Second largest maximal cliques in small Paley graphs of square order
Abstract
There is a conjecture that the second largest maximal cliques in Paley graphs of square order have size , where , and split into two orbits under the full group of automorphisms whenever (a symmetric description for these two orbits is known). However, some extra second largest maximal cliques (of this size) exist in whenever . In this paper we analyse the algebraic and geometric structure of the extra cliques.
keywords:
Paley graph, maximal cliquesMSC:
[2020] 05C25 , 11T301 Introduction
Let be an odd prime power such that , and let be the finite filed of order with primitive root . The Paley graph of order , denoted by , is an undirected graph defined on the elements of the finite field such that two vertices are adjacent if and only if the difference of these two vertices is a nonzero square in the multiplicative group . The Paley graph is known to be a self-complementary arc-transitive strongly regular graph with smallest eigenvalue . According to the Delsarte-Hoffman bound [5], the size of a maximum independent set of a Paley graph is at most . Since Paley graph is self-complementary, the size of a maximum clique in is also at most .
Through out this paper, set . Then for . Now, we only study Paley graph of square order, which is denoted by . For a Paley graph , the Delsarte-Hoffman bound applied to gives that the size of a maximum independent set (a maximum clique) is . It is obvious that the subfield of order forms a clique in Paley graph . In 1984, Blokhuis [2] studied maximum cliques (of order ) in Paley graphs and proved that these cliques are isomorphic to the subfield . In 1996, Baker et al. [1] provided a construction of maximal cliques of size for . These cliques are maximal but not maximum and the cliques with this structure are not the only ones. They proposed a conjecture that there are no maximal cliques of size in , where for . In 2009, Kiermaier and Kurz [9] considered integral point sets in affine planes over finite field and provided two maximal integral point sets and proved their maximality. In 2018, Goryainov et al. [6] provided a construction of maximal cliques of size for . By Magma [3], they found that for , the graph contains exactly two non-equivalent (under the action of the automorphism group) maximal cliques of size for , and these cliques are the second largest. In 2022, Goryainov et al. [7] established a linear fractional correspondence between these two types of maximal cliques of size for in . In 2024, Brouwer et al. [4] generalised the result by Baker et al. [1] to the collinearity graphs of the Desargusian nets (in this paper we show that their construction gives maximal cliques of size in for , which are constructed from two intersecting lines.
In [6], the number of orbits on the maximal cliques of size in was computed for , and the results are summarised in the following table.
| Clique Size | |||||||||
| Number of Orbits |
2 Preliminaries
In this section, we recall some basic facts about the affine planes and finite fields.
2.1 Affine Plane
An affine plane is a point-line incidence structure. Let denote the affine plane, whose points are vectors of the -dimensional vector over , and the lines are the additive shifts of -dimensional subspaces of . It is well known that each line in contains points and there are lines through each point. There are points and lines in .
2.2 Finite fields
Note that can be viewed as a quadratic extension over . Set and let be the extension of by adding a root of the irreducible polynomial over . Then every element in can be uniquely written as , for some . Moreover, can naturally be viewed as a -dimensional vector spaces with basis and over . Define : by for all and in . It is easy to prove that is a vector space isomorphism. Now we can identify the points of as the elements of and the line in can be viewed as , where and are fixed. We say a line of this form has a slope and note that the difference between any two points in is a scalar multiple of . A line is called quadratic line (non-quadratic line) if the slope of this line is a square (non-square) element in . For a quadratic line, the difference between any two distinct elements from this line is a square element in . A Paley graph constructed on the points of , and any two distinct points in are adjacent if and only if their difference is a square element in . This implies that in are adjacent if and only if they are incident to a common line with square slope and the line through and is a quadratic line. Let be a primitive element in the finite field and be a primitive element in the subfield . Note that and any element in is square in . This further implies that the line is a clique of size in .
This must be throughout this paper, we set to be the set of square elements in and . Then we have that .
Lemma 2.1.
([7], Proposition 1.) Through any point of , there pass lines. Moreover, of these lines are quadratic and of these lines are non-quadratic.
Lemma 2.2.
([8], Theorem 9.1.) The automorphism group of Paley graph acts arc-transitively, and the equality
holds, where is the set of square elements in .
The group preserves the sets of quadratic and non-quadratic lines and acts on each of them transitively.
Lemma 2.3.
Let be an odd prime power, be a divisor of and be the subgroup of order in . Then the following statements are hold.
(1) If is even, then .
(2) If is odd, then .
Proof (1) If is even, for any , , then . It follows that .
(2) On the contrary, assume that there exists an element . Then and , this implies , a contradiction.
Followed by the above notations, the following lemma is obvious.
Lemma 2.4.
([7], Proposition 2.)
(1) The element is a square in if and only if .
(2) The element is a square in if and only if .
3 Constructions
In this section, we propose the constructions of maximal cliques in Paley graph of size for , where . Moreover, we give some numerical information of these cliques by computing the stabilizer of each clique under the action of the automorphism group . In this section, we set denote the dihedral group of order , and set denote the cyclic group of order . Throughout this section, by denote the stabilizer of the automorphism group acting on the set of cliques, where is a clique of the Paley graph .
3.1 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that . Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 1.
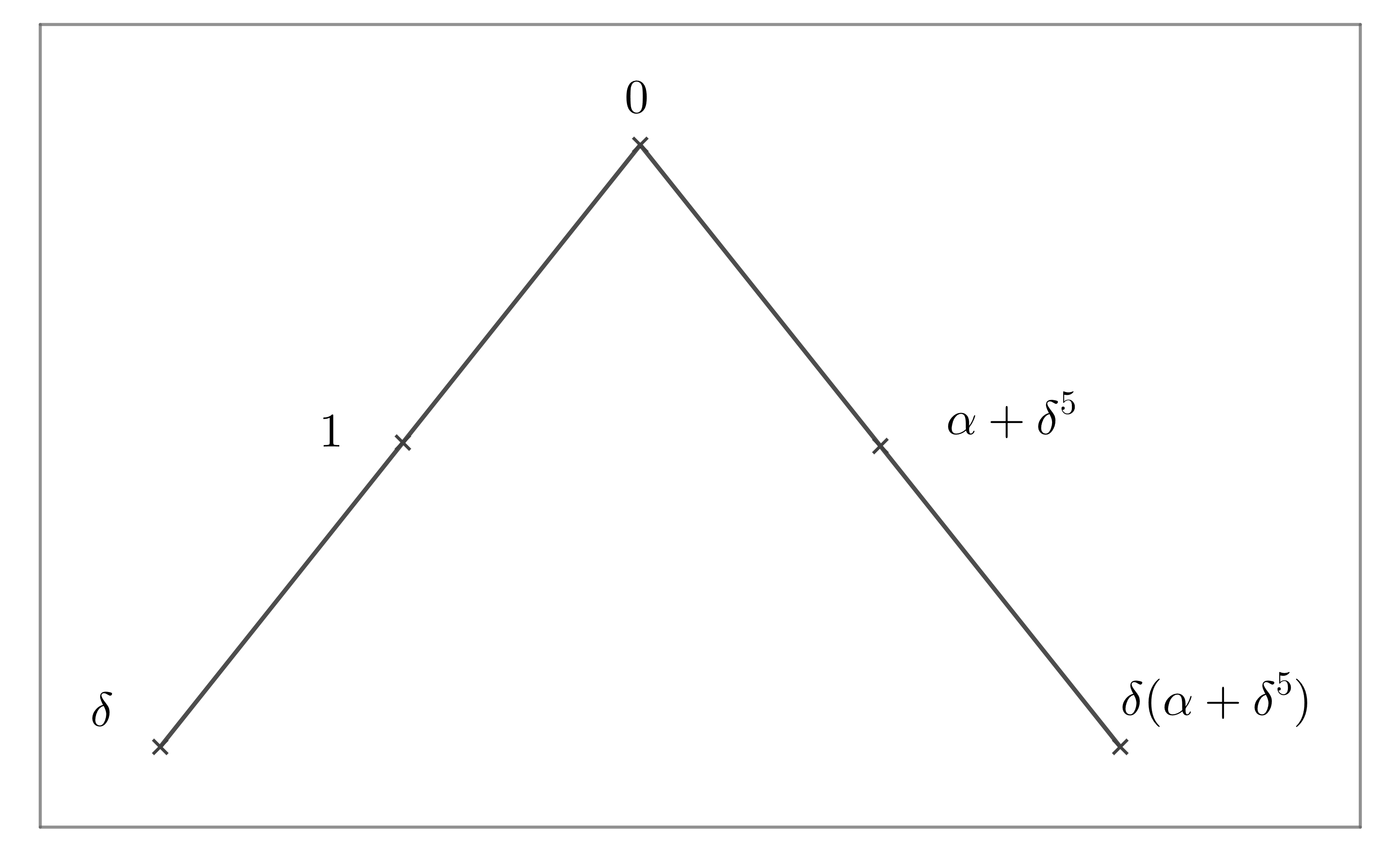
Lemma 3.1.
Set be the orbit of acting on the cliques with . Then , where for any . Moreover, .
Proof Note that for any , , where , , . If , then and . Set be the subset of two intersection lines, which are presented in Fig 1. Then . It follows that either , or , .
If and , then we have that and . It follows that for any . Now, is the identity automorphism.
If and , then by the same arguments as in the first case we have that and . Then we have that for any . It follows that .
Now, we have that . The action of on the points in clique is presented in the following table.
| 0 | |||||
| 0 | 1 |
Note that , so we have that .
Set for , where and .
Lemma 3.2.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of two lines in the clique is . If , then and .
If , then and .
If , then either , or , .
Case 1: If and , then and . Now with , then either or . If , then , a contradiction. If , then we have that followed from , a contradiction.
Case 2: If , , then we have that , a contradiction.
Followed from the above arguments, we have that , because .
3.2 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that and .
3.2.1 -construction
Let be a subgroup of with order . Then .
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 2.
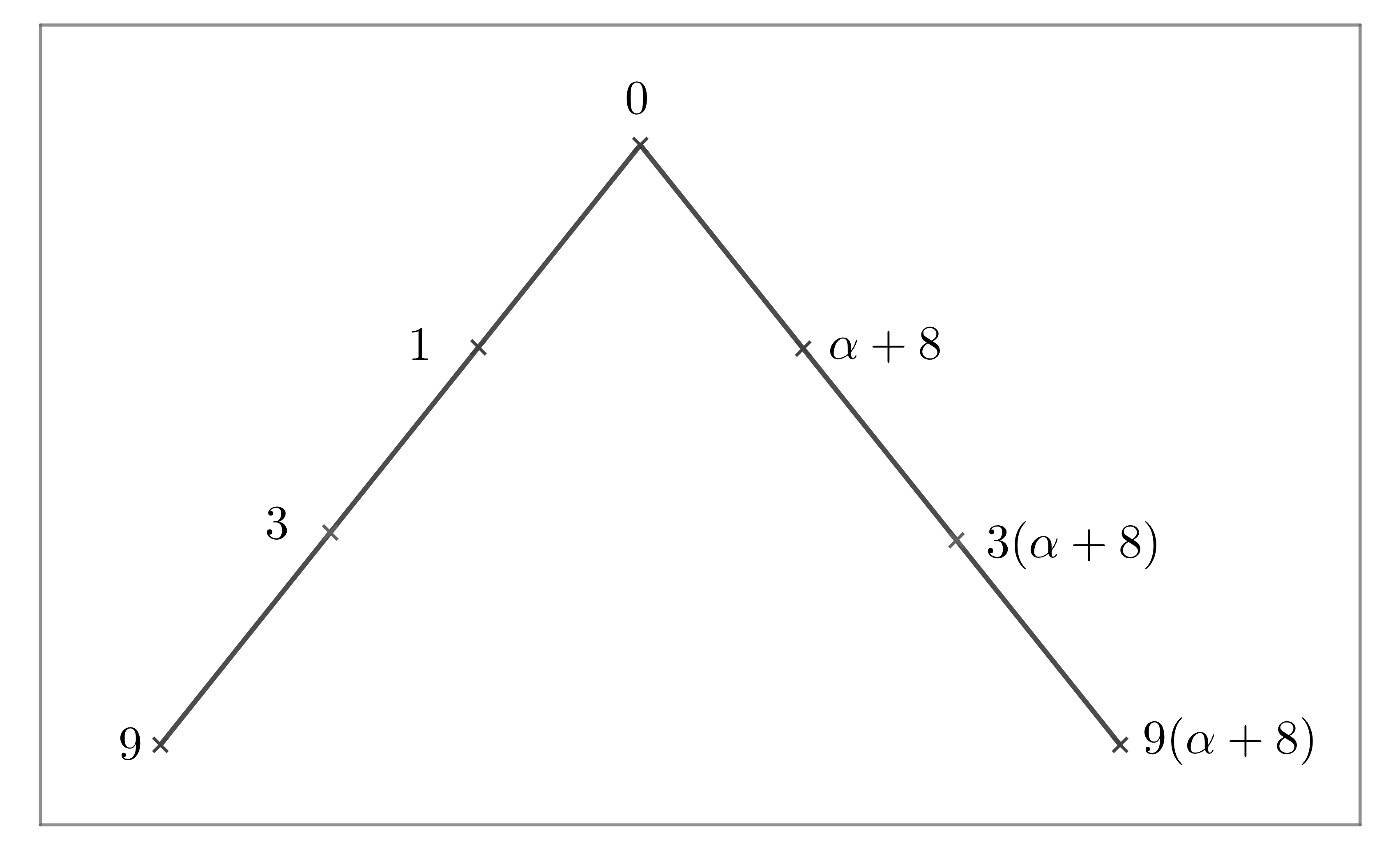
Lemma 3.3.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . If , then and . Set be the subset of two lines, which are presented in Fig 2. Then . It follows that either , or , .
If , , then we have that and . It follows that and . So with .
If , , then we have that and , then and . So with .
Let , , , , , for any . Set and . Then , , . Then . The action of and on the points in clique is presented by the following table.
| 0 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 0 |
Followed by the above arguments, we know that and . Then , where , for any .
Note that , so we have that .
Set , where , and .
Lemma 3.4.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of two lines in the clique is . If , then and .
If and , then . If , then and ; if , then , a contradiction; if , then , a contradiction.
If and , then , a contradiction.
Followed from the above arguments, we have that , because .
3.2.2 -construction
Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 3.
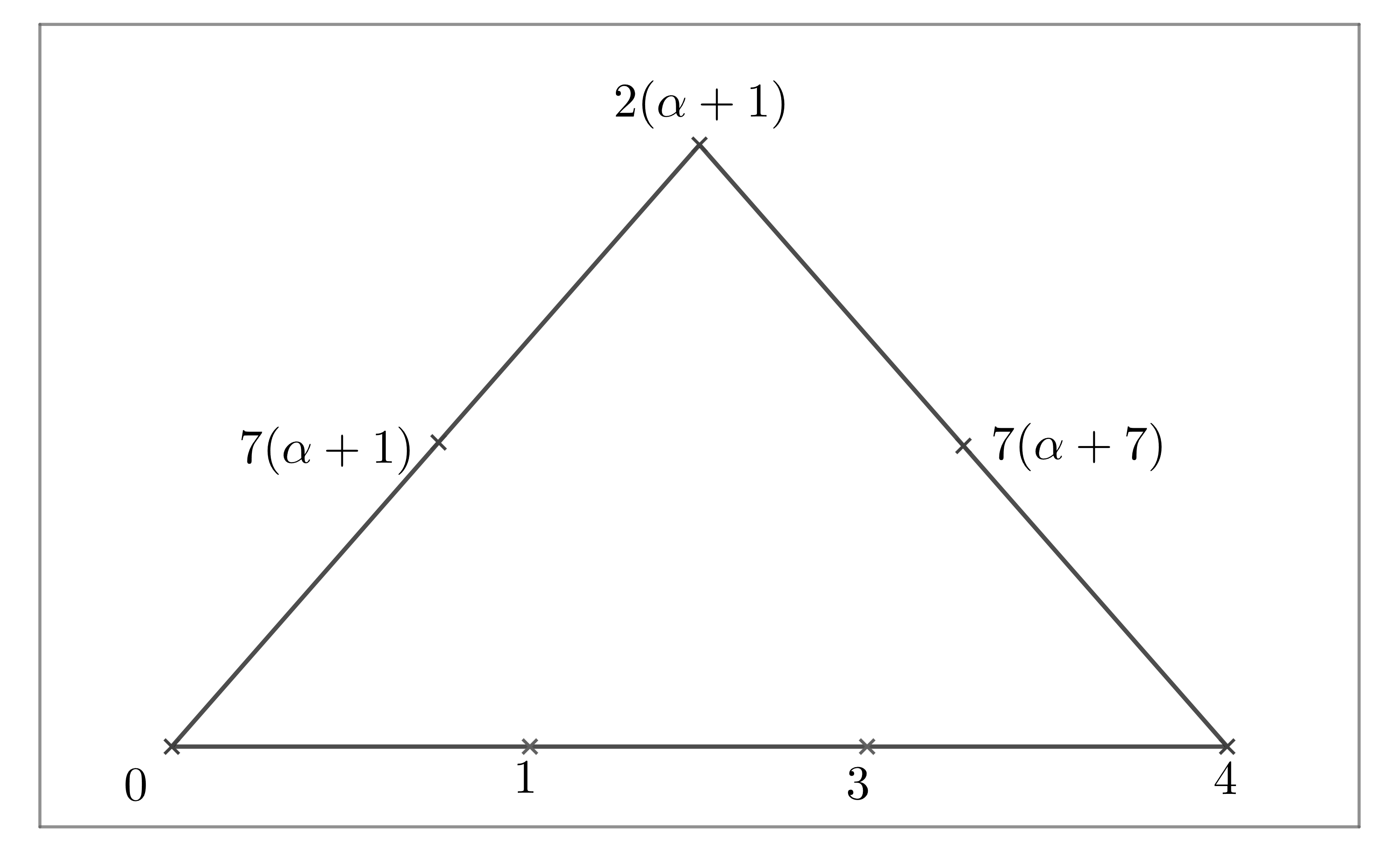
Lemma 3.5.
Set be the orbit of acting on the cliques with . Then , where for any . Moreover, .
Proof Note that for any , , where , , . If , then . Set be the two special intersecting points in clique , then . It follows that either , or , .
If and , then we have that , . Then , and . It follows that for any .
If and . Then , and . Moreover, we have that and . Then we have that for any and .
The action of on the point in clique is presented by the following table.
| 0 | |||||||
| 4 | 0 |
Followed by the above arguments, we get that and , where for any . Note that , so we have that .
Set where and .
Lemma 3.6.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if and where , .
If , then and the two special intersecting points . If and , then , a contradiction. Now, we have and . And then , because .
3.3 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that and .
3.3.1 -construction
Let be a subgroup in . Then .
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 4.
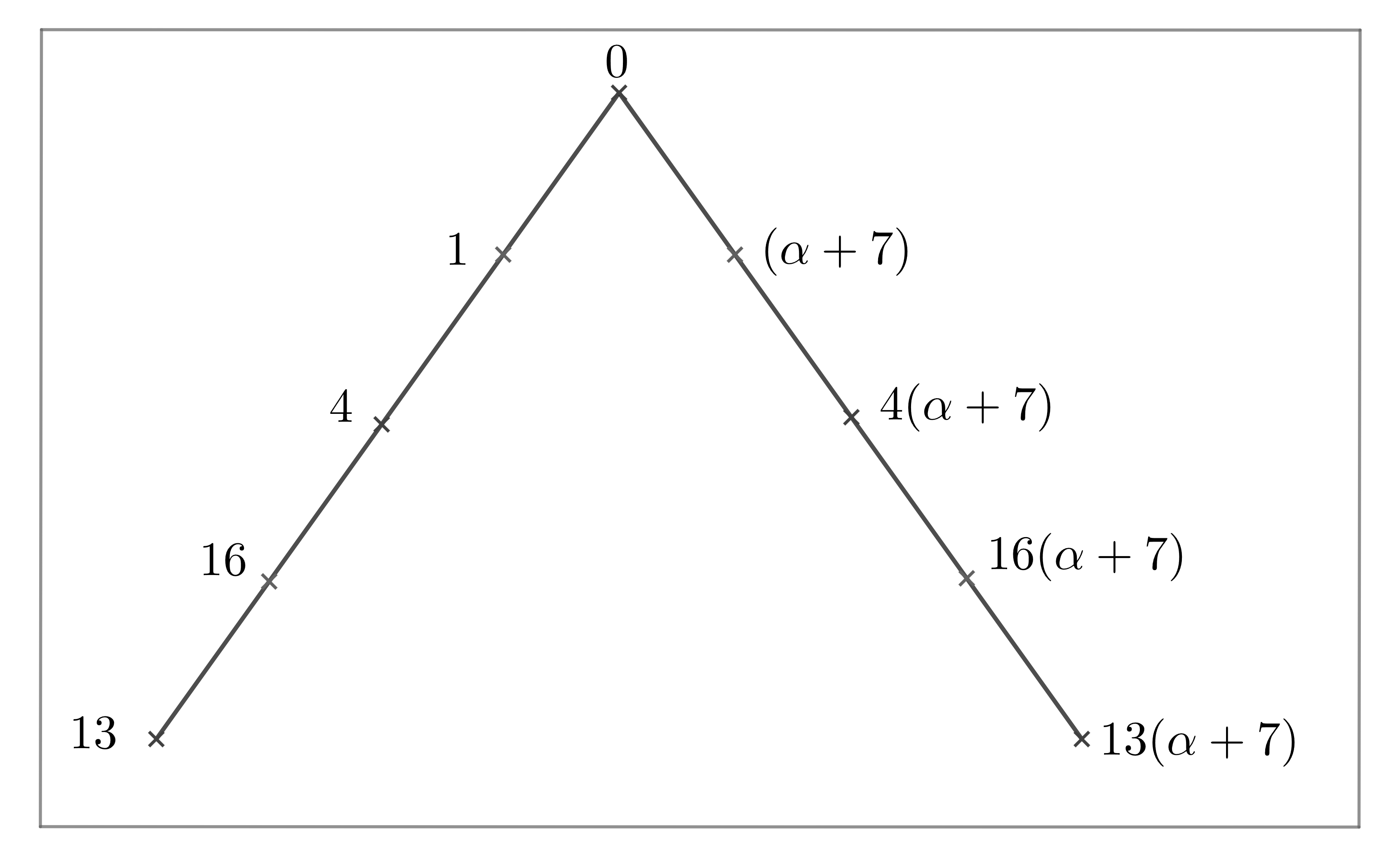
Lemma 3.7.
Set be the orbit of acting on the cliques with . Then , where for any . Moreover, .
Proof Note that for any , , where , , . If , then and . Set be the subset of two lines, which are presented in Fig 4. Then . It follows that either , or , .
If , , we have that and , then and . So that with .
If , , we have that and , then and . So that with .
Set . Then and . The action of on the points of clique is presented in the following table.
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 |
Followed by the above arguments, we know that . Then , where for any .
Note that , so we have that .
Set where , , .
Lemma 3.8.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of two lines in the clique is . If , then and the two special lines .
If and , then . If , then and ; if , then , a contradiction; if , then , a contradiction; if , then , a contradiction.
If and , then , a contradiction. Now, we have and .
Followed from the above arguments, we have that , because .
3.3.2 -construction
Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 5.
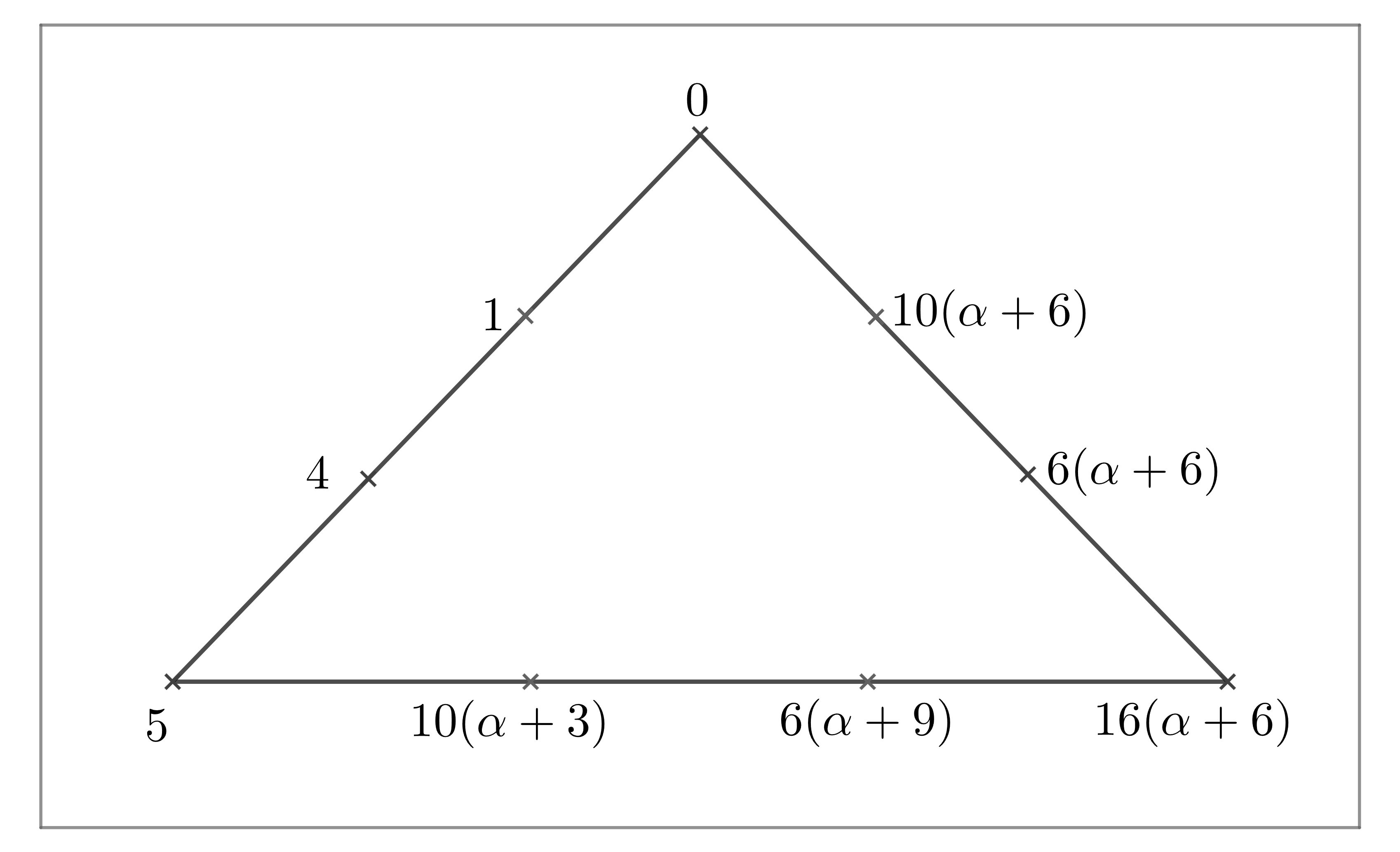
Lemma 3.9.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . Set be the three intersecting points in clique . Then . It follows six cases.
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
Set , , then we have that , , and . The action of and on the points in the clique is presented in the following table.
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Followed by the above arguments, we know that and , then where and for any .
Note that , so we have that .
Set where , .
Lemma 3.10.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . If , now we will prove that if and only if , where , .
If , then the three special points . If and , then , a contradiction. Now, we have . From Lemma 3.9, we have that , where permutate the three intersecting points. And then , because .
3.3.3 -construction
Let be a subgroup in with . Then .
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 6.
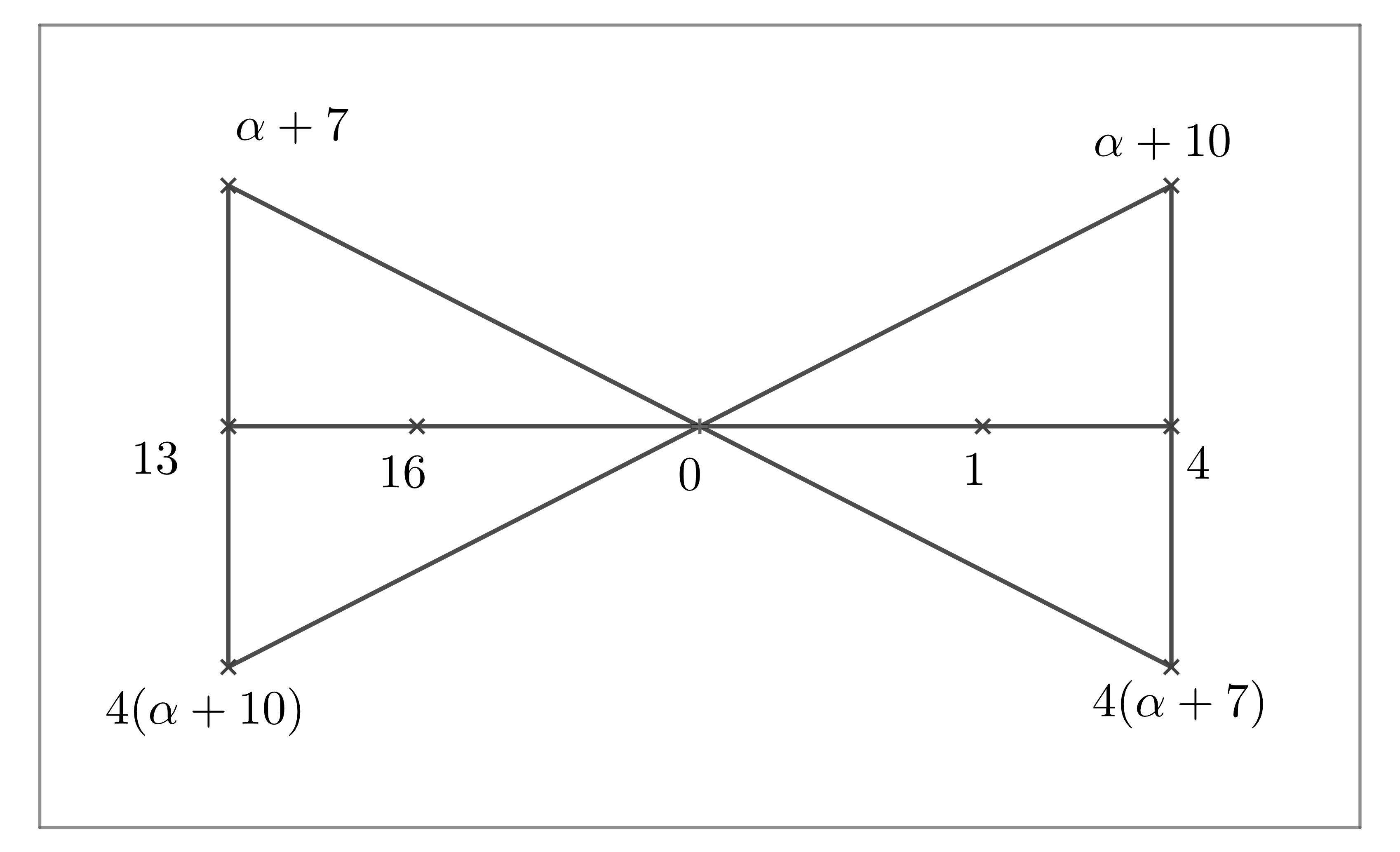
Lemma 3.11.
Set be the orbit of acting on the cliques with . Then , where for any . Moreover, .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of three lines, and one of these lines contains five points in this clique. If , then and . And , we have that , then . So that with , . Set be a subset in and be the subset of two lines, which are presented in Fig 6. Then . It follows that either , or , .
If and , then we have that and , then and . So for any .
If and , then we have that and , then and . So for any .
The action of acting on the points in the clique is presented by the following table.
| 0 | |||||||||
| 0 |
Followed by the above arguments, we know that and . Then where for any .
Note that , so we have that .
Set where , .
Lemma 3.12.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if and , where and .
Note that the intersecting point of three special lines in the clique is . If , then and the subset of two lines . If and , then ; if and , then , a contradiction. Now, we have .
And then , because .
3.3.4 -construction
Let be a subgroup in with . Then .
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 7.
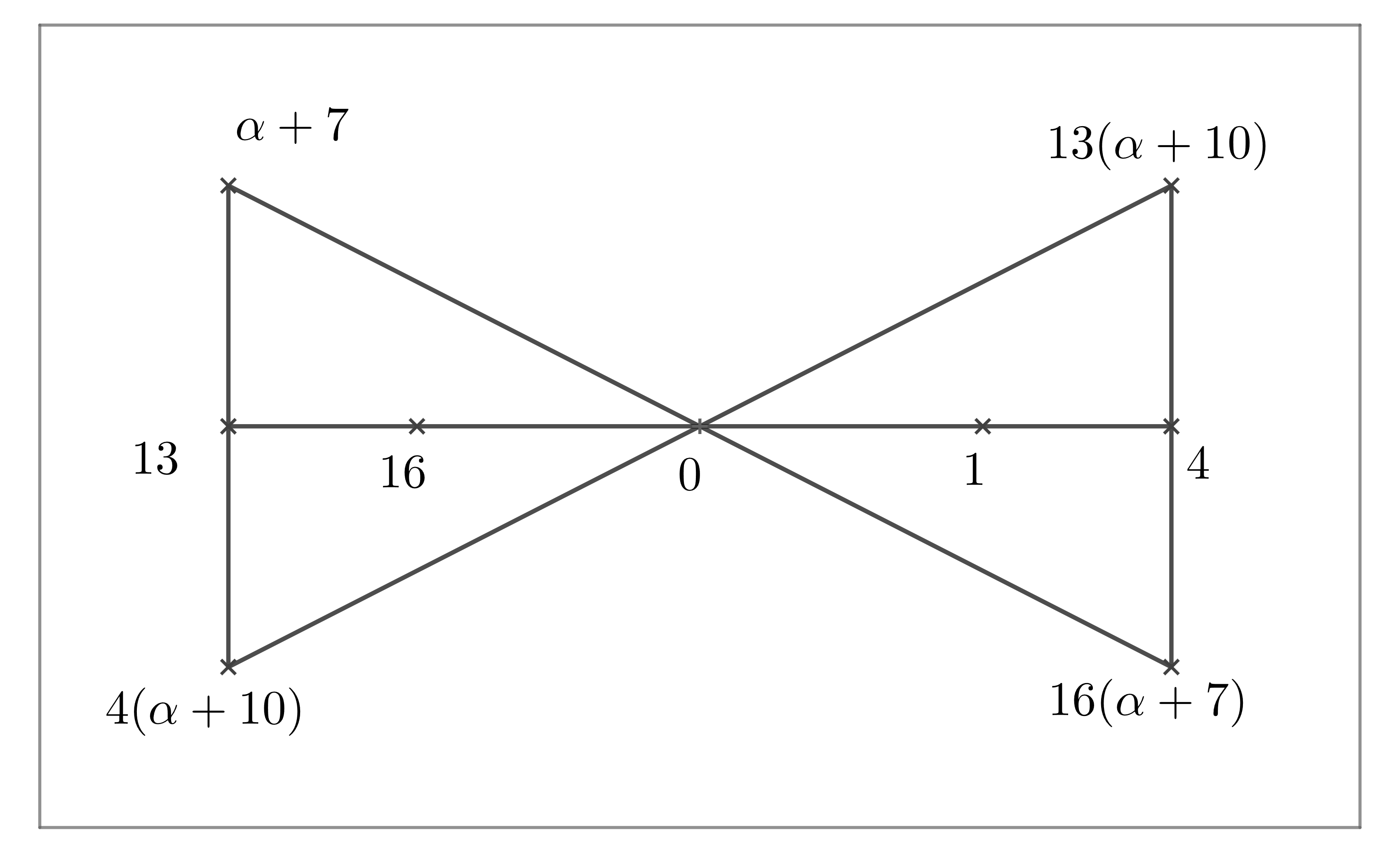
Remarks: There exists other lines that contain at least three points in . They are: ,.
Lemma 3.13.
Set be the orbit of acting on the cliques with . Then , where for any . Moreover, .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of three lines, and one of these lines contains five points in this clique. If , then and . And , we have that , then . So that with , . Let be a subset in and . Set be the subset of two lines, which are presented in Fig 7. Then . It follows that either , or , .
If and , then we have that and , then and . Now set and for any .
If and , then we have that and , then and . Now set , for any .
Set , now we have that and . The action of on the points in clique is presented in the following table.
| 0 | |||||||||
| 0 |
Followed by the above arguments, we know that and then where for any .
Note that , so we have that .
Set where , , .
Lemma 3.14.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of three lines in the clique is . If , then and . Now we have that . It follows that and .
And then , because .
3.3.5 -construction
Let be a subgroup in with . Then .
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 8.
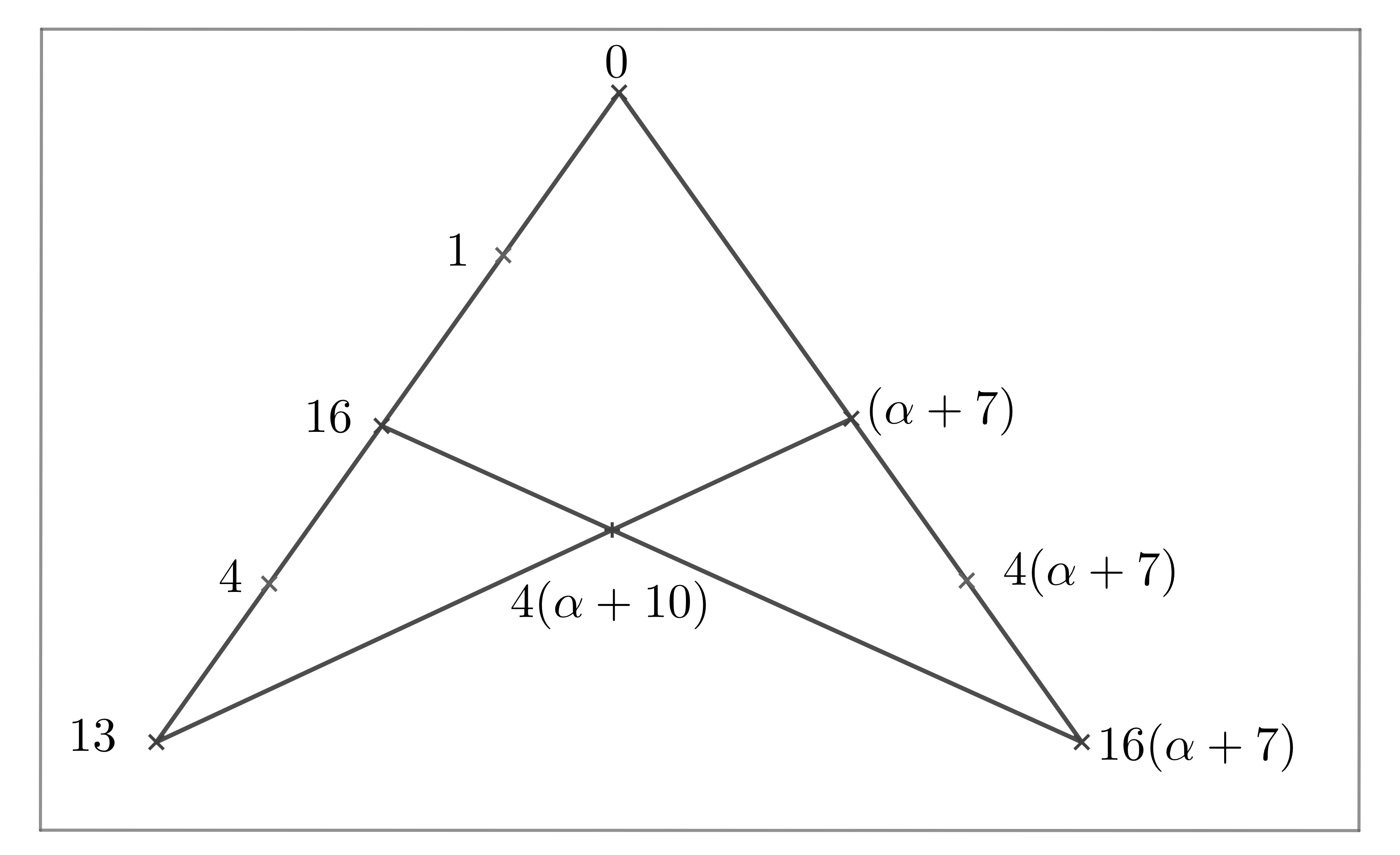
Lemma 3.15.
Set be the orbit of acting on the cliques with . Then and .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of two lines, where one line contain five points in this clique and the other line contain four points; the point in the clique is a intersecting point of two lines, which contain three points separately in this clique. If , then , . So we have that and , then and . Followed by the above arguments, we know that .
Note that , so we have that .
Set for , where and .
Lemma 3.16.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and . If , then , the subset and . Then , and we have and .
And then , because .
3.3.6 -construction
Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 9.
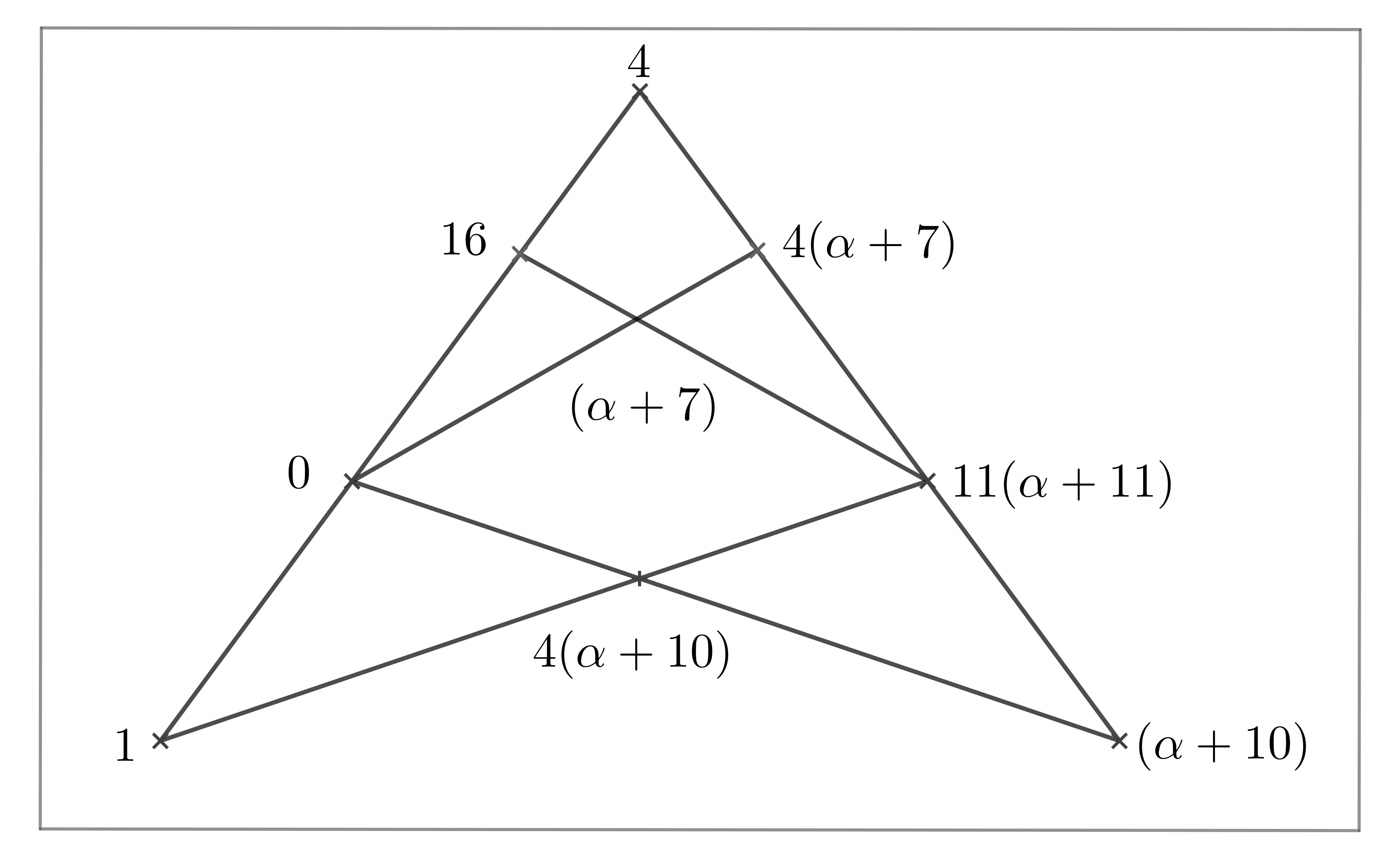
Lemma 3.17.
Set be the orbit of acting on the cliques with . Then where for any . Moreover, .
Proof Note that for any , , where , , . If , then and . Set be the two special points which are the intersecting points of three lines in clique . Then . It follows that either , or , .
If and , then we have that , and . So that for any .
If and , then we have that , and . So that and ,
The action of acting on the points in the clique is presented by the following table.
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Followed by the above arguments, we know that then where with .
Note that , so we have that .
Set where , .
Lemma 3.18.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , where and .
If , then and the two special points . If and , then and . If and , then , a contradiction. Now, we have and .
And then , because .
3.3.7 -construction
Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 10.
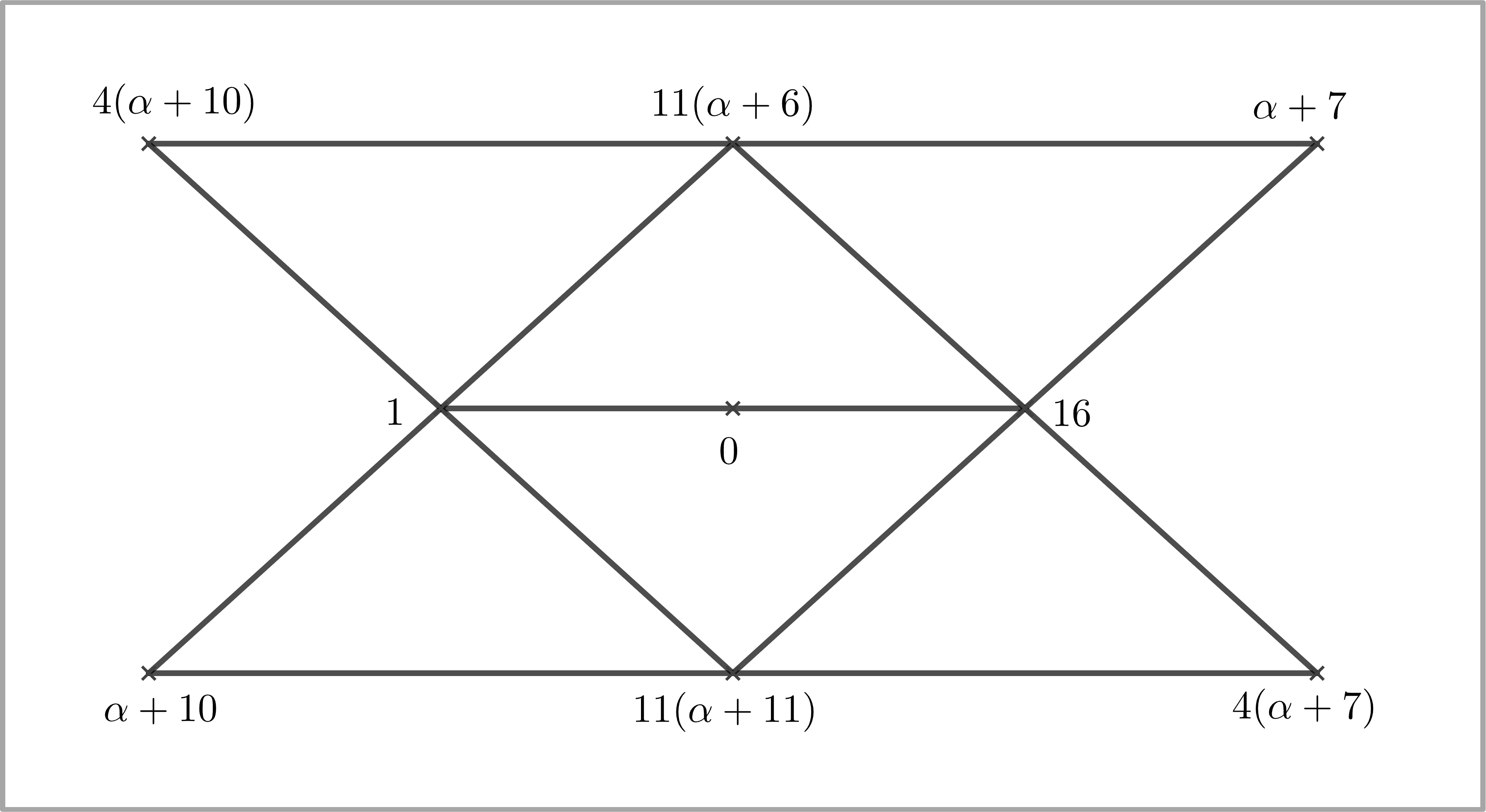
Remarks: There exists other lines that contain at least three points in . They are: and .
Lemma 3.19.
Set be the orbit of acting on the cliques with . Then where and for any . Moreover, .
Proof Note that for any , , where , , . Set be the three intersecting points in the clique , where for any , there does not exist , such that belong to a line. Then for any . Now we have the following six cases.
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
Let , , then we have that , , then . The action of and acting on the points of clique is presented in the following table.
| 0 | 1 | 16 | |||||||
|---|---|---|---|---|---|---|---|---|---|
Followed by the above arguments, we know that and , then where and with .
Note that , so we have that .
Set where , .
Lemma 3.20.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . If , now we will prove that if and only if , where .
If , then . If and then , a contradiction. Now, we have .
From Lemma 3.19, we have that , and .
And then , because .
3.4 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that and . Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 11.
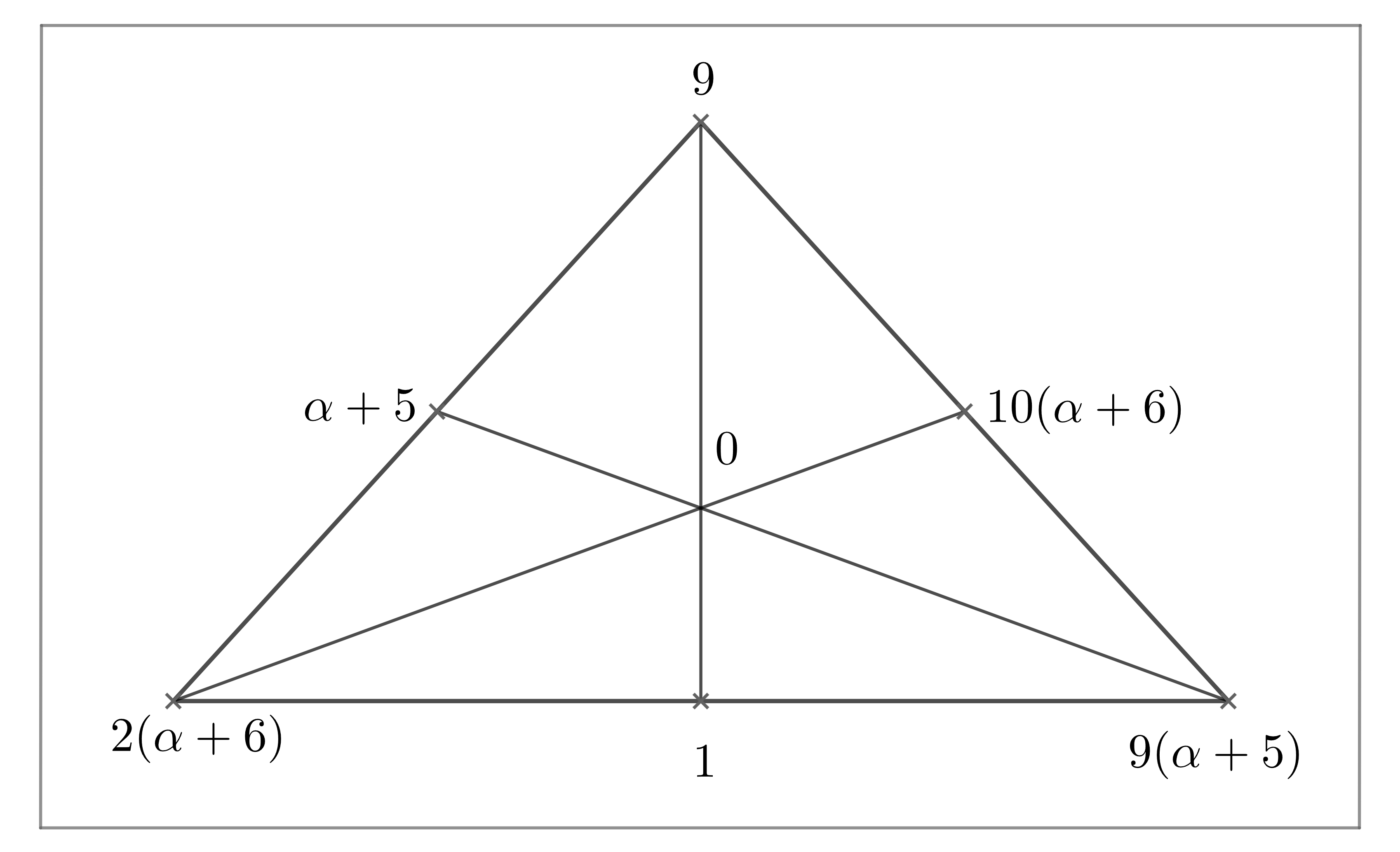
Lemma 3.21.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . Set be the three special points which are the intersecting points of two lines in clique . Then . Now we have the following six cases.
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
If , and , then we have that , and . It follows that for any .
Set , , then we have that , , , then . The action of and on the points of clique is presented in the following table.
| 0 | 1 | 9 | |||||
|---|---|---|---|---|---|---|---|
Followed by the above arguments, we know that and , then where , with .
Note that , so we have that .
Set for , where and .
Lemma 3.22.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
If , then and the three special intersecting points . If , then and ; if , then we can get a contradiction; if , then we can get a contradiction. Now, we have and .
And then , because .
3.5 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that and .
3.5.1 -construction
Let be a subset in . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 12.
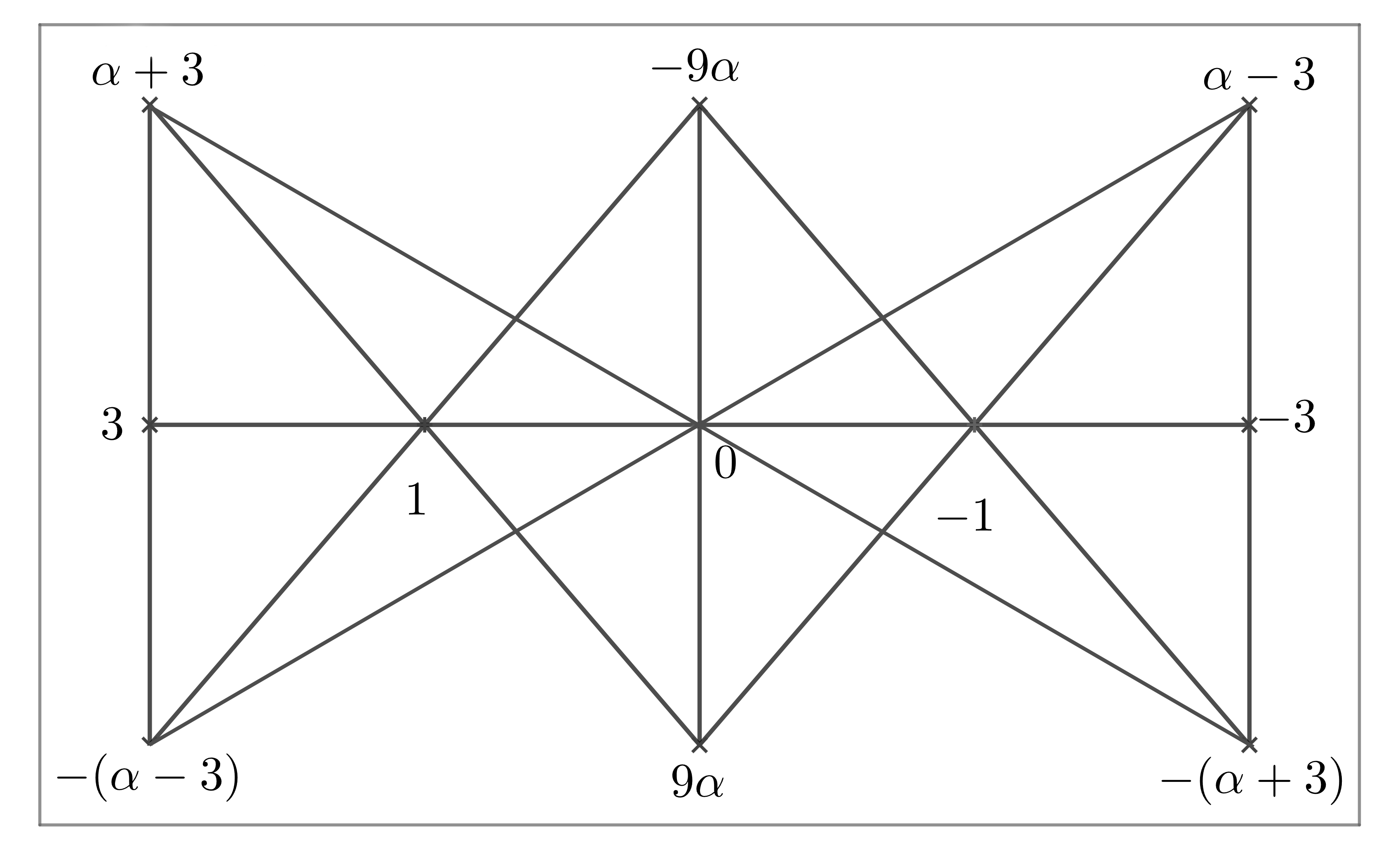
Remarks: There exists other lines that contain at least three points in .
They are:,,,.
Lemma 3.23.
Set be the orbit of acting on the cliques with . Then , where , for any . Moreover, .
Proof Note that for any , , where , , . Set be the three special points which are the intersecting points of four lines in Figure 12, and one of these lines contain five points in the clique. Then . Now we have the following six cases.
If , and , then we have that , and . Let and for any for any .
If , and , then we have that , and . Let and for any for any .
If , and , then there are no solutions for and . If , and , then there are no solutions for and . If , and , then there are no solutions for and . If , and , then there are no solutions for and .
Set , . Then we have that , and . The action of and on the points in the clique is presented in the following table.
| 0 | 1 | -1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -1 | 1 | |||||||||
| 0 | 1 | -1 |
Followed by the above arguments, we know that and , then where , for any .
Note that , so we have that .
Set where , , .
Lemma 3.24.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
If , then and the subset of a line . Then , and we have that and .
And then , because .
3.5.2 -construction
Let be a subset , Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 13.
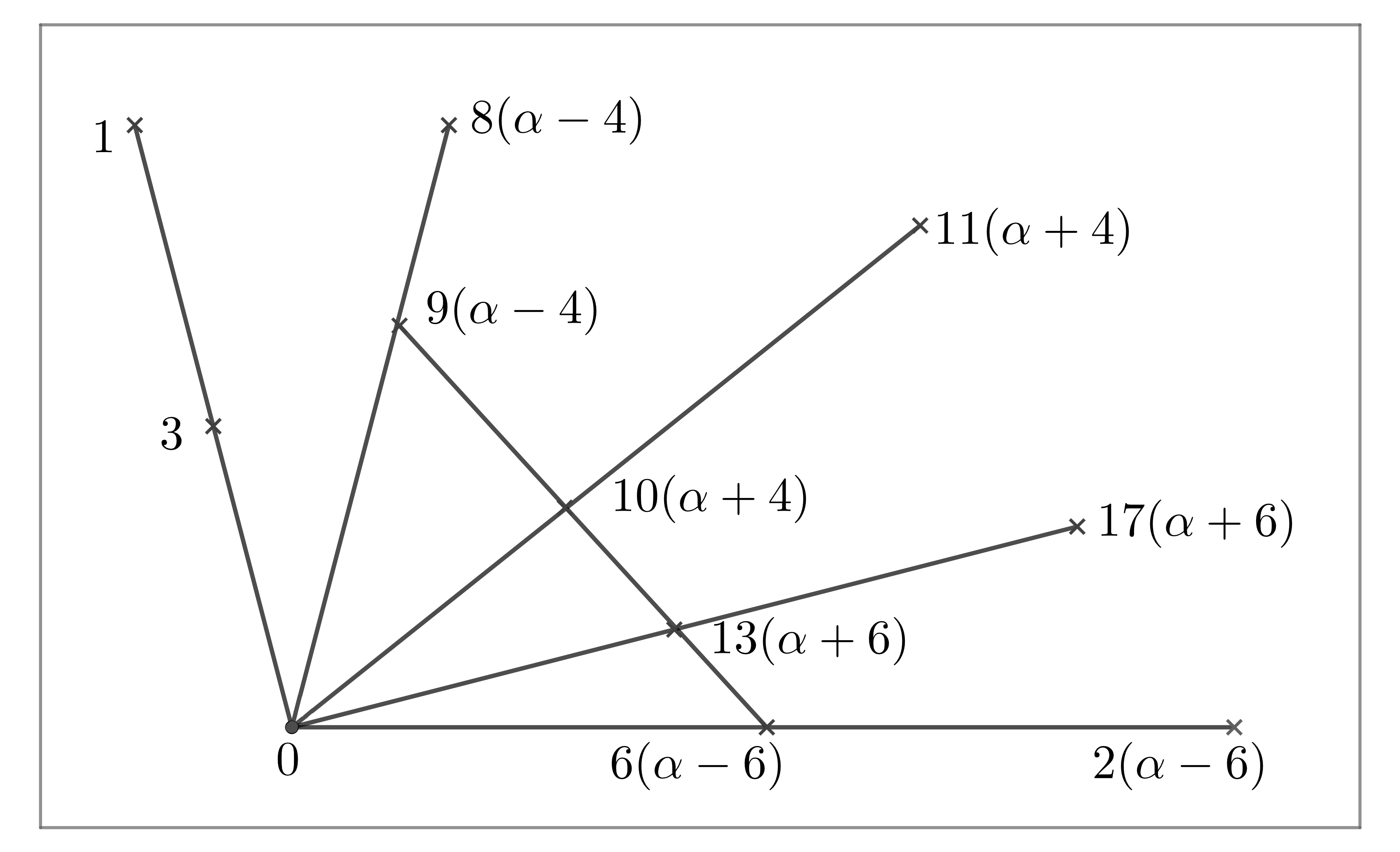
Remarks: There exists other lines that contain at least three points in . They are:,,,.
Lemma 3.25.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of five lines, which contain three points in this clique. If , then and . Set be the subset of five lines in clique , which are presented in Fig 13. Then .
If , then we have that , . It follows that . Set and for any .
If , then we have that , . It follows that . Set and for any .
Similarly, we have that , , , , , .
Set , , then we have that , , , then . The action of and acting on the points in clique is presented by the following table.
| 0 | 1 | 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | |||||||||||
| 0 |
Followed by the above arguments, we know that and . Then , where and with .
Note that , so we have that .
Set for , where and .
Lemma 3.26.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersecting point of five lines in the clique is . If , then and the subset of five lines . Then , we have that and .
And then , because .
3.6 Maximal cliques in Paley graph
We can choose a primitive element and be a root of the irreducible polynomial over , such that and .
3.6.1 -construction
Let H= be a subset . Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 14
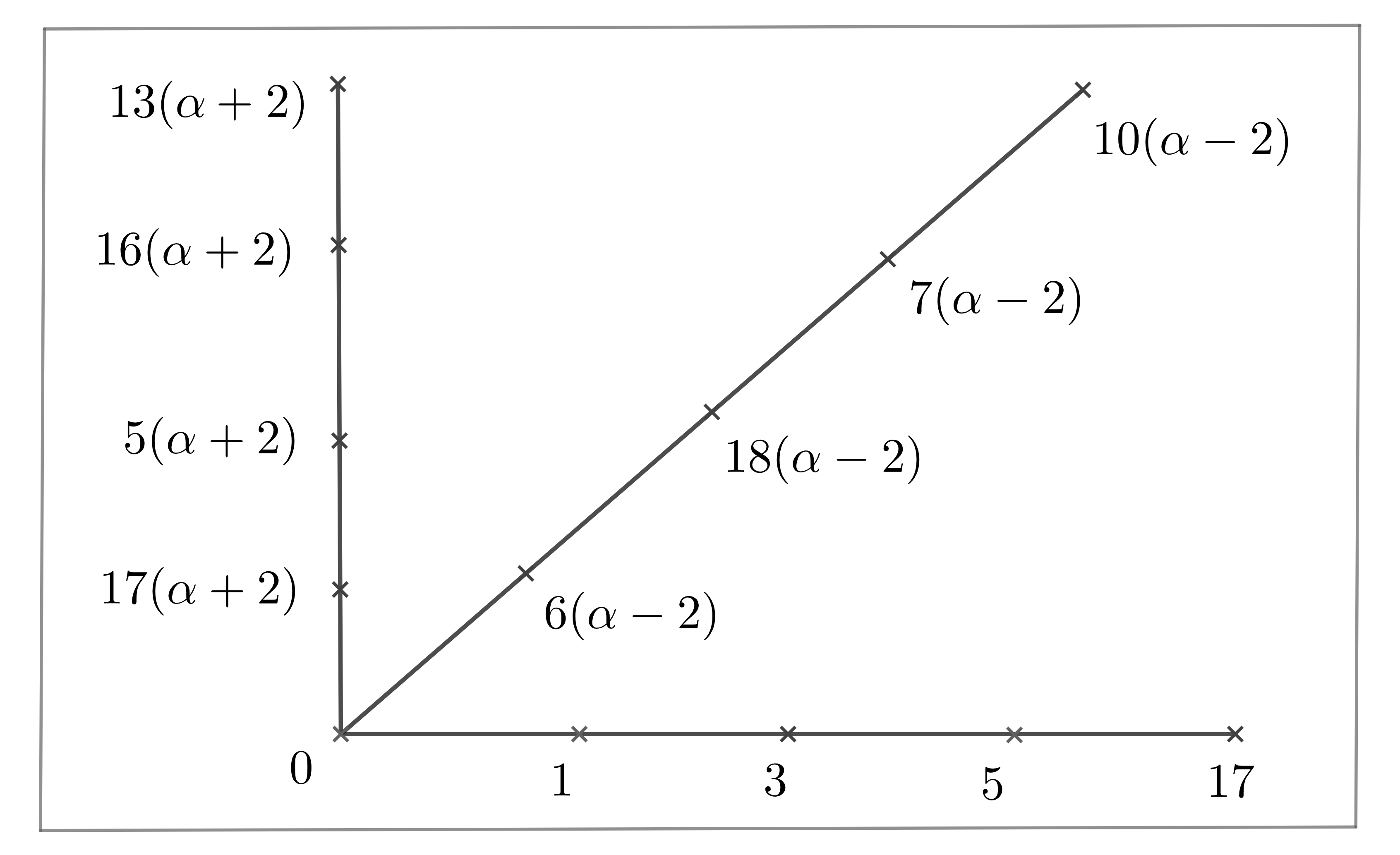
Remarks: There exists other lines that contain at least three points in . They are:, , , , , ,,,.
Lemma 3.27.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of three lines, which contain five points in this clique. If , then and . Set be the subset of three lines, which are presented in Fig 14. Then . Now we have the following six cases.
If , and , then we have that and . It follows that for any .
If , and , then we have that and . It follows that for any .
If , and , then we have that and . It follows that for any .
If , and , then we have that and . It follows that for any .
If , and , then we have that and . It follows that for any .
If , and , then we have that and . It follows that for any .
Set , with , then we have that , , then . The action of and acting on the points in clique is presented in the following table.
| 0 | 1 | 3 | 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | |||||||||||||
| 0 | 1 | 3 | 5 | 17 |
Followed by the above arguments, we know that and , then where , with .
Note that , so we have that .
Set for , where and .
Lemma 3.28.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of three lines in the clique is . If , then and the subset of three lines . Then , and we have that and .
And then , because .
3.6.2 -construction
Let be a subset , Set be a subset of finite field . By Magma, we have that is a maximal clique in with size for . The structure of the clique is presented in Fig 15.
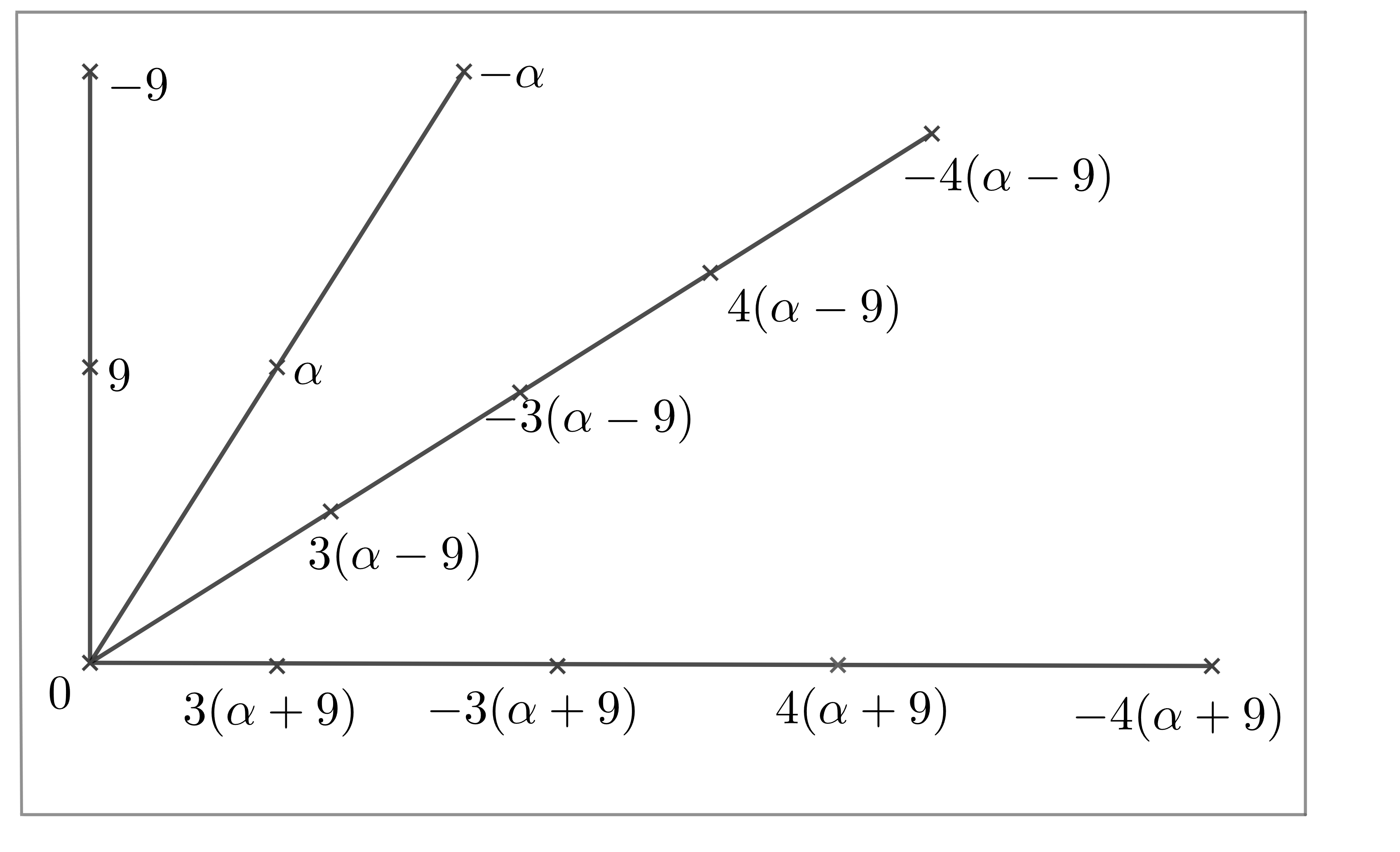
Remarks: There exists other lines that contain at least three points in . They are:, ,, , , , ,
Lemma 3.29.
Set be the orbit of acting on the cliques with . Then , where and for any . Moreover, .
Proof Note that for any , , where , , . Note that the point in the clique is a intersecting point of two lines, which contain five points in this clique. If , then and . Set be the two short lines in clique , which have a common point . Then .
If and , then we have that , and . Set , , and for any .
If and , then we have that , and . Set , , and for any .
Let , , then we have that , , then . The action of and on the points in clique is presented in the following table.
| 0 | 9 | -9 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -9 | 9 | |||||||||||
| 0 | 9 | -9 |
Followed by the above arguments, we know that and , then where and with .
Note that , so we have that .
Set for , where and .
Lemma 3.30.
Set be the orbit of acting on the cliques with . Then .
Proof It is obvious that . Now we will prove that if and only if , and , where , and .
Note that the intersection point of three lines in the clique is . If , then and the subset of two lines , then . We have that , .
And then for , because .
4 Conclusion
In this section we give a table that summarises the descriptions of the extra maximal cliques given in this paper, and formulate a problem.
Set be a representative element of the set of cliques with size , where .
| 9 | ||
| 13 | ||
| 13 | ||
| 17 | ||
| 17 | ||
| 17 | ||
| 17 | ||
| 17 | ||
| 17 | ||
| 17 | ||
| 11 | ||
| 19 | ||
| 19 | ||
| 23 | ||
| 23 |
Problem 1.
Is there any extension of the maximal cliques described above to infinitely many values of (these cliques would not be necessarily second largest for )?
Acknowledgments
Huye Chen is supported by National Natural Science Foundation of China (12301446).
References
- [1] R.D. Baker, G.L. Ebert, J. Hemmeter, A. Woldar, Maximal cliques in the Paley graph of square order, Journal of Statistical Planning and Inference, 56 (1996), 33-38.
- [2] A. Blokhuis, On subsets of with square differences, Indagationes Mathematicae (Proceedings), 46 (1984), 369-372.
- [3] W. Bosma, J. Cannon, and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235–265.
- [4] A. E. Brouwer, S. Goryainov, L. Shalaginov and C. H. Yip, Cliques in Paley graphs of square order and in Peisert graphs, in preparation.
- [5] P. Delsarte, An algebraic approach to the association schemes of coding theory, Philips Res. Rep.Suppl. 10 (1973).
- [6] S.V. Goryainov, V.V. Kabanov, L.V. Shalaginov, A.A. Valyuzhenich, On eigenfunctions and maximal cliques of Paley graphs of square order, Finite Fields and Their Applications, 52 (2018), 361-369.
- [7] S. Goryainov, A. Masley, L. Shalaginov, On a correspondence between maximal cliques in Paley graphs of square order, Discrete Mathematics, 345 (2022).
- [8] G.A. Jones, Paley and the Paley Graphs, in: G. Jones, I. Ponomarenko, J. Širáň(Eds.), Isomorphisms, Symmetry and Computations in Algebraic Graph Theory, WAGT 2016, in: Springer Proceedings in Mathematics & Statistics, vol. 305, Springer, Cham, 2020, pp. 155-183.
- [9] M. Kiermaier, S. Kurz, Maximal integral point sets in affine planes over finite fields, Discrete Mathematics, 309 (2009), 4564-4575.