Searching via conservation laws
Abstract
To distinguish and in the experiments, we propose two methods based on the conservation laws. I. From the angular momentum conservation, a nonzero helicity of of would be an evidence of . II. Since is kinematically forbidden, provides a clean channel to probe . Particularly, our results show that is promising to be observed at LHC via . On the other hand, we find that , which is also feasible to be measured at the forthcoming experiments at HL-LHC and FCC-hh.
I introduction
The meson is unique in the Standard Model (SM) as its members are composed of heavy quarks with two different flavors, beauty () and charm (). The mesons lie intermediate between () and () states both in mass and size, while the different quark flavors leads to much richer dynamics. On the other hand, the ground state of mesons, unlike the charmonium and bottomonium, cannot annihilate into gluons or photons, providing an idea place to examine the heavy quarks. Study on the mesons can deepen our understanding of both the strong and the weak interactions, revealing the underlying physics of the heavy quark dynamics. Last but not least , it provides a unique hunting ground for searching new physics beyond the SM.
The ground state of meson was first observed by the CDF Collaboration at Fermilab Abe:1998fb in 1998, and there have been continuous measurements on both the mass CDF:2007umr ; LHCb:2012ihf ; LHCb:2020ayi and the lifetime CDF:2006kbk ; D0:2008thm via the exclusive decay and the semileptonic decay . In 2014, the ATLAS Collaboration reported a structure with the mass of MeV Aad:2014laa , which is consistent with the value predicted for . In 2019, the excited was confirmed and states have been observed in the invariant mass spectrum by the CMS and LHCb Collaborations, with their masses determined to be and MeV Sirunyan:2019osb ; Aaij:2019ldo , respectively. The decays to directly, and the state decay to followed by . Since the soft photon in the intermediate decay was not reconstructed, the mass of meson appears lower than that of . This peculiar behaviors of the mass hierarchy makes uniquely important in studying the meson family.
In the following, we will abbreviate as so long as it does not cause confusion. Study on the can complete the precise measurements of the spectrum of the family, and the confirmation of its existence is of great importance for the understanding of strong interaction dynamics at low energy. On the mass of , the theoretical predictions range discrepantly from to MeV Ding:2021dwh ; Eichten:1994gt ; Godfrey:2004ya ; Mathur:2018epb ; Li:2019tbn ; Asghar:2019qjl ; Eichten:2019gig , and an experimental measurement is still lacking. The dominant decay mode has not yet been observed, partly due to the noisy soft photon background of the hadron collider. To identify in the experiments, one of the important tasks is to distinguish them from . In this study, we propose two methods based on the conservation laws:
-
•
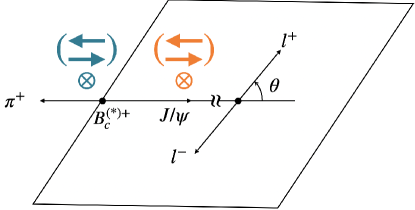
From the angular momentum conservation, the can only possess a zero helicity from as is spin-0. In contrast, the of can have either positive, zero, or negative helicities (see Fig. 1).
-
•
As is kinematically forbidden, provides a clean channel.
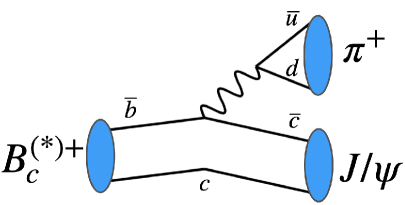
Their responsible quark diagrams at the tree level are given in Fig. 2 , where the hadronizations take place in the blue regions. As the W boson is color blind, the decays are color allowed and color suppressed, respectively.
II Helicity Formalism
To extract the helicity information of as well as calculate the branching fractions, we give the helicity formalism of the decays in this section. The helicity information of can be obtained from with . The advantage of the helicity analysis is that it can easily cooperate with the sequential decays and has a clear view of physical meaning Gutsche:2013oea .
Taking the initial as unpolarized, the angular distributions of are given as
| (1) |
where are the helicity amplitudes with the subscripts denoting the helicity of , the Wigner -matrix for , defined in the helicity frame of (see Fig. 1), and
| (2) |
Here, has the physical meaning of the nonzero-polarized fraction of . Notice that are forbidden by the angular momentum conservation, resulting in
| (3) |
To further extract the helicity information, we define
| (4) |
where is chosen to satisfy
| (5) |
which is found to be .
The experiments of are polluted by the off-shell contributions from at LHC. Thus, we define the event-average as
| (6) |
as well as the event-average nonzero-polarized fraction as
| (7) |
with
| (8) |
where is the number of the observed events in . The second equality in Eq. (6) is attributed to Eq. (3) .
To get an estimation on the experiments, we calculate the amplitudes within the factorization framework. The helicity amplitudes of are given as
| (9) |
where is for the 4-momentum of the hadron in the subscript, and the Fermi and the pion decay constants, the effective Wilson coefficient for the color-allowed decays, the angular momentum at the direction, and indicates .
On the other hand, the helicity amplitudes of are given as
| (10) |
where is the effective Wilson coefficient for the color-suppressed decays, the decay constant, and the polarization 4-vector of with its helicity.
Finally, the decay width for is given as
| (11) |
whereas the decay widths of with the daughter vector meson having helicity are given as
| (12) |
The total decays widths of and can be easily obtained by adding up the contributions from .
III Numerical analysis
The meson transition matrix elements require the knowledge of the hadron wave functions. In this work, we employ the ones from the homogeneous bag model, in which the center motions of the hadrons in the original bag model are removed Geng:2020ofy . The bag radius and the quark masses can be extracted from the mass spectra, which are found to be Zhang:2021yul
| (13) |
The details of the calculation can be found in the Appendix. In this study, and are taken from the experiments and the Lattice QCD Chen:2020qma ; pdg
| (14) |
and the effective Wilson coefficients are taken to be
| (15) |
The results are given in Table I , where we also include , which can be safely approximated as with the lifetime of . The calculated lifetime is consistent with most of the literature Li:2019tbn ; consistent , but significantly smaller than the one from the nonrelativistic potential model Eichten:1994gt , and twice larger than the one from the relativistic independent quark model twice . Nonetheless, a large part of the uncertainties that arises from the hadron wave functions is canceled in the branching ratios of , as the lifetime is calculated under the same framework.
| Channel | Helicity | ||
|---|---|---|---|
| Total | |||
| Total | 1 | ||
| Total |
Our is consistent with the relativistic quark model BcRQ , but two times smaller compared to most of the literature Jpsipip , which can be partly attributed to that we use a smaller . As our estimation is a more conservative one, the angular analysis is promising to be carried out in the experiments for there are more data points to reconstruct the distribution than we expect.
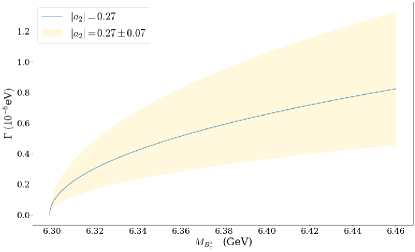
The decay of is color suppressed and suffers large uncertainties from as well as . In particular, as is close to the mass threshold of , the decay width can range from to eV, depending on . The dependency on as well as the uncertainties caused by are plotted in Fig. 3. Taking MeV, the calculated decay width is given in Table 1, which is consistent with Ref. Search , within the range of the error.
From Table 1, for we obtain
| (16) |
in which the theoretical uncertainty is canceled for the correlations between . The cross section of meson at the LHC is expected to be Chang:1992jb . At an integrated luminosity of during LHC Run-2, during LHC Run-3, and after High Luminosity upgrade (HL-LHC) Apollinari:2017lan , the numbers of events are , and , resulting in , , and events of , respectively. Taking the branching ratios pdg , there are expected to be , , and events of being able to be reconstructed at LHC Run-2, LHC Run-3 and HL-LHC, respectively.
By choosing with the invariant mass of , most of the off-shell contribution from would be filtered, in which is expected to be less than 20 at running LHC from the Fig. 1 of Ref. LHCb:2016vni 111In fact, at the bottom right figure, there appears to have a little bump around MeV.. Thus, and can be safely taken as equal in the simulation.
We generate the pseudodata based on the experimental conditions at LHC Run-2, LHC Run-3, and HL-LHC. The off-shell contributions from are also included with as discussed in the previous paragraph. The numbers of the events are plotted against in Fig. 4 , and the numerical results of and are given in Table 2 . Our analysis show that there would be a signal of nonzero at LHC Run-2 , and a signal at HL-LHC, which would be a solid evidence of .
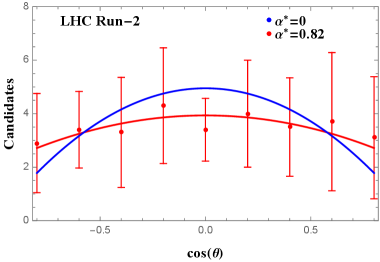
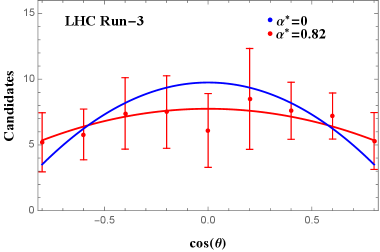
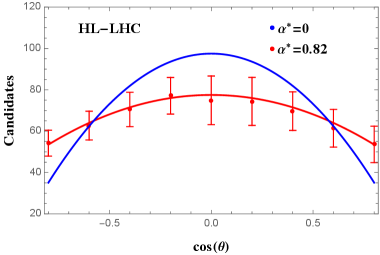
| LHC Run-2 | 33 | ||
|---|---|---|---|
| LHC Run-3 | 65 | ||
| HL-LHC | 650 |
On the other hand, at the forthcoming experiments at FCC-hh FCC:2018vvp , the number of events are expected to be . Hence, there would be about and events at HL-LHC and FCC-hh, respectively, which would be sufficient for the experiments to determine the mass.
IV Conclusions
Utilizing the conservation laws, we propose two novel methods for distinguishing and in the experiments. The calculated branching fractions of and are compatible with the literature, indicating that our analysis is reliable. The nonzero polarized fraction of from has been found to be . Furthermore, the branching fractions of and have been obtained as and , respectively. To calculate the lifetime of , we have found that eV with the homogeneous bag model, consistent with most of the literature.
We have shown that would be promising to be measured at HL-LHC as well as FCC-hh. To examine the feasibilities of the measurements, we have conducted simulations based on the experimental conditions. Remarkably, we have shown that the helicity analysis on is ready to be performed at LHC. Thus, we urge the experimentalists to probe the angular distributions of in the region of MeV, which can be served as an evidence of .
Acknowledgments
The authors would like to acknowledge the helpful discussion with Chao-Qiang Geng, Ying-Rui Hou and Cong-Feng Qiao.
Appendix : The baryon wave functions
Here, we give the meson wave functions of the homogeneous bag model, which are used in the calculation of the transition matrix elements in the main text. In the original version of the bag model, both the asymptotic freedom and the confinement of the QCD are described by the bag radius, . The quarks are confined in the bag but moving freely within it, satisfying the free Dirac equation
| (17) |
For low-lying hadrons, we can take the wave functions to be spherical, and we arrive at
| (18) |
where is the quark flavor, the normalizing constant, the two component spinor, the magnitude of the 3-momentum, and with the quark energy. The antiquark wave functions are obtained by taking the charge conjugate.
At the boundary of the bag the current shall vanish, which give us the boundary condition, read as
| (19) |
In analogy to the familiar infinite square well, is quantized, satisfying
| (20) |
We concern the low-lying hadrons only and therefore take the minimum of . At the massless and the heavy quark limits we have
| (21) |
respectively. A meson can be constructed by confining a quark and an antiquark to a same bag. By considering the bag energy, zero point energy, and the interaction between quarks, the bag model can successfully explain most of the low-lying hadron masses as well as the ratios of the magnetic dipole moments Zhang:2021yul .
However, despite the success on the hadron masses, the wave functions of the bag model are problematic when it comes to decays. As the description of a static bag is essentially localized, the hadron wave function cannot be the momentum eigenstates, and thus the transition matrix elements cannot be consistently calculated. This problem has been resolved with the linear superposition of infinite bags by one of the authors (Liu), and with it the experimental branching ratios of and can be well explained Geng:2020ofy .
In the homogeneous bag model, the meson wave functions at rest are given as
| (22) |
where is the normalizing constant, and in the superscript denotes the charge conjugate. The wave function in Eq. (22) is manifestly invariant under the space translation and therefore describes a meson at rest. The wave functions with nonzero momenta can be easily obtained by Lorentz boost.
By demanding the normalization condition
| (23) |
we find
| (24) |
with and the hadron momentum and mass, respectively.
With the wave functions, the meson transition matrix elements can be computed straightforwardly. For simplicity we take as an example. The results of can be obtained by taking the CP conjugate as CP is conserved in the transition. The transition matrix elements read as
| (25) | |||||
with
| (26) |
Here, the calculation is taken at the Briet frame where and have the velocity and , respectively. Although the derivation is quite tedious (see Ref. Geng:2020ofy for an example), their physical meaning can be easily understood:
-
•
is the overall normalizing constant along with the momentum conservation.
-
•
is the overlapping coefficient attributed by the spectator quark between the initial and the final states. Note that their centers of the bags are separated at a distance of .
-
•
is the matrix element of the (axial) vector current at the quark level, where the centers of the bags are separated at a distance of .
Here, the exponential in the integrals would oscillate violently at large velocity, causing a suppression that is a punishment for not being at the same speed. The matrix elements of can be calculated in the same manner.
References
- (1) F. Abe et al. [CDF Collaboration], Phys. Rev. D 58, 112004 (1998).
- (2) T. Aaltonen et al. [CDF], Phys. Rev. Lett. 100, 182002 (2008).
- (3) R. Aaij et al. [LHCb], Phys. Rev. Lett. 109, 232001 (2012).
- (4) R. Aaij et al. [LHCb], JHEP 07, 123 (2020).
- (5) A. Abulencia et al. [CDF], Phys. Rev. Lett. 97, 012002 (2006).
- (6) V. M. Abazov et al. [D0], Phys. Rev. Lett. 102, 092001 (2009).
- (7) G. Aad et al. [ATLAS Collaboration], Phys. Rev. Lett. 113, 212004 (2014).
- (8) A. M. Sirunyan et al. [CMS Collaboration], Phys. Rev. Lett. 122, 132001 (2019).
- (9) R. Aaij et al. [LHCb], Phys. Rev. Lett. 122, 232001 (2019)
- (10) E. J. Eichten and C. Quigg, Phys. Rev. D 49, 5845 (1994).
- (11) E. J. Eichten and C. Quigg, Phys. Rev. D 99, 054025 (2019).
- (12) S. Godfrey, Phys. Rev. D 70, 054017 (2004).
- (13) R. Ding, B. D. Wan, Z. Q. Chen, G. L. Wang and C. F. Qiao, Phys. Lett. B 816, 136277 (2021).
- (14) N. Mathur, M. Padmanath and S. Mondal, Phys. Rev. Lett. 121, 20, 202002 (2018).
- (15) Q. Li, M. S. Liu, L. S. Lu, Q. F. Lü, L. C. Gui and X. H. Zhong, Phys. Rev. D 99, 096020 (2019).
- (16) I. Asghar, F. Akram, B. Masud and M. A. Sultan, Phys. Rev. D 100, 096002 (2019).
- (17) P. Bialas, J. G. Körner, M. Kramer and K. Zalewski, Z. Phys. C 57, 115-134 (1993); T. Gutsche, M. A. Ivanov, J. G. Körner, V. E. Lyubovitskij and P. Santorelli, Phys. Rev. D 87, 074031 (2013); T. Gutsche, M. A. Ivanov, J. G. Körner, V. E. Lyubovitskij and P. Santorelli, Phys. Rev. D 88, 114018 (2013).
- (18) C. Q. Geng, C. W. Liu and T. H. Tsai, Phys. Rev. D 102, 034033 (2020); C. Q. Geng and C. W. Liu, JHEP 11, 104 (2021); C. W. Liu and C. Q. Geng, JHEP 01, 128 (2022).
- (19) T. A. DeGrand, R. L. Jaffe, K. Johnson and J. E. Kiskis, Phys. Rev. D 12, 2060 (1975); W. X. Zhang, H. Xu and D. Jia, Phys. Rev. D 104, 114011 (2021).
- (20) P. A. Zyla et al. [Particle Data Group], PTEP 2020, 083C01 (2020).
- (21) Y. Chen et al. [QCD], Chin. Phys. C 45, 023109 (2021).
- (22) S. S. Gershtein, V. V. Kiselev, A. K. Likhoded and A. V. Tkabladze, Phys. Rev. D 51, 3613 (1995); L. P. Fulcher, Phys. Rev. D 60, 074006 (1999); D. Ebert, R. N. Faustov and V. O. Galkin, Phys. Rev. D 67, 014027 (2003); Z. G. Wang, Eur. Phys. J. C 73, 2559 (2013).
- (23) S. Patnaik, P. C. Dash, S. Kar, S. Patra and N. Barik, Phys. Rev. D 96, 116010 (2017).
- (24) D. Ebert, R. N. Faustov and V. O. Galkin, Phys. Rev. D 68, 094020 (2003).
- (25) C. H. Chang and Y. Q. Chen, Phys. Rev. D 49, 3399 (1994); V. V. Kiselev, A. K. Likhoded and A. I. Onishchenko, Nucl. Phys. B 569, 473 (2000); A. Abd El-Hady, J. H. Munoz and J. P. Vary, Phys. Rev. D 62, 014019 (2000); P. Colangelo and F. De Fazio, Phys. Rev. D 61, 034012 (2000); M. A. Ivanov, J. G. Krner and P. Santorelli, Phys. Rev. D 73, 054024 (2006); A. Issadykov and M. A. Ivanov, Phys. Lett. B 783, 178 (2018); W. Cheng, Y. Zhang, L. Zeng, H. B. Fu and X. G. Wu, Chin. Phys. C 46, 053103 (2022).
- (26) J. Sun, Y. Yang, N. Wang, Q. Chang and G. Lu, Phys. Rev. D 95, 074032 (2017).
- (27) C. H. Chang and Y. Q. Chen, Phys. Rev. D 48, 4086(1993).
- (28) G. Apollinari, I. Béjar Alonso, O. Brüning, P. Fessia, M. Lamont, L. Rossi and L. Tavian, Report No. CERN-2017-007-M.
- (29) A. Abada et al. [FCC], Eur. Phys. J. ST 228, 755-1107 (2019).
- (30) R. Aaij et al. [LHCb], JHEP 09, 153 (2016).