The Belle Collaboration

The decay $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ (charge-conjugate processes are implied throughout this letter) is of interest for the testing of Lepton Flavor Universality (LFU) and for searches of physics beyond the Standard Model (SM). This decay is highly suppressed in the SM and can only proceed via a flavor-changing neutral current, with a predicted branching fraction of order $\mathcal{O}(10^{-7})$ [1]. The branching fraction can be enhanced if new physics (NP) effects contribute [2, 3, 4, 5]. The flavor-changing neutral current processes such as $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ can provide very powerful tests for the SM and its extensions. In particular, the decay is a third-generation equivalent of the $B^{0}\rightarrow K^{\ast 0}\ell^{+}\ell^{-}$ decay, where $\ell$ is an electron or a muon. Hence, compared with electron and muon modes, the decay is expected to be more sensitive to new physics in a model which has a coupling proportionate to the particle mass [6] or only couples to the third generation [7].

Semileptonic $B$ decay measurements in recent years show significant deviations from SM expectations, for both charged and neutral current transitions. The first type of transition has been measured in the decay $b\rightarrow c\ell\bar{\nu}_{\ell}$ via $R(D^{(*)})=[\mathcal{B}(B\rightarrow D^{(*)}\tau^{+}\nu_{\tau})]/[\mathcal{B}(B\rightarrow D^{(*)}\ell^{+}\nu_{\ell})]$ by the BaBar [8, 9], Belle [10, 11, 12, 13] and LHCb [14, 15] experiments. While these decays are tree-level processes, which are not very sensitive to NP, the measured results show a deviation of about three standard deviations, 3$\sigma$, from the SM predictions (combined significance) [16]. The neutral current transition $b\rightarrow s\ell^{+}\ell^{-}$ is highly suppressed in the SM and very sensitive to NP. The LFU ratio between muon and electron in the decay mode $B\rightarrow K^{(*)}\ell^{+}\ell^{-}$ as measured by Belle [17, 18, 19] and BaBar [20] are consistent with the SM, while LHCb result [21, 22, 23] is 3.1$\sigma$ lower than the SM prediction. Many theoretical models are introduced to explain these anomalies such as the NP contribution to the Wilson coefficients [3, 4] and the leptoquark model [5]. These approaches lead to an enhancement of the $b\rightarrow s\tau^{+}\tau^{-}$ branching fraction up to $1$-$5\times 10^{-4}$, 3 orders of magnitude larger than the SM predictions. The predicted branching fraction of $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ is larger than that of $B^{+}\rightarrow K^{+}\tau^{+}\tau^{-}$ as shown in Ref. [3].

The presence of at least two neutrinos in the final state originating from the decays of $\tau^{+}\tau^{-}$ pair make analysis of the decay challenging. To date only a search for the decay $B^{+}\rightarrow K^{+}\tau^{+}\tau^{-}$ has been conducted by the BaBar collaboration setting an upper limit $\mathcal{B}(B^{+}\rightarrow K^{+}\tau^{+}\tau^{-})<2.25\times 10^{-3}$ at 90% confidence level (CL) [24].

In this letter, we present the first search for the rare decay $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$. Our analysis is based on the complete data set collected at the center of mass (c.m.) energy equal to the $\Upsilon(4S)$ resonance mass by the Belle detector [25] at the KEKB asymmetric-energy $e^{+}e^{-}$ collider [26]. This data sample corresponds to an integrated luminosity of 711 $\rm fb^{-1}$, containing $772\times 10^{6}B\bar{B}$ pairs. We use a full reconstruction technique [27] in this analysis where the companion $B$ meson in the process $e^{+}e^{-}\rightarrow\Upsilon(4S)\rightarrow B\bar{B}$ is reconstructed in hadronic decay modes, referred to as $B_{\rm tag}$. We then search for the signal $B$ meson, $B_{\rm sig}$, in the rest of the event not used in the $B_{\rm tag}$ reconstruction.

The Belle detector [25] is a large-solid-angle magnetic spectrometer consisting of a silicon vertex detector (SVD), a 50-layer central drift chamber (CDC), an array of aerogel threshold Cherenkov counters (ACC), a barrel-like arrangement of time-of-flight scintillation counters (TOF), and an electromagnetic calorimeter comprised of CsI(Tl) crystals (ECL). All these components are located inside a superconducting solenoid coil that provides a 1.5 T magnetic field. An iron flux-return located outside of the coil is instrumented with resistive plate chambers to detect $K_{L}^{0}$ mesons and to identify muons (KLM).

We use Monte Carlo (MC) simulation samples, generated with EvtGen [28], to optimize the signal selection, determine the selection efficiencies, as well as to obtain the signal and background fitting models. The detector response is simulated using GEANT3 [29]. Simulated events are overlaid with random trigger data taken for each run period to reproduce the effect of beam-associated backgrounds. A signal sample containing 50 million $\Upsilon(4S)\rightarrow B^{0}\bar{B}^{0}$ events is generated where one $B$ decays to all possible final states, according to its measured or estimated branching fractions [30], and the other decays via $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$, using the model described in Ref. [31]. Background MC samples consist of $B^{+}B^{-}$, $B^{0}\bar{B}^{0}$, and continuum $e^{+}e^{-}\rightarrow q\bar{q}$ ($q=u,d,s,c$), where the size of each sample is six times larger than that of collision data. Rare $B$ meson decay processes such as charmless hadronic, radiative, and electroweak decays are simulated separately in a sample designated Rare B. Semileptonic $b\rightarrow u\ell\nu$ decays are simulated in a dedicated $u\ell\nu$ sample. The sizes of the $Rare~{}B$ and $u\ell\nu$ samples are 50 and 20 times larger than that of collision data, respectively.

A candidate $B_{\rm tag}$ meson is reconstructed in one of the 489 hadronic decay channel using a hierarchical NeuroBayes-based (NB) full-reconstruction algorithm [27]. In this algorithm, the continuum backgrounds are suppressed by employed event shape variables such as the polar angle of $B_{\rm tag}$, the cosine of the angle between the thrust axis [32] and z-direction, and the modified second Fox-Wolfram moment [33]. All the input variables which used during the reconstruction are mapped to a single classifier output, ${\cal O}_{\rm NB}$, which represents the quality of $B_{\rm tag}$, ranges from zero for combinatorial background and continuum events to unity for an unambiguous $B_{\rm tag}$. Event selection also exploits the energy difference $\Delta E=E_{\rm Btag}-E_{\rm cm}/2$ and the beam-energy-constrained mass $M_{\rm bc}=\sqrt{(E_{\rm cm}/2)^{2}/c^{4}-|\vec{p}_{\rm Btag}|^{2}/c^{2}}$, where $E_{\rm cm}$ is the $e^{+}e^{-}$ energy, and $E_{\rm Btag}$ and $\vec{p}_{\rm Btag}$ are the reconstructed energy and momentum of the $B_{\rm tag}$ candidate, respectively. All the quantities are measured in the c.m. frame. We require each $B_{\rm tag}$ candidate to satisfy $\ln({\cal O}_{\rm NB})>-7$, $|\Delta E|<0.06$ GeV, and $5.275<M_{\rm bc}<5.290$ GeV/$c^{2}$. The net tagging efficiency which is defined as number of truly reconstructed B-tag divided for total number of generated event is 0.24%. It is slightly higher than that reported in Ref. [27], due to lower average particle multiplicity in this signal sample compared to generic sample. The signal side of the $B^{0}\rightarrow K^{\ast 0}\tau^{-}\tau^{+}$ sample contains of leptons and only two hadron tracks. The possibility of the interference from signal side to the tag side reconstruction is lower than that of the generic samples, where both $B$ mesons decay generically. The tagging efficiency is calibrated by comparing the known branching fraction from PDG [30] of the decays $B\rightarrow D^{(*)}\ell\nu_{\ell}$ and the measured values which use this hadron tag reconstruction method [34].

For events where a $B_{\rm tag}$ is reconstructed, we search for the decay $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ in the rest of the event. The remaining tracks are examined to remove duplicate ones due to the curling of low transverse momentum particles ($p_{t}<0.3$ GeV/$c$). A pair of tracks is considered as duplicate if the cosine of the angle between them is either larger than 0.9 or smaller than 0.1, and the difference in transverse momentum is less than 0.1 GeV/$c$. All tracks are constrained to originate from the interaction point (IP) by the requirements $|dr|<2$ cm and $|dz|<4$ cm, where $dr$ and $dz$ are the impact parameter with respect to IP in the transverse and longitudinal directions, respectively. We select events as signal candidates if there are four remaining tracks with zero net charge. The number of signal candidates doubles after removing duplicate tracks.

We reconstruct candidate $K^{\ast 0}$ mesons from $K^{\ast 0}\rightarrow K^{+}\pi^{-}$ decays using two of the four remaining tracks. We identify kaons and pions based on combined information from the CDC, ACC, and TOF [35]. A charged track is identified as a kaon if the likelihood ratio $\mathcal{R}_{K}=\mathcal{L}_{K}/(\mathcal{L}_{K}+\mathcal{L}_{\pi})>0.6$, and as a pion if $\mathcal{R}_{K}<0.4$, where $\mathcal{L}_{i}$ is the PID likelihood for the particle type $i$. The momenta of $K^{+}$ and $\pi^{-}$ candidates are required to be greater than 0.1 GeV/$c$. The flavor of the reconstructed $K^{\ast 0}$ and hence the corresponding flavor of $B_{\rm sig}$ is required to be opposite to that of $B_{\rm tag}$. This requirement rejects 20% of the events. We fit the vertex for $K^{\ast 0}$ candidates, and reject candidates if the vertex fit fails. If more than one $K^{\ast 0}$ candidate is successfully reconstructed, the one having the reconstructed mass closest to the known $K^{\ast 0}$ mass is retained. We require the mass of the reconstructed $K^{\ast 0}$ candidate to be in the range [0.8, 1.0] GeV/$c^{2}$, which is approximately twice the decay width of $K^{\ast 0}$. We consider three $\tau$ decay modes in this analysis: $\tau^{-}\rightarrow e^{-}\bar{\nu}_{e}\nu_{\tau}$, $\tau^{-}\rightarrow\mu^{-}\bar{\nu}_{\mu}\nu_{\tau}$, and $\tau^{-}\rightarrow\pi^{-}\nu_{\tau}$, resulting in six different decay topologies: $K^{\ast 0}e^{+}e^{-}$, $K^{\ast 0}e^{\mp}\mu^{\pm}$, $K^{\ast 0}\mu^{+}\mu^{-}$, $K^{\ast 0}e^{\mp}\pi^{\pm}$, $K^{\ast 0}\mu^{\mp}\pi^{\pm}$, and $K^{\ast 0}\pi^{+}\pi^{-}$. We regard the two remaining tracks not used in the $B_{\rm tag}$ or the $K^{\ast 0}$ candidates as $\tau$ decay products. The reconstructed mass of these two tracks is required to be less than 2.5 GeV/$c^{2}$.

All the tracks and clusters in a signal event are used for the reconstruction of $B_{\rm tag}$ and $B_{\rm sig}$. However, there are still tracks and clusters from beam background and possible duplicate tracking reconstruction. We require that there be no extra $\pi^{0}$ nor $K_{S}^{0}$ candidates, and at most one $K_{L}^{0}$ candidate cluster, to allow for beam-associated backgrounds or electronic noise. We reconstruct $K_{L}^{0}$ candidates based on the hit patterns in the KLM subdetector not associated with any charged track. A $\pi^{0}$ candidate is reconstructed from $\pi^{0}\rightarrow\gamma\gamma$ in which neither daughter photon is included in the reconstructed $B_{\rm tag}$ and whose reconstructed mass is within 25 MeV/$c^{2}$ of the nominal $\pi^{0}$ mass [30], corresponding to $3\sigma$ of the $\pi^{0}$ mass resolution. Energy of photon candidates must exceed 50 MeV and we require their shower shape, characterized as the ratio of total energy detected in a $3\times 3$ versus $5\times 5$ array of ECL crystals in which the center crystal has the maximum detected energy, to be larger than 0.75. We reconstruct candidate $K_{S}^{0}$ from $K_{S}^{0}\rightarrow\pi^{+}\pi^{-}$ decays, where the reconstructed mass is within 15 MeV/$c^{2}$ of the nominal mass, corresponding to $3\sigma$ of $K_{S}^{0}$ mass resolution.

We determine the number of signal candidates by fitting the distribution of extra calorimeter energy, $E_{\rm ECL}^{\rm extra}$, which is defined as the total energy of the neutral clusters detected in the ECL not associated with either $B_{\rm tag}$ or $B_{\rm sig}$. We reduce the contribution of beam-associated backgrounds while estimating $E_{\rm ECL}^{\rm extra}$ by only counting clusters with energy greater than 0.15, 0.05 and 0.10 GeV for the backward, barrel, and forward regions, respectively. In signal events $E_{\rm ECL}^{\rm extra}$ should be zero or have a small value due to the residual energy from beam-associated backgrounds or mismatched tracks. Background events tend to have larger values due to contributions from additional neutral clusters. We select events with $E_{\rm ECL}^{\rm extra}<0.2$ GeV as the signal region and those with $E_{\rm ECL}^{\rm extra}<2$ GeV for sideband studies. The selection criteria in this study are chosen to maximize the search sensitivity in the signal region following the Punzi figure of merit [36].

In the c.m. frame, the $B_{\rm tag}$ and $B_{\rm sig}$ have opposite flight directions, and the $B_{\rm tag}$ is fully reconstructed and its four-vector is determined. The momentum of $B_{\rm sig}$ is thus derived from the $B_{\rm tag}$ reconstruction. Its direction is opposite the $B_{\rm tag}$ and its magnitude is calculated as $|\vec{p}_{B\rm{sig}}|=\sqrt{(E_{\rm{cm}}/2)^{2}/c^{2}-m_{B}^{2}c^{2}}$, where $\vec{p}_{B\rm{sig}}$ is the momentum vector of $B_{\rm sig}$, $E_{\rm{cm}}/2$ is the beam energy measured in c.m frame, and $m_{B}$ is the nominal $B^{0}$ meson mass [30]. We calculate the $\tau^{+}\tau^{-}$ pair invariant mass, $M_{\tau^{+}\tau^{-}}$, by subtracting the reconstructed $K^{\ast 0}$ c.m. four-vector from the $B_{\rm sig}$’s giving its kinematic limits. We require $M_{\tau^{+}\tau^{-}}$ to be greater than 3.55 GeV/$c^{2}$ to suppress combinatorial background.

After the selections above, the remaining background is final-state dependent. We classify the remaining events into signal modes based on final-state particles for further background suppression. We identify electron candidates using an electron likelihood ratio, $\mathcal{R}_{e}=\mathcal{L}_{e}/(\mathcal{L}_{e}+\mathcal{L}_{\bar{e}})$, $\bar{e}$ indicates non-electron hypothesis. $\mathcal{L}_{e}$ ($\mathcal{L}_{\bar{e}}$) are calculated based on $dE/dx$ information from the CDC, the ratio of the energy deposited in the ECL to the momentum measured by the CDC and SVD, the shower shape in the ECL, hit information from the ACC, and matching between the position of the charged track and the ECL cluster [37]. Muon candidates are identified using a muon likelihood ratio, $\mathcal{R}_{\mu}=\mathcal{L}_{\mu}/(\mathcal{L}_{\mu}+\mathcal{L}_{\pi}+\mathcal{L}_{K})$, which is estimated based on the difference between the range of the track in KLM, estimated assuming no hadronic interactions, and the actual range observed in the KLM. A $\chi^{2}$ from extrapolating a track to the signals identified in the KLM using a Kalman filter also contributes to the likelihood [38]. Tracks are identified as electrons if $\mathcal{R}_{e}>0.8$, as muons if not satisfying the electron requirement and have $\mathcal{R}_{\mu}>0.8$, and as a pion if not either an electron or a muon. The average of electron (muon) identification efficiency for the selection $\mathcal{R}_{e(\mu)}>0.8$ is 92 (92)% with pion fake rate of 0.25 (2.5)%. In the signal decay modes $K^{\ast 0}\pi^{+}\pi^{-}$ and $K^{\ast 0}\ell^{\pm}\pi^{\mp}$, there remains a large background contribution from the decay $B^{0}\rightarrow D^{(*)-}\ell^{+}\nu_{\ell}$, where $D^{(*)-}\rightarrow K^{\ast 0}\pi^{-}(\pi^{0})$. We suppress this by requiring the invariant mass $M_{K^{\ast 0}\pi^{-}}$ to lie outside the $D^{-}$ mass region, $M_{K^{\ast 0}\pi^{-}}<1.84$ GeV/$c^{2}$ or $M_{K^{\ast 0}\pi^{-}}>1.94$ GeV/$c^{2}$, where $M_{K^{\ast 0}\pi^{-}}$ is the combination of the $K^{\ast 0}$ candidate and a track that is opposite to the charge of the kaon candidate in the $K^{\ast 0}$ decay. Combinatorial background is also significant in these signal modes, and so the ${\cal O}_{\rm NB}$ selection criterion is tightened to ${\ln(\cal O}_{\rm NB})>-4$ for these modes.

After we apply above selection criteria, our simulation predicts that the remaining backgrounds with low $E_{\rm ECL}^{\rm extra}$ are primarily $B^{0}\bar{B}^{0}$ events in which a $B_{\rm tag}$ is properly reconstructed opposite $B^{0}\rightarrow D^{-}\ell^{+}\nu_{\ell}$ decaying to $D^{-}\rightarrow K^{\ast 0}\ell^{-}\bar{\nu}_{\ell}$. Such events have the same final-state particles as signal events. The different number of missing neutrinos results in a different missing mass distribution, $M_{\rm miss}$. We calculate this by subtracting the measured part of the four-momentum of $B_{\rm sig}$ from the derived four-momentum of $B_{\rm sig}$ from the recoil against $B_{\rm tag}$. In addition to the missing mass, we find $M_{K^{\ast 0}\pi^{-}}$ is also powerful distinguishing signal from the remaining background. For $K^{\ast 0}\ell^{-}\ell^{+}$ modes, we calculate $M_{K^{\ast 0}\pi^{-}}$ by combining the negatively charged lepton with the $K^{\ast 0}$ assuming a pion mass. We optimize selection criteria based on $M_{\rm miss}^{2}$ and $M_{K^{\ast 0}\pi^{-}}$ together mode-by-mode. These are summarized in Table 1. Since the number of missing neutrinos from the $K^{\ast 0}\pi^{+}\pi^{-}$ mode is the same as that from the $B^{0}\rightarrow D^{-}\ell^{+}\nu_{\ell}$ background, the $M_{\rm miss}^{2}$ is ineffective in rejecting this background. We only apply the selection $M_{\rm miss}^{2}<9$ $\rm{GeV}^{2}/c^{4}$ to reject combinatorial background which is significant in this mode. Despite the continuum suppression performed by the full reconstruction algorithm, a small fraction of continuum events remains in the $K^{\ast 0}\pi^{+}\pi^{-}$ signal mode. In this case, further constraints on the event shape are imposed. Specifically, the event thrust is required to be smaller than 0.85, the cosine of the angle between the thrust of $B_{\rm sig}$ and that of $B_{\rm tag}$ must be smaller than 0.85, and the modified second Fox-Wolfram moment is required to be less than 0.4.

We estimate the signal reconstruction efficiency after applying all of the selection criteria and $B_{\rm tag}$ efficiency corrections. The overall selection efficiency, determined using simulated $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ decays, is approximately $(1.23\pm 0.05)\times 10^{-5}$, where the uncertainty is statistical. The signal yield is extracted with a binned extended maximum-likelihood fit to the $E_{\rm ECL}^{\rm extra}$ distribution, with a bin width of 0.1 GeV. The probability density functions (PDFs) for signal and background components are taken from MC expectations after applying the B-tag efficiency correction. To reduce the uncertainty due to low statistics, a simulation sample three times larger than the data is used to construct the background PDFs, the signal PDF is derived from 50 million $\Upsilon(4S)\rightarrow B^{0}\bar{B}^{0}$ signal events, and signal modes are combined in the fit. The $B^{+}B^{-}$ and $B^{0}\bar{B}^{0}$ samples are normalized to the data and their ratio is fixed in the fit. Contributions from $Rare~{}B$ and $u\ell\nu_{\ell}$ components in the final sample are negligible, and are normalized to the number of $B\bar{B}$ pairs and fixed in the fit. We float the $B\bar{B}$, continuum, and signal normalizations. We have validated the fitting procedure in tests with MC samples.

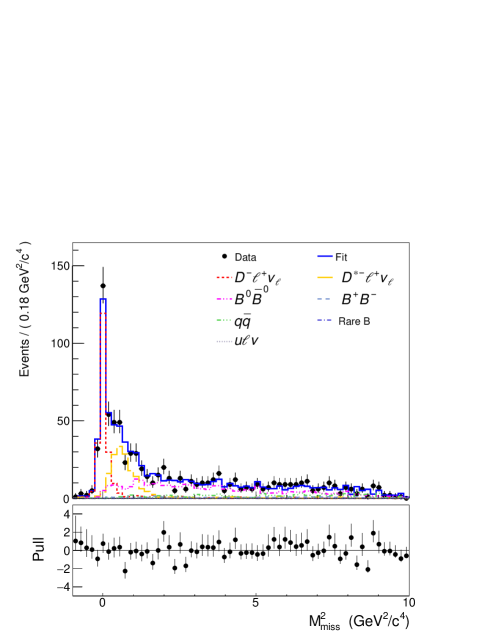
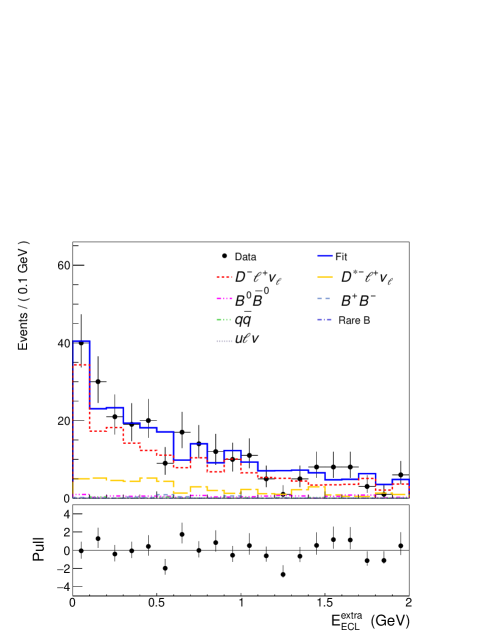
We test the analysis procedure and shape of the simulated $E_{\rm ECL}^{\rm extra}$ distribution using $B^{0}\rightarrow D^{-}\ell^{+}\nu_{\ell}$ decays, with $D^{-}\rightarrow K^{\ast 0}\pi^{-}$. The analysis steps and selection criteria for the decay are the same as those for the $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ decay, except the requirement on $M_{\rm miss}^{2}$ is removed and the selection on $M_{K^{\ast 0}\pi^{-}}$ is reversed, requiring $1.84<M_{K^{\ast 0}\pi^{-}}<1.94$ GeV/$c^{2}$. We divided the sample into the two sub-samples, one with $M_{\rm miss}^{2}<0.5$ $\rm{GeV}^{2}/c^{4}$ and the other with $M_{\rm miss}^{2}>0.5$ $\rm{GeV}^{2}/c^{4}$. The first sub-sample where events are mainly from $B^{0}\rightarrow D^{-}\ell^{+}\nu_{\ell}$ is useful for checking the signal shape. The latter containing mostly background events is used for validate the background shape. Within statistics, the signal and background models obtained from simulation are in good agreement with the data and are used to model the signal and background in the final fit. As a cross-check, we measure the branching fraction of the decay $B^{0}\rightarrow D^{-}\ell^{+}\nu_{\ell}$ from a fit to the $E_{\rm ECL}^{\rm extra}$ distributions, similar to our search for the decay $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$, and also to the $M_{\rm miss}^{2}$ distribution. Results of these fits are shown in Fig. 1. The branching fraction measured by fitting to $E_{\rm ECL}^{\rm extra}$ for the first sub-sample is $(2.45\pm 0.17)\%$ and to $M_{\rm miss}^{2}$ is $(2.37\pm 0.15)\%$, where the quoted uncertainties are statistical only. The results are in good agreement with the world average of $2.31\pm 0.10$% [30]. We obtained a zero signal for the fit to $E_{\rm ECL}^{\rm extra}$ distribution of the second sub-sample ($M_{\rm miss}^{2}>0.5$ $\rm{GeV}^{2}/c^{4}$) as expected.

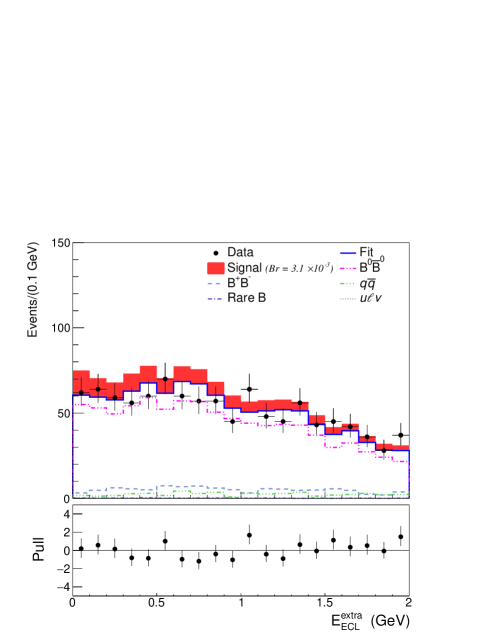
We perform the fit to $E_{\rm ECL}^{\rm extra}$ for the decay $B^{0}\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ using the procedure as described above, where all signal modes have been combined. The numbers of signal and background events in the signal window [0; 0.2] GeV obtained from the fit are $N_{\rm sig}=-4.9\pm 6.0$ and $N_{\rm bkg}=122.4\pm 4.9$, respectively. We find no evidence for a signal. Data are consistent with background as shown in Fig. 2, where the background-only model is fitted to data and a signal with branching fraction of $3.1\times 10^{-3}$ is superimposed on the top.

Systematic uncertainties on the number of background events, the signal reconstruction efficiency, and number of $B\bar{B}$ pairs arise from several sources and affect the branching fraction upper limit. The uncertainty on number of $B\bar{B}$ pairs is 1.8%. The statistical uncertainty on the selection efficiency due to limited MC sample size is estimated to be 4.0%. The uncertainty associated with the $B_{\rm tag}$ efficiency is 5.1%, which is estimated using various decays as studied in Ref. [34]. Tracking uncertainty is assigned to be 1.4% for the four $B_{\rm sig}$ charged tracks. The uncertainty due to the charged track selection is estimated to be 4.1%. Particle identification impacts $K^{\ast 0}$ reconstruction and signal mode separation, hence the uncertainties from electron, muon, and pion identification are weighted following their fraction in the signal mode. The total particle identification uncertainty is 2.55%. The difference in reconstruction efficiency for $\pi^{0}$ and $K_{S}^{0}$ leads to a systematic uncertainty in application of the corresponding vetoes. Their uncertainties are estimated to be 0.17% and 1.56% for $\pi^{0}$ and $K_{S}^{0}$, respectively. The uncertainty on the branching fraction of $\tau$ is 0.57%. The total systematic uncertainty is 8.5% calculated by summing the above uncertainties in quadrature.

The systematic uncertainty due to the statistical error of the PDF templates is estimated by varying bin contents of the templates following the Poisson distribution and repeating the fit to the data. This step is repeated 1000 times for each of the PDF. The standard deviation of the number of signal distribution obtained from the fits is considered as systematics uncertainty. The total uncertainty is 4.59 events.

The signal yield obtained from the extended maximum-likelihood fit is translated into an upper limit on the $B\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ branching fraction using the CLs method [39, 40]. We account for statistical and systematic uncertainties on the number of background events and signal efficiencies by modeling them as Gaussian functions with standard deviations given by their uncertainties. Our observed upper limit on the $B\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ branching fraction is $3.1\times 10^{-3}$ at 90% CL.

In conclusion, we have performed a search for the decay $B\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$ using the full Belle data set collected at the c.m. energy of the $\Upsilon(4S)$ resonance. We find no signal and set an upper limit on the branching fraction to be $3.1\times 10^{-3}$ at 90% CL. This is the first experimental limit on the decay $B\rightarrow K^{\ast 0}\tau^{+}\tau^{-}$.

We thank the KEKB group for the excellent operation of the accelerator; the KEK cryogenics group for the efficient operation of the solenoid; and the KEK computer group, and the Pacific Northwest National Laboratory (PNNL) Environmental Molecular Sciences Laboratory (EMSL) computing group for strong computing support; and the National Institute of Informatics, and Science Information NETwork 5 (SINET5) for valuable network support. We acknowledge support from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan, the Japan Society for the Promotion of Science (JSPS), and the Tau-Lepton Physics Research Center of Nagoya University; the Australian Research Council including grants DP180102629, DP170102389, DP170102204, DP150103061, FT130100303; Austrian Federal Ministry of Education, Science and Research (FWF) and FWF Austrian Science Fund No. P 31361-N36; the National Natural Science Foundation of China under Contracts No. 11435013, No. 11475187, No. 11521505, No. 11575017, No. 11675166, No. 11705209; Key Research Program of Frontier Sciences, Chinese Academy of Sciences (CAS), Grant No. QYZDJ-SSW-SLH011; the CAS Center for Excellence in Particle Physics (CCEPP); the Shanghai Science and Technology Committee (STCSM) under Grant No. 19ZR1403000; the Ministry of Education, Youth and Sports of the Czech Republic under Contract No. LTT17020; Horizon 2020 ERC Advanced Grant No. 884719 and ERC Starting Grant No. 947006 “InterLeptons” (European Union); the Carl Zeiss Foundation, the Deutsche Forschungsgemeinschaft, the Excellence Cluster Universe, and the VolkswagenStiftung; the Department of Atomic Energy (Project Identification No. RTI 4002) and the Department of Science and Technology of India; the Istituto Nazionale di Fisica Nucleare of Italy; National Research Foundation (NRF) of Korea Grant Nos. 2016R1D1A1B01010135, 2016R1D1A1B02012900, 2018R1A2B3003643, 2018R1A6A1A06024970, 2019K1A3A7A09033840, 2019R1I1A3A01058933, 2021R1A6A1A03043957, 2021R1F1A1060423, 2021R1F1A1064008; Radiation Science Research Institute, Foreign Large-size Research Facility Application Supporting project, the Global Science Experimental Data Hub Center of the Korea Institute of Science and Technology Information and KREONET/GLORIAD; the Polish Ministry of Science and Higher Education and the National Science Center; the Ministry of Science and Higher Education of the Russian Federation, Agreement 14.W03.31.0026, and the HSE University Basic Research Program, Moscow; University of Tabuk research grants S-1440-0321, S-0256-1438, and S-0280-1439 (Saudi Arabia); the Slovenian Research Agency Grant Nos. J1-9124 and P1-0135; Ikerbasque, Basque Foundation for Science, Spain; the Swiss National Science Foundation; the Ministry of Education and the Ministry of Science and Technology of Taiwan; and the United States Department of Energy and the National Science Foundation.