Frame Equivariance in Dynamics Modeling and Reinforcement Learning
Abstract
In this paper, we aim to explore the potential of symmetries in improving the understanding of continuous control tasks in the 3D environment, such as locomotion. The existing work in reinforcement learning on symmetry focuses on pixel-level symmetries in 2D environments or is limited to value-based planning. Instead, we considers continuous state and action spaces and continuous symmetry groups, focusing on translational and rotational symmetries. We propose a pipeline to use these symmetries in learning dynamics and control, with the goal of exploiting the underlying symmetry structure to improve dynamics modeling and model-based planning.
1 Motivation
Symmetries have recently been explicitly included into some machine learning algorithms, such as translational equivariance of convolution neural networks (CNNs) on image segmentation. Symmetries can provide regularities from the laws of physics, including physics-related tasks such as modeling dynamics. However, it has not been widely explored in the context of control of dynamical system, such as continuous control tasks in reinforcement learning.
In exiting work, van_der_pol_mdp_2020, mondal_group_2020 initiate the study of symmetry in deep reinforcement learning, after [ravindran_symmetries_nodate, zinkevich_symmetry_2001]. They focus on pixel-level symmetries in the CartPole task or Atari games, such as left-right reflection or discrete rotations. Nevertheless, such level of symmetry does not unveil the symmetry of the underlying dynamical system. zhao_integrating_2022 study discrete symmetry in model-based planning on 2D discrete grid, which uses the symmetry of 2D grid (4 rotations and 2 reflections). However, it is constrained to 2D grid and value-based planning, which cannot trivially extend to continuous control case that needs sampling-based planning.
This motivates to further move ahead to continuous state and action spaces and continuous symmetry groups and ask: can we make use of the symmetry structure of the 3D space to improve dynamics modeling and model-based planning/control? In this work, we aim to exploit the underlying symmetry structure of those continuous control tasks, through the lens of symmetry. We focus on the tasks in the 3D environment, which include locomotion and manipulation and simulate the needs of our 3D physical world. We consider translational and rotational symmetries in the 3D space, which are related to conservation of linear and angular momentum. To this end, we propose a pipeline to use these symmetries in learning dynamics and control.
2 Related work
Symmetry in RL and state abstraction.
Symmetries widely exist in various domains and have been exploited in classic planning algorithms and model checking [fox_detection_1999, fox_extending_2002, pochter_exploiting_2011, domshlak_enhanced_nodate, shleyfman_heuristics_2015, holldobler_empirical_2015, sievers_structural_nodate, sievers_theoretical_2019, fiser_operator_2019]. zinkevich_symmetry_2001 show the invariance of value function for an MDP with symmetry. However, these algorithms have a fundamental issue with the exploitation of symmetries, as they explicitly construct equivalence classes of symmetric states, which are intractable (NP-hard) in maintaining symmetries in trajectory rollout and forward search [narayanamurthy_hardness_2008] and incompatible with differentiable pipelines for representation learning. To address this issue, recent work has explored state abstraction for symmetry, such as coarsest state abstraction that aggregates symmetric states into equivalence classes, studied in MDP homomorphisms and bisimulation [ravindran2004algebraic, ferns_metrics_2004, li_towards_2006]. However, these methods usually require perfect MDP dynamics knowledge and do not scale well due to the complexity of constructing and maintaining abstraction mappings [van2020mdp]. Several recent studies have integrated symmetry into RL based on MDP homomorphisms [ravindran2004algebraic]. van2020mdp integrate symmetry by equivariant policy network, which avoids the difficulties in handling symmetry in forward search. Earlier, mondal_group_2020 have separately applied similar idea earlier while not using MDP homomorphisms. park_learning_2022 learn equivariant transition models, but do not consider planning. zhao_toward_2022 focus on permutation symmetry in object-oriented transition models. The direct precedent is [zhao_integrating_2022], which studies 2D discrete symmetry on 2D grid with a value-based planning approach.
Geometric deep learning.
Geometric deep learning studies how to preserve geometric properties, such as symmetry and curvature [bronstein_geometric_2021]. Equivariant neural networks have been developed for preserving the symmetries in data. cohen_group_2016 introduce G-CNNs, followed by Steerable CNNs [cohen_steerable_2016] which generalizes from scalar feature fields to vector fields with induced representations. kondor_generalization_2018, cohen_general_2020 study theory on equivariant maps and convolutions. weiler_general_2021 propose to solve kernel constraints under arbitrary representations for and its subgroups by decomposing into irreducible representations, named -CNN. brandstetter_geometric_2022 propose steerable message passing GNNs that use equivariant steerable features, while satorras_en_2021 only use invariant scalar features when building -equivariant graph networks. brandstetter_geometric_2022 develop steerable message passing graph networks for 3D space.
Learned dynamics or physics for model-based planning.
battaglia_interaction_2016 proposed a framework for learning the interaction dynamics between objects in a scene, based on the notion of relational inductive biases. battaglia_relational_2018, this framework was extended to include relational networks for learning the dynamics between objects in a graph-based representation. sanchez-gonzalez_graph_2018 also focused on learning dynamics in a graph-based representation, proposing a graph neural network model for physics simulation. li_learning_2019 developd particle-based dynamics network that focuses on learning the physical interactions between particles in a simulation, allowing for the generation of realistic animations and predictions of future states.
3 Problem Formulation
3.1 Preliminaries
Symmetry groups and equivariance. A symmetry group is defined as a set together with a binary composition map satisfying the axioms of associativity, identity, and inverse. A (left) group action of on a set is defined as the mapping which is compatible with composition. Given a function and acting on and , then is -equivariant if it commutes with group actions: . In the special case the action on is trivial , then holds, and we say is -invariant.
3.2 Graph Representation of a Dynamical System
We consider a dynamical system that models a robot in a 3D physical world. One example is locomotion, where a robot learns to move on a ground that provides support, with gravity directed downwards. The robot is represented by connected links (bodies) and joints (actuators). Suppose the system is modeled by a discrete-time Markov decision process (MDP) as . As done in Interaction Network [battaglia_interaction_2016] or Graph Network [sanchez-gonzalez_graph_2018], we could represent the robot state at each time step as a geometric graph .
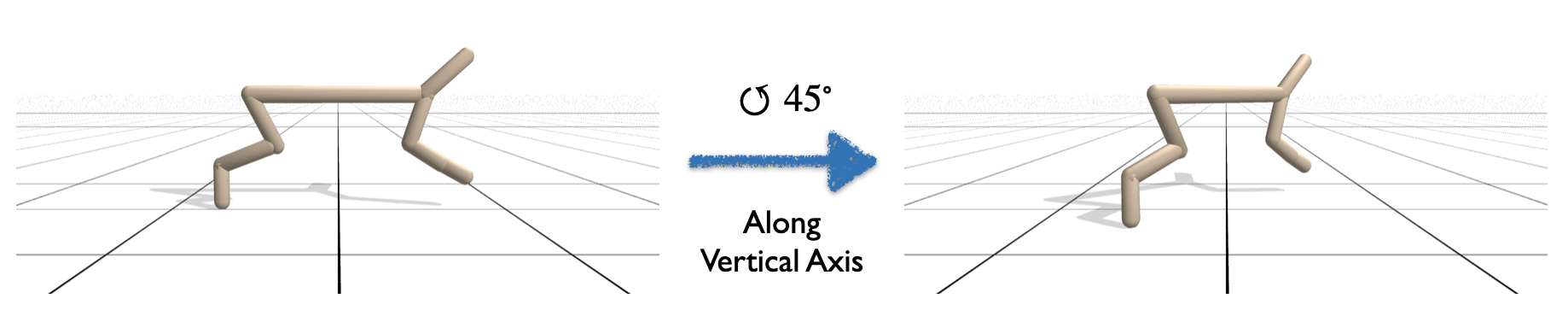
This geometric graph lives in a 3D geometric space, allowing for rotation and translation transformations. The graph nodes are links with features of positions, orientations, linear velocity, and angular velocity. The edges describe the joints between links, where actuation is provided as edge feature. As an example, we can rotate the half cheetah along the vertical axis, where all nodes and edges are rotated correspondingly, as shown in the figure.
The frame symmetry in 3D is the focus of our interest. It implies that even if we change the reference frame by moving in different directions or locations, the robot does not need to relearn how to walk or run. The frame symmetry represents the proper transformations of the entire 3D world, represented as , the group of 3D continuous translations and rotations.
However, the robot is subject to external forces that may break symmetry, such as gravity, contact, and actuation forces. Despite these forces, the symmetry can still be maintained if they are included as inputs to the system along with the robot state, during rotation or translation. The network learns from data that has only rotation symmetry along the gravity axis. We include these factors as global features to the geometric graph, which is transformed along with the graph. We explain how to transform the graph and its features in the next section.
3.3 Symmetry in Continuous Control
In this section, we outlines the symmetry under consideration in the continuous control tasks and how we explore that. [ravindran2004algebraic, ravindran_symmetries_nodate, zinkevich_symmetry_2001] explore symmetry in MDPs with no function approximation like neural networks. [van2020mdp, mondal_group_2020] initiate the exploration of symmetry in model-free (deep) RL by using equivariant policy networks. [zhao_integrating_2022] study symmetry in value-based planning on 2D grid. We extend it and focus on MDPs with continuous state and action spaces and sampling-based control/planning algorithms.
Symmetry properties.
The symmetry properties in MDPs are specified by equivariance of the transition and reward functions, studied in zinkevich_symmetry_2001, ravindran2004algebraic, van2020mdp, zhao_integrating_2022:
| (1) | ||||
| (2) |
Note that how the group acts on states and actions is called group representation, and is decided by the space or . zhao_integrating_2022 study path planning and take maps as a part of input. On high level, this takes into consideration all “symmetry breaking” factors, such as obstacles in path planning that are represented by input occupancy maps . In typical continuous control tasks, such as locomotion and manipulation, the symmetry breaking factors include external forces, such as gravity, contact (e.g., with ground), and actuation forces (from control motors).
4 Frame Equivariance in Dynamics Model and Control
Our high-level objective is to investigate the advantages of symmetry structures in dynamic systems for enhancing continuous control and planning. Additionally, we seek to minimize the complexity of task-specific design for symmetry, reducing the barriers to implementing equivariant methods and avoiding any unnecessary burdens.
Overview.
When symmetry presents in the dynamical system, the optimal policy and value functions are also equivariant [ravindran2004algebraic, ravindran_symmetries_nodate, zinkevich_symmetry_2001, van2020mdp]. The existence of symmetry helps shrink the hypothesis spaces and reduced generalization gap. In this section, we propose an approach to make use of symmetry in sampling-based planning methods, such as model predictive control (MPC).
Our formulation is an extension to the prior work on symmetric planning [zhao_integrating_2022], which designs a principled approach to consider discrete symmetry. Specifically, they focus on path planning in 2D discrete grids () with a discrete symmetry group () consisting of rotations and reflections for value-based planning. The key insight is that all functions defined on signals () are steerable by the group. Additionally, equivariant mappings between these signals can be represented as convolutions and other operations (e.g., , , ), which can be implemented using CNNs.
Our work generalizes to 3D continuous space and the continuous symmetry group that contains isometric proper transformations of the 3D space. The robot acts in continuous action space, which necessitates the consideration of sampling-based method.
4.1 Dynamics Model with Equivariance
To use frame equivariance in control, there are three key steps [zhao_integrating_2022]: (1) specify the symmetry group in the system, (2) learn a -equivariant dynamics model , and (3) incorporate symmetry into continuous control. In the second step, using equivariant model induces equivariant Bellman operator: . Albeit the previous two steps are analogous to prior work, the third step is not trivial because of the nature of sampling-based approaches. We explain it in the next subsection.
Since we use graph-based representation of the system, we make use of equivariant message passing networks for implementing the dynamics network. Specifically, we use steerable -equivariant message passing network [brandstetter_geometric_2022]. Compared to using invariant scalar features, steerable networks allow to use higher-order equivariant steerable features, enabling better expressivity. We briefly explain how we use steerable message passing network and specify -representations for state and action features. We omit the details on hidden layers and more.
Group acting on geometric graphs.
In order to understand how the group acts on the states and actions represented by geometric graphs , we discuss the group representations of rotations and translations. We focus on the representations of rotations, . We say a vector is steerable if there exists a matrix that can transform for group elements by . In short, the representations of can be decomposed into irreducible representations, or Wigner-D matrices with dimensions . We say a vector transformed by -th matrix as type- steerable vector. A type- steerable feature is a scalar (trivial representation), and a type- feature is steerable by rotation matrices (standard representation).
The graph nodes are links with features of positions (3D, type- feature), orientations (quaternion, acts by group composition), linear velocity (3D, type- feature), and angular velocity (also 3D vector space, tangent space, type- feature). The edge features include actions, which are typically scalars or type- features. We also include gravity direction as a type- global feature, which is also transformed correspondingly. We also include additional features, computed from quantities like positions and velocities, similar to [brandstetter_geometric_2022].
4.2 Control with Symmetry
In prior work [zhao_integrating_2022], they developed Symmetric Value Iteration Network (SymVIN) for path planning on 2D grid . The network iteratively apply learned Bellman operators to reach a fixed point . Since every step is equivariant, the entire value iteration process is equivariant:
| (3) |
where is the occupancy map and goal input . Since Bellman operators are a sequence of (linear) equivariant operations on steerable signals, the whole process can be implemented using steerable convolution networks [cohen_steerable_2016, weiler_general_2021].
Intuitively, SymVIN relate maps under four discrete rotations and two reflections, so if a map is rotated, it does not need to relearn the optimal plan or actions. Analogously, we aim to develop a control method that considers the frame equivariance of 3D space. One practical setup is locomotion on some terrain. The symmetry of locomotion task is that a robot does not to learn how to walk when facing different directions and locations, while instead share information between all directions and locations of .
Symmetry in MPC. Our goal is to exploit frame symmetry of the underlying space in the planning algorithm. For sampling-based planning, symmetries enable two types of benefits.
-
1.
Forward search. When sampling a trajectory in the ground MDP, we equivariantly know the outcome of all trajectories under symmetries: . This saves computation when the group is “large”. However, while this is important for discrete case, it is negligible for continuous state space.
-
2.
Value backup. Symmetries allow us to reuse knowledge between equivalent state, as and . Intuitively, facing different directions do not change how a robot walks.
In continuous control, the second type of consideration is crucial. Since the optimal policy and value functions are equivariant (or invariant), we constrain the function approximation to be only the set of equivariant functions.
Planning with MPC. We use model predictive control as a sampling-based planning approach for continuous actions. We use MPPI (Model Predictive Path Integral) control method [williams_model_2015, williams_aggressive_2016, williams_model_2017, williams_information_2017], as also done in [hansen_temporal_2022]. We sample trajectories with horizon using the learned dynamics model with actions from a learned policy, and estimate the expectation of total return . Importantly, if we rotate the entire trajectory by , we know the return is invariant since it is a scalar:
| (4) | ||||
| (5) |
We can then update the action selection policy by using top- trajectories, which is a Gaussian distribution with learned mean and variance. To capture the symmetry here, we use equivariant policy network and invariant value network in estimating values and optimal actions.
Benefits of symmetry in continuous control. There are some benefits of explicitly considering symmetry in continuous control. The possibility of hitting orbits is negligible, so there is no need for orbit-search on symmetric states in forward search in continuous control. Additionally, the model predictive control algorithm implicitly plans in a smaller continuous MDP [ravindran2004algebraic]. Furthermore, from equivariant network literature [elesedy_provably_2021], the generalization gap for learned equivariant policy and value networks are smaller, which allows them to generalize better.
5 Discussion
In this work, we provide a principled guideline to consider the continuous frame symmetry in sampling-based planning and control in 3D environments, which extends the prior work of path planning with value-based planning on 2D grid with 2D discrete symmetry. As a working project, we are still working on tuning results for equivariant dynamics and symmetric control methods.
We include some notes on implementation side. For predicting dynamics, we base our code off of brandstetter_geometric_2022 and use a Steerable-E(3)-GNN, which is an E(3)-equivariant message passing network that uses steerable features and also injects additional physical quantities into the node and edge updates. In our Brax environments, the task is to use the current state and action to predict the next state. We modify the original observation and set the state to be each joint’s angular position, orientation, angular velocity, and joint angles and transform them if necessary to all be of type . We use the state as node input features and use the actions as edge features as they act on the nodes. Note that our Brax environments is in 3D, but has some symmetry breaking elements such as gravity and the ground. We thus include gravity and the ground into the state as well in order to make the environment symmetric with respect to E(3). We test on the Brax Ant domain, which contains joints.
Appendix A Outline
Temporary pages for note. Include an outline here.