Screening of nucleon electric dipole moments in atomic systems

The observation of a permanent electric dipole moment (EDM) of an atom implies the existence of parity ($P$) and time-reversal ($T$) violating interactions between constituent particles. The atomic EDM is defined by

where $e$ is the elementary charge and $\bm{r}_{i}^{\prime}$ indicates the coordinates of the atomic electrons. The interaction of the atomic EDM with an external electric field causes an energy shift to be measured [1, 2].

Although the nuclear EDM and the intrinsic EDMs of electrons and nucleons are independently coupled to the external electric field $\bm{E}_{\text{ext}}$ as

they are obscured by the internal interactions with the electrons. Here $\bm{d}^{(e)}_{i}$ and $\bm{d}_{a}$ are the intrinsic EDMs of electrons and nucleons, respectively, and the nuclear EDM is defined by

where $\bm{r}_{a}$ indicates the proton coordinates. In particular, the energy shift due to the EDM of a point-like nucleus is canceled by the contribution from the atomic EDM induced by the internal interaction of the nuclear EDM with the electrons. However, $P$, $T$-odd nucleon-nucleon ($NN$) interactions allow a finite-size nucleus to have the nuclear Schiff moment as well as the nuclear EDM. Since the atomic EDM induced by the interaction of the Schiff moment with the electrons survives the screening, the atomic EDMs particularly of diamagnetic atoms are sensitive to $P$, $T$-odd $NN$ interactions [3, 4, 5, 6]. The screening mechanism of the nuclear EDM induced by the $P$, $T$-odd meson-exchange $NN$ ($\pi NN$) interaction is reviewed in this section.

The Hamiltonian of an atomic system that conserves $P$ and $T$ symmetries is written as

where $H_{\text{nucl}}$ denotes $P$, $T$-even $NN$ interactions. The electron kinetic term $T_{e}$ and the electron-electron interactions $V^{(ee)}$ are not relevant to the nuclear $P$, $T$ violation of interest. The electrostatic interaction between the electrons and the protons is

If $r_{i}^{\prime}>r_{a}$, then each term can be expanded as

The atomic Hamiltonian $H_{\text{atom}}$ does not contain the odd-$l$ electron-nucleon ($eN$) interactions denoted by $V^{(eN)}_{\text{odd}-l}$, which vanish unless $P$ and $T$ symmetries are both violated in the nucleus.

The nuclear ground state in the existence of the $P$, $T$-odd $\pi NN$ interaction $\widetilde{V}_{\pi NN}$ is given by

where $E^{(N)}_{\text{g.s.}}$ and $E^{(N)}_{n}$ denote the energies of the ground state $\big{|}\psi^{(N)}_{\text{g.s.}}\big{\rangle}$ and excited states $\big{|}\psi^{(N)}_{n}\big{\rangle}$ of the nuclear Hamiltonian $H_{\text{nucl}}$, respectively. As well as the atomic EDM is generated by $P$, $T$-violations in the electron system, the $P$, $T$-odd $\pi NN$ interaction can induce the nuclear EDM. The external interaction of the nuclear EDM represented in Fig. 1 causes the energy shift

where the coupling constants $\overline{g}_{\pi NN}$ and $q_{N}$ specify the perturbative interactions.

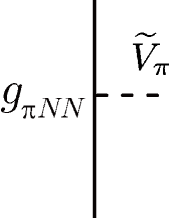
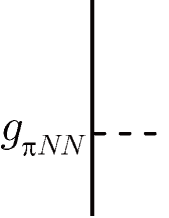
The $P$, $T$-odd $\pi NN$ interaction also induces the odd-$l$ $eN$ interactions $V^{(eN)}_{\text{odd}-l}$, which violate $P$ and $T$ symmetries in the electron system. Consequently, the atomic EDM contributes to the energy shift in third order perturbation as

This process is represented in Fig. 1. The eigenstates of the atomic system in the existence of the $P$, $T$-odd $\pi NN$ interaction are expressed except for the Clebsch-Gordan coefficients as

where $\big{|}\psi^{(e)}_{\text{g.s.}}\big{\rangle}$ and $\big{|}\psi^{(e)}_{m}\big{\rangle}$ denote the ground state and excited states of the electron system described by $H_{e}$ with the energies $E^{(e)}_{\text{g.s.}}$ and $E^{(e)}_{m}$, respectively.

Here I summarize the notations used in this paper. The superscripts $(A)$, $(N)$, and $(e)$ represent the atomic, nuclear, and electron systems, respectively. $P$, $T$-odd interactions and $P$, $T$-violated wave functions are denoted by $\widetilde{V}$ and $\big{|}\widetilde{\psi}\big{\rangle}$, respectively.

The screening of the nuclear EDM is demonstrated by using a Hermitian operator [7]

where

The nuclear EDM interactions in Eqs. (9) and (10) are transformed as

and

The $eN$ interactions of a point-like nucleus consist of the $l=0,1$ components, which are explicitly given by

The last equality in Eq. (16) follows from the fact that the operator $U_{\text{nucl}}$ commutes with the electron kinetic term $T_{e}$ and the interactions between electrons $V^{(ee)}$.

Although the same transformations are realized even if one adopts

instead of $U_{\text{nucl}}$, the resulting nuclear moment is a more complicated two-body operator than the Schiff moment (24).

Using the transformations (15) and (16), the third-order effect (10) is transformed as

where the first term implies the screening of the nuclear EDM. The remaining terms caused by the finite-size effect can be nonzero in the “point-like nucleus limit”, where

Here $R$ is the nuclear radius.

Considering $l\leq 3$, one obtains

where the nuclear part is separated from the electron part as explained in Appendix A. The expectation value of the nuclear Schiff moment is given by

The explicit form of the Schiff moment operator is

where the charge mean values are defined by

and

is the quadrupole moment of proton. Since the $P$, $T$-odd $\pi NN$ interaction is scalar, only the $z$-component $S_{z}$ can have nonzero values. The third term of the Schiff moment operator (24) must vanish in spin $\frac{1}{2}$ nuclei including ¹⁹⁹Hg.

In conclusion of this section, the leading order contribution from the $P$, $T$-odd $\pi NN$ interaction is given by

This result implies that the interaction of the Schiff moment with the electrons denoted by $V_{\text{NSM-1}}$ induces the atomic EDM that survives the screening. The third-order process is illustrated in Fig. 2.

The Schiff moments $S_{1}$ of actinide nuclei would be enhanced thanks to octupole correlations and the parity doubling of the ground states [8]. It is expected from recent nuclear many-body calculations [9, 10, 11, 12] that the Schiff moment of ²²⁵Ra is greater than that of ¹⁹⁹Hg by orders of magnitude, although the uncertainty is still large.

There are several attempts to identify the leading order contribution from the intrinsic EDMs of nucleons to the atomic EDM. In particular, the Schiff moment of ¹⁹⁹Hg that originates from the nucleon EDM was computed in the random phase approximation [13]. Using their result, an upper bound on the neutron EDM was evaluated from the experimental limit on the atomic EDM as $d_{n}<1.6\times 10^{-26}e\text{cm}$ [14, *Graner2017-erratum]. This constraint is competitive with a recent direct measurement $d_{n}<1.8\times 10^{-26}e\text{cm}$ [16]. On the other hand, it was claimed that the nucleon EDMs in a neutral atom are completely screened [17, 18]. In this section, I demonstrate that the screening of the nucleon EDMs is incomplete in the point-like nucleus limit.

Figure 3 represents the direct coupling of the nucleon EDMs to the external electric field. This first-order contribution is given by

where $\bm{d}_{a}$ denotes the nucleon EDMs.

The internal interaction of the nucleon EDMs with the electrons

violate $P$ and $T$ symmetries in the electron system. Thus, the induced atomic EDM contributes to the energy shift in second order perturbation as

This process is represented in Fig. 3. The internal interaction (30), which is expanded for $r_{i}^{\prime}>r_{a}$ as

is restricted to the even-$l$ components because $P$ and $T$ symmetries are not violated in the nuclear system.

The ground state and excited states of the atomic Hamiltonian $H_{\text{atom}}$ without $P$, $T$-odd interactions are expressed as

respectively.

I introduce a Hermitian operator

where in contrast to $\langle\bm{d}_{\text{nucl}}\rangle$ in Eq. (13),

is the expectation value in the ground state of $H_{\text{nucl}}$ conserving $P$ and $T$ symmetries. The external interaction of the nucleon EDMs (29) is transformed as

The $l=0$ component of the internal interaction (30), which is explicitly given by

is transformed as

where $[U_{N},T_{e}]=0$ and $[U_{N},V^{(ee)}]=0$ are used. Substituting (39) into (31), one can find

The right-hand side vanishes for a point-like nucleus, where the $eN$ interactions in Eqs. (6) and (30) are restricted to $l\leq 1$. The complete screening of a point-like nucleus is valid even if the nucleons are relativistic [19].

The remaining second-order process in Eq. (40) is illustrated in Fig. 4. In the point-like nucleus limit, the finite-size effect is given up to $l=2$ by

as derived in Appendix B. The nuclear moment $\bm{S}_{2}$ is also called the Schiff moment, and given by

Using the independent particle model (IPM) [12], one obtains

which is consistent with the previous evaluation [8] $S_{2}\simeq 2.2d_{n}\,(\text{fm}^{2})$. This quantity was calculated as $S_{2}=(1.895\pm 0.035)d_{n}\,(\text{fm}^{2})$ in the random phase approximation [13].

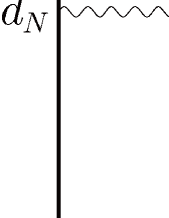
As discussed in Sec. II, the atomic EDM is sensitive to the Schiff moment $S_{2}$, which stems from the screening effect of the nucleon EDMs themselves. In addition to the nucleon EDMs, the nuclear EDM is independently coupled to the external electric field as shown in Eq. (2). The nuclear EDM is induced not only by the $\pi NN$ interaction but also by the interaction between the nucleon EDMs and the protons

A similar argument as in Sec. I shows that this contribution represented in Fig. 5 is screened by the third-order processes represented in Fig. 5. The finite-size effect leads to the next-to-leading order contribution of the nucleon EDM to the Schiff moment

where the operator $\bm{S}_{3}$ is the same as $\bm{S}_{1}$. This correction is evaluated as

in the IPM.

I have examined the screening of the intrinsic EDMs of nucleons and the nuclear EDM in a neutral atom. In the point-like nucleus limit, the Schiff moment of a finite-size nucleus induces the atomic EDM that circumvents the screening. The total Schiff moment is given by

where $S_{2}$ and $S_{3}$ are due to the nucleon EDM. The nucleon EDM contributions provide constraints on the short-range component, whereas the $P$, $T$-odd $\pi NN$ interaction contributes to the nucleon EDM in the leading order chiral perturbation theory [20, *Crewther1980-erratum, 22, 2].

The leading order contribution $S_{2}$ stems from the screening of the nucleon EDMs themselves. The nuclear EDM is induced by the interaction of the nucleon EDMs with the protons as well as the $P$, $T$-odd $\pi NN$ interaction. The screening of the nuclear EDM gives rise to the next-to-leading order contribution to the Schiff moment $S_{3}$. This correction to the Schiff moment of ¹⁹⁹Hg is of the order of $5\%$ in the IPM. Here, nuclear octupole correlations would enhance $S_{3}$ as well as $S_{1}$, which is induced by the $\pi NN$ interaction, by orders of magnitude. Consequently, the dependence of the Schiff moment on the nucleon EDM can be dominated by $S_{3}$ rather than $S_{2}$ in octupole deformed nuclei.