Schwinger Pair Production in QCD from Flavor-Dependent Contact Interaction Model of Quarks
Abstract
We study the Schwinger mechanism in QCD i.e., the quark-antiquark pair production rate in the presence of pure electric field strength , for a higher number of colors and flavors . In this context, our unified formalism is based on the Schwinger-Dyson equations, flavor-dependent symmetry preserving vector-vector contact interaction model of quarks, and an optimal time regularization scheme. For fixed and , the dynamically quark mass decreases as we increase and near at and above the pseudo-critical electric field , the chiral symmetry is restored and quarks becomes unconfined. The pair production rate becomes stable and grows quickly above . For fixed and upon increasing the dynamical mass suppresses and as a result, the reduces to its smaller values, the pair production rate tends to initiates and grows quickly for smaller values of . In contrast, for fixed and upon increasing , the dynamical chiral symmetry is restored for larger and larger values of and at , the transition changes from smooth cross-over to the first order at some critical endpoint (). Consequently, the quark-antiquark production rate needs higher values of for the stable and quick growth as we increase . Our findings are satisfactory and in agreement with already predicted results for pair production rate (for fixed and ) by other reliable effective models of QCD.
Keywords:
Chiral symmetry breaking, confinement, electric field, Schwinger-Dyson equations, QCD phase diagram
1 Introduction
Historically, the phenomenon of electron-positron pair production from a non-perturbative vacuum in the presence of electric field strength (where is an electric charge) was first introduced by Fritz Sauter [1], Heisenberg and Euler [2]. However, the complete theoretical framework provided by Julian Schwinger in the field of quantum electrodynamics (QED) [3], and named after him as the Schwinger effect or Schwinger mechanism. Later on, this phenomenon has been widely studied in the field of quantum chromodynamics (QCD), see for example, Refs. [4, 5, 6, 7, 8]. As we know that the QCD is a theory of strong color force among the quarks and gluons possess two special properties: The asymptotic freedom (i.e., the quarks interacts weakly
at a short distancesor high energy scale) and the quark confinement
(i.e., the quarks interacts strongly at a large distance or low energy scale).
The Schwinger effect in QCD is thus, the production of quark-antiquark pairs in the presence of a strong electric field . The quark-antiquark pair production can be calculated from the Schwinger pair production rate and is, defined as the probability, per unit time and per unit
volume that a quark-antiquark pair is created by the constant electric
field .
Another important property of low-energy QCD is
the dynamical chiral symmetry breaking, which is related to the dynamical mass generation of the quarks. The strong electric field tends to restore the dynamical chiral symmetry and as a result, the dynamically generated quark mass suppresses with the increase of . It can be understood by realizing that being closer together, the quark and antiquark pairs are reaching the asymptotic freedom regime faster by reducing the interaction strength as the intensity of the electric field increases. Such a phenomenon is sometimes referred to as the chiral electric inhibition effect [9, 6, 10, 11, 12, 13, 14], or the chiral electric rotation effect [15] or inverse electric catalysis(IEC) [16, 17, 18]. The nature of the dynamical chiral symmetry breaking–restoration and confinement–deconfinement phase transition is of second-order when the bare quark mass (i.e., in the chiral limit) while cross-over when . It has been argued in Refs. [13, 14, 17] that the pair production rate , increases quickly near some pseudo-critical electric field , where the chiral symmetry is restored.
The study of the effect of the electric field on the chiral phase transition plays a significant role in Heavy-Ion Collision experiments. In such experiments, the magnitude of the electric and magnetic fields produced with the same order of magnitude ( to Gauss) [19, 20, 21, 22] in the event-by-event collisions using Au Au at RHIC-BNL, and in a non-central Heavy-Ion collision of Pb Pb in ALICE-LHC. Besides, experiments with asymmetric
Cu Au collisions, it is believed that the strong
electric field is supposed to be created in the overlapping region [23, 24, 25]. It happens because there are different numbers
of electric charges in each nuclei, which may be
due to the charge dipole formed in
the early stage of the collision. Some other phenomena like the chiral electric separation effect [26, 27], the particle polarization effect [28, 29, 30], etc., which may emerge due to the generation of vector and/or axial current in the presence of strong electromagnetic fields.
It is illustrative to approximate the created number of
charged quark-antiquark pairs in the
QGP produces in Heavy Ion collision, because in the QGP phase the dynamical chirl symmetry restores and the deconfinement occurs.
According to advance numerical
simulations, the electric fields created in Au Au
collisions at center-of-mass energy GeV
due to the fluctuation is of
the order
while in PbPb collisions at
TeV is of the order
[20]. Then by assuming
the space-time volume of the QGP is of the order ,
the total pair creation number is , and [31], gives us a clear indication of the importance of Schwinger pair production of quark
and antiquark in Heavy Ion Collisions.
It is well understood that the QCD exhibits confinement and chiral symmetry breaking with
the small number of light quark
flavors . However, for larger
, Lattice QCD simulation [32, 33, 34, 35, 36],
as well as the continuum methods of QCD [37, 38, 39, 40, 41, 42, 18, 43], predicted that there is a critical value
above which the chiral symmetry is restored and quarks become
unconfined. It has been discussed in detail in Ref. [18] that the critical number of flavors suppresses with the increase of temperature and enhances with the increasing magnetic field . Even the QCD phase diagram at finite temperature and density suppresses with the increase of light quark flavors, see for an instance Ref. [42]. Besides the higher number of light quark flavors, QCD with a larger number of colors in the
fundamental representation also plays a significant role. It has been demonstrated in Ref. [18, 42] that the
chiral symmetry is dynamically broken above a critical value , as a result, the dynamically generated mass increases
near and above . Increasing the number of colors also enhances the critical temperature and the critical chemical potential of the chiral phase transition in the QCD phase diagram [18]. Both and magnetic field strengthen the generation of the dynamical masses of the quarks
[42].
It will be more significant to study the dynamical chiral symmetry breaking and Schwinger effect in pure electric field background for a higher number of light quark flavors and for a large number of colors , which has not yet been studied so far, as far as we know. It may have a stronger impact not only on the theoretical ground but also in Heavy-Ion Collision experiments where a large number of light flavors of quark-antiquark pairs are produced.
Our main objective of this work is to study the quark-antiquark pair production rate in the presence of a pure electric field background for a higher number of light quark flavors and colors . For this purpose, we use the Schwinger-Dyson equation in the rainbow-ladder truncation, in the Landau gauge, the symmetry preserving flavour-dependent confining vector-vector contact interaction model of quarks [18],
and the Schwinger optimal time regularization scheme [3]. The pseudo-critical electrical field strength , the critical number of flavors and the critical number of colors for chiral symmetry breaking-restoration can be obtained from the peak of the correspondence gradient of dynamical quark mass, whereas the confinement-deconfinement can be triggered from the peaks of correspondence gradient of the confining length scale [44, 18, 42]. It
should be noted that the chiral symmetry restoration and
deconfinement occur simultaneously in this model [45, 44, 18, 42].
This manuscript is organized as follows: In Sec. 2, we present the general formalism for the flavor-dependent contact interaction model and QCD gap equation. In Sec. 3, We discuss the gap equation and the the Schwinger pair production rate in the presence of electric field for a large number of flavors and colors . In Sec. 4, we present the numerical solution of the gap equation and the Schwinger pair production rate in the presence of for a higher number of and . In the last Sec. 5, we present the summary and future perspective of our work.
2 General formalism and flavor-dependent Contact Interaction model
The Schwinger-Dyson equations (SDE) for the dressed-quark propagator , is given by:
| (1) |
where , is the bare quark propagator and is the dressed quark propagator. The is the self energy and is given by
| (2) |
where is the dressed quark-gluon vertex and is the QCD coupling constant. The is the gluon propagator in the Landau gauge with is the metric tensor in Euclidean space, is the gluon scalar function and is the gluon four momentum. The is the current quark mass, which may set equal to zero (i.e., ) in the chiral limit. The ’s are the Gell-Mann matrices and in the representation, the Gell-Mann’s matrices satisfies the following identity:
| (3) |
here is the unit matrix. In this work, we use the symmetry preserving flavor-dependent confining contact interaction model [42, 43] for the gluon propagator (in Landau gauge) in the infrared region where the gluons dynamically acquire a mass [46, 47, 48, 49, 50], is given by
| (4) |
the is the infrared enhanced interaction strength parameter, MeV is the gluon mass scale [51]. The is some guess values of critical number of
flavors. In Ref. [42, 43], the value of has been set and it ranging from , to obtained the desired number of critical number above which the dynamical symmetry restored and deconfinement occurred. It has been
argued in the Ref. [42] that the appearance of the parameter is
because of the factor in Eq. (4).
With a particular choice of the flavor-dependent model Eq. (4), the dynamical quark mass function is merely a constant and the
the dressed quark propagator takes
into a very simple form [52]:
| (5) |
It is because the wave function renormalization trivially tends to unity in this case, and the quark mass function become momentum independent:
| (6) |
Where is the dynamical mass and . After simplifying Eq. (6), we have
| (7) |
The quark-anitquark condensate which serves as an order parameter for the dynamical chiral symmetry breaking in this truncation, can be written as
| (8) |
Using , performing the trivial integration’s and using the variable in Eq. (7), we have
| (9) |
The above integral in Eq. (9) is divergent and we need to regularize it. In the present scenario we use the Schwinger proper-time regularization procedure [3]. In this procedure, we take the exponent integrand’s denominator and then introduce an additional infrared cutoff, in addition to the conventional ultraviolet that is normally used in NJL model Studies. Accordingly, the confinement is implemented through an infrared cut-off [53]. The significance of adopting the mentioned regularization procedure is, the quadratic and logarithmic divergences remove and the axial-vector Ward-Takahashi identity [54, 55] is satisfied. From Eq. (9), the integrand’s denominator reduced to:
| (10) | |||||
Here, is an ultra-violet regulator, which plays the dynamical role and sets the scale for all dimensional quantities.
The stands for the infrared regulator whose non zero value implements confinement by ensuring the absence of quarks production thresholds [56]. Hence referred to as the confinement scale [44]. From Eq. (10), it is now clear that the location of the original pole is at , which is canceled by the numerator.
Thus the propagator is free from real as well as the complex poles, which is consistent with the definition of confinement i.e., “an excitation
described by a pole-less propagator would never reach its
mass-shell” [53].
After integration over ‘s’, the gap equation Eq. (9) is reduced to:
| (11) |
where
| (12) |
with , is the incomplete Gamma function. The above equation Eq. (11), is the gap equation in vacuum which is regularized in the Schwinger proper time regularization scheme with two regulators. The confinement in this model can be triggered from the confining length scale [44, 18, 42]:
| (13) |
where is the dynamical mass for fixed , . Here is the generalized color and flavor dependent dynamical mass. As, the is introduced in the
model to mimic confinement by ensuring the absence of quarks production thresholds, so in the presence of and , it
is required to vary slightly with both and . Thus the entanglement between dynamical chiral symmetry breaking and confinement is expressed through an explicit and -dependent regulator i.e., , in the infrared.
For chiral quarks (i.e., ), the confining scale diverges at the chiral symmetry restoration region.
Next we discuss the general formalism of the gap equation and the Schwinger pair production rate in the in the presence of electric field and in the presence of electric field and for higher and .
3 Gap equation and Schwinger pair production rate in the presence of electric field
In this section, we discuss the gap equation in the presence of a uniform and homogeneous pure electric field . In QCD Lagrangian, the interaction with pure electric field embedded in the covariant derivative,
| (14) |
with is refers to the electric charges of and -quark, respectively. We choose the symmetric gauge vector potential , to obtain the resulting electric field along the z-axis. The gap equation in the presence of pure electric field continues to form Eq. (6), where is now dressed with electric field , that is, [3, 11, 13, 15, 57], and is given as
| (15) |
Where ’s are the Dirac gamma matrices. Taking the trace “Tr” of the of the propagator Eq. (15), inserting it in Eq. (6) and after carrying out the the integration over ’s, the gap equation in the electric field and with the flavor-dependent contact interaction model of quark [42] is given by
| (16) |
Next, we separate the vacuum and electric field dependent part by using the vacuum subtraction scheme[11, 13], as given by
| (17) | |||||
The vacuum integral can be regularized with the two regulators as in Eq. (11), and thus the Eq. (17) can be reduced to:
| (18) | |||||
The Eq. (18) can also be written as
| (19) | |||||
As we have already regularized the integral in Eq. (18), using the vacuum subtraction scheme but we still have poles associated with the tangent term in the denominator of our gap equation when with . Upon taking the principle value (real value) of the integral [11], given in Eq. (19), we have
| (20) |
with
| (21) |
The effective potential , can be obtained by integrating the Eq. (19) over dynamical mass :
| (22) | |||||
We noted that there are infinite poles in the effective potential too which are due to the contribution of the Schwinger pair production in the presence of the tangent (electric field-related) term . These poles yields the effective potential to be complex with its imaginary part giving the Schwinger pair production rate [3, 16, 13, 14]. The third term in the Eq. (22) can be further simplified by using the following trigonometric relation:
| (23) |
Using Eq. (23) in Eq. (23), we have
| (24) | |||||
The Schwinger pair production rate , corresponds to the imaginary part of the effective potential Eq. (24), and is thus, given by
| (25) |
which does not depend on the number of color or the number of flavors explicitly. However, since the dynamical quark mass depends on both and as it is obvious from the gap equation Eq. (17), they will affect the quark-antiquark pair production rate implicitly through . The numerical solution of the gap equation and the Schwinger pair production rate will be discussed in the next section.
4 Numerical Results
In this section, we present the numerical results of the gap equation at zero electric field and in the presence of electric field for higher and . We use the following set of flavor-dependent contact interaction model parameters [42] i.e., , ,
and bare quark mass GeV. For fixed and , we have obtained the dynamical mass GeV and the
condensate GeV3. It should be noted that these parameters were fitted to reproduce the light mesons properties [49].
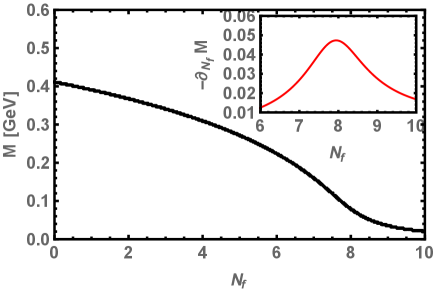
Next, we solve the gap equation Eq.(11) for various and at fix as shown in the Fig. 1. The dynamical mass monotonically decreases as we increase the as depicted in Fig. 1(a). The plot inside the Fig. 1(a), represents the flavor-gradient of the dynamical mass , whose peak is at , which is a critical number of flavors where near and above the dynamical chiral symmetry restored. In Fig. 1(b), we show the dynamical mass as a function of the number of colors for fix . This plot represents that the dynamical chiral symmetry broken near or above some critical value of . The is obtained from the peak of the color-gradient of the mass function . These findings are consistent with results obtained in [42, 43].
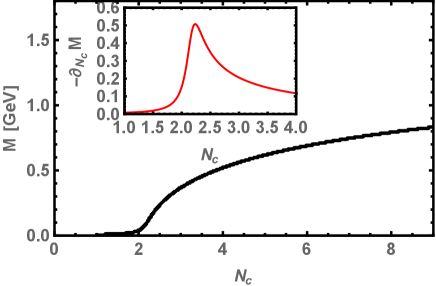
(6(b)) The behavior of the dynamical quark mass and its color-gradient as a function of number of colors and for fixed . From the peak of the , it is clear that the dynamical chiral symmetry is broken above .
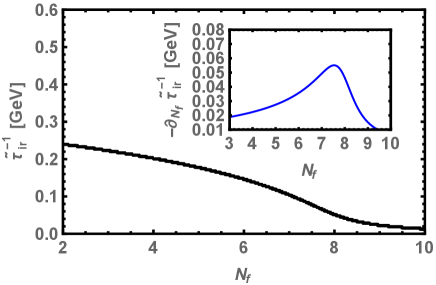
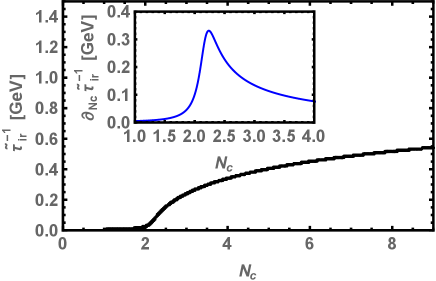
The inverse of the confining length scale and its flavor-gradient plotted for various and for fixed are plotted in Fig. 2(a). The confinement can be triggered from flavor-gradient , whose peak is at , and is approximated as a critical number of flavors above which the quark become unconfined. In Fig. 2(b), we show the inverse confining length scale as a function of the various number of colors for fix . This plot represents that the confinement occurs near and above at some critical value of . The critical for the confinement is obtained from the peak of the color gradient .
Next, we solve the gap equation Eq. (17), in the presence of electric field and plotted the dynamical mass as a function of , for the various number of flavors and for fix as depicted in Fig. 3(a). The dynamical mass decreases as we increase the electric field as we expected. Upon increasing the , the plateau of dynamical quark mass as a function of suppresses for larger values of . There is no dynamical mass generation above , this is because both electric field and restore the dynamical chiral symmetry and quarks becomes unconfined.
In Fig. 3(b), we plotted the dynamical quark mass as a function of electric field strength for various and for fixed . The increasing enhances the plateau of the dynamical mass as a function of . For , the mass plots show the discontinuities in the dynamical symmetry restoration region where the nature of smooth cross-over phase transition changes to the first order. This may be due to the strong competition that occurs between and (i.e. strong electric field tends to restore the dynamical chiral symmetry whereas larger enhance the dynamical chiral symmetry breaking.
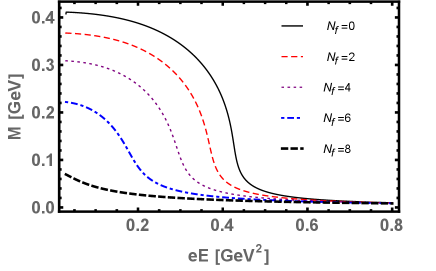
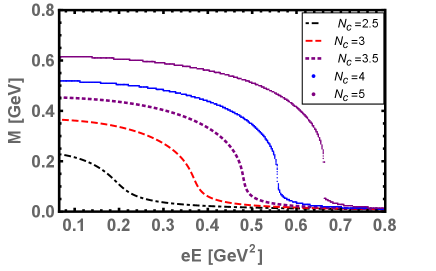
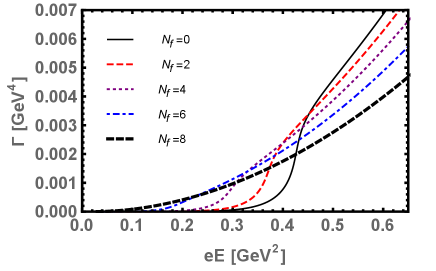
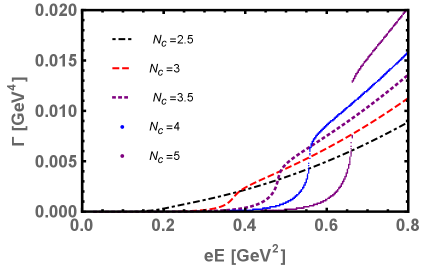
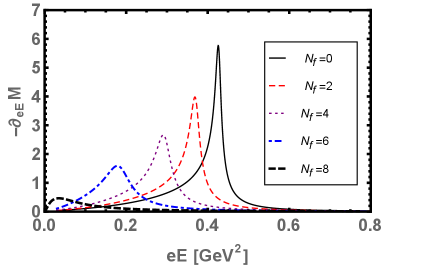
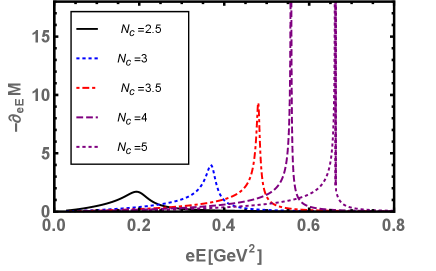
The Schwinger pair production rate “” Eq. (25), as a function of electric field strength , for various and for fix is shown in the Fig. 4(a). This figure clearly demonstrate that after some critical value , where near at and above the dynamical symmetry restored and the deconfinement occurred, the pair production rate “” grows faster due to the weakening of the chiral condensates. In this situation, the QCD vacuum becomes more unstable and the pair of quark-antiquark becomes more likely to produces. Upon increasing the number of flavors , the pair production rate grows faster and shifted towards the lower values of electric field . This is because, both the and restore the dynamical chiral symmetry. Although, there is an unstable slow enhancement of pair production rate for small but become stable and faster for higher values of In Fig. 4(b), we plotted the quark-antiquark pair production rate“” as a function of for various but at this time we fix the number of flavors . Upon increasing the number of colors , the production rate grows slowly and higher values of are needed for a stable and faster production rate. This is because, enhances the dynamical chiral symmetry breaking. For , the discontinuity occurs in the production rate near and above the chiral symmetry restoration and deconfinement region. This may be due to the strong competition between and , i.e., on one hand, the strong electric field tends to restore the dynamical chiral symmetry whereas the tends to break it.
We then obtained the pseudo-critical electric field for the chiral symmetry breaking -restoration from the electric field-gradient as a function of for various and at fixed , as depicted in Fig. 5(a). The peaks of the shift towards lower values of the electric field . In Fig. 5(b), we plotted the electric field gradient as a function of for various and at fixed . Upon increasing , the peaks shift towards higher values of .
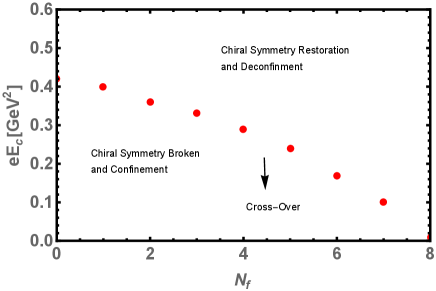
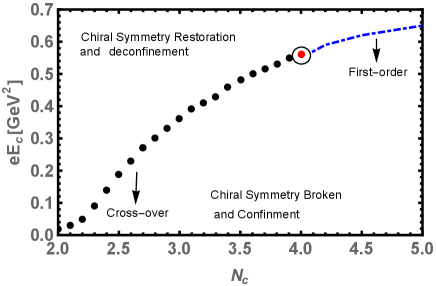
We then obtained the pseudo-critical electric field for the chiral symmetry restoration/deconfinement different , and draw a phase diagram in plane a shown in the Fig. 6(a). The pseudo-critical electric field decreases as we increase , the nature of the chiral phase transition is of smooth cross-over. In Fig. 6(b), we sketch the phase diagram in plane, the critical grows upon increasing the number of colors . The transition is of smooth cross-over until the critical endpoint where it suddenly changes to the first-order. The phase diagram also shows that the quark-antiquark pair production grows quickly after pseudo-critical electric field and how it varies with the flavors and colors. Our finding for and , agrees well with the growth of the quark-antiquark production rate studied through another effective model of low energy QCD [31, 14].
In the next section, we discuss the summery and future perspectives of the this work.
5 Summery and Perspectives
In this work, we have studied the impact of
pure electric
field on the color-flavor chiral phase transitions and investigated the Schwinger quark-antiquark pair production rate for the higher number of colors and number flavors . For this purpose, we
implemented the Schwinger-Dyson formulation of QCD,
with a gap equation kernel comprising a symmetry-preserving
vector-vector flavor-dependent contact interaction model of quarks
in a rainbow-ladder truncation. Subsequently, we adopted
the well-known Schwinger proper-time regularization
procedure. The outcome of this study is presented as
follows:
First, we reproduced the results of dynamical chiral symmetry restoration for large with fixed , where we evaluated the critical number of flavors . Further, we explore the dynamical symmetry breaking for a higher number of colors but kept and found the critical number of colors .
Second, we consider the influence of the pure electric field , where we have explored the dynamical chiral symmetry restoration and deconfinement for various numbers of flavors and colors . The plateau of the mass as a function of the electric field is noted to suppress upon increasing the number of flavors. Whereas upon increasing the number of colors, the dynamical mass as a function of enhances and at some , we found the discontinuity in the chiral symmetry restoration region.
Next, We obtained the Schwinger pair production (quark-antiquark) rate as a function of the pure electric field for various and . For fixed , and upon varying the , we found that quark-antiquark production rate grows quickly
when we cross a pseudo-critical electric field . As a result, the
pair production rate
tends to initiates at lower values of for larger values of . Hence, the pseudo-critical electric field reduced in magnitude upon increasing the number of flavors . This is because both and restored the dynamical chiral symmetry. While for fixed and upon increasing , the Schwinger pair production
tends to initiate at larger values of for higher values of . It is interesting to note that for , the discontinuity occurred in the production rate in the region where the chiral symmetry is restored. This may be due to the strong competition that occurred between and . Thus, the pseudo-critical enhances as the number of colors increases. The transition is of smooth cross-over until the critical endpoint , where it suddenly changes to the first order. Our finding for and agrees well with the behaviour of the pair production rate studied through other effective models of low energy QCD.
Qualitatively and quantitatively, the predictions of the
presented flavor-dependent contact interaction model for fixed and agree well with results obtained from
other effective QCD models. Soon, we plan to extend this
work to study the Schwinger pair production rate in hot and dense matter QCD in the presence of background fields. We are also interested in extending this work
to study the properties of light hadrons in the
background fields etc.
6 Acknowledgments
We acknowledge A. Bashir and A. Raya for their guidance and valuable suggestions in the process of completion of this work. We also thank to the colleagues of the Institute of Physics, Gomal University (Pakistan).
References
References
- [1] Sauter F 1931 Z. Phys. 69 742–764
- [2] Heisenberg W and Euler H 1936 Z. Phys. 98 714–732 (Preprint physics/0605038)
- [3] Schwinger J S 1951 Phys. Rev. 82 664–679
- [4] Yildiz A and Cox P H 1980 Phys. Rev. D 21 1095
- [5] Cox P H and Yildiz A 1985 Phys. Rev. D 32 819–820
- [6] Suganuma H and Tatsumi T 1991 Annals Phys. 208 470–508
- [7] Suganuma H and Tatsumi T 1993 Prog. Theor. Phys. 90 379–404
- [8] Tanji N 2009 Annals Phys. 324 1691–1736 (Preprint 0810.4429)
- [9] Klevansky S P and Lemmer R H 1988 Phys. Rev. D38 3559–3565
- [10] Klimenko K G 1992 Theor. Math. Phys. 90 1–6 [Teor. Mat. Fiz.90,3(1992)]
- [11] Klevansky S P 1992 Rev. Mod. Phys. 64 649–708
- [12] Babansky A Yu, Gorbar E V and Shchepanyuk G V 1998 Phys. Lett. B419 272–278 (Preprint hep-th/9705218)
- [13] Cao G and Huang X G 2016 Phys. Rev. D 93 016007 (Preprint 1510.05125)
- [14] Tavares W R and Avancini S S 2018 Phys. Rev. D 97 094001 (Preprint 1801.10566)
- [15] Wang L and Cao G 2018 Phys. Rev. D97 034014 (Preprint 1712.09780)
- [16] Ruggieri M and Peng G X 2016 Phys. Rev. D93 094021 (Preprint 1602.08994)
- [17] Tavares W R, Farias R L S and Avancini S S 2020 Phys. Rev. D 101 016017 (Preprint 1912.00305)
- [18] Ahmad A 2021 Chin. Phys. C 45 073109 (Preprint 2009.09482)
- [19] Bzdak A and Skokov V 2012 Phys. Lett. B710 171–174 (Preprint 1111.1949)
- [20] Deng W T and Huang X G 2012 Phys. Rev. C 85 044907 (Preprint 1201.5108)
- [21] Bloczynski J, Huang X G, Zhang X and Liao J 2013 Phys. Lett. B718 1529–1535 (Preprint 1209.6594)
- [22] Bloczynski J, Huang X G, Zhang X and Liao J 2015 Nucl. Phys. A939 85–100 (Preprint 1311.5451)
- [23] Hirono Y, Hongo M and Hirano T 2014 Phys. Rev. C 90 021903 (Preprint 1211.1114)
- [24] Voronyuk V, Toneev V D, Voloshin S A and Cassing W 2014 Phys. Rev. C 90 064903 (Preprint 1410.1402)
- [25] Deng W T and Huang X G 2015 Phys. Lett. B 742 296–302 (Preprint 1411.2733)
- [26] Huang X G and Liao J 2013 Phys. Rev. Lett. 110 232302 (Preprint 1303.7192)
- [27] Jiang Y, Huang X G and Liao J 2015 Phys. Rev. D91 045001 (Preprint 1409.6395)
- [28] Karpenko I and Becattini F 2017 Eur. Phys. J. C77 213 (Preprint 1610.04717)
- [29] Xia X L, Li H, Tang Z B and Wang Q 2018 Phys. Rev. C98 024905 (Preprint 1803.00867)
- [30] Wei D X, Deng W T and Huang X G 2019 Phys. Rev. C99 014905 (Preprint 1810.00151)
- [31] Cao G and Zhuang P 2015 Phys. Rev. D 92 105030 (Preprint 1505.05307)
- [32] Appelquist T et al. (LSD) 2014 Phys. Rev. D 90 114502 (Preprint 1405.4752)
- [33] Hayakawa M, Ishikawa K I, Osaki Y, Takeda S, Uno S and Yamada N 2011 Phys. Rev. D 83 074509 (Preprint 1011.2577)
- [34] Cheng A, Hasenfratz A, Petropoulos G and Schaich D 2013 JHEP 07 061 (Preprint 1301.1355)
- [35] Hasenfratz A and Schaich D 2018 JHEP 02 132 (Preprint 1610.10004)
- [36] Appelquist T et al. (Lattice Strong Dynamics) 2019 Phys. Rev. D 99 014509 (Preprint 1807.08411)
- [37] Bashir A, Raya A and Rodriguez-Quintero J 2013 Physical Review D 88 054003
- [38] Appelquist T, Cohen A G and Schmaltz M 1999 Phys. Rev. D 60 045003 (Preprint hep-th/9901109)
- [39] Hopfer M, Fischer C S and Alkofer R 2014 JHEP 11 035 (Preprint 1405.7031)
- [40] Doff A and Natale A A 2016 Phys. Rev. D 94 076005 (Preprint 1610.02564)
- [41] Binosi D, Roberts C D and Rodriguez-Quintero J 2017 Phys. Rev. D 95 114009 (Preprint 1611.03523)
- [42] Ahmad A, Bashir A, Bedolla M A and Cobos-Martínez J J 2021 J. Phys. G 48 075002 (Preprint 2008.03847)
- [43] Ahmad A and Murad A 2022 Chin. Phys. C 46 083109 (Preprint 2201.09980)
- [44] Ahmad A and Raya A 2016 J. Phys. G43 065002 (Preprint 1602.06448)
- [45] Marquez F, Ahmad A, Buballa M and Raya A 2015 Phys. Lett. B747 529–535 (Preprint 1504.06730)
- [46] Langfeld K, Kettner C and Reinhardt H 1996 Nucl. Phys. A 608 331–355 (Preprint hep-ph/9603264)
- [47] Cornwall J M 1982 Phys. Rev. D 26 1453
- [48] Aguilar A C, Binosi D and Papavassiliou J 2016 Front. Phys. (Beijing) 11 111203 (Preprint 1511.08361)
- [49] Gutierrez-Guerrero L X, Bashir A, Cloet I C and Roberts C D 2010 Phys. Rev. C81 065202 (Preprint 1002.1968)
- [50] Kohyama H 2016 (Preprint 1602.09056)
- [51] Boucaud P, Leroy J P, Yaouanc A L, Micheli J, Pene O and Rodriguez-Quintero J 2012 Few Body Syst. 53 387–436 (Preprint 1109.1936)
- [52] Ahmad A, Ayala A, Bashir A, Gutiérrez E and Raya A 2015 J. Phys. Conf. Ser. 651 012018
- [53] Ebert D, Feldmann T and Reinhardt H 1996 Phys. Lett. B388 154–160 (Preprint hep-ph/9608223)
- [54] Ward J C 1950 Phys. Rev. 78 182
- [55] Takahashi Y 1957 Nuovo Cim. 6 371
- [56] Roberts C D, Bhagwat M S, Holl A and Wright S V 2007 Eur. Phys. J. ST 140 53–116 (Preprint 0802.0217)
- [57] Cao G 2021 Eur. Phys. J. A 57 264 (Preprint 2103.00456)