Scattering of low energy neutrinos and antineutrinos by neon and argon

There is significant interest in the low energy O(10 keV) scattering of electron neutrinos and antineutrinos by atomic electrons

for which the binding of the atomic electron cannot be ignored and one can expect modifications of the free electron scattering formulae. One example is the study of possible electromagnetic properties of neutrinos, such as magnetic and electric dipole moments, using low energy scattering of neutrinos and antineutrinos [1, 2]. For a review of neutrino-atom collisions, see [3].

Of particular interest is the ionization of atoms by neutrinos and antineutrinos. Ionization cross sections calculated for H, He and Ne were found [4] to be smaller than the corresponding free electron cross sections, and the calculations were then extended [5] to the electron spectra for H, He and Ne, and integrated ionization cross sections for H, He, Ne and Xe.

These calculations treat the $\nu_{e}$-electron scattering process as a probability weighted scattering by a free electron of mass $\tilde{m}$, where

$E_{e_{i}}=m_{e}+\epsilon$ is the energy of the initial bound electron, where $\epsilon$ is the binding energy, and the momentum $\mathbf{p}_{e_{i}}$ is determined by the probability amplitude $|\Psi_{n_{i}l_{i}m_{i}}(\mathbf{p}_{e_{i}})|^{2}$, where $\Psi_{n_{i}l_{i}m_{i}}(\mathbf{p}_{e_{i}})$ is the momentum-space atomic wave function. Spin-independent non-relativistic atomic wave functions are used for the initial electron and Coulombic effects on the final electron are ignored. These calculations destroy the relationship between the neutrino helicities and the orbital and spin angular momenta of the atomic electrons. Some of these issues have been addressed by [6, 7, 8] and their approach is closest in spirit to the present calculations.

The theory of scattering of neutrinos and antineutrinos by bound electrons which maintains the full collision dynamics has recently been developed [9]. The scattering is formulated in configuation space using the Bound Interaction Picture [10, 11], rather than the usual formulation in the Interaction Picture in momentum space as appropriate to scattering by free electrons. The energy spectra of ionization electrons produced by scattering of neutrinos and antineutrinos with energies of 5, 10, 20, and 30 keV by hydrogen, helium and neon were calculated using Dirac screened Coulombic eigenfunctions. The results were significantly different to those of [5] and indicated that binding effects from both the initial bound state and the final continuum state are important.

Very recently, a second quantization formalism has been developed [12] to include atomic effects in the electron recoil signal for dark matter or neutrino scattering. Although the neutrino scattering amplitude includes more general interactions than the $W$- and $Z$- exchange of the Standard Model, the formalism treats the atomic electrons as non-relativistic and includes the electron spin through a non-relativistic approximation to the four-component Dirac eigenfunction which ignores coupling between the spin and orbital angular momenta.

This paper reports further applications of the Bound Interaction Picture theory [9], to a new calculation of the energy spectra for neon, as the original calculation used some screening constants which underestimated the effects of screening in the inner subshells, and to scattering by argon as it is the basis of current and near-future experiments sensitive to neutrino-electron scattering.

The general formalism for the scattering of neutrinos and antineutrinos by atomic electrons is summarized in Sec. II, and the radial matrix elements which occur in the atomic electron scattering tensor discussed in Sec. III. Results for the energy spectra of the ionization electrons produced in scattering from neon and argon are presented and discussed in Sec. IV, and Sec. V contains a summary and conclusions for the investigation.

The scattering of neutrinos by atomic electrons involves both $W$- and $Z$- boson exchange. The total $S$-matrix in the Bound Interaction Picture for $\nu_{e}$ scattering at low momentum transfers $k^{2}\ll M_{A}^{2}$, where $A=W,Z$, is [9]

where the atomic electron scattering amplitude is

the quantity

incorporates energy conservation, $\mathbf{q}=\mathbf{p}_{\nu_{i}}-\mathbf{p}_{\nu_{f}}$ is the momentum transfer from the neutrino, and

is the neutrino scattering amplitude. Here $\phi^{(+)}_{n}(\mathbf{x})$ is the positive energy eigenfunction for an electron in a state of the external field $A^{(\mathrm{ext})}$ specified by the quantum numbers $n$, and $u^{(s)}(\mathbf{p}_{\nu})$ are the plane wave spinors describing a neutrino with momentum $\mathbf{p}_{\nu}$ and helicity $s$. The natural unit system $\hbar=c=1$ is used throughout, the scalar product of two 4-vectors is $A\cdot B\equiv g^{\alpha\beta}A_{\alpha}B_{\beta}=A_{0}B_{0}-\mathbf{A}\cdot\mathbf{B}$, the Dirac matrices $\gamma^{\alpha},(\alpha=0,1,2,3)$ satisfy $\{\gamma^{\alpha},\gamma^{\beta}\}=2g^{\alpha\beta}$, and $\gamma_{5}\equiv i\gamma^{0}\gamma^{1}\gamma^{2}\gamma^{3}$.

The electron mixing parameters are

where

and $\theta_{W}$ is the weak mixing angle.

For scattering of antineutrinos, $M^{(\nu)}$ is replaced by

where $v^{(s)}(\mathbf{p}_{\nu})$ is the antineutrino plane wave spinor, and $\delta(E_{fi}^{(\nu)})$ is replaced by $\delta(E_{fi}^{(\bar{\nu})})$.

We assume the atomic electron moves in a spherically symmetric potential $V(r)=eA^{(\mathrm{ext})}(r)$, for which the Dirac equation has eigenfunctions of the form [13]

where $(r,\theta,\varphi)=(r,\Omega)$ are spherical polar coordinates, and $\chi^{\mu}_{\kappa}(\Omega)$ are the spinor spherical harmonics

Here $C(j_{1},j_{2},j_{3},m_{1},m_{2},m_{3})$ is a Clebsch-Gordon coefficient, and $\chi_{m_{s}}$ are the two component Pauli spinors. The total angular momentum $j$ and orbital angular momentum $l_{\kappa}$ are obtained from the quantum number $\kappa$ by

where $\kappa$ takes all non-zero integral values. The radial functions satisfy

The energy spectrum of the ionized electrons is [9]

where

and it is understood that $E_{\nu_{f}}=E_{i}+E_{\nu_{i}}-E_{f}$. The neutrino scattering tensor is

where $s_{i}=s_{f}=-1/2$. The atomic electron scattering tensor is

where $\tilde{\mathbf{q}}\equiv(0,0,q)$ and $q\equiv|\mathbf{q}|$. The quantities $L^{\beta\alpha}_{v_{e}v_{e}}$, etc involve [9] various angular momentum coupling coefficients and the radial integrals

The scattering of antineutrinos involves

where $v^{(s)}(\mathbf{p}_{\nu})$ is the antineutrino plane wave spinor, and $s_{i}=s_{f}=+1/2$.

The radial integrals (II) involve the Dirac radial functions $g_{\kappa,E}(r)$ and $f_{\kappa,E}(r)$ for the initial bound electron and the final continuum electron. We assume a potential of a Coulombic form $V(r)=-\alpha Z_{\mathrm{eff}}/r$, where $Z_{\mathrm{eff}}$ is an effective nuclear charge. The radial Dirac equations (13) then have analytic solutions [13] in terms of confluent hypergeometric functions ${}_{1}F_{1}(a,c,z)$.

As scattering by electrons in the ground states of Ne and Ar involve only K-, L- and M- shell electrons, we can use the simplified expressions [13, 14]

where

and the initial state energy $E_{i}$ is

The dimensionless coefficients $(c_{i},a_{i},N_{i})$ for the K-shell ($n=1,\kappa_{i}=-1$), L_I - subshell ($n=2,\kappa_{i}=-1$), L_II -subshell ($n=2,\kappa_{i}=+1$), L_III -subshell ($n=2,\kappa_{i}=-2$), M_I - subshell ($n=3,\kappa_{i}=-1$), M_II -subshell ($n=3,\kappa_{i}=+1$), and M_III -subshell ($n=3,\kappa_{i}=-2$) are listed in Table I.

The screening effects of the electrons in the filled K- shell, L-subshells and M-subshells are represented by an effective nuclear charge of the form $Z_{\mathrm{eff}}=Z-s_{i}$, a procedure that should be reasonable for small principal quantum number $n$ and small $n-l$ [15]. These screening constants $s_{i}$ are taken from the fits [16] of Dirac single electron eigenfunctions to empirical binding energies. For neon, they are 2.016 (K-shell), 6.254 (L_I -subshell), and 7.482 (L_II- and L_III- subshells). For argon, the constants are 2.721 (K-shell), 8.248 (L_I -subshell), 9.470 (L_II- and L_III- subshells), 13.603 (M_I -subshell), and 14.771 (M_II- and M_III- subshells).

The final electron continuum states involve the hypergeometric function ${}_{1}F_{1}(a,c,z)$ where $a=\gamma_{f}+1+iy$, $c=2\gamma_{f}+1$, $z=2ip_{f}r$, and

We choose to integrate the Dirac equation directly to obtain the continuum states rather than evaluate the hypergeometric functions as $a$ and $z$ are complex and the computation of ${}_{1}F_{1}(a,c,z)$ would involve the summation of a slowly convergent complex series for each required value of $z$. For each shell and subshell calculation, the continuum state electrons are assumed to move in the same potential as the bound state electrons [17].

The energy spectra $d\sigma/dE_{f}$ of the ionization electrons have been calculated as a function of the electron kinetic energy $\epsilon_{f}=E_{f}-m_{e}$. Results are obtained for scattering of 5, 10, 20, and 30 keV neutrino energies by the ground state systems Ne($1s^{2}2s^{2}2p^{6}$) and Ar($1s^{2}2s^{2}2p^{6}3s^{2}3p^{6}$), where the electrons are considered as independent scattering centers.

The energy spectra are compared to those for scattering from free electrons, for which [4]

where $m_{e}\leq E_{f}\leq m_{e}+\epsilon_{f}^{\mathrm{max}}$ and the maximum kinetic energy is

The total cross section for scattering off free electrons is [4]

The expressions for $\bar{\nu}_{e}$ scattering can be obtained by the interchange $\bar{a}_{e}\leftrightarrow-\bar{a}_{e}$ in (36) and (38).

Results for $\nu_{e}$ and $\bar{\nu}_{e}$ scattering by Ne are given in Table II, and by Ar in Table III. The energy spectra and cross sections are expressed as ratios

and $\sigma^{(\nu)}/Z\sigma^{(\nu)}_{(\mathrm{Free})}$, to the corresponding quantities for scattering by $Z$ free electrons. Tables and plots of the energy spectra for scattering from free electrons are given in [9].

The energy spectra ratios for scattering of neutrinos by Ne and Ar are shown in Figs 1 and 2 respectively. Plots for scattering of antineutrinos are not shown as they differ only very slightly from those for scattering by neutrinos. The energy spectra ratios become constant at low kinetic energies and can safely be extrapolated to lower kinetic energies.

The present spectra for Ne have the same general form as those calculated in [5], but have a much smoother structure and are significantly lower, representing a stronger dependence on atomic binding effects.

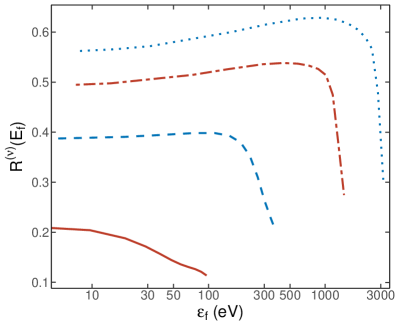
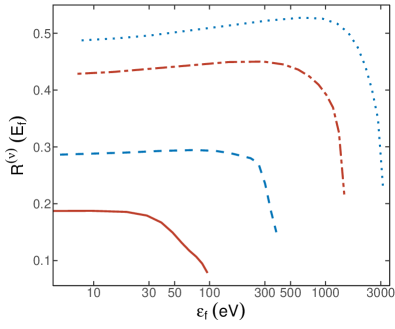
The largest binding energy of 3.2059 keV, for the K-shell of argon, is less than the lowest incident neutrino energy of $E_{\nu_{i}}$= 5 keV considered in the present calculations. Consequently, all occupied shells and subshells contribute to the energy spectra although, for the lower neutrino energies, the contributions from the inner shell and subshells will be small. For neon, the K-shell contributions at 5 keV and 10 keV are only O($10^{-3}$) and O($10^{-2}$) respectively. At all neutrino energies, the L_I subshell gives the largest contribution, and the L_II and L_III contributions are quite similar. For argon, the K-shell contributions at 5 keV and 10 keV are O($10^{-5}$) and O($10^{-3}$) respectively, and the L-subshell contributions at 5 keV are O($10^{-2}$). The M_I subshell contribution is dominant at all energies, the L_II and L_III contributions are similar, as are the M_II and M_III contributions.

The major computational challenge is to obtain satisfactory convergence in the sum over $\kappa_{f}$, as the convergence decreases with increasing $\epsilon_{f}$. The imposed practical limit $|\kappa_{f}|\leq 50$ ensured the fractional contributions of the neglected terms were less than $1\times 10^{-4}$ for $\epsilon_{f}\lesssim 1.4$ keV in the Ne spectra, and for $\epsilon_{f}\lesssim 0.6$ keV in the Ne spectra. However, for the higher energies, the convergence decreased and the contributions of the neglected terms increased to $1\times 10^{-3}$ for the L subshells of Ne, and $1\times 10^{-2}$ for the M subshells of Ar, so the numbers shown for these higher energies are slight underestimates.

The binding effects in the spectra increase with atomic number, decrease with increasing $E_{\nu_{i}}$ and, for each $E_{\nu_{i}}$, are most significant at the high electron energy end of the spectrum. The sharp decrease in the spectra at the high energy end is due to the minimizaion of the range $2E_{\nu_{f}}$ of the $q^{2}$ integration in (14) at $E_{f}^{\mathrm{max}}$. Also, for this region, $q\approx E_{\nu_{i}}$, so that the high energy tail will increase as $E_{\nu_{i}}$ increases.

The integrated cross sections

where $E_{l}=m_{e}$ and $E_{u}=m_{e}+\epsilon_{f}^{\mathrm{max}}$, can be estimated from the calculated energy spectra. We assume the spectra at $E_{f}=m_{e}$ are the same as at $m_{e}+0.01\epsilon_{f}^{\mathrm{max}}$. These integrated cross sections are given in the tables, expressed as ratios to the integrated cross sections $Z\sigma^{(\nu)}_{(\mathrm{Free})}$ (Eqn (38)) for $Z$ free electrons.

The recently developed [9] theory of scattering of low energy neutrinos and antineutrinos by atomic electrons, which uses the Bound Interaction Picture in configuration space to fully implement the relationship between the neutrino helicities and the orbital and spin angular momenta of the atomic electrons, has been applied here to the scattering by the ground state systems Ne($1s^{2}2s^{2}2p^{6}$) and Ar($1s^{2}2s^{2}2p^{6}3s^{2}3p^{6}$).

The energy spectra $d\sigma/dE_{f}$ of the ionization electrons produced in the scattering of electron neutrinos and antineutrinos with energies 5, 10, 20 and 30 keV have been calculated. Results are also obtained for the integrated cross sections. Screened point-Coulomb radial eigenfunctions have been used, with the continuum state eigenfunctions calculated by direct integration of the Dirac equations. The results here for Ne replace those given in [9] which were calculated using some screening constants which underestimated the effects of screening in the inner subshells. The new spectra ratios for neon are larger than the original ratios by $\approx 0.03$ to $\approx 0.14$, with the greatest increases occurring at $E_{\nu_{i}}$ = 10 keV.

The calculated energy spectra show that binding effects increase with atomic number, decrease with increasing $E_{\nu_{i}}$ and, for each $E_{\nu_{i}}$, are greatest at the high electron energy end of the spectrum. The neutrino and antineutrino energy spectra are very similar, with small difference of $\lesssim 1\%$.

Binding effects are still very significant at $E_{\nu_{i}}=30$ keV, the integrated spectra ratios being $\lesssim 0.6$ and $\lesssim 0.5$ for Ne and Ar respectively. Extension of the calculations to higher neutrino energies to study the further decrease of binding effects would require a substantial increase in the maximum value of $|\kappa_{f}|$ used as the $\kappa_{f}$ convergence is very slow at higher energies, which is not practical.

The largest uncertainty in the present calculations arises from the choice of the potential $V(r)$ for the atomic electron, and the consequent form of the radial functions $g(r)$ and $f(r)$ used in the evaluation of the radial matrix elements (II). The choice of a Coulombic potential with an effective nuclear charge $Z_{\mathrm{eff}}=Z-s_{i}$ to account for electron screening effects is convenient and should be accurate for the small values of $n$ and $n-l$ occurring in the ground states of neon and argon [15]. However, if increased accuracy is required, or extension to, for example, xenon is considered, then self-consistent relativistic radial eigenfunctions [18, 19] would be needed.

Relativistic self-consistent field theory includes [18] the effects of magnetic interactions between electrons and retardation of the inter-electronic Coulomb repulsion, as described by the Breit operator. This operator is treated as a first order perturbation to an unperturbed Hamiltonian which is a sum of the Dirac central field Coulombic Hamiltonians for each electron and the total Coulombic inter-electronic interaction. The magnetic and retardation terms are of order $(v/c)^{2}$ compared to the inter-electronic repulsion term, which is of order $(\alpha^{2}Z)m_{e}c^{2}$. Their contribution is therefore of order $(\alpha^{4}Z^{3})m_{e}c^{2}$ and increases strongly with $Z$. Detailed calculations are discussed in section 7.2 of [14].

The scattering of dark matter (DM) particles by atomic electrons is a promising method for detecting the particles forming the DM component of the Milky Way, and the theoretical treatment of this process shares many features with that for neutrino scattering by atomic electrons. The response of argon and xenon targets has been studied by [20] by treating the atomic electrons and DM particle as non-relativistic, with a general interaction constructed to satisfy Galilean and rotational invariance. The DarkSide-50 experiment [21] uses an argon target and they have presented a non-relativistic analysis for a vector mediator based upon atomic and DM form factors. The conversion of a sterile neutrino DM particle into an active neutrino via inelastic scattering with an atomic electron has been considered by [12] using a non-relativistic second quantization formalism based upon a four-fermion coupling and a mediator which could be scalar, pseudo-scalar, vector or axial vector.

The formalism developed in [9], which considers only vector and axial vector couplings, could be readily adapted to the $Z$-mediated scattering of a fermionic WIMP DM particle such as the neutralino $\chi$. The neutrino scattering tensor $L^{(\nu)}_{\beta\alpha}$ would be replaced by the appropriate tensor $L^{(\chi)}_{\beta\alpha}$ for the neutralino, the admixture of vector and axial vector contributions altered to accommodate the neutralino couplings, and changes made to the normalization factors for the plane wave spinors. Generalization to scalar and pseudo-scalar couplings is possible but would require substantial modifications to the formalism, especially to the angular momentum matrix elements.