Scaling theory of charge transport and thermoelectric response in disordered 2D electron systems: From weak to strong localization

The scaling theory for the Anderson localization [19], i.e., Abraham–Anderson–Licciardello–Ramakrishnan (AALR) theory [20], indicates that the conductance in a disordered system at $T=0$ follows a differential equation:

where $g$ is the dimensionless conductance scaled by the universal conductance $e^{2}/h$ ($e$: elementary charge, $h$: Planck’s constant), $L$ is the length of the system, and $\beta(g)$ is assumed to be a smoothly and monotonically increasing function with respect to $g$.

In the large-$g$ limit, $g$ obeys the classical Ohm’s law as $g=\sigma L^{d-2}$, where $\sigma$ is conductivity and $d$ is the spatial dimension of the system. From Eq. (1), we see that the $\beta$ function in this limit is given by $\beta(g)=d-2$; the asymptotic behavior of $\beta(g)$ is therefore expressed as $\beta(g)\approx d-2-\alpha/g$, where the expansion coefficient $\alpha$ is a positive constant on the order of unity. On the other hand, in the small-$g$ limit, the electronic states are localized because of disorder and $g$ decreases exponentially with $L$ as $g\sim e^{-L/\xi}$, where $\xi$ is the localization length, resulting in $\beta(g)\approx\ln g$ in this limit. Thus, in the two limits, the $\beta$ function is given by

for $d$-dimensional systems. In three-dimensional (3D) systems ($d=3$), where conducting and localized states are sharply separated across the mobility edge, different theoretical schemes are needed for each state. By contrast, the 2D systems ($d=2$) of present interest exhibit $g(L)\to 0$ in the limit of $L$; that is, the electronic states are always localized. If $L$ is finite and varied, $g(L)$ is expected to crossover from metallic to insulating behaviors as $L$ is increased. Actually, this expectation has been confirmed through studies on the frequency ($\omega$) dependences of conductance for $L=\infty$ at $T=0$ by Vollhardt and Wolfle [21] and by Kawabata [22] using the self-consistent (SC) theory. Notably, the SC theory is governed by a single parameter, $\lambda=\frac{\hbar}{\varepsilon_{\rm F}\tau}$ (where $\varepsilon_{\rm F}$ is the Fermi energy and $\tau$ is the elastic scattering time), which characterizes the scattering strength in quantum transport, and turns out to be capable of describing not only metallic but also insulating states. Regarding the $T$ dependence of conductance, however, we need to develop a different theoretical scheme. Once at finite temperatures, $g(T)$ can be non zero even for $L=\infty$ and the $T$ dependence of $g(T)$ exhibits a crossover from essentially metallic WL with $\ln T$ to SL with exponential $T$ dependences. The characteristic temperature of this crossover depends on the carrier density.

To address the WL–SL crossover in 2D systems, we first consider $T=0$ and introduce the following $\beta$ function as a smoothly and monotonically increasing function that asymptotically behaves as in Eq. (4) in both limits of $g\to 0$ and $g\to\infty$:

To solve the differential equation in Eq. (1) with $\beta(g)$ in Eq. (5), we impose $g(L_{0})=g_{0}$ as the boundary condition, where $L_{0}$ is the microscopic characteristic length that is much larger than the mean free path and $g_{0}$ is the conductance at length scale $L_{0}$. Under this condition, Eq. (1) can be rewritten as

By solving Eq. (6) with Eq. (5), we obtain the $L$ dependence of $g$ at $T=0$.

To extend this theory to finite $T$, Anderson, Abrahams, and Ramakrishnan (AAR) proposed replacing the system length $L$ in Eq. (6) with a characteristic length $L_{\phi}$ (hereafter referred to as the dephasing length) over which an electron remains in an eigenstate [23] . In the diffusive transport in the WL regime, $L_{\phi}$ is given by $L_{\phi}=\sqrt{D\tau_{\phi}}$ with diffusion coefficient $D$ and dephasing time $\tau_{\phi}$. Because the dephasing time generally depends on $T$ as $\tau_{\phi}\propto T^{-2p}$ with a positive constant $p$, the $T$-dependence of $L_{\phi}$ is given by $L_{\phi}\propto T^{-p}$. In the present work, we adopt $L_{\phi}$ as a single parameter to describe the $T$ dependences, similar to $\lambda=\frac{\hbar}{\varepsilon_{\rm F}\tau}$ in $L=\infty$ at $T=0$ in the SC theory, and express it as

in terms of three different parameters: the temperature $T_{\rm d}$ characterizing the WL-SL crossover and the dephasing length $L_{\rm d}$ at $T=T_{\rm d}$ and the exponent $p$ of the temperature dependence. This expression is possible because the $T$ dependence of conductance in a 2D system, unlike that in a 3D system with the mobility edge, exhibits a gradual change from logarithmic to exponential behavior in the $\omega$ dependences of the conductance as $T$ decreases.

In the WL limit, where $g_{0}$ is large and $g_{0}\gg\alpha\ln(L_{\phi}/L_{0})=\alpha p\ln(T_{\rm WL}/T)$ is satisfied, the differential equation in Eq. (6), with $L_{\phi}(\varepsilon,T)$ substituted for $L$, can be solved analytically. The spectral conductance $g(\varepsilon,T)$ is given by

with

resulting in the well-known logarithmic correction to conductance as long as $T<T_{\rm WL}(\varepsilon)$. On the other hand, in the SL limit where $g_{0}$ is small ($\alpha/g_{0}\gg 1$), the differential equation can also be analytically solved, enabling $g(\varepsilon,T)$ to be expressed as

for $T\ll T_{\rm SL}(\varepsilon)$, where $T_{\rm SL}(\varepsilon)$ is defined as

The electrical conductivity and the Seebeck coefficient can be expressed in terms of $g(\varepsilon,T)$ as follows. In linear response theory, the electrical current density ${\bm{j}}$ under the electric field ${\bm{E}}$ and the temperature gradient $\nabla T$ can be described by $\displaystyle{\bm{j}}=L_{11}{\bm{E}}-L_{12}({\nabla T}/{T})$. Here, the electrical conductivity $L_{11}(=\sigma)$ and the thermoelectric conductivity $L_{12}$ can be expressed by the following Sommerfeld-Bethe (SB) relation based on the Kubo–Luttinger theory [24, 25] under the assumption that the heat current is carried only by electrons.

where the factor of 2 accounts for the spin degree of freedom, $L$ and $A_{\rm c}$ represent the length and cross-sectional area of the system, respectively, $f_{0}$ denotes the Fermi–Dirac distribution function, and $\mu$ is the chemical potential. Notably, the SB relation was originally derived from the Boltzmann transport theory (BTT); however, it is valid even for strongly disordered systems that cannot be treated by the BTT [26]. Using Eq. (12) and Eq. (13), we can describe the Seebeck coefficient by

Here, we note that the $\varepsilon$ dependences of $g(\varepsilon,T)$ results from those of $g_{0}$, $p$, $T_{\rm WL}$ and $T_{\rm SL}$ in the present scheme. When the $\varepsilon$ dependence of $g(\varepsilon,T)$ within $k_{\rm B}T$ is weak and can be approximated as linear with respect to $\varepsilon$, i.e., $g(\varepsilon,T)\approx g(\mu,T)+g^{\prime}(\mu,T)(\epsilon-\mu)$, the Seebeck coefficients in the two limits are respectively given as

and

Here, $S_{0}^{\rm WL}(\mu)$, $A(\mu)$ and $S_{0}^{\rm SL}(\mu)$, $B(\mu)$ are respectively given by

with $\Delta(\mu)=\alpha\frac{p(\mu)}{g^{\prime}_{0}(\mu)}\frac{T^{\prime}_{\rm WL}(\mu)}{T_{\rm WL}(\mu)}$, and

Thus, $S_{\rm WL}(T)$ is proportional to $T$, whereas $S_{\rm SL}(T)$ is proportional to $T^{1-p}$ and both of which have logarithmic corrections.

We here compare the present theory to the experimental data for PBTTT thin films obtained by two different carrier-doping methods: the electrochemical doping method [15] and the chemical doping method [9]. For the ECT fabricated by Ito et al. [15], the channel length between the source and drain electrodes is $L=140$ $\mu$m, the channel width is $W=2$ mm, and the film thickness is $t=17$ nm. On the other hand, for the PBTTT device fabricated by Watanabe et al. [9], $L=300$ $\mu$m, $W=80$ $\mu$m, and $t=40$ nm. Note that the lamellar spacing of PBTTT (a distance between two layers in the PBTTT with a multi layered 2D structure) is $d_{l}=2$ nm; thus, the cross-sectional area of a single layer in Eqs. (12) and (13) is given by $A_{\rm c}\equiv Wd_{l}$.

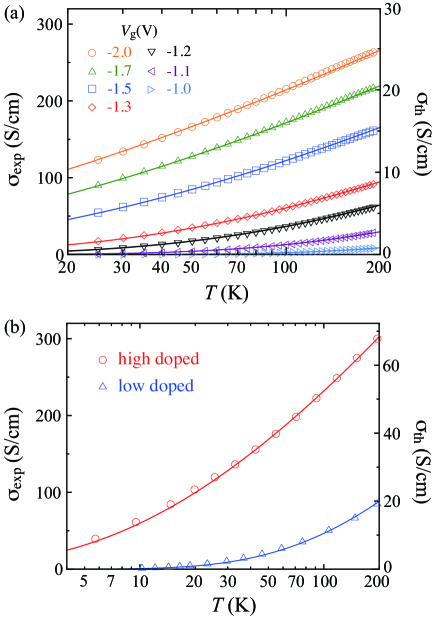
Figure 1(a) presents the experimental electrical conductivity, $\sigma_{\rm exp}(T)$, under various gate voltages, $V_{g}$, as measured using the ECT setup [15]. $\sigma_{\rm exp}(T)$ increases monotonically with increasing $|V_{g}|$ at a fixed $T$, which is reasonable because the hole density increases. We also observe that $\sigma_{\rm exp}(T)$ is proportional to $\ln T$ in the higher-$T$ region and deviates from this logarithmic behavior as $T$ decreases, which we ascribe to a precursor to the WL–SL crossover. The solid curves in Fig. 1(a) represent the $T$ dependences of theoretical results $\sigma_{\rm th}(T)$ based on the assumption of $L_{0}=4$nm, $\alpha=1.0$, and $T_{\rm d}=20$K, where $T_{d}$ is chosen as a typical temperature at which $\sigma_{\rm exp}(T)$ in Fig. 1 deviates from the logarithmic behavior. The three qualitatively different parameters ($g_{0}$, $L_{\rm d}$, and $p$) obtained by fitting to experimental data are listed in TABLE 1, showing convincing agreement, except for the difference between the absolute values of $\sigma_{\rm exp}$ and $\sigma_{\rm th}$. We consider that the difference is due to uncontrolled sample conditions, such as layer numbers and types of spatial disorder.

Figure 1(b) shows the electrical conductivity of PBTTT thin films chemically doped at two different doping levels. The marks represent experimental data [9] and the solid curves are the present theoretical results based on the same assumption of $L_{0}=4$nm, $\alpha=1.0$, $T_{\rm d}=20$K. The values of the three parameters ($g_{0}$, $L_{\rm d}$ and $p$) are listed in TABLE 2. The theoretical curves are in excellent agreement with the experimental data, except for the difference between their absolute values, similar to Fig. 1(a).

As $V_{g}$ changes from $V_{g}=-1.0$ V to $-2.0$ V, $g_{0}$ increases monotonically from $0.55$ to $2.55$, which reflects the carrier density and the strength of disorder scattering, as characterized by parameter $\lambda$ under the SC theory. This result suggests that, under these experimental conditions, the electrons in the PBTTT thin film are situated more or less in the WL regime rather than in the SL regime. The data in TABLE 1 also show that the dephasing length $L_{\rm d}$ increases and the exponent $p$ decreases because of the delocalization of electrons with increasing $|V_{g}|$. Similar tendencies in $p$ and $L_{d}$ are observed in the data in TABLE 2. Thus, the experimental data obtained by different carrier-doping methods can be understood in a unified manner using the three parameters $g_{0}$, $L_{\rm d}$ and $p$.

As shown in TABLE 1 and TABLE 2, the exponent is $p\sim{0.4}$ which implies that $\tau^{-1}_{\phi}$ is almost proportional to $T$ in the crossover regime where diffusive motions are assumed in the microscopic region. This $T$ dependence might indicate that Coulomb interaction is the dominant scattering processes in this regime [28, 29, 30]. It is of interest to see that the present result of $p\sim 1/2$ based on quantum transport is close to that argued by Efros and Shklovskii [31], whose approach was based on the idea of VRH caused by electron–electron scattering. Such an interesting possibility of interaction effects in the crossover regime between conducting and localized regimes is a very particular property of 2D systems, in contrast to a sharp, though continuous, critical transition between them in 3D systems as analyzed recently for the Seebeck coefficient taking into account the energy dependences of the localization length near the mobility edge [33]. It is to be noted that $p=1/3$ in a 2D Mott VRH [32], where the electron hopping between localized states is caused by electron–phonon scattering.

We here discuss the $T$ dependence of $S(T)$ data for PBTTT thin films obtained by the electrochemical doping method [15] and the chemical doping method [9]. Figure 2(a) shows the experimental $S(T)$ of the PBTTT-based ECT under various $V_{g}$ [15]. The $S(T)$ for all $V_{g}$ are proportional to $T$ in the high-$T$ region, where the electrical conductivity varies as $\sigma(T)\propto\ln T$, reflecting the WL. By fitting the experimental data using $S(T)=S_{0}^{\rm WL}\frac{T}{T_{\rm WL}}$ in Eq. (15), we determined $S_{0}^{\rm WL}$ and $T_{\rm WL}$, as listed in TABLE 3, where $T_{\rm WL}$ can be obtained from Eq. (9). Both $S_{0}^{\rm WL}$ and $T_{\rm WL}$ increase as $V_{g}$ (or $g_{0}$) increases, as expected from Eqs. (9) and (17). In the low-$T$ region for low-doped cases of $V_{g}=1.0$V and $1.1$V, $S(T)$ is expected to deviate from $T$-linear behavior; however, corresponding experimental data are not available.

Figure 2(b) shows the $S(T)$ for chemically carrier-doped PBTTT films [9]. In the case of high doping, $S(T)$ is proportional to $T$ within a wide $T$ region from 30 to 200 K, reflecting the WL. By contrast, in the case of low doping, $S(T)$ is also linear with respect to $T$ in the high-$T$ region but deviates from the $T$-linear behavior in the low-$T$ region (the fitting parameters $S_{0}^{\rm WL}$ and $T_{\rm WL}$ for the high- and low-doped cases are summarized in TABLE 4). In the low-$T$ region, $S(T)$ appears to vary as $S(T)\propto T^{1-p^{*}}$ with $p^{*}\sim 0.3$. Notably, the $T$-dependence of $S(T)$ follows a power-law behavior, which is a characteristic feature of SL as shown in Eq. (16), even though the electrons in this low-doped PBTTT thin film are not in the fully SL regime but are somewhat more localized than in the WL regime.