Scaling laws of the out-of-time-order correlators at the transition to the spontaneous -symmetry breaking in a Floquet system
Abstract
We investigate both numerically and analytically the dynamics of out-of-time-order correlators (OTOCs) in a non-Hermitian kicked rotor model, addressing the scaling laws of the time dependence of OTOCs at the transition to the spontaneous symmetry breaking. In the unbroken phase of symmetry, the OTOCs increase monotonically and eventually saturate with time, demonstrating the freezing of information scrambling. Just beyond the phase transition points, the OTOCs increase in the power-laws of time, with the exponent larger than two. Interestingly, the quadratic growth of OTOCs with time emerges when the system is far beyond the phase transition points. Above numerical findings have been validated by our theoretical analysis, which provides a general framework with important implications for Floquet engineering and the information scrambling in chaotic systems.
pacs:
03.65.-w, 03.65. YZ, 05.45.-a, 05.45.MtI Introduction
Non-Hermiticity has been regarded as a fundamental modification to the conventional quantum mechanics Markum99 ; Stephanov99 ; Berry2004 ; Graefe2008 ; Rotter2009 ; Ott2013 ; Harsh2014 , a subclass of which with symmetry even displays the transition from the real energy spectrum to complex one. Such intrinsic spontaneous -symmetry breaking occurs at the exceptional points (EP), at which both the eigenstates and eigenvalues coalesce Bender1998 ; Bender2002 ; Mosta2002 ; Bender2007 ; Mosta2010 ; Harsh2010 ; Ganainy2018 ; Klaiman2008 ; Musslimani2008 . The existence of EP leads to rich physics, such as the enhancement of precision in quantum sensors Cai20 , the topological phase transition Bergholtz21 ; ZhongWang18 ; Mzhao1 ; FYu ; Mzhao2 , the nonadiabatic transition FengYu21 ; WYWang22 , and the unidirectional propagation of light YinHuang , just to name a few. Theoretical advances have enabled exponential realizations of symmetric systems in various fields, such as optical settings Sergi2014 ; Makris2008 ; Ganainy2007 ; Guo2009 ; Regensburger2012 ; Hodaei2014 ; Feng2014 ; Jiahua2016 ; Longhi2009 ; Longhi2010 ; Ruter2010 ; YongmeiXue , electronic circuits Stegmaier2021 , and optomechanical systems Luxy15 . Moreover, the extension of Floquet-driven systems to the symmetric regime has opened up unique opportunities for understanding fundamental concepts such as quantum chaos Bender09 and quantum-classical transition Bender10 ; wlzhao23a . Interestingly, chaos is found to facilitate the scaling law of the spontaneous symmetry breaking in a symmetric kicked rotor (PTKR) model West2010 . This system even displays ballistic energy diffusion Longhi2017 and the quantized acceleration of momentum current Zhao19 , which enriches our understanding on the unique transport phenomena in the presence of chaos.
The dynamics of OTOCs, originally introduced by Lakin et al., in the study of quasiclassical theory of superconductivity Larkin1969 , has received extensive studies in the fields of high energy physics Roberts2016 ; Maldacena2016 ; Polchinski2016 , condensed matter physics Bohrdt2016 ; Garttner2017 ; Banerjee2017 ; Shen2017 ; Fan2017 ; Huang2017 and quantum information Li2017 ; Weinstein22 ; Hu23 . It has been found that OTOCs can effectively detect quantum chaos Pappalardi22 ; GMata18 ; JiaoziWang21 ; Kidd2021 , quantum thermalization Balachandran21 , and information scrambling Harris2022 ; Roberts2022 ; Zhang2019 ; Yan2020 ; Patel2017 ; WLZhao23 . In the semiclassical limit, the exponential growth of OTOCs is governed by the Lyapunov exponent of classical chaos, which demonstrates a route of quantum-classical correspondence Hashimoto2017 . In Floquet-driven systems, OTOCs has been used to diagnose dynamical quantum phase transition Zamani2022 and entanglement Martin2018 ; Lewis-Swan2019 . Intrinsically, we previously found a quantized response of OTOCs when varying the kicking potential of the PTKR model WlZhao22 . State-of-art experimental advances have observed different kinds of OTOCs in the setting of nuclear magnetic resonance Wei2018 ; Nie2019 , trapping ions Landsman2019 and qubit under Floquet engineering Zhao2021 .
In this context, we both numerically and analytically investigate the dynamics of OTOCs when the PTKR model is in different phases of -symmetry. We use a machine learning method, namely a long short-term memory network (LSTM), to classify the phase diagram of -symmetry breaking and extract the phase boundary in a wide range of system parameters. We find that in the unbroken phase of symmetry, OTOCs increase monotonically with time evolution and eventually saturate, demonstrating the freezing of operator growth. We analytically prove that the saturation of OTOCs is a power-law function of the real part of the kicking potential. In the broken phase of the symmetry, we find a power-law increase of OTOCs with time, for which the characteristic exponent is larger than two when the system is just beyond the phase transition point, and is equal to two for the system far beyond the phase transition point. Through the detailed analysis of the wavepacket’s dynamics in the time reversal process, we uncover the mechanisms of both the dynamical localization and the power-law increase of OTOCs. Our investigations reveal that the dynamics of OTOCs can be utilized to diagnose spontaneous -symmetry breaking.
The paper is organized as follows. In Sec. II, we describe the PTKR model and show the scaling-law of spontaneous -symmetry breaking. In Sec. III, we show the scaling-laws of the dynamics of OTOCs at the transition to the -symmetry breaking. Sec. IV contains the theoretical analysis of the scaling-laws of OTOCs. The conclusion and discussion are presented in Sec. V.
II Transition to spontaneous -symmetry breaking in Floquet systems
II.1 Model
The Hamiltonian of the PTKR model in dimensionless unites reads
| (1) |
where the kicking potential satisfies the -symmetric condition Longhi2017 ; West2010 ; Zhao19 . The parameters and indicate the strength of the real and imaginary parts of the kick potential, respectively. The is angular momentum operator, is the angle coordinate, and denotes the effective planck constant. The time is integer, indicating kicking numbers. The eigenequation of angular momentum operator is with eigenstate and eigenvalue . On the basis of , an arbitrary quantum state can be expanded as .
For time-periodic systems, i.e., , the Floquet theory predicts the eigenequation of the evolution operator , where the eigenphase is referred to as quasienergy. One-period time evolution of a quantum state of the PTKR system is given by with the Floquet operator
| (2) |
This demonstrates that in numerical simulations, one period evolution is split into two steps, namely the kicking evolution and the free evolution . The kick evolution is realized in angle coordinate space, i.e., . Then, one can utilize the fast Fourier transform to change the state to angular momentum space, thereby obtaining its component on the eigenstate . Finally, the free evolution is conducted in angular momentum space, i.e., . By repeating the same procedure, one can get the quantum state at arbitrary time Casati79 .
II.2 Spontaneous -symmetry breaking
It is straightforward to prove that the Floquet operator of the PTKR satisfies the symmetry , where and are the parity and time reversal operators, respectively. Based on conventional understanding of quantum mechanics, one asserts that the two operators, i.e., and have simultaneous eigenstates, that is to say, the quasieigenstate is also the eigenstate of the operator, i.e., . This conclusion is indeed valid for positive quasienergies . However, a notable feature of the PTKR system is that complex quasienergies emerge when the strength of the imaginary part of the complex potential exceeds a threshold value, i.e., Longhi2017 ; West2010 ; Zhao19 . The threshold value is just the exceptional points of the system. It can be proven that the quasieigenstate is no longer an eigenstate of the operator due to the complex quasienergies, thus demonstrating the spontaneous -symmetry breaking. An intrinsic quality of the PTKR system is that symmetry is helpful in protecting the real spectrum of the Floquet operator.
We assume that the initial state is expanded as . Then, after the th kick, the quantum state has the expression , whose norm exponentially increases with time due to positive . We numerically investigate the time evolution of for different . Without loss of generality, we choose a Gaussian wavepacket, i.e., with as the initial state in numerical simulations. Figure 1(a) shows that for very small (e.g., and 0.05), the value of equals almost to unity with time evolution, which implies that quasienergies are all real. Interestingly, for sufficiently large (e.g., ), increases exponentially with time, i.e., , and the growth rate increases with the increase of . The non-unitary feature of the Floquet operator, , leads to the growth of the norm. A rough estimation of the norm yields a time dependence of the form , indicating the relation of the growth rate , which is confirmed by our numerical results [see inset in Figure 1(a)]. We further investigate the long-time average value of the norm, , for a wide range of . Figure 1(b) shows that, for a specific (e.g., ), remains at unity for smaller than a threshold value , beyond which it monotonically increases with . It is reasonable to believe that the threshold value corresponds to the emergence of spontaneous -symmetry breaking.
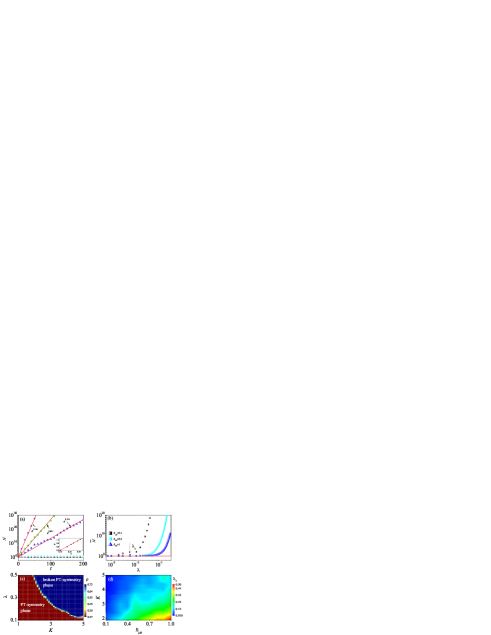
Recently, the long short-term memory (LSTM) network has been exploited to extract the character of time series and thus to predict the phase diagram of quantum diffusion Mano21 . Based on the character of the time evolution of , we conducted supervised training on the LSTM network and used it to evaluate the feature of , namely, whether or not, for different system parameters. This highly effective machine learning method outputs the probability of the time series to be exponentially increasing or not, which can predict the phase diagram of spontaneous -symmetry breaking. Interestingly, our results show that the increases with the increase of both and [see Fig. 1(c)]. We identify two phases in the parameters space , the boundary of which is clearly visible in Fig. 1(c). We further investigate the for different and . Our results demonstrate that the critical parameter increases with the increase of and decreases with the increase of [see Fig. 1(d)]. This behavior is rooted in the fact that the mean spacing level of the quasienergies of the quantum kicked rotor (QKR) model is proportional to West2010 . The smaller the is, the easier it is for the non-Hermitian parameter to cause the coalescence of two quasienergies, implying the relation .
III Scaling laws of the OTOCs at the transition to the spontaneous -symmetry breaking
The OTOCs are defined by , with the operators and being evaluated in the Heisenberg picture Chen2017 ; Hashimoto2017 ; Dora2017 ; Mata2018 ; Alavirad2018 ; Swingle2016 ; Hafezi2016 ; Li2017 ; Garttner2017 . The average, i.e., , is taken over an initial state Heyl2018 . In this work, we consider the case where both and are angular momentum operators, i.e., . We use a Gaussian wavepacket, i.e., with as the initial state. It is worth noting that, as opposed to static-lattice systems, periodically-driven systems have no thermal states, as the temperature grows to infinity with time evolution D'Alessio14 . Thus, there is no need to average over the initially thermal states in the definition of in our system WlZhao22 ; WLZhao21 .
Straightforward derivation yields the equivalence
| (3) |
where the two-points correlators, namely, the first two terms in right side are defined by
| (4) |
| (5) |
and the four-points correlator is
| (6) |
with and Ueda2018 . The symbol denotes the real part of a complex variable.
To obtain the state , three steps must be carried out: i) the forward evolution from to , i.e. , ii) the action of the operator on the state , i.e. , and iii) the backward evolution from to , i.e. . The expectation value of the square of the momentum can then be calculated using to obtain [see Eq. (4)]. To numerically simulate , the operator should first be applied to the initial state , yielding the new state . Then, the forward evolution is conducted, i.e., . Subsequently, the action of is performed on , obtaining , afterwards, the time-reversal is applied to , resulting in . Using Eq. (5), can then be calculated by evaluating the norm of . Lastly, the term [seen in Eq. (6)] can be determined using the two states and , which is usually complex since they are not identical.
In the -symmetry breaking phase, the norm of the quantum state increases exponentially with time regardless of the forward or backward evolution. To address this issue and eliminate its contribution to the OTOCs, we normalize the time-evolved state. For the forward evolution of , we set the norm of the quantum state to be the same as that of the initial state, i.e., with . The backward evolution starts from the state , whose norm is the mean energy of the state . Thus, it is reasonable to take the norm of the quantum state during the backward evolution to be , i.e., . In short, the norm of the time-evolved state for both the forward and backward evolution is equal to that of the state it starts from. If the same normalization procedure is applied to the evolution of , then we will have and () for the forward and time reversal evolutions, respectively.

In order to understand the effects of -symmetry breaking on the dynamics of , we numerically investigated the time evolution of for different . Figure 2(a) shows that, for values of smaller than the phase transition point (e.g., ), the increases gradually up to saturation. Interestingly, for slightly larger than , the increases in a power-law of time, i.e., with [see with in Fig. 2(a)]. We dub this phenomenon as a super-quadratic growth (SQG) of . When the value of is much larger than the phase transition point, i.e., [e.g., and 0.9 in Fig.2(a)], the quadratic growth (QG) of OTOCs emerges. We further investigate the exponent for different . Our results show that is zero for , increases abruptly to a maximum value greater than two for slightly larger than , and finally saturates to two for sufficiently large [e.g., see in Fig. 2(b)]. It is evident that the scaling-law of OTOCs reveals the emergence of the spontaneous -symmetry breaking and unveils the correlation between information scrambling and the -symmetry phase transition.
IV Theoretical analysis of the dynamics of OTOCs
IV.1 Mechanism of the saturation of for
We numerically investigate the time evolution of the three parts of the OTOCs, i.e., , , and for . Figure 3(a) shows that the time dependence of and almost overlap, displaying rapid growth up to saturation. Since the real part of , i.e., fluctuates between positive and negative values, we plot the absolute value in Fig. 3(b). Both and saturate after a very short time evolution. Importantly, is at least 4 orders of magnitude larger than both and , leading to a perfect consistency between and . Consequently, based on Eq. (3), we can safely use the approximation
| (7) |
where denotes the exceptional value of energy of the state divided by its norm .

The normalization procedure for time reversal yields the equivalence , which shows that the value of is just the mean energy of the state at the time . For , the quasienergies are all real, thus the dynamics of the PTKR is the same as that of the Hermitian QKR. A noteworthy characteristic of the QKR’s energy diffusion is the phenomenon of DL, i.e. the mean energy gradually approaches to saturation level with increasing time due to quantum coherence. It is reasonable to believe that the mechanism of DL suppresses the growth of both and , and therefore leads to the saturation of .
To confirm this conjecture, we consider a specific time, i.e., , and numerically trace the evolution of for both the forward () and backward () evolution. Figure 4(a) shows that for , increases rapidly to saturation during forward time evolution from to , then jumps to a specific value at the start of the time reversal (i.e., at ) before finally saturating for the backward evolution from to . This clearly demonstrates the emergence of the DL, which is also reflected by the probability density distribution in momentum space. We compare the momentum distributions at the end of the forward evolution (i.e., ) and the end of time reversal (i.e., ) in Fig. 4(b). One can see that the two quantum states almost overlap with each other, both of which are exponentially localized in momentum space, i.e., [see Fig. 4(b)]. A rough estimation yields and . Plugging the two relations into Eq. (7), we can immediately get the estimation of the OTOCs, i.e., . It is known that the localization length is in a quadratic function of , i.e., Izrailev90 , which results in the relation
| (8) |
This clearly demonstrates that the is time-independent after the long term evolution, verifying our numerical results in Fig. 2(a) and Fig. 3(a).
To provide evidence of our analytical prediction, we investigate the time-averaged value of OTOCs, i.e., , numerically for different . In the numerical simulations, we ensure that is large enough for the long-term saturation of to be well quantified by . Our numerical results show that for a specific , increases in a power-law of [see Fig. 3(c)], which is well described by our theoretical prediction in Eq. (8). This is a strong indication of the validity of our analytical analysis. Our findings of the dependence of the OTOCs on the kick strength provide an opportunity to control the operator growth with an external driven potential.

The discontinuous jump in the mean square momentum, , at , the beginning of time reversal, is due to the action of the operator on the quantum state . This action generates the quantum state , for which the mean value is given by . The exponentially-localized shape of the quantum state, [see Fig. 4(b)], allows us to obtain the expectation values and , which quantitatively explains the discontinuous increase in the mean energy from to .
IV.2 Mechanism of the SQG of for
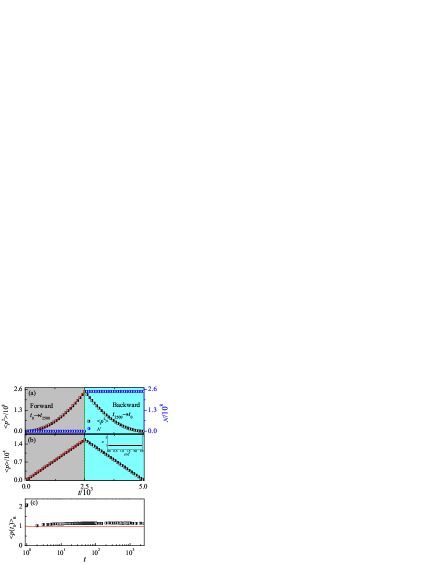
Figure 5(a) shows the time evolution of , , , and for just larger than the -symmetry phase transition point . It is clear that the time dependence of corresponds perfectly to that of , both of which increase following the SQG . The time evolution of displays the QG, i.e., , while follows the SQG . In addition, one can see that is larger than both and by approximately four orders of magnitude. Therefore, it is sufficient to analyze the time evolution of the term to uncover the mechanism of the SQG of .

Since the value of at a specific time is dependent on both the mean energy and the norm of the state at the end of time reversal [see Eq. (7)], we numerically calculate the forward and backward time evolution of , , and with a fixed (e.g., in Fig. 6). Figure 6(a) demonstrates that the mean energy diffuses ballistically with time during the forward evolution , and it displays the intrinsic time reversal during . Meanwhile, the mean momentum linearly increases for , and linearly decays for [see Fig. 6(b)]. Moreover, Fig. 6(a) reveals that the norm remains unity, i.e., , during the forward evolution and equals the mean energy at the time , i.e., during the time reversal. Taking the ballistic diffusion of energy into account, the following equivalence can be derived
| (9) |
In order to measure the degree of time reversal for a fixed , we define the ratio of mean energy between forward () and backward () time evolution as
| (10) |
where and () denote the mean square of momentum for the forward evolution and time reversal, respectively. The inset in Fig. 6(b) shows that is very large (i.e., for ) and approaches almost one with time evolution. This reveals that the mean energy at the end of time reversal is much greater than that at the initial time, i.e., . We further investigate the time evolution of , and find [see Fig. 6(c)] that the increases in the power-law of time
| (11) |
Substituting Eqs. (9) and (11) into Eq. (7) yields the SQG of OTOCs
| (12) |
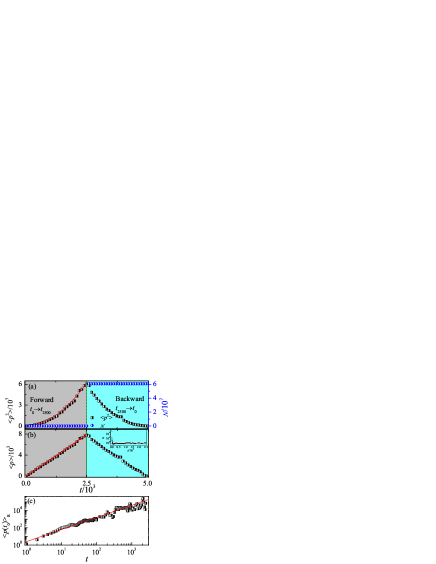
Figure 7 shows the probability density distribution of the state at forward and backward evolution in both the real and momentum space. The initial state is a Gaussian wavepacket centered at and [see Figs. 7(a) and (b)]. Interestingly, one can observe that the quantum state is mainly distributed in the region for both the forward and backward evolution. This is due to the fact that the action of the Floquet operator of the kicking term on a quantum state, i.e., helps to amplify the state within the region as . Assuming that the real part of the kicking potential provides the driven force , the PTKR experiences a positive magnitude force during the forward evolution, thus the momentum grows with time, as shown in Fig. 6(b). For the time reversal, the sign of kick strength flips, i.e., , so the mean momentum decreases with time evolution. Our conjecture is supported by the numerical results of momentum distributions. Figures 7(b), (d) and (f) show that the wavepacket, like a soliton, moves to the positive direction in momentum space for , resulting in [in Fig. 6(b)], and moves back to the opposite direction for . In addition, the width of the wavepacket in momentum space is so narrow that one can safely use the approximation , which is verified by our numerical results in Figs. 6(a).

IV.3 Mechanism of the QG of for
We numerically investigate the time evolution of , , , and for . As shown in Fig. 5(b), all of them increase in the way of QG (i.e., ). We use the ratios and to quantify the differences among , , and . Our investigation show that both of them are larger than one, specifically and [see the inset in Fig. 5]. This suggests that contributes mainly to the , which is verified by the good agreement between and [see Fig. 5(b)]. To reveal the mechanism of the QG of , we proceed to analyze the time evolution of by thoroughly investigating both the forward and backward evolution of the mean values , , and the norm for a given .
Figure 8(a) shows that the mean energy exhibits ballistic diffusion , during the forward evolution from to , and decays as the inverse of a quadratic function, with , during the backward evolution from to . This decay is symmetric with respect to the of . The dynamics of the mean momentum also exhibits perfect time reversal, namely it linearly increases as during and decreases linearly during . The ratio remains close to one throughout the time evolution, except at the end, i.e., [see the inset in Fig. 8(b)], providing a clear evidence of time reversal. For the forward evolution from to , the norm is equal to unity, while for the interval , it is equal to the value of , i.e., [see Fig. 8(a)]. By utilizing the ballistic diffusion of mean energy, we establish the relationship , where is an arbitrary time. We further evaluate the behavior of for different . As shown in Fig. 8(c), the remains almost constant at a value of one, indicating that it is independent of time. Plugging in the values of and into Eq. (7), we obtain the QG of OTOCs
| (13) |
The time reversal of a wavepacket’s dynamics is clearly seen in the evolution of its momentum distributions. For the forward time evolution, the quantum state is localized at the point [seen in Figs. 9(a), (c) and (e)], which is the result of the localization-effect of the imaginary part of the Floquet operator . With the wavepacket mimicking a classical particle, it experiences a kicking force of magnitude , resulting in a constant acceleration of momentum , which is reflected in the linear growth of momentum. This phenomenon of the directed current is also seen in the propagation of momentum distributions in Figs. 9(b), (d) and (f), where a soliton can be observed moving unidirectionally towards the positive direction in momentum space.
During the backward evolution, the wavepacket of the real space remains centered at , with a width much smaller than the corresponding state at the time of forward evolution [see Figs. 9(a), (c) and (e)]. As the particle is exposed to the kicking force with during time reversal, its momentum decreases linearly in time, which is also reflected in the propagation of the wavepackets in momentum space [Figs. 9(b), (d) and (f)]. It is evident that the is in perfect overlap with the , apart from the initial state [see Figs. 9(b)]. The width of is considerably larger than that of , leading to the ratio of energy being larger than one, i.e., [see the inset in Fig. 8(b)].
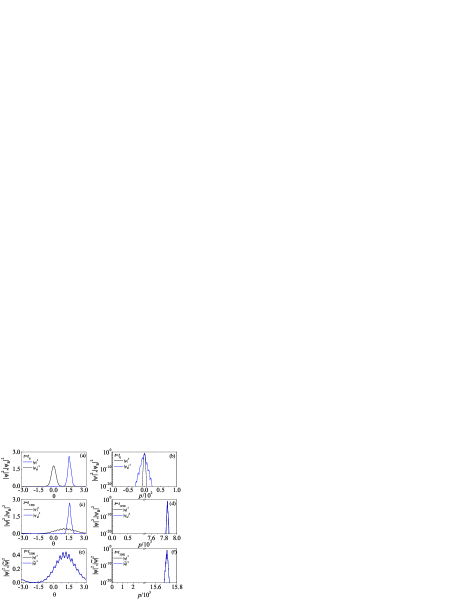
V Conclusion and discussion
In this work, we investigate the dynamics of OTOCs in a PTKR model and achieve its scaling laws in different phases of symmetry. We use the time series of the norm to train a LSTM, which enables us to extract a clear phase diagram of -symmetry breaking, with a phase boundary at . For , we find that the DL of energy diffusion suppresses the growth of OTOCs, and prove analytically the dependence of OTOCs on the kicking strength, i.e., . At the vicinity of the phase transition points, i.e., , we observe a SQG of OTOCs, i.e., with an exponent . Interestingly, a QG of OTOCs, i.e., emerges for . We elucidate the mechanisms of both the SQG and QG by analyzing the time-reversed wavepacket’s dynamics. Our results demonstrate that the spontaneous -symmetry breaking profoundly affects the dynamics of OTOCs, providing an unprecedented opportunity for diagnosing the spontaneous -symmetry breaking with OTOCs.
In recent years, the OTOCs have been widely used to investigate the operator growth in quantum mapping systems Moudgalya19 , the information scrambling in spin chains TianciZhou20 , and the quantum thermalization in many-body chaotic systems KenXuanWei19 . Theoretical studies have demonstrated that the QKR model is mathematically equivalent to the kicked Heisenberg spin XXZ chain Boness10 , indicating a connection between the magnon dynamics and quantum diffusion of chaotic systems. Our findings therefore bridge the gap between the information scrambling in condensed matter physics and the operator growth in quantum chaotic systems. This also paves the way for the experimental observation of OTOCs dynamics in chaotic systems using spin chain platforms.
ACKNOWLEDGMENTS
Wen-Lei Zhao is supported by the National Natural Science Foundation of China (Grant Nos. 12065009), the Natural Science Foundation of Jiangxi province (Grant Nos. 20224ACB201006 and 20224BAB201023) and the Science and Technology Planning Project of Ganzhou City (Grant No. 202101095077). Jie Liu is supported by the NSAF (Contract No. U1930403).
References
- (1) H. Markum, R. Pullirsch, and T. Wettig, Non-Hermitian Random Matrix Theory and Lattice QCD with Chemical Potential, Phys. Rev. Lett. 83, 484 (1999).
- (2) N. Hatano and David R. Nelson, Localization Transitions in Non-Hermitian Quantum Mechanics, Phys. Rev. Lett. 77, 570 (1996).
- (3) M. Berry, Physics of Nonhermitian Degeneracies, Czech. J. Phys. 54, 1039 (2004).
- (4) E. M. Graefe, H. J. Korsch, and A. E. Niederle, Mean-field dynamics of a non-Hermitian Bose-Hubbard dimer, Phys. Rev. Lett. 101, 150408 (2008).
- (5) I. Rotter, A non-Hermitian Hamilton operator and the physics of open quantum systems, J. Phys. A 42, 153001 (2009).
- (6) G. Barontini, R. Labouvie, F. Stubenrauch, A. Vogler, V. Guarrera, and H. Ott, Controlling the Dynamics of an Open Many-Body Quantum System with Localized Dissipation, Phys. Rev. Lett. 110, 035302 (2013).
- (7) K. Jones-Smith and H. Mathur, Relativistic Non-Hermitian Quantum Mechanics, Phys. Rev. D89, 125014 (2014).
- (8) C. M. Bender and S. Boettcher, Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry, Phys. Rev. Lett. 80, 5243 (1998).
- (9) C. M. Bender, D. C. Brody, and H. F. Jones, Complex Extension of Quantum Mechanics, Phys. Rev. Lett. 89, 270401 (2002).
- (10) A. Mostafazadeh, Pseudo-Hermiticity versus PT-symmetry. II. A complete characterization of non-Hermitian Hamiltonians with a real spectrum, J. Math. Phys. (N.Y.), 43, 2814 (2002).
- (11) C. M. Bender, Making sense of non-Hermitian Hamiltonians, Rep. Prog. Phys. 70, 947 (2007).
- (12) A. Mostafazadeh, Pseudo-hermitian representation of quantum mechanics, Int. J. Geom. Meth. Mod. Phys. 07, 1191 (2010).
- (13) K. Jones-Smith and H. Mathur, Non-Hermitian quantum Hamiltonians with PT symmetry, Phys. Rev. A82, 042101 (2010).
- (14) R. El-Ganainy, K. G. Makris, M. Khajavikhan, Z. H. Musslimani, S. Rotter, and D. N. Christodoulides, Non-Hermitian physics and PT symmetry, Nat. Phys. 14, 11 (2018).
- (15) S. Klaiman, U. Günther, and N. Moiseyev, Visualization of Branch Points in PT-Symmetric Waveguides, Phys. Rev. Lett. 101, 080402 (2008).
- (16) Z. H. Musslimani, K. G. Makris, R. El-Ganainy, and D. N. Christodoulides, Optical Solitons in PT Periodic Potentials, Phys. Rev. Lett. 100, 030402 (2008).
- (17) Y. Chu, Y. Liu, H. Liu, and J. Cai, Quantum Sensing with a Single-Qubit Pseudo-Hermitian System, Phys. Rev. Lett. 124, 020501 (2020).
- (18) E. J. Bergholtz, J. C. Budich, and F. K. Kunst, Exceptional topology of non-Hermitian systems, Rev. Mod. Phys. 93, 015005 (2021).
- (19) S. Yao and Z. Wang, Edge States and Topological Invariants of Non-Hermitian Systems, Phys. Rev. Lett. 121, 086803 (2018).
- (20) X. M. Zhao, C. X. Guo, M. L. Yang, H.Wang,W. M. Liu, and S. P. Kou, Anomalous non-Abelian statistics for non-Hermitian generalization of Majorana zero modes, Phys. Rev. B104, 214502 (2021).
- (21) Z. F. Yu, J. K. Xue, L. Zhuang, J. Zhao, and W. M. Liu, Non-Hermitian spectrum and multistability in exciton-polariton condensates, Phys. Rev. B104, 235408 (2021).
- (22) X. M. Zhao, C. X. Guo, S. P. Kou, L. Zhuang, and W. M. Liu, Defective Majorana zero modes in a non-Hermitian Kitaev chain, Phys. Rev. B104, 205131 (2021).
- (23) F. Yu, X. L. Zhang, Z. N. Tian, Q. D. Chen, and H. B. Sun, General Rules Governing the Dynamical Encircling of an Arbitrary Number of Exceptional Points, Phys. Rev. Lett. 127, 253901 (2021).
- (24) W. Y. Wang, B. Sun, and J. Liu, Adiabaticity in nonreciprocal Landau-Zener tunneling, Phys. Rev. A106, 063708 (2022).
- (25) Y. Huang, Y. Shen, C. Min, S. Fan and G. Veronis, Unidirectional reflectionless light propagation at exceptional points, Nanophotonics 6, 977 (2017).
- (26) K. G. Zloshchastiev, and A. Sergi, Comparison and unification of non-Hermitian and Lindblad approaches with applications to open quantum optical systems, J. Mod. Opt. 61, 1298 (2014).
- (27) K. G. Makris, R. El-Ganainy, D. N. Christodoulides, and Z. H. Musslimani, Beam Dynamics in PT Symmetric Optical Lattices, Phys. Rev. Lett. 100, 103904 (2008).
- (28) R. El-Ganainy, K. G. Makris, D. N. Christodoulides, and Z. H. Musslimani, Theory of coupled optical PT-symmetric structures, Opt. Lett. 32, 2632 (2007).
- (29) A. Guo, G. J. Salamo, D. Duchesne, R. Morandotti, M. Volatier-Ravat, V. Aimez, G. A. Siviloglou, and D. N. Christodoulides, Observation of PT-Symmetry Breaking in Complex Optical Potentials, Phys. Rev. Lett. 103, 093902 (2009).
- (30) A. Regensburger, C. Bersch, M.-A. Miri, G. Onishchukov, D. N. Christodoulides, and U. Peschel, Parity-time synthetic photonic lattices, Nature 488, 167 (2012).
- (31) H. Hodaei, M. A. Miri, M. Heinrich, and M. Khajavikhan, Parity-time-symmetric microring lasers, Science 346, 975 (2014).
- (32) L. Feng, Z. J. Wong, R. M. Ma, Y . Wang, and X. Zhang, Single-mode laser by parity-time symmetry breaking, Science 346, 972 (2014).
- (33) J. Li, R. Yu, C. Ding, and Y. Wu, PT-symmetry-induced evolution of sharp asymmetric line shapes and high-sensitivity refractive index sensors in a three-cavity array, Phys. Rev. A93, 023814 (2016).
- (34) S. Longhi, Bloch Oscillations in Complex Crystals with PT Symmetry, Phys. Rev. Lett. 103, 123601 (2009).
- (35) S. Longhi, Optical Realization of Relativistic Non-Hermitian Quantum Mechanics, Phys. Rev. Lett. 105, 013903 (2010).
- (36) C. E. Rüter, K. G. Makris, R. El-Ganainy, D. N. Christodoulides, M. Segev, and D. Kip, Observation of parity-time symmetry in optics, Nat. Phys. 6, 192 (2010).
- (37) Y. Xue, C. Hang, Y. He, Z. Bai, Y. Jiao, G. Huang, J. Zhao, and S. Jia, Experimental observation of partial parity-time symmetry and its phase transition with a laser-driven cesium atomic gas, Phys. Rev. A105, 053516 (2022).
- (38) A. Stegmaier, S. Imhof, and T. Helbig, Topological Defect Engineering and PT Symmetry in Non-Hermitian Electrical Circuits, Phys. Rev. Lett. 126, 215302 (2021).
- (39) X. Y. Lü, H. Jing, J. Y. Ma, and Y. Wu, PT-Symmetry-Breaking Chaos in Optomechanics Phys. Rev. Lett. 114, 253601 (2015).
- (40) C. M. Bender, J. Feinberg, D. W. Hook, et al, Chaotic systems in complex phase space, Pramana - J Phys 73, 453 (2009).
- (41) C. M. Bender, D. W. Hook, P. N. Meisinger, and Q. H. Wang, Complex Correspondence Principle, Phys. Rev. Lett. 104, 061601 (2010).
- (42) W. Zhao and H. Zhang, Dynamical stability in a non-Hermitian kicked rotor model, Symmetry 15, 113 (2013).
- (43) C. T. West, T. Kottos, and T. Prosen, PT-Symmetric Wave Chaos, Phys. Rev. Lett. 104, 054102 (2010).
- (44) S. Longhi, Localization, quantum resonances, and ratchet acceleration in a periodically kicked PT -symmetric quantum rotator, Phys. Rev. A95 012125 (2017).
- (45) W. L. Zhao, J. Wang, X. Wang, and P. Tong, Directed momentum current induced by the PT-symmetric driving, Phys. Rev. E99, 042201 (2019).
- (46) A. Larkin and Y. N. Ovchinnikov, Quasiclassical method in the theory of superconductivity, Sov. Phys. JETP 28, 1200 (1969).
- (47) D. A. Roberts, and B. Swingle, Lieb-Robinson bound and the butterfly effect in quantum field theories, Phys. Rev. Lett. 117, 091602 (2016).
- (48) J. Maldacena and D. Stanford, Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D94, 106002 (2016).
- (49) J. Polchinski and V. Rosenhaus, The spectrum in the Sachdev-Ye-Kitaev model, J. High Energ. Phys 2016, 1 (2016).
- (50) A. Bohrdt, C. Mendl, M. Endres, and M. Knap, Scrambling and thermalization in a diffusive quantum many-body system, New J. Phys. 19, 063001 (2017).
- (51) M. Gärttner, J. G. Bohnet, A. Safavi-Naini, M. L. Wall, J. J. Bollinger, and A. M. Rey, Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet, Nat. Phys. 13, 781 (2017).
- (52) S. Banerjee and E. Altman, Solvable model for a dynamical quantum phase transition from fast to slow scrambling, Phys. Rev. B95, 134302 (2017).
- (53) H. Shen, P. Zhang, R. Fan, and H. Zhai, Out-of-time-order correlation at a quantum phase transition, Phys. Rev. B96, 054503 (2017).
- (54) R. Fan, P. Zhang, H. Shen, and H. Zhai, Out-of-time-order correlation for many-body localization, Science Bulletin 62, 707 (2017).
- (55) Y. Huang, Y.-L. Zhang, and X. Chen, Out-of-Time- Ordered Correlators in Many-Body Localized Systems, Ann. Phys. (Berlin) 529, 1600318 (2017).
- (56) J. Li, R. Fan, H. Wang, B. Ye, B. Zeng, H. Zhai, X. Peng, and J. Du, Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator, Phys. Rev. X 7, 031011 (2017).
- (57) Z. Weinstein, S. P. Kelly, J. Marino, E. Altman, Scrambling Transition in a Radiative Random Unitary Circuit, arXiv:2210.14242 quant-ph.
- (58) Xi. Hu, T. Luo, and D. Zhang, Quantum algorithm for evaluating operator size with Bell measurements, Phys. Rev. A107, 022407 (2023).
- (59) S. Pappalardi, J. Kurchan, Low temperature quantum bounds on simple models, SciPost Phys. 13, 006 (2022).
- (60) I. García-Mata, M. Saraceno, R. A. Jalabert, A. J. Roncaglia, and D. A. Wisniacki, Chaos Signatures in the Short and Long Time Behavior of the Out-of-Time Ordered Correlator, Phys. Rev. Lett. 121, 210601 (2018).
- (61) J. Wang, G. Benenti, G. Casati, and W. G. Wang, Quantum chaos and the correspondence principle, Phys. Rev. E103, L030201 (2021).
- (62) R. A. Kidd, A. Safavi-Naini, and J. F. Corney, Saddle-point scrambling without thermalization, Phys. Rev. A103, 033304 (2021).
- (63) V. Balachandran, G. Benenti, G. Casati, and D. Poletti, From the eigenstate thermalization hypothesis to algebraic relaxation of OTOCs in systems with conserved quantities, Phys. Rev. B104, 104306 (2021).
- (64) J. Harris, Bin Yan, and N. A. Sinitsyn, Benchmarking Information Scrambling, Phys. Rev. Lett. 129, 050602 (2022).
- (65) J. Braumüller, et al, Probing quantum information propagation with out-of-time-ordered correlators, Nat. Phys. 18, 172 (2022).
- (66) Y. L. Zhang, Y. Huang, and X. Chen, Information scrambling in chaotic systems with dissipation, Phys. Rev. B99, 014303 (2019).
- (67) B. Yan, and N. A. Sinitsyn, Recovery of damaged information and the out-of-time-ordered correlators, Phys. Rev. Lett. 125, 040605 (2020).
- (68) A. A. Patel, D. Chowdhury, S. Sachdev, and B. Swingle, Quantum butterfly effect in weakly interacting diffusive metals, Phys. Rev. X 7, 031047 (2017).
- (69) W. Zhao and R. Wang, Scaling laws of out-of-time-order correlators in a non-Hermitian kicked rotor model, Front. Phys 11, 1130225 (2023).
- (70) K. Hashimoto, K. Murata, and R. Yoshii, Out-of-time-order correlators in quantum mechanics, J. High Energ. Phys. 2017, 138 (2017).
- (71) S. Zamani, R. Jafari, and A. Langari, Out-of-time-order correlations and floquet dynamical quantum phase transition, Phys. Rev. B105, 094304 (2022).
- (72) Martin Grttner, P. Hauke, and A. M. Rey, Relating Out-of-Time-Order Correlations to Entanglement via Multiple-Quantum Coherences, Phys. Rev. Lett. 120, 040402 (2018).
- (73) R. J. Lewis-Swan, A. Safavi-Naini, A. M. Kaufman, and A. M. Rey, Dynamics of Quantum Information, Nat. Rev. Phys. 1, 627 (2019).
- (74) W. L. Zhao, Quantization of out-of-time-ordered correlators in non-Hermitian chaotic systems, Phys. Rev. Research 4, 023004 (2022)
- (75) K. X. Wei, C. Ramanathan, and P. Cappellaro, Exploring Localization in Nuclear Spin Chains, Phys. Rev. Lett. 120, 070501 (2018).
- (76) X. Nie, Z. Zhang, X. Zhao, T. Xin, D. Lu, and J. Li, Detecting scrambling via statistical correlations between randomized measurements on an NMR quantum simulator arXiv:1903.12237.
- (77) K. A. Landsman, C. Figgatt, T. Schuster, N. M. Linke, B. Yoshida, N. Y. Yao, and C. Monroe, Verified quantum information scrambling, Nature, 567, 61 (2019).
- (78) S. K. Zhao, Z. Y. Ge, Z. Xiang, G. M. Xue, and S. P, Zhao, Probing Operator Spreading via Floquet Engineering in a Superconducting Circuit arXiv.2108.01276.
- (79) G. Casati, B. V. Chirikov, F. M. Izrailev, and J. Ford, Stochastic Behavior in Classical and Quantum Hamiltonian Systems, edited by G. Casati and J. Ford, Lecture Notes in Physics, Vol. 93 (Springer, Berlin, 1979).
- (80) T. Mano and T. Ohtsuki, Machine learning the dynamics of quantum kicked rotor, Annals of Physics, 435, 168500 (2021).
- (81) X. Chen, T. Zhou, D. A. Huse, and E. Fradkin, Out-of-time-order correlations in many-body localized and thermal phases, Ann. Phys. 529, 1600332.
- (82) B. Dóra and R. Moessner, Out-of-time-ordered density correlators in Luttinger liquids, Phys. Rev. Lett. 119, 026802 (2017).
- (83) I. García-Mata, M. Saraceno, R. A. Jalabert, A. J. Roncaglia, and D. A. Wisniacki, Chaos signatures in the short and long time behavior of the out-of-time ordered correlator, Phys. Rev. Lett. 121, 210601 (2018).
- (84) Y. Alavirad and A. Lavasani, Scrambling in the Dicke model, Phys. Rev. A99, 043602. (2018).
- (85) B. Swingle, G. Bentsen, M. Schleier-Smith, and P. Hayden, Measuring the scrambling of quantum information, Phys. Rev. A94, 040302 (2016).
- (86) G. Zhu, M. Hafezi, and T. Grover, Measurement of many-body chaos using a quantum clock, Phys. Rev. A94, 062329 (2016).
- (87) M. Heyl, F. Pollmann, and B. Dóra, Detecting equilibrium and dynamical quantum phase transitions in Ising chains via out-of-time-ordered correlators, Phys. Rev. Lett. 121, 016801 (2018).
- (88) L. D’Alessio and M. Rigol, Long-time Behavior of Isolated Periodically Driven Interacting Lattice Systems, Phys. Rev. X 4, 041048 (2014).
- (89) W. L. Zhao, Y. Hu, Z. Li, and Q. Wang, Super-exponential growth of Out-of-time-ordered correlators, Phys. Rev. B103, 184311 (2021).
- (90) R. Hamazaki, K. Fujimoto, and M. Ueda, Operator Noncommutativity and Irreversibility in Quantum Chaos arXiv:1807.02360.
- (91) F.M. Izrailev, Simple modelds of quantum chaos: spectrum and eigenfunctions, Phys. Rep. 196, 299 (1990), and references therein.
- (92) S. Moudgalya, T. Devakul, C. W. von Keyserlingk, and S. L. Sondhi, Operator spreading in quantum maps, Phys. Rev. B, 99 094312 (2019).
- (93) T. Zhou, S. Xu, X. Chen, A. Guo, and B. Swingle, Operator Lévy Flight: Light Cones in Chaotic Long-Range Interacting Systems, Phys. Rev. Lett. , 124, 180601 (2020).
- (94) K. X. Wei, P. Peng, O. Shtanko, I. Marvian, S. Lloyd, C. Ramanathan, and P. Cappellaro, Emergent Prethermalization Signatures in Out-of-Time Ordered Correlations, Phys. Rev. Lett. 123, 090605 (2019).
- (95) T. Boness, K. Kudo, and T. S. Monteiro, Doubly excited ferromagnetic spin-chain as a pair of coupled kicked rotors, Phys. Rev. E81, 046201 (2010).