Scalable Set Encoding with Universal Mini-Batch Consistency and
Unbiased Full Set Gradient Approximation
Abstract
Recent work on mini-batch consistency (MBC) for set functions has brought attention to the need for sequentially processing and aggregating chunks of a partitioned set while guaranteeing the same output for all partitions. However, existing constraints on MBC architectures lead to models with limited expressive power. Additionally, prior work has not addressed how to deal with large sets during training when the full set gradient is required. To address these issues, we propose a Universally MBC (UMBC) class of set functions which can be used in conjunction with arbitrary non-MBC components while still satisfying MBC, enabling a wider range of function classes to be used in MBC settings. Furthermore, we propose an efficient MBC training algorithm which gives an unbiased approximation of the full set gradient and has a constant memory overhead for any set size for both train- and test-time. We conduct extensive experiments including image completion, text classification, unsupervised clustering, and cancer detection on high-resolution images to verify the efficiency and efficacy of our scalable set encoding framework. Our code is available at github.com/jeffwillette/umbc
1 Introduction
For a variety of problems for which deep models can be applied, unordered sets naturally arise as an input. For example, a set of words in a document (Jurafsky & Martin, 2008) and sets of patches within an image for multiple instance learning (Quellec et al., 2017). Functions which encode sets are commonly known as set encoders, and most previously proposed set encoding functions (Zaheer et al., 2017; Lee et al., 2019) have implicitly assumed that the whole set can fit into memory and be accessed in a single chunk. However, this is not a realistic assumption if it is necessary to process large sets or streaming data. As shown in Figure 2(a), Set Transformer (Lee et al., 2019) cannot properly handle streaming data and suffers performance degradation. Please see Figure 8 for more qualitative examples. Bruno et al. (2021) identified this problem, and introduced the mini-batch consistency (MBC) property which dictates that an MBC set encoding model must be able to sequentially process subsets from a partition of a set while guaranteeing the same output over any partitioning scheme, as illustrated in Figure 1. In order to satisfy the MBC property, they devised an attention-based MBC model, the Slot Set Encoder (SSE).





Although SSE satisfies MBC, there are several limitations. First, it has limited expressive power due to the constraints imposed on its architecture. Instead of the conventional softmax attention (Vaswani et al., 2017), the attention of SSE is restricted to using a sigmoid for attention without normalization over the rows of the attention matrix, which may be undesirable for applications requiring convex combinations of inputs. Moreover, the Hierarchical SSE is a composition of pure MBC functions and thus cannot utilize more expressive non-MBC models, such as those utilizing self-attention. Another crucial limitation of the SSE is its limited scalability during training. Training models with large sets requires computing gradients over the full set which can be computationally prohibitive. SSE proposes to randomly sample a small subset for gradient computation, which is a biased estimator of the full set gradient as we show in Section A.8.
To tackle these limitations of SSE, we propose Universal MBC (UMBC) set functions which enable utilizing a broader range of functions while still satisfying the MBC property. Firstly, we relax the restriction to the sigmoid on the activation functions for attention and show that cross-attention with a wider class of activation functions, including the softmax, is MBC. Moreover, we re-interpret UMBC’s output as a set, which as we show in Figures 1 and 3, universally allows for the application of non-MBC set encoders when processing UMBC’s output sets, resulting in more expressive functions while maintaining the MBC property. For a concrete example, UMBC used in conjunction with the (non-MBC) Set Transformer (ST) produces consistent output for any partition of a set as shown in Figure 3, and outperforms all other MBC models for clustering streaming data as illustrated in Figure 2.
Lastly, for training MBC models, we propose a novel and scalable algorithm to approximate full set gradient. Specifically, we obtain the full set representation by partitioning the set into subsets and aggregating the subset representations while only considering a portion of the subsets for gradient computation. We find this leads to a constant memory overhead for computing the gradient with a fixed size subset, and is an unbiased estimator of the full set gradient.
To verify the efficacy and efficiency of our proposed UMBC framework and full set gradient approximation algorithm, we perform extensive experiments on a variety of tasks including image completion, text classification, unsupervised clustering, and cancer detection on high-resolution images. Furthermore, we theoretically show that UMBC is a universal approximator of continuous permutation invariant functions under some mild assumptions and the proposed training algorithm minimizes the total loss of the full set version by making progress toward its stationary points. We summarize our contributions as follows:
-
•
We propose a UMBC framework which allows for a broad class of activation functions, including softmax, for attention and also enables utilizing non-MBC functions in conjuction with UMBC while satisfying MBC, resulting in more expressive and less restrictive architectures.
-
•
We propose an efficient training algorithm with a constant memory overhead for any set size by deriving an unbiased estimator of the full set gradient which empirically performs comparably to using the full set gradient.
-
•
We theoretically show that UMBC is a universal approximator to continuous permutation invariant functions under mild assumptions and our algorithm minimizes the full set total loss by making progress toward its stationary points.

2 Related Work
Set Encoding. Deep learning for set structured data has been an active research topic since the introduction of DeepSets (Zaheer et al., 2017), which solidified the requirements of deep set functions, namely permutation equivariant feature extraction and permutation invariant set pooling. Zaheer et al. (2017) have shown that under certain conditions, functions which satisfy the aforementioned requirements act as universal approximators for functions of sets. Subsequently, the Set Transformer (Lee et al., 2019) applied attention (Vaswani et al., 2017) to sets, which has proven to be a powerful tool for set functions. Self-attentive set functions excel on tasks where independently processing set elements may fail to capture pairwise interactions between elements. Subsequent works which utilize pairwise set element interactions include optimal transport (Mialon et al., 2021) and expectation maximization (Kim, 2022). Other notable approaches to permutation invariant set pooling include featurewise sorting (Zhang et al., 2020), and canonical orderings of set elements (Murphy et al., 2019).
Mini-Batch Consistency (MBC). Every method mentioned in the preceding paragraph suffers from an architectural bias which limits them to seeing and processing the whole set in a single chunk. Bruno et al. (2021) identified this problem, and highlighted the necessity for MBC which guarantees that processing and aggregating each subset from a set partition results in the same representation as encoding the entire set at once (Definition 3.2). This is important in settings where the data may not fit into memory due to either large data or limited on-devices resources. In addition to identifying the MBC property, Bruno et al. (2021) also proposed the Slot Set Encoder (SSE) which utilizes cross attention between learnable ‘slots’ and set elements in conjunction with simple activation functions in order to achieve an MBC model. As shown in Table 1, however, SSE cannot utilize self-attention to model pairwise interactions of set elements due to the constraints imposed on its architecture, which makes it less expressive than the Set Transformer.
3 Method
In this section, we describe the problem we target and provide a formulation for UMBC models along with a derivation of our unbiased full set gradient approximation algorithm. All proofs of theorems are deferred to Appendix A.
3.1 Preliminaries
Let be a -dimensional vector space over and let be the power set of . We focus on a collection of finite sets , which is a subset of such that . We want to construct a parametric function satisfying permutation invariance. Specifically, given a set , the output of the function is a fixed sized representation which is invariant to all permutations of the indices . For supervised learning, we define a task specific decoder and optimize parameters and to minimize the loss
| (1) |
on training data , where is a label for the input set and denotes a loss function.
Definition 3.1 (Permutation Invariance).
Let be the set of all permutations of , i.e. where . A function is permutation invariant iff for all and for all permutation .
We further assume that the cardinality of a set is sufficiently large, such that loading and processing the whole set at once is computationally prohibitive. For non-MBC models, a naïve approach to solve this problem would be to encode a small subset of the full set as an approximation, leading to a possibly suboptimal representation of the full set. Instead, Bruno et al. (2021) propose a mini-batch consistent (MBC) set encoder, the Slot Set Encoder (SSE), to piecewise process disjoint subsets of the full set and aggregate them to obtain a consistent full set representation.
Definition 3.2 (Mini-Batch Consistency).
We say a function is mini-batch consistent iff for any , there is a function such that for any partition of the set ,
| (2) |
Models which satisfy the MBC property can partition a set into subsets, encode, and then aggregate the subset representations to achieve the exact same output as encoding the full set. Due to constraints on the architecture of the SSE, however, on certain tasks the SSE shows weaker performance than non-MBC set encoders such as Set Transformer (Lee et al., 2019) which utilizes self attention. To tackle this limitation, we propose Universal MBC (UMBC) set encoders which are both MBC and also allow for the use of arbitrary non-MBC set functions while still satisfying MBC property.
3.2 Universal Mini-Batch Consistent Set Encoder
In this section, we provide a formulation of our UMBC set encoder . Given an input set , we represent it as a matrix whose rows are elements in the set, and independently process each element with as , where is a deep feature extractor. We then compute the un-normalized attention score between a set of learnable slots and as:
| (3) |
where is an element-wise activation function with for all , LN denotes layer normalization (Ba et al., 2016), and are parameters which are part of . For simplicity, we omit biases for , and . With the un-normalized attention score , we can define a map
| (4) |
for , where is defined by either which normalizes the columns or the identity mapping . The choice of depends on the desired activation function . Alternatively, similar to slot attention (Locatello et al., 2020), we can make the function stochastic by sampling with reparameterization (Kingma & Welling, 2013) for , where are part of the parameters . If we sample with a sigmoid for and for normalization, and then apply a pooling function (sum, mean, min, or max) to the columns of , we achieve a function equivalent to the SSE, where is -th row of .
However, SSE has some drawbacks. First, since the attention score of is independent to the other attention scores for , it is impossible for the rows of to be convex coefficients as the softmax outputs in conventional attention (Vaswani et al., 2017). Notably, in some of our experiments, the constrained attention activation originally used in the SSE, which we call slot-sigmoid, significantly degrades generalization performance. Furthermore, stacking hierarchical SSE layers has been shown to harm performance (Bruno et al., 2021), which limits the power of the overall model.
To overcome these limitations of the SSE, we propose a Universal Mini-Batch Consistent (UMBC) set encoder by allowing the set function to also use arbitrary non-MBC functions. Firstly, we propose normalizing the attention matrix over rows to consider dependency among different elements of the set in the attention operation:
| (5) | |||
| (6) |
where . We prove that a UMBC set encoder is permutation invariant, equivariant, and MBC.
Theorem 3.3.
A UMBC function is permutation invariant.
Any strictly positive elementwise function is a valid . For an instance, if we use the identity mapping with , the attention matrix is equivalent to applying the softmax to each row of , which is hypothesized to break the MBC property by Bruno et al. (2021). However, we show that this does not break the MBC property in Appendix A.2. Intuitively, since
| (7) |
holds for any partition of the set , we can iteratively process each subset and aggregate them without losing any information of , i.e., is MBC even when normalizing over the elements of the set. Note that the operation outlined above is mathematically equivalent to the softmax, but uses a non-standard implementation. We discuss the implementation and list 5 such valid attention activation functions which satisfy the MBC property in Appendix I.
Theorem 3.4.
Given the slots , a UMBC set encoder is mini-batch consistent.
Lastly, we may consider the output of a UMBC set encoder as either a fixed vector or a set of elements. Under the set interpretation, we may therefore apply subsequent functions on the set of cardinality . To provide a valid input to subsequent set encoders, it is sufficient to view UMBC as a set to set function for each set , which is permutation equivariant w.r.t. the slots .
Definition 3.5.
A function is said to be permutation equivariant iff for all and for all , where contains all permutations of , and denote -th row of and , respectively.
Theorem 3.6.
For each input , is equivariant w.r.t. permutations of the slots .
A key insight is that we can leverage non-MBC set encoders such as Set Transformer after a UMBC layer to improve expressive power of an MBC model while still satisfying MBC (Definition 3.2). As a result, with some assumptions, a UMBC set encoder used in combination with any continuously sum decomposable (Zaheer et al., 2017) permutation invariant deep neural network is a universal approximator of the class of continuously sum decomposable functions.
Theorem 3.7.
Let and restrict the domain to . Suppose that the nonlinear activation function of has nonzero Taylor coefficients up to degree . Then, UMBC used in conjunction with any continuously sum-decomposable permutation-invariant deep neural network with nonlinear activation functions that are not polynomials of finite degrees is a universal approximator of the class of functions .
Although we use a non-MBC set encoder on top of UMBC, this does not violate the MBC property. Since we may obtain by sequentially processing each subset of and the resulting set with cardinality is assumed small enough to load in memory, we can directly provide the MBC output of UMBC to the non-MBC set encoder.
Corollary 3.8.
Let be a (non-MBC) set encoder and let be a UMBC set encoder. Then is mini-batch consistent.
For notational convenience, we write to indicate the composition of a set encoder and a decoder , throughout the paper. Similarly, the parameter denotes .
3.3 Stochastic Approximation of the Full Set Gradient
Although we can leverage SSE or UMBC at test-time by sequentially processing subsets to obtain the full set representation , at train-time it is infeasible to utilize the gradient of the loss (equation 1) w.r.t. the full set. Computation of the full set gradient with automatic differentiation requires storing the entire computation graph for all forward passes of each subset from denoted as a partition of a set , which incurs a prohibitive computational cost for large sets. As a simple approximation, Bruno et al. (2021) propose randomly sampling a single subset and computing the gradient of the loss based on a single subset at each iteration.
Remark 3.9.
Let be a partition of set and be a subset of . Then the gradient of is a biased estimation of the full set gradient and leads to a suboptimal solution in our experiments. Please see Appendix A.8 for further details.
In order to tackle this issue, we propose an unbiased estimation of the full set gradient which incurs a constant memory overhead. Firstly, we uniformly and independently sample a mini-batch from the training dataset for every iteration . We denote this process by Then, for each , we sample a mini-batch from the partition of , i.e., all are drawn independently and uniformly from . Denote this process by . Instead of storing the computational graph of all forward passes of subsets in the partition of a set , we apply StopGrad to all subsets as follows:
| (8) | ||||
| (9) |
where, for any function , the symbol denotes a constant with its value being , i.e., . For simplicity, we omit the superscript if there is no ambiguity. Finally, we update both the parameter and of the respective encoder and decoder using the gradient of the following functions, respectively at :
| (10) | ||||
| (11) |
We outline our proposed training method in Algorithm 1. Note that we can apply our algorithm to any set encoder for which a full set representation can be decomposed into a summation of subset representations as in equation 7 such as Deepsets with sum or mean pooling, or SSE which are in fact special cases of UMBC. Furthermore, we can apply the algorithm to any differentiable non-MBC set encoder if we simply place a UMBC layer before the non-MBC function. As a consequence of the operation, if we set , our method incurs the same computation graph storage cost as randomly sampling a single subset. Moreover, and are unbiased estimators of and , respectively.
Theorem 3.10.
For any , and are unbiased estimators of and as follows:
| (12) | ||||
| (13) |
where the first expectation is taken for , and the second expectation is taken for for all .
4 Experiments




4.1 Amortized Clustering
We consider amortized clustering on a dataset generated from Mixture of Gaussians (MoGs) (See Appendix C for dataset construction details). Given a set sampled from a MoGs, the goal is to output the mixing coefficients, and Gaussian mean and variance, which minimizes the negative log-likelihood of the set as follows:
| (14) | |||
| (15) |
where denotes a mean vector and a diagonal covariance matrix for -th Gaussian, and is -th mixing coefficient. Note that there is no label since it is an unsupervised clustering problem. We optimize the parameters of the set encoder to minimize the loss over a batch, .
Setup. We evaluate training with the full set gradient vs. the unbiased estimation of the full set gradient. In this setting, for gradient computation, MBC models use a subset of 8 elements from a full set of 1024 elements. Non MBC models such as Set Transformer (ST), FSpool (Zhang et al., 2020), and Diff EM (Kim, 2022) are also trained with the set of 8 elements. We compare our UMBC model against Deepsets, SSE, Set Transformer, FSPool, and Diff EM. Note that at test-time all non-MBC models process every 8 element subset from the full set independently and aggregate the representations with mean pooling.
| Model | MBC | NLL() | Memory (Kb) | Time (Ms) |
|---|---|---|---|---|
| DeepSets | ✓ | |||
| SSE | ✓ | |||
| SSE (Hierarchical) | ✓ | |||
| FSPool | ✗ | |||
| Diff EM | ✗ | |||
| Set Transformer (ST) | ✗ | |||
| UMBC + FSPool | ✓ | |||
| UMBC + Diff EM | ✓ | |||
| UMBC + ST | ✓ |
Results. In Figure 4, interestingly, the unbiased estimation of the full set gradient (red) is almost indistinguishable from the full set gradient (blue) for DeepSets and UMBC, while there is a significant gap for SSE. In all cases, the unbiased estimation of the full set gradient outperforms training with the biased gradient approximation with only the set of 8 elements per random sample (green), which is proposed by Bruno et al. (2021). Lastly, as shown in Table 2, we compare all models in terms of generalization performance (NLL), memory usage, and wall-clock time for processing a single subset. All non-MBC models show underperformance due to their violation of the MBC property. However, if we utilize ‘UMBC+’ compositions, the composition becomes MBC with significantly improved performance and little added overhead for memory and time complexity. In contrast, a composition of pure MBC functions, the Hierarchical SSE degrades the performance of SSE. Notably, UMBC with Set Transformer outperforms all other models whereas Set Transformer alone achieves the worst NLL. These results verify expressive power of UMBC in conjuction with non-MBC models.




4.2 Image Completion
In this task, we are given a set of RGB pixel values of an image as well as the corresponding 2-dimensional coordinates normalized to be in . The goal of the task is to predict RGB pixel values of all coordinates of the image. Specifically, given a context set processed by the set encoder, we obtain the set representation . Then, a decoder which utilizes both the set representation and the target coordinates, learns to predict a mean and variance for each coordinate of the image as , where . Then we compute the negative log-likelihood of the label set :
| (16) |
where is a univariate Gaussian probability density function. Finally, we optimize and to minimize the loss .
Setup. In our experiments, we impose the restriction that a set encoder is only allowed to compute the gradient with 100 elements of a context set during training and the model can only process 100 elements of the context set at once at test time. We train the set encoders in a Conditional Neural Process (Garnelo et al., 2018) framework, using images from the CelebA dataset (Liu et al., 2015). We vary the cardinality of the context set size and compare the negative log-likelihood (NLL) of each model. For baselines, we compare our UMBC set encoder against: Deepsets, SSE, Hierarchical SSE, Set Transformer (ST), FSPool, and Diff EM. For our UMBC, we use the softmax for in equation 3 and place the ST after the UMBC layer.
Results. First, as shown in Figure 5(a), our UMBC + ST model outperforms all baselines, empirically verifying the expressive power of UMBC. SSE underperforms in terms of NLL due to its constrained architecture. Moreover, stacking hierarchical SSE layers degrades the performance of SSE for larger sets. Note that all MBC set encoders (Deepsets, SSE, Hierarchical SSE and UMBC) in Figure 5(a) are trained with our proposed unbiased gradient approximation in Algorithm 1. On the other hand, we train non-MBC models such as Set Transformer (ST), FSPool, and Diff EM with a randomly sampled subset of 100 elements, and perform mean pooling over all subset representations at test-time to approximate an MBC model.
Additionally, Figure 5(b) shows GPU memory usage for each model while processing sets of varying cardinalities without a memory constraint. The marker size is proportional to the set cardinality. Notably, all four MBC models incur a constant memory overhead to process any set size, as we can apply StopGrad to most of the subset, and compute an unbiased gradient estimate with a fixed sized subset (100). However, memory overhead for all non-MBC models is a function of set size. Thus, Set Transformer uses more than twice the memory of UMBC to achieve a similar log-likelihood on a set of 500 elements.
Lastly, in Figure 5(c), we show how our proposed unbiased training algorithm (red) improves the generalization performance of UMBC models compared to training with a limited subset of 100 elements (green). Notably, the performance of our algorithm is indistinguishable from that of training models with the full set gradient (blue). We present similar plots for Deepsets and SSE in Figures 11(a) and 11(b). Across all models, our training algorithm significantly and consistently improves performance compared to training with random subsets of 100 elements, while requiring the same amount of memory. These empirical results verify both efficiency and effectiveness of our proposed method.
| Model | F1 | MBC | Memory (MB) |
|---|---|---|---|
| Longformer | ✗ | ||
| ToBERT | ✗ | ||
| DeepSets w/ 100 | ✓ | ||
| DeepSets w/ full | ✓ | ||
| SSE w/ 100 | ✓ | ||
| SSE w/ full | ✓ | ||
| UMBC + BERT w/ 100 | 70.48 | ✓ | |
| UMBC + BERT w/ full | 70.23 | ✓ |
4.3 Long Document Classification
In this task, we are given a long document consisting of an average of words. The goal of this task is to predict a binary multi-label of the document, where is the number of classes. We ignore the order of words and consider the document as a multiset of words, i.e., a set allowing duplicate elements. Specifically, given a training dataset , we process each set with the set encoder to obtain the set representation . We then use a decoder to output the probability of each class and compute the cross entropy loss:
|
|
(17) |
where and denotes the sigmoid function. Finally we optimize and to minimize the loss .
Setup. All models are trained on the inverted EURLEX dataset (Chalkidis et al., 2019) consisting of long legal documents divided into sections. The order of sections are inverted following prior work (Park et al., 2022). To predict a label, we give the whole document to the model without any truncation. We compare the micro F1 of each model.
We compare UMBC to Deepsets, SSE, ToBERT (Pappagari et al., 2019), and Longformer (Beltagy et al., 2020). For Deepsets and SSE, we use the pre-trained word embedding from BERT (Devlin et al., 2019) without positional encoding and 2 layer fully connected (FC) networks for feature extractor . We use another 3 layer FC network for the decoder. For UMBC, we use the same feature extractor as SSE but instead use the pre-trained BERT as a decoder, with a randomly initialized linear classifier. We remove the positional encoding of BERT for UMBC to ignore word order. For all the MBC models, we train them both with full set denoted as “w/ full” and with our gradient approximation method on a subset of 100 elements denoted as “w/ 100”.

Results. As shown in Table 3, our proposed UMBC outperforms all baselines including non-MBC models — Longformer and ToBERT which require excessive amounts of GPU memory for training models with long sequences. This result again verifies the expressive power of UMBC with BERT (a non-MBC model) for long document classification. Moreover, with significantly less GPU memory, all MBC models (Deepsets, SSE, and UMBC) trained with our unbiased gradient approximation using a subset of 100 elements, achieve similar performance to the models trained with full set. Lastly, in Figure 6, we plot the micro F1 score as a function of the cardinality of the subset used for gradient computation when training the UMBC model. Our proposed unbiased gradient approximation (red) shows consistent performance for all subset cardinalities. In contrast, training the model with a small random subset (green) is unstable, resulting in underperformance and higher F1 variance.
| Model | MBC | Accuracy | AUROC | Accuracy | AUROC |
| Pretrain | MBC Finetune | ||||
| DS-MIL | ✗ | - | - | ||
| AB-MIL | ✗ | - | - | ||
| DeepSets | ✓ | ||||
| SSE | ✓ | ||||
| UMBC + ST | ✓ | ||||
4.4 Multiple Instance Learning (MIL)
In MIL, we are given a ‘bag’ of instances with a corresponding bag label, but no labels for each instance within the bag. Labels should not depend on the order of the instances, i.e., MIL can be recast as a set classification problem. Specifically, given a set , the goal is to predict its binary label . For this task, we obtain two streams of set representations and compute the cross entropy loss from the decoder output as:
| (18) | |||
| (19) |
where and are parameters and is the cross entropy loss described in equation 17 with . We optimize all parameters to minimize the loss . At test time, we predict a label for a set as:
| (20) |
where , , is the sigmoid function, is indicator function and is threshold tuned on the validation set.
Setup. We evaluate all models on the Camelyon16 Whole Slide Image cancer detection dataset (Bejnordi et al., 2017). Each instance consists of a high resolution image of tissue from a medical scan which is pre-processed into patches of RGB pixels. After pre-processing, the average number of patches in a single set is over 9,300 (7.3GB), making each input roughly equivalent to processing 1% of ImageNet1k (Deng et al., 2009). The largest input in the training set contains 32,382 patches (25.4 GB). We utilize a ResNet18 (He et al., 2016) which is pretrained on Camelyon16 (Li et al., 2021) via SimCLR (Chen et al., 2020) as a backbone feature extractor whose weights can be downloaded from this repository111https://github.com/binli123/dsmil-wsi. Our goal is to first pretrain MBC set encoders on the extracted features, and then use the unbiased estimation of the full set gradient to fine-tune the feature extractor on the full input sets. We evaluate the performance of UMBC against non-MBC MIL baselines: DS-MIL (Li et al., 2021) and AB-MIL (Ilse et al., 2018), as well as MBC baselines: DeepSets and SSE.
Results. As shown in Table 4, our UMBC model achieves the best accuracy and competitive AUROC score. Note that SSE shows the worst performance due to its constrained architecture, which even underperforms DeepSets in this task. These empirical results again verify the expressive power of our UMBC model. Moreover, we can further improve the performance of UMBC via fine-tuning the backbone network, ResNet18, which is only feasible as a consequence of our unbiased full set gradient approximation which incurs constant memory overhead. However, it is not possible for the non-MBC models to fine-tune with the ResNet18 since it is computationally prohibitive to compute the gradient of the ResNet18 with sets consisting of tens of thousands of patches with resolution.
4.5 Ablation Study
To validate effectiveness of activation functions for attention in equation 3, we train UMBC + Set Transformer with different activation functions listed in Table 15 for the amortized clustering and MIL pretraining tasks. As shown in Figures 7 and 7, softmax attention outperforms all the other activation functions whereas the slot-sigmoid used for attention in SSE underperforms. This experiment highlights the importance of choosing the proper activation function for attention, which is enabled by our UMBC framework.

| Activation | Acc. | AUC |
|---|---|---|
| slot-sigmoid | ||
| slot-exp | ||
| sigmoid | ||
| slot-softmax | ||
| softmax | 87.91 | 0.874 |
5 Limitations and Future Work
One potential limitation of our method is a higher time complexity needed for our proposed unbiased gradient estimation during mini-batch training. If represents the size of a single subset, and represents the size of the whole set, then the naive sampling strategy of Bruno et al. (2021) has a time complexity of while our full set gradient approximation has a complexity of during training since we must process the full set. However, we note some things we gain in exchange for this higher time complexity below.
Our unbiased gradient approximation can achieve higher performance than the biased sampling of a single subset as denoted in our experiments (specifically, see Figures 4, 5(c) and 6). Additionally, due to the stop gradient operation in Equation 9, UMBC achieves a constant memory overhead for any training set size. Our experiment in Figure 5(b) shows a constant memory overhead for SSE and DeepSets only because we apply our unbiased gradient approximation to those models in that experiment. The original models as they were presented in the original works do not have a constant memory overhead. As a result, our method can process huge sets during training, and practically any GPU size can be accommodated by adjusting the size of the gradient set. For example, the average set in the experiment on Camelyon16 contains 9329 patches (7.3 GB), while the largest input in the training set contains 32,382 patches (25.46 GB). Even though the set sizes are large, models can be trained on all inputs using a single 12GB GPU due to the constant memory overhead.
Another potential limitation is that UMBC (and SSE) use a cross attention layer with parameterized slots in order to achieve an MBC model. However, the fixed parameters, which are independent to the input set, can be seen as a type of bottleneck in the attention layer which is not present in traditional self-attention. Therefore we look forward to seeing future work which may find ways to make the slot parameters depend on the input set, which may increase overall model expressivity.
6 Conclusion
In order to overcome the limited expressive power and training scalability of existing MBC set functions, such as DeepSets and SSE, we have proposed Universal MBC set functions that allow mixing both MBC and non-MBC components to leverage a broader range of architectures which increases model expressivity while universally maintaining the MBC property. Additionally, we generalized MBC attention activation functions, showing that many functions, including the softmax, are MBC. Furthermore, for training scalability, we have proposed an unbiased approximation to the full set gradient with a constant memory overhead for processing a set of any size. Lastly, we have performed extensive experiments to verify the efficiency and efficacy of our scalable set encoding framework, and theoretically shown that UMBC is a universal approximator of continuous permutation invariant functions and converges to stationary points of the total loss with the full set.
Acknowledgements
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No.2019-0-00075, Artificial Intelligence Graduate School Program(KAIST)), the Engineering Research Center Program through the National Research Foundation of Korea (NRF) funded by the Korean Government MSIT (NRF-2018R1A5A1059921), Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No. 2021-0-02068, Artificial Intelligence Innovation Hub), Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No. 2022-0-00184, Development and Study of AI Technologies to Inexpensively Conform to Evolving Policy on Ethics), Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No.2022-0-00713), and Samsung Electronics (IO201214-08145-01)
References
- Ba et al. (2016) Ba, J. L., Kiros, J. R., and Hinton, G. E. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.
- Bejnordi et al. (2017) Bejnordi, B. E., Veta, M., Van Diest, P. J., Van Ginneken, B., Karssemeijer, N., Litjens, G., Van Der Laak, J. A., Hermsen, M., Manson, Q. F., Balkenhol, M., et al. Diagnostic assessment of deep learning algorithms for detection of lymph node metastases in women with breast cancer. Jama, 318(22):2199–2210, 2017.
- Beltagy et al. (2020) Beltagy, I., Peters, M. E., and Cohan, A. Longformer: The long-document transformer. arXiv preprint arXiv:2004.05150, 2020.
- Bruno et al. (2021) Bruno, A., Willette, J., Lee, J., and Hwang, S. J. Mini-batch consistent slot set encoder for scalable set encoding. Advances in Neural Information Processing Systems, 34:21365–21374, 2021.
- Chalkidis et al. (2019) Chalkidis, I., Fergadiotis, E., Malakasiotis, P., and Androutsopoulos, I. Large-scale multi-label text classification on EU legislation. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pp. 6314–6322. Association for Computational Linguistics, 2019.
- Chen et al. (2020) Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pp. 1597–1607. PMLR, 2020.
- Deng et al. (2009) Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pp. 248–255. Ieee, 2009.
- Devlin et al. (2019) Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of NAACL-HLT, pp. 4171–4186, 2019.
- Fehrman et al. (2020) Fehrman, B., Gess, B., and Jentzen, A. Convergence rates for the stochastic gradient descent method for non-convex objective functions. Journal of Machine Learning Research, 21:136, 2020.
- Garnelo et al. (2018) Garnelo, M., Rosenbaum, D., Maddison, C., Ramalho, T., Saxton, D., Shanahan, M., Teh, Y. W., Rezende, D., and Eslami, S. A. Conditional neural processes. In International Conference on Machine Learning, pp. 1704–1713. PMLR, 2018.
- He et al. (2016) He, K., Zhang, X., Ren, S., and Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778, 2016.
- Ilse et al. (2018) Ilse, M., Tomczak, J., and Welling, M. Attention-based deep multiple instance learning. In International conference on machine learning, pp. 2127–2136. PMLR, 2018.
- Jurafsky & Martin (2008) Jurafsky, D. and Martin, J. H. Speech and language processing: An introduction to speech recognition, computational linguistics and natural language processing. Upper Saddle River, NJ: Prentice Hall, 2008.
- Kawaguchi et al. (2022) Kawaguchi, K., Zhang, L., and Deng, Z. Understanding dynamics of nonlinear representation learning and its application. Neural Computation, 34(4):991–1018, 2022.
- Kim (2022) Kim, M. Differentiable expectation-maximization for set representation learning. In International Conference on Learning Representations, 2022.
- Kingma & Ba (2015) Kingma, D. P. and Ba, J. Adam: A method for stochastic optimization. In International Conference on Learning Representations, 2015.
- Kingma & Welling (2013) Kingma, D. P. and Welling, M. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
- Lee et al. (2019) Lee, J., Lee, Y., Kim, J., Kosiorek, A., Choi, S., and Teh, Y. W. Set transformer: A framework for attention-based permutation-invariant neural networks. In International conference on machine learning, pp. 3744–3753. PMLR, 2019.
- Lee et al. (2016) Lee, J. D., Simchowitz, M., Jordan, M. I., and Recht, B. Gradient descent only converges to minimizers. In Conference on learning theory, pp. 1246–1257. PMLR, 2016.
- Li et al. (2021) Li, B., Li, Y., and Eliceiri, K. W. Dual-stream multiple instance learning network for whole slide image classification with self-supervised contrastive learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 14318–14328, 2021.
- Liu et al. (2015) Liu, Z., Luo, P., Wang, X., and Tang, X. Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision (ICCV), December 2015.
- Locatello et al. (2020) Locatello, F., Weissenborn, D., Unterthiner, T., Mahendran, A., Heigold, G., Uszkoreit, J., Dosovitskiy, A., and Kipf, T. Object-centric learning with slot attention. Advances in Neural Information Processing Systems, 33:11525–11538, 2020.
- Loshchilov & Hutter (2019) Loshchilov, I. and Hutter, F. Decoupled weight decay regularization. In International Conference on Learning Representations, 2019.
- Mertikopoulos et al. (2020) Mertikopoulos, P., Hallak, N., Kavis, A., and Cevher, V. On the almost sure convergence of stochastic gradient descent in non-convex problems. Advances in Neural Information Processing Systems, 33:1117–1128, 2020.
- Mialon et al. (2021) Mialon, G., Chen, D., d’Aspremont, A., and Mairal, J. A trainable optimal transport embedding for feature aggregation and its relationship to attention. In International Conference on Learning Representations, 2021.
- Murphy et al. (2019) Murphy, R. L., Srinivasan, B., Rao, V., and Ribeiro, B. Janossy pooling: Learning deep permutation-invariant functions for variable-size inputs. In International Conference on Learning Representations, 2019.
- Pappagari et al. (2019) Pappagari, R., Zelasko, P., Villalba, J., Carmiel, Y., and Dehak, N. Hierarchical transformers for long document classification. In 2019 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), pp. 838–844. IEEE, 2019.
- Park et al. (2022) Park, H., Vyas, Y., and Shah, K. Efficient classification of long documents using transformers. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pp. 702–709, 2022.
- Pinkus (1999) Pinkus, A. Approximation theory of the MLP model in neural networks. Acta numerica, 8:143–195, 1999.
- Quellec et al. (2017) Quellec, G., Cazuguel, G., Cochener, B., and Lamard, M. Multiple-instance learning for medical image and video analysis. IEEE reviews in biomedical engineering, 10:213–234, 2017.
- Rolnick & Tegmark (2018) Rolnick, D. and Tegmark, M. The power of deeper networks for expressing natural functions. In International Conference on Learning Representations, 2018.
- Vaswani et al. (2017) Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. Attention is all you need. Advances in neural information processing systems, 30, 2017.
- Wagstaff et al. (2022) Wagstaff, E., Fuchs, F. B., Engelcke, M., Osborne, M. A., and Posner, I. Universal approximation of functions on sets. Journal of Machine Learning Research, 23(151):1–56, 2022.
- Zaheer et al. (2017) Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. R., and Smola, A. J. Deep sets. Advances in neural information processing systems, 30, 2017.
- Zhang et al. (2020) Zhang, Y., Hare, J., and Prügel-Bennett, A. Fspool: Learning set representations with featurewise sort pooling. In International Conference on Learning Representations, 2020.
Appendix A Proofs
A.1 Proof of Theorem 3.3
Proof.
Let be a set of all permutations on and let be given. For a given set , and permutation , we can construct a permutation matrix such that
Since we apply the feature extractor independently to each element of the set ,
With an elementwise, strictly positive activation function ,
For , the un-normalized attention score with the permutation is
Since is the identity mapping, for .
Now, we consider the matrix multiplication of
Since
is permutation invariant. Since , is also invariant with respect to the permutation of input , which leads to the conclusion that
is permutation invariant.
∎
A.2 Proof for Theorem 3.4
Proof.
Let input set be given and let be a partition of with , i.e., and for . Since a Universal MBC set encoder is permutation invariant, without loss of generality we can assume that,
| (21) |
where and for . Then we can express the matrix as follows:
| (22) |
where for since is independent to for all .
Since
the following equality holds
| (23) | ||||
Thus, is mini-batch consistent.
A.3 Proof of Corollary 3.8
Proof.
Let be an arbitrary set encoder and let be a UMBC set encoder. Given a set and a partition , we get
as shown in section A.2. We assume that is small enough so that we can load in memory after we compute . As a consequence, we can directly evaluate without partitioning into smaller subsets and aggregating .
is mini-batch consistent.
∎
A.4 Proof of Theorem 3.6
Proof.
Let be a permutation on and let be a set of all permutations on . Define a matrix
with the input set and the given slots . Then we can identify a permutation matrix such that,
Since the query with the permutation is , the un-normalized attention score with the permutation matrix is
Since the normalization matrix is a function of the slots , we define a new normalization matrix by permuting the slots with the given permutation matrix as
where for . Note that
and .
Then we get since
The last equality holds since -th row of the permutation matrix has a single non-zero entry which is 1. Thus,
which implies that
Finally, combining all the pieces, we get
is permutation equivariant. ∎
A.5 Proof of Theorem 3.7
Proof.
Following the previous proofs (Zaheer et al., 2017; Wagstaff et al., 2022) for uncountable set , we assume a set size is fixed. In other words, we restrict the domain to . Let be given. By using the proof of Theorem 13 from Wagstaff et al. (2022) (with a more detailed proof in Zaheer et al., 2017), the function is continuously sum-decomposable via as:
for all , where is invertible and defined by
and is continuous and defined by
We want to show that UMBC with some continuously decomposable permutation invariant deep neural network can approximate the function by showing that and are approximated by components of the UMBC model. Let be a continuously decomposable permutation invariant deep neural network defined by
where , is a deep neural network, and is defined by
with some deep neural network . First, we want to show that Deepsets with average pooling is a special case of UMBC. Set the slots as the zero matrix , and . Then by using Lemma 1 from Lee et al. (2019), becomes average pooling, i.e.,
Then the composition of UMBC and becomes continuously sum-decomposable function as follows:
where is -th row of . By defining and ,
Since is continuous and is compact, is compact. Since is compact and is continuous, and the nonlinearity of is not a polynomial of finite degree, Theorem 3.1 of (Pinkus, 1999) implies the following (as a network with one hidden layer can be approximated by a network of greater depth by using the same construction for the first layer and approximating the identity function with later layers): for any , there exists and parameters of such that if the width of is at least , then . Combining these, we have that
where depends on the width of . Since the nonlinearity of has nonzero Taylor coefficients up to degree , the proof of Theorem 3.4 of (Rolnick & Tegmark, 2018) implies the following: there exists such that if the width of is at least , for every , there exists parameters of such that for . Let us fix the width of to be at least . By the triangle inequality,
for all . It implies that for every there exists the parameters of such that
Since is continuous and is compact, is compact. Since and are compact, is compact. Define by for all . Replacing with ,
Since is compact and is continuous on , is uniformly continuous. Thus, for any there is a such that
Since with an arbitrary small , we can take a small such that , i.e. for all . Then ,
It implies that
Thus, we get
where depends on the width of , while is arbitrarily small with a fixed width of (due to the universal approximation result with a bounded width of Rolnick & Tegmark, 2018). Let be given. Then, we set to be sufficiently large to ensure that and set , obtaining
Since was arbitrary, this proves the following desired result: (a formal restatement of this theorem) suppose that the nonlinear activation function of has nonzero Taylor coefficients up to degree . Let be a continuously-decomposable permutation-invariant deep neural network with the nonlinear activation functions that are not polynomials of finite degrees. Then, there exists such that if the width of is at least , then for any , there exists for which the following statement holds: if the width of is at least , then there exist trainable parameters of and satisfying
∎
A.6 Proof for Theorem 3.10
is defined by
for all , where is -th row of defined in equation 4 and is -th component of which is defined in equation 5.
Proof.
From the mini-batch consistency and definition of and , we have that for any partition procedure ,
By using this and defining and , where is -th row of , the chain rule along with the linearity of the derivative operator yields that for any partition procedure ,
| (25) | ||||
Similarly, by defining and ,
| (26) | ||||
Let be fixed. By the linearity of expectation, we have that
| (27) |
where
Below, we further analyze the following factors in the right-hand side of this equation:
Denote the elements of as . Then,
Since is drawn independently and uniformly from the elements of , we have that
Substituting this into the right-hand side of the preceding equation, we have that
Similarly,
Substituting these into ,
By using this in equation 27 and defining we have that
Thus, expanding the definition of ,
Here, since and for any partition procedure from the mini-batch consistency, we have that
| (28) | ||||
By comparing equation equation 25 and equation equation 28, we conclude that
Since was arbitrary, this holds for any .
Now we want to show equation 13 holds for any . Since and for all ,
| (29) |
Since we independently and uniformly sample from and is constant with respect to the sampling,
| (30) |
A.7 Unbiased Estimation of Full Set Gradient for MIL
Corollary A.1.
For multiple instance learning, given a training set , we define the loss as follows:
For every iteration we sample a mini-batch of training data and sample random partition . Then we sample a mini-batch of subsets . Let and define a function by . Similar to equation 9 we define as,
Then we update the parameters and using the gradient of the following functions as
where is a learning rate. If we assume that there exists a unique maximum value for each and sample a single subset from for , i.e. , then the following holds:
| (32) | ||||
| (33) | ||||
| (34) |
Proof.
It is enough to show the equation 32 and 33 hold since we have already proved equation 34, which does not depend on , in Theorem 3.10. By defining , where for , and ,
for any partition for all . Similarly, we define , where for , and . Let be fixed and define,
With linearity of expectation and properties of the max operation, we have that
| (35) |
Note that we partition the set and there is a unique maximum value. Thus, only one subset includes the element leading to the maximum value . If we do not choose such a subset , the gradient in equation 35 becomes zero. Since we sample uniformly a single subset from , i.e. , we get
| (36) |
If we apply the right hand side of equation 36 to equation 35, we obtain
With the chain rule, we get,
Since we have already shown that
| (37) |
in Theorem 3.10, it suffices to show that
| (38) |
For the left hand side of equation 38, we have that
| (39) | ||||
For the right hand side of equation 38, with linearity of expectation, we obtain
| (40) |
Now we expand the summand in the right hand side,
| (41) |
Now we apply the right hand side of equation 41 to equation 40. Then we get,
| (42) | ||||
Finally combining equation 37 and equation 42, we arrive at the the conclusion:
∎
A.8 SSE’s Training Method Is a Biased Approximation to the Full Set Gradient
In this section, we show that sampling a single subset, and computing the gradient as an approximation to the gradient of , which is proposed by Bruno et al. (2021), is a biased estimation of full set gradient. Since with an attention activation function comprised of and a sigmoid for is equivalent to a Slot Set Encoder, and is a special case of UMBC, we focus on the gradient of . Specifically, at every iteration , we sample a mini-batch from the training dataset . We choose a partition for each and sample a single subset from the partition . If we compute the gradient of the loss as
| (43) |
then it is a biased estimation of , where is defined by .
Proof.
The gradient of with respect to the parameter is
| (44) | ||||
for a partition of the set , where is defined by . However, the expectation of equation 43 is not equal to the full set gradient in equation 44:
| (45) | ||||
To see why this is the case, we analyze the case of real valued function with and a squared loss function
Since is sum decomposable, i.e. where , the full set gradient from equation 44 becomes,
| (46) | ||||
Assume that and we sample a single subset from the partition for all and . Then gradient of the subsampling a single subset from equation 45 becomes,
| (47) | ||||
Therefore, the random subsampling of a a single subset in the method proposed by Bruno et al. (2021) is not an unbiased estimate of the gradient of the full set. ∎
Appendix B Optimization
Define and . We assume that for all . Let be a sequence generated by with an initial point and a step size sequence , where for with an open convex set . Here, is an open set and thus it is allowed to choose (or any other open convex set). We do not assume that the loss function or model is convex. We also do not make any assumption on the initial point . To analyze the optimization behavior formally, we consider the following standard assumption in the literature (Lee et al., 2016; Mertikopoulos et al., 2020; Fehrman et al., 2020):
Assumption B.1.
There exist such that for any , , and ,
We use the following lemma on a general function from a previous work (Kawaguchi et al., 2022, Lemma 2):
Lemma B.2.
For any differentiable function with an open convex set , if for all , then
| (48) |
In turn, Lemma B.2 implies the following lemma:
Lemma B.3.
For any differentiable function with an open convex set such that for all , the following holds: for all such that ,
| (49) |
Proof.
Since (nonnegative), if , the desired statement holds. Thus, we consider the remaining case of in the rest of this proof. We invoke Lemma B.2 with , yielding
By rearranging, this implies that . ∎
Since we are dealing with a general non-convex and non-invex function (as the choice of architecture and loss is very flexible) where gradient-based optimization might only converge to a stationary point (to avoid the curse of dimensionality), we consider the convergence in terms of stationary points of :
Theorem B.4.
Suppose that Assumption B.1 holds and the step size sequence satisfies . Then, there exists a constant independent of such that
Proof.
Using this and Theorem 3.10 along with Jensen’s inequality, we have that for any ,
Thus, satisfies the conditions of Lemma B.2 and Lemma B.3. Since for , using Lemma B.2 for the function , we have that
Using ,
Using Lemma B.3 for , we have that
Define . Using the linearity and monotonicity of expectation,
where the second inequality follows from Theorem 3.10 and where is the expectation of the maximum ratio .
Taking expectation over with the law of total expectation ,
| (50) |
Since , this implies that
where the last inequality follows from for all . Applying this inequality recursively over , it holds that for any ,
Using this inequality in equation 50,
Rearranging and summing over with,
where we define . Since and for all ,
This implies that
Since and , this implies that there exists a constant independent of such that
∎
For example, if with and , then we have .
Appendix C Details on the Mixture of Gaussians Amortized Clustering Experiment
We used a modified version of the MoG amortized clustering dataset which was used by Lee et al. (2019). We modified the experiment, adding separate, random covariance parameters into the procedure in order to make a more difficult dataset. Specifically, to sample a single task for a problem with classes,
-
1.
Sample set size for the batch .
-
2.
Sample class priors with .
-
3.
Sample class labels for .
-
4.
Generate cluster centers , where for and .
-
5.
Generate cluster covariance matrices , where for and .
-
6.
For all , if , sample data
In our MoG experiments, we set . The Motivational Example in Figure 2 also used the MoG dataset, and performed MBC testing of the set transformer corresponding to the procedure outlined in Appendix E






C.1 Streaming Settings
The four total streaming settings in Figures 2 and 8 are described below:
-
•
single point stream streams each point in the set one by one. This causes the most severe under-performance by non-MBC models.
-
•
class stream streams an entire class at once. Models which make complex pairwise comparisons cannot compare the input class with any other clusters, thereby degrading performance of models such as the Set Transformer.
-
•
chunk stream streams 8 random points at a time from the dataset, Providing, random and limited information to non-MBC models.
-
•
one each stream streams a set consisting of a single instance from each class. non-MBC models can see examples of each class, but with a limited sample size, therefore non-MBC models such as Set Transformer fail to make accurate predictions.
C.2 Experimental Setup
We train each model for epochs, with each epoch containing iterations. We use the Adam optimizer with a learning rate of and no weight decay. We do not perform early stopping. We make a single learning rate adjustment at epoch which adjusts the learning rate to . When measuring NLL for results, we measure the NLL of the full set of points. Unless otherwise specified, UMBC models use the softmax activation function. We list the architectures in Sections C.2, C.2 and C.2. All models have an additional linear output which outputs parameters for the Gaussian mixture outlined in Equation 14.
| Output Size | Layers | Amount |
|---|---|---|
| Input Set | ||
| Linear(2, 128), ReLU | ||
| Set Encoder | ||
| Decoder |
| Name | Set Encoder | Output Size | Set Decoder | Output Size |
|---|---|---|---|---|
| DeepSets (Zaheer et al., 2017) | Mean Pooling | Linear, ReLU | ||
| SSE (Bruno et al., 2021) | Slot Set Encoder | Linear, ReLU | ||
| FSPool (Zhang et al., 2020) | Featurewise Sort Pooling | Linear, ReLU | ||
| Diff. EM. (Kim, 2022) | Expectation Maximization Layer | Linear, ReLU | 128 | |
| Set Transformer (Lee et al., 2019) | Pooling by Multihead Attention | Set Attention Block |
| Name | MBC Set Encoder | Output Size | non-MBC Set Encoder | Output Size | Set Decoder | Output Size |
|---|---|---|---|---|---|---|
| (Ours) UMBC+FSPool | UMBC Layer | Featurewise Sort Pooling | Linear, ReLU | |||
| (Ours) UMBC+Diff EM | UMBC Layer | Expectation Maximization Layer | Linear, ReLU | |||
| (Ours) UMBC+Set Transformer | UMBC Layer | Set Attention Block | Linear, ReLU |
Appendix D Measuring the Variance of Pooled Features
In Figure 3, we show the quantitative effect on the pooled representation between the plain Set Transformer, UMBC+Set Transformer, FSPool and DiffEM. The UMBC model always shows 0 variance, while the non-MBC models produce variance between aggregated encodings of random partitions. For a single chunk, however, non-MBC models show no variance, as random partitions of a single chunk would be equivalent to permuting the elements within the chunk (i.e. non-MBC models still produce an encoding which is permutation invariant). The variance increases drastically when the set is partitioned into two chunks and then the behavior differs between the non-MBC models. Set Transformer happens to show decreasing variance as the number of chunks increases. Note that as the number of chunks increases, the cardinality of each chunk decreases. Therefore, the variance decreases as the chunk cardinality also decreases, but this does not indicate that the models is performing better. For example, in Figure 2, when a singleton set is input to the Set Transformer, the predictions become almost meaningless even though they may have lower variance. The procedure for aggregating the encodings of set partitions for the non-MBC models is outlined in Appendix E.
| Distribution | Dimension | Number of Points |
|---|---|---|
| Normal(0, 1) | ||
| Uniform(-3, 3) | ||
| Exponential(1) | ||
| Cauchy(0, 1) |
| Number of Chunks | ||||||
| Elements per Chunk |
To perform this experiment, we used a randomly initialized model with hidden units, and sampled set elements from four different distributions in order to make a total set size of . We then created 100 random partitions for various chunk sizes. Chunk sizes and distributions are shown in Figure 10. We then encode the whole set in chunks and and report the observed variance over the 100 different random partitions at each of the various chunk sizes (Figure 3). Note that the encoded set representation is a vector and Figure 3 shows a scalar value. To achieve this, we take the feature-wise variance over the 100 encodings and report the mean and standard deviation over the feature dimension. Specifically, given representing all 100 encodings with , we compute feature-wise variance as
for . We then achieve the values of y-axis and error bars in Figure 3 by a mean and standard deviation over the feature dimension,
| (51) |
Appendix E A Note on MBC Testing of non-MBC models
In the qualitative experiments Figures 2 and 3, we apply MBC testing to non-MBC models in order to study the effects of using non-MBC models in MBC settings. Non-MBC models do not prescribe a way to accomplish this in the original works, so we took the approach of processing each chunk up until the pooled representation. We then performed mean pooling over the encoded chunks in the following way. Let be an input set and let be a partition of the set , i.e. with for . Denote a non-MBC set encoding function, then our pseudo-MBC testing procedure is as follows,
| (52) |




Appendix F Details on the Image Completion Experiments
F.1 Additional Experimental Results
In figure Figure 11, we evaluate our proposed unbiased full set gradient approximation algorithm (red) with Deepsets, Slot Set Encoder (SSE) and UMBC + Set Transformer (ST) and compare our algorithm against the one training with a randomly sampled subset of 100 elements , which is a biased estimator, (green) and the one computing full set gradient (blue). Across all models, our unbiased estimator significantly outperforms the models trained with a randomly sampled subset. Notably, the model trained with our proposed algorithm is indistinguishable from the model trained with full set gradient while our method only incurs constant memory overhead for any set size. These empirical results again verify efficiency of our unbiased full set gradient approximation.
F.2 Experimental Setup
We train all models on CelebA dataset for 200,000 steps with Adam optimizer (Kingma & Ba, 2015) and 256 batch size but no weight decay. We set the learning rate to and use a cosine annealing learning rate schedule. In Sections F.2 and F.2, we specify the architecture of Conditional Neural Process with UMBC + Set Transformer. We use slots and set dimension of each slot to . For the attention layer, we use the softmax for the activation function and set the dimension of attention output to . As an input to the set encoder, we concatenate the coordinates of each and the corresponding pixel value from the context for , resulting in a matrix.
| Output Size | Layers |
|---|---|
| Input Set Representation and Coordinates | |
| Tile & Concatenate | |
| Linear(130, 128), ReLU | |
| Linear(128, 128), ReLU | |
| Linear(128, 128), ReLU | |
| Linear(128, 128), ReLU | |
| Linear(128, 6) |
Appendix G Details on the Long Document Classification Experiments
We train all models for 30 epochs with AdamW optimizer (Loshchilov & Hutter, 2019) and batch size 8. We use constant learning rate . For our UMBC model, we pretrain the model while freezing BERT for 30 epochs and finetune the whole model for another 30 epochs. In Table 11, we specify architecture of UMBC + BERT (Devlin et al., 2019) without positional encoding. We use slots and set dimension of each slot to . We use slot-sigmoid for the activation function and set the dimension of the attention output to .
| Output Size | Layers |
|---|---|
| Input Document | |
| Word Embedding | |
| Layer Normalization | |
| Linear(768,768), ReLU | |
| Linear(768,768), ReLU | |
| UMBC Layer | |
| Layer Normalization | |
| BERT w/o Positional Encoding (Devlin et al., 2019) | |
| [CLS] token Pooler | |
| Dropout(0.1), Linear(768, 4271) |
Appendix H Details on the Camelyon16 Experiments



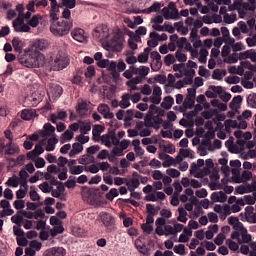
The Camelyon16 Whole Slide Image dataset consists of 270 training instances and 129 validation instances. The dataset was created for a competition, and therefore the test set is hidden. We therefore follow the example set by previous works (Li et al., 2021) and report performance achieved on the validation set. For preprocessing, we consider the slide magnification setting, and use OTSU’s thresholding method to detect regions containing tissue within the WSI. We then split the activated regions into non overlapping patches of size . An example of single input patches can be seen in Figure 12. The largest input set contains image patches which are each . All patch extraction code can be found in the supplementary file. Table 14 contains statistics related to the numbers of patches per input for the training and the test set as well as the distribution of positive and negative labels.
H.1 Experimental Setup
We use a ResNet18 (He et al., 2016) which was pretrained with self-supervised contrastive learning (Chen et al., 2020) by Li et al. (2021). The pretrained ResNet18 weights can be downloaded from this repository. Following the classification experiments done by Lee et al. (2019), we place dropout layers before and after the PMA layer of the Set Transformer in our UMBC model. We will describe our pretraining and finetuning steps below in detail.
| Output Size | Layers | Name | Amount |
| Input Set | Bag of Instances | ||
| ResNet18(InstanceNorm) | Feature Extractor | ||
| Linear, ReLU, Linear | Projection | ||
| Linear, Max Pooling | Instance Classifier | ||
| Set Encoding Function | Bag Classifier | ||
| Set Decoder | Bag Classifier |
Pretraining.
For pretraining, we extract the features from the pretrained ResNet18 and only train the respective MIL models (Section H.1) on the extracted features. We pretrain for 200 epochs with the Adam optimizer which uses a learning rate of and a cosine annealing learning rate decay which reaches the minimum at . We use , and for Adam. We train with a batch size of 1 on a single GPU, and save the model which showed the best performance on the validation set, where the performance metric is . Other details can be found in Section 4.4. These results can be seen in the left column of Table 4.
Finetuning.
For finetuning, we use our unbiased gradient approximation algorithm with a chunk size of . We freeze the pretrained MIL head and only finetune the backbone resnet model. Therefore, we sequentially process each chunk for each input set until the entire set has been processed. We train for 10 total epochs, and use the AdamW optimizer with a learning rate of , and a weight decay of which is not applied to bias or layernorm parameters. We use a one epoch linear warmup, and then a cosine annealing learning rate decay at every iteration which reaches a minimum at . We train on 1 GPU, with a batch size of 1 and with a single instance on each GPU.
| Metric | Train | Test |
|---|---|---|
| Mean | 9,329 | 9,376 |
| Min | 154 | 1558 |
| Max | 32,382 | 37,345 |
| Metric | Train | Test |
|---|---|---|
| Positive () | 110 | 49 |
| Negative () | 160 | 80 |
Appendix I Generalizing Attention Activations
As shown in Equation 7, any attention activation function which can be expressed as a strictly positive elementwise function combined with sum decomposable normalization constants and represents a valid attention activation function. Table 15 shows 5 such functions with their respective normalization constants, although there are an infinite number of possible functions which can be used.
The softmax operation we propose which is outlined immediately before Theorem 3.4 is mathematically equivalent to the standard softmax which is commonly implemented in deep learning libraries because and have the same domain, the same codomain, and for all . Therefore the functions are mathematically equivalent, even though the implementations are not. Our proposed function requires separately applying the exponential, and storing and updating the normalization constant while is generally implemented in such a way that everything is done in a single operation.
Appendix J Algorithm
We outline our unbiased full set gradient approximation here.