Scalable Method for Eliminating Residual $ZZ$ Interaction between Superconducting Qubits

Scalable quantum information processing relies on simultaneous implementation of high-fidelity quantum operations. Unfortunately, unwanted crosstalk effects become inevitable in a quantum processor with a high degree of integration, compromising quantum operational fidelity and ultimately limiting scalability. Recent progress with superconducting qubits has shown that by leveraging a tunable-coupling architecture, various crosstalk phenomena can be efficiently reduced while fast two-qubit gates are enabled Yan et al. (2018); Arute et al. (2019). However, residual longitudinal or $ZZ$ interaction – by which the frequency of a qubit depends on the state of the other – may still exist due to the fact that superconducting qubits are not so well-defined two-level systems by nature and the computational states are more or less affected by noncomputational states that are energetically close. Such unwanted $ZZ$ interaction will result in spectator errors Sundaresan et al. (2020); Krinner et al. (2020); Cai et al. (2021); Zajac et al. (2021), correlated errors Postler et al. (2018); von Lüpke et al. (2020), and coherent phase errors during intermittent idling operations Barends et al. (2016); Kandala et al. (2019); Gong et al. (2019); Karamlou et al. (2021). Notably, quantum error correction usually necessitates relatively lengthy reset and feedback operations, making it extremely susceptible to these coherent errors accrued during idling Huang et al. (2020); Bultink et al. (2020); Andersen et al. (2020); Chen et al. (2021).

There are several methods for $ZZ$ suppression or cancellation, such as, among the passive ones, the use of large qubit-qubit detuning DiCarlo et al. (2009); Collodo et al. (2020); Xu et al. (2020), qubits with opposite anharmonicity signs Zhao et al. (2020); Ku et al. (2020); Xu and Ansari (2021), and multiple coupling paths Mundada et al. (2019); Li et al. (2020); Kandala et al. (2021); Zhao et al. (2021); Sete et al. (2021); Stehlik et al. (2021); Xu and Ansari (2022). These methods either result in incomplete cancellation or heavily rely on design and fabrication precision which can be hard to achieve in practice. There are also a few active methods. One approach is to apply dynamical-decoupling sequences during long idling periods at the expense of additional gates Jurcevic et al. (2021); Tripathi et al. (2021). It is, however, unclear how to best implement dynamical-decoupling protocols in the context of a highly connected qubit array. Another approach, which utilizes the ac Stark effect by off-resonantly driving the qubits, has been demonstrated in recent experiments at a small scale Noguchi et al. (2020); Mitchell et al. (2021); Wei et al. (2021); Xiong et al. (2022). Although suitable for architecture with fixed-frequency qubits, the Stark method requires independent drives applied to at least one – sometimes both – of the two qubits in order to cancel the $ZZ$ coupling between this particular qubit pair. In a high-connectivity qubit array such as two-dimensional grid where the number of nearest-neighbor connections is more than the number of qubits, this method becomes inextensible due to the lack of degrees of freedom in control. In addition, directly driving the qubit may induce spurious excitation and leakage to the target qubit and its surroundings, especially in a frequency-crowded system.

In this Letter, we propose and experimentally demonstrate a practically scalable and noninvasive method for cancelling residual $ZZ$ interaction between fixed-frequency superconducting qubits. In contrast to previous approaches that utilize ac Stark shift by driving the qubits, we apply a weak microwave drive to the intermediate coupler instead. On a device with two transmon qubits connected to a cavity bus coupler, we show complete removal of residual $ZZ$ interaction from measurement of two-qubit entangling phases and $ZZ$ correlations. We also perform simultaneous randomized benchmarking (RB) experiments with interleaved idling operations to extract idling gate fidelity which shows full-scale improvement, reaching the coherence limit.

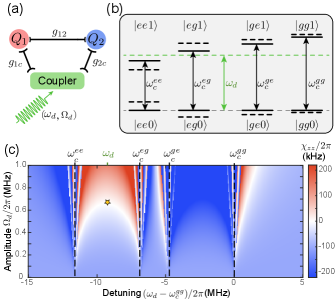
Consider a general model described in Fig. 1(a), where two qubits $Q_{1}$ and $Q_{2}$ couple to an intermediate coupler $C$ with a coupling strength of $g_{1c}$ and $g_{2c}$, respectively, as well as to each other with a coupling strength $g_{12}$. The static Hamiltonian can be written as ($\hbar=1$):

where $\omega_{i}$ ($i\in\{1,2,c\}$) is the bare frequency of the qubits or coupler, $\eta_{i}$ is the anharmonicity of each mode, and $a_{i}$ ($a_{i}^{\dagger}$) is the corresponding annihilation (creation) operator. In the dispersive limit, where $g_{ij}\ll\left|\omega_{i}-\omega_{j}\right|$, we can conveniently diagonalize the Hamiltonian and truncate it to the relevant subspace:

which is expressed in the rotating frame of the qubits. For clarity, we use $\left|g\right\rangle$ ($\left|e\right\rangle$) to denote the ground (excited) state of the qubits and $\left|0\right\rangle$, $\left|1\right\rangle$, $\left|2\right\rangle$… to denote the coupler state. $\omega_{c}^{mn}$ is the 0-1 transition frequency of the coupler with the two qubits in state $\left|mn\right\rangle$. In general, the four values of $\omega_{c}^{mn}$ are different as illustrated in Fig. 1(b). We shall later exploit such inhomogeneity for $ZZ$ cancellation. $\chi_{zz}^{\mathrm{static}}$ is the residual $ZZ$ coupling, which results from a finite effective coupling between the two qubits and causes unwanted $ZZ$ interaction during idling periods. Detailed discussions about $\chi_{zz}^{\mathrm{static}}$ can be found in Ref. Chu and Yan (2021).

To eliminate $\chi_{zz}^{\mathrm{static}}$ from the system, we apply a microwave drive $\frac{\Omega_{d}}{2}\left(a_{c}^{\dagger}\textrm{e}^{-\textrm{i}\omega_{d}t}+a_{c}\textrm{e}^{\textrm{i}\omega_{d}t}\right)$ to the coupler, where $\omega_{d}$ is the drive frequency and $\Omega_{d}$ is the drive amplitude or equivalent Rabi frequency. Such a drive near the coupler frequency induces the ac Stark effect, which causes an energy shift of each computational state $\left|mn0\right\rangle$ according to

where $\Delta_{mn}=\omega_{d}-\omega_{c}^{mn}$ is the respective detuning. The sign of the shift $\delta_{mn}$ is the same as the sign of $\Delta_{mn}$. Given the proper choice of $\omega_{d}$ and $\Omega_{d}$, the residual $ZZ$ term $\chi_{zz}^{\mathrm{static}}$ can be offset by the combined Stark shifts,

giving zero net $ZZ$ coupling.

In our experimental device, two fixed-frequency transmon qubits ($\omega_{1}/2\pi=5.627$ GHz and $\omega_{2}/2\pi=4.353$ GHz) couple to a common 3D cavity ($\omega_{c}/2\pi=6.363$ GHz, $\eta_{c}/2\pi=-123$ kHz), a nontunable coupler, with coupling strengths $g_{1c}/2\pi=119$ MHz and $g_{2c}/2\pi=228$ MHz, and also directly couple to each other with a direct coupling strength $g_{12}/2\pi=16$ MHz. The resulting static or residual $ZZ$ coupling is $\chi_{zz}^{\mathrm{static}}/2\pi=-103$ kHz, which is highly consistent with the estimated one ($-101.3$ kHz) Sup . The state-dependent coupler frequencies are $\omega_{c}^{gg}/2\pi=6.363$ GHz, $\omega_{c}^{eg}=\omega_{c}^{gg}+\chi_{1}$, $\omega_{c}^{ge}=\omega_{c}^{gg}+\chi_{2}$, and $\omega_{c}^{ee}=\omega_{c}^{gg}+\chi_{1}+\chi_{2}$, where $\chi_{1}/2\pi=-6.79$ MHz and $\chi_{2}/2\pi=-4.80$ MHz are the dispersive shifts between each qubit and the coupler (see Supplemental Material Sup for more details about the device parameters and experimental setup). For such a spectral configuration, it can be easily seen from Fig. 1(b) that choosing $\omega_{d}$ between $\omega_{c}^{ee}$ and $\omega_{c}^{eg}$ is the most efficient way to leverage the transition frequency inhomogeneity for creating a positive $\chi_{zz}^{\mathrm{drive}}$ to offset $\chi_{zz}^{\mathrm{static}}$. Figure 1(c) plots the numerically simulated net $ZZ$ coupling $\chi_{zz}$ as a function of the drive frequency and amplitude, in which the optimal choice for $ZZ$ cancellation is identified (starred) according to the objective of keeping the drive as weak as possible relative to the detunings, i.e., $\Omega_{d}\ll|\Delta_{mn}|$, to avoid exciting the coupler.

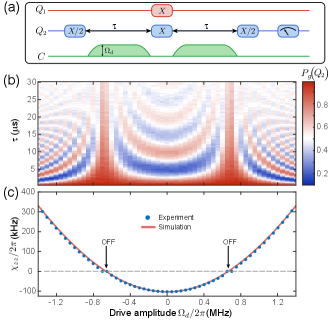
To calibrate the cancellation drive, we follow the simulation result to fix $\omega_{d}=(\omega_{c}^{ee}+\omega_{c}^{eg})/2$ and measure $\chi_{zz}$ as a function of $\Omega_{d}$ using the pulse sequence depicted in Fig. 2(a). For the cancellation pulse, we use a relatively slow rise and fall (300 ns for each) in order to avoid adding significant excitation upon the thermal level ($\sim$1%) to the cavity (see Supplemental Material Sup for more details). The sequence performs a Ramsey-like experiment on the target qubit $Q_{2}$ but with additional $\pi$ pulses simultaneously applied to both qubits in the middle of the sequence Chow et al. (2013); Xiong et al. (2022). In this way, the final phase of $Q_{2}$ encodes the entangling $ZZ$ phase accumulated during idling while the local $Z$ phase is echoed away for both qubits. Figure 2(b) shows the measured Ramsey fringes as a function of the drive amplitude $\Omega_{d}$. The oscillation frequency is equivalent to the net $ZZ$ coupling $\chi_{zz}$. As the drive amplitude is increased from zero (either direction), the oscillation first slows down from $\chi_{zz}^{\mathrm{static}}$ to be almost invisible and then comes back again, suggesting that $\chi_{zz}$ has been tuned continuously from negative to positive. The extracted $\chi_{zz}$ from the fit is shown in Fig. 2(c) and agrees well with prediction. The identified optimal drive amplitude $\Omega_{d}/2\pi\approx 0.66$ MHz (the coupling-OFF point) is adopted in the cancellation drive for subsequent experiments. Note that the flattened curve around the “OFF” bias, on the one hand, results from the inaccurate fitting of the Ramsey oscillation frequency near the zero $ZZ$ region, and on the other hand, may be due to the breakdown of the perturbation approximation beyond the dispersive regime Ku et al. (2020); Ansari (2019).

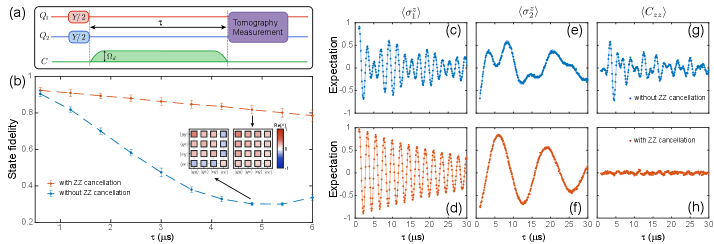
To validate the cancellation, we first measure the entangling phase accrued when idling both qubits. By preparing the system in the product state $\left(\left|gg\right\rangle+\left|ge\right\rangle+\left|eg\right\rangle+\left|ee\right\rangle\right)/2$, we perform the two-qubit state tomography after idling for a variable time $\tau$ (Fig. 3(a)). The state fidelity of the measured density matrices at different $\tau$ with and without the $ZZ$ cancellation drive are compared in Fig. 3(b). For $\tau=4.8\,\mu$s, the two-qubit entangling phase is near its maximum, which is $\chi_{zz}^{\mathrm{static}}\tau\approx\pi$ in the case of no cancellation. With the cancellation drive, such a conditional phase-flip error is corrected. The state fidelity with cancellation shows a smooth decay with idling duration, implying that the cancellation performance is stable. One set of calibrated parameters can be used for idling operation of variable length.

We also look into other relevant observables to verify the removal of two-qubit correlations by our cancellation drive. In a similar experiment as Fig. 3(a), we set a small detuning of $-0.5$ MHz ($+0.1$ MHz) to the microwave drives on qubit $Q_{1}$ ($Q_{2}$) in order to render a fringe pattern. At a varying delay time $\tau$, we compute the ensemble average of single-qubit observables $\left\langle\sigma_{1}^{z}\right\rangle$ and $\left\langle\sigma_{2}^{z}\right\rangle$, as well as their correlation $\left\langle C_{zz}\right\rangle=\left\langle\sigma_{1}^{z}\sigma_{2}^{z}\right\rangle-\left\langle\sigma_{1}^{z}\right\rangle\left\langle\sigma_{2}^{z}\right\rangle$. Without the cancellation drive, the Ramsey fringe exhibits a beating pattern as shown in Figs. 3(c, e), which results from the mixing of precession frequencies due to the presence of nonzero $\chi_{zz}^{\mathrm{static}}$. These beatings are, however, gone when the cancellation drive is applied (Figs. 3(d, f)), verifying complete $ZZ$ removal. It can also be seen that the measured two-qubit $ZZ$ correlation functions have been significantly suppressed with the cancellation drive (Figs. 3(g, h)). All data show good agreement with numerical simulation.

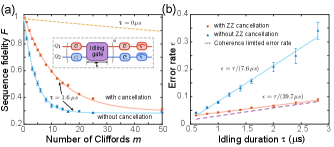
Finally, to benchmark the impact of residual $ZZ$ interaction on the fidelity of a general quantum circuit with intermittent idling operations and the improvement we can gain from our cancellation protocol, we implement the simultaneous Clifford-based RB experiment with interleaved idling gates Barends et al. (2014). As shown in the inset of Fig. 4(a), the circuit performs simultaneous single-qubit RB with an idling gate of variable length $\tau$ inserted in each Clifford cycle. Figure 4(a) shows an example of the measured sequence fidelity $F$ versus the number of Clifford cycles $m$ averaged over 80 randomizations for the case of $\tau=1.6~{}\mu$s. Comparing the interleaved case with the reference case ($\tau=0$), we obtain the idling gate error rate $\epsilon=\frac{3}{4}(1-p_{\mathrm{int}}/p_{\mathrm{ref}})$, where $p_{\mathrm{int}}$ and $p_{\mathrm{ref}}$ are from fitting the corresponding fidelity decay curve to $F=Ap^{m}+B$. Figure 4(b) compares the idling gate error rate with and without the cancellation drive at various idling gate durations $\tau$. It clearly shows significant error mitigation using the $ZZ$ cancellation drive across the entire range of $\tau$ up to $2.8~{}\mu$s. In the case without cancellation, the gate error rate has a strong $\tau$-dependence, $\epsilon=\tau/(7.6\,\mu\mathrm{s})$, which implies that, even without any active gate operation, the circuit fidelity can drop rapidly with extended idling periods. After adding the cancellation drive, the $\tau$-dependence is reduced by about 5 times to $\epsilon=\tau/(39.7\,\mu\mathrm{s})$, which agrees with the coherence limit $\epsilon\approx\frac{1}{3}(\tau/T_{1}^{Q_{1}})+\frac{1}{3}(\tau/T_{1}^{Q_{2}})$ O’Malley et al. (2015), with $T_{1}^{Q_{1}}$ and $T_{1}^{Q_{2}}$ the energy relaxation times of qubits $Q_{1}$ and $Q_{2}$, respectively. Such a full-scale improvement demonstrates the effectiveness of our cancellation protocol which removes almost all errors caused by the residual $ZZ$ interaction.

To summarize, we discuss the pros and cons of our method. First, our method is truly scalable given the one-to-one proportionality between the number of drives and number of connections. This is a clear advantage over previous methods based on directly driving the qubits. Second, the cancellation drive is noninvasive to the qubits because the drive frequency – near coupler frequency – is in a distinct band from the qubits. Third, the drive also causes negligible perturbation to the coupler state as it requires only a weak drive – in our demonstrated case, an equivalent Rabi frequency of 0.66 MHz – given a proper choice of drive parameters. Actually, adiabatic rising and falling edges as used in our pulse further prohibits excitation of the coupler. Fourth, our method is compatible with both nontunable and tunable couplers. Since the latter requires a local control line anyway, our method should not add any additional complexity in design. The cost of our method is the extra microwave drive that needs to be synthesized from room-temperature electronics. We believe, however, that our method will be useful in addressing unwanted $ZZ$ crosstalk in scalable devices, complementing other methods such as dynamical decoupling.