Scalable and Sample Efficient Distributed Policy Gradient Algorithms in Multi-Agent Networked Systems
Abstract
This paper studies a class of multi-agent reinforcement learning (MARL) problems where the reward that an agent receives depends on the states of other agents, but the next state only depends on the agent’s own current state and action. We name it REC-MARL standing for REward-Coupled Multi-Agent Reinforcement Learning. REC-MARL has a range of important applications such as real-time access control and distributed power control in wireless networks. This paper presents a distributed policy gradient algorithm for REC-MARL. The proposed algorithm is distributed in two aspects: (i) the learned policy is a distributed policy that maps a local state of an agent to its local action and (ii) the learning/training is distributed, during which each agent updates its policy based on its own and neighbors’ information. The learned algorithm achieves a stationary policy and its iterative complexity bounds depend on the dimension of local states and actions. The experimental results of our algorithm for the real-time access control and power control in wireless networks show that our policy significantly outperforms the state-of-the-art algorithms and well-known benchmarks.
1 Introduction
Multi-Agent Reinforcement Learning, or MARL for short, considers a reinforcement learning problem where multiple agents interact with each other and with the environment to finish a common task or achieve a common objective. The key difference between MARL and single-agent RL is that each agent in MARL only observes a subset of the state and receives an individual reward and does not have global information. Examples include multi-access networks where each user senses the collision locally, but needs to coordinate with each other to maximize the network throughput, or power control in wireless networks where each wireless node can only measure its local interference but they need to collectively decide the transmit power levels to maximize a network-wide utility, or task offloading in edge computing where each user observes its local quality of service (QoS) but they coordinate tasks offloaded to edge servers to maintain a high QoS for the network, or a team of robots where each robot can only sense its own surrounding environment, but the robot team needs to cooperate and coordinate for accomplishing a rescue task.
MARL raises two fundamental aspects that are different from single-agent RL. The first aspect is the policy space (the set of policies that are feasible) is restricted to local policies since each agent has to decide an action based on information available to the agent. The second aspect of MARL is that while distributed learning, e.g. distributed policy gradient, is desired, it is impossible in general MARL because an agent does not know the global state and rewards. One popular approach to address the second issue is the centralized learning and distributed execution paradigm [8], where data samples are collected by a central entity and the central entity uses data from all agents to learn a local policy. Therefore, the learning occurs at the central entity, but the learned policy is a local policy.
In this paper, we consider a special class of MARL, which we call REward-Coupled Multi-Agent Reinforcement Learning (REC-MARL). In REC-MARL, the problem is coupled through the reward functions. More specifically, the reward function of agent depends on agent ’s state and action and its neighbors’ states and actions. However, the next state of agent only depends on agent s current state and action, and is independent of other agents’ states and actions. In contrast, in general MARL, the transition kernels of the agents are coupled, so the next state of an agent depends on other agents’ states and actions.
While REC-MARL is more restrictive than MARL, a number of applications of MARL are actually REC-MARL. In wireless networks, where agents are network nodes or devices, and the state of an agent is could be its queue length or transmit power, the state only depends on an agent’s current state and its current action (see Section 2 for detailed description). For REC-MARL, this paper proposes distributed policy gradient algorithms and establish the local convergence (i.e. the algorithms achieve a stationary policy). The main contributions are summarized as follows.
-
•
We establish perfect decomposition of value functions and policy gradients in Lemmas 1 and 2, respectively, where we show that the global value functions (policy-gradients) can be written as a summation of local value functions (policy gradients). This decomposition significantly reduces the complexity of value functions and motivates our distributed multi-agent policy gradient algorithms.
-
•
We propose a Temporal-Difference (TD) learning based regularized distributed multi-agent policy gradient algorithm, named TD-RDAC in Algorithm 2. We proved in Theorem 2 that TD-RDAC achieves the local convergence with the rate which only depends on the maximum sizes of local state and action spaces, instead of the sizes of the global action and state spaces.
-
•
We apply TD-RDAC to the applications of real-time access and power control in ad hoc wireless networks, both are well-known challenging networking resource management problems. Our experiments show that TD-RDAC significantly outperforms the state-of-the-art algorithm [20] and well-known benchmarks [2, 21] in these two applications.
Related Work
MARL for networking: MARL have been applied to various networking applications (e.g., content caching [25], packet routing [23], video transcoding and transmission [3], transportation network control [6]). The work [25] proposed a multi-agent advantage actor-critic algorithm for large-scale video caching at network edge and it reduced the content access latency and traffic cost. The proposed algorithm requires the knowledge of neighbors’ policies, which is usually not observable. [23] studied packet routing problem in WAN and applied MARL to minimize the average packet completion time. The method adopted dynamic consensus algorithm to estimate the global reward, which incurs a heavy communication overhead. The work [3] proposed a multi-agent actor-critic algorithm for crowd-sourced livecast services and improved the average throughput and the transmission delay performance. The proposed algorithm requires a centralized controller to maintain the global state information. The most related work is [6], which utilized spatial discount factor to decouple the correlation of distant agents and designed networked MARL solution in traffic signal control and cooperative cruise control. However, it requires a dedicated communication module to maintain a local estimation of global state, which again incurs large communication cost. Moreover, the theoretical performance of these algorithms in [25, 23, 3, 6] are not investigated.
Provable MARL: There have been a great amount of works addressing the issues of scalability and sample complexity in MARL. A popular paradigm is the centralized learning and distributed execution (see e.g. [8]), where agents share a centralized critic but have individual actors. Both the critic and the actors are trained at a central server, but the actors are local policies that lead to a distributed implementation. [29] proposed a decentralized actor-critic algorithm for a cooperative scenario, where each agent has its individual critic and actor with a shared global state. The proposed algorithm converges an stationary point of the objective function. Motivated by [29], [4] and [10] provided a finite-time analysis of decentralized actor-critic algorithms in the infinity-horizon discounted-reward MDPs and average-reward MDPs, respectively. [30] studied a policy gradient algorithm for multi-agent stochastic games, where each agent maximizes its reward by taking actions independently based on the global state. It established its local convergence for general stochastic games and its global convergence for Markov potential games. The centralized critic or shared states (even with decentralized actors) require collecting global information and centralized training. The work [19] exploits the network structure to develop a localized or scalable actor-critic (SAC) framework that is proved to achieve -approximation of a stationary point in -discounted-reward MDPs. [20] and [13] extended SAC framework in [19] into the settings of infinity-horizon average-reward MDPs and stochastic/time-varying communication graphs. The SAC framework in [19] is efficient in implementing the paradigm of distributed learning and distributed execution. It is also worth mentioning that in a recent work [31], the authors studied a kernel-coupled setting and established that the localized policy-gradient converges to a neighborhood of global optimal policy, where the distance to the global optimality depends on the number of hops, , polynomially and could be a constant when is small. Another line of research in MARL that addresses the scalability issue is the mean-field approximation (MFA) [9, 7, 27], where agents are homogeneous and an individual agent interacts or games with the approximated “mean” behavior. However, the MFA approach is only applicable to a homogeneous system. Finally, [16] and [26] studied weakly-coupled MDPs, where individual MDPs are independent and coupled through constraints, instead of coupled reward as in ours.
Different from these existing works, this paper considers reward-coupled multi-agent Reinforcement learning (REC-MARL), establishes the local convergence of policy gradient algorithms with both distributed learning and distributed implementation, and demonstrates its efficiency in classical and challenging resource management problems.
2 Model
We consider a multi-agent system where the agents are connected by an interactive graph with and being the set of nodes and edges, respectively. The system consists of agents who are connected with edges in Each agent is associated with a -discounted Markov decision process of where is the state space, is the action space, is the reward function, and is the transition kernel. Define the neighbourhood of agent (including itself) to be Define the states and actions of the neighbors of agent to be and respectively. We next formally define the REward-Couple Multi-Agent Reinforcement Learning.
REC-MARL: The reward of agent depends on its neighbors’ states and actions The transition kernel of agent only depends on its own state and action Agent uses a local policy where is the probability of taking action in state
Given a REC-MARL problem, the global state space is with the global action space is with the global reward function is the transition kernel is with
In this paper, we study the softmax policy parameterized by that is
The global policy with is as follows
In this paper, we study -discounted infinite-horizon Markov decision processes (MDP) with being the state and action of the MDP at time For a global policy its value function, action value function (-function), and advantage function given the initial state and action () are defined below:
Let be the initial state distribution. Define Further define the discounted occupancy measure to be
| (1) |
We seek policies with distributed learning and distributed execution in this paper. We will decompose the global -function as a sum of local -functions so that the agents can collectively optimize the local policy. Before presenting the details of our solution, we introduce two representative applications in wireless networks: real-time access control and distributed power control.
Real-time access control in wireless networks: Consider a wireless access network with nodes (agents) and access points as shown in Figure 1(a). At the beginning of each time slot, a packet arrives at node with probability . The packet is associated with deadline is the successful transmitting probability when transmitting to access point A packet is removed if either it is sent to an access point (not necessarily delivered successfully) or it expires. At each time, each node decides whether to transmit a packet to one of the access points or keeping silence. A collision happens if multiple nodes send packets to the same access point simultaneously. Therefore, the throughput of a node depends not only on its decision but also its neighboring nodes’ decisions. In particular, the throughput of node is
| (2) |
where indicate if node transmits a packet to its access point The goal of real-time access control is to maximize the network throughput.
The problem of real-time access control is challenging because i) the throughput functions are non-convex and highly-coupled functions of other nodes’ decisions and ii) the system parameters are unknown (e.g., and ). This problem can be formulated as a REC-MARL problem. In particular for node/agent the MDP formulation is the state of agent is the queue length with being the number of packets with the remaining time ; the action is with (one of access point of agent ); is the reward for agent is its next queue state.
Distributed power control in wireless network: The other application of REC-MARL is distributed power control in wireless networks. Consider a network with wireless links (agents) as shown in Figure 1(b). Each link can control the transmission rate by adapting its power level, and neighboring links interfere with each other. Therefore, the transmission rate of a link depends not only on its transmit power but also its neighboring links’ transmit power. In particular, the reward/utility of link is its transmission rate minus a linear power cost:
| (3) |
where is the channel gain from node to is the power of node is the power of noise at user and are the trade-off parameters. The goal of distributed power control to maximize the total rewards for the network.
The distributed power control is also challenging because the reward function is non-convex and highly-coupled, and the channel condition is unknown and dynamic. This problem can also be formulated as a REC-MARL problem. In particular for link/agent the MDP formulation is the state of agent is the power level with ( is the maximum power constraint); the action is (keep, decrease, or increase the power level by one); is the reward for agent is the next power level.
In the following, we present distributed multi-agent reinforcement learning algorithms that can be used to solve these two problems and show that our algorithm outperforms the existing benchmarks.
3 Decomposition of Value and Policy Gradient Functions
To implement a paradigm of distributed learning and distributed execution, we first establish the decomposition of value and policy gradient functions in Lemma 1 and Lemma 2, respectively. The value and policy gradient functions could be represented locally and computed/estimated via exchange information with their neighbors.
3.1 Decomposition of value functions
We decompose the global value () functions into the individual value () functions and show they only depend on its neighborhood in Lemma 1. The proof could be found in Appendix A.1.
Lemma 1
Given a multi-agent network, where each agent is associated with a -discounted Markov decision process defined by the neighborhood of agent is defined by the network reward function is and the transition kernel is The policy of a network is with each agent using a local policy we have
3.2 Decomposition of Policy Gradient
We show that policy gradient function can also be decomposed exactly as -function. Recall the definitions of and and we first state the classical policy gradient theorem in [24].
Theorem 1 ([24])
Let be a policy parameterized by for a -discounted Markov decision process, we have the policy gradient to be
Theorem 1 has motivated policy gradient methods in the single-agent setting (e.g., [12]) and multi-agent setting (e.g., [14]). However, it is infeasible to be applied for a large-scale multi-agent network due to the large global state space. Therefore, we decompose the policy gradient in the following lemma. The proof can be found in Appendix A.2.
Lemma 2
Given a multi-agent network, where each agent is associated with a -discounted Markov decision process defined by the neighborhood of agent is defined by the network reward function is and the transition kernel is The policy of a network is with each agent using a local policy we have
Remark 2
Lemma 2 implies that policy gradient of agent could be computed/estimated via exchanging information or with its neighbors. This decomposition is the key to implement the efficient paradigm of distributed learning and distributed execution and motivate the algorithms in the following sections.
4 Distributed Multi-Agent Policy Gradient Algorithms
In this section, we introduce distributed policy gradient based algorithms (DPG) for the multi-agent system. Before introducing the algorithms, we assume that the initial state distribution induced by our policy is strictly positive:
Assumption 1
The initial state distribution satisfies for any agent
This assumption imposes the sufficient exploration for the state space for each agent and is common in the literature [1, 15]. We first propose a regularized distributed policy gradient algorithm assuming the access of an inexact gradient, and then introduce TD-learning methods to estimate the gradient.
4.1 Regularized Distributed Policy Gradient Algorithm with Inexact Gradient
Assume an estimated gradient at any time we study relative entropy regularized objective for the network as in [1, 28] that
where is a positive constant and is the regularizer to prevent the probability of taking action at state approaches to a small quantity for any agent With the regularized value function we present a DPG with the inexact gradient in Algorithm 1, where the inexact gradient is usually estimated with TD-learning methods (see Section 4.2).
By analyzing the dynamics of in Algorithm 1, we can establish the upper bound on the cumulative in Theorem 2. The proof can be found in Appendix B.
Theorem 2
Let and We have Algorithm 1 with the learning rate such that
Theorem 2 implies a local convergence result of Algorithm 1 given a reasonable good gradient estimator, e.g., which is related to the quality of estimated value functions according to Lemma 2. Next, we utilize TD-learning to estimate value functions, provide an actor-critic type of algorithm, and establish its local convergence.
4.2 Regularized Distributed Actor Critic Algorithm
Motivated by [19], we utilize TD-learning to estimate the gradient according to Lemma 2 and provide an actor-critic type of algorithm (TD-RDAC) for multi-agent setting in Algorithm 2. From Lemma 2, we have
For each agent it requires to aggregate the advantage functions (or the estimator) from its neighbors, i.e., for any to estimate the gradient or The actor-critic algorithm is summarized in Algorithm 2. It contains outer loops and inner loops. The lines to perform TD learning to estimate value function for each individual agent. The line is to compute TD-error based on the learned value function for each agent. The line is to estimate the policy gradient by aggregating its neighbors’ TD-error. The line is to update the policy parameters. The inner loops (lines to ) will be run rounds.
Intuitively, Algorithm 2 requires a large number of inner loops to guarantee the convergence of value function such that the estimated policy gradient is accurate. Before proving the local convergence results of Algorithm 2, we introduce a common Assumption 2 (e.g., [22, 18]) on the mixing time of Markov decision process.
Assumption 2
Assume be a Markov chain with the geometric mixing time under any policy i.e., there exists a constant such that for any the total variance distance of and satisfies
To avoid the complicated conditions on and we present the order-wise results in Theorem 3. The proofs and the detailed requirements on and can be found in Appendix C.
Theorem 3
Suppose large and Let the learning rate be We have Algorithm 2 such that
5 Experiments
In this section, we evaluate TD-RDAC for real-time access control problem and distributed power control problem in wireless networks as described in Section 2.
Real-time access control in wireless network: We consider the reward/utility of node defined in (2). We compared Algorithm 2 with the ALOHA algorithm [21] and a scalable actor critic (SAC) in [20]. The classical distributed solution to this problem is the localized ALOHA algorithm [21], where node sends the earliest packet with a certain probability and the packet is sent to a random access point in its available set, with probability proportional to and inversely proportional to the number of nodes that can potentially transmit to access point Note to compare ALOHA algorithm [21] and SAC in [20], we apply Algorithm 2 into a slightly different setting where a packet is removed from its queue if either it is delivered successfully or expired.
In our experiment, we considered two types of network topology: a line network and a grid network as shown in the lefthhand side of Figure 2. The tabular method is used to represent value functions since the size of the table is tractable in this experiment.
The line network has nodes and access points as shown in the left-up of Figure 2. We considered two settings in the line network with the same arrival probability but distinct success transmission probabilities to represent reliable/unreliable environments. Specifically, the arrival probabilities are the transmission probabilities of the reliable/unreliable environments are and respectively. The deadline of packets is We ran different instances with different random seeds and the shaded region represents the confidence interval. We observe our algorithm increases steady in Figures 3(a) and 3(b) and outperforms both SAC algorithm in [20] and ALOHA algorithm in the reliable and unreliable environment, where the converged rewards of (our algorithm v.s. SAC v.s. ALOHA) are ( v.s. v.s. ) and ( v.s. v.s. ) for the reliable and unreliable environment, respectively.
The grid network is similar as in [20], shown in the left-bottom of Figure 2. The network has nodes and access points. The arrival probability of node and success transmission probability of access point are generated uniformly random from The deadline of packets is also set We observe our algorithm again increases steady in Figure 3(c) even with the relatively dense environment and outperforms both SAC algorithm in [20] and ALOHA algorithm [21], where the converged rewards of (our algorithm v.s. SAC v.s. ALOHA) are ( v.s. v.s. ).




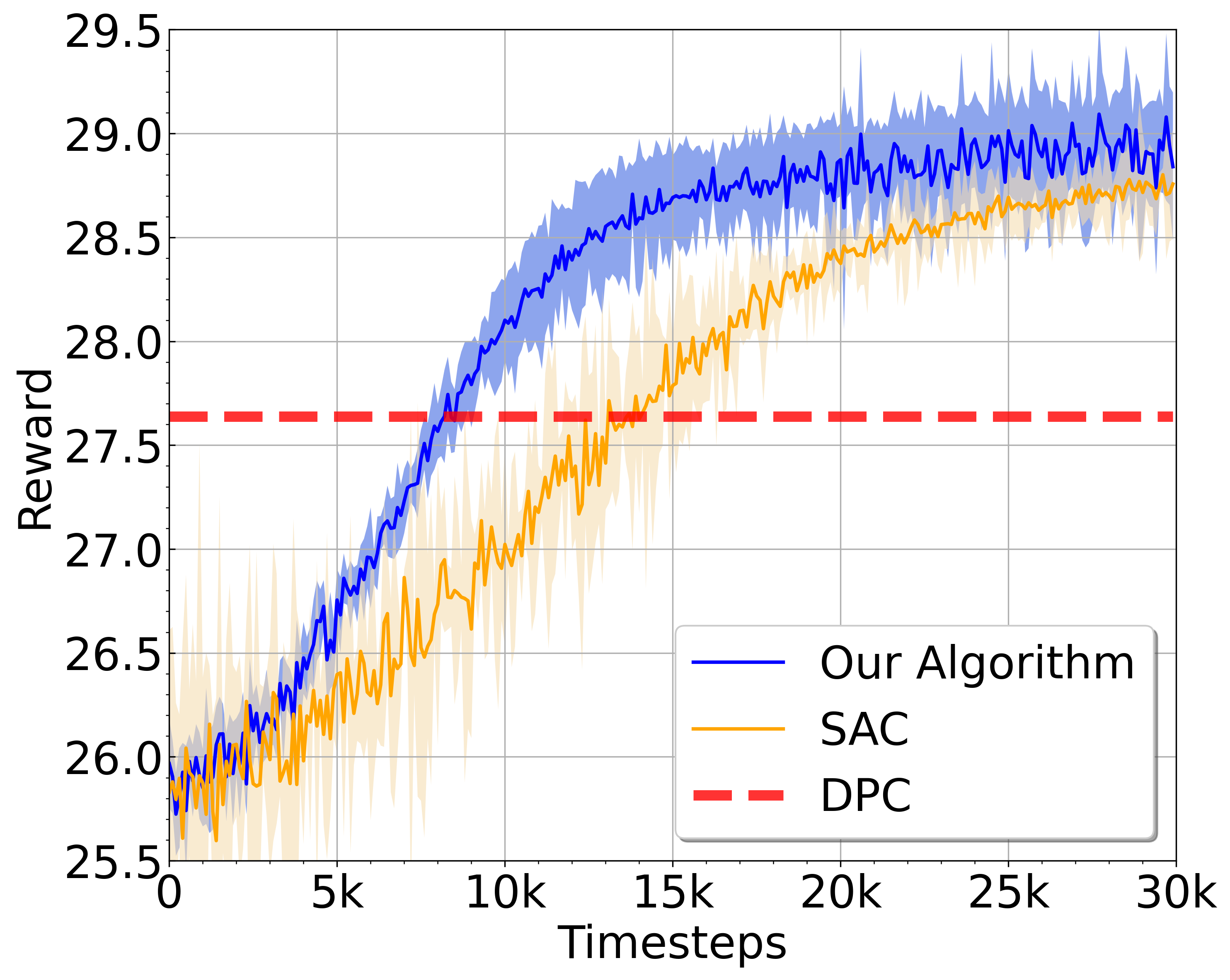

Distributed power control in wireless network: We considered the reward/utility of each agent is the difference between a logarithmic function of signal-interference-noise ratio (SINR) and a linear pricing function proportional to the transmitted power as in (3). In the literature, the problem has been formulated as a linear pricing game [2] and [5]. We compared Algorithm 2 with the DPC algorithm [2] and SAC in [20]. In our experiment, we first studied a setting with -link ( grids) where the tabular method is tractable to represent value functions. Then we studied two settings: -link and -link as shown in the right-hand side of Figure 2, where we use blue circles to denote links. For both settings, we use neural network (NN) approximation for value functions. With NN approximation, we utilized the replay buffer [17] and double-Q learning [11] to stabilize the learning process.
For the reward/utility in (3), we set and with as the fading factor and is the distance between nodes and The average power of the noise is We set the trade-off parameter For each environment, we ran different instances with different random seeds and the shaded region represents the confidence interval.
For -nodes network, we represent value functions with tables in Algorithm 2. We observe the learning processes are quite stable in Figure 4(a). We observe our algorithm outperforms the SAC and DPC algorithm as the training time increases: the converged reward are ( v.s. v.s. ). For 9-nodes , we approximate value functions with neural networks in Algorithm 2. We observe Algorithm 2 outperforms the SAC and DPC algorithms as the training time increases in Figure 4(b) ( v.s. v.s. ). For 25 nodes, Figure 4(c) shows the results with a heterogeneous topology. Again, we observe our algorithm increases steady in Figure 4(c) and outperforms the SAC and DPC algorithms ( v.s. v.s. ).
Finally, we note that both ALOHA and DPC algorithms are model-based algorithm and the agents need to know the systems parameters (success transmitting probability in the real-time access control problem and channel gains and interference levels in the power control problem) while our algorithm is model-free and does not need to know these parameters.
6 Conclusion
In this paper, we studied a weakly-coupled multi-agent reinforcement learning problem where agents’ reward functions are coupled but the transition kernels are not. We propose TD-learning based regularized multi-agent policy actor-critic algorithm (TD-RDAC) that achieve the local convergence result. We demonstrated the effectiveness of TD-RDAC with two important applications in wireless networks: real-time access control and distributed power control and showed that our algorithm outperforms the existing benchmarks in the literature.
Acknowledgements
The authors are very grateful to Rui Hu for his insightful discussion and comments.
References
- [1] Alekh Agarwal, Sham M Kakade, Jason D Lee, and Gaurav Mahajan. Optimality and approximation with policy gradient methods in markov decision processes. In Proceedings of Thirty Third Conference on Learning Theory, 2020.
- [2] Tansu Alpcan, Tamer Başar, R. Srikant, and Eitan Altman. CDMA uplink power control as a non-cooperative game. Proceedings of the IEEE Conference on Decision and Control, 2001.
- [3] Xingyan Chen, Changqiao Xu, Mu Wang, Zhonghui Wu, Shujie Yang, Lujie Zhong, and Gabriel-Miro Muntean. A universal transcoding and transmission method for livecast with networked multi-agent reinforcement learning. In IEEE Conference on Computer Communications, 2021.
- [4] Ziyi Chen, Yi Zhou, Rong-Rong Chen, and Shaofeng Zou. Sample and communication-efficient decentralized actor-critic algorithms with finite-time analysis. In Proceedings of the 39th International Conference on Machine Learning, 2022.
- [5] Mung Chiang, Prashanth Hande, Tian Lan, and Chee Wei Tan. Power control in wireless cellular networks. Foundations and Trends® in Networking, 2008.
- [6] Tianshu Chu, Sandeep Chinchali, and Sachin Katti. Multi-agent reinforcement learning for networked system control. In International Conference on Learning Representations, 2020.
- [7] Romuald Elie, Pérolat Julien, Mathieu Laurière, Matthieu Geist, and Olivier Pietquin. On the convergence of model free learning in mean field games. AAAI Conference on Artificial Intelligence, 2020.
- [8] Jakob Foerster, Gregory Farquhar, Triantafyllos Afouras, Nantas Nardelli, and Shimon Whiteson. Counterfactual multi-agent policy gradients. AAAI Conference on Artificial Intelligence, 2018.
- [9] Xin Guo, Anran Hu, Renyuan Xu, and Junzi Zhang. Learning mean-field games. In Advances in Neural Information Processing Systems, 2019.
- [10] FNU Hairi, Jia Liu, and Songtao Lu. Finite-time convergence and sample complexity of multi-agent actor-critic reinforcement learning with average reward. In The Tenth International Conference on Learning Representations, 2022.
- [11] Hado van Hasselt, Arthur Guez, and David Silver. Deep reinforcement learning with double q-learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, 2016.
- [12] Vijay Konda and John Tsitsiklis. Actor-critic algorithms. In S. Solla, T. Leen, and K. Müller, editors, Advances in Neural Information Processing Systems, volume 12. MIT Press, 2000.
- [13] Yiheng Lin, Guannan Qu, Longbo Huang, and Adam Wierman. Multi-agent reinforcement learning in stochastic networked systems. In Advances in Neural Information Processing Systems, 2021.
- [14] Ryan Lowe, Yi Wu, Aviv Tamar, Jean Harb, Pieter Abbeel, and Igor Mordatch. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017.
- [15] Jincheng Mei, Chenjun Xiao, Csaba Szepesvari, and Dale Schuurmans. On the global convergence rates of softmax policy gradient methods. In Proceedings of the 37th International Conference on Machine Learning, 2020.
- [16] Nicolas Meuleau, Milos Hauskrecht, Kee-Eung Kim, Leonid Peshkin, Leslie Pack Kaelbling, Thomas Dean, and Craig Boutilier. Solving very large weakly coupled markov decision processes. American Association for Artificial Intelligence, 1998.
- [17] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. Playing atari with deep reinforcement learning. In International Conference on Neural Information Processing Systems, 2013.
- [18] Guannan Qu, Yiheng Lin, Adam Wierman, and Na Li. Scalable multi-agent reinforcement learning for networked systems with average reward. arXiv preprint arXiv:2006.06626, 2020.
- [19] Guannan Qu, Adam Wierman, and Na Li. Scalable reinforcement learning of localized policies for multi-agent networked systems. In Proceedings of the 2nd Conference on Learning for Dynamics and Control, 2020.
- [20] Guannan Qu, Adam Wierman, and Na Li. Scalable reinforcement learning for multiagent networked systems. Operations Research, 2022.
- [21] Lawrence G. Roberts. Aloha packet system with and without slots and capture. SIGCOMM Comput. Commun. Rev., 1975.
- [22] R. Srikant and Lei Ying. Finite-time error bounds for linear stochastic approximation and TD learning. In Proceedings of the 22nd Annual Conference on Learning Theory (COLT), 2019.
- [23] Shan Sun, Mariam Kiran, and Wei Ren. MAMRL: Exploiting multi-agent meta reinforcement learning in WAN traffic engineering. arXiv preprint arXiv:2111.15087, 2021.
- [24] Richard S. Sutton, David McAllester, Satinder Singh, and Yishay Mansour. Policy gradient methods for reinforcement learning with function approximation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, 1999.
- [25] Fangxin Wang, Feng Wang, Jiangchuan Liu, Ryan Shea, and Lifeng Sun. Intelligent video caching at network edge: A multi-agent deep reinforcement learning approach. In IEEE Conference on Computer Communications, 2020.
- [26] Xiaohan Wei, Hao Yu, and Michael J. Neely. Online learning in weakly coupled markov decision processes: A convergence time study. Proc. ACM Meas. Anal. Comput. Syst., apr 2018.
- [27] Qiaomin Xie, Zhuoran Yang, Zhaoran Wang, and Andreea Minca. Learning while playing in mean-field games: Convergence and optimality. In Proceedings of the 38th International Conference on Machine Learning, 2021.
- [28] Junzi Zhang, Jongho Kim, Brendan O’Donoghue, and Stephen Boyd. Sample efficient reinforcement learning with reinforce. In Proceedings of the AAAI Conference on Artificial Intelligence, 2021.
- [29] Kaiqing Zhang, Zhuoran Yang, Han Liu, Tong Zhang, and Tamer Basar. Fully decentralized multi-agent reinforcement learning with networked agents. In Proceedings of the 35th International Conference on Machine Learning, 2018.
- [30] Runyu Zhang, Zhaolin Ren, and Na Li. Gradient play in multi-agent markov stochastic games: Stationary points and convergence. arXiv preprint arXiv:2106.00198, 2021.
- [31] Yizhou Zhang, Guannan Qu, Pan Xu, Yiheng Lin, Zaiwei Chen, and Adam Wierman. Global convergence of localized policy iteration in networked multi-agent reinforcement learning. arXiv preprint arXiv:2211.17116, 11 2022.
Appendix A Decomposition of Value Functions
A.1 Proof of Lemma 1
Proof 1
We provide the proof of the decomposition on -function and the similar argument holds for the value function According to the definitions of reward and -function, we have
where the second equality holds because the reward and transition of agent only depends on its neighbors’ states and actions since for any trajectories of agent until we have
and it implies only depends on
A.2 Proof of Lemma 2
Appendix B Proof of Theorem 2
To prove Theorem 2, we first prove the smoothness of regularized value function.
B.1 Smoothness of function
Recall the definition of function
where We show is -smoothness in Lemma 3 and is -smoothness in Lemma 4, respectively, which imply is smoothness.
Lemma 3 (Smoothness)
Under Algorithm 1, we have to be smoothness, i.e.,
Proof 3
The Bellman equation (for a network) is
Let
Let be a vector with only the th entry being one and zeros for other entries. The Bellman equation can be wrote as
which implies satisfies
where is the identity matrix. Let and we have With a bit abuse of notation, let and We need to compute the first-order gradient
where we use the derivative of inverse matrix and the second-order gradient
Therefore, we need to establish the upper bounds on
which require to compute
Recall Let’s compute
where the last equality holds because
and it implies
Therefore, we have
Next, let’s compute
where we need to compute
and
Then we have
and
| (4) | ||||
| (5) | ||||
| (6) |
which implies
| (7) |
Now it is good to bound
Finally, we have
which completes the proof.
Lemma 4
Under Algorithm 1, we have is -smoothness.
Proof 4
We have for any such that
which implies
Finally we have
which completes the proof.
B.2 Proving Theorem 2
Recall and Given and we have
Since we have
which implies
Take summation and we have
Appendix C Proof of Theorem 3
Recall the estimated gradient and the true gradient to be
Further define and to decompose policy gradient as follows:
The error is decomposed to be
where the error is related to the estimated TD-error and its true TD-error under policy the error is related to the sample-based TD-error estimation and its expected one; the error is related to the truncated error of estimated state occupancy measure.
To prove Theorem 3, we establish the following lemma that relates to the errors of and
Lemma 5
Under Algorithm 1, we have
Proof 5
Define Therefore, we have
Recall the values of and where , we have
which implies that
| (8) |
Next, we provide the upper bound on Note that
and
We immediately have
Finally, we complete the proof by substituting the upper bound into (8).
In the following subsections, we provide the upper bounds on the error terms in Lemma 5. We define and occasionally abbreviate the index in for a simple notation.
C.1 Bounds on and
Lemma 6
Proof 6
As in the proof of Lemma 5, it could be verified that are bounded by the term
Therefore, all these error terms of and are also bounded by
which completes the proof.
C.2 Bound on
Lemma 7
Proof 7
The sequence of is a martingale difference sequence with respect to because it satisfies
-
•
-
•
Therefore, we use Azuma–Hoeffding inequality for the sequence such that
which completes the proof.
C.3 Bound on
Lemma 8
Proof 8
We have
C.4 Bounds on
Lemma 9
Proof 9
Recall the error
which implies that
where the third inequality holds because and the last inequality holds because and the last inequality holds because of the definition of TD-error
Since is directly related to the estimation error of value function, we follow [22] to establish a finite-time analysis of We write down a linear representation of value function updating as in [22]. Define and a vector with the th entry being one and zeros otherwise. We abbreviate and for the simple notation because we evaluate a fixed policy for any and the following derivation holds for any We represent with parameter Recall the value function updates in Algorithm 2 as follows
which can be wrote down in a linear form
Define and we have
| (9) |
Define a matrix to be with the column being and to be a diagonal matrix with where is the stationary distribution of Markov chain to be the transition kernel matrix and to be a vector with being the th entry. Further define and The corresponding (shift) ODE of (9) is
where its equilibrium is and it is also the solution to Bellman equation, i.e.,
Then we study by leveraging the drift analysis as in [22]. The Lyapunov equation of ODE is with a positive symmetric where and are the largest and smallest eigenvalues of
Based on Assumption 2, let be the mixing time such that total variance distance of and is less than that is
Based on these definitions, we state Theorem in [22] as follows.
Theorem 4 (Theorem in [22])
For any and such that we have the following finite-time bound:
By setting we can invoke Theorem in [22] and have the following lemma.
Lemma 10
For any such that we have the estimation error of value functions
Proof 10
Let and in Theorem 4, we have
which completes the proof because of the linear representation of the value function
C.5 Proving Theorem 3
Let and We consider a small and a large such that and Combine all lemmas together, we have
the last inequality holds because
which completes the proof of Theorem 3 by