Same sign trilepton as signature of charged Higgs in two Higgs doublet model
Abstract
We explored the prospect of looking for a fermiophobic charged Higgs () via the same sign trilepton signal at the LHC. A fermiophobic scenario appears in the type-I two Higgs doublet model where the coupling of the with the Standard Model fermions is inversely proportional to . Almost all the experimental searches rely on the fermionic production and decay of the charged Higgs. Consequently, the limit on for fermiophobic scenarios is non-existent unless is small. We show that for a fermiophobic case, the electroweak production of is dominant for most of the parameter space. Subsequent bosonic decay of the charged and neutral Higgses give rise to the same sign trilepton signal. With a thorough phenomenological analysis, we demonstrate that the same sign trilepton signal can be an excellent complementary search to explore the high regions.
Keywords:
Two Higgs Doublet Models, Charged Higgs, Fermiophobic Higgs, Same sign trilepton1 Introduction
Extension of the Higgs sector is ubiquitous in physics beyond the Standard Model (BSM), and two Higgs Doublet Model (2HDM) is one of the simplest extensions containing two scalar doublets instead of one for electroweak symmetry breaking. To avoid the dangerous flavour changing neutral current, the Yukawa interactions are restrictedGunion:1989we ; Djouadi:2005gj ; Branco:2011iw and the phenomenology of the BSM scalars vary based on the Yukawa structure. A charged Higgs boson () would be one of the most striking signals of an extended Higgs sector like 2HDM. The Large Hadron Collider (LHC) has performed several searches for the charged Higgs. For most of the cases the collider studies look for produced in association with a top quark and decays to jets or leptons ATLAS:2013uxj ; ATLAS:2014otc ; CMS:2015lsf ; CMS:2015yvc ; ATLAS:2016avi ; ATLAS:2018gfm ; ATLAS:2018ntn ; CMS:2018dzl ; CMS:2019bfg ; ATLAS:2020jqj ; ATLAS:2021upq . Production of a charged Higgs via vector boson fusion is also explored in CMS:2017fgp ; ATLAS:2018iui . Discovery prospects of charged Higgs in model independent framework are studied in Coleppa_2020 ; Coleppa:2021wjx .
The LHC searches are motivated by the Yukawa structure of type-II 2HDM and supersymmetry. Thus these searches can not explore an extensive part of phenomenology where the is fermiophobic. The type-I 2HDM at the large is one of the simplest realizations of fermiophobic scalars. In this scenario, the typical production of charged Higgs via the top channel becomes very low. As a result, the existing limit on charged Higgs in the type-I 2HDM is essentially non-existent for larger than five Chen:2019pkq ; Kling:2020hmi . Thus, to investigate the vast region with large , we need to look for independent channels. Hence, exploration of bosonic decay of the BSM scalars is essential, which is governed by the gauge coupling. Another aspect that determines the signature of a is the BSM scalar spectrum. If a BSM scalar lighter than exist, then the signature of the varies accordingly.
The importance of the bosonic decay model of the has been identified before. The decay of to and a neutral scalar has been studied for both type-II and type-I 2HDM model with associated production of charged Higgs Coleppa:2014cca ; Enberg:2014pua ; Kling:2015uba ; Akeroyd:2016ymd ; Arhrib:2016wpw ; Alves:2017snd ; Arhrib:2019ywg ; Arhrib:2020tqk ; Sanyal:2019xcp and in linear colliders Akeroyd_1999 ; Demirci_2020 . For fermiophobic cases, the coupling is suppressed, and the channel becomes irrelevant for large . On the other hand, the electroweak production of Kanemura:2001hz ; Cao:2003tr ; Belyaev:2006rf ; Chun:2018vsn ; Bahl:2021str in association with a neutral (pseudo)scalar depends on the gauge coupling and dominates over the top associated production at large . In type-I 2HDM, the electroweak production of a light charged Higgs can give rise to multi-photon or multi-boson final state Arhrib:2017wmo ; Enberg:2018pye ; Enberg:2018nfv ; Arhrib:2021xmc ; Wang:2021pxc ; Akeroyd:2003bt ; Akeroyd_2004 . However, if the BSM scalars are heavier than the observed Higgs boson, they dominantly decay to a pair of massive gauge bosons, and these analyses can not be applied. Hence it is crucial to consider how to look for a if it is heavier than the SM Higgs boson to understand the experimental discovery potential of a charged Higgs.
Our goal is to present a complementary search strategy for the charged and neutral Higgses, which are heavier than the SM Higgs boson and display fermiophobic nature. We consider electroweak production of the charged Higgs and its subsequent decay to the heavy CP even neutral scalar . We found that this channel remains dominant for a wide range of parameter space and give rise to a distinctive final state. Although it is possible to explore the final state via trilepton signature, the signature will be overwhelmed by the huge background coming from and channels. Going further to four lepton final state decreases the signal cross-section significantly, and it will compete with another substantial background.
In this work, we have shown that the most promising signal is the same sign trilepton (SS3L) final state. Background for this process is rare. We have done a realistic analysis of the SS3L final state for the fermiophobic BSM sector by using the type-I 2HDM as a proxy scenario. We show that the proposed signal will discover or rule out a significant parameter space for BSM scalars even at an integrated luminosity of 300 . The exclusion bounds can be as low as , and any larger than that will be covered by the high luminosity LHC with an integrated luminosity of 3000 . The proposed signal complement the existing search strategies to expand the reach of LHC searches for charged Higgs. To show robustness of our study, we have studied the scenarios for three different mass gaps between charged Higgs and the heavy CP even neutral scalar. For a mass gap of 120 GeV, all relevant processes apart from is on-shell and when mass gap is 85 GeV, the process becomes off-shell. It is possible to accommodate even lower mass gap of 60 GeV where all the processes including become off-shell.
The paper is organized as follows: In Sec. 2 we briefly discuss the type-I 2HDM model, including the existing theoretical and experimental bounds on the parameter space. Then we motivate towards the possible SS3L signature in Sec. 3 where we also provide the details of the collider analysis. The results are presented in Sec. 4 and we conclude in Sec. 5.
2 The Model and Experimental Bounds
Here we give a brief overview of the type-I 2HDM and discuss possible phenomenology and experimental constraints.
2.1 The 2HDM Type-I Model
The 2HDM model consists of two scalar doublets and with hypercharge Gunion:1989we ; Djouadi:2005gj ; Branco:2011iw . Flavor changing neutral current (FCNC) interaction appears at tree level when both the doublets couple to the fermions. It is possible to suppress FCNC at tree level by imposing an additional symmetry such that and . The fermions are also charged appropriately under the discrete symmetry. The symmetric scalar potential is,
| (1) | |||||
The symmetry is softly broken by the dimensionful coupling and we have considered the parameters and to be real assuming CP invariance. We parameterize the doublets in the following way,
| (2) |
The scalar spectrum consists of five massive states, two CP-even neutral scalars and , one CP-odd pseudoscalar , and a pair of charged Higgs . The mass eigenstates can be expressed in terms of the gauge eigenstates:
| (3) |
Here , etc. and . The CP-even state is identified as the SM-like Higgs boson with mass GeV.
| 2HDM | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| type-I |
Based on the charge assignment of the fermions, there are four possible types of Yukawa structures, and in this article, we will consider the type-I 2HDM, where the fermions are even under symmetry and thus couple only with . The relevant Yukawa Lagrangian is given by,
| (4) |
where . After the symmetry breaking, we can write the Yukawa Lagrangian in terms of mass eigenstates,
| (5) | |||||
Here the up-type quarks, down-type quarks, and charged leptons are denoted as , , and respectively. The Yukawa multiplicative factors () for the type-I scenario are given in Tab. 1. Note that we can write couling of with fermions () as . Hence the BSM Higgs becomes fermiophobic when . We will use this relation later in our analysis.
For completeness, let us provide the relevant scalar couplings. In 2HDM, the couplings of scalars with a pair of gauge bosons are given by Gunion:1989we ; Djouadi:2005gj :
| (6) |
where = . The couplings of boson with the neutral scalars are,
| (7) |
where and are outgoing four-momenta of the first and the second scalars, respectively, and . Couplings involving the charged scalar is given by,
| (8) |
The trilinear scalar coupling which governs the decay of heavy Higgs to a pair of SM Higgs bosons is PhysRevD.77.115013
| (9) |
2.2 Theoretical Constraints
The quartic couplings in Eq. 1 are restricted by vacuum stability of the potential, tree unitarity and perturbativity. The conditions are,
-
•
Perturbativity :
-
•
Vacuum stability Gunion:2002zf :
(10) -
•
Unitarity constraints are discussed in Kanemura:1993hm ; Akeroyd:2000wc .
We have used the 2HDMC-1.8.0 Eriksson:2009ws package to check the above constraints before any phenomenological analysis.
The presence of two Higgs doublets modifies the electroweak oblique parameters Peskin:1991sw . The -parameter restricts large mass splitting among the components of the doublet, and we have assumed that the pseudoscalar is degenerate with the charged Higgs (), thus evading the precision constraints.
2.3 Experimental Constraints
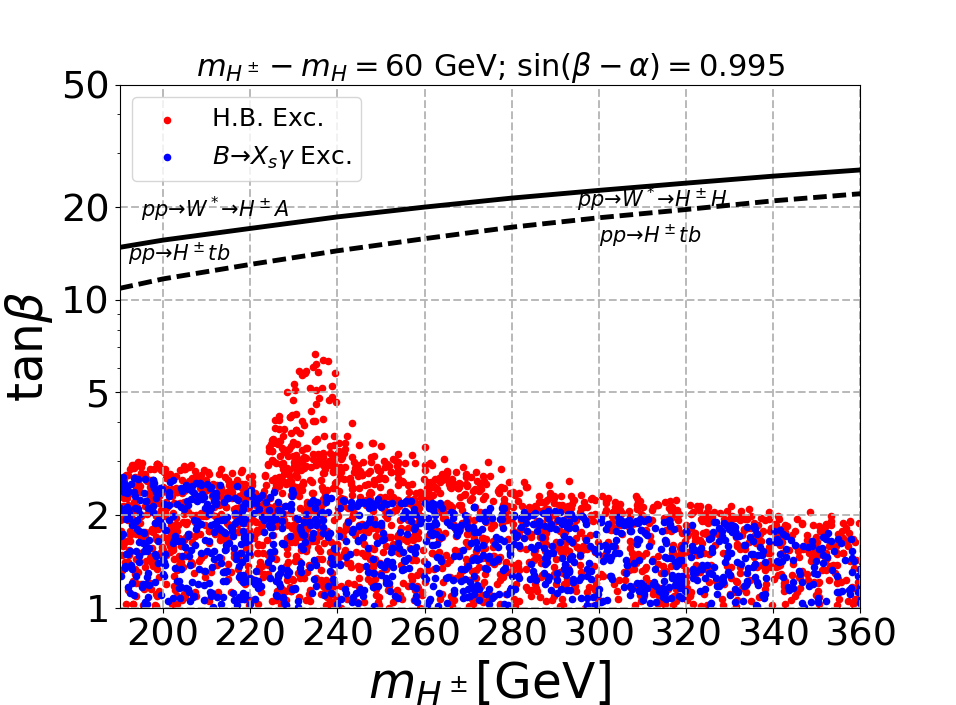
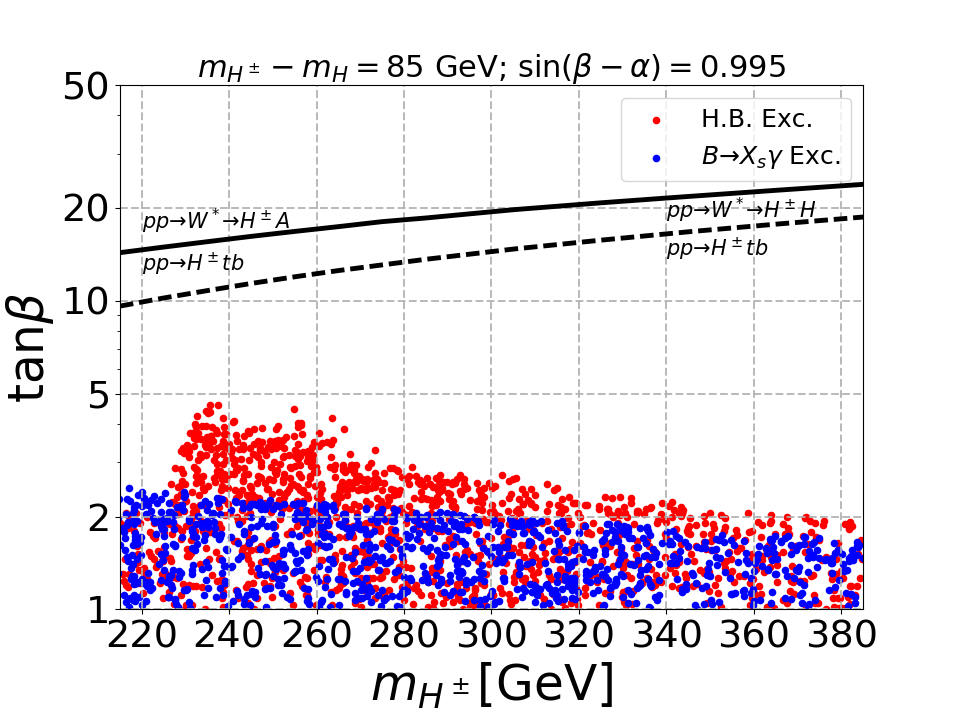
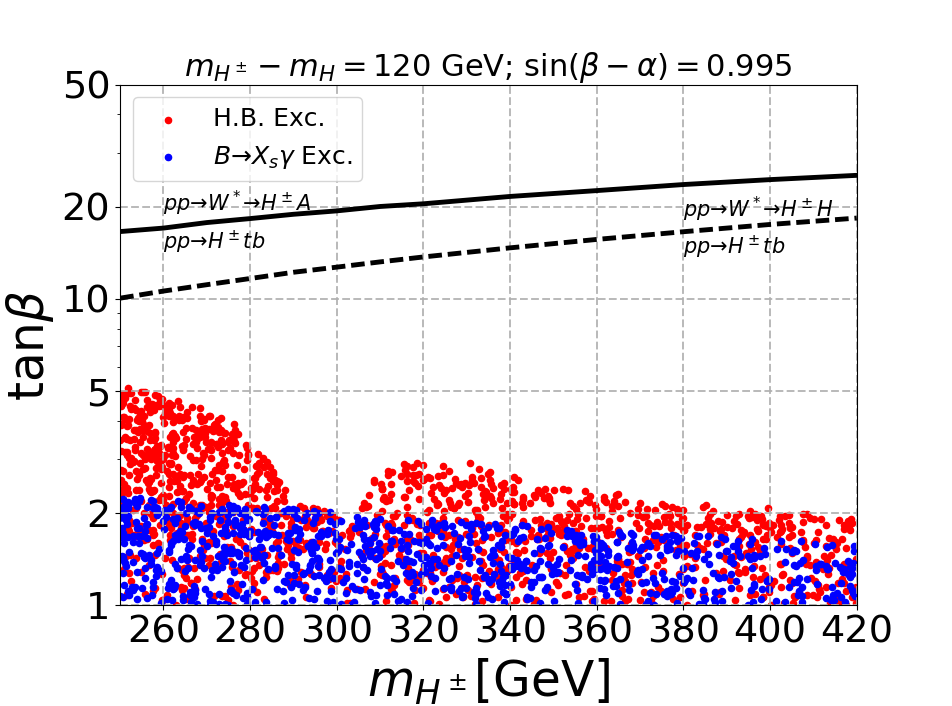
To obtain the limits coming from experimental searches at the LHC, we have used the public code HiggsBounds-5.10.2 Bechtle:2013wla ; Bechtle:2020pkv . We are interested in the scenario where the CP-even Higgs is lighter than and which are degenerate. For our analysis we choose three mass differences, viz. 60 GeV, 85 GeV and 120 GeV. A wider mass gap makes heavy and the production cross-section decreases. We choose the mixing angle . We then scan the CP-even heavy Higgs in the range GeV, and . We used HiggsSignals-2.6.2 Bechtle_2014 ; Bechtle:2020uwn to satisfy the SM Higgs signal strength measurements and since we are very close to the alignment limit which is , the above mentioned parameter space easily satisfy the constraints on the SM Higgs boson measurements.
In Fig. 1 we have shown exclusion in plane for different mass gaps between and . The red points depict the limit coming from LHC measurements and we found that the constraint on the plane is governed by the following LHC searches as obtained by HiggsBounds-5.10.2: ATLAS:2015kpj ; CMS:2018xvc , ATLAS:2018oht , CMS:2015mca , CMS:2017vpy or ATLAS:2014jdv , ATLAS:2018ntn and also the SM Higgs boson decay to 4-leptons CMS:2013wyb . In the 2HDM scenario the observation of HFLAV:2016hnz ; Misiak:2017bgg constrain the charged Higgs mass and the limit is shown in blue points using the package SUPERISO-2.5 Mahmoudi_2009 . For the type-I 2HDM scenario, the production of neutral Higgses () via gluon fusion as well as the production of charged Higgs via the top associated channel () is suppressed by . Hence, the limit coming from present LHC searches (red points) primarily restricts the small region, and the limits will remain weak even in HL-LHC Chen:2019pkq . We would like to point out that the limit coming from is the strongest when all the BSM scalars are degenerate Kling:2020hmi . However, in our case, the decay of the pseudoscalar to channel is substantial, and consequently, the experimental sensitivity is poor. Similarly, the exclusion is weak due to the fermiophobic nature of fermionic coupling of . In the top left (mass gap of 60 GeV) of Fig. 1 when the decay opens up, the exlusion limit becomes stronger which is clearly visible when crosses 220 GeV. The same argument applies to the top right panel (mass gap of 85 GeV). In the bottom panel (mass gap of 120 GeV) is always open, but the limit becomes weak as increases. The limit again becomes strong when opens up and this explains the dip in the exclusion region obtained from HiggsBounds-5.10.2.
From Fig. 1 it is evident that the existing LHC search strategies are inadequate, and we need to explore possible signatures which will be effective in the high regime. As increases, the production of in association with top quark decreases but the electroweak(EW) production is independent of . The black solid and dashed lines in Fig. 1 depict when the EW process dominates over top quark processes, and it is evident that we need to consider the EW process for large . In the next section, we have explored the phenomenology of produced alongside and . We will show that the exploration via gauge boson channels can significantly enhance the reach of LHC for the search.
3 Same sign trilepton as probe of charged Higgs
In the previous section, we demonstrated that the existing LHC limit on the BSM scalars in the type-I 2HDM is rather weak. We can improve it by exploring the EW production of and its decay into gauge bosons. Here we will show that the most promising channel is the same sign trilepton (SS3L) final state. Such signal originates via the following processes111Another possible source of SS3L is through the charged Higgs pair creation mode: . However, the charged Higgs pair production via channel is much smaller than the charged current channel and hence does not affect our result.:
| (11) |
Here is any additional jets and/or leptons. Since the pseudoscalar is degenerate with , the bottom process will be subdominant compared to the channel. Before going into the phenomenological study of the signal, let us first discuss the decay of the BSM Higgs to the gauge bosons. We compute the decay widths and the branching ratios using 2HDMC-1.8.0.
3.1 Bosonic decays of the Higgs bosons
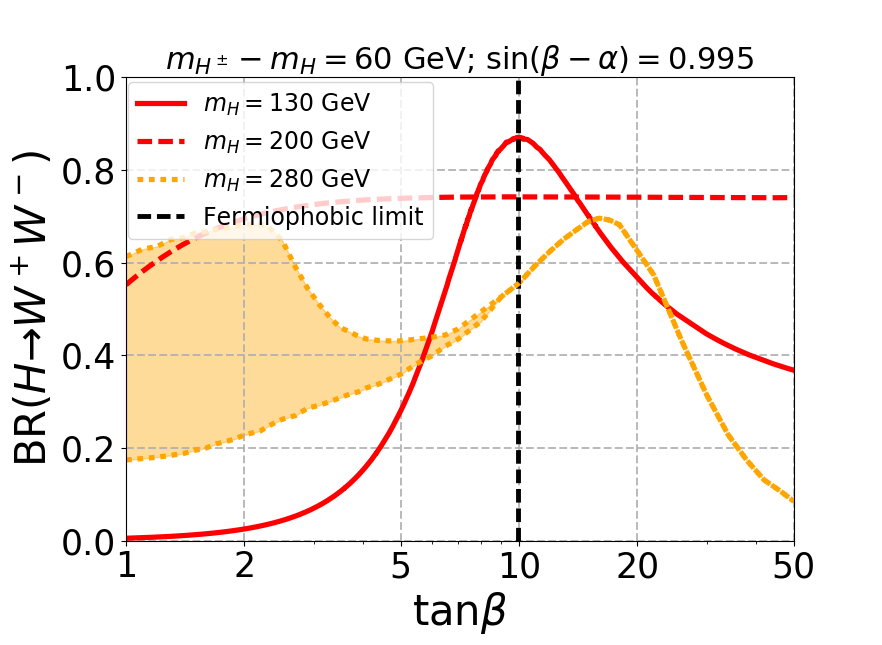
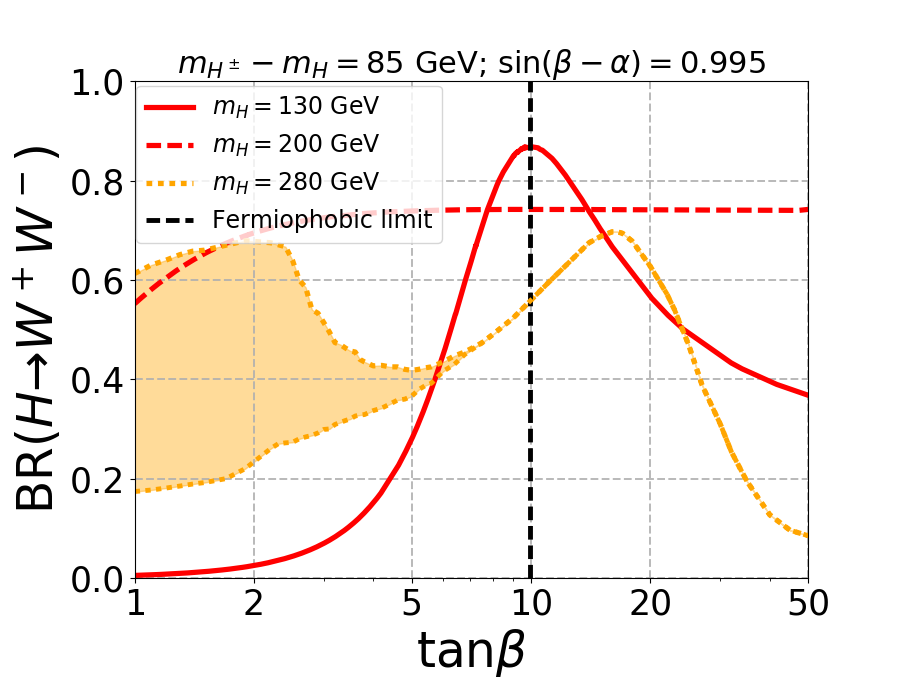
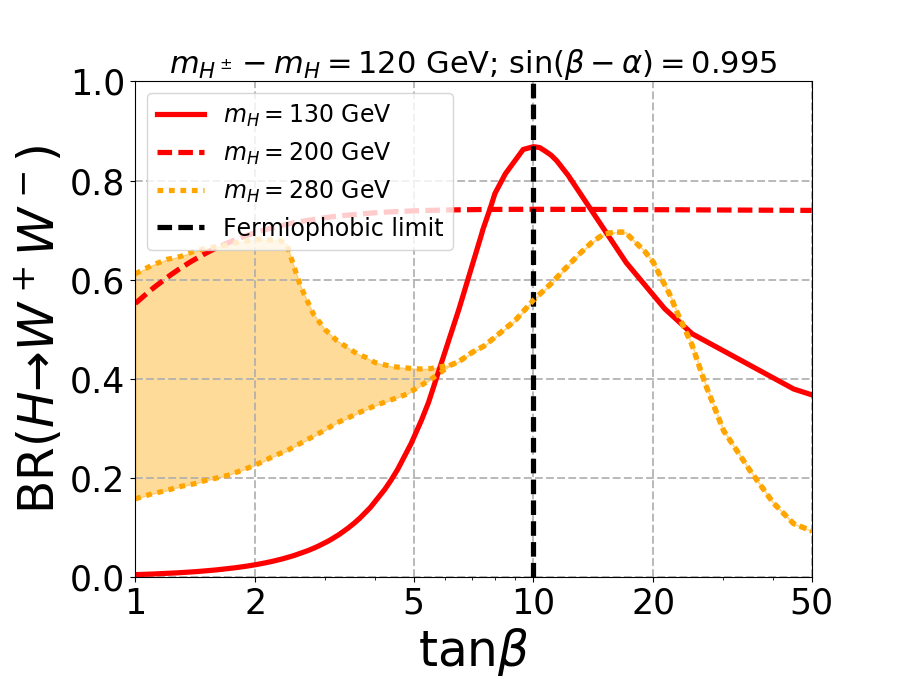
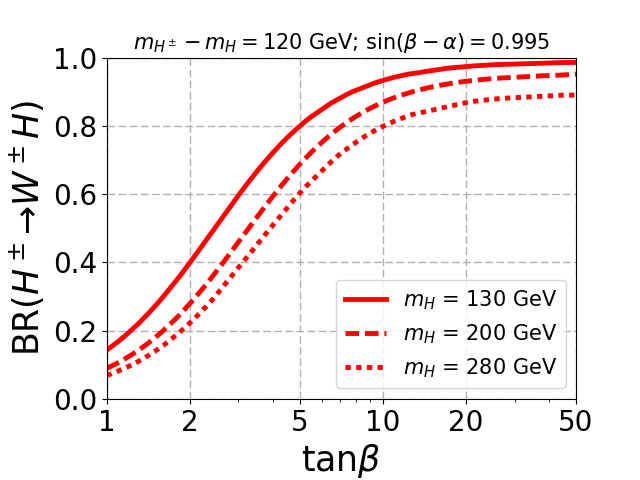
In Fig. 2 the branching ratios of additional Higgs bosons are shown for different mass differences, where we fix . The top panel shows the decay of to final state for different as a function of . When is smaller than (solid red curve), the branching ratio peaks only at the fermiophobic limit (indicated by the vertical black dashed line), which occurs for when . As we move away from the fermiophobic limit, the branching ratio decreases slightly but remains large enough to be explored at the LHC. As increases and on-shell decay to pair opens up, becomes the dominant decay mode irrespective of as shown by the red-dashed curves in the top panel. When the di-Higgs channel opens up, which decreases the branching ratio. The coupling as shown in Eq. 9 depends on , and for small , the allowed range of varies substantially, which changes the decay width. Consequently, the BR() also varies, which is shown by the yellow region. As increases, the value of approaches to satisfy the stability and perturbativity constraints, and the yellow regions become a single curve. When becomes very large, the coupling dominates, which decrease the branching substantially. The figures in the top planel look independent of mass gap since the mass gap changes the masses of (and ) which affects only the di-photon branching ratio, a loop suppressed process.
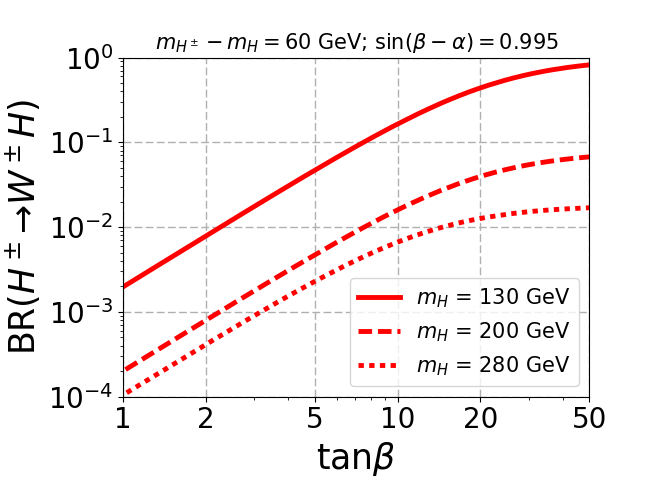
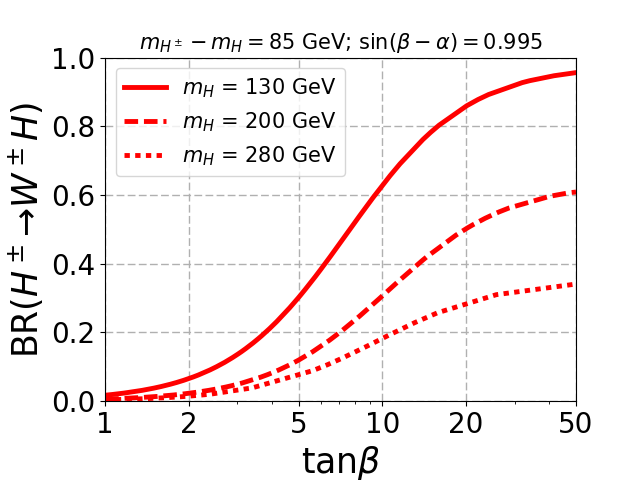
The middle panel in Fig. 2 shows the branching ratio of charged Higgs to channel. As increases, the decay to channel decreases, and BR() as well as BR() increases. For the mass gap of 60 GeV and 85 GeV, the kinematic suppression is strong enough to decrease BR() as (and therefore ) increases. When the mass gap increases (120 GeV), the kinematic suppression becomes irrelevant, and BR() becomes dominant since decay to is suppressed.
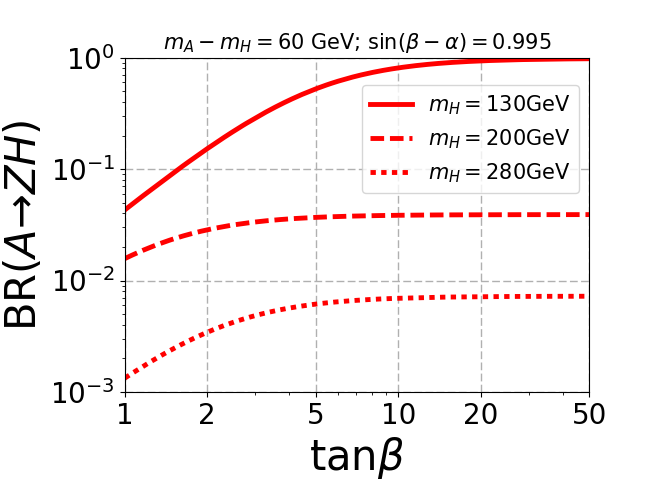
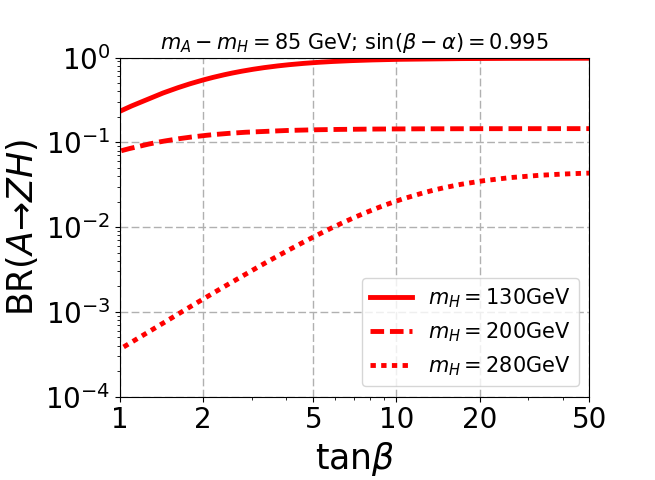
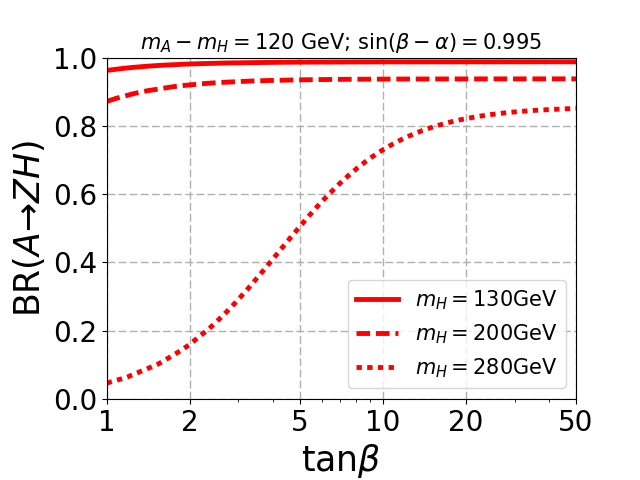
The lower panel in Fig. 2 depicts the decay of pseudoscalar to channel. When the mass gap is smaller than the required for on-shell production of , the decay dominates despite suppression. As the mass gap increases, mostly decays to , as shown in the right plot of the bottom panel. When opens up, the branching ratio decreases substantially for low , which is evident in the red dotted curves.
From Fig. 2 it is evident that branching ratio of the bosonic decay channels with respect to the mass of (and therefore ) decreases as the mass gap decreases. In addition the selection efficiency of the decay products coming from the off-shell decay of and will be very low as we decrease the mass gap. Thus, the signal process is not suitable for very small mass gap where both the dominant and the subdominant channels are mediated through off-shell decays of and . Hence, we have not considered GeV despite the large production cross-section of . Note that, for small mass gap the decay of becomes dominant and might be useful.
3.2 Event Generation and Signal Selection
| Signal cross-sections at TeV | |||||||
|---|---|---|---|---|---|---|---|
| Selection cuts | MG5 | SS3L | & | & | -veto | b-veto | |
| GeV | Signal 1 [fb] | 0.741 | 0.00237 | 0.00113 | 0.000975 | 0.000962 | 0.0007 |
| Signal 2 [fb] | 0.0537 | 0.000224 | 0.0000698 | 0.0000604 | 0.0000590 | 0.0000406 | |
| GeV | Signal 1 [fb] | 9.18 | 0.0372 | 0.0205 | 0.0186 | 0.0182 | 0.0131 |
| Signal 2 [fb] | 1.2 | 0.00754 | 0.0048 | 0.00418 | 0.00399 | 0.00276 | |
| GeV | Signal 1 [fb] | 15.84 | 0.0668 | 0.0405 | 0.0370 | 0.0364 | 0.0260 |
| Signal 2 [fb] | 6.13 | 0.0374 | 0.0252 | 0.0229 | 0.0190 | 0.0113 | |
As discussed at the beginning of the section, the charged Higgs will be produced via the following process: and the subsequent bosonic decay of the Higgses yield the same sign trilepton signal () in association with additional jets and/or leptons. We applied uniform K-factor of 1.35 Bahl:2021str for the signal cross-section. For event generation, the type-I 2HDM model is implemented in FeynRules-2.3Alloul:2013bka and both the signal and the background events are generated using [email protected]Alwall:2011uj ; Alwall:2014hca . We used PYTHIA-8.2 Sjostrand:2006za ; Sjostrand:2014zea for showering and hadronization, and for detector simulation we used Delphes-3.4.2deFavereau:2013fsa using anti-kt algorithm Cacciari:2008gp for jet clustering with radius parameter and GeV. In Delphes we have used the following lepton identification and isolation criteria:
-
•
Electrons and muons should have GeV and the electron efficiency is taken as 95% and 90% for and respectively. Efficiency for muon is 98% when and 95% if .
-
•
The lepton isolation () is defined as the ratio of the sum of of all objects within a cone with to the of the lepton. We demand that .
Selection criteria: A signal event is selected based on the following selection criteria:
-
•
SS3L: We select events with three isolated leading leptons () with same sign.
-
•
Lepton cuts: We impose the transverse momentum on the SS3L signal as, GeV, GeV and respectively where leptons are ordered according to the transverse momentum.
-
•
Missing energy cut: We impose a nominal MET cut GeV to reduce events with jets as fake leptons.
-
•
Lepton and jet separation cuts: We impose the lepton-lepton separation, and lepton-jet separation cuts, where .
-
•
-veto: If additional leptons with opposite sign to the tagged three same sign leptons are present in an event, we veto such events if any opposite-sign same flavor lepton pair combination satisfy the invariant mass condition GeV.
-
•
-veto: We veto events if there are any tagged -jets. This minimizes the background comes from processes.
In Tab. 2 we have shown the cut flow for both the signals given in Eq. 3 where Signal 1 (Signal 2) refers to the production channels. For benchmark points we fixed GeV, and with three mass gaps GeV, 85 GeV and 120 GeV. As the mass gap increases, the cross-section increases due to the increase of BR() and BR(). For the mass gap of 60 GeV large kinematic suppression comes in both the signals and for the mass gap of 85 GeV the kinematic suppression comes mostly to the subdominant () signal.
| Background cross-sections at TeV | ||||||
| Backgrounds | MG5 | SS3L | & | & | -veto | -veto |
| jets [fb] | 1360.80 | 0.0543 | 0.0122 | 0.0073 | 0.0065 | 0.0061 |
| jets [fb] | 246.55 | 0.00991 | 0.00122 | 0.00083 | 0.00065 | 0.00061 |
| jets [fb] | 0.781 | 0.00881 | 0.00555 | 0.00525 | 0.001667 | 0.00155 |
| jets [fb] | 0.218 | 0.00210 | 0.000783 | 0.000616 | 0.000432 | 0.00041 |
| jets [fb] | 20.51 | 0.00842 | 0.00095 | 0.000875 | 0.000875 | 0.000123 |
| jets [fb] | 62.57 | 0.0878 | 0.0118 | 0.0103 | 0.0103 | 0.0018 |
| jets [fb] | 92.08 | 0.0321 | 0.00705 | 0.00648 | 0.00583 | 0.00092 |
3.3 Background Estimation
The SM backgrounds can be divided into irreducible and reducible backgrounds. The relevant irreducible backgrounds are + jets (K-factor = 1.85 Alwall:2014hca ), + jets (K-factor = 1.18 Alwall:2014hca ), + jets (K-factor = 1.31 Alwall:2014hca ), + jets (K-factor = 1.18 Alwall:2014hca ) and + jets (K-factor = 1.17 LHCHiggsCrossSectionWorkingGroup:2016ypw ). The relevant reducible backgrounds are + jets (K-factor = 1.3 Campanario:2010hp ), + jets (K-factor = 1.7 Cascioli:2014yka ), + jets (K-factor = 1.17 LHCHiggsCrossSectionWorkingGroup:2016ypw ), + jets (K-factor = 1.22 Maltoni:2015ena ) and + jets (K-factor = 1.44 Maltoni:2015ena ). We generated all the background events matched up to one parton using the MLM scheme Artoisenet_2013 . The cross-sections and the cut flow for the dominant backgrounds at TeV according to the above mentioned selection cuts are given in Tab. 3. The subdominant backgrounds contribute only at the order of . The total background cross-section at TeV is 0.01161 . For both the signal and the backgrounds we have included the decay of boson to lepton, which can further decay to light leptons and contribute to signal and background processes.
4 Results and Discussion
To set the exclusion limits on our signal, we compute the significance () for exclusion using a likelihood ratio method Cowan:2010js given by:
| (12) |
To estimate the discovery reach, we compute the following significance,
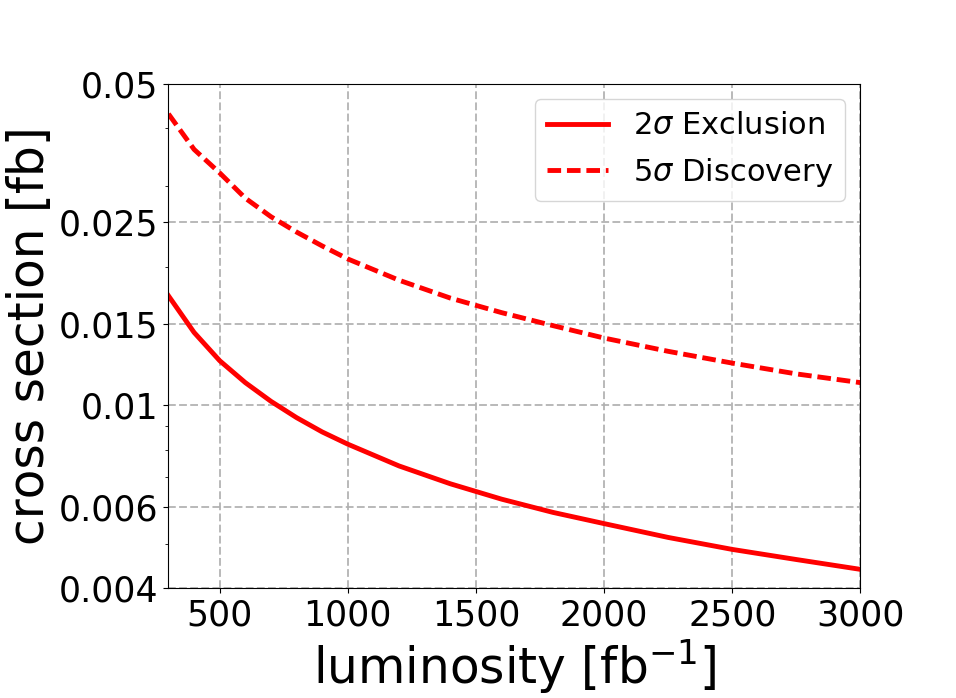
For exclusion we demand and for discovery we demand . In Fig 3 we shows the signal cross-sections required for exclusion and discovery as a function of integrated luminosity.
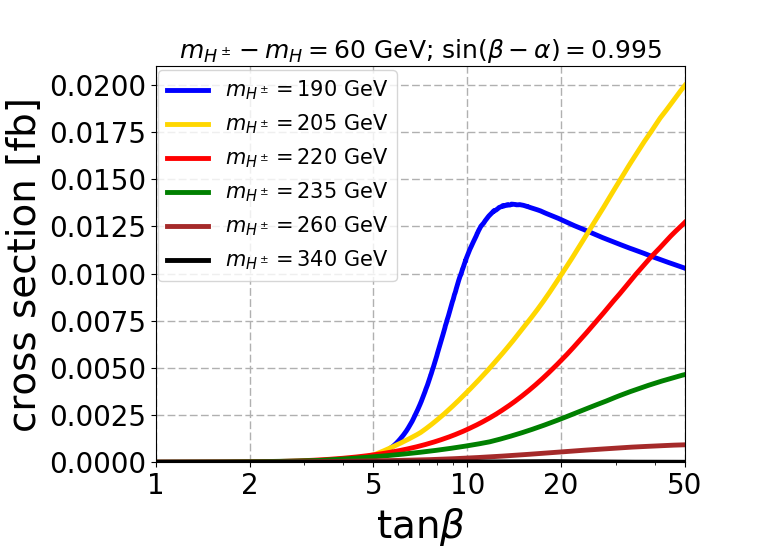
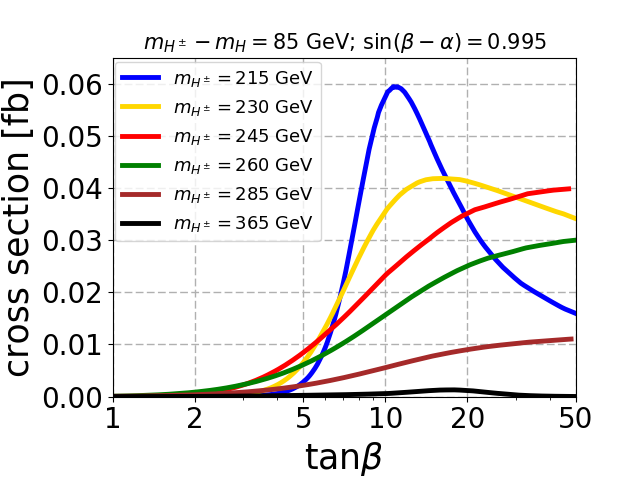
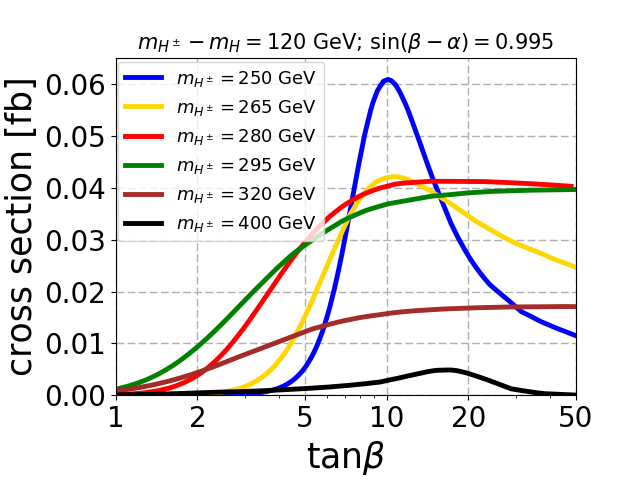
After applying the selection cuts, the same sign trilepton signal cross-section for different charged Higgs mass is shown in Fig. 4 for a mass gap of 60 GeV(top left), 85 GeV(top right) and 120 GeV (bottom). For all the plots we fix , and the fermiophobic limit for such the fermiophobic limit happens at as described in Sec. 2.1 and manifest in the top panel of Fig. 2 for GeV. This is prominent when mass of and in turn mass of is the lowest and depicted in blue curve.
As the mass of the BSM heavy Higgs increases, the remains large for any and the cross-section remains large beyond the fermiophobic region, which is depicted in red and green curves in Fig. 4. Notice that for the mass gap of 60 GeV, the cross-section shown by yellow curve for GeV is large at high compared to the blue curve for GeV. This is because the is sizable only for . When the mass of and therefore is least, peaks at where is low resulting to a low signal cross-section. This is the case for GeV as shown in blue curve. When mass of increases, saturates beyond , and consequently becomes large at high which pushes the yellow curve beyond the blue curve. For the mass gap of 120 GeV, the saturates at a lower compared to the mass gaps of 60 GeV and 85 GeV. Hence the signal cross-section also saturates at a lower . This is clear from the red, green and brown curves of the three mass gaps. The same argument explains why the width of the blue curve, which corresponds to GeV is minimum for the mass gap of 120 GeV and maximum for the mass gap of 60 GeV. Finally, when the decay comes into play, the signal cross-section decreases rapidly as shown by the black curves for all the mass gaps.
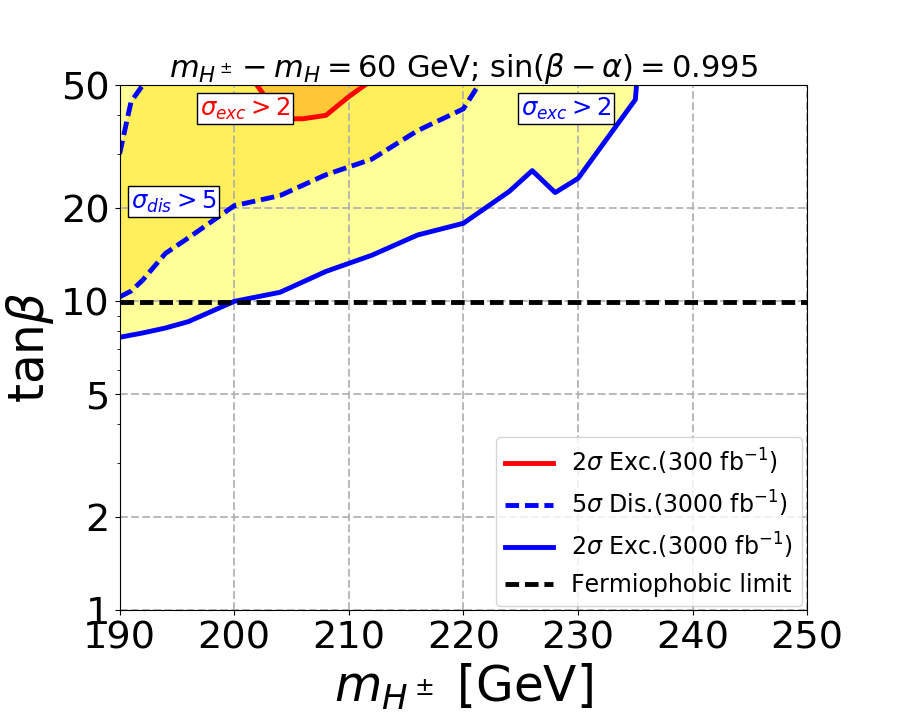
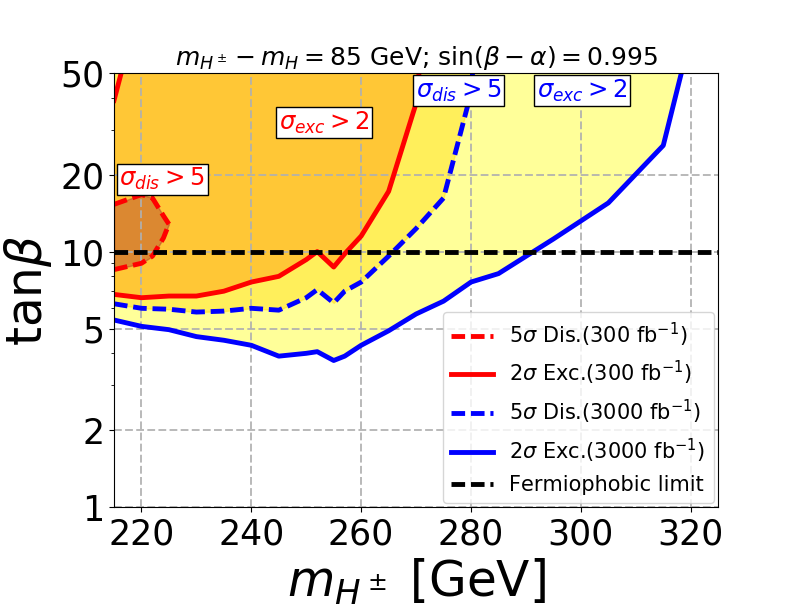
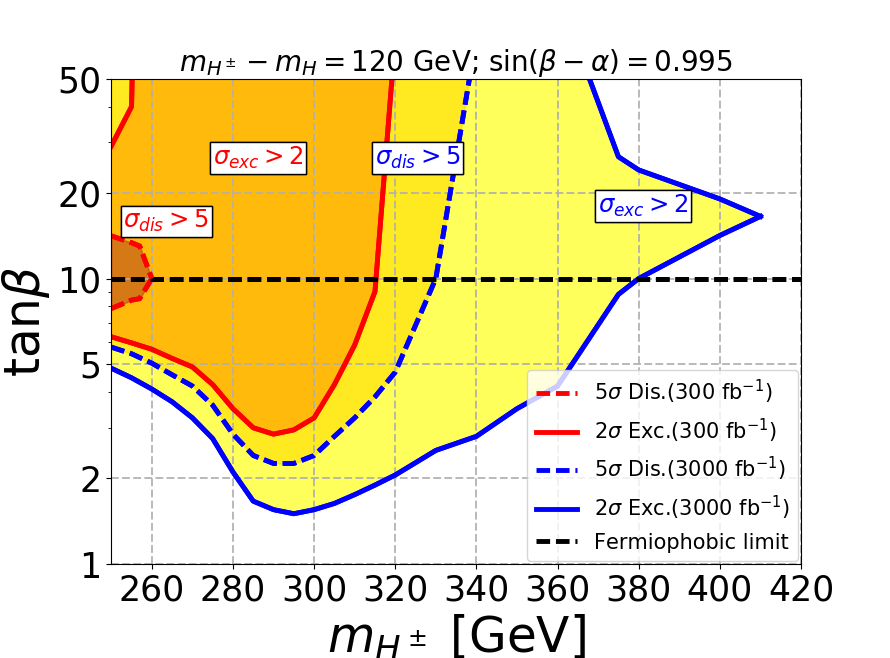
Now we will show our main result of exclusion and discovery region in plane for the different mass gaps. In Fig. 5 we displayed the reach of LHC for three mass gaps where . The fermiophobic limit corresponds to and is shown in the horizontal black dashed line. The exclusion(discovery) contours are depicted by solid(dashed) curves and red(blue) curves corresponds to integrated luminosity of 300(3000).
For the mass gap of 60 GeV, the low at the fermiophobic limit of makes the signal cross-section low as mentioned before. Hence the signal is not enough for discovery at 300 as seen in top left figure. For the mass gaps of 85 GeV and 120 GeV, the discovery regions at 300 are confined only for low mass where the signal cross-sections are large. We also observe a dip in the discovery regions at 3000 and exclusion regions at 300 and 3000 due to the enhancement to the signal coming from the on-shell mode. The on-shell effect can also be seen for mass gap of 60 GeV by the presence of a dip in the exclusion region at 3000. From the plots, it is evident that the SS3L signal is capable of excluding a substantial parameter space at the large region. As the mass gap increases, the decay to saturates at a lower value of , which pushes the limits to lower region and thus excludes even larger parameter space. This is most evident for the mass gap of 120 GeV as shown in the bottom panel. Also for the mass gap of 120 GeV, when the mass of is large, we can not exclude the large region as the decay dominates at large , and our signal becomes irrelevant.
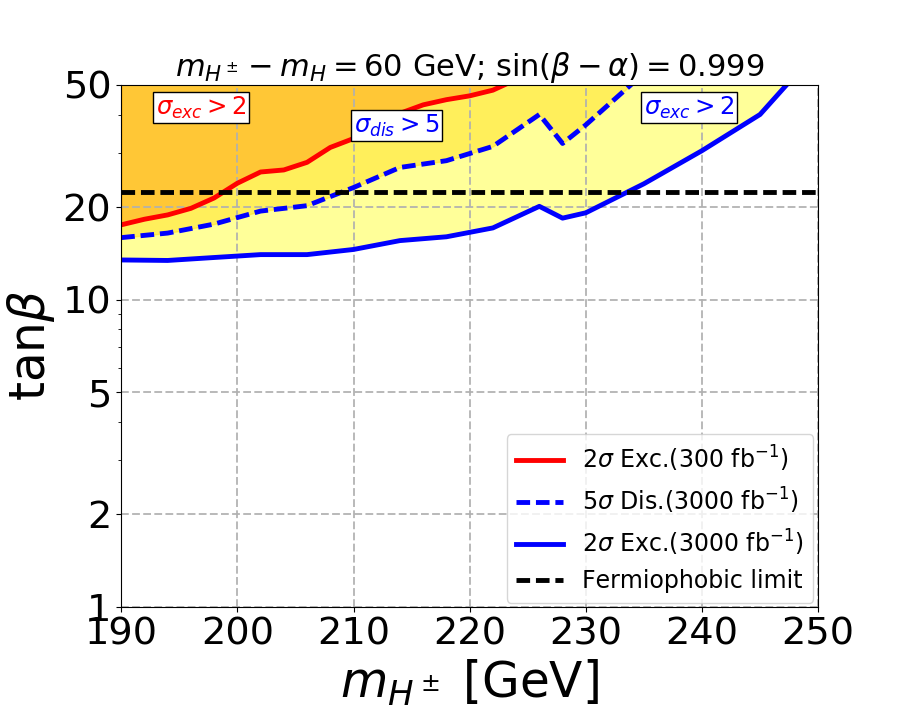
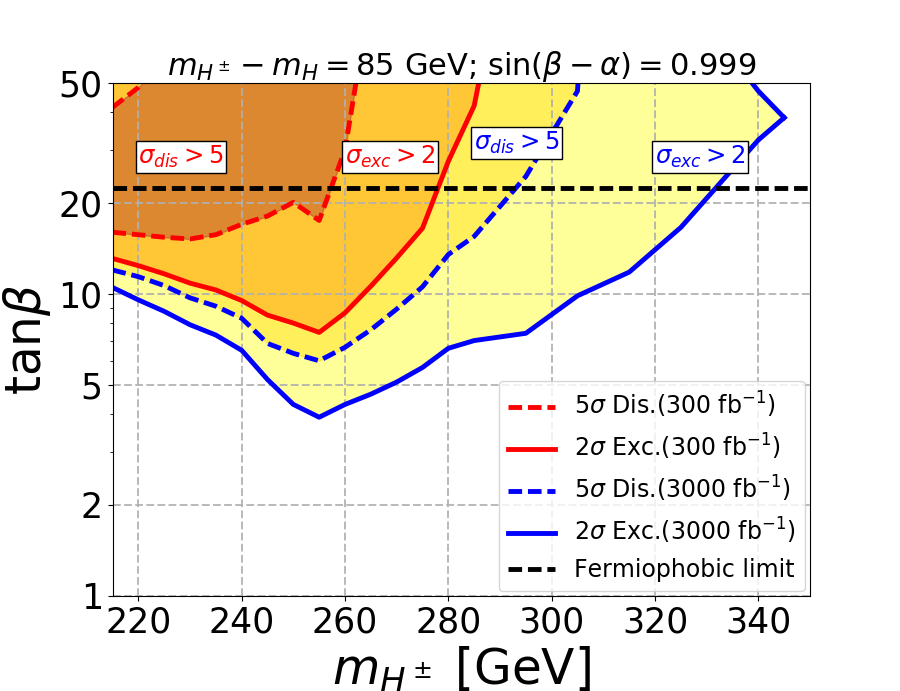
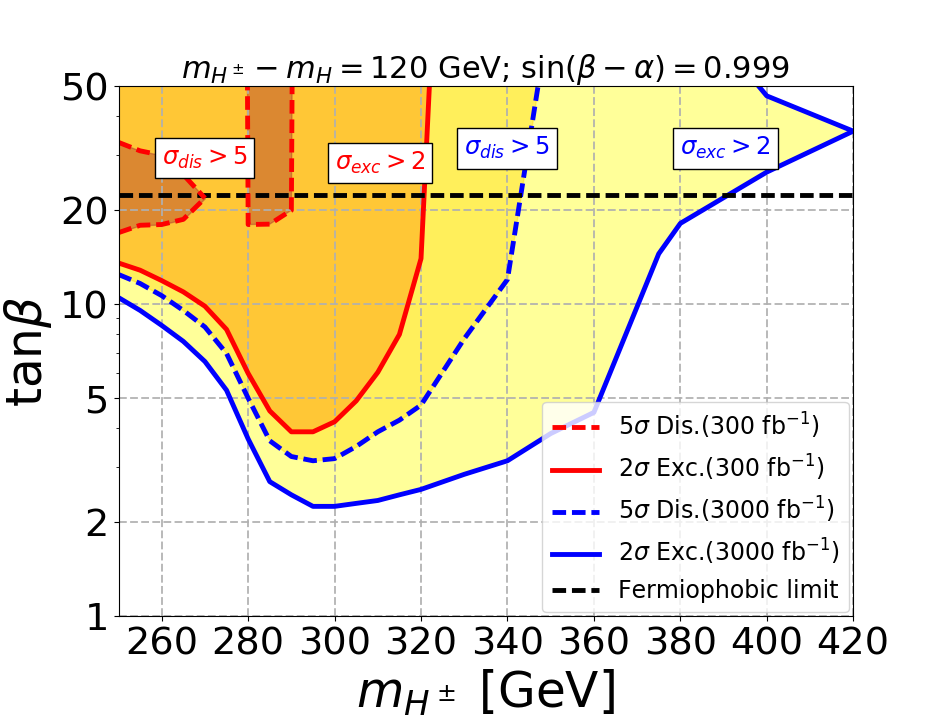
To show how the proposed signal works even closer to the alignment limit, we have performed the phenomenological analysis for . The limit becomes stronger in this scenario because of the following reasons:
-
•
The coupling is proportional to , the production cross-section and the branching ratio of increases in this case.
-
•
remains dominant even with suppression since the fermionic decay modes of is suppressed.
-
•
The subdominant signal is enhanced as the coupling is proportional to .
-
•
, being proportional to becomes small and decay is suppressed when allowed.
Effectively, the exclusion and discovery limits become stronger for . This is evident from Fig. 6, specially for the mass gap of 60 GeV the exclusion region at 300 is much more enhanced. Also the discovery regions at 300 for the mass gap of 85 GeV and 120 GeV are more enhanced. The discovery region at 300 for the mass gap of 120 GeV shows a discontinuity as for small the cross-section is large and it again reappears when decay to on-shell pair is open. Just like the case of , the limits become most stringent when the on-shell decay of opens up showing a dip around GeV. In Fig. 6 the fermiophobic limit corresponds to . Since the value of for fermiophobic limit has moved upwards, we expect the exclusion and discovery regions to shift to higher , which is quite visible for the discovery regions at 300 for the mass gaps of 85 GeV and 120 GeV. Similarly the discovery and exclusion regions at 3000 for the mass gap of 60 GeV are shifted upwards. However, the overall signal cross-sections have increased due to the enhancement of , the shift of the discovery regions at 3000 and exclusion regions at 300 and 3000 for the mass gap of 85 GeV and 120 GeV are negligible.
5 Conclusion
Observation of a charged Higgs at the LHC will indicate the presence of an extended Higgs sector. The search strategies of looking for a charged Higgs at the LHC dominantly depends on the coupling. However, the coupling can be small for a fermiophobic scenario like the type-I 2HDM model. As a result, the limit on a charged Higgs is non-existent unless is close to unity. Here we proposed the same sign trilepton signal to complement the existing searches. The SS3L signature appears when a charged Higgs is produced via electroweak interaction in association with or and subsequently decays to heavy gauge bosons. By performing a detailed phenomenological analysis, we demonstrate that our proposed signal is capable of extending the reach of LHC up to a very high region for charged Higgs mass of up to 400 GeV. The decay of the BSM scalars and depends on the mass gap among themselves and to cover a large model parameter space we studied three mass gaps between and , viz. 60 GeV, 85 GeV and 120 GeV, which covers complete off-shell to fully on-shell decay of various BSM scalars. We also showed that the dependency of the signal on mixing angle is relatively weak, and a slight deviation from the alignment limit is enough to explore the SS3L signature. If the deviation from the alignment limit is significant, then the proposed signal will not work efficiently as both the couplings and couplings are proportional to . Also, the exact fermiophobic limit will move towards the low region, which is already constrained via the search in association with the top quark.
Acknowledgments
The authors would like to thank Ravindra Kumar Verma for some useful comments and discussions. T.M. was supported by a KIAS Individual Grant PG073502 at Korea Institute for Advanced Study. P.S. was supported by the appointment to the JRG Program at the APCTP through the Science and Technology Promotion Fund and Lottery Fund of the Korean Government. This was also supported by the Korean Local Governments - Gyeongsangbuk-do Province and Pohang City.
References
- (1) J. F. Gunion, H. E. Haber, G. L. Kane and S. Dawson, The Higgs Hunter’s Guide, vol. 80. 2000.
- (2) A. Djouadi, The Anatomy of electro-weak symmetry breaking. II. The Higgs bosons in the minimal supersymmetric model, Phys. Rept. 459 (2008) 1 [hep-ph/0503173].
- (3) G. C. Branco, P. M. Ferreira, L. Lavoura, M. N. Rebelo, M. Sher and J. P. Silva, Theory and phenomenology of two-Higgs-doublet models, Phys. Rept. 516 (2012) 1 [1106.0034].
- (4) ATLAS collaboration, Search for a light charged Higgs boson in the decay channel in events using pp collisions at = 7 TeV with the ATLAS detector, Eur. Phys. J. C 73 (2013) 2465 [1302.3694].
- (5) ATLAS collaboration, Search for charged Higgs bosons decaying via in fully hadronic final states using collision data at TeV with the ATLAS detector, JHEP 03 (2015) 088 [1412.6663].
- (6) CMS collaboration, Search for a charged Higgs boson in pp collisions at TeV, JHEP 11 (2015) 018 [1508.07774].
- (7) CMS collaboration, Search for a light charged Higgs boson decaying to in pp collisions at TeV, JHEP 12 (2015) 178 [1510.04252].
- (8) ATLAS collaboration, Search for charged Higgs bosons produced in association with a top quark and decaying via using collision data recorded at TeV by the ATLAS detector, Phys. Lett. B 759 (2016) 555 [1603.09203].
- (9) ATLAS collaboration, Search for charged Higgs bosons decaying via in the +jets and +lepton final states with 36 fb-1 of collision data recorded at TeV with the ATLAS experiment, JHEP 09 (2018) 139 [1807.07915].
- (10) ATLAS collaboration, Search for charged Higgs bosons decaying into top and bottom quarks at = 13 TeV with the ATLAS detector, JHEP 11 (2018) 085 [1808.03599].
- (11) CMS collaboration, Search for a charged Higgs boson decaying to charm and bottom quarks in proton-proton collisions at TeV, JHEP 11 (2018) 115 [1808.06575].
- (12) CMS collaboration, Search for charged Higgs bosons in the H± decay channel in proton-proton collisions at 13 TeV, JHEP 07 (2019) 142 [1903.04560].
- (13) ATLAS collaboration, Search for charged Higgs bosons decaying into a top-quark and a bottom-quark at = 13 TeV with the ATLAS detector, .
- (14) ATLAS collaboration, Search for charged Higgs bosons decaying into a top quark and a bottom quark at = 13 TeV with the ATLAS detector, JHEP 06 (2021) 145 [2102.10076].
- (15) CMS collaboration, Search for Charged Higgs Bosons Produced via Vector Boson Fusion and Decaying into a Pair of and Bosons Using Collisions at , Phys. Rev. Lett. 119 (2017) 141802 [1705.02942].
- (16) ATLAS collaboration, Search for resonant production in the fully leptonic final state in proton-proton collisions at TeV with the ATLAS detector, Phys. Lett. B 787 (2018) 68 [1806.01532].
- (17) B. Coleppa, A. Sarkar and S. K. Rai, Charged higgs boson discovery prospects, Physical Review D 101 (2020) .
- (18) B. Coleppa, G. B. Krishna and A. Sarkar, Charged Higgs Prospects In Extended Gauge Models, 2107.03993.
- (19) N. Chen, T. Han, S. Li, S. Su, W. Su and Y. Wu, Type-I 2HDM under the Higgs and Electroweak Precision Measurements, JHEP 08 (2020) 131 [1912.01431].
- (20) F. Kling, S. Su and W. Su, 2HDM Neutral Scalars under the LHC, JHEP 06 (2020) 163 [2004.04172].
- (21) B. Coleppa, F. Kling and S. Su, Charged Higgs search via channel, JHEP 12 (2014) 148 [1408.4119].
- (22) R. Enberg, W. Klemm, S. Moretti, S. Munir and G. Wouda, Charged Higgs boson in the Higgs channel at the Large Hadron Collider, Nucl. Phys. B 893 (2015) 420 [1412.5814].
- (23) F. Kling, A. Pyarelal and S. Su, Light Charged Higgs Bosons to AW/HW via Top Decay, JHEP 11 (2015) 051 [1504.06624].
- (24) A. G. Akeroyd et al., Prospects for charged Higgs searches at the LHC, Eur. Phys. J. C 77 (2017) 276 [1607.01320].
- (25) A. Arhrib, R. Benbrik and S. Moretti, Bosonic Decays of Charged Higgs Bosons in a 2HDM Type-I, Eur. Phys. J. C 77 (2017) 621 [1607.02402].
- (26) D. S. M. Alves, S. El Hedri, A. M. Taki and N. Weiner, Charged Higgs Signals in Searches, Phys. Rev. D 96 (2017) 075032 [1703.06834].
- (27) A. Arhrib, K. Cheung and C.-T. Lu, Same-sign charged Higgs boson pair production in bosonic decay channels at the HL-LHC and HE-LHC, Phys. Rev. D 102 (2020) 095026 [1910.02571].
- (28) A. Arhrib, R. Benbrik, H. Harouiz, S. Moretti, Y. Wang and Q.-S. Yan, Implications of a light charged Higgs boson at the LHC run III in the 2HDM, Phys. Rev. D 102 (2020) 115040 [2003.11108].
- (29) P. Sanyal, Limits on the Charged Higgs Parameters in the Two Higgs Doublet Model using CMS TeV Results, Eur. Phys. J. C 79 (2019) 913 [1906.02520].
- (30) A. Akeroyd, Three-body decays of higgs bosons at lep2 and application to a hidden fermiophobic higgs, Nuclear Physics B 544 (1999) 557–575.
- (31) M. Demirci, Precise predictions for charged higgs boson pair production in photon-photon collisions, Nuclear Physics B 961 (2020) 115235.
- (32) S. Kanemura and C. P. Yuan, Testing supersymmetry in the associated production of CP odd and charged Higgs bosons, Phys. Lett. B 530 (2002) 188 [hep-ph/0112165].
- (33) Q.-H. Cao, S. Kanemura and C. P. Yuan, Associated production of CP odd and charged Higgs bosons at hadron colliders, Phys. Rev. D 69 (2004) 075008 [hep-ph/0311083].
- (34) A. Belyaev, Q.-H. Cao, D. Nomura, K. Tobe and C. P. Yuan, Light MSSM Higgs boson scenario and its test at hadron colliders, Phys. Rev. Lett. 100 (2008) 061801 [hep-ph/0609079].
- (35) E. J. Chun, S. Dwivedi, T. Mondal, B. Mukhopadhyaya and S. K. Rai, Reconstructing heavy Higgs boson masses in a type X two-Higgs-doublet model with a light pseudoscalar particle, Phys. Rev. D98 (2018) 075008 [1807.05379].
- (36) H. Bahl, T. Stefaniak and J. Wittbrodt, The forgotten channels: charged Higgs boson decays to a W± and a non-SM-like Higgs boson, JHEP 06 (2021) 183 [2103.07484].
- (37) A. Arhrib, R. Benbrik, R. Enberg, W. Klemm, S. Moretti and S. Munir, Identifying a light charged Higgs boson at the LHC Run II, Phys. Lett. B 774 (2017) 591 [1706.01964].
- (38) R. Enberg, W. Klemm, S. Moretti and S. Munir, Electroweak production of multiple (pseudo)scalars in the 2HDM, Eur. Phys. J. C 79 (2019) 512 [1812.01147].
- (39) R. Enberg, W. Klemm, S. Moretti and S. Munir, Signatures of the Type-I 2HDM at the LHC, PoS CORFU2018 (2018) 013 [1812.08623].
- (40) A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti, Y. Wang et al., New Discovery Modes for a Light Charged Higgs Boson at the LHC, 2106.13656.
- (41) Y. Wang, A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti et al., Analysis of in the 2HDM Type-I at the LHC, 2107.01451.
- (42) A. G. Akeroyd and M. A. Diaz, Searching for a light fermiophobic Higgs boson at the Tevatron, Phys. Rev. D 67 (2003) 095007 [hep-ph/0301203].
- (43) A. G. Akeroyd, M. A. Díaz and F. J. Pacheco, Double fermiophobic higgs boson production at the cern lhc and a linear collider, Physical Review D 70 (2004) .
- (44) A. Arhrib, R. Benbrik and C.-W. Chiang, Probing triple higgs couplings of the two higgs doublet model at a linear collider, Phys. Rev. D 77 (2008) 115013.
- (45) J. F. Gunion and H. E. Haber, The CP conserving two Higgs doublet model: The Approach to the decoupling limit, Phys. Rev. D67 (2003) 075019 [hep-ph/0207010].
- (46) S. Kanemura, T. Kubota and E. Takasugi, Lee-Quigg-Thacker bounds for Higgs boson masses in a two doublet model, Phys. Lett. B 313 (1993) 155 [hep-ph/9303263].
- (47) A. G. Akeroyd, A. Arhrib and E.-M. Naimi, Note on tree level unitarity in the general two Higgs doublet model, Phys. Lett. B 490 (2000) 119 [hep-ph/0006035].
- (48) D. Eriksson, J. Rathsman and O. Stal, 2HDMC: Two-Higgs-Doublet Model Calculator Physics and Manual, Comput. Phys. Commun. 181 (2010) 189 [0902.0851].
- (49) M. E. Peskin and T. Takeuchi, Estimation of oblique electroweak corrections, Phys. Rev. D 46 (1992) 381.
- (50) P. Bechtle, O. Brein, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein et al., : Improved Tests of Extended Higgs Sectors against Exclusion Bounds from LEP, the Tevatron and the LHC, Eur. Phys. J. C 74 (2014) 2693 [1311.0055].
- (51) P. Bechtle, D. Dercks, S. Heinemeyer, T. Klingl, T. Stefaniak, G. Weiglein et al., HiggsBounds-5: Testing Higgs Sectors in the LHC 13 TeV Era, Eur. Phys. J. C 80 (2020) 1211 [2006.06007].
- (52) P. Bechtle, S. Heinemeyer, O. Stål, T. Stefaniak and G. Weiglein, Higgssignals: Confronting arbitrary higgs sectors with measurements at the tevatron and the lhc, The European Physical Journal C 74 (2014) .
- (53) P. Bechtle, S. Heinemeyer, T. Klingl, T. Stefaniak, G. Weiglein and J. Wittbrodt, HiggsSignals-2: Probing new physics with precision Higgs measurements in the LHC 13 TeV era, Eur. Phys. J. C 81 (2021) 145 [2012.09197].
- (54) ATLAS collaboration, Search for a CP-odd Higgs boson decaying to Zh in pp collisions at TeV with the ATLAS detector, Phys. Lett. B 744 (2015) 163 [1502.04478].
- (55) CMS collaboration, Search for a heavy pseudoscalar boson decaying to a Z boson and a Higgs boson at sqrt(s)=13 TeV, .
- (56) ATLAS collaboration, Search for a heavy Higgs boson decaying into a boson and another heavy Higgs boson in the final state in collisions at TeV with the ATLAS detector, Phys. Lett. B 783 (2018) 392 [1804.01126].
- (57) CMS collaboration, Search for additional neutral Higgs bosons decaying to a pair of tau leptons in collisions at = 7 and 8 TeV, .
- (58) CMS collaboration, Search for a new scalar resonance decaying to a pair of Z bosons in proton-proton collisions at = 13 TeV, .
- (59) ATLAS collaboration, Search for Scalar Diphoton Resonances in the Mass Range GeV with the ATLAS Detector in Collision Data at = 8 , Phys. Rev. Lett. 113 (2014) 171801 [1407.6583].
- (60) CMS collaboration, Properties of the Higgs-like boson in the decay H to ZZ to 4l in pp collisions at sqrt s =7 and 8 TeV, .
- (61) HFLAV collaboration, Averages of -hadron, -hadron, and -lepton properties as of summer 2016, Eur. Phys. J. C 77 (2017) 895 [1612.07233].
- (62) M. Misiak and M. Steinhauser, Weak radiative decays of the B meson and bounds on in the Two-Higgs-Doublet Model, Eur. Phys. J. C 77 (2017) 201 [1702.04571].
- (63) F. Mahmoudi, Superiso v2.3: A program for calculating flavor physics observables in supersymmetry, Computer Physics Communications 180 (2009) 1579–1613.
- (64) A. Alloul, N. D. Christensen, C. Degrande, C. Duhr and B. Fuks, FeynRules 2.0 - A complete toolbox for tree-level phenomenology, Comput. Phys. Commun. 185 (2014) 2250 [1310.1921].
- (65) J. Alwall, M. Herquet, F. Maltoni, O. Mattelaer and T. Stelzer, MadGraph 5 : Going Beyond, JHEP 06 (2011) 128 [1106.0522].
- (66) J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations, JHEP 07 (2014) 079 [1405.0301].
- (67) T. Sjostrand, S. Mrenna and P. Z. Skands, PYTHIA 6.4 Physics and Manual, JHEP 05 (2006) 026 [hep-ph/0603175].
- (68) T. Sjöstrand, S. Ask, J. R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An Introduction to PYTHIA 8.2, Comput. Phys. Commun. 191 (2015) 159 [1410.3012].
- (69) DELPHES 3 collaboration, DELPHES 3, A modular framework for fast simulation of a generic collider experiment, JHEP 02 (2014) 057 [1307.6346].
- (70) M. Cacciari, G. P. Salam and G. Soyez, The Anti-k(t) jet clustering algorithm, JHEP 04 (2008) 063 [0802.1189].
- (71) LHC Higgs Cross Section Working Group collaboration, Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector, 1610.07922.
- (72) F. Campanario, C. Englert, S. Kallweit, M. Spannowsky and D. Zeppenfeld, NLO QCD corrections to WZ+jet production with leptonic decays, JHEP 07 (2010) 076 [1006.0390].
- (73) F. Cascioli, T. Gehrmann, M. Grazzini, S. Kallweit, P. Maierhöfer, A. von Manteuffel et al., ZZ production at hadron colliders in NNLO QCD, Phys. Lett. B735 (2014) 311 [1405.2219].
- (74) F. Maltoni, D. Pagani and I. Tsinikos, Associated production of a top-quark pair with vector bosons at NLO in QCD: impact on searches at the LHC, JHEP 02 (2016) 113 [1507.05640].
- (75) P. Artoisenet, R. Frederix, O. Mattelaer and R. Rietkerk, Automatic spin-entangled decays of heavy resonances in monte carlo simulations, Journal of High Energy Physics 2013 (2013) .
- (76) G. Cowan, K. Cranmer, E. Gross and O. Vitells, Asymptotic formulae for likelihood-based tests of new physics, Eur. Phys. J. C 71 (2011) 1554 [1007.1727].