S-stable foliations on flow-spines with transverse Reeb flow

A polyhedron $P$ is said to be simple if every point on $P$ has a neighborhood represented by one of the models shown in Figure 2. Each connected component of the set of points with the model (i) is called a region, that with the model (ii) is called a triple line and that with the model (iii) is called a true vertex, which we call a vertex for short. Let $S(P)$ denote the union of triple lines and vertices of $P$, which is called the singular set of $P$. A triple line is either an open arc, called an edge, or a circle. A simple polyhedron $P$ is said to be standard¹¹1It is also called a special polyhedron. if every connected component of $P\setminus S(P)$ is homeomorphic to an open disk and every triple line is an open arc.

Let $P$ be a simple polyhedron embedded in an oriented, $3$-manifold $M$ and assume that each region of $P$ is orientable. An assignment of orientations to the regions of $P$ such that for any triple line the three orientations induced from those of the adjacent regions do not coincide is called a branching. A simple polyhedron equipped with a branching is called a branched polyhedron. If a branched polyhedron is standard then it is called a branched standard polyhedron. For a branched polyhedron $P$, we define the orientation of each triple line of $S(P)$ by the orientation induced from the two adjacent regions, see Figure 3.

A region of a branched simple polyhedron is called a preferred region if the orientations of all edges on its boundary are opposite to the one induced from the orientation of the region defined by the branching of $P$.

Let $M$ be a closed, connected, oriented $3$-manifold and $P$ be a simple polyhedron embedded in $M$. The polyhedron $P$ is called a spine of $M$ if $M\setminus\text{Int\,}B$ collapses to $P$, where $B$ is a $3$-ball in $M\setminus P$. If a spine is standard (resp. branched) then it is called a standard (resp. branched) spine.

The singular set $S(P)$ of a branched simple polyhedron $P$ can be regarded as the image of an immersion of a finite number of circles. The immersion has only normal crossings as shown in Figure 3. A flow-spine is defined from a non-singular flow in a closed, connected, oriented, smooth $3$-manifold and a disk $D$ intersecting all orbits of the flow transversely by floating the boundary of $D$ smoothly until it arrives in the disk $D$ itself. See [8] for the precise definition (cf. [9]). By the construction, the flow is positively transverse to the flow-spine. We can easily see that a branched simple polyhedron $P$ is a flow-spine if and only if $S(P)$ is the image of an immersion of one circle.

Let $P$ be a branched simple polyhedron. To have a $1$-form $\beta$ on $P$ with $d\beta>0$, $P$ need satisfy the following admissibility condition. Let $R_{1},\ldots,R_{n}$ be the regions of $P$. Regions and triple lines of $P$ are oriented by the branching. Let $\bar{R}_{i}$ be the metric completion of $R_{i}$ with the path metric inherited from a Riemannian metric on $R_{i}$. Let $\kappa_{i}:\bar{R}_{i}\to P$ be the natural extension of the inclusion $R_{i}\to P$.

We introduce a lemma that is useful for determining singularities of foliations on flow-spines. Let $P$ be a flow-spine of a closed, oriented, smooth $3$-manifold $M$ and $\mathcal{F}$ be a foliation on $P$ with only elliptic and hyperbolic singularities. Assume that $\mathcal{F}$ is tangent to $S(P)$ at a finite number of points in the interior of triple lines and the singularities do not lie on $S(P)$. Let $e$ be the number of elliptic singularities, $h$ be the number of hyperbolic singularities and $t_{+}$ and $t_{-}$ be the numbers of simple tangency points of $\mathcal{F}$ with index $+1$ and $-1$, respectively.

The branched polyhedron $A$ obtained from the neighborhood of the singular set shown in Figure 9 by attaching two disks $D_{1}$ and $D_{2}$ is called the abalone. This is a flow-spine of $S^{3}$. We can easily see that $(E_{1},E_{2})\in C(A)$ if and only if

This system of inequalities has a solution, for example $(-1,13)\in\mathbb{R}^{2}$. Hence $A$ is admissible.

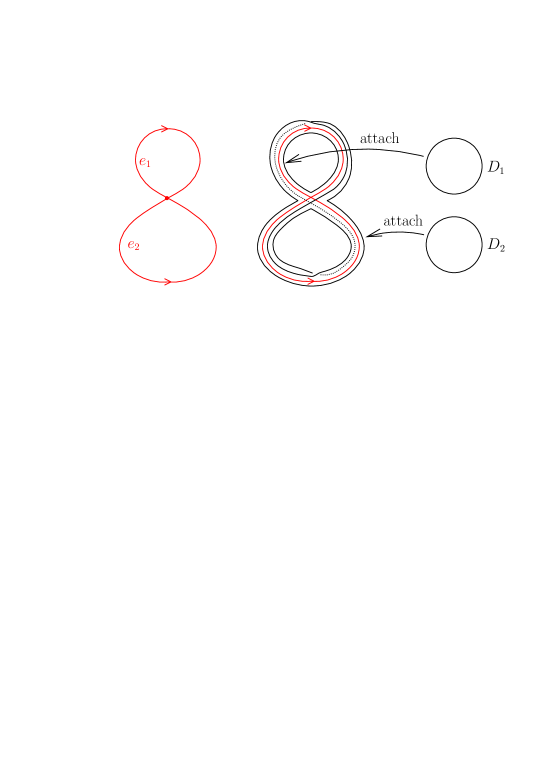
We give an S-stable foliation on $A$ defined by a $1$-form $\beta$ with $d\beta>0$ explicitly. Set $(E_{1},E_{2})=(-1,13)\in C(A)$. According to the construction in the proof of Theorem 1.1, one can construct an S-stable foliation on $\mathrm{Nbd}(S(A);A)$ defined by a $1$-form $\beta_{0}$ with $d\beta_{0}>0$ as the left two figures in Figure 10. Let $R_{1}$ and $R_{2}$ be the regions of $A$ containing $D_{1}$ and $D_{2}$, respectively. We describe four leaves on $R_{2}$ as shown on the right in Figure 10. We denote these leaves by $\ell_{1},\ldots,\ell_{4}$. For each $\ell_{i}$, we can find a $1$-form $\beta_{\ell_{i}}$ on $\mathrm{Nbd}(\ell_{i};R_{2})$ so that $\beta_{\ell_{i}}=\beta_{0}$ on $\mathrm{Nbd}(\ell_{i};R_{2})\cap\mathrm{Nbd}(\partial R_{2};R_{2})$ and $\ell_{i}$ is a leaf of the foliation defined by $\beta_{\ell_{i}}=0$.

We decompose $\partial R_{2}$ into $15$ arcs by the endpoints of the leaves $\ell_{1},\ldots,\ell_{4}$, the tangent points of these leaves with $\partial R_{2}$ and the vertices on $\partial R_{2}$. We label these arcs as $a_{1},\ldots,a_{15}$ as shown on the right in Figure 10. For the arcs $a_{1},\ldots,a_{15}$, we assign real numbers $A_{1},\ldots,A_{15}$ so that

and

and $(A_{4},A_{5},A_{6})=(A_{10},A_{11},A_{12})$. The five equalities mean that the assignment of real numbers to $a_{1},\ldots,a_{15}$ is a refinement of the assignment of those to $e_{1}$ and $e_{2}$. The nine inequalities mean that, for each region bounded by $\partial R_{2}\cup\bigcup_{i=1}^{4}\ell_{i}$, the sum of the real numbers along its boundary is positive, which is necessary for applying Lemma 3.4. Note that we set the real number assigned to $\ell_{i}$ to be $0$ since $\ell_{i}$ will be a leaf of the foliation obtained by a $1$-form. The last equality is needed since, for each $i=4,5,6$, the two edges $a_{i}$ and $a_{i+6}$ correspond to the same arc on the edge $e_{1}$ divided by the two simple tangency points. This system of equalities and inequalities has a solution, for example as

Let $\beta^{\prime}$ be a $1$-form defined on a small neighborhood $N$ of $S(P)\cup(\cup_{i=1}^{4}\ell_{i})$ in $P$ so that

• •

  $d\beta^{\prime}>0$ on $N$,

• •

  the characteristic foliation on $N$ has leaves shown on the right in Figure 10,

• •

  $\int_{a_{j}}\beta^{\prime}=A_{j}$ for $j=1,\ldots,15$.

Such a $1$-form can be easily constructed as in the proof of Theorem 1.1 (cf. [9, the proof of Lemma 6.3]). We may extend $\beta^{\prime}$ to the whole $P$ by applying Lemma 3.4.

Consider a foliation on $A$ shown in Figure 11, which coincides with the one defined by $\beta^{\prime}$ on $N$. It has two elliptic singularities with positive divergence and no hyperbolic singularities (cf. Lemma 6.1). It is not difficult to find a $1$-form $\beta$ on $P$ with $d\beta>0$ that defines the foliation in the figure. For example, let $R$ be the region on $R_{2}$ bounded by the leaves $\ell_{3}$ and $\ell_{4}$ and the edges $a_{11}$ and $a_{14}$ and regard $R$ as a rectangle with coordinates $(x,y)$ so that the foliation is parallel to the $x$-axis. On $\mathrm{Nbd}(\partial R;R)$, $\beta$ is given in the form $\varphi(x,y)dy$, where $\varphi(x,y)$ is a smooth function on $\mathrm{Nbd}(\partial R;R)$ with $\frac{\partial\varphi}{\partial x}(x,y)>0$. Remark that $\int_{a_{11}}\varphi(x,y)dy=A_{11}$, $\int_{a_{14}}\varphi(x,y)dy=A_{14}$ and $A_{11}+A_{14}>0$. We observe the graph of the function $\varphi(x,y)$ on $\mathrm{Nbd}(\partial R;R)$, and extend it to the whole $R$ so that $\frac{\partial\varphi}{\partial x}(x,y)>0$. The $1$-form $\varphi(x,y)dy$ defines the foliation on $R$ and satisfies $d(\varphi(x,y)dy)>0$.

The region $R^{\prime}$ bounded by the leaf $\ell_{4}$ and the edges $a_{12}$ and $a_{13}$ has one elliptic singularity with positive divergence. For any region $T$ bounded by an arc on $a_{12}\cup a_{13}$ and two leaves connecting the elliptic singularity and the endpoints of the arc, the $1$-form $\beta$ that we are going to make should satisfy $\int_{T}d\beta>0$. Therefore, the assignment to the edges $a_{12}$ and $a_{13}$ must satisfy the inequalities $A_{12}>0$ and $A_{13}>0$. Under this setting, the $1$-form on $R^{\prime}$ with required property can be found by the same way as before.

Applying the same construction for other regions bounded by the E-cycles and the leaves $\ell_{1},\ldots,\ell_{4}$, we can obtain a $1$-form $\beta$ on $A$ that defines the foliation in Figure 11 and satisfies $d\beta>0$. The DS-diagram with this S-stable foliation is described in Figure 12.

The foliation in Figure 11 has two simple tangency points on $e_{1}$. Since $R_{1}$ is a preferred region, due to Theorem 1.2, we can conclude that there is no S-stable foliation defined by a $1$-form $\beta$ with $d\beta>0$ and with less simple tangency points.

A characteristic foliation of the flow-spine of the Poincaré homology $3$-sphere whose DS-diagram is the dodecahedron is observed by the first author in [5] by the same manner.

Let $P$ be the branched simple polyhedron obtained from the branched polyhedron with boundary described in Figure 13 by attaching four disks along the four connected components of the boundary of $P$. It has three vertices, six edges and four disk regions. The orientations of the edges $e_{1},\ldots,e_{6}$ in the figure are those induced from the adjacent regions by the rule in Figure 3. The Euler characteristic of $P$ is $3-6+4=1$, and hence the Euler characteristic of the boundary of a thickening of $P$ is $2$. We may easily verify that the boundary of a thickening of $P$ is connected and hence it is $S^{2}$. This means that $P$ is a branched standard spine of a closed, oriented $3$-manifold. We can check that the DS-diagram of this spine, forgetting the branching, is the diagram (1-10) in [7] and conclude that the $3$-manifold is $S^{3}$.

The region containing the disk $D_{0}$ in the figure is a preferred region. The defining inequalities of $C(P)$ are $E_{6}>0$, $-E_{2}-E_{3}>0$, $E_{1}+E_{2}-E_{6}>0$ and $E_{2}+2E_{3}+E_{4}+E_{5}+E_{6}>0$. This system of inequalities has a solution, for example as $(6,1,-2,-1,-1,6)\in\mathbb{R}^{6}$. Hence $P$ is admissible. We choose the projections $\mathrm{pr}_{v_{i}}$ for each of vertices $v_{1}$, $v_{2}$ and $v_{3}$ so that their H-pieces become as shown in Figure 14. Under this setting, we can obtain an $S$-stable foliation defined by a $1$-form $\beta$ with $d\beta>0$ and without simple tangency points.

We here give an S-stable foliation on $P$ defined by a $1$-form $\beta$ with $d\beta>0$ and without simple tangency points on $P$ explicitly. Set

Let $R_{1},R_{2},R_{3},R_{4}$ be the regions of $P$ bounded by the sequences of edges $\{e_{6}\}$, $\{-e_{2},-e_{3}\}$, $\{e_{1},e_{2},-e_{5},-e_{6},e_{5}\}$ and $\{e_{1},e_{4},e_{5},e_{3},-e_{1},e_{3},e_{4},e_{6},-e_{4},e_{2}\}$, respectively, see Figure 15. Draw four leaves $\ell_{1},\ell_{2},\ell_{3}$ and $\ell_{4}$ as shown in the figure. The edge $e_{1}$ on the boundary of $R_{3}$ divides into two oriented arcs by an endpoint of $\ell_{1}$, named $a_{1}$ and $a_{2}$ as in the figure. Similarly, we name $a_{3},a_{4},a_{5},a_{6},a_{7}$ and $a_{8}$ as in the figure. For these arcs $a_{1},\ldots,a_{8}$, we assign real numbers $A_{1},\ldots,A_{8}$ as

so that they satisfy $A_{1}+A_{2}=A_{5}+A_{6}=E_{1}$, $A_{3}+A_{4}=A_{7}+A_{8}=E_{6}$ and

Thus, this assignment satisfies the required conditions for obtaining a $1$-form $\beta$ with $d\beta>0$ on $P$. We may draw a foliation in the regions $R_{1},\ldots,R_{4}$ described in Figure 15 so that $R_{1}$ has only one elliptic singularity in the middle and the other regions have no singularity, and there exists a $1$-form $\beta$ with $d\beta>0$ on $P$ which gives this foliation as in the case of abalone. There are two “tangency points” on the boundary of $R_{3}$ described in Figure 15, one is at the intersection of the edges $e_{5}$ and $e_{1}$ and the other is of the edges $e_{5}$ and $e_{6}$, and the boundary of $R_{4}$ also has two “tangency points”. The “tangency point” at the intersection of $e_{5}$ and $e_{1}$ appears in a neighborhood of the vertex $v_{1}$ shown on the left in Figure 14, where the leaves of the foliation given by $\beta=0$ is horizontal. The other three “tangency points” appear by the same reason. Therefore, these leaves are transverse to the singular set of $P$ and the foliation given in Figure 15 has no simple tangency points. The DS-diagram with this S-stable foliation is described in Figure 12.