Robustness of Helical Hinge States of Weak Second-Order Topological Insulators

Introduction.$-$Topological insulators (TIs) characterized by topological invariants and robust boundary states have attracted great interest because of their exotic properties. The band invention resulting in non-zero Chern numbers of a band is the central theme of topological materials. The non-zero topological invariants give rise to a bulk-boundary correspondence and the necessity of gapless boundary states in the band gap. The standard paradigm of the first-order TIs (FOTIs) claims that a $d-$dimensional insulator with band inversion has $(d-1)-$dimensional in-gap boundary states haldane_prl_1988 ; kane_prl_2005 ; kane_prl_20051 ; bernevig_science_2006 ; konig_science_2007 ; Roth_science_2009 ; hasan_rmp_2010 ; Moore_nature_2010 ; qi_rmp_2011 ; chang_science_2013 . In three-dimensions (3D), FOTIs are strong (weak) when the number of surface Dirac cones is odd (even). A weak FOTI (WFOTI) has zero principle $\mathbb{Z}_{2}$ index $\nu_{0}$, at least one non-zero weak indexes $(\nu_{1},\nu_{2},\nu_{3})$, and an even number of Dirac cones on surfaces not perpendicular to $(\nu_{1},\nu_{2},\nu_{3})$. With this understanding of FOTIs, most recent activities have been focused on higher-order TIs with a generalized bulk-boundary correspondence zhang_prl_2013 ; benalcazar_science_2017 ; peng_prb_2017 ; langbehn_prl_2017 ; song_prl_2017 ; schindler_sciadv_2018 ; ezawa_prl_2018 ; liu_prl_2019 ; Zhangrx_prl_2019 ; zhang_prl_2019 ; lee_prl_2019 ; varjas_prl_2019 ; luo_prl_2019 ; kudo_prl_2019 ; chen_pra_2019 ; Queiroz_prl_2019 ; li_npj_2019 ; chen_prl_2020 ; araki_prb_2019 ; su_cpb_2019 ; agarwala_prr_2020 ; agarwala_arxiv_2020 . The new paradigm is that, with band inversions on a $d$-dimensional manifold and its sub-manifolds, gapped bands in the manifold and its sub-manifolds of dimensions larger than $d-n$ can have gapless states in a boundary sub-manifold of dimension $d-n$. For example, a 3D second-order TI has gapless states on the sample hinges inside its bulk and surface band gaps benalcazar_science_2017 ; langbehn_prl_2017 ; song_prl_2017 ; schindler_sciadv_2018 ; liu_prl_2019 ; Zhangrx_prl_2019 ; Queiroz_prl_2019 . These hinge states have been predicted and observed in real materials, e.g., bismuth crystals schindler_natphys_2018 and magnetic axion insulator Bi_2-xSm_xSe₃ yue_natphys_2019 .

As a well-accepted paradigm, hinge states appear at the intersections of two surfaces of different topological classes when the surface Dirac cones of a 3D FOTI are gapped. Hinge states could be either chiral langbehn_prl_2017 or helical song_prl_2017 ; schindler_sciadv_2018 ; Zhangrx_prl_2019 ; Queiroz_prl_2019 , depending on whether the number of surface Dirac cones is odd or even. Robustness of those states against disorders is a fundamental issue because disorders exist inevitable in all materials and hinge states must survive in disorders in order to be a genuine state. Chiral hinge states can survive in random media due to the absence of backward scattering wang_arxiv_2020 , while inter-spin/valley scatterings are allowed in helical hinge states and may result in the disappearance of these states through Anderson localizations at an infinitesimally weak disorder. The occurrence of this scenario, however, contradicts a general belief that the in-gap hinge states should persist at finite disorders until the surface state gap closes sheng_prl_2006 ; li_prl_2009 ; trifunovic_prx_2019 . Hence, whether disorder-induced backward scatterings can destroy the helical hinge states is not clear and should be examined.

In this letter, we report a weak second-order TI (WSOTI) generated from a WFOTI through band inversion of surface states and with mirror symmetry. Different from other reported helical hinge states song_prl_2017 ; Zhangrx_prl_2019 ; schindler_sciadv_2018 ; Queiroz_prl_2019 that lock the momentum with spins, carriers in different valleys of WSOTIs move to the opposite directions along a hinge. In clean cases, such helical hinge states are characterized by the quantized valley-Chern number. They survive in the presence of weak but finite disorders, similar to the surface states in WFOTIs. Helical hinge states can be identified by the dominate occupation probability on hinges and negligible occupation probability in the bulks and on the surfaces. With increasing disorders, a gap-closing transition from WSOTI to WFOTI happens at a critical disorder $W_{c1}$ at which gaps of surface Dirac cones close. Moreover, with further increasing disorders from $W_{c1}$, the WFOTI becomes a diffusive metal (DM), and finally an Anderson insulator (AI). Electronic transport through helical hinge states is also studied. We find that the quantum resistance is the sum of an intrinsic contribution from the topological states and an extrinsic part from the inter-valley scatterings that is proportional to system sizes. These results cast the authenticity of helical hinge states that provide a way to manipulate the valley degree of freedom.

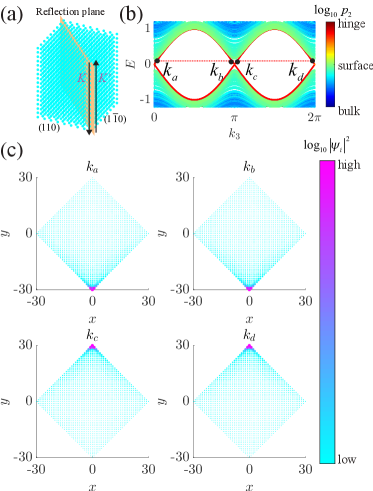
Clean WSOTI.$-$A clean WSOTI can be modelled by the following Hamiltonian in the momentum space

Here, $\Gamma^{\mu=1,2,3,4,5}=(s_{1}\otimes\sigma_{1},s_{2}\otimes\sigma_{1},s_{3}\otimes\sigma_{1},I_{2}\otimes\sigma_{3},I_{2}\otimes\sigma_{2})$ are the four-by-four non-unique gamma matrices with $s_{\mu}$ and $\sigma_{\mu}$ being the Pauli matrices acting on spin and orbital spaces, respectively. $I_{\mathcal{D}}$ is the identity matrix of dimension $\mathcal{D}$. Hopping energy $t=1$ is chosen as the energy unit. Equation (1) is invariant under the reflection symmetry of $\Gamma^{54}=I_{2}\otimes\sigma_{1}$, i.e., $\Gamma^{54}h(k_{1},k_{2},k_{3})\Gamma^{54}=h(-k_{1},k_{2},k_{3})$. For $B=0$ and $M\in(0,2)$, Eq. (1) is a reflection-symmetric WFOTI with the reflection plane on $x=0$ and characterized by the $\mathbb{Z}_{2}$ indexes $(\nu_{0},\nu_{1}\nu_{2}\nu_{3})=(0,001)$ fu_prb_2007 ; chiu_prb_2013 ; morimoto_prb_2013 . Such $\mathbb{Z}_{2}$ index guarantees two Dirac cones on the surfaces not perpendicular to the vector $(0,0,1)$, e.g., $yz$-facets. For $B>0$, the last term within the surface state subspace acts like an effective Dirac mass langbehn_prl_2017 . To see it, we derive the low-energy effective Hamiltonian of the surface Dirac cones on the $yz$-facets with open boundary condition (OBC) applied in the $x-$direction. Such effective Hamiltonian, expanded around two Dirac cones (valleys) $\bm{K}=(0,0)$ and $\bm{K}^{\prime}=(\pm\pi,\pm\pi)$, reads (See Supplemental Materials supp )

with $h_{\mathbb{S}}(\bm{p}_{\parallel})=tp_{2}\tau_{1}+tp_{3}\tau_{3}+(B-t^{\prime 2}p^{2}_{2}/2)\tau_{2}$. $\tau_{1,2,3}$ are the Pauli matrices in the basis of the zero-energy surface states wave functions. The upper and lower blocks are for $\bm{K}$ and $\bm{K}^{\prime}$ related by the pseudo- time-reversal symmetry represented by $\mathcal{T}=-i\tau_{2}\mathcal{C}$ with $\mathcal{C}$ being complex conjugate. In what follows, we denote $\bm{K}$ and $\bm{K}^{\prime}$ by $\eta_{i}=\pm 1$. If the two facets are separated by a distance, the Newton mass $t^{\prime}$ decays exponentially with the distance such that the band inversion is prevented. While, if they encounter at the reflection plane $x=0$, $t^{\prime}=t/2$. Equation (2) has been widely used to describe quantum spin Hall systems, e.g. HgTe/CdTe quantum well, where the helical states come in Kramer pairs with spin-momentum locked bernevig_science_2006 . Analogously, we expect helical states appear on the reflection plane as well but with a valley-momentum locked, i.e., electrons in hinge channels that behave as massless relativistic particles with a given valley pseudo-spin is locked to its propagating direction, see Fig. 1(a).

Figure 1(b) shows the energy spectrum $E(k_{3})$ of model (1) on a rectangle sample of size $L_{\parallel}/\sqrt{2}\times L_{\parallel}/\sqrt{2}\times L_{\perp}$ with periodic boundary condition (PBC) in $z-$direction and OBCs on surfaces perpendicular to $(110)$ and $(1\bar{1}0)$. Colors in Fig. 1(b) encode the common logarithmic of participation ratio, defined as $\mathcal{P}_{2}(E)=1/\sum_{\bm{i}}|\psi_{\bm{i}}(E)|^{4}$. Here $|\psi_{\bm{i}}(E)|$ is the normalized wave function amplitude of energy $E$ at site $\bm{i}$. $\mathcal{P}_{2}$ measures the number of sites occupied by state of $E$ wang_pra_1989 ; wang_prl_2015 ; pixley_prl_2015 and allows one to distinguish hinge states from the bulk and surface states easily. Clearly, for $M=t$ and $B=0.2t$, two pairs of gapless hinge modes appear. Those near $k_{3}=0$ ($k_{3}=\pi$) are described by the up (down) block of Eq. (2) supp . Wave function distributions of four specific hinge states $k_{a,b,c,d}$ of energy $E=0.02t$ are shown in Fig. 1(c). States of $k_{a}$ and $k_{b}$ ($k_{c}$ and $k_{d}$), respectively propagating along $\pm z-$directions, are localized on the same hinge $x=0,y=L_{\parallel}/2$ ($x=0,y=-L_{\parallel}/2$).

In quantum spin Hall systems where spin $s_{z}$ is a good quantum number, spin-Chern numbers play the role of topological invariant. Similarly, we employ the valley-Chern number $C_{\text{valley}}$ to measure the topology of the surface states in clean limit that tells the emergence of helical hinge states. $C_{\text{valley}}$, widely used in layered-graphene systems by studying the valley Hall effect zhang_prl_2011 ; ezawa_prb_2013 ; zhang_pnas_2013 , is defined as

with $C_{\bm{K}}$ and $C_{\bm{K}^{\prime}}$ being the valley-Chern number for $\bm{K}$ and $\bm{K}^{\prime}$, respectively. The summation of the Berry curvature over all occupied states of electrons in a valley $\eta_{i}$ gives $C_{\eta_{i}}=\eta_{i}\text{sgn}[B]/2=\pm 1/2$ supp . Thus, the valley-Chern number is quantized to 1.

Stability against disorders.$-$To study the robustness of the helical hinge states against disorders, we add a random on-site potential $V=\sum_{\bm{i}}c^{\dagger}_{\bm{i}}v_{\bm{i}}I_{4}c_{\bm{i}}$ to the lattice model of Hamiltonian Eq. (1), where $c^{\dagger}_{\bm{i}}$ ($c_{\bm{i}}$) is the electron creation (annihilation) operator at site $\bm{i}$. $v_{\bm{i}}$ distributes randomly in the range of $[-W/2,W/2]$. Disorders break the lattice translational symmetry so that $C_{\text{valley}}$ is not good any more. Yet, we can still use the $L_{\parallel}=L_{\perp}=L$ dependence of $\eta_{W,L}(E)=\langle\sum_{\bm{i}\in\text{Hinge}}|\psi_{\bm{i},E}(W,L)|^{2}\rangle$ to characterize hinge states, where the sum is over all the lattice sites on two hinges of $x=0,y=\pm L/2$ and $\langle\cdots\rangle$ denotes ensemble average. $\eta_{W,L}(E)$ measures the distribution on the hinges. Naturally, for states with dominated occupation probability on hinges, $\eta_{W,L}(E)$ approaches a finite value for $L\gg 1$; while for surface and bulk states, $\eta_{W,L}(E)$ should decrease with $L$ algebraically.

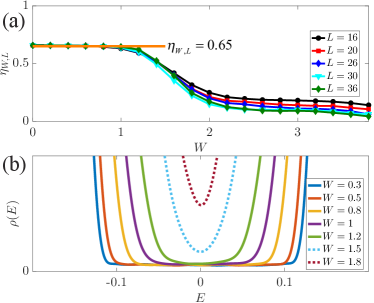
Let us focus on $E=0$. The obtained $\eta_{W,L}$ as a function of $W$ for various $L$ are shown in Fig. 2(a) wf ; kwant ; scipy . Apparently, there exists a critical disorder $W_{c1}/t\simeq 1.2\pm 0.2$ below which all curves merge and form a plateau at $\eta_{W,L}\simeq 0.65$, see the orange line. Mergence and plateau of $\eta_{W,L}$ are strong indications of helical hinge states at a finite disorder. For $W>W_{c1}$, $\eta_{W,L}$ decreases with $L$. As shown below, they are surface states for $W>W_{c1}$, featured by a finite size-independent occupation probability on surfaces as $L\to\infty$.

More insights can be obtained by investigating how disorders affect the gap of surface states through the self-consistent Born approximation (SCBA) chen_prl_2015 ; liu_prl_2016 , where the self-energy is given by

We write $\Sigma$ as $\Sigma=\Sigma_{0}I_{4}+\sum^{5}_{\mu=1}\Sigma_{\mu}\gamma^{\mu}$ with $\gamma^{1,2,3,4,5}=(\tau_{1}\otimes I_{2},\tau_{3}\otimes I_{2},\tau_{2}\otimes\sigma_{3},\tau_{2}\otimes\sigma_{3},\tau_{1}\otimes\sigma_{3},\tau_{3}\otimes\sigma_{3})$. For $E=0$, $\Sigma_{1,3,4,5}=0$ and $\Sigma_{0}$ is a pure imaginary number, i.e., $\Sigma_{0}=i(-1/\tau)$. Then, we obtain supp ; shindou_prb_2009

where the Dirac mass is renormalized as $\tilde{B}=B+\Sigma_{2}$. Here, $\tau$ is the life-time of the zero-energy surface states, i.e., $\rho_{\text{surface}}(E=0)\propto 1/\tau$. For $W<W_{c1}$, $1/\tau=0$ and surface states are gapped at $E=0$. While for $W>W_{c1}$, finite $\tau$ solutions are allowed and $\rho_{\text{surface}}(E=0)\neq 0$. Thus, with increasing $W$, we expect the WSOTI undergoes a gap-closing transition at the critical disorder $W_{c1}$ whose approximate solution is determined from Eq. (5) with $\tilde{B}=B$ is $W_{c1}=t(24\pi/(\ln[16\sqrt{2}/B]))^{1/2}$ supp . The closed-form solution indicates that $W_{c1}$ increases with $B$, which measures the width of surface gap, and explains qualitatively Fig. 2(a).

Dispersion relation of the hinge states in clean limit is linear in $p_{3}$ near two valleys (see Supplemental Materials supp ). Since disorders do not change the linear dispersion relation within the framework of SCBA, we expect a constant density of helical hinge states for $|E|<\Delta_{1}$ with $\Delta_{1}$ being the gap of surface states for $W<W_{c1}$. This behavior is confirmed by numerical calculations of the average density of states (DOS), defined as $\rho(E)=\langle(\sum^{8L^{3}}_{q=1}\delta(E-E_{q}))\rangle/(8L^{3})$ with $E_{q}$ being the eigenvalues of the systems. We calculate $\rho(E)$ through the kernel polynomial method kpm ; DOS and plot those for $L=200$ and various $W/t$ from 0.3 to 1.8 in Fig. 2(b). Indeed, $\rho(E)$ is independent of $W$ and $E$ within $|E|<\Delta_{1}$ and $W<W_{c1}$, while $\Delta_{1}$ decreases with $W$. For $W>W_{c1}\simeq 1.2t$, the constant $\rho(E)$ fades, and $\rho(E=0)$ increases with $W$. Hence, the constant DOS can be another fingerprint of the helical hinge states, akin to chiral hinge states wang_arxiv_2020 .

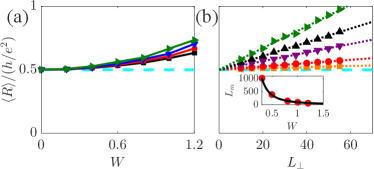
Electronic transport.$-$We have also investigated the electronic transport through helical hinge states by using the Landauer-Bttiker formula conductance ; macKinnon_zphb_1985 to calculate the two-terminal resistance $R$ of the Hall bar connected by two semi-infinite leads along $z-$direction. We focus on $W<W_{c1}$ and $E=0$. Figure 3(a) plots the $\langle R\rangle$ versus $W$ for various $L_{\parallel}=L_{\perp}=L$. For $W=0$, $R$ displays perfect quantum plateau at $h/(2e^{2})$. In the presence of disorders, $\langle R\rangle$ notably increases with $W$ and $L$, even for very small disorders. Furthermore, we investigate how $\langle R\rangle$ depends on system sizes. Figure 3(b) shows $\langle R\rangle$ as a function of $L_{\perp}$ for various $W$ and a fixed $L_{\parallel}$. We find that $\langle R\rangle$ is linearly increased with $L_{\perp}$ and can be well described by the following formula

with $L_{m}$ being a characteristics length, but independent of $L_{\parallel}$, see data in Supplemental Materials supp . Remarkably, very similar features have also been observed in quantum spin Hall systems with spin dephasings jiang_prl_2009 .

Equation (6) can be understood as follows. Unlike chiral hinge states, helical hinge states always suffer from the inter-valley scattering caused by short-range disorders such that the resistance plateau at $W=0$ are destroyed. Indeed, one can treat Eq. (6) as a combination of an intrinsic resistance $h/(2C_{\text{valley}}e^{2})$ coming from the non-trivial topology of surface states and an extrinsic resistance due to the inter-valley scattering. The latter should be proportional to $L_{\perp}$ and independent of $L_{\parallel}$. While, $L_{m}$ is a length acting like mean free length, i.e., $L_{m}\sim v_{g}\tau_{m}$ with $1/\tau_{m}$ being the inter-valley scattering rate and $v_{g}$ being the group velocity. Through Fermi Golden rule, we obtain $L_{m}\sim t^{2}/W^{2}$ (see Supplemental Materials supp ), which accords well with numerical data, as shown in the inset of Fig. 3(b).

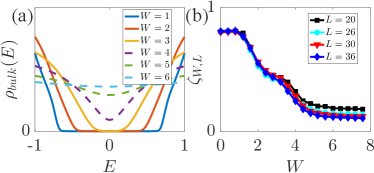
Strong disorders.$-$To have a complete picture, we study the fate of WSOTIs under stronger disorders. For $W>W_{c1}$, the surface energy gap $\Delta_{1}$ is closed while the bulk energy gap $\Delta_{2}$ remains finite. The system becomes a WFOTI. The conclusion is confirmed by demonstrating that the mid-bulk-gap states are localized on the surfaces. Akin to WSOTIs, WFOTIs survive up to a higher disorder $W_{c2}$ at which $\Delta_{2}=0$ and the system transforms into a DM beyond $W_{c2}$. Figure 4(a) shows the calculated density of bulk states $\rho_{\text{bulk}}(E)$, obtained by applying with PBCs on all directions so that no surface and hinge states are allowed, for various disorders $W>W_{c1}$. Clearly, there is always a finite bulk gap for $W<W_{c2}\simeq 3t$. Also, these results demonstrate that the non-zero $\rho(E)$ around $E=0$ for $W>W_{c1}$ shown in Fig. 2(b) is from the contributions of surface states.

Stronger evidence of the WFOTI-DM transition is given in Fig. 4(b), which displays $\zeta_{W,L}=\langle\sum_{\bm{i}\in\text{Surface}}|\psi_{\bm{i},E=0}(W,L)|^{2}\rangle$ as a function of $W$ for various $L_{\parallel}=L_{\perp}=L$. One should not be confused $\zeta_{W,L}$, the distribution of state $E=0$ on surfaces, with $\eta_{W,L}$ of the distribution on hinges. The identification of the nature of state $E=0$ thus can be guided by the following observations: (1) For hinge and surface states, $\zeta_{W,L}$ proceeds toward a finite constant in $L\to\infty$; (2) For bulk states, $\zeta_{W,L}$ decreases with $L$ and scales with $L$ as $1/L$ for large enough systems. Following such criteria, we determine $W_{c2}\simeq 3t$ such that the system is a WFOTI for $W_{c2}>W\geq W_{c1}$, while becomes a DM for $W\geq W_{c2}$.

Anderson localization occurs at an extremely strong disorders $W_{c3}>W_{c2}$, and the system becomes an insulator for $W>W_{c3}$. We numerically determine $W_{c3}/t=20\pm 1$ and the critical exponent $\nu=1.5\pm 0.1$ through the finite-size scaling analysis of the ensemble-average PR, $\mathcal{P}_{2}(E=0)$, see Supplemental Materials supp . The obtained critical exponent $\nu$ is closed to that of Gaussian unitary ensemble established before wang_arxiv_2020 ; kawarabayashi_prb_1998 .

Material relevance.$-$The WSOTI is a direct consequence of the band inversion of surface states of WFOTIs. Remarkably, a recent experiment verified the emergency of WFOTI phase in quasi-one-dimensional bismuth iodide with the same $Z_{2}$-index studied here noguchi_nature_2019 . Besides, it is found that band inversion of surface states can happen in bismuth with respect to certain crystal symmetries schindler_natphys_2018 ; yue_natphys_2019 . We thus expect bismuth is an ideal material to search for the helical hinge states. Rather than electronic systems, WSOTIs may be also found in other systems like photons, where the WFOTI has already been visualized yang_nature_2019 and a band inversion can be artificially induced in principle.

Conclusion.$-$In short, we have theoretically demonstrated the genuineness of WSOTIs with valley-momentum locked helical hinge states. Such hinge states are featured by the quantized valley-Chern number in clean limit and are robust against disorders until the band gap of surface states collapses. However, the normal quantized conductance of 1D channel is destroyed by disorders. With further increasing disorder, quantum transitions from WSOTI to WFOTI and from WFOTI to DM happen in order. At very strong disorders, the system becomes a insulator through the Anderson localization transition.