Robust Self-Supervised Extrinsic Self-Calibration
Abstract
Autonomous vehicles and robots need to operate over a wide variety of scenarios in order to complete tasks efficiently and safely. Multi-camera self-supervised monocular depth estimation from videos is a promising way to reason about the environment, as it generates metrically scaled geometric predictions from visual data without requiring additional sensors. However, most works assume well-calibrated extrinsics to fully leverage this multi-camera setup, even though accurate and efficient calibration is still a challenging problem. In this work, we introduce a novel method for extrinsic calibration that builds upon the principles of self-supervised monocular depth and ego-motion learning. Our proposed curriculum learning strategy uses monocular depth and pose estimators with velocity supervision to estimate extrinsics, and then jointly learns extrinsic calibration along with depth and pose for a set of overlapping cameras rigidly attached to a moving vehicle. Experiments on a benchmark multi-camera dataset (DDAD) demonstrate that our method enables self-calibration in various scenes robustly and efficiently compared to a traditional vision-based pose estimation pipeline. Furthermore, we demonstrate the benefits of extrinsics self-calibration as a way to improve depth prediction via joint optimization. The project page: https://sites.google.com/view/tri-sesc
[Self-supervised learning with velocity supervision]
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e3d8368b-e183-4d11-839e-42a68a1edfb5/1_selfsup_v2.png) [Extrinsic estimation]
[Extrinsic estimation]
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e3d8368b-e183-4d11-839e-42a68a1edfb5/2_estimation_v2.png) [Self-calibration via joint optimization]
[Self-calibration via joint optimization]
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e3d8368b-e183-4d11-839e-42a68a1edfb5/3_joint_optim_v2.png) Our proposed method for self-supervised extrinsic self-calibration (SESC).
(a) First, scale-aware depth and ego-motion predictors are acquired via self-supervised learning with instantaneous velocity supervision. (b) Afterwards, the extrinsic parameters are optimized using predictions from the learned depth and ego-motion networks. (c) Finally, all the networks and extrinsic parameters are jointly optimized to complete the self-calibration.
Our proposed method for self-supervised extrinsic self-calibration (SESC).
(a) First, scale-aware depth and ego-motion predictors are acquired via self-supervised learning with instantaneous velocity supervision. (b) Afterwards, the extrinsic parameters are optimized using predictions from the learned depth and ego-motion networks. (c) Finally, all the networks and extrinsic parameters are jointly optimized to complete the self-calibration.
I Introduction
Having access to accurate geometric information surrounding an autonomous system is crucial for perception and planning tasks. Predicting dense depth maps from images is a promising way to generate this surrounding geometric information, as cameras are cheap, have low power consumption, and can be easily placed anywhere. Images are also useful for a number of other downstream tasks, such as detection, semantic segmentation, and tracking. To achieve the goal of dense depth prediction, self-supervised depth and ego-motion learning methods [1, 2] are attractive because self-supervision is not restricted to high-quality labeled data, and can instead be trained on raw image sequences without ground-truth point clouds. Moreover, to cover a wide field of view, research to extend the methods to a multi-camera setting has also emerged [3, 4] as this learning principle is not restricted to the number of cameras. Importantly, studies have demonstrated that even if the overlap between two images from different cameras is small, provided that accurate extrinsics are available, multi-camera constraints still lead to improvements over monocular baselines [3].
However, despite the fact that multi-camera training improves self-supervised learning, it still requires known extrinsics, which in turn requires laborious camera calibration, typically involving the manual collection of images containing known calibration targets [5]. In contrast to the manual, target-based calibration approach, recent work has shown that monocular intrinsics calibration can be achieved in a self-supervised way [6, 7, 8], though self-supervised architectures utilizing extrinsics still use ground-truth data. To tackle the problem, in this paper we propose Self-Supervised Extrinsic Self-Calibration (SESC): a novel methodology for extrinsic self-calibration that extends the self-supervised depth and ego-motion learning paradigm. Utilizing pretrained scale-aware depth networks (obtained using the vehicle’s instantaneous velocity [9, 10]), and a curriculum learning strategy, we are able to estimate accurate, metrically-scaled extrinsics from unlabeled image sequences, without expensive optimization or bundle adjustment. Contrary to standard extrinsic calibration pipelines, which require specific tools (including calibration targets [5]) or time-consuming computation (bundle adjustment [11]), we use photometric consistency as a training objective. As a result, we can self-calibrate a multi-camera system without depending on the supervision of 3D sensors or any manual labor.
Experimental results show that our approach produces more robust calibration on a variety of real-world driving scenes compared to a standard structure-from-motion tool (COLMAP [12]). Moreover, our results also reveal specific difficulties and limitations in each sequence, both quantitatively and qualitatively. Finally, we also provide evidence that our predicted extrinsics improves depth estimation performance via the joint self-supervised optimization of extrinsics alongside depth and ego-motion.
In summary, we propose SESC (Self-Supervised Extrinsic Self-Calibration), and our contributions are as follows:
-
•
We introduce a novel camera extrinsics self-calibration technique for wide-baseline multi-camera systems utilizing the self-supervised monocular depth estimation paradigm (See Figure Robust Self-Supervised Extrinsic Self-Calibration for overview).
- •
- •
II Related Work
Multi-Camera Wide-baseline Depth Estimation. Early works on learning-based depth estimation from a single image were fully supervised [14, 15], requiring ground truth depth maps for training. After that, the need for large amounts of high-quality annotated data led research efforts towards self-supervised depth estimation [1, 16]. Zhou et al. [1] formulated this as a joint optimization problem of depth and ego-motion estimation via photometric consistency using STN [17]. Godard et al. [2] developed strategies to alleviate some of the inherent problems that come from structure-from-motion learning, while other works focused on architecture design [9], presence of dynamic objects [18], and uncertainty estimation [19]. Importantly, all these works were limited to the monocular setting, in which the field of view is limited to be that of a single camera.
To achieve self-supervised wide-baseline depth estimation, FSM [3] proposed the use of spatial-temporal photometric and pose consistency across cameras. Differently from other methods, FSM [3] does not require large amounts of overlap between cameras or 360° images [20], which allows for more flexibility in the mechanical design of the system and the integration of other vision-based perceptual modules. Subsequently, other methods were proposed to improve multi-camera depth estimation performance, in terms of architecture, method of prediction, and loss function design [4, 21, 22]. However, all these works assume well-calibrated multi-camera extrinsics, which is a strong assumption in many practical scenarios [5]. Thus, a reliable and efficient method is required in order to fully realize the benefit of calibrated extrinsic parameters in multi-camera depth estimation.
Camera Calibration via Photometric Consistency Traditional approaches to camera calibration are target-based: images of well-known patterns such as AprilTags [23] and checkerboards are captured and used to solve a correspondence matching problem by optimizing the relationship between camera parameters and observations. Even though recent open-source tools have facilitated this process and made it more efficient [24, 25], the need for tools and a pre-designed structure makes it difficult to run the calibration procedure without access to the system itself [26]. Recently, a targetless strategy using image features from the surrounding environment was proposed in [11, 27]. By using COLMAP [12] and additional optimization, Liu et al. achieved calibration from arbitrary images independently of the initial guess or the use of tools or/and pre-structured environments. However, this is still (1) a time-consuming process, that requires feature extraction and matching; and (2) it frequently fails to achieve proper convergence [3], thus making it difficult to efficiently and robustly apply this method to large-scale real-world datasets. Motivated by this fact, we propose a novel deep learning-based strategy that does not require explicit feature extraction and matching (which is usually sparse and non-differentiable), and achieves robust convergence for a variety of domains by utilizing dense and more informative geometric constraints [28, 29]. Especially, using the photometric consistency between two images as a training objective removes the dependency on additional pose labels for supervision [29] or 3D sensory input like LiDAR [27]. Furthermore, as our learned depth and ego-motion networks can be directly applied to other camera configurations, we can simultaneously and efficiently calibrate multi-camera systems.
Photometric consistency provides a strong training signal that can be used as proxy supervision to learn several different geometry-based tasks. In particular, by optimizing image reconstruction [28, 30, 31] or depth estimation [6, 7, 8] networks, previous works have shown that it is possible also to learn intrinsic and/or extrinsic camera parameters. Since mitigation of learning difficulties in a dynamic environment [2] and relatively fast inference time is attractive for efficient calibration in various real-world environments, we chose the latter group, which explicitly learns depth (and the corresponding ego-motion) and camera parameters. Our method is most similar to the self-supervised self-calibration work from [8], where the authors demonstrated that camera intrinsics could be jointly learned alongside a depth and pose networks by minimizing the photometric loss in a single-camera setting. Here, we extend the self-calibration of intrinsics to the multi-camera setting, then show that it is possible to jointly learn intrinsic and extrinsic parameters alongside depth and pose, improving depth estimation in a multi-camera setting.
III Methodology
We now describe SESC, our proposed framework to learn depth, ego-motion, and extrinsic camera parameters jointly in a self-supervised manner. First, we formulate the problem and summarize the standard method of self-supervised monocular depth and ego-motion learning. Next, we introduce our extensions towards multi-camera self-supervised extrinsic self-calibration, describing the challenges of this new setting. Finally, we present a curriculum learning method that leverages the learned extrinsics to further improve the depth and pose estimates. We assume a set of cameras rigidly attached to a vehicle, with arbitrary relative position and overlap between pairs. We also assume the instantaneous velocity of the vehicle and whether each camera is pointing backward or not.
III-A Self-Supervised Depth and Ego-motion Training
Self-supervised depth and ego-motion learning is defined as the joint optimization of a depth network, which maps a target image to a depth map , as well as a pose network, that predicts the relative transformation from a context to target frames. The synthesized target image is obtained via reprojection [1] using , , camera intrinsics , and the context image . The photometric reprojection error is then calculated as:
| (1) |
Here, is the photometric reprojection loss [1, 16], and the SSIM term measures the structure similarity of two images [32]. This reprojection error provides the photometric consistency constraint we use as the self-supervised training objective. In addition, to promote smoothness in the predicted depth map, a regularization term is added to the above reprojection error [9, 16]:
| (2) |
To address our multi-camera setup, we follow [3] and define spatio-temporal constraints via photometric consistency between reprojected camera images across the spatial (i.e. between different cameras) as well as temporal axes (i.e. between different timesteps).
III-B Self-Supervised Extrinsic Self-Calibration
In the discussion below, we index cameras by subscripts and temporal indices (video frames) by superscripts. Also, pose refers to the motion of the vehicle, while extrinsics refers to the poses of cameras on the rig with respect to a vehicle coordinate frame. Note that we chose Euler angles as a representation for extrinsics because of their simplicity, but other parameterizations are possible.
First, we will review the pose consistency loss proposed in [3] which assumes calibrated extrinsic, and then extend it to our self-calibration setting. Given a camera , the pose network predicts its transformation from the current frame to a temporally adjacent frame (usually ). Assuming that all cameras are rigidly attached to the vehicle, their motion should be consistent when observed from the vehicle coordinate system, i.e. the motion of the vehicle estimated from in camera should be the same as the motion observed in camera (given that the cameras are rigidly attached). Given the known extrinsics and , respectively, we can transform the vehicle pose estimated using the pose network predictions from camera () into camera using:
| (3) |
The above transformation can be used to transform pose predictions from all cameras into the coordinates of camera , which is the label we give to the forward-facing camera. Given that there is inconsistency in the pose predictions, FSM [3] defines a pose consistency loss as the weighted sum of pair-wise translation and rotation errors:
| (4) |
where .
In the above equation, is the number of cameras, and and are respectively the translation and rotation weighting parameters. In [3], the squared difference is applied for both and after converting the rotation matrix to Euler angles. For the fully-calibrated setting in [3], this consistency constraint is used to improve the pose as well as depth network predictions.
Pose Consistency for Extrinsics Learning: Here extrinsics refer to the poses of the cameras on the rig with respect to the vehicle coordinate frame, which in our experiments is chosen as the origin of the front camera. Therefore, is . Note that the camera extrinsics are present in Equation 3 and thus in Equation 4; this can be used as a differentiable constraint on the extrinsic parameters, and we use it to guide extrinsics learning. However, naively learning extrinsics from scratch, guided by Equation 4, causes extrinsics learning to fail because of a property of the pose network: the predicted rotation is close to the identity matrix when the images are densely sampled and the camera moves in a straight line, which is common in driving scenarios. Next, we describe our initialization technique to alleviate this and enable joint depth, pose, and extrinsics estimation.
Consider this early training scenario where the predicted pose and , plugging Equation 3 into Equation 4 will look like:
| (5) |
Here the rotation matrices are represented as Euler angles such that . If the ego-motion in the dataset is only composed of forward or backward motion (giving ), and the camera is looking backwards relatively to camera (which gives ), the above approximation shows that there is no useful gradient for . Therefore, we set only for the initialization of the back-looking camera, and set for the others.
Note that the approximation in Equation 5 also reveals another limitation of our training procedure: it is difficult to get the gradient of the translation vector . Thus, we learn the camera translations in a sequential manner, first estimating the rotation and then learning the translation (followed by end-to-end finetuning), please refer to Figure 1 and Section III-C for more details.
| Stage | Optimization | Loss | |||
|---|---|---|---|---|---|
| depth | ego-motion | extrinsics | Photo | Pose | |
| Monodepth Pretraining | ✓ | ✓ | - | ✓ | ✓ |
| Rotation Estimation | - | Fix | ✓ | - | ✓ |
| Extrinsic Estimation | Fix | ✓ | ✓ | ✓ | ✓ |
| End-to-end Training | ✓ | ✓ | ✓ | ✓ | ✓ |
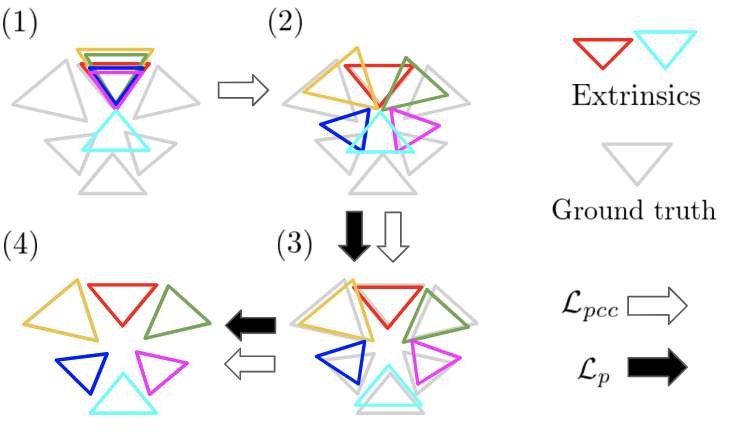
III-C Curriculum Learning
Jointly learning depth, pose, and extrinsics from scratch is a highly underconstrained problem, and empirically we have observed that a naive approach fails to converge in the self-supervised setting. Thus, we propose a curriculum schedule composed of different learning modules (depth, ego-motion, and extrinsic parameters) and objectives to minimize (photometric loss and pose consistency loss), designed to enable self-supervised learning in this novel setting. Table I summarizes the different stages of our proposed curriculum learning schedule and Figure 1 shows the extrinsics update flow. Below we describe each stage in detail and quantify their impact in the experiments section.
III-C1 Monodepth Pretraining
We train our depth and pose estimators following monodepth2 [2]. Removing the scale ambiguity in depth and ego-motion learning is an important factor in our self-calibration strategy, as a way to make the target extrinsics metrically scaled. To inject metric scale without any calibration procedure, similar to Kumar et al. [10], we normalize the output of the pose network and multiply it by the magnitude of the relative translation. The relative translation is obtained using ground-truth velocity, defined as the instantaneous velocity divided by the image sampling frequency.
III-C2 Rotation Estimation
III-C3 Extrinsic Estimation
In this stage, all extrinsic parameters and the pose network are jointly optimized using both the photometric and pose consistency losses.
III-C4 End-to-end Training
Finally, the entire architecture (including the depth network) is jointly optimized with extrinsics parameters using the photometric and pose consistency losses.
IV Experiments
We compare SESC to strong baselines for depth estimation as well as camera calibration. We aim to show (1) that SESC achieves competitive extrinsic calibration in a challenging multi-camera setting where each camera shares an arbitrary amount of field of view overlap as well as in the simplest multi-camera setup of a stereo pair; and (2) that the extrinsic calibration learned by SESC in turn helps improve monocular depth estimation in the self-supervised setting.
       (c) Camera placement of DDAD
(c) Camera placement of DDAD
|
IV-A Datasets
DDAD [9]. DDAD (Dense Depth for Autonomous Driving) is a dataset with images recorded by cameras mounted around the vehicle, forming a field of view. It has a total of training samples (composed of sequences each with or images) and validation samples (composed of sequences each with or images). All cameras are synchronized at Hz, which facilitates self-supervised learning in a multi-camera setting. In all our experiments, images are downsampled to a resolution of , and evaluated at distances of up to 200 meters. Furthermore, because the training sequences were collected using different vehicles in different cities, we learn instead per-sequence extrinsic parameters, as a way to investigate the performance of our self-calibration method in different scenarios. As reported in [3], the DDAD dataset has several areas with self-occlusion from the vehicle body, which can harm monocular self-supervised learning. Thus, we use the same self-occlusion masking protocol for training. The ground-truth depth maps are used only for evaluation. In contrast to temporally adjacent image pairs that share field of view, the overlap area of spatial- and spatiotemporal-image pairs only shares .
KITTI [13]. The KITTI dataset is the standard benchmark for depth and ego-motion estimation. We train our model on the Eigen train split [1] containing images per camera and validate on the test split containing images. Images are reshaped to , and evaluated at distances up to 80m with the garg crop [1]. Extrinsics are learned according to timestamp date, so five configurations are trained from 2011_09_26 to 2011_10_03. A target image and corresponding image always overlap about .
IV-B Implementation Details
Our models were implemented using PyTorch [33] and trained across eight NVIDIA A100 GPUs of GB per device. Previous and subsequent frames are used as temporal context. Color jittering and left-right image flips are applied as data augmentation for the depth network.
For the Monodepth Pretraining stage, we use the Adam optimizer [34] with learning rate for both the depth and pose networks, a batch size , and train for a total of epochs. Note that this step is done using pretrained weights, obtained by training standard self-supervised monocular depth and ego-motion networks considering each camera independently, without weak velocity supervision. Empirically, we found that the direct learning of scaled depth and ego-motion creates instability in the training pipeline.
After pretraining the scale-aware model, we begin the extrinsic learning stage with the following parameters: per GPU, the SGD optimizer is used with for the Rotation Estimation stage, the Adam optimizer is used for the Extrinsic Estimation stage with the for the pose network and for the extrinsics parameters, and the Adam optimizer is also used for the last joint optimization with for the depth and pose networks and for the extrinsic parameters. The number of epochs is set to 10 for the Rotation Estimation and Extrinsic Estimation stages, and 5 for the End-to-end Training stage. For the pose consistency, the translation term is formulated following [3], and the geodesic loss [35] is used as the rotation term. We set in all experiments.
For the network architectures, following [2], we used a ResNet18-based depth and pose networks. Additionally, we introduce “per-camera” extrinsic parameters, which are optimized during training. We evaluate SESC on datasets which consist of sequences collected by vehicles that have the same sensory setup, but slight variations in their extrinsic parameters across sequences due to calibration differences as well as temporal variations. To account for this, we estimate one set of per-camera parameters over the whole dataset, as well as a per-camera residual which is optimized for each sequence.
| Method | [m] | |||||
|---|---|---|---|---|---|---|
| F.Left | F.Right | B.Left | B.Right | Back | Avg. | |
| COLMAP | FAILED | |||||
| COLMAP* | 6.070 | 2.430 | 2.200 | 2.240 | 2.470 | 3.080 |
| COLMAP** | 0.117 | 0.282 | 0.210 | 0.308 | 0.262 | 0.236 |
| SESC (I) | 0.155 | 0.240 | 0.167 | 0.263 | 0.217 | 0.208 |
| SESC | 0.116 | 0.129 | 0.174 | 0.192 | 0.187 | 0.160 |
| Method | [°] | |||||
|---|---|---|---|---|---|---|
| F.Left | F.Right | B.Left | B.Right | Back | Avg. | |
| COLMAP | FAILED | |||||
| COLMAP* | 2.011 | 1.612 | 1.727 | 1.750 | 1.196 | 1.640 |
| COLMAP** | 1.251 | 0.873 | 1.016 | 0.937 | 0.434 | 0.903 |
| SESC (I) | 1.724 | 2.022 | 1.078 | 2.577 | 1.449 | 1.770 |
| SESC | 0.573 | 0.514 | 0.576 | 0.787 | 0.628 | 0.616 |
IV-C Multi-camera extrinsic self-calibration on DDAD
Extrinsics Calibration Performance. Our results are summarized in Table II, and we note that SESC achieves on average m translation error and below rotation error for extrinsic calibration. We compare SESC with COLMAP [12], a widely used structure-from-motion library.
Since COLMAP predicts intrinsics as well as extrinsics, we present a version of our method, denoted by SESC(I), where we also learn the intrinsics for all the cameras in a self-supervised manner, following the approach described in Fang et al. [8]: the ground-truth intrinsic parameters are replaced with a learnable parameter vector which is optimized jointly with the other networks. The intrinsics are initialized using the image resolution (i.e. ), following [8], and we learn one parameter vector for each camera which is optimized across the entire dataset. The Adam optimizer with is applied to these parameters in all stages except Rotation Estimation. We note that this version of our model also achieves competitive results even in this very challenging setting of unknown intrinsics and extrinsics.
We run COLMAP separately on each DDAD sequence, and we metrically scale COLMAP predictions by adjusting their magnitude based on ground-truth relative translation, to ensure a fair comparison with our method. In all experiments, we run bundle adjustment with the rig_bundle_adjuster option and set each camera model as pinhole, to account for the fact that all cameras are rigidly attached to the vehicle and can be modeled using a pinhole geometry.
| Model | Abs.Rel. (Metric) | ||||||
|---|---|---|---|---|---|---|---|
| Front | F.Left | F.Right | B.Left | B.Right | Back | Avg. | |
| Monodepth+v | 0.169 | 0.203 | 0.228 | 0.235 | 0.238 | 0.206 | 0.213 |
| SESC | 0.165 | 0.196 | 0.219 | 0.216 | 0.222 | 0.209 | 0.205 |
| SESC | 0.161 | 0.195 | 0.216 | 0.215 | 0.221 | 0.207 | 0.202 |
| FSM [3] | 0.130 | 0.201 | 0.224 | 0.229 | 0.240 | 0.186 | 0.201 |
Table II shows a quantitative comparison between the two methods. We observed that COLMAP did not converge in all sequences. Furthermore, even when it converged, the translation error produced by COLMAP was very large (up to a few meters) in several sequences. Therefore, for a more nuanced comparison, we also report COLMAP results on the sequences where convergence was reached (for a total of sequences, marked as COLMAP*), and those in which the translation error is smaller than m (for a total of sequences, marked as COLMAP**). We note that our method outperforms COLMAP** on translation error and is competitive on orientation error. Note that both SESC (I) and SESC were able to converge in all sequences from the same initialization, as an indication that it is more robust to different environment conditions. Moreover, the total training time of our method is hours for the whole dataset, while COLMAP required hours ( hour per sequence if it converged, otherwise more time is required, up to 4 hours).
A qualitative comparison between our calibrated camera extrinsics and COLMAP is shown in Figure 2, alongside our predicted point clouds. These sequences are from significantly different settings: (a) a street scene at low speeds with mostly parked cars, and (b) a highway scene at high speeds with many dynamic objects. The latter is very challenging for COLMAP, as motion blur and the presence of dynamic objects makes it difficult to perform feature matching. Even though our method also degrades in this challenging setting, compared to the simpler former setting, we are still able to reasonably estimate camera extrinsics and depth maps.
Depth Estimation Evaluation. Next, we evaluate SESC on the task of depth estimation, to answer the question of whether our self-calibrated extrinsics can be used as proxy to ground-truth extrinsics and improve depth estimation performance by leveraging cross-camera constraints. These results are reported in Table III, including variations of our depth network trained in different conditions. In Monodepth+v we directly use the backbone from the Monodepth Pretraining stage. SESC is trained using the same curriculum and number of epochs as SESC but without optimizing extrinsics; we include this baseline to highlight the fact that learning intrinsics via our method leads to improved depth performance, and that the increase is not due to additional training of the depth and ego-motion networks. SESC and SESC are trained times using randomly generated seeds and the same hyperparameters, and we also report the mean of these runs. Finally, we also include FSM [3] results obtained using the same ResNet18-based backbone.
These result shows that SESC, which optimizes extrinsics as well as depth and ego-motion networks, improves depth estimation performance compared to the baseline of SESC . Furthermore, these results also show that SESC is competitive with methods that use ground-truth extrinsics, such as FSM [3]. In fact, our model outperforms FSM in several cameras (especially B.Right) although we use the same depth backbones. We hypothesize this is due to a slight miscalibration in the provided ground-truth extrinsics. In summary, our results are evidence that the learned extrinsics generated by SESC can contribute to improvements in depth estimation without requiring additional information or explicit cross-camera calibration [3].

| Stage | ||||||
|---|---|---|---|---|---|---|
| F.Left | F.Right | B.Left | B.Right | Back | Avg. | |
| 1. Monodepth Pre. | 0.197 | 0.706 | 0.476 | 0.836 | 1.466 | 0.736 |
| 2. Rotation Est. | 0.221 | 0.678 | 0.355 | 0.737 | 1.215 | 0.641 |
| 3. Extrinsic Est. | 0.119 | 0.130 | 0.176 | 0.200 | 0.191 | 0.163 |
| 4. E2E (SESC) | 0.116 | 0.129 | 0.174 | 0.192 | 0.187 | 0.160 |
| Extrinsic Est. 2 | 0.248 | 0.478 | 0.534 | 0.683 | 0.729 | 0.534 |
| E2E 3 | 0.154 | 0.577 | 0.266 | 0.691 | 1.036 | 0.545 |
| Stage | ||||||
|---|---|---|---|---|---|---|
| F.Left | F.Right | B.Left | B.Right | Back | Avg. | |
| 1. Monodepth Pre. | 50.21 | 56.17 | 121.6 | 127.8 | 2.753 | 71.71 |
| 2. Rotation Est. | 1.856 | 1.050 | 2.264 | 2.935 | 1.393 | 1.900 |
| 3. Extrinsic Est. | 0.658 | 0.692 | 0.781 | 0.977 | 0.808 | 0.783 |
| 4. E2E (SESC) | 0.573 | 0.514 | 0.576 | 0.787 | 0.628 | 0.616 |
| Extrinsic Est. 2 | 2.734 | 3.969 | 9.188 | 9.814 | 27.64 | 10.67 |
| E2E 3 | 0.711 | 0.938 | 0.969 | 1.293 | 1.205 | 1.023 |
Effect of Curriculum Learning. In Table IV, we investigate the effects of our proposed curriculum strategy on the DDAD dataset to show that it enables the learning of extrinsic parameters without task-specific prior knowledge. In this process, the first stage (Rotation Estimation) promotes the proper initialization of camera orientation from initial values. Afterwards, the second stage (Extrinsic Estimation) significantly reduces translation error while also improving rotation. Finally, the joint optimization further improves accuracy, including depth estimation performance.
By ablating both the Rotation Estimation (see Extrinsic Est. 2) and Extrinsic Estimation (see E2E 3) stages we show that SESC effectively decreases translation and rotation error at each training stage.
IV-D Stereo-camera extrinsic self-calibration on KITTI
Table V shows the estimated error of our predicted extrinsic parameters in each learning stage, for the KITTI stereo setup. Even in this “simplest” calibration case, our proposed method improves performance through the proposed stages of our curriculum, achieving a final error of 0.018[m]. The depth estimation performance of the model is shown in Table VI. SESC achieves better results on all metrics compared to the baseline of SESC (which does not use predicted extrinsics). In addition, SESC is competitive with the current state-of-the-art, even though it relaxes the stereo-camera assumption and does not have access to information about the stereo baseline.
| Stage | [m] | [°] |
|---|---|---|
| Monodepth Pretraining | 0.541 | 0.000 |
| Rotation Estimation | 0.538 | 0.201 |
| Extrinsic Estimation | 0.031 | 0.068 |
| End-to-end Training (SESC) | 0.018 | 0.039 |
| Method | Abs Rel | Sq Rel | RMSE | |
|---|---|---|---|---|
| SESC | 0.114 | 0.831 | 4.788 | 0.863 |
| SESC | 0.113 | 0.819 | 4.777 | 0.864 |
| PackNet-SfM (M+v) [9] | 0.111 | 0.829 | 4.788 | 0.864 |
| FisheyeDistanceNet [10] | 0.117 | 0.867 | 4.739 | 0.869 |
| FSM [3] | 0.108 | 0.737 | 4.615 | 0.872 |
V Limitations
As SESC relies on the self-supervised learning of depth and ego-motion, there are some settings that are challenging, due to limitations in the photometric loss used as training objective. For example, SESC fails to properly calibrate sequences in which there are frequent complete stops, e.g. as shown in Figure 3 (seq:000032). Since self-supervised depth and pose networks rely on camera ego-motion, these sequences do not provide any meaningful source of supervision for our self-supervised training procedure, leading to a failure in calibration.
VI Conclusion
We propose a novel methodology for camera extrinsic calibration based on self-supervised depth and ego-motion learning, focusing on efficiency and robustness. Our experimental evaluation on driving benchmarks demonstrates that applying our proposed curriculum learning strategy, composed of Monodepth Pretraining, Rotation Estimation, Extrinsic Estimation, and End-to-end Training, makes it possible to simultaneously learn depth, ego-motion and extrinsic parameters over more than one hundred data collection sequences, while achieving performance comparable to traditional structure-from-motion systems. Furthermore, depth estimation experiments demonstrate that our predicted extrinsics can be used to improve depth estimation performance without requiring additional information in the form of ground-truth extrinsics.
References
- [1] T. Zhou, M. Brown, N. Snavely, and D. G. Lowe, “Unsupervised learning of depth and ego-motion from video,” in CVPR, 2017.
- [2] C. Godard, O. Mac Aodha, M. Firman, and G. J. Brostow, “Digging into self-supervised monocular depth estimation,” in ICCV, 2019.
- [3] V. Guizilini, I. Vasiljevic, R. Ambrus, G. Shakhnarovich, and A. Gaidon, “Full surround monodepth from multiple cameras,” IEEE Robotics and Automation Letters, vol. 7, no. 2, pp. 5397–5404, 2022.
- [4] J. H. Kim, J. Hur, T. P. Nguyen, and S.-G. Jeong, “Self-supervised surround-view depth estimation with volumetric feature fusion,” in NeurIPS, 2022.
- [5] Y. Chen, L. Zhang, Y. Shen, B. N. Zhao, and Y. Zhou, “Extrinsic self-calibration of the surround-view system: A weakly supervised approach,” IEEE Transactions on Multimedia, pp. 1–1, 2022.
- [6] A. Gordon, H. Li, R. Jonschkowski, and A. Angelova, “Depth from videos in the wild: Unsupervised monocular depth learning from unknown cameras,” in CVPR, 2019.
- [7] I. Vasiljevic, V. Guizilini, R. Ambrus, S. Pillai, W. Burgard, G. Shakhnarovich, and A. Gaidon, “Neural ray surfaces for self-supervised learning of depth and ego-motion,” in 3DV, 2020.
- [8] J. Fang, I. Vasiljevic, V. Guizilini, R. Ambrus, G. Shakhnarovich, A. Gaidon, and M. R. Walter, “Self-supervised camera self-calibration from video,” in ICRA, 2022, pp. 8468–8475.
- [9] V. Guizilini, R. Ambrus, S. Pillai, A. Raventos, and A. Gaidon, “3d packing for self-supervised monocular depth estimation,” in CVPR, 2020.
- [10] V. R. Kumar, S. A. Hiremath, M. Bach, S. Milz, C. Witt, C. Pinard, S. Yogamani, and P. Mäder, “Fisheyedistancenet: Self-supervised scale-aware distance estimation using monocular fisheye camera for autonomous driving,” in ICRA, 2020, pp. 574–581.
- [11] Y. Lin, V. Larsson, M. Geppert, Z. Kukelova, M. Pollefeys, and T. Sattler, “Infrastructure-based Multi-Camera Calibration using Radial Projections,” in ECCV, 2020.
- [12] J. L. Schonberger and J.-M. Frahm, “Structure-from-motion revisited,” in CVPR, 2016.
- [13] A. Geiger, P. Lenz, and R. Urtasun, “Are we ready for autonomous driving? the kitti vision benchmark suite,” in CVPR, 2012.
- [14] D. Eigen, C. Puhrsch, and R. Fergus, “Depth map prediction from a single image using a multi-scale deep network,” in NeurIPS, 2014.
- [15] I. Laina, C. Rupprecht, V. Belagiannis, F. Tombari, and N. Navab, “Deeper depth prediction with fully convolutional residual networks,” in 3DV, 2016, pp. 239–248.
- [16] C. Godard, O. Mac Aodha, and G. J. Brostow, “Unsupervised monocular depth estimation with left-right consistency,” in CVPR, 2017.
- [17] M. Jaderberg, K. Simonyan, A. Zisserman, and k. kavukcuoglu, “Spatial transformer networks,” in NeurIPS, vol. 28, 2015.
- [18] T.-W. Hui, “Rm-depth: Unsupervised learning of recurrent monocular depth in dynamic scenes,” in CVPR, 2022, pp. 1665–1674.
- [19] J. Hornauer and V. Belagiannis, “Gradient-based uncertainty for monocular depth estimation,” ECCV, 2022.
- [20] M. Rey–Area, M. Yuan, and C. Richardt, “360monodepth: High-resolution 360° monocular depth estimation,” in CVPR, 2022.
- [21] J. Xu, X. Liu, Y. Bai, J. Jiang, K. Wang, X. Chen, and X. Ji, “Multi-camera collaborative depth prediction via consistent structure estimation,” in ACM Multimedia, 2022, p. 2730–2738.
- [22] Y. Wei, L. Zhao, W. Zheng, Z. Zhu, Y. Rao, G. Huang, J. Lu, and J. Zhou, “Surrounddepth: Entangling surrounding views for self-supervised multi-camera depth estimation,” CoRL, 2022.
- [23] E. Olson, “Apriltag: A robust and flexible visual fiducial system,” in ICRA, 2011, pp. 3400–3407.
- [24] J. Rehder, J. Nikolic, T. Schneider, T. Hinzmann, and R. Siegwart, “Extending kalibr: Calibrating the extrinsics of multiple imus and of individual axes,” in ICRA, 2016, pp. 4304–4311.
- [25] F. Rameau, J. Park, O. Bailo, and I. S. Kweon, “Mc-calib: A generic and robust calibration toolbox for multi-camera systems,” Computer Vision and Image Understanding, vol. 217, 3 2022.
- [26] G. Koo, W. Jung, and N. Doh, “A two-step optimization for extrinsic calibration of multiple camera system (mcs) using depth-weighted normalized points,” IEEE Robotics and Automation Letters, 2021.
- [27] H. Hu, F. Han, F. Bieder, J.-H. Pauls, and C. Stiller, “Tescalib: Targetless extrinsic self-calibration of lidar and stereo camera for automated driving vehicles with uncertainty analysis,” in IROS, 2022.
- [28] Y. Jeong, S. Ahn, C. Choy, A. Anandkumar, M. Cho, and J. Park, “Self-calibrating neural radiance fields,” in ICCV, 2021.
- [29] J. Y. Zhang, D. Ramanan, and S. Tulsiani, “RelPose: Predicting probabilistic relative rotation for single objects in the wild,” in ECCV, 2022.
- [30] L. Yen-Chen, P. Florence, J. T. Barron, A. Rodriguez, P. Isola, and T.-Y. Lin, “iNeRF: Inverting neural radiance fields for pose estimation,” in IROS, 2021, pp. 1323–1330.
- [31] C.-H. Lin, W.-C. Ma, A. Torralba, and S. Lucey, “Barf: Bundle-adjusting neural radiance fields,” in ICCV, 2021.
- [32] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: from error visibility to structural similarity,” IEEE transactions on image processing, 2004.
- [33] A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga, and A. Lerer, “Automatic differentiation in pytorch,” in NeurIPS, 2017.
- [34] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014.
- [35] T. Hempel, A. A. Abdelrahman, and A. Al-Hamadi, “6d rotation representation for unconstrained head pose estimation,” in ICIP, 2022, pp. 2496–2500.