$R^{\nu}_{K^{(*)}}$ and non-standard neutrino interactions

Rare $B$ decays play an important role in understanding the dynamics of the standard model (SM) as well as being a fertile ground for the search for new physics. The $B\to K^{(*)}\nu\bar{\nu}$ decays are amongst the cleanest modes to search for new physics due to their well controlled theoretical uncertainty. Experiments at Belle and Babar have already published upper limits on these modes at 2-3 times the SM rate and further improvement is expected from Belle-II, which can reach a sensitivity on the branching ratios of about 10% with 50 ab^-1 [1]. Interesting constraints for certain BSM physics can be obtained already with current bounds.

We consider two types of models that add incoherently to the SM rates. First we entertain the possibility of a fourth light neutrino that couples to SM fields through a non-universal $Z^{\prime}$. We find that existing constraints on the model allow enhancements of the $B\to K^{(*)}\nu\bar{\nu}$ rates by up to factors of two and that these are correlated with the $B_{s}\to\tau^{+}\tau^{-}$ mode which could reach a rate up to six times larger than in the SM.

We then consider possible contributions from neutrino flavour violating final states in the context of scalar and vector leptoquarks. These contributions are correlated to the charged lepton flavour violating (CLFV) modes $B_{s}\to\ell\ell^{\prime}$ and $B\to K^{(*)}\ell\ell^{\prime}$ and we find that the current limits on $B\to K^{(*)}\nu\bar{\nu}$ are more restrictive for modes with tau-leptons. The leptoquark scenario also correlates $B\to K^{(*)}\nu\bar{\nu}$ to the neutral and charged B anomalies, as has been extensively discussed in the literature, and we comment on this.

Within the SM the effective Hamiltonian responsible for the $B\to K^{(*)}\nu\bar{\nu}$ transitions originates at lowest order from box and penguin diagrams and is usually written as [2]

	$\displaystyle{\cal H}_{SM}$	$\displaystyle=-\frac{4G_{F}}{\sqrt{2}}V_{tb}V^{\star}_{ts}C_{L}^{SM}\sum_{i}{\cal O}^{ii}_{L}+{\rm~{}h.c.}$
	$\displaystyle{\cal O}^{ii}_{L}$	$\displaystyle=\frac{e^{2}}{16\pi^{2}}(\bar{s}\gamma_{\mu}P_{L}b)(\bar{\nu}_{i}\gamma^{\mu}(1-\gamma_{5})\nu_{i}),$		(1)

with an accurately known Wilson coefficient that is independent of the neutrino flavour and that including NLO QCD corrections [3] and two-loop electroweak corrections [4] is given by

$\displaystyle C_{L}^{SM}=-\frac{X(x_{t})}{s^{2}_{W}},\quad X(x_{t})=1.469\pm 0.017.$

(2)

Typical SM predictions obtained with flavio are¹¹1These numbers agree within errors with published numbers as in [5, 1]. Neglecting isospin breaking, the neutral and charged modes have the same rates so we choose to present the two modes with the strongest experimental limits.

$\displaystyle\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})_{SM}=(4.4\pm 0.7)\times 10^{-6},\quad\mathcal{B}(B^{0}\to K^{*0}\nu\bar{\nu})_{SM}=(9.5\pm 1.0)\times 10^{-6}.$

(3)

We list the best current experimental constraints on these modes in Table 1.

Belle-II is expected to improve these limits, and has produced a preliminary result $\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})\leq 4.1\times 10^{-5}$ at the 90% confidence level [9]. They have averaged this result with the previous ones to arrive at $\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})=(1.1\pm 0.4)\times 10^{-5}$ [9]. For the $K^{*}$ channel, Belle has also combined the charged and neutral modes to obtain the limit $\mathcal{B}(B\to K^{*}\nu\bar{\nu})\leq 2.7\times 10^{-5}$ [8] but here we will use the limit in Table 1. These results are usually presented as ratios, for which we obtain

$\displaystyle R^{\nu}_{K}=\frac{\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})}{\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})_{SM}}=2.5\pm 1.0,\quad R^{\nu}_{K^{*}}=\frac{\mathcal{B}(B\to K^{*0}\nu\bar{\nu})}{\mathcal{B}(B\to K^{*0}\nu\bar{\nu})_{SM}}\leq 1.9.$

(4)

The second number is simply the ratio of the limit in Table 1 and the central value in Eq. 3 and somewhat lower than what is used in [10].

We can parameterise any new physics relevant for these decays through an effective Hamiltonian at the $b$ mass scale. The effective theory originates in extensions of the SM containing new particles at or above the electroweak scale that have been integrated out. In general, this results in additional contributions to $C_{L}$ in Eq. 2 as well as in new operators. Because our discussion is tied to two types of models, we only need to consider the following

	$\displaystyle{\cal H}_{NP}=-\frac{4G_{F}}{\sqrt{2}}V_{tb}V^{\star}_{ts}\frac{e^{2}}{16\pi^{2}}$	$\displaystyle\sum_{ij}\left(C_{L}^{ij}{\cal O}_{L}^{ij}+C_{R}^{ij}{\cal O}_{R}^{ij}+C_{L}^{\prime~{}ij}{\cal O}_{L}^{\prime~{}ij}+C_{R}^{\prime~{}ij}{\cal O}_{R}^{\prime~{}ij}\right.$
		$\displaystyle+\left.C_{9}^{ij}{\cal O}_{9}^{ij}+C_{10}^{ij}{\cal O}_{10}^{ij}+C_{9^{\prime}}^{ij}{\cal O}_{9^{\prime}}^{ij}+C_{10^{\prime}}^{ij}{\cal O}_{10^{\prime}}^{ij}\right)+{\rm~{}h.c.}$		(5)

where the operators are

	$\displaystyle{\cal O}_{L}^{ij}$	$\displaystyle=(\bar{s}_{L}\gamma_{\mu}b_{L})(\bar{\nu}_{i}\gamma^{\mu}(1-\gamma_{5})\nu_{j})$	$\displaystyle{\cal O}_{R}^{ij}$	$\displaystyle=(\bar{s}_{R}\gamma_{\mu}b_{R})(\bar{\nu}_{i}\gamma^{\mu}(1-\gamma_{5})\nu_{j})$
	$\displaystyle{\cal O}_{L}^{\prime~{}ij}$	$\displaystyle=(\bar{s}_{L}\gamma_{\mu}b_{L})(\bar{\nu}_{i}\gamma^{\mu}(1+\gamma_{5})\nu_{j})$	$\displaystyle{\cal O}_{R}^{\prime~{}ij}$	$\displaystyle=(\bar{s}_{R}\gamma_{\mu}b_{R})(\bar{\nu}_{i}\gamma^{\mu}(1+\gamma_{5})\nu_{j})$
	$\displaystyle{\cal O}_{9}^{ij}$	$\displaystyle=(\bar{s}_{L}\gamma_{\mu}b_{L})(\bar{\ell}_{i}\gamma^{\mu}\ell_{j})$	$\displaystyle{\cal O}_{10}^{ij}$	$\displaystyle=(\bar{s}_{L}\gamma_{\mu}b_{L})(\bar{\ell}_{i}\gamma^{\mu}\gamma_{5}\ell_{j})$
	$\displaystyle{\cal O}_{9^{\prime}}^{ij}$	$\displaystyle=(\bar{s}_{R}\gamma_{\mu}b_{R})(\bar{\ell}_{i}\gamma^{\mu}\ell_{j})$	$\displaystyle{\cal O}_{10^{\prime}}^{ij}$	$\displaystyle=(\bar{s}_{R}\gamma_{\mu}b_{R})(\bar{\ell}_{i}\gamma^{\mu}\gamma_{5}\ell_{j})$		(6)

The Wilson coefficients are defined so that they only contain NP contributions and the SM is counted separately through Eq. 2. The list in Eq. 6 includes ${\cal O}^{(\prime)}_{L}$, ${\cal O}^{(\prime)}_{R}$, which contribute to $B^{(*)}\to K^{(*)}\nu\bar{\nu}$. It excludes operators with scalar and tensor neutrino bi-linears that have been considered in [10] because they do not appear in the models we discuss. The operators with charged leptons appear in the models we discuss with coefficients that are related to $C_{L,R}^{(\prime)ij}$. The flavour diagonal operators ${\cal O}^{(\prime)\mu\mu}_{9,10}$ affect $b\to s\mu\bar{\mu}$ decays including the $B\to K^{(*)}\mu\bar{\mu}$ anomalies and have been studied extensively in that context.

We can classify the contributions to $B\to K^{(*)}\nu\bar{\nu}$ from these operators into two types: those that interfere with the SM, ${\cal O}_{L,R}^{ii}$; and those that do not, ${\cal O}_{L,R}^{i\neq j}$ and ${\cal O}^{\prime~{}ij}_{L,R}$. In $B\to K\nu\bar{\nu}$ only the vector current enters the hadronic matrix element so that the contributions to the rate from ${\cal O}_{L}^{ij}$ and ${\cal O}_{R}^{ij}$ are the same. Similarly for those from ${\cal O}_{L}^{\prime~{}ij}$ and ${\cal O}_{R}^{\prime~{}ij}$. At the same time, the different neutrino chirality eliminates interference between the primed and un-primed-operators for massless neutrinos. The only operators that interfere with the SM are thus the diagonal ones (in neutrino flavour) ${\cal O}_{L}^{ii}$ and ${\cal O}_{R}^{ii}$. The rates can be evaluated numerically using $\tt flavio$ [11], and the central value (uncertainty will be shown in the figures) is given approximately by

	$\displaystyle\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})\times 10^{6}$	$\displaystyle\approx 4.39-0.457~{}{\rm Re}\sum_{i}\left(C^{ii}_{L}+C^{ii}_{R}\right)$
		$\displaystyle+0.0357~{}\sum_{ij}\left(\left|C^{ij}_{L}+C^{ij}_{R}\right|^{2}+\left|C_{L}^{\prime~{}ij}+C_{R}^{\prime~{}ij}\right|^{2}\right)$		(7)

In $B\to K^{*}\nu\bar{\nu}$ both the vector and axial-vector currents enter the hadronic matrix element resulting in different contributions for ${\cal O}_{L}^{ij}$ and ${\cal O}_{R}^{ij}$ as well as for ${\cal O}_{L}^{\prime~{}ij}$ and ${\cal O}_{R}^{\prime~{}ij}$. Numerically, the rate is approximately given by

	$\displaystyle\mathcal{B}(B^{0}\to K^{\star 0}\nu\bar{\nu})\times 10^{6}$	$\displaystyle\approx 9.53+{\rm Re}\sum_{i}\left(-0.993~{}C^{ii}_{L}+0.661~{}C^{ii}_{R}\right)$
		$\displaystyle+\sum_{ij}\left(0.0775\left({C^{ij}_{L}}^{2}+{C^{ij}_{R}}^{2}+{C_{L}^{\prime~{}ij}}^{2}+{C_{R}^{\prime~{}ij}}^{2}\right)-0.103\left(C^{ij}_{L}C^{ij}_{R}+C_{L}^{\prime~{}ij}C_{R}^{\prime~{}ij}\right)\right)$		(8)

The parametric uncertainty in these predictions, as estimated by flavio is illustrated in Fig. 1²²2The uncertainty in these predictions is around 15% and is mostly due to the form factors for the $B\to K$ and $B\to K^{*}$ hadronic transitions, which are responsible for about 10%, while the value of $V_{cb}$ contributes an additional 5%.. We show $\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})$ as a function of $C_{L}^{33}$ (the figure is identical for $C_{L,R}^{ii}$) and as a function of $C_{L}^{23}$ (the figure is identical for $C_{L}^{i\neq j}$ and $C_{L,R}^{\prime~{}ij}$). The red band marks the experimental combination $\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})=(1.1\pm 0.4)\times 10^{-5}$ [9] and the green band the SM in Eq. 3 at 1$\sigma$. For $\mathcal{B}(B^{0}\to K^{\star 0}\nu\bar{\nu})$ we show the dependence on $C_{L}^{33}$ (same for all $C_{L}^{ii}$), $C_{R}^{33}$ (same for all $C_{R}^{ii}$) and $C_{L}^{23}$ (same for all $C_{L}^{i\neq j}$ and $C_{L,R}^{\prime~{}ij}$). In this case the red line shows the 90% c.l. experimental upper bound from Table 1 and the green band the SM at 1$\sigma$.

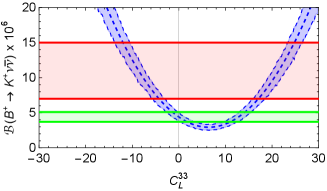
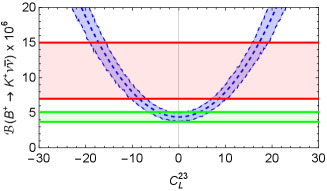
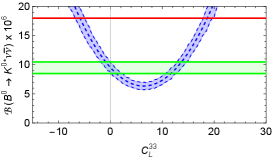
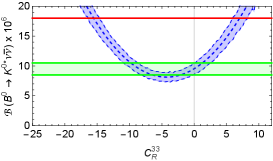
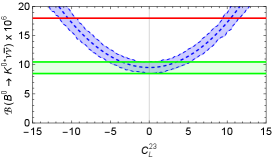
For example, new physics contributions allowed by the value of $\mathcal{B}(B^{+}\to K^{+}\nu\bar{\nu})$ in Eq. 7 at the 1$\sigma$ level and taking only one non-zero parameter at a time are shown in Table 2 and can also be read off Fig. 1.

The first type of new physics we consider that can increase the SM value of $B\to K^{(*)}\nu\bar{\nu}$ consists of new light neutrinos. In fact, modes with neutrino pairs in the final state count the number of light neutrinos in the SM due to lepton universality. The existence of new light neutrinos is severely constrained by measurements of the invisible $Z$ width and by cosmological considerations. Assuming lepton universality, the former implies that $N_{\nu}=2.9840\pm 0.0082$ [12]. Cosmological constraints depend on other parameters and, for example, $\Delta N_{eff}<0.77$ for a Hubble constant $H_{0}=71.3^{+1.9}_{-2.2}$ km/s/Mpc [13].

It is possible to avoid these limits with a light sterile neutrino that interacts with the SM through a $Z^{\prime}$. The contribution of this neutrino to the $Z$ width neutrino count is proportional to the square of the $Z-Z^{\prime}$ mixing parameter and can thus be negligibly small. In addition, if the $Z^{\prime}$ is non-universal and couples predominantly to the third generation SM fermions, the new neutrino reaches thermal equilibrium with SM particles at a temperature near the $\tau$-lepton mass. However, at the time of big-bang nucleosynthesis the temperature is about 1 MeV and this difference results in a suppression of the contribution of this neutrino to $\Delta N_{eff}$ to a safe level, $\Delta N_{eff}<0.1$ [14].

We have previously constructed a detailed example of a model with these properties [15, 16] so we do not repeat the details here. The $Z^{\prime}$ is responsible for two new operators that contribute to $B\to K^{(*)}\nu\bar{\nu}$ and to $B_{s}\to\tau^{+}\tau^{-}$ [17]:

	$\displaystyle{\cal H}_{T}$	$\displaystyle=-\frac{G_{F}}{\sqrt{2}}2s^{2}_{W}\frac{M_{Z}^{2}}{M_{Z^{\prime}}^{2}}\cot^{2}\theta_{R}V^{d*}_{Rbs}V^{d}_{Rbb}\bar{s}_{R}\gamma_{\mu}b_{R}\ \left(\bar{\nu}_{R3}\gamma^{\mu}\nu_{R3}-\bar{\tau}_{R}\gamma^{\mu}\tau_{R}\right)$
	$\displaystyle{\cal H}_{L}$	$\displaystyle=-\frac{G_{F}}{\sqrt{2}}\frac{\alpha}{\pi}\frac{M_{Z}^{2}}{M_{Z^{\prime}}^{2}}\cot^{2}\theta_{R}V^{*}_{ts}V_{tb}I(\lambda_{t},\lambda_{H})\bar{s}_{L}\gamma_{\mu}b_{L}\ \left(\bar{\nu}_{R3}\gamma^{\mu}\nu_{R3}-\bar{\tau}_{R}\gamma^{\mu}\tau_{R}\right)$		(9)

In the notation of Eq. 5, the Wilson coefficients that result in this model are thus:

	$\displaystyle C_{L}^{\prime~{}\tau\tau}=-C_{9}^{\tau\tau}=-C_{10}^{\tau\tau}$	$\displaystyle=2\left(\frac{m_{Z}^{2}}{m_{Z^{\prime}}^{2}}\right)\cot^{2}\theta_{R}I(\lambda_{t},\lambda_{H})$
	$\displaystyle C_{R}^{\prime~{}\tau\tau}=-C_{9^{\prime}}^{\tau\tau}=-C_{10^{\prime}}^{\tau\tau}$	$\displaystyle=4\left(\frac{V^{d*}_{Rbs}V^{d}_{Rbb}}{V_{tb}V^{\star}_{ts}}\right)\left(\frac{m_{Z}^{2}}{m_{Z^{\prime}}^{2}}\right)\cot^{2}\theta_{R}\frac{\pi s^{2}_{W}}{\alpha}.$		(10)

The first operator in Eq. 9 originates in a flavour changing tree-level exchange of the $Z^{\prime}$. The parameters that appear in this result are: the $Z^{\prime}$ mass; a ratio parameterising the strength of the new interaction relative to the weak interaction, $\cot\theta_{R}$; and two elements of the matrix that rotates the down-type quarks between the weak and the mass bases. The second operator in Eq. 9 arises from a new penguin diagram and depends on details of the scalar sector through the Inami-Lim function $I(\lambda_{t},\lambda_{H})$ [18]. The existing constraints on these parameters can be summarised as:

• •

  A combination of perturbative unitarity [15] and LHC non-production of $Z^{\prime}$ from $b\bar{b}$ annihilation [19] restrict the overall strength of the new interaction to

  $\displaystyle\left(\frac{m_{Z}^{2}}{m_{Z^{\prime}}^{2}}\right)\cot^{2}\theta_{R}\lesssim 0.15.$

  (11)

• •

  $B_{s}$ mixing constrains $|V^{d}_{Rbs}V^{d*}_{Rbb}|$ and $I(\lambda_{t},\lambda_{H})$ [17]. Both the SM calculation and the experimental situation regarding $\Delta M_{B_{s}}$ have changed significantly so we repeat that analysis here.

In terms of the parameters of interest, the effective Hamiltonian below the $Z^{\prime}$ scale is:

	$\displaystyle{\cal H}=$	$\displaystyle\frac{G_{F}}{\sqrt{2}}\left(\frac{m_{Z}^{2}}{m_{Z^{\prime}}^{2}}\right)\cot^{2}\theta_{R}\left(\left(\frac{\alpha}{2\pi s_{W}}V^{*}_{tb}V_{ts}\right)^{2}I(\lambda_{t},\lambda_{H})^{2}~{}{\cal O}_{LL}\right.$
		$\displaystyle+\left.s_{W}^{2}(V^{d}_{Rbs}V^{d*}_{Rbb})^{2}~{}{\cal O}_{RR}+2s_{W}\left(\frac{\alpha}{2\pi s_{W}}V^{*}_{tb}V_{ts}\right)I(\lambda_{t},\lambda_{H})(V^{d}_{Rbs}V^{d*}_{Rbb})~{}{\cal O}_{LR}\right)$		(12)

with the usual $\Delta B=2$ operators:

$\displaystyle{\cal O}_{LL,RR}=(\bar{s}_{L,R}\gamma_{\mu}b_{L,R})(\bar{s}_{L,R}\gamma_{\mu}b_{L,R}),\quad{\cal O}_{LR}=(\bar{s}_{L}\gamma_{\mu}b_{L})(\bar{s}_{R}\gamma_{\mu}b_{R}).$

(13)

QCD renormalisation group running modifies the Wilson coefficients and introduces one more operator at the $b$ scale, ${\cal O}_{SLR}=(\bar{s}_{R}b_{L})(\bar{s}_{L}b_{R})$. Making use of flavio once more, we find

$$\frac{\Delta M_{B_{s}}}{(\Delta M_{B_{s}})_{SM}}\approx 1+1.5\times 10^{-4}I(\lambda_{t},\lambda_{H})^{2}-8.2~{}I(\lambda_{t},\lambda_{H})|V^{d}_{Rbs}V^{d*}_{Rbb}|+3282.~{}|V^{d}_{Rbs}V^{d*}_{Rbb}|^{2}.$$

(14)

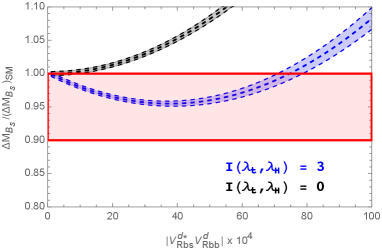
The current experimental average $\Delta M_{B_{s}}=(17.741\pm 0.020){\rm~{}ps}^{-1}$ [20] combined with a recent SM prediction $(\Delta M_{B_{s}})_{SM}=(18.4^{+0.7}_{-1.2}){\rm~{}ps}^{-1}$ [21] results in $\Delta M_{B_{s}}/(\Delta M_{B_{s}})_{SM}=0.96^{+0.4}_{-0.6}$ and we compare this ratio to the prediction of Eq. 14 in Fig. 2 for $I(\lambda_{t},\lambda_{H})=0$ and $I(\lambda_{t},\lambda_{H})=3$. These two values were chosen because a scan over the parameters in the model [18] suggests $-2\lesssim I(\lambda_{t},\lambda_{H})\lesssim 3$ as a range for the Inami-Lim function. The allowed range for $C_{L,R}^{\prime\tau\tau}$, assuming that $V^{d}_{Rbs}V^{d*}_{Rbb}$ is real, is then showed in the right panel of Fig. 2. The key point is that the tree level $Z^{\prime}$ exchange tends to increase $\Delta M_{B_{s}}$ over its SM value and this is severely constrained by current data. It is the new penguin contribution to ${\cal O}_{LR}$ and ${\cal O}_{SLR}$ that allows $\Delta M_{B_{s}}$ to drift below its SM value. As can be seen from Eq. 14, allowing $V^{d}_{Rbs}V^{d*}_{Rbb}$ to have a phase can augment the allowed parameter range but a complete phenomenological study of this general case is beyond the scope of the present work.

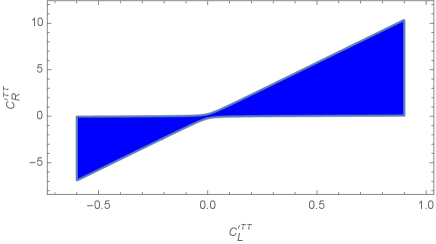
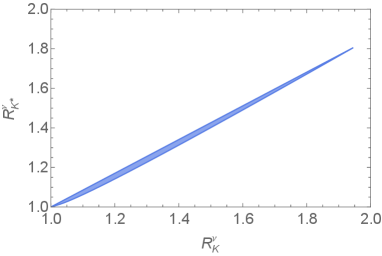
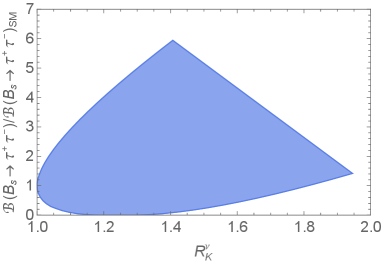
The allowed region in $C_{L,R}^{\prime\tau\tau}$ shown in Fig. 2 results in an increase of the $B\to K^{(*)}\nu\bar{\nu}$ rates over their SM value and this is shown in the left panel of Fig. 3. The figure indicates a near perfect correlation between the two neutrino modes and the largest values, near two, are obtained for the upper-right corner of the region in Fig. 2. Interestingly, the same model with the constraint of Eq. 11 can no longer enhance $K\to\pi\nu\bar{\nu}$ modes by more than a few percent.³³3In the notation of [22] it predicts $\tilde{X}\leq 0.1$. The main difference between these two cases is the strong constraint on $V^{d*}_{Rbd}$ (from $B_{d}$ mixing) that enters $K\to\pi\nu\bar{\nu}$ in place of $V^{d*}_{Rbb}$ which can be close to one.

The model predicts through Eq. 10 a correlation between $B\to K^{(*)}\nu\bar{\nu}$ modes and $B_{s}\to\tau^{+}\tau^{-}$. The latter currently only has a weak experimental limit from LHCb $\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})\leq 6.8\times 10^{-3}$ at 95%c.l. [23]. The prediction can be written in a very simple form because only the hadronic axial vector current contributes,

$\displaystyle\frac{\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})}{\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})_{SM}}=\left(1+\frac{(C_{10}^{\tau\tau}-C_{10^{\prime}}^{\tau\tau})}{C_{10}^{\tau\tau SM}}\right)^{2}.$

(15)

The allowed parameter region seen in Fig. 2, combined with $C_{10}^{\tau\tau SM}=-Y(x_{t})/s_{W}^{2}\sim-4.3$ [3], implies that the model allows

$$\frac{\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})}{\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})_{SM}}\lesssim 6.$$

(16)

This can be read off Fig. 3 which illustrates the correlation with $R^{\nu}_{K}$. On the other hand, the model also allows for $(C_{10^{\prime}}^{\tau\tau}-C_{10}^{\tau\tau})\sim-4$ where the $\mathcal{B}(B_{s}\to\tau^{+}\tau^{-})$ is significantly suppressed with respect to its SM value.

The corresponding Wilson coefficients affecting the modes $b\to s\mu^{+}\mu^{-}$ exhibiting anomalies, $C_{9,10,9^{\prime},10^{\prime}}^{\mu\mu}$ are suppressed with respect to$C_{9,10,9^{\prime},10^{\prime}}^{\tau\tau}$ by factors $|V^{\ell}_{R3\mu}|^{2}$ which can be very small [24]. For this reason, this model yields predictions for $b\to s\mu^{+}\mu^{-}$ processes that are very similar to the SM. Correlations between these dimuon modes and $b\to s\nu\bar{\nu}$ modes have also been explored in other models [25, 26].

In this section we consider models that can increase $R^{\nu}_{K^{(*)}}$ by producing final states with neutrino pairs of different lepton flavour, but with only the three SM neutrinos. The starting point is then scalar $S$ and vector $V$ leptoquarks with couplings to SM fermions which include a left-handed neutrino $\nu_{L}$ of any flavour. They are [27, 28] ,

	$\displaystyle{\cal L}_{S}=$	$\displaystyle\lambda_{LS_{0}}\bar{q}^{c}_{L}i\tau_{2}\ell_{L}S_{0}^{\dagger}+\lambda_{L\tilde{S}_{1/2}}\bar{d}_{R}\ell_{L}\tilde{S}^{\dagger}_{1/2}+\lambda_{LS_{1}}\bar{q}^{c}_{L}i\tau_{2}\vec{\tau}\cdot\vec{S}^{\dagger}_{1}\ell_{L}+{\rm~{}h.~{}c}.\;,$
	$\displaystyle{\cal L}_{V}=$	$\displaystyle\lambda_{LV_{1/2}}\bar{d}_{R}^{c}\gamma_{\mu}\ell_{L}V^{\dagger\mu}_{1/2}+\lambda_{LV_{1}}\bar{q}_{L}\gamma_{\mu}\vec{\tau}\cdot\vec{V}^{\dagger\mu}_{1}\ell_{L}+{\rm~{}h.~{}c.}\;,$		(17)

where the leptoquark fields and their transformation properties under the SM group are given by

	$\displaystyle S^{\dagger}_{0}$	$\displaystyle=S_{0}^{1/3}:(\bar{3},1,1/3)$
	$\displaystyle\tilde{S}_{1/2}^{\dagger}$	$\displaystyle=\left(\tilde{S}_{1/2}^{-1/3},\tilde{S}_{1/2}^{2/3}\right):(3,2,1/6)$
	$\displaystyle\vec{\tau}\cdot\vec{S}_{1}^{\dagger}$	$\displaystyle=\left(\begin{array}[]{cc}S^{1/3}_{1}&\sqrt{2}S^{4/3}_{1}\\ \sqrt{2}S^{-2/3}_{1}&-S^{1/3}_{1}\end{array}\right):(\bar{3},3,1/3)$		(20)
	$\displaystyle V_{1/2}^{\dagger}$	$\displaystyle=\left(V_{1/2}^{1/3},V_{1/2}^{4/3}\right):(\bar{3},2,5/6)$
	$\displaystyle\vec{\tau}\cdot\vec{V}_{1}^{\dagger}$	$\displaystyle=\left(\begin{array}[]{cc}V^{2/3}_{1}&\sqrt{2}V^{5/3}_{1}\\ \sqrt{2}V^{-1/3}_{1}&-V^{2/3}_{1}\end{array}\right):(3,3,2/3)$		(23)

Exchange of these particles at tree-level, assuming leptoquark multiplets that are degenerate in mass, generates the following effective Lagrangian

	$\displaystyle{\cal L}_{eff}$	$\displaystyle=\frac{\lambda^{ij}_{LS_{0}}\lambda^{*kl}_{LS_{0}}}{2m_{S_{0}}^{2}}\left(\bar{d}_{Lk}\gamma_{\mu}d_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+\bar{u}_{Lk}\gamma_{\mu}u_{Li}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}-\bar{u}_{Lk}\gamma_{\mu}d_{Li}\bar{e}_{L_{l}}\gamma^{\mu}\nu_{Lj}-\bar{d}_{Lk}\gamma_{\mu}u_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}e_{Lj}\right)$
		$\displaystyle+\frac{\lambda^{ij}_{LS_{1}}\lambda^{*kl}_{LS_{1}}}{2m_{S_{1}}^{2}}\left(\bar{d}_{Lk}\gamma_{\mu}d_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+2\bar{d}_{Lk}\gamma_{\mu}d_{Li}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}+2\bar{u}_{Lk}\gamma_{\mu}u_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+\bar{u}_{Lk}\gamma_{\mu}u_{Li}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}\right)$
		$\displaystyle-\frac{\lambda^{kj}_{LV_{1}}\lambda^{*il}_{LV_{1}}}{m_{V_{1}}^{2}}\left(2\bar{d}_{Lk}\gamma_{\mu}d_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+\bar{d}_{Lk}\gamma_{\mu}d_{Li}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}+\bar{u}_{Lk}\gamma_{\mu}u_{Li}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+2\bar{u}_{Lk}\gamma_{\mu}u_{Li}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}\right)$
		$\displaystyle-\frac{\lambda^{kj}_{L\tilde{S}_{1/2}}\lambda^{*il}_{L\tilde{S}_{1/2}}}{2m_{S_{1/2}}^{2}}\left(\bar{d}_{Rk}\gamma_{\mu}d_{Ri}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+\bar{d}_{Rk}\gamma_{\mu}d_{Ri}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}\right)$
		$\displaystyle+\frac{\lambda^{ij}_{LV_{1/2}}\lambda^{*kl}_{LV_{1/2}}}{m_{V_{1/2}}^{2}}\left(\bar{d}_{Rk}\gamma_{\mu}d_{Ri}\bar{\nu}_{L_{l}}\gamma^{\mu}\nu_{Lj}+\bar{d}_{Rk}\gamma_{\mu}d_{Ri}\bar{e}_{L_{l}}\gamma^{\mu}e_{Lj}\right).$		(24)

If the fermions in Eq. 24 are in their weak eigenstate basis, rotation to the mass eigenstate basis will introduce mixing angles. Here we will work with $\lambda^{ij}_{I}$ defined in a basis in which the down-type fermions are already mass eigenstates [29]. The $\nu$ and up-type quarks need to be further rotated by $u_{Lk}=(V^{*}_{KM})_{km}u_{Lm}$, and $\nu_{Lk}=(V_{PMNS})_{km}\nu_{Lm}$ respectively. However, since the neutrino flavour is not measured, working in either their weak or mass basis yields the same results. Collecting the Wilson coefficients for Eq. 6 gives,

	$\displaystyle C_{L}^{ij}$	$\displaystyle=\frac{\pi}{\sqrt{2}\alpha G_{F}V_{tb}V_{ts}^{*}}\left(\frac{\lambda^{3j}_{LS_{0}}\lambda^{*2i}_{LS_{0}}}{2m_{S_{0}}^{2}}+\frac{\lambda^{3j}_{LS_{1}}\lambda^{*2i}_{LS_{1}}}{2m_{S_{1}}^{2}}-2\frac{\lambda^{2j}_{LV_{1}}\lambda^{*3i}_{LV_{1}}}{m_{V_{1}}^{2}}\right),$
	$\displaystyle C_{R}^{ij}$	$\displaystyle=C_{9^{\prime}}^{ij}=-C_{10^{\prime}}^{ij}=\frac{\pi}{\sqrt{2}\alpha G_{F}V_{tb}V_{ts}^{*}}\left(-\frac{\lambda^{2j}_{L\tilde{S}_{1/2}}\lambda^{*3i}_{L\tilde{S}_{1/2}}}{2m_{S_{1/2}}^{2}}+\frac{\lambda^{3j}_{LV_{1/2}}\lambda^{*2i}_{LV_{1/2}}}{m_{V_{1/2}}^{2}}\right),$
	$\displaystyle C_{9}^{ij}$	$\displaystyle=-C_{10}^{ij}=\frac{\pi}{\sqrt{2}\alpha G_{F}V_{tb}V_{ts}^{*}}\left(\frac{\lambda^{3j}_{LS_{1}}\lambda^{*2i}_{LS_{1}}}{m_{S_{1}}^{2}}-\frac{\lambda^{2j}_{LV_{1}}\lambda^{*3i}_{LV_{1}}}{m_{V_{1}}^{2}}\right).$		(25)

All of these leptoquarks contribute to $R^{\nu}_{K^{(*)}}$ but their contributions are correlated with different modes [30, 31, 32, 33]. We begin with the lepton flavour number violating case which adds incoherently to the SM values for $R^{\nu}_{K^{(*)}}$. There are several CLFV modes with existing experimental upper bounds and we list them in Table 3. The corresponding predictions using Eq. 25 are

	$\displaystyle\mathcal{B}(B_{s}\to e^{\pm}\mu^{\mp})$	$\displaystyle\approx.98\left(C_{10}^{\mu e~{}2}+C_{10^{\prime}}^{e\mu~{}2}+C_{10^{\prime}}^{\mu e~{}2}+C_{10}^{e\mu~{}2}\right)\times 10^{-10}$
	$\displaystyle\mathcal{B}(B_{s}\to\mu^{\pm}\tau^{\mp})$	$\displaystyle\approx.22\left(C_{10}^{\mu\tau~{}2}+C_{10^{\prime}}^{\tau\mu~{}2}+C_{10^{\prime}}^{\mu\tau~{}2}+C_{10}^{\tau\mu~{}2}\right)\times 10^{-7}$
	$\displaystyle\mathcal{B}(B^{+}\to K^{+}e^{-}\mu^{+})$	$\displaystyle\approx 0.18\left((C_{10}^{\mu e}+C_{10^{\prime}}^{\mu e})^{2}+(C_{9}^{\mu e}+C_{9^{\prime}}^{\mu e})^{2}\right)\times 10^{-7}$
	$\displaystyle\mathcal{B}(B^{+}\to K^{+}\tau^{+}e^{-})$	$\displaystyle\approx 0.114\left((C_{10}^{e\tau}+C_{10^{\prime}}^{e\tau})^{2}+(C_{9}^{e\tau}+C_{9^{\prime}}^{e\tau})^{2}\right)\times 10^{-7}$
	$\displaystyle\mathcal{B}(B^{+}\to K^{+}\tau^{+}\mu^{-})$	$\displaystyle\approx\left(0.117(C_{10}^{\mu\tau}+C_{10^{\prime}}^{\mu\tau})^{2}+0.111(C_{9}^{\mu\tau}+C_{9^{\prime}}^{\mu\tau})^{2}\right)\times 10^{-7}$
	$\displaystyle\mathcal{B}(B^{+}\to K^{*+}e^{-}\mu^{+})$	$\displaystyle\approx 0.18\left((C_{10}^{\mu e}+C_{10^{\prime}}^{\mu e})^{2}+(C_{9}^{\mu e}+C_{9^{\prime}}^{\mu e})^{2}\right)\times 10^{-7}$
	$\displaystyle\mathcal{B}(B^{0}\to K^{*0}e^{-}\mu^{+})$	$\displaystyle\approx 0.18\left((C_{10}^{\mu e}+C_{10^{\prime}}^{\mu e})^{2}+(C_{9}^{\mu e}+C_{9^{\prime}}^{\mu e})^{2}\right)\times 10^{-7}$		(26)

The best current experimental bounds on these modes as given in [20] are listed in Table 3 along with the constraints they impose on the Wilson coefficients taken one non-zero at a time.