spacing=nonfrench
RisGraph: A Real-Time Streaming System for Evolving Graphs to Support Sub-millisecond Per-update Analysis at Millions Ops/s
Abstract.
Evolving graphs in the real world are large-scale and constantly changing, as hundreds of thousands of updates may come every second. Monotonic algorithms such as Reachability and Shortest Path are widely used in real-time analytics to gain both static and temporal insights and can be accelerated by incremental computing. Existing streaming systems adopt the incremental computing model and achieve either low latency or high throughput, but not both. However, both high throughput and low latency are required in real scenarios such as financial fraud detection.
This paper presents RisGraph, a real-time streaming system that provides low-latency analysis for each update with high throughput. RisGraph addresses the challenge with localized data access and inter-update parallelism. We propose a data structure named Indexed Adjacency Lists and use sparse arrays and Hybrid Parallel Mode to enable localized data access. To achieve inter-update parallelism, we propose a domain-specific concurrency control mechanism based on the classification of safe and unsafe updates.
Experiments show that RisGraph can ingest millions of updates per second for graphs with several hundred million vertices and billions of edges, and the P999 processing time latency is within 20 milliseconds. RisGraph achieves orders-of-magnitude improvement on throughput when analyses are executed for each update without batching, and performs better than existing systems with batches of up to 20 million updates.
1. Introduction
Graphs have currently drawn broad interests in both academic and industrial communities. Real-world graphs are evolving graphs in general, for example, social networks, financial networks, and web graphs. Evolving graphs are continuously changing (Ntoulas et al., 2004; Garg et al., 2009; Chen et al., 2009; Armstrong et al., 2013), as the updates could come at a high rate, reaching tens or hundreds of thousands of updates per second (twi, [n.d.]; Qiu et al., 2018; tma, [n.d.]).
Evolving graphs include both static and temporal information and can provide valuable insights with analytical algorithms. For example, in some e-commerce or social network analytics (Erling et al., 2015; Jiang et al., 2016; Khalil et al., 2016; Cen et al., 2020), users are modeled into vertices, and the trust relationships between them are modeled into weighted edges. Analyzing shortest paths can discover suspicious users within short distances (Khalil et al., 2016) from known malicious users. Incoming interactions or transactions are converted into a series of graph updates. Updates modify the graph and change the analysis results. High throughput is essential to keep pace with incoming updates (reaching hundreds of thousands of updates per second). Meanwhile, real-time analysis is necessary to detect suspicious users and prevent fraud or harmful information from these users in time (typically within tens of milliseconds (Qiu et al., 2018)).
Monotonic algorithms (Vora et al., 2017) are commonly used (Xu and Chen, 2004; Erling et al., 2015; Khalil et al., 2016; Wang et al., 2019) in evolving graph analytics, which include Reachability, Breadth-First Search, Shortest Path, Connected Components, and Min/Max Label Propagation. It requires scanning a large amount of data or even the entire graph to recompute monotonic algorithms on each snapshot of evolving graphs. For example, the processing time of the shortest path is of the order of seconds on graphs with millions of vertices and billions of edges (Kumar and Huang, 2019; Shun and Blelloch, 2013; Zhu et al., 2016). The idea of incremental computing can accelerate monotonic algorithms by leveraging previous results to reduce redundant computing.
Existing Solutions.
In recent years, several incremental graph computing models (McSherry et al., 2013; Shi et al., 2016; Sengupta et al., 2016; Vora et al., 2017) are proposed, which work well on monotonic algorithms. Among them, KickStarter (Vora et al., 2017) and Differential Dataflow (Murray et al., 2013; McSherry et al., 2013) are state-of-the-art representatives. KickStarter proposes an incremental graph computing model for monotonic algorithms, while Differential Dataflow presents a generalized incremental model without graph-awareness. They effectively shorten the processing time of monotonic algorithms from a few seconds to milliseconds when updating a single edge on power-law graphs with billions of edges, such as social networks (Mislove et al., 2007), web graphs (Albert et al., 1999), and financial graphs (Qiu et al., 2018).
However, for graph analytics of Internet-scale, the performance of existing systems still have a large gap to fulfill the throughput requirement which would demand ingesting hundreds of thousands of updates every second. KickStarter and Differential Dataflow can handle only about one thousand updates per second if they analyze every time the graph changes (per-update analysis). They rely on batching to trade latency for higher throughput, benefiting from larger concurrency and lower overheads. Moreover, they provide a batch-update mode to further optimize throughput, which reduces the frequency of analyzing and produces only one aggregated final result for each batch.
Unfortunately, the high throughput of KickStarter and Differential Dataflow relies on large batches and amplifies latency, even if batch-update mode is enabled. We take Breadth-First Search (BFS) on Twitter-2010 (Leskovec and Krevl, 2014) as an example. To meet 20 ms latency requirement (real-time analysis (Qiu et al., 2018)), the throughput of these systems is only about 1K ops/s. To provide throughput of 100K ops/s, they need to batch more than 20K updates, and the average processing time grows to more than 150 ms. Therefore, existing streaming graph systems cannot simultaneously fulfill latency and throughput requirements by batching.
Meanwhile, batch-update mode processes a batch of updates as a whole, skipping intermediate states which are potentially useful in some scenarios such as financial fraud detection (Qiu et al., 2018) and transaction conformity (Barga et al., 2007; Meehan et al., 2015).
Compared to batching, per-update analysis is friendly to latency, produces up-to-date results, and provides the most accurate and detailed information. It only leaves one open question: how to provide high throughput in per-update analysis.
Open Challenges.
A per-update system faces challenges of combining two kinds of workloads in a fine-grained manner for each update, which include modifying the graph structure and incrementally analyzing based on the updated graph. Different from batch-update systems (Cheng et al., 2012; Sengupta et al., 2016; Vora et al., 2017; Sheng et al., 2018; Mariappan and Vora, 2019), per-update analysis does not ingest multiple updates as a whole or analyzes them together. Therefore, per-update systems cannot reuse existing techniques designed for batching or benefit from batched updates, such as amortizing overheads across multiple updates.
The goal of high throughput and low latency requires the system to efficiently conduct both kinds of workloads. When modifying the graph, it needs to apply each update to a data structure and provide an updated graph ready for analysis in a short time. To enable real-time analysis for each update, the system requires a graph-aware design that leverages the locality of individual updates, rather than that utilizes the typical technique of entire graph scanning. Besides, it requires a new mechanism to enable parallelism for per-update processing, which is also important to achieve high throughput without batching.
Guiding Ideas.
We propose two guiding ideas to address the challenge, localized data access and inter-update parallelism.
The idea of localized data access comes from the observation that commonly used graph-aware techniques for graph streaming systems still require unnecessary entire graph scans (Sengupta et al., 2016; Vora et al., 2017; Kumar and Huang, 2019; Mariappan and Vora, 2019). If we can avoid these scans by only accessing the necessary vertices affected by updates, we will gain much better performance, thus we propose to use data structures called Indexed Adjacency Lists and sparse arrays to enable localized accesses.
We further improve throughput by processing updates in parallel (inter-update parallelism) while maintaining the per-update semantics to applications. We propose an algorithm to identify updates that can be safely executed in parallel and execute the rest of updates one by one to keep low latency, as well as atomicity, isolation, and correctness of per-update analysis.
Contributions.
We summarize our contributions as follows.
-
•
We propose a data structure for graphs named Indexed Adjacency Lists, which provides efficient analytical performance and supports microsecond-level updates. It consists of a dynamic array of arrays and indexes of edges, to store edges in a continuous memory layout and also ensure average O(1) time complexity for each update (Section 3.1).
-
•
During incremental computing, we track active vertices and updated results with sparse arrays to eliminate redundant overheads of scanning all the vertices and achieve localized data access. For better analytical performance, we further propose Hybrid Parallel Mode, which adaptively uses edge-parallel and vertex-parallel strategies through a linear classifier (Section 3.2).
-
•
We propose a domain-specific concurrency control mechanism to support parallelism among multiple updates with low overheads, thus improve throughput. It leverages the incremental model and intermediate data structures to identify non-conflicting updates before processing them (Section 4).
Based on the above core ideas, we design and implement a real-time graph streaming system for monotonic algorithms called RisGraph. For graphs with hundreds of millions of vertices and billions of edges, RisGraph can ingest millions of updates per second on a single commodity machine for monotonic algorithms like Breadth-First Search (BFS), Single Source Shortest Path (SSSP), Single Source Widest Path (SSWP) and Weakly Connected Component (WCC). Meanwhile, RisGraph ensures that more than 99.9% updates can be processed within 20 milliseconds without breaking per-update analysis semantics. It provides 2-4 orders of magnitude improvement over existing solutions for per-update analysis. Besides, it performs better than KickStarter and Differential Dataflow in batch-update scenarios with up to 20M updates per batch.
2. High-Level Architecture

RisGraph adopts a four-tier architecture, as shown in Figure 1.
The top layer is an interactive interface that allows users to interact with RisGraph in a fine-grained manner. Users submit graph updates to RisGraph and receive analysis results for each update.
A scheduler stands below the interface to control the execution of updates from multiple clients. It monitors processing latency and dynamically schedules updates based on statistics. The goal of the scheduler is to fulfill predefined expected tail latency and achieve balanced trade-off between throughput and latency.
At the core of RisGraph is the localized execution engine, which processes each update from the scheduler through localized data accesses (see Section 3). It includes a graph updating engine and a graph computing engine. Graph updating engine can apply updates to the graph concurrently. After updating the graph, the graph computing engine performs parallel incremental computing to synchronize analysis results based on the latest graph structure.
Independent from the execution engine, a standalone concurrency control module ensures per-update analysis semantics, as well as correctness, atomicity and isolation. To achieve inter-update parallelism, we propose a domain-specific mechanism which picks out non-conflicting updates before execution (see Section 4).
An in-memory store as an underlying layer manages all necessary data, including graph store, tree and value store, and history store. Graph store maintains the current graph and supports efficient modification and analysis. To support incremental computing, tree and value store handles the latest and temporary computing states for each vertex. History store traces all result changes by versioning, to generate consistent result views for each update.
Finally, monotonic algorithms define the analysis tasks maintained by RisGraph. Algorithm API in RisGraph makes graph monotonic algorithms easy to write. The execution engine and concurrency control module leverage Algorithm API to perform incremental computing.
| init_val | (vid) | init_value |
|---|---|---|
| gen_next | (edge, src_value) | next_value |
| need_upd | (vid, cur_value, next_value) | is_needed |
| ins/del_edge | (edge) | version_id |
| ins/del_vertex | (vertex_id) | version_id |
| txn_updates | (updates) | version_id |
| get_value | (version_id, vertex_id) | value |
| get_parent | (version_id, vertex_id) | edge |
| get_current_version | ( ) | version_id |
| get_modified_vertices | (version_id) | vertex_ids |
| release_history | (version_id) |
| BFS | SSSP | SSWP | WCC | |
|---|---|---|---|---|
| init_val | vid | |||
| gen_next | src_val | |||
| need_upd |
Algorithm API.
RisGraph focuses on monotonic algorithms. Monotonic algorithms employ intermediate values to monotonically approximate and finally reach accurate results from initial values. After applying edge insertions, computing can start from current results instead of initial values. These results are valid intermediate values and save computation by giving a closer approximation. KickStarter (Vora et al., 2017) further discovers that all known monotonic graph algorithms, such as Reachability, Shortest Path, Weakly Connected Components, Widest Path, and Min/Max Label Propagation, can be incrementally computed by maintaining a dependency tree (or forest). The dependency tree shows a vertex’s result depends on its parent and the edge between them. Deleting an edge on the dependency tree will invalidate the subtree rooted at the destination. Trimmed approximation technique proposed by KickStarter can generate valid approximations for invalidated vertices.
RisGraph adopts the dependency tree model and the trimmed approximation technique. Similar to KickStarter, RisGraph provides user-friendly API to describe monotonic algorithms as shown in the upper part of Table 1. init_val defines initial values for each vertex. gen_next uses an edge and its source vertex to generate a next possible value for its destination vertex. need_upd decides whether a vertex’s value should be updated. Table 2 shows implementation of Breadth-First Search, Single Source Shortest Path, Single Source Widest Path and Weakly Connected Component.
Interactive API.
RisGraph supports vertex/edge insertions and deletions, with guarantees of correctness, atomicity, isolation and per-update analysis semantics. For each operation, RisGraph responds with a view of the results afterwards. Result views are versioned snapshots maintained by RisGraph, to enable consistent read operations on different vertices. Optionally, RisGraph provides durability with write-ahead logs (WAL) and also sequential consistency for better user-friendliness. Besides single edge/vertex updates, RisGraph can also handle transactions (see Section 4).
The lower part of Table 1 lists RisGraph’s Interactive API. Users call ins / del_edge and ins / del_vertex to send updates to RisGraph. txn_updates is the API to describe a transaction or an atomic batch of updates, which is a contiguous sub-sequence of a stream that must be treated as an indivisible unit (Meehan et al., 2015). After RisGraph processes an update or a transaction, it will return a version ID of the result snapshot. Users can get consistent results and dependency trees according to the version ID and vertex ID by get_value and get_parent. RisGraph supports querying the current version (get_current_version) and vertices that have been modified in any specific version (get_modified_vertices). RisGraph holds historical snapshots for each session, and requires users to actively report the latest unused versions for garbage collections (GC). release_history marks previous snapshots before its version ID as no longer used for its session.

Example of RisGraph API.
Figure 2 shows an example of detecting suspicious users by Shortest Path algorithm. Two interactive API calls generate three result versions. At the bottom, Algorithm API calls incrementally maintain the shortest path to Vertices 4 and 5. The example also shows that detailed information provided by per-update analysis is important. It is able to find Vertex 4 suspicious when an edge is inserted in Version 1 under per-update analysis. However, it would miss the detection with batch-update mode if the system skips Version 1 and only checks Version 2.
3. Localized Data Access
Different from batch-update systems, per-update analysis systems need to perform analysis for each update, thus cannot amortize the overhead of batch processing among multiple updates. To address this challenge, we design RisGraph with localized data access, which means only accessing necessary vertices, including the vertices with results to update and the neighbours of the updated vertices when calculating new results. The rationale behind localized data access is that incremental computing only needs to access part of the vertices, but improper data structures would require partial computing to access the entire graph. The system should use proper data structures to avoid unnecessary operations.
RisGraph provides 2-4 orders of magnitude improvement in our evaluation by both utilizing graph awareness and localizing data access. We make new design for the graph store and the graph computing engine, to eliminate redundant scanning.
3.1. Graph Store
For per-update analysis, graph store needs to handle each individual update and provide an updated graph ready for efficient analysis in a short time. Existing literature (Zhu et al., 2020; Kumar and Huang, 2019) has shown that using an array of arrays to store adjacency lists can support updates and provide comparable computing performance of compressed sparse row (CSR). Graph streaming systems such as GraphOne (Kumar and Huang, 2019), GraphBolt (Mariappan and Vora, 2019) and KickStarter also adopt an array of arrays as their graph store. However, their data structures cannot satisfy localized data access because they scan all the vertices when applying updates, even if processing a single update. With bloom filters, LiveGraph (Zhu et al., 2020) supports fine-grained edge insertions well but suffers from scanning edges on hubs (the high-degree vertices) when deleting edges.
Indexed Adjacency Lists.
RisGraph proposes a data structure named Indexed Adjacency Lists as shown in Figure 3, which uses an array of arrays to store edges for efficient analyzing and also maintains indexes of edges to address the shortcomings of the existing approaches. In RisGraph, each vertex has a dynamic array (doubling capacity when full) to store its outgoing edges, including destination vertex IDs and edge data. Arrays ensure that all the outgoing edges of a vertex are continuously stored, which is critical for efficient analysis (Zhu et al., 2020). However, arrays suffer from edge lookups by scanning for fine-grained updates. To accelerate lookups, RisGraph maintains Key-Value pairs of DstVidOffset for edges, indicating edge locations in arrays. Indexes are created only for vertices whose degree is larger than a threshold, providing a trade-off between memory consumption and lookup performance by filtering out low-degree vertices in power-law graphs (see Section 5).
RisGraph uses Hash Table as the default indexes because our data structure with Hash Table provides an average time complexity for each update. Also, indexes do not hurt RisGraph’s analyzing performance because the graph computing engine can directly access adjacency lists without involving indexes.
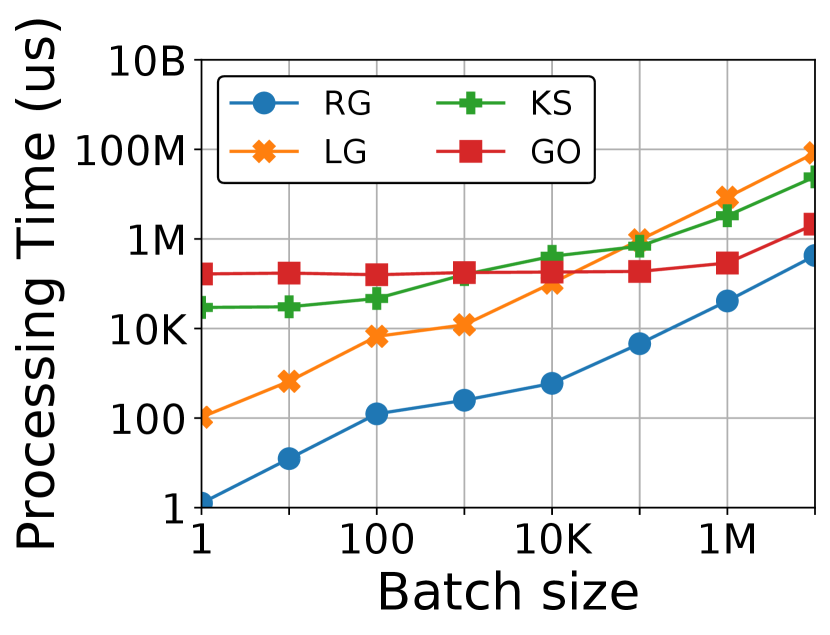
Figure 4 shows the performance of graph store when processing on Twitter-2010. The experimental setup is the same as Section 6. For insertions and deletions of an edge, the average latency for updating the graph store of RisGraph is several microseconds. Because of the significant improvement in performance, it is worthy of adding indexes in RisGraph’s data structure, at the cost of about 3.25x memory footprints of the raw data.
Under single edge updates, RisGraph’s graph store outperforms KickStarter and GraphOne more than thousands of times, thanks to the elimination of overheads on scanning vertices. Compared to LiveGraph, RisGraph reduces the average latency of edge insertions by 89.7% and deletions by 98.8%. The indexes of RisGraph can directly locate edges without scanning, which is friendly to deletions and also solves false-positive issue in LiveGraph (e.g. scanning average 541 edges per edge insertion on Twitter-2010). For batch updates, it is interesting to see that RisGraph performs better than other systems when the batch size does not exceed 100K.


3.2. Graph Computing Engine
After updating the graph, the incremental computing can be expressed by the vertex-centric model (Malewicz et al., 2010). Some optimizations on vertex-centric frameworks have been widely discussed, for example, various methods in parallelization schemes, traversal directions, and data layouts. They target the optimization of computing on the whole graph, so the designs and trade-offs do not fully meet incremental graph computing. We focus on localizing data access to fit in the incremental computing scenario.
Sparse Arrays.
In vertex-centric graph computing, the most commonly used operation is the push operation (Beamer et al., 2012; Besta et al., 2017). It iteratively performs on active vertices, whose states need to propagate. In each iteration, the push operation traverses the edges of the active vertices, updates the state of the destination vertices, and activates some destination vertices for the next iteration.
Recent graph processing systems (Zhu et al., 2016; ZhangYunming et al., 2018) and graph stores (Kumar and Huang, 2019; Zhu et al., 2020) prefer dense arrays or bitmaps to store active vertices because dense representations perform better than sparse arrays in graph computing. Figure 5 shows an example of dense array and sparse array. KickStarter also uses bitmaps, however, checking the entire vertex set and clearing the bitmaps are expensive for incremental computing. For example, clearing and checking bitmaps take KickStarter 90.3% of the BFS computation time on Twitter-2010.

For per-update analysis and incremental computing, sparse arrays can avoid accessing unnecessary vertices and reduce the average computing time from more than 50 ms to a few microseconds. In other cases, they can still improve computing performance when the batch-size is less than 200K on Twitter-2010. The reason is that sparse arrays are not optimal, but still acceptable for many active vertices or even the entire set (Shun and Blelloch, 2013). For example, to compute BFS on Twitter-2010 directly instead of incrementally, it takes RisGraph 2.21 s, while it takes GraphOne 0.76 s with dense arrays.
In summary, sparse arrays provide orders of magnitude improvement for per-update analysis and handle most batch sizes well. Meanwhile, sparse arrays are also acceptable for corner cases or even whole-graph analysis. Taking BFS on Twitter-2010 as an example, RisGraph’s performance only drops by 26.6% with batches of 200M edges and drops by 65.6% when re-computing BFS. Therefore, we choose sparse arrays to store active vertices.
We also manage to localize data access in other parts of the computation. For example, incremental computing relies on the previous version of results. In our implementation, we use sparse arrays to track updates on results, while KickStarter copies the entire vertex set for every new iteration of analysis.


Hybrid Parallel Mode.
With sparse arrays, there are two parallel modes for push operations, vertex-parallel and edge-parallel. Vertex-parallel takes active vertices as parallel units, while edge-parallel is fine-grained that parallelizes across all edges instead of just vertices, as shown in Figure 6. A common conclusion in graph computing is that vertex-parallel is always better than edge-parallel (ZhangYunming et al., 2018). However, edge-parallel sometimes outperforms vertex-parallel in incremental computing, especially considering skewed distributions of degrees in power-law graphs. Edge-parallel loses some locality of edges, but can provide more parallelism and better load balance when the number of active vertices is small.
Figure 7 shows the results of comparing edge-parallel and vertex-parallel on the UK-2007 (Boldi and Vigna, 2004; Boldi et al., 2011) dataset running four different algorithms (BFS, SSSP, SSWP and WCC). The x-axis is the number of active vertices, and the y-axis is the out-degrees of active vertices. We average the time of push operations, and only keep the results where the difference is more significant than 20% (filtering out 32% results). Red dots indicate where edge-parallel outperforms, and blue crosses show that where vertex-parallel wins. When there are fewer active vertices and more active edges (top left corner of the figure), edge-parallel is better than vertex-parallel.
We integrate edge-parallel and vertex-parallel by a linear classifier (the black straight line in Figure 7), which is trained by linear regression. In our evaluations, the hybrid mode outperforms 24.2% than the commonly used vertex-parallel only mode.
4. Inter-update Parallelism
RisGraph has significantly cut the average processing time of per-update analysis by localized data access to about one-thousandth of the existing systems, which naturally turn into about 1000 throughput improvement (see Section 6.4 for evaluation). However, the current design of single writer mechanism processes updates one by one under per-update analysis and limits RisGraph’s throughput because incremental computing depends on the previous results. To further improve the throughput, we investigate how to process updates in parallel among multiple clients or user sessions while preserving the correctness and analysis frequency.
A general approach is to employ transaction techniques from databases for parallel updates and analysis. Concurrency control mechanisms provide ACID properties and guarantee the correctness by serializable isolation. Nevertheless, general read/write-set based concurrency control mechanisms are not practical in our scenario. When processing power-law graphs, the sizes of read/write sets are much larger than typical transaction sizes in online transaction processing (OLTP) databases. For example, the average size of read/write sets exceeds one hundred and sometimes reaches millions, when incrementally analyzing shortest paths on UK-2007.
Observation.
| Graph Dataset | Abbr. | Vertices | Edges | Temporal | Type | Root | Visited |
|---|---|---|---|---|---|---|---|
| HepPh (Rossi and Ahmed, 2015) | PH | 281K | 4.60M | ✓ | Collab. | 1 | 98% |
| Wiki (Rossi and Ahmed, 2015) | WK | 2.13M | 9.00M | ✓ | Int. | 0 | 89% |
| Flickr (Rossi and Ahmed, 2015) | FC | 2.30M | 33.1M | ✓ | Social | 1 | 82% |
| StackOverflow (Leskovec and Krevl, 2014) | SO | 2.60M | 63.5M | ✓ | Int. | 0 | 78% |
| BitCoin (Rossi and Ahmed, 2015) | BC | 24.6M | 123M | ✓ | Txn. | 2 | 49% |
| SNB-SF-1000 (Erling et al., 2015) | SB | 3.14M | 202M | ✓ | Social | 0 | 84% |
| LinkBench (Armstrong et al., 2013) | LB | 128M | 560M | ✓ | Social | 0 | 26% |
| Twitter-2010 (Leskovec and Krevl, 2014) | TT | 41.7M | 1.47B | Social | 0 | 83% | |
| Subdomain (noa, [n.d.]c) | SD | 102M | 2.04B | Web | 0 | 67% | |
| UK-2007 (Boldi and Vigna, 2004; Boldi et al., 2011) | UK | 106M | 3.74B | Web | 0 | 91% |
| BFS | SSSP | SSWP | WCC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10% | 50% | 90% | 10% | 50% | 90% | 10% | 50% | 90% | 10% | 50% | 90% | |
| PH | 0.03 | 0.03 | 0.01 | 0.03 | 0.03 | 0.01 | 0.02 | 0.04 | 0.03 | 0.04 | 0.02 | 0.01 |
| WK | 0.07 | 0.06 | 0.11 | 0.07 | 0.05 | 0.13 | 0.07 | 0.04 | 0.12 | 0.13 | 0.10 | 0.10 |
| FC | 0.00 | 0.01 | 0.06 | 0.00 | 0.01 | 0.06 | 0.00 | 0.01 | 0.05 | 0.11 | 0.04 | 0.03 |
| SO | 0.07 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.08 | 0.04 | 0.05 |
| BC | 0.00 | 0.10 | 0.15 | 0.00 | 0.11 | 0.18 | 0.00 | 0.09 | 0.15 | 0.45 | 0.47 | 0.50 |
| SB | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.02 | 0.11 | 0.04 | 0.03 |
| LB | 0.00 | 0.03 | 0.09 | 0.00 | 0.03 | 0.09 | 0.00 | 0.03 | 0.09 | 0.22 | 0.16 | 0.12 |
| TT | 0.00 | 0.03 | 0.02 | 0.00 | 0.04 | 0.02 | 0.00 | 0.03 | 0.02 | 0.18 | 0.03 | 0.01 |
| SD | 0.00 | 0.04 | 0.03 | 0.00 | 0.04 | 0.03 | 0.00 | 0.03 | 0.03 | 0.23 | 0.05 | 0.03 |
| UK | 0.00 | 0.02 | 0.02 | 0.00 | 0.02 | 0.02 | 0.00 | 0.02 | 0.02 | 0.19 | 0.03 | 0.02 |
According to the incremental computing model, the results of all vertices only depend on the edges on the dependency tree. Since each vertex has at most one parent in the dependency tree, there are at most (number of vertices) edges on the tree, rather than (total edges in the graph). The other edges are irrelevant to the results, therefore, the modification of these edges will not change any result.
This fact inspires us and leads to a natural question, how much the updates will change the results. We analyze four algorithms (BFS, SSSP, SSWP and WCC) on ten graphs listed in Table 4. We also vary the number of initially loaded edges (), including 10%, 50% and 90% of edges, to show the effect of the average degree (). The method of generating updates and varying degrees is the same as the evaluation in Section 6. Table 4 also enumerates the roots selection and the percentage of visited vertices from the root for BFS, SSSP and SSWP with 90% edges.
We find that only a small part of updates change the results for most cases, as shown in Table 4. The proportion of updates which modify the results is less than 20% in 115 combinations of algorithms and datasets (120 experiments in total). In 100/120 experiments, the proportion is less than 10%. 77/120 experiments show that less than 5% updates modify results.
The observation guides us to propose a domain specific concurrency control mechanism for monotonic algorithms to avoid tracing memory accesses. We name the updates which do not change any results as safe updates. Correspondingly, unsafe updates modify results or the dependency tree. If we identify safe updates and only process them in parallel, not only can we preserve the correctness of per-update analysis, but also improve the throughput.
Classification of Updates.
Figure 8 shows an example of safe updates and unsafe updates. Dark red arc arrows in the figure represent the dependency tree of the selected monotonic algorithm. Formally, given a directed graph and the current dependency tree , an update to the graph is considered safe if and only if it fits in the following categories:
(1) ins_vertex(v) or del_vertex(v) for any vertex . The operation is valid only when is a isolated vertex (users must first delete all edges related to before deleting ), thus will not affect the results in monotonic algorithms (Vora et al., 2017).
(2) del_edge(e) for , such as the edge . These deletions will not modify the dependency tree, and therefore will not change any result. In contrast, deleting or will invalidate the states of or respectively.
(3) ins_edge(e) for when need_upd(vt, vt.data, gen_next(e, vs.data)) is false. Taking edge insertion as an example, we first compute the new result of the destination from the source and the new edge . The insertion is safe if cannot produce a better result than the current result of .
All other types of updates are unsafe. In summary, the classification only depends on updating edges, sources and destinations. The classification of updates is light-weight in RisGraph because it does not require any scanning.
Epoch Loop Schema and Inter-update Parallelism.


Then we design an epoch loop schema, which takes advantage of the parallelism brought by classification to improve throughput and ensure correctness. In each epoch, RisGraph processes all safe updates in parallel first and then handles all unsafe updates one by one. Figure 9 shows RisGraph’s epoch loop schema when processing updates from multiple sessions. There are six updates from three asynchronous sessions in the figure. RisGraph classifies the updates into safe (S), unsafe (U), and next-epoch (N). After an unsafe update, all updates in the same session are next-epoch updates, which means they should be re-classified in the next epoch because any unsafe operation could modify the results and change classifications of updates behind it. RisGraph processes multiple safe updates in parallel, exploiting inter-update parallelism. In contrast, RisGraph handles unsafe updates one by one and performs parallel incremental computing (intra-update parallelism) for each update.
For better user-friendliness, RisGraph guarantees updates from a session will be executed by the same order of the updates and provides sequential consistency. However, it may lead to starvation. If some sessions keep producing safe updates, RisGraph will make unsafe updates starved. In order to solve the starvation and also provide predictable processing time, we design a scheduler for RisGraph. RisGraph’s scheduler controls the size of each epoch, and try to satisfy the user’s desired tail latency (processing-time latency (Karimov et al., 2018)) as much as possible, which is discussed in Section 5.
In our experiments (Section 6.2), RisGraph’s throughput is 14.1 better than the throughput without the inter-update parallelism, while the 99.9th percentile (P999) latency is under 20 ms. The results show that the epoch loop schema, inter-update parallelism, and scheduler can effectively optimize RisGraph’s throughput.
Supporting Transactions and Multiple Algorithms.
We have shown that RisGraph can support the situation where all updates are single vertex or edge updates, and only one algorithm is online in the system at a time. Sometimes, users also expect the support of transactions or atomic batches containing multiple updates and also running multiple algorithms at the same time. To support write transactions, we classify and process updates of a transaction as a whole. A write-only transaction is safe only when all of its write operations are safe, such as a transaction consisting of inserting a vertex and deleting the edge in Figure 8. As for read-write transactions, although they are not typical for streaming systems, RisGraph can still support them by treating them as unsafe transactions and processing them individually by blocking other sessions (just long-term unsafe updates in the epoch loops).
Similar to write-only transactions, when maintaining multiple algorithms simultaneously, an update is safe only when it is safe for every algorithm. The proportion of safe updates would decrease with larger transactions or more algorithms, which reduces the throughput brought from the inter-update parallelism. Compared with updates without being packed into transactions, RisGraph’s throughput reduces by 51.1% on average when the size of each transaction is 16. In any case, even if all transactions or updates are unsafe, localized data access can still provide thousands of times throughput of existing systems.
5. Implementation
Graph Store.
RisGraph proposes Indexed Adjacency Lists. Each vertex maintains its outgoing edges in an dynamic array (doubling capacity when full). Adjacency lists store directed edges, consist of the destination vertex IDs, the weight of each edge and the number of duplicated edges (the destination and the weight are both the same). RisGraph also stores a transpose graph required by the incremental model. Each vertex, whose degree is greater than a threshold, also contains an index, which represents the location of the edge in the list. The key of an edge is a pair of its destination vertex ID and its weight. The threshold provides a trade-off between memory consumption and lookup performance. We search it in the power of two to maximize performance divided by the square root of the memory usage (more performance-oriented). In our implementations, the threshold is 512. Users can search a better threshold based on their data, hardware, and requirements.
When inserting an edge, RisGraph first checks whether the edge exists in adjacency lists from edge indexes. If the edge exists, RisGraph only modifies the number of duplicated edges; otherwise RisGraph appends the new edge to the adjacency list and updates the index. For deleting an edge, RisGraph modifies the number of edges after searching from indexes. RisGraph keeps tomb (deleted) edges first, and recycle them and their indexes when doubling the adjacency list. RisGraph recycles the vertex IDs of deleted vertices into a pool. When inserting vertex, RisGraph either uses an ID from the recycling pool or assigns a new vertex ID.
RisGraph uses Hash Table111Implemented by Google Dense Hashmap (https://bit.ly/3rWs6yr) and MurmurHash3 as the default indexes to obtain the average time complexity of insertions and deletions. There are also many alternative data structures that can replace Hash Table for indexes, such as BTree and ARTree (Leis et al., 2013) (the adaptive radix tree). According to the theoretical complexity and our experiments, the performance of Hash Table is the best in general. To maximize performance, we choose Hash Table by default although it is non-optimal in memory consumption. RisGraph can also utilize other data structures for indexes if the memory capacity is a constraint.
Tree and Value Store.
RisGraph stores dependency trees by parent pointer trees (Wikipedia contributors, 2019). Similar to KickStarter, each vertex maintains at most one bottom-up pointer to its parent on the dependency tree. It is efficient to classify updates by checking whether the updating edge is a bottom-up pointer on the dependency tree with parent pointer trees. During computing, modifications on parent pointer trees are also more lightweight than top-down pointer trees. With top-down pointers, updating the value of a vertex requires locking three vertices. On the contrary, parent pointer trees lock or atomically update the modified vertex only once.
History Store.
The history store consists of a doubly-linked list from new versions to old versions for each vertex, and sparse arrays for each version to trace modifications of the results. Linked lists are similar to version chaining in multi-versioned databases, which are generally efficient in practice (Wu et al., 2017).
The history store only maintains short-term historical information, to provide consistent snapshots of the results. Every second, RisGraph chooses the latest useless version among versions released by every session, marks the version and the previous versions as garbage, and then aggressively recycles them from sparse arrays. For linked lists, RisGraph performs lazy garbage collection, which means RisGraph only recycles garbage from the tail of a vertex’s linked list when a new version updates this vertex.
Graph Computing Engine.
RisGraph chooses sparse arrays to store active vertices and converts them to bitmaps only when performing pull operations (checking all incoming edges for each vertex). We create a separate sparse array for each thread, which helps eliminating the overhead of synchronization and contention among multiple threads.
For push operations, we propose a hybrid mode supported by a linear regression based classifier to adaptively choose the proper edge-parallel or vertex-parallel mode. In our implementation, we train the classifier based on UK-2007 dataset, and it works well on other graphs. In our evaluation, the hybrid mode reduces RisGraph’s computing time by 24.2% compared to vertex-parallel only mode, showing the effectiveness of the classifier. Users can also train the classifier by their datasets and algorithms. Online training would bring additional overhead, so we choose to fix the parameters first and leave online training as our future work.
Scheduler.
The purpose of the scheduler in RisGraph is to avoid starvation and also to achieve the highest possible throughput automatically under an expected tail latency. Avoidance of starvation has been discussed in Section 4, so we focus on how the scheduler improves throughput while maintaining the latency demand.
The scheduler would first try to pack as many safe updates in an epoch-loop as possible to maximize throughput. It may break the latency constraint without a latency control, so the scheduler uses two heuristics to abort parallel execution of safe updates and turns to process unsafe updates. One is when the waiting time of the earliest unsafe update in the queue almost exceeds the target latency. In our implementation, we set the target latency to 0.8 times the user-specified latency limitation. Another one is when the number of unprocessed unsafe updates reached a dynamic threshold. RisGraph adjusts the threshold based on historical information. If the proportion of qualified updates (under the latency limitation) is higher than the target after the last adjustment, the scheduler will slowly increase the threshold. Otherwise, if the proportion is lower than the goal, the scheduler will quickly decrease the threshold. In our implementation, the initial threshold is the number of physical threads, and RisGraph adjusts the threshold every three epoch-loops. RisGraph increases the threshold by 1% each time, and when decreasing, adjusts the threshold by 10%. Since the scheduler is self-adjusting, it can support various algorithms and datasets.
In our experiments, the scheduler can meet the latency requirement, and get a good trade-off between latency and throughput.
6. Evaluation
6.1. Experimental Setup
We evaluate RisGraph by four algorithms implemented by Algorithm API in Table 2, including Breadth-First Search (BFS), Single Source Shortest Path (SSSP), Single Source Widest Path (SSWP) and Weakly Connected Component (WCC), on ten graph datasets in Table 4. LinkBench (128M vertices) and LDBC SNB (SF1000) are interactive datasets from graph database benchmarks (Armstrong et al., 2013; Erling et al., 2015), consisting of a pre-populated graph and incoming updates. For the other datasets, we split the edge set similar to KickStarter, GraphBolt, and SAMS (Then et al., 2017), by pre-populating a part of edges and treating the other edges as updates. We load 90% edges first, select 10% edges as the deletion updates from loaded edges, and treat the remaining (10%) edges as the insertion updates. If datasets are timestamped, we choose the latest 10% as the insertion set and the oldest 10% as the deletion set; otherwise, we randomly select edges as updates. The ratio of insertions to deletions is 50% by default, and we alternately request insertions and deletions of each edge. We also name the entire pre-loaded graphs in LinkBench and SNB as graphs with 90% edges for alignment of the results.
We set up experiments on two dual-socket servers, running RisGraph and clients respectively. Each server has two Intel Xeon Gold 6126 CPU (12 physical cores per CPU), 576GB main memory, an Intel Optane P4800X 750GB SSD, an 100Gb/s Infiniband NIC, and runs Ubuntu 18.04 with Linux 4.15 kernel.
6.2. Performance of RisGraph
We evaluate the performance of RisGraph by a group of emulated synchronous users, similar to TPC-C (noa, [n.d.]b). Remote clients interact with RisGraph by RPCs. To eliminate the impact of the network, clients connect to RisGraph by Infiniband network and a light-weight RPC framework with the RDMA technique. Each client maintains multiple sessions, which represent emulated users. The users repeatedly send a single update and wait for the response. Here we focus on edge insertions and edge deletions because they can express all types of updates regarding edges and vertices.
Latency (more precisely, processing-time latency (Karimov et al., 2018)) is measured on the client side and defined as the elapsed time between the request and response. We calculate throughput by the total execution time and the number of updates. The latency requirement is that at least 99.9% of updates should receive responses in 20 milliseconds. Such a strict latency target requires the system to provide sufficient real-time ability. Updates in the evaluation are insertions and deletions with only a single edge, which evaluate the performance with the minimal granularity of updates and analysis.
All modules in RisGraph are enabled, including the write-ahead log, the scheduler and the history store. On the next page, Figure 10 indicates average latency and throughput when doubling the number of sessions from 48 (number of the hardware threads) until RisGraph cannot satisfy the target latency, which is up to 6144 (6448) sessions. Black crosses show where RisGraph breaks the latency limitation. With more sessions, RisGraph gets more opportunities to schedule and execute safe updates in parallel for each epoch, so RisGraph can get higher throughput.
Figure 10 lists detailed metrics when throughput reaches the peak. In Figure 10, T. represents throughput, while Mean and P999 are average latency and tail latency, respectively. RisGraph’s throughput reaches hundreds of thousands or millions of updates per second, meanwhile, the P999 latency is under 20 milliseconds. These results indicate that the designs of RisGraph can provide high throughput under per-update analysis.
RisGraph’s throughput is close to 100K ops/s without the inter-update parallelism, and can additionally improve by 15.5 for BFS, 9.93 for SSSP, 15.3 for SSWP, 17.1 for WCC, and 14.1 in overall when inter-update parallelism is enabled. Even if unsafe updates reach 49.7% of the updates (WCC on Bitcoin), it can still provide 3.25 speedup. The improvements show that the epoch loop schema, inter-update parallelism, and scheduler can effectively optimize the throughput for per-update analysis.

| BFS | SSSP | SSWP | WCC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T. (op/s) | Mean (us) | P999 (ms) | T. (op/s) | Mean (us) | P999 (ms) | T. (op/s) | Mean (us) | P999 (ms) | T. (op/s) | Mean (us) | P999 (ms) | |
| HepPh (PH) | 2.95M | 258.44 | 12.13 | 2.56M | 348.62 | 18.59 | 2.28M | 416.78 | 19.92 | 3.28M | 244.63 | 6.234 |
| Wiki (WK) | 1.42M | 492.96 | 10.34 | 794K | 883.53 | 10.33 | 1.20M | 1171.4 | 15.32 | 1.26M | 1124.2 | 8.384 |
| Flickr (FC) | 1.25M | 552.97 | 15.28 | 944K | 752.21 | 10.34 | 2.17M | 602.25 | 9.901 | 2.56M | 530.92 | 7.584 |
| StackOverflow (SO) | 1.86M | 747.43 | 19.89 | 1.93M | 1240.7 | 19.76 | 1.14M | 1260.6 | 18.75 | 2.55M | 893.12 | 17.00 |
| BitCoin (BC) | 1.05M | 1356.9 | 19.64 | 1.03M | 1363.5 | 19.58 | 1.49M | 935.56 | 16.52 | 432K | 6614.2 | 16.72 |
| SNB-SF-1000 (SB) | 4.51M | 601.72 | 14.43 | 2.02M | 722.34 | 18.98 | 4.01M | 660.22 | 12.37 | 2.94M | 1726.5 | 18.84 |
| LinkBench (LB) | 1.67M | 401.54 | 14.93 | 1.59M | 425.11 | 18.85 | 1.42M | 432.46 | 18.53 | 1.61M | 1773.2 | 18.52 |
| Twitter-2010 (TT) | 3.42M | 777.90 | 19.51 | 3.04M | 903.07 | 18.37 | 3.63M | 729.36 | 17.92 | 3.93M | 682.75 | 18.13 |
| Subdomain (SD) | 2.82M | 956.91 | 18.72 | 989K | 742.90 | 18.71 | 3.14M | 862.07 | 18.38 | 3.11M | 881.11 | 18.50 |
| UK-2007 (UK) | 1.22M | 600.17 | 18.22 | 288K | 640.68 | 17.86 | 1.21M | 610.28 | 18.68 | 3.86M | 1327.4 | 18.14 |
Performance under Different Configurations.
Next, we adjust the number of pre-populated edges (representing the size of the sliding window), the proportion of insertions and deletions, and the size of the transactions to evaluate the robustness of the system. In this paragraph, we only present the geometric average of the peak throughput relative to the default configuration for each algorithm on the next page, due to the page limit.
Our experiments keep the same number of edges as the pre-loaded size and perform sliding updates. The pre-loaded size can indicate the size of the sliding window. By default, we pre-populate 90% of the graph. Table 7 lists relative throughputs when the pre-populated part is 10% and 50% graph. For BFS, SSSP and SSWP, RisGraph gets throughput benefit with 10% and 50% pre-loaded edges because fewer edges result in less visited vertices from the root. For WCC, the performance drops 15% with 50% edges and 66% with 10% edges because fewer edges build up sparser graph than 90% edges, make the connected component unstable, generate more unsafe updates (see Table 4) and require more computing.
Table 7 shows the performance with varying percentage of edge insertions, compared to the performance with 50% insertions. From the table, RisGraph provides higher throughput as the proportion of insertions increases. The reason is that deletions need to reset results following to the dependency tree, while insertions do not.
We also evaluate RisGraph using transactions of different sizes. The latency constraint is that at least 99.9% of updates should receive responses in 20 milliseconds. Each transaction contains a fixed number of updates. If the latency exceeds the transaction size multiplied by 20 milliseconds, the transaction is timeout. We still use the number of updates per second to express throughput. Table 7 lists the results. When processing larger transactions, the throughput of RisGraph will drop to a maximum of 61% (WCC and 16 updates per transaction). The reason is that larger transactions lead to lower proportions of safe transactions, which reduces the benefits from inter-updates parallel. Nevertheless, RisGraph still supports several hundred thousands of updates per second.
| BFS | SSSP | SSWP | WCC | |
|---|---|---|---|---|
| 50% | 1.29 | 1.35 | 1.46 | 0.85 |
| 10% | 2.23 | 3.29 | 2.26 | 0.34 |
| BFS | SSSP | SSWP | WCC | BFS | SSSP | SSWP | WCC | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 0.72 | 0.79 | 0.88 | 0.67 | 75% | 1.09 | 1.01 | 1.04 | 1.10 | |
| 25% | 0.92 | 0.83 | 0.93 | 0.71 | 100% | 1.20 | 1.08 | 1.15 | 1.34 |
| BFS | SSSP | SSWP | WCC | BFS | SSSP | SSWP | WCC | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.87 | 0.85 | 0.97 | 0.79 | 8 | 0.59 | 0.67 | 0.62 | 0.48 | |
| 4 | 0.70 | 0.76 | 0.78 | 0.59 | 16 | 0.46 | 0.63 | 0.51 | 0.39 |
Finally, we evaluate RisGraph when maintaining multiple algorithms simultaneously. RisGraph maintains BFS, SSSP, SSWP and excludes WCC because these three algorithms require directed edges, but WCC requires undirected edges. We set the latency constraints to P999 and 60 milliseconds. The throughput is 1.20M ops/s for HepPh, 107K ops/s for Wiki, 391K ops/s for Flickr, 719K ops/s for StackOverflow, 429K ops/s for Bitcoin, 1.89M ops/s for LDBC-SNB, 288K ops/s for LinkBench, 1.61M ops/s for Twitter-2010, 891K ops/s for Subdomain and 363K ops/s for UK-2007.
The above results show that RisGraph can handle various workloads robustly.



Performance Case Study.
We take Twitter-2010 dataset as an example and present more performance details for RisGraph.
We first examine the multi-core scalability of RisGraph under an increasing number of threads, as shown in Figure 11. RisGraph’s throughput scales smoothly with more cores until 24 physical cores are occupied, and further improves about 13.5% with hyper threading. As a result, RisGraph’s throughput speedup is 17.6 for BFS, 17.8 for SSSP, 15.4 for SSWP and 17.7 for WCC with 24 physical cores (48 hyper threads).
We then look into RisGraph’s performance breakdown of components. Figure 11 illustrates that RisGraph provides similar breakdowns under different algorithms. On an average of four algorithms, graph updating engine (UpdEng) and computing engine (CmpEng), as the core of RisGraph, take 36.4% and 29.2% of the wall time respectively. To trace results, history store (HisStore) costs 5.7% of the time. The concurrency control module (CC) and the scheduler (Sched) are very lightweight and only bring a total of 3.6% overheads. WAL provides durability and network interacts with clients, which occupy 14.0% and 11.1% time, respectively.
We also trace RisGraph’s throughput (T.), timeout updates with more than 20 ms latency and the scheduler’s threshold over time when maintaining BFS on Twitter-2010, as shown in Figure 12. It shows that the scheduler can self-adjust its threshold to meet a tail-latency requirement and provide a good throughput over time.
6.3. Comparison of Implementation Choices
To verify that our implementation choices are effective, we evaluate alternative choices by the algorithms and datasets used in Section 6.2. The scheduler and history store are disabled in this part. We classify updates first, apply all safe updates in parallel, and then apply unsafe updates one by one. The purpose is to separate safe and unsafe updates, and to show the impact of different designs.
Graph Computing Engine.
We first evaluate the graph computing engine by comparing it with the performance of vertex-parallel, edge-parallel and the hybrid-parallel strategies. We focus on unsafe updates and keep the adjacency lists stored by arrays to eliminate the impact of data structures.


Figure 13 lists the speedup compared with vertex-parallel. We measure the slowest 1% updates first because the graph computing engine is the bottleneck for these updates, and they mainly affect RisGraph’s tail latency. According to Figure 13, edge-parallel is better than vertex-parallel in some cases, which validates our discussion in Section 3.2. Hybrid-parallel can integrate the advantages of vertex-parallel and edge-parallel well and provide better performance. It can accelerate computing up to 1.99 times, except for WCC on StackOverflow (a slight drop of 0.8%).
The performance (geometrically averaged) of edge-parallel outperforms vertex-parallel by 3.9%. The hybrid-parallel strategy can achieve more improvements than edge-parallel, reaching 1.24 times speedup over vertex-parallel and 1.19 times over edge-parallel. For all unsafe updates, the performance advantages are 4.8% and 6.1%.
Graph Store.
We next evaluate six alternative data structures for the graph store. IA_Suffix means the adjacency lists are stored in arrays and corresponding indexes. IO_Suffix represents that RisGraph only stores edges in the indexes. We evaluate three indexes, Dense Hash Table (Hash), BTree and ARTree.
Table 8 shows the relative overall performance measured from various data structures. The baseline is IA_Hash used by RisGraph. We calculate the geometric average of the relative performance to reflect the overall performance.
For safe updates, IA_Hash and IO_Hash provide higher performance when processing graph updates because the time complexity of Hash Table is better than other indexes. IO_Hash reduces the overhead by about 7% compared to IA_Hash because IO_Hash does not maintain additional compact adjacency lists. RisGraph pays overheads for adjacency lists to optimize the computing because unsafe updates (with computing) mainly determine the tail latency of per-update analysis and take an average 2.59 times longer than safe updates under large batches. The additional adjacency lists give IA_Hash a 17% advantage for unsafe updates. Overall, RisGraph’s default data structure (IA_Hash) performs well.
| Index with Array (IA) | Index Only (IO) | |||||
|---|---|---|---|---|---|---|
| ARTree | BTree | Hash | ARTree | BTree | Hash | |
| Safe | 0.91 | 0.79 | 1.00 | 0.94 | 0.81 | 1.07 |
| Unsafe | 0.93 | 0.96 | 1.00 | 0.48 | 0.76 | 0.83 |
| Overall | 0.92 | 0.90 | 1.00 | 0.57 | 0.78 | 0.89 |
Memory Consumption.
| Index with Array (IA) | Index Only (IO) | |||||
|---|---|---|---|---|---|---|
| ARTree | BTree | Hash | ARTree | BTree | Hash | |
| Unweighted | 3.63 | 2.36 | 3.25 | 3.45 | 2.10 | 2.97 |
| 8B_Weight | 3.45 | 2.50 | 3.38 | 3.13 | 2.17 | 3.04 |
Table 9 shows the memory consumption of RisGraph. We compare RisGraph’s memory footprint with raw-data (16 Bytes per edge for Unweighted graphs and 24 Bytes per edge for 8B_Weight graphs) and geometrically average them. RisGraph spends 3.25 memory on unweighted graphs and 3.38 memory on weighted graphs. RisGraph’s indexes brings most of the memory overhead, but they are necessary to support both fast insertions and deletions, which are discussed in Section 3.1. In order to support efficient bi-direct traversal at the same time, RisGraph maintains a transpose (reverse) of the directed graph, which doubles the memory occupation. The adjacency lists only occupy less than 0.5 of raw-data memory according to the comparison of IA_Hash with IO_Hash because they only store the destination vertices. Meanwhile, RisGraph only creates indexes for vertices whose degree exceeds the threshold to balance the memory consumption and performance. If a compact memory footprint is necessary, it is a wise choice to replace Hash Table (IA_Hash) with BTree (IA_BTree), which can reduce memory usage by about 1.15 times raw-data and lose 22% performance at the same time.
Since RisGraph is an in-memory system, we also explore how to scale for larger datasets. We try to extend RisGraph to support out-of-core processing. We use mmap to build a prototype that swaps to an SSD (Intel P3608 4TB SSD). We choose IA_BTree as the data structure and run UK-2014 (Boldi and Vigna, 2004; Boldi et al., 2011) (788M vertices, 47.6B edges, 710GB raw data). For WCC, it can process 262K safe updates per second. The average time of unsafe updates is 147 us, and the P999 latency is 2091 us, showing that scaling up to disks is a feasible solution. We take scaling up and scaling out as our future work.



6.4. Comparisons with Existing Systems
We also evaluate the performance of RisGraph compared with other streaming systems with batched updates. The goal is to evaluate the performance of RisGraph when the scenarios allow batching updates together and also reducing analysis frequency. We choose KickStarter222A module of GraphBolt, is available at https://bit.ly/34JgiX8, commit 190d15a. and Differential Dataflow333The latest implementation on Rust from https://bit.ly/3hK8xnv, commit 704bee. as baselines in this evaluation. Both of them officially provide BFS implementations, and we implement SSSP for Differential Dataflow based on its BFS code. Batch-update mode is enabled when it provides better performance. In all implementations, vertex IDs are 64-bit integers to generally support large graphs which may contain more than 4 billion vertices. RisGraph processes updates in batches and also disable WALs and tracing history for fair comparison.
We compare the performance of systems with different sizes of batches, from two updates (one edge insertion and one edge deletion) to 200M updates. The metric is the processing time of ingesting updates and performing analysis for each batch. And the throughput is calculated by the processing time and the batch size.
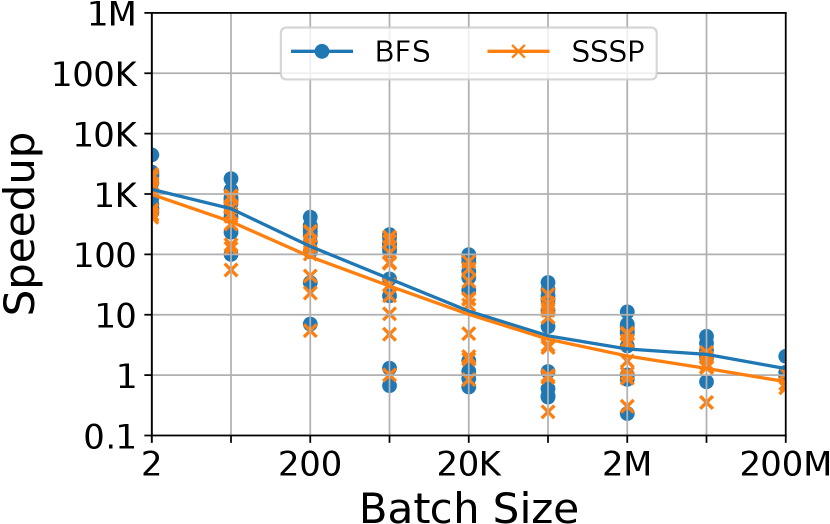
Figure 14 and Figure 14 show the geometric mean of speedups for all datasets and their distributions. RisGraph with batching outperforms KickStarter 13.8K times (from 587 with SSSP-HepPh to 588K with BFS-Bitcoin) and Differential Dataflow 1.06K times (from 365 with SSSP-HepPh to 4.45K with BFS-Bitcoin) on average when the batch-size is 2 (nearly per-update analysis).
As the batch size increases, RisGraph’s advantage gradually decreases. RisGraph keeps the advantage until the batch size is larger than 20M, but such a large batch seriously hurt the latency and analyzing frequency. Taking BFS on Twitter-2010 (Figure 14 and Figure 14) as an example, it takes GraphOne 0.76 s to re-compute BFS once, which is about RisGraph’s processing time on a batch of 2M updates. This example shows that incremental computing does not always optimize the analyzing performance when processing large batches, so it is reasonable to focus the design of RisGraph on fine-grained updates and analyses.
Compared with KickStarter, RisGraph’s performance improvement mainly credits to our localized data access (Section 3). RisGraph outperforms Differential Dataflow primarily due to specialized graph-aware engine and incremental model. For example, it takes Differential Dataflow 78 the processing time to re-compute BFS on Twitter-2010 compared to RisGraph.
7. Discussion
Affected Areas Could Be Small.
In our evaluation, RisGraph can ingest up to millions of updates per second and provide per-update incremental analysis, thanks to localized data access and inter-update parallelism. Its performance surprises us and prompts us to study how each update modifies the results. We use affected area (Fan et al., 2011; Fan et al., 2017) (AFF) as a tool to model computing costs. The affected area is the area modified or inspected (accessed) by an update.
Incremental computing assumes that the affected area of each update is relatively small compared to the entire graph. Several incremental graph computing models (McSherry et al., 2013; Shi et al., 2016; Sengupta et al., 2016; Vora et al., 2017) can accelerate monotonic algorithms in practical, but they still lack sufficient discussion and analysis of affected areas.
We try to give some mathematical bounds of affected areas. Because of the variety of graphs, updates, and algorithms, to mathematically bound affected areas for general monotonic algorithms is challenging. We only find a preliminary, yet optimistic bound based on an assumption. We assume that updating edges are uniformly sampled from all edges in the graph.
Consider a directed graph and a rooted tree in the graph , in which edges point from parents to children. The rooted tree represents the dependency tree of monotonic algorithms. For any vertex , we define , where is the subtree of rooted at if , and otherwise. The size of is denoted by , satisfying .
For any directed edge in , let and ( is the total degree of in , and is the indicator function), respectively representing the upper bound of vertices that need to be modified after is inserted or removed, and edges related to these vertices. bounds the area modified by , and bounds the area inspected by .
When is sampled uniformly from the edge set , the mean AFFV can be written as:
where is the depth of in (the distance between and ), is the diameter (the length of the longest path) of , and is the mean degree of . So that could be bounded by . In power-law graphs, is often small (Milgram, 1967; Cohen and Havlin, 2003; Leskovec et al., 2005; Leskovec et al., 2010). And in evolving graphs, will decrease while will increase over time, according to Densification Laws and Shrinking Diameters (Leskovec et al., 2005).
Similarly, the mean AFFE can be calculated as:
which can also be bounded by .
The results above guarantee mathematically that if we choose edges randomly for each update, only few vertices will be modified in average, and few vertices and edges will be accessed to perform the post-update analysis, thus showing the efficiency of incremental monotonic algorithms on power-law graphs.
Performance with Non-power-law Graphs.
Existing hierarchical algorithms (Sanders and Schultes, 2005; Nannicini and Liberti, [n.d.]; Wang et al., 2019) can efficiently limit the computing into a small neighbouring area for non-power-law graphs such as roadmaps. However, they cannot deal with power-law graphs efficiently because of hubs in power-law graphs. RisGraph focus on taking one step forward to support power-law graphs efficiently based on incremental computing. Meanwhile, RisGraph can also handle per-update incremental analysis on non-power-law graphs.
We evaluate RisGraph with the USA road network (Rossi and Ahmed, 2015), which is a non-power-law roadmap. There are 23.9M vertices and 28.9M edges in the USA dataset, and the experimental setup is the same as Section 6.1. The throughput is 26.7K ops/s for BFS, 4.10K ops/s for SSSP, 154K ops/s for SSWP, and 10.4K ops/s for WCC.
8. Related Work
Graph Computing on Static Graphs.
A large number of systems (Low et al., 2010; Gonzalez et al., 2012; Kyrola et al., 2012; Shun and Blelloch, 2013; Gonzalez et al., 2014; Zhu et al., 2015; Zhu et al., 2016; Ai et al., 2017; Maass et al., 2017; Wang et al., 2017; Shi et al., 2018; ZhangYunming et al., 2018; Mukkara et al., 2018; Lin et al., 2018; Chen et al., 2019; Vora, 2019) focus on graph computing with static graphs. These systems are designed for efficient graph analytics on entire graphs, but they suffer from ETL overheads with evolving graphs.
Dynamic Graph Stores.
Graph databases (neo, [n.d.]; tit, [n.d.]; ori, [n.d.]; ara, [n.d.]; Bronson et al., 2013; Sun et al., 2015; Gurajada et al., 2014; Dubey et al., 2016; Carter et al., 2019) mainly target transactional workloads, which rarely query and modify a large number of vertices or edges. Some recent work (Jindal et al., 2015; Kimura et al., 2017; Fan et al., 2015; Zhao and Yu, 2017; Zhu et al., 2020) propose to optimize analytical workloads in graph databases as well. Several graph computing engines (Prabhakaran et al., 2012; Han et al., 2014; Miao et al., 2015; Macko et al., 2015; Iyer et al., 2016; Vora et al., 2016; Then et al., 2017; Kumar and Huang, 2019) are also designed to support evolving graphs. These systems can handle graph update workloads. However, they are limited by recomputing on entire graphs for analytical workloads due to lack of incremental computing.
Generalized Streaming Systems.
Several generalized streaming systems, such as Storm (noa, [n.d.]a) and Flink (Katsifodimos and Schelter, 2016), allow users to incrementally process unbounded streams. Spark Streaming (Zaharia et al., 2013) utilizes small batches to handle streaming data and provide second-scale latency. It is not easy for users to develop incremental iterative graph algorithms based on these systems, such as monotonic algorithms. Differential Dataflow (McSherry et al., 2013), together with Naiad (Murray et al., 2013), carries out a generalized computational model that supports executing iterative and incremental computations with low latency. However, general-purpose systems lose opportunities to specialize and optimize for graph workloads.
Graph Streaming Systems.
Kineograph (Cheng et al., 2012) and GraphInc (Cai et al., 2012) are systems that enable incremental computation for graph mining. Qiu et al. (Qiu et al., 2018) design a real-time streaming system called GraphS for cycle detection. These systems lack support for monotonic algorithms like shortest path. Tornado (Shi et al., 2016) processes user queries by branching the execution and computing results incrementally while ingesting graph structure updates. However, it might lead to incorrect results in the presence of edge deletions when maintaining some monotonic algorithms such as WCC and SSWP (Vora et al., 2017).
KickStarter (Vora et al., 2017) provides correct incremental computation for monotonic algorithms by tracing dependencies and trimmed approximations. GraPU (Sheng et al., 2018) accelerates batch-update monotonic algorithms by components-based classification and in-buffer precomputation. GraphIn (Sengupta et al., 2016) incorporates an I-GAS model that processes fixed-size batches of updates incrementally. GraphBolt (Mariappan and Vora, 2019) proposes a generalized incremental model to handle non-monotonic algorithms like Belief Propagation, but involves more overheads than KickStarter for monotonic algorithms. These systems support monotonic algorithms, but all of them are designed for batch-update analysis. RisGraph targets per-update analysis to provide milliseconds tail-latency and detailed information in comparison.
9. Conclusion
In this paper, we present RisGraph, a real-time streaming system that efficiently supports per-update incremental analysis for monotonic algorithms on evolving graphs. The main ideas of RisGraph are localized data access and inter-update parallelism, which are critical to achieve high throughput and low latency simultaneously.
Acknowledgements.
We sincerely thank all SIGMOD reviewers for their insightful comments and suggestions. We also appreciate suggestions from Yaqin Li, Yanzheng Cai, Xuanhe Zhou, Bowen Yu, Songtao Yang, Jidong Zhai, Xiaosong Ma, and Marco Serafini. This work is partially supported by NSFC 61525202 and BAAI scholar program. Corresponding authors are Wentao Han and Wenguang Chen.References
- (1)
- noa ([n.d.]a) [n.d.]a. Apache Storm. https://storm.apache.org
- tma ([n.d.]) [n.d.]. China’s Singles’ Day shopping spree sees robust sales. https://bit.ly/31FrAJU [Online; accessed 6-January-2020; https://bit.ly/31FrAJU].
- ori ([n.d.]) [n.d.]. Graph Database — Multi-Model Database — OrientDB. [Online; accessed 6-January-2020; http://orientdb.com].
- ara ([n.d.]) [n.d.]. Multi-model highly available NoSQL database - ArangoDB. [Online; accessed 6-January-2020; http://orientdb.com].
- neo ([n.d.]) [n.d.]. Neo4j Graph Platform - The Leader in Graph Databases. [Online; accessed 6-January-2020; https://neo4j.com].
- twi ([n.d.]) [n.d.]. New Tweets per second record, and how! https://bit.ly/3b9zePQ [Online; accessed 6-January-2020; https://bit.ly/3b9zePQ].
- tit ([n.d.]) [n.d.]. TITAN: Distributed Graph Database. [Online; accessed 6-January-2020; http://titan.thinkaurelius.com/].
- noa ([n.d.]b) [n.d.]b. TPC-C - Overview of the TPC-C Benchmark. http://www.tpc.org/tpcc/detail.asp [Online; accessed 6-January-2020; http://www.tpc.org/tpcc/detail.asp].
- noa ([n.d.]c) [n.d.]c. WDC - Download the 2012 Hyperlink Graph. https://bit.ly/2Dby2Po [Online; accessed 6-January-2020; https://bit.ly/2Dby2Po].
- Ai et al. (2017) Zhiyuan Ai, Mingxing Zhang, Yongwei Wu, Xuehai Qian, Kang Chen, and Weimin Zheng. 2017. Squeezing out All the Value of Loaded Data: An Out-of-core Graph Processing System with Reduced Disk I/O. 125–137. https://www.usenix.org/conference/atc17/technical-sessions/presentation/ai
- Albert et al. (1999) Réka Albert, Hawoong Jeong, and Albert-László Barabási. 1999. Internet: Diameter of the world-wide web. nature 401, 6749 (1999), 130.
- Armstrong et al. (2013) Timothy G. Armstrong, Vamsi Ponnekanti, Dhruba Borthakur, and Mark Callaghan. 2013. LinkBench: A Database Benchmark Based on the Facebook Social Graph. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data (SIGMOD ’13). ACM, New York, NY, USA, 1185–1196. https://doi.org/10.1145/2463676.2465296 event-place: New York, New York, USA.
- Barga et al. (2007) Roger S. Barga, Jonathan Goldstein, Mohamed Ali, and Mingsheng Hong. 2007. Consistent Streaming Through Time: A Vision for Event Stream Processing. In In CIDR. 363–374.
- Beamer et al. (2012) Scott Beamer, Krste Asanović, and David Patterson. 2012. Direction-optimizing breadth-first search. In Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis (SC ’12). IEEE Computer Society Press, Washington, DC, USA, 1–10.
- Besta et al. (2017) Maciej Besta, Michał Podstawski, Linus Groner, Edgar Solomonik, and Torsten Hoefler. 2017. To Push or To Pull: On Reducing Communication and Synchronization in Graph Computations. In Proceedings of the 26th International Symposium on High-Performance Parallel and Distributed Computing (HPDC ’17). Association for Computing Machinery, New York, NY, USA, 93–104. https://doi.org/10.1145/3078597.3078616
- Boldi et al. (2011) Paolo Boldi, Marco Rosa, Massimo Santini, and Sebastiano Vigna. 2011. Layered label propagation: a multiresolution coordinate-free ordering for compressing social networks. In Proceedings of the 20th international conference on World wide web (WWW ’11). Association for Computing Machinery, New York, NY, USA, 587–596. https://doi.org/10.1145/1963405.1963488
- Boldi and Vigna (2004) P. Boldi and S. Vigna. 2004. The webgraph framework I: compression techniques. In Proceedings of the 13th international conference on World Wide Web (WWW ’04). Association for Computing Machinery, New York, NY, USA, 595–602. https://doi.org/10.1145/988672.988752
- Bronson et al. (2013) Nathan Bronson, Zach Amsden, George Cabrera, Prasad Chakka, Peter Dimov, Hui Ding, Jack Ferris, Anthony Giardullo, Sachin Kulkarni, Harry Li, Mark Marchukov, Dmitri Petrov, Lovro Puzar, Yee Jiun Song, and Venkat Venkataramani. 2013. {TAO}: Facebook’s Distributed Data Store for the Social Graph. In 2013 USENIX Annual Technical Conference (USENIX ATC 13). USENIX Association, San Jose, CA, 49–60. https://www.usenix.org/conference/atc13/technical-sessions/presentation/bronson
- Cai et al. (2012) Zhuhua Cai, Dionysios Logothetis, and Georgos Siganos. 2012. Facilitating Real-Time Graph Mining. In Proceedings of the Fourth International Workshop on Cloud Data Management (CloudDB ’12). Association for Computing Machinery, New York, NY, USA, 1–8. https://doi.org/10.1145/2390021.2390023 event-place: Maui, Hawaii, USA.
- Carter et al. (2019) Andrew Carter, Andrew Rodriguez, Yiming Yang, and Scott Meyer. 2019. Nanosecond Indexing of Graph Data With Hash Maps and VLists. In Proceedings of the 2019 International Conference on Management of Data (SIGMOD ’19). ACM, New York, NY, USA, 623–635. https://doi.org/10.1145/3299869.3314044 event-place: Amsterdam, Netherlands.
- Cen et al. (2020) Yukuo Cen, Jing Zhang, Gaofei Wang, Yujie Qian, Chuizheng Meng, Zonghong Dai, Hongxia Yang, and Jie Tang. 2020. Trust Relationship Prediction in Alibaba E-Commerce Platform. IEEE Transactions on Knowledge and Data Engineering 32, 5 (May 2020), 1024–1035. https://doi.org/10.1109/TKDE.2019.2893939 Conference Name: IEEE Transactions on Knowledge and Data Engineering.
- Chen et al. (2019) Rong Chen, Jiaxin Shi, Yanzhe Chen, Binyu Zang, Haibing Guan, and Haibo Chen. 2019. PowerLyra: Differentiated Graph Computation and Partitioning on Skewed Graphs. ACM Trans. Parallel Comput. 5, 3 (2019). https://doi.org/10.1145/3298989
- Chen et al. (2009) Zaiben Chen, Heng Tao Shen, Xiaofang Zhou, and Jeffrey Xu Yu. 2009. Monitoring path nearest neighbor in road networks. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of data (SIGMOD ’09). Association for Computing Machinery, New York, NY, USA, 591–602. https://doi.org/10.1145/1559845.1559907
- Cheng et al. (2012) Raymond Cheng, Ji Hong, Aapo Kyrola, Youshan Miao, Xuetian Weng, Ming Wu, Fan Yang, Lidong Zhou, Feng Zhao, and Enhong Chen. 2012. Kineograph: Taking the Pulse of a Fast-changing and Connected World. In Proceedings of the 7th ACM European Conference on Computer Systems (EuroSys ’12). ACM, New York, NY, USA, 85–98. https://doi.org/10.1145/2168836.2168846 event-place: Bern, Switzerland.
- Cohen and Havlin (2003) Reuven Cohen and Shlomo Havlin. 2003. Scale-Free Networks Are Ultrasmall. Physical Review Letters 90, 5 (Feb. 2003), 058701. https://doi.org/10.1103/PhysRevLett.90.058701
- Dubey et al. (2016) Ayush Dubey, Greg D. Hill, Robert Escriva, and Emin Gün Sirer. 2016. Weaver: A High-Performance, Transactional Graph Database Based on Refinable Timestamps. Proc. VLDB Endow. 9, 11 (July 2016), 852–863. https://doi.org/10.14778/2983200.2983202
- Erling et al. (2015) Orri Erling, Alex Averbuch, Josep Larriba-Pey, Hassan Chafi, Andrey Gubichev, Arnau Prat, Minh-Duc Pham, and Peter Boncz. 2015. The LDBC Social Network Benchmark: Interactive Workload. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data (SIGMOD ’15). Association for Computing Machinery, New York, NY, USA, 619–630. https://doi.org/10.1145/2723372.2742786
- Fan et al. (2015) Jing Fan, Adalbert Gerald Soosai Raj, and Jignesh M Patel. 2015. The Case Against Specialized Graph Analytics Engines.. In CIDR.
- Fan et al. (2017) Wenfei Fan, Chunming Hu, and Chao Tian. 2017. Incremental Graph Computations: Doable and Undoable. In Proceedings of the 2017 ACM International Conference on Management of Data (SIGMOD ’17). ACM, New York, NY, USA, 155–169. https://doi.org/10.1145/3035918.3035944 event-place: Chicago, Illinois, USA.
- Fan et al. (2011) Wenfei Fan, Jianzhong Li, Jizhou Luo, Zijing Tan, Xin Wang, and Yinghui Wu. 2011. Incremental Graph Pattern Matching. In Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data (SIGMOD ’11). ACM, New York, NY, USA, 925–936. https://doi.org/10.1145/1989323.1989420 event-place: Athens, Greece.
- Garg et al. (2009) Sanchit Garg, Trinabh Gupta, Niklas Carlsson, and Anirban Mahanti. 2009. Evolution of an online social aggregation network: an empirical study. In Proceedings of the 9th ACM SIGCOMM conference on Internet measurement (IMC ’09). Association for Computing Machinery, New York, NY, USA, 315–321. https://doi.org/10.1145/1644893.1644931
- Gonzalez et al. (2012) Joseph E. Gonzalez, Yucheng Low, Haijie Gu, Danny Bickson, and Carlos Guestrin. 2012. PowerGraph: Distributed Graph-Parallel Computation on Natural Graphs. In 10th USENIX Symposium on Operating Systems Design and Implementation (OSDI 12). USENIX Association, Hollywood, CA, 17–30. https://www.usenix.org/node/170825
- Gonzalez et al. (2014) Joseph E. Gonzalez, Reynold S. Xin, Ankur Dave, Daniel Crankshaw, Michael J. Franklin, and Ion Stoica. 2014. GraphX: Graph Processing in a Distributed Dataflow Framework. In 11th USENIX Symposium on Operating Systems Design and Implementation (OSDI 14). USENIX Association, Broomfield, CO, 599–613. https://www.usenix.org/node/186217
- Gurajada et al. (2014) Sairam Gurajada, Stephan Seufert, Iris Miliaraki, and Martin Theobald. 2014. TriAD: A Distributed Shared-Nothing RDF Engine Based on Asynchronous Message Passing. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data (Snowbird, Utah, USA) (SIGMOD ’14). Association for Computing Machinery, New York, NY, USA, 289–300. https://doi.org/10.1145/2588555.2610511
- Han et al. (2014) Wentao Han, Youshan Miao, Kaiwei Li, Ming Wu, Fan Yang, Lidong Zhou, Vijayan Prabhakaran, Wenguang Chen, and Enhong Chen. 2014. Chronos: A Graph Engine for Temporal Graph Analysis. In Proceedings of the Ninth European Conference on Computer Systems (EuroSys ’14). ACM, New York, NY, USA, 1:1–1:14. https://doi.org/10.1145/2592798.2592799 event-place: Amsterdam, The Netherlands.
- Iyer et al. (2016) Anand Padmanabha Iyer, Li Erran Li, Tathagata Das, and Ion Stoica. 2016. Time-Evolving Graph Processing at Scale. In Proceedings of the Fourth International Workshop on Graph Data Management Experiences and Systems (GRADES ’16). Association for Computing Machinery, New York, NY, USA. https://doi.org/10.1145/2960414.2960419 event-place: Redwood Shores, California.
- Jiang et al. (2016) Wenjun Jiang, Guojun Wang, Md Zakirul Alam Bhuiyan, and Jie Wu. 2016. Understanding Graph-Based Trust Evaluation in Online Social Networks: Methodologies and Challenges. Comput. Surveys 49, 1 (May 2016), 10:1–10:35. https://doi.org/10.1145/2906151
- Jindal et al. (2015) A. Jindal, S. Madden, M. Castellanos, and M. Hsu. 2015. Graph analytics using vertica relational database. In 2015 IEEE International Conference on Big Data (Big Data). 1191–1200. https://doi.org/10.1109/BigData.2015.7363873
- Karimov et al. (2018) Jeyhun Karimov, Tilmann Rabl, Asterios Katsifodimos, Roman Samarev, Henri Heiskanen, and Volker Markl. 2018. Benchmarking Distributed Stream Data Processing Systems. In 2018 IEEE 34th International Conference on Data Engineering (ICDE). 1507–1518. https://doi.org/10.1109/ICDE.2018.00169 ISSN: 2375-026X.
- Katsifodimos and Schelter (2016) A. Katsifodimos and S. Schelter. 2016. Apache Flink: Stream Analytics at Scale. In 2016 IEEE International Conference on Cloud Engineering Workshop (IC2EW). 193–193. https://doi.org/10.1109/IC2EW.2016.56
- Khalil et al. (2016) Issa Khalil, Ting Yu, and Bei Guan. 2016. Discovering Malicious Domains through Passive DNS Data Graph Analysis. In Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security (ASIA CCS ’16). Association for Computing Machinery, New York, NY, USA, 663–674. https://doi.org/10.1145/2897845.2897877
- Kimura et al. (2017) Hideaki Kimura, Alkis Simitsis, and Kevin Wilkinson. 2017. Janus: Transaction Processing of Navigation and Analytic Graph Queries on Many-core Servers. (2017). http://cidrdb.org/cidr2017/papers/p104-kimura-cidr17.pdf
- Kumar and Huang (2019) Pradeep Kumar and H. Howie Huang. 2019. GraphOne: A Data Store for Real-time Analytics on Evolving Graphs. In 17th USENIX Conference on File and Storage Technologies (FAST 19). USENIX Association, Boston, MA, 249–263. https://www.usenix.org/conference/fast19/presentation/kumar
- Kyrola et al. (2012) Aapo Kyrola, Guy Blelloch, and Carlos Guestrin. 2012. GraphChi: Large-Scale Graph Computation on Just a {PC}. 31–46. https://www.usenix.org/node/170824
- Leis et al. (2013) Viktor Leis, Alfons Kemper, and Thomas Neumann. 2013. The adaptive radix tree: ARTful indexing for main-memory databases. In 2013 IEEE 29th International Conference on Data Engineering (ICDE). 38–49. https://doi.org/10.1109/ICDE.2013.6544812 ISSN: 1063-6382.
- Leskovec et al. (2010) Jure Leskovec, Deepayan Chakrabarti, Jon Kleinberg, Christos Faloutsos, and Zoubin Ghahramani. 2010. Kronecker Graphs: An Approach to Modeling Networks. J. Mach. Learn. Res. 11 (March 2010), 985–1042. http://dl.acm.org/citation.cfm?id=1756006.1756039
- Leskovec et al. (2005) Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. 2005. Graphs over time: densification laws, shrinking diameters and possible explanations. In Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining (KDD ’05). Association for Computing Machinery, New York, NY, USA, 177–187. https://doi.org/10.1145/1081870.1081893
- Leskovec and Krevl (2014) Jure Leskovec and Andrej Krevl. 2014. SNAP Datasets: Stanford Large Network Dataset Collection. http://snap.stanford.edu/data.
- Lin et al. (2018) Heng Lin, Xiaowei Zhu, Bowen Yu, Xiongchao Tang, Wei Xue, Wenguang Chen, Lufei Zhang, Torsten Hoefler, Xiaosong Ma, Xin Liu, Weimin Zheng, and Jingfang Xu. 2018. ShenTu: Processing Multi-Trillion Edge Graphs on Millions of Cores in Seconds. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis (Dallas, Texas) (SC ’18). IEEE Press, Article 56, 11 pages.
- Low et al. (2010) Yucheng Low, Joseph Gonzalez, Aapo Kyrola, Danny Bickson, Carlos Guestrin, and Joseph Hellerstein. 2010. GraphLab: A New Framework for Parallel Machine Learning. In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence (UAI’10). AUAI Press, Arlington, Virginia, USA, 340–349. event-place: Catalina Island, CA.
- Maass et al. (2017) Steffen Maass, Changwoo Min, Sanidhya Kashyap, Woonhak Kang, Mohan Kumar, and Taesoo Kim. 2017. Mosaic: Processing a Trillion-Edge Graph on a Single Machine. In Proceedings of the Twelfth European Conference on Computer Systems (EuroSys ’17). Association for Computing Machinery, New York, NY, USA, 527–543. https://doi.org/10.1145/3064176.3064191 event-place: Belgrade, Serbia.
- Macko et al. (2015) Peter Macko, Virendra J. Marathe, Daniel W. Margo, and Margo I. Seltzer. 2015. LLAMA: Efficient graph analytics using Large Multiversioned Arrays. In 2015 IEEE 31st International Conference on Data Engineering. 363–374. https://doi.org/10.1109/ICDE.2015.7113298 ISSN: 2375-026X.
- Malewicz et al. (2010) Grzegorz Malewicz, Matthew H. Austern, Aart J.C Bik, James C. Dehnert, Ilan Horn, Naty Leiser, and Grzegorz Czajkowski. 2010. Pregel: a system for large-scale graph processing. In Proceedings of the 2010 ACM SIGMOD International Conference on Management of data (SIGMOD ’10). Association for Computing Machinery, New York, NY, USA, 135–146. https://doi.org/10.1145/1807167.1807184
- Mariappan and Vora (2019) Mugilan Mariappan and Keval Vora. 2019. GraphBolt: Dependency-Driven Synchronous Processing of Streaming Graphs. In Proceedings of the Fourteenth EuroSys Conference 2019 (Dresden, Germany) (EuroSys ’19). Association for Computing Machinery, New York, NY, USA, Article 25, 16 pages. https://doi.org/10.1145/3302424.3303974
- McSherry et al. (2013) Frank McSherry, Derek Murray, Rebecca Isaacs, and Michael Isard. 2013. Differential dataflow. In Proceedings of CIDR 2013. https://www.microsoft.com/en-us/research/publication/differential-dataflow/
- Meehan et al. (2015) John Meehan, Nesime Tatbul, Stan Zdonik, Cansu Aslantas, Ugur Cetintemel, Jiang Du, Tim Kraska, Samuel Madden, David Maier, Andrew Pavlo, Michael Stonebraker, Kristin Tufte, and Hao Wang. 2015. S-Store: streaming meets transaction processing. Proceedings of the VLDB Endowment 8, 13 (Sept. 2015), 2134–2145. https://doi.org/10.14778/2831360.2831367
- Miao et al. (2015) Youshan Miao, Wentao Han, Kaiwei Li, Ming Wu, Fan Yang, Lidong Zhou, Vijayan Prabhakaran, Enhong Chen, and Wenguang Chen. 2015. ImmortalGraph: A System for Storage and Analysis of Temporal Graphs. ACM Trans. Storage 11, 3, Article 14 (July 2015), 34 pages. https://doi.org/10.1145/2700302
- Milgram (1967) Stanley Milgram. 1967. The small world problem. Psychology today 2, 1 (1967), 60–67.
- Mislove et al. (2007) Alan Mislove, Massimiliano Marcon, Krishna P. Gummadi, Peter Druschel, and Bobby Bhattacharjee. 2007. Measurement and Analysis of Online Social Networks. In Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement (San Diego, California, USA) (IMC ’07). Association for Computing Machinery, New York, NY, USA, 29–42. https://doi.org/10.1145/1298306.1298311
- Mukkara et al. (2018) Anurag Mukkara, Nathan Beckmann, Maleen Abeydeera, Xiaosong Ma, and Daniel Sanchez. 2018. Exploiting Locality in Graph Analytics through Hardware-Accelerated Traversal Scheduling. In Proceedings of the 51st Annual IEEE/ACM International Symposium on Microarchitecture (MICRO-51). IEEE Press, 1–14. https://doi.org/10.1109/MICRO.2018.00010 event-place: Fukuoka, Japan.
- Murray et al. (2013) Derek G. Murray, Frank McSherry, Rebecca Isaacs, Michael Isard, Paul Barham, and Martín Abadi. 2013. Naiad: A Timely Dataflow System. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles (SOSP ’13). ACM, New York, NY, USA, 439–455. https://doi.org/10.1145/2517349.2522738 event-place: Farminton, Pennsylvania.
- Nannicini and Liberti ([n.d.]) Giacomo Nannicini and Leo Liberti. [n.d.]. Shortest paths on dynamic graphs. 15 ([n. d.]). https://doi.org/10.1111/j.1475-3995.2008.00649.x
- Ntoulas et al. (2004) Alexandros Ntoulas, Junghoo Cho, and Christopher Olston. 2004. What’s new on the web? the evolution of the web from a search engine perspective. In Proceedings of the 13th international conference on World Wide Web (WWW ’04). Association for Computing Machinery, New York, NY, USA, 1–12. https://doi.org/10.1145/988672.988674
- Prabhakaran et al. (2012) Vijayan Prabhakaran, Ming Wu, Xuetian Weng, Frank McSherry, Lidong Zhou, and Maya Haradasan. 2012. Managing Large Graphs on Multi-Cores with Graph Awareness. 41–52. https://www.usenix.org/conference/atc12/technical-sessions/presentation/prabhakaran
- Qiu et al. (2018) Xiafei Qiu, Wubin Cen, Zhengping Qian, You Peng, Ying Zhang, Xuemin Lin, and Jingren Zhou. 2018. Real-time Constrained Cycle Detection in Large Dynamic Graphs. Proc. VLDB Endow. 11, 12 (Aug. 2018), 1876–1888. https://doi.org/10.14778/3229863.3229874
- Rossi and Ahmed (2015) Ryan Rossi and Nesreen Ahmed. 2015. The network data repository with interactive graph analytics and visualization. In Twenty-Ninth AAAI Conference on Artificial Intelligence.
- Sanders and Schultes (2005) Peter Sanders and Dominik Schultes. 2005. Highway Hierarchies Hasten Exact Shortest Path Queries. In Proceedings of the 13th Annual European Conference on Algorithms (Palma de Mallorca, Spain) (ESA’05). Springer-Verlag, Berlin, Heidelberg, 568–579. https://doi.org/10.1007/11561071_51
- Sengupta et al. (2016) Dipanjan Sengupta, Narayanan Sundaram, Xia Zhu, Theodore L. Willke, Jeffrey Young, Matthew Wolf, and Karsten Schwan. 2016. GraphIn: An Online High Performance Incremental Graph Processing Framework. In Proceedings of the 22nd International Conference on Euro-Par 2016: Parallel Processing - Volume 9833. Springer-Verlag, Berlin, Heidelberg, 319–333. https://doi.org/10.1007/978-3-319-43659-3_24
- Sheng et al. (2018) Feng Sheng, Qiang Cao, Haoran Cai, Jie Yao, and Changsheng Xie. 2018. GraPU: Accelerate Streaming Graph Analysis through Preprocessing Buffered Updates. In Proceedings of the ACM Symposium on Cloud Computing (Carlsbad, CA, USA) (SoCC ’18). Association for Computing Machinery, New York, NY, USA, 301–312. https://doi.org/10.1145/3267809.3267811
- Shi et al. (2016) Xiaogang Shi, Bin Cui, Yingxia Shao, and Yunhai Tong. 2016. Tornado: A System For Real-Time Iterative Analysis Over Evolving Data. In Proceedings of the 2016 International Conference on Management of Data (SIGMOD ’16). Association for Computing Machinery, New York, NY, USA, 417–430. https://doi.org/10.1145/2882903.2882950
- Shi et al. (2018) Xuanhua Shi, Zhigao Zheng, Yongluan Zhou, Hai Jin, Ligang He, Bo Liu, and Qiang-Sheng Hua. 2018. Graph Processing on GPUs: A Survey. ACM Comput. Surv. 50, 6 (2018). https://doi.org/10.1145/3128571
- Shun and Blelloch (2013) Julian Shun and Guy E. Blelloch. 2013. Ligra: A Lightweight Graph Processing Framework for Shared Memory. In Proceedings of the 18th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP ’13). Association for Computing Machinery, New York, NY, USA, 135–146. https://doi.org/10.1145/2442516.2442530 event-place: Shenzhen, China.
- Sun et al. (2015) Wen Sun, Achille Fokoue, Kavitha Srinivas, Anastasios Kementsietsidis, Gang Hu, and Guotong Xie. 2015. SQLGraph: An Efficient Relational-Based Property Graph Store. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data (Melbourne, Victoria, Australia) (SIGMOD ’15). Association for Computing Machinery, New York, NY, USA, 1887–1901. https://doi.org/10.1145/2723372.2723732
- Then et al. (2017) Manuel Then, Timo Kersten, Stephan Günnemann, Alfons Kemper, and Thomas Neumann. 2017. Automatic algorithm transformation for efficient multi-snapshot analytics on temporal graphs. Proceedings of the VLDB Endowment 10, 8 (April 2017), 877–888. https://doi.org/10.14778/3090163.3090166
- Vora (2019) Keval Vora. 2019. LUMOS: Dependency-Driven Disk-based Graph Processing. In 2019 USENIX Annual Technical Conference (USENIX ATC 19). USENIX Association, Renton, WA, 429–442. https://www.usenix.org/conference/atc19/presentation/vora
- Vora et al. (2016) Keval Vora, Rajiv Gupta, and Guoqing Xu. 2016. Synergistic Analysis of Evolving Graphs. ACM Trans. Archit. Code Optim. 13, 4, Article 32 (Oct. 2016), 27 pages. https://doi.org/10.1145/2992784
- Vora et al. (2017) Keval Vora, Rajiv Gupta, and Guoqing Xu. 2017. KickStarter: Fast and Accurate Computations on Streaming Graphs via Trimmed Approximations. SIGARCH Comput. Archit. News 45, 1 (April 2017), 237–251. https://doi.org/10.1145/3093337.3037748
- Wang et al. (2017) Kai Wang, Aftab Hussain, Zhiqiang Zuo, Guoqing Xu, and Ardalan Amiri Sani. 2017. Graspan: A Single-Machine Disk-Based Graph System for Interprocedural Static Analyses of Large-Scale Systems Code. SIGPLAN Not. 52, 4 (April 2017), 389–404. https://doi.org/10.1145/3093336.3037744
- Wang et al. (2019) Yong Wang, Guoliang Li, and Nan Tang. 2019. Querying shortest paths on time dependent road networks. Proceedings of the VLDB Endowment 12, 11 (July 2019), 1249–1261. https://doi.org/10.14778/3342263.3342265
- Wikipedia contributors (2019) Wikipedia contributors. 2019. Parent pointer tree — Wikipedia, The Free Encyclopedia. https://bit.ly/32AzgMS [Online; accessed 16-January-2020].
- Wu et al. (2017) Yingjun Wu, Joy Arulraj, Jiexi Lin, Ran Xian, and Andrew Pavlo. 2017. An Empirical Evaluation of In-memory Multi-version Concurrency Control. Proc. VLDB Endow. 10, 7 (March 2017), 781–792. https://doi.org/10.14778/3067421.3067427
- Xu and Chen (2004) Jennifer J. Xu and Hsinchun Chen. 2004. Fighting organized crimes: using shortest-path algorithms to identify associations in criminal networks. Decision Support Systems 38, 3 (Dec. 2004), 473–487. https://doi.org/10.1016/S0167-9236(03)00117-9
- Zaharia et al. (2013) Matei Zaharia, Tathagata Das, Haoyuan Li, Timothy Hunter, Scott Shenker, and Ion Stoica. 2013. Discretized streams: fault-tolerant streaming computation at scale. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles (SOSP ’13). Association for Computing Machinery, New York, NY, USA, 423–438. https://doi.org/10.1145/2517349.2522737
- ZhangYunming et al. (2018) ZhangYunming, YangMengjiao, BaghdadiRiyadh, KamilShoaib, ShunJulian, and AmarasingheSaman. 2018. GraphIt: a high-performance graph DSL. Proceedings of the ACM on Programming Languages (Oct. 2018). https://dl.acm.org/doi/abs/10.1145/3276491
- Zhao and Yu (2017) Kangfei Zhao and Jeffrey Xu Yu. 2017. All-in-One: Graph Processing in RDBMSs Revisited. In Proceedings of the 2017 ACM International Conference on Management of Data (Chicago, Illinois, USA) (SIGMOD ’17). Association for Computing Machinery, New York, NY, USA, 1165–1180. https://doi.org/10.1145/3035918.3035943
- Zhu et al. (2016) Xiaowei Zhu, Wenguang Chen, Weimin Zheng, and Xiaosong Ma. 2016. Gemini: A Computation-Centric Distributed Graph Processing System. In 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16). USENIX Association, Savannah, GA, 301–316. https://www.usenix.org/conference/osdi16/technical-sessions/presentation/zhu
- Zhu et al. (2020) Xiaowei Zhu, Guanyu Feng, Marco Serafini, Xiaosong Ma, Jiping Yu, Lei Xie, Ashraf Aboulnaga, and Wenguang Chen. 2020. LiveGraph: A Transactional Graph Storage System with Purely Sequential Adjacency List Scans. Proc. VLDB Endow. 13, 7 (March 2020), 1020–1034. https://doi.org/10.14778/3384345.3384351
- Zhu et al. (2015) Xiaowei Zhu, Wentao Han, and Wenguang Chen. 2015. GridGraph: Large-Scale Graph Processing on a Single Machine Using 2-Level Hierarchical Partitioning. In 2015 USENIX Annual Technical Conference (USENIX ATC 15). USENIX Association, Santa Clara, CA, 375–386. https://www.usenix.org/conference/atc15/technical-session/presentation/zhu