RIS-Aided Interference Cancellation for Joint Device-to-Device and Cellular Communications

With the proliferation of mobile users and devices, joint device-to-device (D2D) and cellular communication has been envisioned as a promising technology for enhancing spectral efficiency in future wireless networks [1]. In this technology, devices and cellular users operate on the same spectrum, and therefore significantly improve the network spectral efficiency. However, the interference management problem is very challenging due to spectrum sharing between the operating devices and cellular users [2, 3, 4]. Fortunately, the D2D interference problem can be effectively addressed by reconfigurable intelligent surfaces (RISs)–a recent innovative technology capable of shaping the wireless channel in desired ways [5, 6]. For example, the works in [7, 8, 9] show that an RIS can be used to effectively null out or mitigate interference in D2D systems. While the work in [7] considers a conventional passive RIS structure which can only change the phase of the incoming signal, the authors in [8, 9] show that a hybrid RIS structure with the capability of simultaneously changing the phase and amplitude of the incoming signal can provide better interference cancellation performance. However, these prior works all consider systems with only D2D links, i.e., there were no active co-channel cellular users present.

RIS-assisted joint D2D and cellular communication has been studied in several recent papers. For example, the works in [10] and [11] perform analyses for RIS-assisted D2D communications under Rician and Nakagami-$m$ fading channels, respectively. The study in [10] investigates the effective capacity and performs mode selection to determine whether the D2D communication is established through an RIS or a base station (BS). The authors of [11] derived closed-form expressions for the outage probability of the D2D links and the resulting diversity order. Unlike [10, 11] which perform system analysis, some other recent papers focus on system design and optimization [12, 13, 14, 15, 16, 17]. In particular, the sum-rate maximization problem was considered in [12, 13, 14, 15] and deep reinforcement learning was used in [12, 14]. However, the works in [12, 14] assume that the BS is equipped with only one antenna and only one D2D pair is allowed to share the spectrum with a single cellular user. Multiple D2D pairs sharing the same spectrum with a cellular user were considered in [13, 15], but it was still assumed that the BS has only one antenna. The sum-rate maximization problem for systems with a multi-antenna BS was studied in [16, 17], but again they assume only one D2D pair sharing the spectrum with one cellular user.

Unlike the aforementioned works which consider the sum-rate maximization problem with relaxed system assumptions, we study a different problem that takes into account the fairness by maximizing the minimum signal-to-interference-plus-noise ratio (SINR) over the cellular users and devices. We also consider a more challenging RIS-assisted joint D2D and cellular communication system where multiple cellular users share the same spectrum with multiple D2D pairs and the BS is also equipped with multiple antennas. The contributions of our paper is summarized as follows:

• •

  First, we adopt a popular alternating optimization (AO) approach and the semi-definite relaxation (SDR) technique to optimize the combining matrix at the BS and the RIS phase shift vector that maximize the minimum SINR over the cellular users and devices.

• •

  Next, we propose an interference cancellation (IC)-based approach whose complexity is much lower than that of the AO algorithm. More specifically, we first derive a representation for the RIS phase shift vector that cancels the interference to the D2D links. Based on this representation, we transform the RIS phase shift optimization problem into an effective D2D channel optimization problem. We show that the AO approach can converge faster and can even give better performance when it uses the proposed IC solution as its initial point.

• •

  We also show that for the case of a single D2D pair, the proposed IC approach can be implemented with limited feedback from the receive device. Finally, we numerically show the gains and benefits of the proposed approaches.

This section develops an AO approach to solve the joint D2D and cellular communication problem in (1). Here, we alternately optimize the BS combiners $\{\mathbf{w}_{k}\}$ and the RIS phase shift $\boldsymbol{\phi}$.

The AO approach presented above is efficient but its computational complexity is high because the BS combiners and the RIS phase shift vector are alternately optimized. In addition, each AO iteration requires use of the Dinkelbach algorithm which is an iterative algorithm itself, and each of its iterations also requires the solution of an SDR optimization problem. Here, we propose an IC approach whose computational complexity is significantly lower than that of the AO algorithm since the proposed IC approach only needs to solve one SDR problem. Details of the proposed IC approach are presented as follows.

Let $\mathbf{F}^{\mathtt{DD}}\in\mathbb{C}^{L\times L}$ be the effective channel from the transmit devices to the receive devices, and define

	$\displaystyle\mathbf{f}^{\mathtt{DD}}=\operatorname{vec}{\left((\mathbf{F}^{\mathtt{DD}})^{T}\right)}$	$\displaystyle=\operatorname{vec}{\left((\mathbf{H}^{\mathtt{DD}})^{T}\right)}+\begin{bmatrix}[0.8]\mathbf{G}^{\mathtt{DD}}_{1}\\ \vdots\\ \mathbf{G}^{\mathtt{DD}}_{L}\end{bmatrix}\boldsymbol{\phi}$
		$\displaystyle=\mathbf{h}^{\mathtt{DD}}+\mathbf{G}^{\mathtt{DD}}\boldsymbol{\phi},$		(10)

where $\mathbf{G}^{\mathtt{DD}}_{\ell}=[\mathbf{g}^{\mathtt{DD}}_{\ell,1},\ldots,\mathbf{g}^{\mathtt{DD}}_{\ell,L}]^{H}$. We use a permutation matrix $\mathbf{P}$ to separate the vector $\mathbf{f}^{\mathtt{DD}}$ into two sub-vectors $\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}$ and $\mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}$ which contain the diagonal and off-diagonal elements of $\mathbf{F}^{\mathtt{DD}}$, respectively. The diagonal elements of $\mathbf{F}^{\mathtt{DD}}$ represent the useful channels for the D2D pairs, while the off-diagonal elements represent the interference channels from other D2D pairs. Hence we use the subscripts ‘$\mathrm{sig}$’ and ‘$\mathrm{itf}$’ to indicate the D2D signal and interference, respectively. This means we can write

$$\begin{bmatrix}[1.2]\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}=\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}+\begin{bmatrix}[1.2]\mathbf{G}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{G}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}\boldsymbol{\phi}$$

(11)

where

$$\begin{bmatrix}[1.2]\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}=\mathbf{P}\mathbf{f}^{\mathtt{DD}},\;\;\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}=\mathbf{P}\mathbf{h}^{\mathtt{DD}},\;\;\begin{bmatrix}[1.2]\mathbf{G}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{G}^{\mathtt{DD}}_{\mathrm{itf}}\end{bmatrix}=\mathbf{P}\mathbf{G}^{\mathtt{DD}}.$$

Similarly, let $\mathbf{F}^{\mathtt{UD}}\in\mathbb{C}^{L\times K}$ be the effective channel from the cellular users to the receive devices, so we can also write

	$\displaystyle\mathbf{f}^{\mathtt{UD}}=\operatorname{vec}{\left((\mathbf{F}^{\mathtt{UD}})^{T}\right)}$	$\displaystyle=\operatorname{vec}{\left((\mathbf{H}^{\mathtt{UD}})^{T}\right)}+\begin{bmatrix}[0.8]\mathbf{G}_{1}^{\mathtt{UD}}\\ \vdots\\ \mathbf{G}_{L}^{\mathtt{UD}}\end{bmatrix}\boldsymbol{\phi}$
		$\displaystyle=\mathbf{h}^{\mathtt{UD}}+\mathbf{G}^{\mathtt{UD}}\boldsymbol{\phi},$		(12)

where $\mathbf{G}_{\ell}^{\mathtt{UD}}=[\mathbf{g}_{\ell,1}^{\mathtt{UD}},\ldots,\mathbf{g}_{\ell,K}^{\mathtt{UD}}]^{H}$.

Combining (11) and (12), we have

$$\begin{bmatrix}[1.2]\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{f}^{\mathtt{UD}}\end{bmatrix}=\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{h}^{\mathtt{UD}}\end{bmatrix}+\underbrace{\begin{bmatrix}[1.2]\mathbf{G}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{G}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{G}^{\mathtt{UD}}\end{bmatrix}}_{\mathbf{A}}\boldsymbol{\phi},$$

(13)

where $\mathbf{A}\in\mathbb{C}^{L(K+L)\times N}$ is a matrix representing the RIS-aided channel. Assuming that $N\geq L(K+L)$, then using (13) we can write the phase shift vector $\boldsymbol{\phi}$ in the following expression:

$$\boldsymbol{\phi}=\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}\left(\begin{bmatrix}[1.2]\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{f}^{\mathtt{UD}}\end{bmatrix}-\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}\\ \mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{h}^{\mathtt{UD}}\end{bmatrix}\right).$$

(14)

Let $[\mathbf{B},\mathbf{C}]\overset{\Delta}{=}\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}$ where $\mathbf{B}\in\mathbb{C}^{N\times L}$ and $\mathbf{C}\in\mathbb{C}^{N\times L(K+L)-L}$, then decompose the right-hand side of (14) as follows:

$\displaystyle\boldsymbol{\phi}$

$\displaystyle=\mathbf{B}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}-\mathbf{B}\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{C}\left(\begin{bmatrix}[1.2]\mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{f}^{\mathtt{UD}}\end{bmatrix}-\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{h}^{\mathtt{UD}}\end{bmatrix}\right).$

(15)

The representation above shows a relationship between the RIS phase shift $\boldsymbol{\phi}$ and the effective device-related channels including the useful D2D channels $\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}$ and the other interference links $\mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}$ and $\mathbf{f}^{\mathtt{UD}}$. If we let $\mathbf{f}^{\mathtt{DD}}_{\mathrm{itf}}=\mathbf{0}$ and $\mathbf{f}^{\mathtt{UD}}=\mathbf{0}$, the RIS solution (15) reduces to an IC $\boldsymbol{\phi}$ solution expressed in terms of $\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}$ as

	$\displaystyle\boldsymbol{\phi}_{\mathrm{IC}}$	$\displaystyle=\mathbf{B}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}-\mathbf{B}\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}-\mathbf{C}\begin{bmatrix}[1.2]\mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}}\\ \mathbf{h}^{\mathtt{UD}}\end{bmatrix}$
		$\displaystyle=\mathbf{B}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{d}$		(16)

where $\mathbf{d}=-\mathbf{B}\mathbf{h}^{\mathtt{DD}}_{\mathrm{sig}}-\mathbf{C}[(\mathbf{h}^{\mathtt{DD}}_{\mathrm{itf}})^{T},\,(\mathbf{h}^{\mathtt{UD}})^{T}]^{T}$. This means that if we could design the RIS phase shifts with (16), the interference to the receive devices will be completely cancelled. In this case, the SINR at the receive device-$\ell$ would simplify to $\mathrm{SINR}_{\ell}^{\mathtt{D}}=p^{\mathtt{D}}_{\ell}|f_{\mathrm{sig},\ell}^{\mathtt{DD}}|^{2}/\sigma_{\mathtt{D}}^{2}$.

With the $\boldsymbol{\phi}_{\mathrm{IC}}$ representation in (16), we can use the Cauchy–Schwarz inequality to find the following upper bound for the SINR of user-$k$:

	$\displaystyle\mathrm{SINR}_{k}^{\mathtt{U}}$	$\displaystyle\leq p^{\mathtt{U}}_{k}\|\mathbf{h}^{\mathtt{UB}}_{k}+\mathbf{G}^{\mathtt{UB}}_{k}\boldsymbol{\phi}_{\mathrm{IC}}\|^{2}/\sigma_{\mathtt{B}}^{2}$		(17)
		$\displaystyle=p^{\mathtt{U}}_{k}\|\mathbf{h}^{\mathtt{UB}}_{k}+\mathbf{G}^{\mathtt{UB}}_{k}(\mathbf{B}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{d})\|^{2}/\sigma_{\mathtt{B}}^{2}$		(18)
		$\displaystyle=p^{\mathtt{U}}_{k}\|\mathbf{Z}_{k}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{q}_{k}\|^{2}/\sigma_{\mathtt{B}}^{2},$		(19)

where $\mathbf{Z}_{k}=\mathbf{G}^{\mathtt{UB}}_{k}\mathbf{B}$ and $\mathbf{q}_{k}=\mathbf{h}^{\mathtt{UB}}_{k}+\mathbf{G}^{\mathtt{UB}}_{k}\mathbf{d}$. Therefore, we propose the following IC-based optimization problem

		$\displaystyle\operatorname*{maximize}_{\{\xi,\;\mathbf{f}_{\mathrm{sig}}^{\mathtt{DD}}\}}$		$\displaystyle\xi$		(20)
		$\displaystyle\operatorname{subject\ to}$		$\displaystyle p^{\mathtt{U}}_{k}\|\mathbf{Z}_{k}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{q}_{k}\|^{2}/\sigma_{\mathtt{B}}^{2}\geq\xi\;\forall k$
		$\displaystyle p^{\mathtt{D}}_{\ell}|f_{\mathrm{sig},\ell}^{\mathtt{DD}}|^{2}/\sigma_{\mathtt{D}}^{2}\geq\xi\;\forall\ell$
		$\displaystyle|\mathbf{b}_{i}^{H}\mathbf{f}_{\mathrm{sig}}^{\mathtt{DD}}+d_{i}|^{2}\leq 1\;\forall i=1,\ldots,N,$

where the constraint $|\mathbf{b}_{i}^{H}\mathbf{f}_{\mathrm{sig}}^{\mathtt{DD}}+d_{i}|^{2}\leq 1$ is equivalent to the constraint $|\phi_{i}|^{2}\leq 1$. Hence, we have transformed the RIS phase shift $\boldsymbol{\phi}$ optimization problem into an effective D2D channel optimization (20) by exploiting the IC representation (16).

The problem in (20) can also be easily solved using SDR. Specifically, let

$$\boldsymbol{\Omega}_{k}=\begin{bmatrix}[1.2]\mathbf{Z}_{k}^{H}\mathbf{Z}_{k}&\mathbf{Z}_{k}^{H}\mathbf{q}_{k}\\ \mathbf{q}_{k}^{H}\mathbf{Z}_{k}&\|\mathbf{q}_{k}\|^{2}\end{bmatrix}\;\text{and}\;\boldsymbol{\Upsilon}_{i}=\begin{bmatrix}[1.2]\mathbf{b}_{i}\mathbf{b}_{i}^{H}&\mathbf{b}_{i}d_{i}\\ \mathbf{b}_{i}^{H}d_{i}^{*}&|d_{i}|^{2}\end{bmatrix},$$

so that

	$\displaystyle\|\mathbf{Z}_{k}\mathbf{f}^{\mathtt{DD}}_{\mathrm{sig}}+\mathbf{q}_{k}\|^{2}=\operatorname{tr}(\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}\boldsymbol{\Omega}_{k})$
	$\displaystyle|\mathbf{b}_{i}^{H}\mathbf{h}_{\mathrm{sig}}^{\mathtt{DD}}+d_{i}|^{2}=\operatorname{tr}(\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}\boldsymbol{\Upsilon}_{i}),$

where $\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}=\mathbf{\tilde{f}}^{\mathtt{DD}}_{\mathrm{sig}}(\mathbf{\tilde{f}}^{\mathtt{DD}}_{\mathrm{sig}})^{T}$ with $\mathbf{\tilde{f}}^{\mathtt{DD}}_{\mathrm{sig}}=[(\mathbf{{f}}^{\mathtt{DD}}_{\mathrm{sig}})^{T},1]^{T}$. Problem (20) can be now relaxed to a convex optimization problem:

		$\displaystyle\operatorname*{maximize}_{\{\xi,\;\mathbf{F}_{\mathrm{sig}}^{\mathtt{DD}}\succeq\mathbf{0}\}}$		$\displaystyle\xi$		(21)
		$\displaystyle\operatorname{subject\ to}$		$\displaystyle p^{\mathtt{U}}_{k}\operatorname{tr}(\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}\boldsymbol{\Omega}_{k})/\sigma_{\mathtt{B}}^{2}\geq\xi\;\forall k$
		$\displaystyle p^{\mathtt{D}}_{\ell}\Re\{\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig},\ell,\ell}\}/\sigma_{\mathtt{D}}^{2}\geq\xi\;\forall\ell$
		$\displaystyle\operatorname{tr}(\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}\boldsymbol{\Upsilon}_{i})\leq 1\;\forall i=1,\ldots,N$
		$\displaystyle\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig},L+1,L+1}=1,$

which again can be solved using SDR. Finally, we need to recover an IC solution $\boldsymbol{\hat{\phi}}_{\mathrm{IC}}$ from $\mathbf{\tilde{F}}^{\mathtt{DD}}_{\mathrm{sig}}$, which can also be done using the Gaussian randomization method. Given a $\boldsymbol{\hat{\phi}}_{\mathrm{IC}}$, the corresponding LMMSE combiner at the BS can be computed.

It can be seen that unlike the AO approach which needs to solve a series of SDR problems, the IC approach involves only one SDR optimization and therefore significantly reduces the computational complexity. We will show later that if the AO approach is initialized with $\boldsymbol{\hat{\phi}}_{\mathrm{IC}}$, it converges more rapidly with better performance compared to using a random initialization.

Limited feedback for single D2D pair: To implement the IC method for the case of multiple device pairs, it is required that each receive device-$\ell$ forwards its estimated CSI including two cascaded channel matrices $\mathbf{G}_{\ell}^{\mathtt{DD}}\in\mathbb{C}^{L\times N}$, $\mathbf{G}_{\ell}^{\mathtt{UD}}\in\mathbb{C}^{K\times N}$ and two direct channel vectors $\mathbf{H}^{\mathtt{DD}}_{\ell,:}\in\mathbb{C}^{1\times L}$, $\mathbf{H}^{\mathtt{UD}}_{\ell,:}\in\mathbb{C}^{1\times K}$ via a control link to the BS, which results in a total number of $(L+K)(N+1)$ complex coefficients to be fed-back.

However, for the case of a single device pair, the representation in (14) can be obtained at the receive device as follows:

$\displaystyle\boldsymbol{{\phi}}$

$\displaystyle=\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}\left(\begin{bmatrix}[1.2]f^{\mathtt{DD}}\\ \mathbf{f}^{\mathtt{UD}}\end{bmatrix}-\begin{bmatrix}[1.2]h^{\mathtt{DD}}\\ \mathbf{h}^{\mathtt{UD}}\end{bmatrix}\right)$

(22)

where $\mathbf{A}=[(\mathbf{g}^{\mathtt{DD}})^{T},\,\mathbf{G}^{\mathtt{UD}}]$ and we have dropped the device index $\ell$ since there is only D2D pair here. By setting $\mathbf{f}^{\mathtt{UD}}=\mathbf{0}$, the $\boldsymbol{\phi}_{\mathrm{IC}}$ representation that cancels the interference at the device is

$\displaystyle\boldsymbol{{\phi}}_{\mathrm{IC}}$

$\displaystyle=\mathbf{b}f^{\mathtt{DD}}+\mathbf{d},$

(23)

where $\mathbf{b}$ is the first column of $\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}$ and $\mathbf{d}=-\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}[h^{\mathtt{DD}},(\mathbf{h}^{\mathtt{UD}})^{T}]^{T}$. This means the receive device can calculate the matrix $\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}$ using its local CSI, then obtain the two corresponding vectors $\mathbf{b}$ and $\mathbf{d}$, which will be forwarded to the BS to solve the RIS phase shift optimization problem:

		$\displaystyle\operatorname*{maximize}_{\{\xi,\;{f}^{\mathtt{DD}}\}}$		$\displaystyle\xi$		(24)
		$\displaystyle\operatorname{subject\ to}$		$\displaystyle p^{\mathtt{U}}_{k}\|\mathbf{z}_{k}{f}^{\mathtt{DD}}+\mathbf{q}_{k}\|^{2}/\sigma_{\mathtt{B}}^{2}\geq\xi\;\forall k$
		$\displaystyle p^{\mathtt{D}}|f^{\mathtt{DD}}|^{2}/\sigma_{\mathtt{D}}^{2}\geq\xi$
		$\displaystyle|b_{i}f^{\mathtt{DD}}+d_{i}|^{2}\leq 1\;\forall i=1,\ldots,N.$

Thus, instead of forwarding the $(K+1)(N+1)$ complex coefficients from $\mathbf{g}^{\mathtt{DD}}\in\mathbb{C}^{N\times 1}$, $\mathbf{G}^{\mathtt{UD}}\in\mathbb{C}^{K\times N}$, $h^{\mathtt{DD}}$, and $\mathbf{h}^{\mathtt{UD}}\in\mathbb{C}^{K\times 1}$, the receive device finds $\mathbf{b}$ and $\mathbf{d}$ and forwards these two vectors to the BS. This only requires transmission of $2N$ complex coefficients, but still guarantees that the BS can solve the RIS phase shift optimization problem.

In this section, we present numerical results to show the superiority and benefits of the proposed IC and IC-AO approaches where IC-AO indicates the AO approach that uses the IC solution $\boldsymbol{\hat{\phi}}_{\mathrm{IC}}$ as an initialization. For the regular AO method, we use a random initial solution for $\boldsymbol{\phi}$. We consider $K=2$ users, $L=2$ device pairs, and $M=8$ antennas at the BS. If not specifically stated, the number of RIS elements is set to $64$. We position the BS and the RIS at the locations $(x,y)=(0,0)$ and $(x,y)=(100,30)$, respectively. The cellular users and transmit devices are randomly located within a circular area whose center is $(x,y)=(200,0)$ with a radius of $25$ m, and we also locate the receive devices randomly also within a circular area centered at $(x,y)=(50,0)$ with the same radius. The transmit power of the cellular users and the transmit devices are set to be the same. The noise power is set to $-169$ dBm/Hz and a bandwidth of $1$ MHz is assumed. The large-scale fading is modeled as $\beta=\beta_{0}(d/d_{0})^{-\eta}$, where $\eta$ is the path loss exponent and $d$ is the distance. We set $\beta_{0}=-30$ dB as the path loss at the reference distance $d_{0}=1$m. The path loss exponent of the user-RIS, TxD-RIS, RIS-RxD, and RIS-BS channel links is set to $2.2$. However, the path loss exponent of the user-BS and TxD-BS channels is set to $4$ and the path loss exponent of the user-RxD and TxD-RxD channels are set to $5$, to model their weak propagation.

In Fig. 1, we show a comparison of the minimum SINR performance and computational complexity as the transmit power changes. It can be seen from Fig. 1(a) that the AO and IC-AO approaches give the same minimum SINRs, which are about $2.5$ to $3$ dB higher than that of the IC approach. However, the computational complexity of the IC approach is much lower than that of AO and IC-AO since the IC approach requires only one iteration while AO and IC-AO require many more iterations as seen in Fig. 1(b). It is also observed that although the AO and IC-AO approaches give the same SINR performance, IC-AO has a lower computational complexity since it requires a smaller number of iterations.

Next, in Fig. 2, we also show a comparison for the minimum SINR performance and computational complexity but with a fixed transmit power of $30$ dBm and the number of RIS elements $N$ is varied. The minimum SINRs for AO and IC-AO are still about $3$-dB higher than that of the IC approach. However, it is interesting that as the number of RIS elements $N$ increases, the IC-AO approach tends to perform better than AO even though IC-AO still requires a smaller number of iterations. This indicates that IC-AO not only converges faster than AO but also converges to better local solutions.

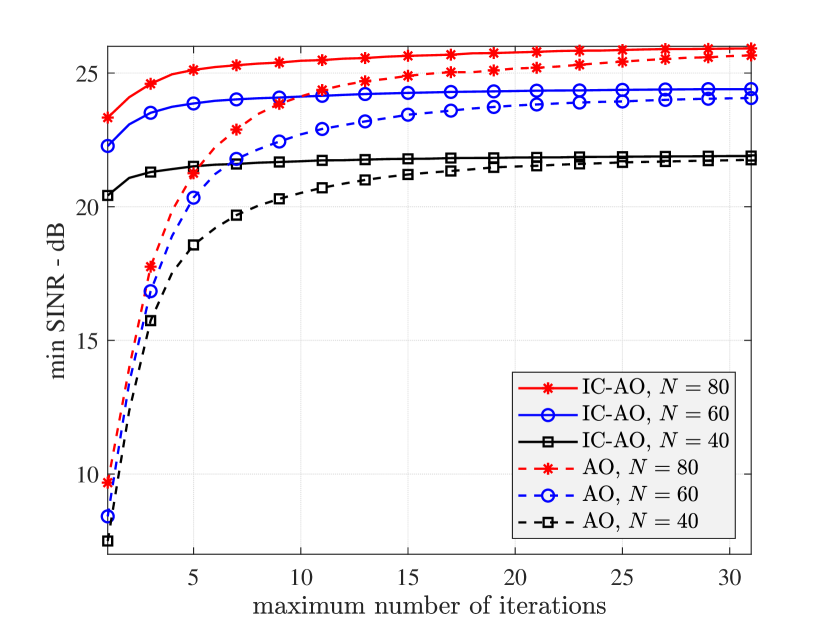
Finally, we show an SINR performance comparison between the AO and IC-AO approaches in Fig. 3 as the maximum number of iterations changes. It is clear that IC-AO converges much faster than AO and if we set a small maximum number of iterations, the performance of IC-AO will be significantly higher than that of AO. For example, if we set the maximum number of iterations to $5$, the IC-AO approach has already nearly converged and its minimum SINRs are about $4$-dB, $3.5$-dB, and $3$-dB higher than that of AO for $N=80$, $60$, $40$, respectively.

This paper has considered a minimum SINR maximization problem in an RIS-aided joint D2D and cellular communication system where the RIS was exploited to simultaneously support the cellular users and the devices. We first presented an AO approach based on the SDR technique to solve the min-max SINR problem. We then derived a representation for the RIS phase shift vector that cancels the interference to the D2D links. Based on the IC representation, we proposed an IC algorithm whose complexity is much lower than that of the AO approach. We also showed that the IC solution can help the AO approach converge faster and achieve better performance. It was also pointed out that for the case of a single D2D pair, the proposed IC approach can be accomplished with limited feedback from the device.