This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Rice’s theorem for generic limit sets of cellular automata

Martin Delacourt
Université d’Orléans, LIFO EA4022, FR-45067 Orléans, France
[email protected]
Abstract

The generic limit set of a cellular automaton is a topologically defined set of configurations that intends to capture the asymptotic behaviours while avoiding atypical ones. It was defined by Milnor then studied by Djenaoui and Guillon first, and by Törmä later. They gave properties of this set related to the dynamics of the cellular automaton, and the maximal complexity of its language. In this paper, we prove that every non trivial property of these generic limit sets of cellular automata is undecidable.

1 Introduction

Cellular automata (CA) are discrete dynamical systems defined by a local rule, introduced in the 40s by John von Neumann [13]. Given a finite alphabet 𝒜\mathcal{A}, the global rule on 𝒜ℤ\mathcal{A}^{\mathbb{Z}} is given by the synchronous application of the local one at every coordinate. They can be seen as models of computation, dynamical systems or many phenomena from different fields, providing links between all of these [5, 9].

The asymptotic behaviour of CA has been studied a lot, mainly using the definition of limit set: the set of points that can be observed arbitrarily far in time. In particular concerning the complexity of this set: it can be non-recursive, the nilpotency problem is undecidable and there is Rice’s theorem on properties of the limit set of CA [6, 7, 8]. Rice’s theorem states that every nontrivial property of the limit set of CA is undecidable. Other definitions were introduced in order to restrain to typical asymptotic behaviour. Milnor proposed the definition of likely limit set and generic limit set in [11] in the more general context of dynamical systems. While the likely limit set is defined in the measure-theoretical world, the generic limit set is a topological variant. Djenaoui and Guillon proved in [4] that both are equal for full-support σ\sigma-ergodic measures in the case of CA.

The generic limit set is the smallest closed subset of the fullshift Σℤ\Sigma^{\mathbb{Z}} containing all limit points of all configurations taken in a comeager subset of Σℤ\Sigma^{\mathbb{Z}}. Djenaoui and Guillon studied the generic limit set in [4], proving results on the structure of generic limit sets related to the directional dynamics of CA. They also provide a combinatorial characterization of the language of the generic limit sets and examples of CA with different limit, generic limit and μ\mu-limit sets. The latter was introduced in [10] by Kůrka and Maass as another measure-theoretical version of limit set.

The μ\mu-limit set is determined by its language which is the set of words that do not disappear in time, relatively to the measure μ\mu. Amongst the results on the μ\mu-limit set, it was proved in [1] that the complexity of the language is at the level 33 of the arithmetical hierarchy (Σ30\Sigma_{3}^{0}), with a complete example, it was also proved that the nilpotency problem is Π30\Pi_{3}^{0}-complete. Rice’s theorem also holds stating that each nontrivial property has at least Π30\Pi_{3}^{0} complexity. A slightly different approach led Hellouin and Sablik to similar results on the limit probability measure in [2].

In [12], Törmä proved computational complexity results on the generic limit sets, in particular an example of a CA with a Σ30\Sigma_{3}^{0}-complete generic limit set, and constraints on the complexity when the dynamics of the CA is too simple on the generic limit set.

In this paper, we prove Rice’s theorem on generic limit sets combining ideas from [8] and [1].

2 Definitions

In this paper, we consider the countable set 𝒬={q0,q1,q2,…}\mathcal{Q}=\{q_{0},q_{1},q_{2},\dots\}. Every finite alphabet will be a finite subset of 𝒬\mathcal{Q}. Given a finite alphabet Σ⊆𝒬\Sigma\subseteq\mathcal{Q} and a radius r∈ℕr\in\mathbb{N}, a local rule is a map δ:Σ2​r+1→Σ\delta:\Sigma^{2r+1}\to\Sigma and a cellular automaton ℱ:Σℤ→Σℤ\mathcal{F}:\Sigma^{\mathbb{Z}}\to\Sigma^{\mathbb{Z}} is the global function associated with some local rule δ\delta: for every c∈Σℤc\in\Sigma^{\mathbb{Z}} and every i∈ℤi\in\mathbb{Z}, ℱ​(c)i=δ​(ci−r,ci−r+1,…,ci+r)\mathcal{F}(c)_{i}=\delta(c_{i-r},c_{i-r+1},\dots,c_{i+r}). We call configurations the elements of Σℤ\Sigma^{\mathbb{Z}}. The orbit of an initial configuration cc under ℱ\mathcal{F} is called a space-time diagram. Time goes upward in the illustrations of this paper.

Define the Cantor topology on Σℤ\Sigma^{\mathbb{Z}} using the distance d​(c,c′)=12id(c,c^{\prime})=\frac{1}{2^{i}} where i=min⁡{j∈ℕ,cj≠cj′​ or ​c−j≠c−j′}i=\min\{j\in\mathbb{N},c_{j}\neq c^{\prime}_{j}\textrm{ or }c_{-j}\neq c^{\prime}_{-j}\}. For any word w∈Σ∗w\in\Sigma^{*}, denote |w||w| the length of ww and [w]i={c∈Σℤ:∀k<|w|,ci+k=wk}[w]_{i}=\{c\in\Sigma^{\mathbb{Z}}:\forall k<|w|,c_{i+k}=w_{k}\} the associated cylinder set, which is a clopen set.

Denote σ\sigma the shift on Σℤ\Sigma^{\mathbb{Z}}, which is the CA such that ∀c∈Σℤ,∀i∈ℤ,σ​(c)i=ci+1\forall c\in\Sigma^{\mathbb{Z}},\forall i\in\mathbb{Z},\sigma(c)_{i}=c_{i+1}. A subshift is a closed σ\sigma-invariant subset of Σℤ\Sigma^{\mathbb{Z}}. A subshift can be equivalently defined by the set of forbidden words, in this case a subshift is the set of configurations that do not belong to any [w]i[w]_{i} where ww is forbidden.

In this paper, a Turing machine works on a semi-infinite (to the right) tape, with a finite alphabet 𝒜\mathcal{A} containing a blank symbol ⊥\bot. It has one initial state q0q_{0} and one final state qfq_{f}. At each step of the computation, the head of the machine reads the symbol at the position on the tape to which it points, and decides the new symbol that is written on the tape, the new state it enters, and its move (one cell at most). It can be simulated by a CA using states that can contain the head of the machine and the tape alphabet. We will here only simulate machines in a finite space in which there is only one head.

2.1 Limit sets of cellular automata

Different definitions of the asymptotic behavior of a CA have been given. The most classical one is the limit set Ωℱ=⋂t∈ℕℱt​(Σℤ)\Omega_{\mathcal{F}}=\bigcap_{t\in\mathbb{N}}\mathcal{F}^{t}(\Sigma^{\mathbb{Z}}) of a CA ℱ\mathcal{F}, that is the set of configurations that can be seen arbitrarily late in time. For any subset X⊆ΣℤX\subseteq\Sigma^{\mathbb{Z}}, define ω​(X)\omega(X) as the set of limit points of orbits of configurations in XX: c∈ω​(X)⇔∃c′∈X,lim inft→∞d​(ℱt​(c′),c)=0c\in\omega(X)\Leftrightarrow\exists c^{\prime}\in X,\liminf_{t\to\infty}d(\mathcal{F}^{t}(c^{\prime}),c)=0. The set ω​(Σℤ)\omega(\Sigma^{\mathbb{Z}}) is called the asymptotic set of ℱ\mathcal{F}.

A subset X⊆ΣℤX\subseteq\Sigma^{\mathbb{Z}} is said to be comeager if it contains a countable intersection of dense open sets. It implies in particular that XX is dense (Baire property).

For X⊆ΣℤX\subseteq\Sigma^{\mathbb{Z}}, define the realm of attraction 𝒟​(X)={c∈Σℤ:ω​(c)⊆X}\mathcal{D}(X)=\{c\in\Sigma^{\mathbb{Z}}:\omega(c)\subseteq X\}. The generic limit set ω~​(ℱ)\tilde{\omega}(\mathcal{F}) of ℱ\mathcal{F} is then defined as the intersection of all closed subsets of Σℤ\Sigma^{\mathbb{Z}} whose realms of attraction are comeager.

The following two examples show differences between all these sets, they were already presented in [4].

Example 2.1 (The Min CA).

Consider the CA ℱ\mathcal{F} of radius 11 on alphabet {0,1}\{0,1\} whose local rule is (x,y,z)↦min⁡(x,y,z)(x,y,z)\mapsto\min{(x,y,z)}. The state 0 is spreading, that is, every cell that sees this state will enter it too. A space-time diagram of the MIN CA is represented in Figure 1.

We have:

  • •

    Ωℱ={c∈{0,1}ℤ:∀i∈ℤ,k∈ℕ∗,c∉[10k1]i]}\Omega_{\mathcal{F}}=\{c\in\{0,1\}^{\mathbb{Z}}:\forall i\in\mathbb{Z},k\in\mathbb{N}^{*},c\notin[10^{k}1]_{i}]\};

  • •

    ω~​(ℱ)={0ℤ}\tilde{\omega}(\mathcal{F})=\{0^{\mathbb{Z}}\} and it is equal to the μ\mu-limit set for a large set of measures containing every non degenerate Markov measure.

Refer to caption
Figure 1: Some part of a space-time diagram of the Min CA, 0 is represented by the white state and 11 by the black state.
Example 2.2 (Gliders).

Consider the CA ℱ\mathcal{F} of radius 11 on alphabet {0,>,<}\{0,>,<\}. The states << and >> are respectively speed −1-1 and 11 signals over a background of 0s. When a << and a >> cross, they both disappear. A space-time diagram of this CA is represented in Figure 2. For a complete description of the rule, see for example [10, Example 3].

We have:

  • •

    Ωℱ={c∈{0,<,>}ℤ:∀i∈ℤ,k∈ℕ,c∉[<0k>]i]}\Omega_{\mathcal{F}}=\{c\in\{0,<,>\}^{\mathbb{Z}}:\forall i\in\mathbb{Z},k\in\mathbb{N},c\notin[<0^{k}>]_{i}]\};

  • •

    ω~​(ℱ)=Ωℱ\tilde{\omega}(\mathcal{F})=\Omega_{\mathcal{F}};

  • •

    the μ\mu-limit set depends here of μ\mu. With μ\mu the uniform Bernoulli measure, it is {0ℤ}\{0^{\mathbb{Z}}\}. If μ\mu is Bernoulli with a bigger probability for << than for >>, then the μ\mu-limit set is {{0,<}ℤ}\{\{0,<\}^{\mathbb{Z}}\}.

Refer to caption
Figure 2: The << and >> states of the Gliders CA are particles going in different directions and annihilating each other when they cross.

2.2 Preliminary properties of generic limit sets of CA

Many properties of generic limit sets were proved either in [11] or in [4] for the particular case of CA.

Proposition 2.3 (Prop 4.2 of [4]).

Given a CA ℱ\mathcal{F}, the realm of attraction of ω~​(ℱ)\tilde{\omega}(\mathcal{F}) is comeager.

Proposition 2.4 (Prop 4.4 of [4]).

Given a CA ℱ\mathcal{F}, ω~​(ℱ)\tilde{\omega}(\mathcal{F}) is a subshift.

Note that the limit set of a CA is also a subshift whereas the asymptotic limit set may not be.

Proposition 2.5 (Cor 4.7 of [4]).

Given a CA ℱ\mathcal{F} on alphabet Σ\Sigma, ω~​(ℱ)=Σℤ⇔ℱ​ is surjective\tilde{\omega}(\mathcal{F})=\Sigma^{\mathbb{Z}}\Leftrightarrow\mathcal{F}\textrm{ is surjective}.

The last result of this section comes from Remark 4.3 of [4] and is reformulated as Lemma 2 of [12]:

Lemma 2.6.

Let ℱ\mathcal{F} be a CA on Σℤ\Sigma^{\mathbb{Z}}. A word s∈Σ∗s\in\Sigma^{*} occurs in ω~​(ℱ)\tilde{\omega}(\mathcal{F}) if and only if there exists a word v∈Σ∗v\in\Sigma^{*} and i∈ℤi\in\mathbb{Z} such that for all u,w∈Σ∗u,w\in\Sigma^{*}, there exist infinitely many t∈ℕt\in\mathbb{N} with ℱt​([u​v​w]i−|u|)∩[s]≠∅\mathcal{F}^{t}([uvw]_{i-|u|})\cap[s]\neq\emptyset.

The word vv is said to enable ss.

3 General structure of the construction

The proof of the main result of this paper relies on a construction already presented in [3, 1, 2]. The present section contains the description of this tool. The idea is to erase most of the content of the initial configuration and start a protected (hence controled) and synchronized evolution. Of course, to ensure that this property holds for any configuration, one needs strong constraints on the dynamics of the CA. Here, we also want to allow a wide variety of dynamics, hence this property shall hold for almost every initial configuration. In the above-cited articles, it was true for μ\mu-almost every configuration, and here we will use a topological variant.

A brief description of this CA ℱ\mathcal{F} follows. Its radius should be at least 22.

3.1 Overview

Some particular state [Uncaptioned image]∈Σ\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt{}\in\Sigma can only appear in the initial configuration: there is no rule that produces it. The states [Uncaptioned image]   will trigger the desired evolution. In order to avoid having to deal with anything unwanted on the initial configuration (like words produced by the evolution of the CA placed in a wrong context), we add a mechanism that cleans the configuration from anything that is not produced by [Uncaptioned image]  . This is achieved through the propagation of large signals that have the information of the time passed since a [Uncaptioned image]   state produced it, that is their age. Then, when two such signals going in opposite directions meet, they compare their ages and only the younger survives.

With this trick, any configuration that contains infinitely many [Uncaptioned image]   on both sides will ultimately be covered by protected areas. The [Uncaptioned image]   states also transform into [Uncaptioned image]∈Σ\vbox to7.0pt{\hbox{\includegraphics{sts}}}\hskip 1.00006pt{}\in\Sigma states, and we consider the words in the space-time diagram that are delimited by [Uncaptioned image]   states produced by [Uncaptioned image]   states, we call them segments. The dynamics of the CA inside a segment only depends on its size. In particular, the simulation of the computation of a given Turing machine can be started on each [Uncaptioned image]   state when it appears.

A close construction with a more precise and complete description can be found in [1, Section 3.1].

3.2 Initialization and counters

The state [Uncaptioned image]   can only appear in the initial configuration: it is not produced by any rule and it disappears immediately. Consider a cell at coordinate ii that contains a [Uncaptioned image]   state in the initial configuration. On each side of the [Uncaptioned image]   state, two signals are sent at speed sfs_{f} and sbs_{b} to the right and symmetrically to the left. The fastest one (speed sfs_{f}) erases everything it encounters except for its symmetrical counterpart. Each couple of signals is seen as one counter whose value is encoded by the distance ⌊k​(sf−sb)⌋\lfloor k(s_{f}-s_{b})\rfloor after kk steps of the CA. The key point is that, at any time, the value of a counter is minimal exactly for counters generated by a [Uncaptioned image]   state.

When two counters meet, they compare their values without being affected until the comparison is done. The comparison process is done via signals bouncing on the borders of the counters. The speed of these inner signals is greater than the speeds (sfs_{f} and sbs_{b}) of the border signals. As the value is encoded by the distance between border signals, it is a geometric comparison illustrated in Figure 3. If one counter is younger than the other one, the older one is deleted (the right one in Figure 3). If they are equal, both counters, that is the 44 signals, are deleted.

Claim 3.1.

For any configuration cc where [Uncaptioned image]   occurs, and any coordinate i∈ℤi\in\mathbb{Z}, denote di=min⁡{|i−j|:cj=[Uncaptioned image]}d_{i}=\min\{|i-j|:c_{j}=\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt\}. Then for any t>sb​dit>s_{b}d_{i} (where sbs_{b} is the speed of the inner border of the counter), ℱt​(c)i\mathcal{F}^{t}(c)_{i} does not contain a counter state.

  • Proof: Each sequence of consecutive [Uncaptioned image]   states creates a left counter at its left extremity and a right counter at its right extremity. They all share a common age which is the minimal one, hence they cannot be crossed by another counter. Thus, at most one of the youngest counters can cross cell ii. And due to the speed of the inner border of the counters, this is done after sb​dis_{b}d_{i} steps.

Refer to caption
Figure 3: When counters meet in OO, signals move at speed 11 towards the borders of the counters that they reach at points CC and C′C^{\prime}. They bounce back until they cross the sign left at point OO. The one that arrives first has crossed the most narrow (hence youngest) one. It bounces once again to erase the opposite counter whose border is reached at point EE.

Last rule of this construction: every [Uncaptioned image]   state that is not surrounded by other [Uncaptioned image]   states on both sides is replaced by a [Uncaptioned image]   state after it gave birth to the counters. Figure 4 shows how a typical initial configuration evolves.

For any time t∈ℕt\in\mathbb{N} and any configuration cc, we call segment a set of consecutive cells from coordinate ii to jj in ℱt​(c)\mathcal{F}^{t}(c) with i,j∈ℤi,j\in\mathbb{Z} such that:

  • •

    ℱt​(c)i=[Uncaptioned image]=ℱt​(c)j\mathcal{F}^{t}(c)_{i}=\vbox to7.0pt{\hbox{\includegraphics{sts}}}\hskip 1.00006pt=\mathcal{F}^{t}(c)_{j}

  • •

    for every i<k<ji<k<j, ℱt​(c)k≠[Uncaptioned image]\mathcal{F}^{t}(c)_{k}\neq\vbox to7.0pt{\hbox{\includegraphics{sts}}}\hskip 1.00006pt

  • •

    ci=[Uncaptioned image]c_{i}=\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt and cj=[Uncaptioned image]c_{j}=\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt.

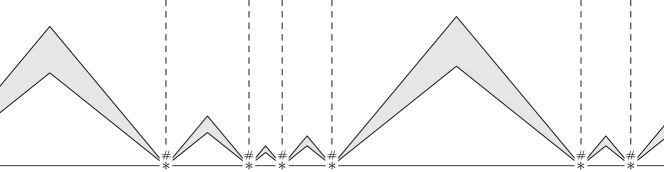
Refer to caption
Figure 4: Starting from a configuration containing infinitely many Refer to caption   states on the left and on the right, the Refer to caption   states generate counters (filled in grey) on both sides that erase everything but another counter going in the opposite direction. These counters eventually meet their opposite and disappear after comparing their ages, hence remain an immaculate configuration with Refer to caption   states in some positions.

Note that if the radius of the CA can be arbitrarily large, any choice of speeds sf>sbs_{f}>s_{b} can be made.

Claim 3.2.

For any s∈ℚs\in\mathbb{Q}, there exists a CA implementing such a construction with speed sb>ss_{b}>s (and hence sfs_{f}).

  • Proof: A big enough radius allows fast enough signals to perform the comparison of counters in due time.

4 Rice’s theorem

Following the steps of the historical proof of Rice and concerning CA, the theorems on limit sets in [8] and μ\mu-limit sets in [3], we first define properties of generic limit sets of CA, then prove that every non trivial such property is undecidable.

The CA used in [3] to prove Rice’s theorem for μ\mu-limit sets also has the general structure presented in the previous section. The difference lies in what is done inside segments. In the case of μ\mu-limit sets (regardless of the choice of μ\mu), it is possible to dedicate a small technical space inside segments to any activity that shouldn’t appear in the μ\mu-limit set, as long as this space tends to disappear in density. This is achieved through larger and larger segments. Nothing prevents the states of this technical space to appear in the generic limit set.

4.1 Properties of generic limit sets of CA

A property of the generic limit set of CA is a set of subshifts and we say that a generic limit set have this property if it belongs to this set. This way, it depends only on the generic limit set: if two CA have the same generic limit set, this common generic limit set either has or not the property. As mentionned earlier, we consider the countable set 𝒬={q0,q1,…}\mathcal{Q}=\{q_{0},q_{1},\dots\}, and every alphabet is a finite subset of 𝒬={q0,q1,…}\mathcal{Q}=\{q_{0},q_{1},\dots\}.

Definition 4.1.

A property 𝒫\mathcal{P} of generic limit sets of cellular automata is a subset of the powerset 𝒫​(𝒬ℤ)\mathscr{P}(\mathcal{Q}^{\mathbb{Z}}). A generic limit set of some cellular automaton is said to have property 𝒫\mathcal{P} if it is in 𝒫\mathcal{P}.

Note that many sets that are not subshifts can belong to a property 𝒫\mathcal{P}, as every generic limit set is a subshift, they do not matter. In particular, every property that does not contain a subshift is equivalent to the empty property that no generic limit set has. A property is said to be trivial when either it contains all generic limit sets or none. The most natural example of a non trivial property is the generic nilpotency, which is given by the family {{qiℤ},i∈ℕ}\{\{q_{i}^{\mathbb{Z}}\},i\in\mathbb{N}\}.

This definition prevents confusions between properties of generic limit sets and properties concerning generic limit sets. For example the property containing every fullshift on finite alphabets is not surjectivity, since the generic limit set of a CA on alphabet Σ\Sigma could be a fullshift on a strictly smaller alphabet. Hence surjectivity is not a property of generic limit sets even if being surjective is equivalent to having a full generic limit set. .

4.2 The theorem

Theorem 4.1.

Every non trivial property of the generic limit sets of CA is undecidable.

This section is dedicated to the proof of Rice’s theorem. It is a many-one (actually one-one) reduction from the Halting problem on empty input for Turing machines. Take a non trivial property 𝒫\mathcal{P} of generic limit sets of CA. Assume for example that 𝒫∩{{qkℤ},k∈ℕ}\mathcal{P}\cap\{\{q_{k}^{\mathbb{Z}}\},k\in\mathbb{N}\} is infinite (the other case leads to a symmetric proof). As 𝒫\mathcal{P} is non trivial, it is possible to choose qn∈𝒬q_{n}\in\mathcal{Q} and a CA ℱ1\mathcal{F}_{1} such that ω~​(ℱ1)∉𝒫\tilde{\omega}(\mathcal{F}_{1})\notin\mathcal{P} and qn∉Σ1q_{n}\notin\Sigma_{1} where Σ1\Sigma_{1} is the alphabet of ℱ1\mathcal{F}_{1}. Denote now ℱ0\mathcal{F}_{0} the CA on alphabet {qn}\{q_{n}\} whose local rule always produces {qn}\{q_{n}\}. Hence ω~​(ℱ0)={qnℤ}∈𝒫\tilde{\omega}(\mathcal{F}_{0})=\{q_{n}^{\mathbb{Z}}\}\in\mathcal{P}.

For any Turing machine MM, we produce a CA ℱM\mathcal{F}_{M} such that:

  • •

    if MM eventually halts on empty input, the generic limit set of ℱM\mathcal{F}_{M} is {qnℤ}\{q_{n}^{\mathbb{Z}}\};

  • •

    if MM never halts on empty input, then the generic limit set of ℱM\mathcal{F}_{M} is ω~​(ℱ1)\tilde{\omega}(\mathcal{F}_{1}).

4.2.1 Construction of ℱM\mathcal{F}_{M}

The CA ℱM\mathcal{F}_{M} contains two layers, one for each of the main tasks. Denote π1\pi_{1} and π2\pi_{2} the projections on the first and second layer. The first layer uses alphabet Σ0\Sigma_{0} and it implements the construction described in Section 3. Denote _\_ the blank state of Σ0\Sigma_{0}. The second layer simulates the CA ℱ1\mathcal{F}_{1}. In some cases, the first layer can be erased, we also add a state qnq_{n}, hence the alphabet of ℱM\mathcal{F}_{M} is Σ=(Σ0×Σ1)∪{qn}∪Σ1\Sigma=(\Sigma_{0}\times\Sigma_{1})\cup\{q_{n}\}\cup\Sigma_{1}.

The set Σ0×Σ1\Sigma_{0}\times\Sigma_{1} can be mapped to a subset of 𝒬∖({qn}∪Σ1)\mathcal{Q}\setminus(\{q_{n}\}\cup\Sigma_{1}) to ensure that Σ⊂𝒬\Sigma\subset\mathcal{Q}. For the clarity of the presentation, we will denote the elements of Σ0×Σ1\Sigma_{0}\times\Sigma_{1} as couples.

The idea is to let ℱ1\mathcal{F}_{1} compute on the second layer (or by itself if the first layer has been erased), while computation on the first layer will either lead to erase this layer or generate a qnq_{n} state that will be spreading (erasing everything but counters) over the whole configuration.

On the first layer, once a [Uncaptioned image]   state appears (from a [Uncaptioned image]   state), a simulation of MM is started on its right. In the general case, another [Uncaptioned image]   state exists further on the right, in which case this simulation takes place in a segment. We will show later that the other case is irrelevant when considering the generic limit set. The simulation evolves freely except if it is blocked by the inner border of a counter, if this happens the simulated Turing head waits until it has enough space to make one more step. A binary counter is started in parallel to the right of the [Uncaptioned image]   state.

The simulation inside a segment should always be finite, it can be interrupted for one of the following reasons.

  • •

    The simulation of MM halts (because MM reaches a final state). Then the state qnq_{n} is written, erasing both layers of ℱM\mathcal{F}_{M}. This state spreads to both of its neighbors erasing everything, even the [Uncaptioned image]   states, except for the inner and outer borders of the counters of the construction of Section 3.

  • •

    It reaches a [Uncaptioned image]   on its right. That is there is not enough space inside the segment and the simulation is aborted. The first layer content of the segment will be erased as explained later.

  • •

    The counter reaches another [Uncaptioned image]   state. The time allowed for the simulation is over and the simulation is aborted. This third case is necessary to avoid problems due to a loop of the Turing machine in a finite space.

The states used for the simulation should not appear in the generic limit set, hence they have to be erased once the simulation halts or is aborted. In the first case, the state qnq_{n} is written in every cell. In the second case, the first layer only is erased. For the same reason, the [Uncaptioned image]   state has to be erased when the simulation is over in both the segments it delimits.

If the simulation is aborted (due to lack of space or end of the allowed time in the segment), an abortion signal is sent in both directions that erases everything of the first layer (except outer or inner border of counters) until it reaches a [Uncaptioned image]   state. A [Uncaptioned image]   state that receives such an abortion signal transforms into a [Uncaptioned image]   state. If a [Uncaptioned image]   state receives an abortion signal, it disappears. The point is to ensure that the abortion signals do not travel too far: if the first abortion signal deletes the [Uncaptioned image]   state on the side of the segment, then the one arriving from the other side will cross. This could lead to the presence of abortion signals in the generic limit set.

Figure 5 is a schematic view of the evolution of CA ℱM\mathcal{F}_{M} on an ordinary initial configuration.

Refer to caption
Figure 5: Starting from the cells in state Refer to caption   in the initial configuration, the counters (grey areas) protect everything above them. Segments are delimited by Refer to caption   states and in each of them a simulation of the computation of a Turing machine takes place (the red curve gives the position of the head). The green curve represents the extension of the binary counter used to limit the time of the simulation. In segment ⓐ, the counter reaches the limit and an abortion signal is sent (blue). In segment ⓑ, the head reaches the right of counter and the simulation is stopped with an abortion signal sent to the left. In segment ⓒ, the Turing machine halts and the spreading state qnq_{n} is written.
Claim 4.2.

There exists an increasing function f:ℕ→ℕf:\mathbb{N}\to\mathbb{N} such that the computation of MM simulated in a segment of length nn either halts or is aborted before time f​(n)f(n).

  • Proof: In a segment of length nn, due to the binary counter, if the simulation of MM has not reached a final state after 2n2^{n} steps, the computation is aborted.

4.2.2 Ensuring a sound computation on the second layer

The proof relies on the fact that, with most initial configurations:

  • •

    if MM halts, there will exist a large enough segment in which the computation has enough space and time to reach its end, thus producing state qnq_{n} that erases everything.

  • •

    if MM does not halt, the computation will be eventually aborted in every segment and only the second layer will remain with a computation of ℱ1\mathcal{F}_{1}.

In order to ensure the second point, we need to deal with the case of qnq_{n} states existing before the counters of Section 3 clean the configuration on the first layer. It can for example happen due to qnq_{n} states on the initial configuration. In this case, the content of the second layer is lost. As it is impossible to control what happens outside the area protected by counters, the counters will not only stop the spreading of qnq_{n} but also write a possible configuration for ℱ1\mathcal{F}_{1}, thus deleting all data that does not descend from the cells containing [Uncaptioned image]   in the first layer of the initial configuration.

Let us assume for simplicity that the radius of ℱ1\mathcal{F}_{1} is 11. For the rest of the proof of the theorem, denote x0x_{0} some state of Σ1\Sigma_{1}. The space-time diagram of ℱ1\mathcal{F}_{1} with initial configuration x0ℤx_{0}^{\mathbb{Z}} is ultimately periodic, contains only uniform configurations and is entirely described by a finite sequence of distinct states (x0,x1,…,xp,…,xp+T,xp)(x_{0},x_{1},\dots,x_{p},\dots,x_{p+T},x_{p}). The counters will write the second layer of the configuration as if every information coming from outside the protected area (between counters) was obtained from the uniform initial configuration x0ℤx_{0}^{\mathbb{Z}}:

  • •

    xtx_{t} at step t≤pt\leq p;

  • •

    xp+(t−p)modTx_{p+(t-p)\mod T} at step t≥pt\geq p.

As a finite amount of information is needed, the local rule of the CA ℱM\mathcal{F}_{M} can be designed to do so. This is illustrated in Figure 6. As said in Claim 3.2, it is possible to use that construction with outer borders of counters moving at speed 11.

If the first layer contains [Uncaptioned image]  , the state on the second layer is not rewritten and is used for the simulation of ℱ1\mathcal{F}_{1}.

Refer to caption
Figure 6: Partial representation of a space-time diagram of ℱM\mathcal{F}_{M}. The red cells are where the counters rewrite the second layer assuming that what does not come from a Refer to caption   state is x0x_{0}. The blue cells are where the computation of ℱ1\mathcal{F}_{1} happens normally on the second layer. The yellow lines are the outer borders of counters, we assume here they have speed 11 for the illustration. Denote δ1\delta_{1} the local rule of ℱ1\mathcal{F}_{1}. Then q′=δ1​(x,y,z)q^{\prime}=\delta_{1}(x,y,z) which are its state (yy) and the ones of its neighbors (xx and zz) at time 0. And q=δ1​(x0,x,y)q=\delta_{1}(x_{0},x,y).

To any initial configuration x∈Σℤx\in\Sigma^{\mathbb{Z}}, corresponds a configuration in Σ1ℤ\Sigma_{1}^{\mathbb{Z}} where all the deleted data is replaced by x0x_{0}. Denote ϕ:Σ→Σ1\phi:\Sigma\to\Sigma_{1} such that:

  • •

    ϕ​([Uncaptioned image],x)=x\phi(\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt,x)=x;

  • •

    ϕ​(s,x)=x0\phi(s,x)=x_{0} when s≠[Uncaptioned image]s\neq\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt;

  • •

    ϕ​(x)=x0\phi(x)=x_{0} when x∈Σ1∪{qn}x\in\Sigma_{1}\cup\{q_{n}\}.

It can be extended to words in Σ∗\Sigma^{*} and configurations in Σℤ\Sigma^{\mathbb{Z}}.

Claim 4.3.

Let cc be a configuration in ΣZ\Sigma^{Z} and i∈ℤi\in\mathbb{Z} a coordinate such that there exists j<i<kj<i<k with cj=[Uncaptioned image]=ckc_{j}=\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt=c_{k}. Then for any t>sb​dit>s_{b}d_{i} (as in Claim 3.1),

π2​(ℱMt​(c)i)∈{ℱ1t​(ϕ​(c))i,qn}\pi_{2}\left(\mathcal{F}_{M}^{t}(c)_{i}\right)\in\left\{\mathcal{F}_{1}^{t}(\phi(c))_{i},q_{n}\right\}

We extend here π2\pi_{2} as the identity to Σ1∪{qn}\Sigma_{1}\cup\{q_{n}\}.

  • Proof: As t>sb​dit>s_{b}d_{i}, the cell at coordinate ii is in the protected area (above [Uncaptioned image]   states or counters) at time tt. Then the second layer has been computed with the rule of ℱ1\mathcal{F}_{1} and the second layer of the configuration rewritten by counters into images of ϕ​(c)\phi(c). The only way to interrupt the computation of ℱ1\mathcal{F}_{1} is to erase the cell and write qnq_{n}, hence the claim.

4.2.3 Proof of the theorem

It remains to prove the next 22 lemmas.

Lemma 4.4.

If MM eventually halts on the empy input, then ω~​(ℱM)=ω~​(ℱ0)∈𝒫\tilde{\omega}(\mathcal{F}_{M})=\tilde{\omega}(\mathcal{F}_{0})\in\mathcal{P}.

Proof.

Suppose that MM eventually halts on the empty input. Then there exists a large enough size SS such that the computation in any segment larger than SS has enough time and space to reach its end. Then the state qnq_{n} appears and spreads at speed 11 in both directions except if it encounters an inner or outer border of a counter.

If some state s∈Σs\in\Sigma occurs in ω~​(ℱM)\tilde{\omega}(\mathcal{F}_{M}) then according to Lemma 2.6, there exists a word vv that enables it when placed at position i∈ℤi\in\mathbb{Z}. Take now u=(_​[Uncaptioned image]​_S​[Uncaptioned image]​_,x0S+4)u=(\_\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt\_^{S}\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt\_,x_{0}^{S+4}), ww the empty word and some c∈[u​v​w]i−|u|c\in[uvw]_{i-|u|}. Counters are generated by the two [Uncaptioned image]   states at coordinates i−(S+3)i-(S+3) and i−2i-2, hence there exists t0∈ℕt_{0}\in\mathbb{N} such that at time t0t_{0}, the cell 0 has been crossed by counters generated by [Uncaptioned image]   states. According to Claim 3.1, it will not contain any state of outer or inner border of a counter anymore. Moreover, a segment is created between coordinates i−(S+3)i-(S+3) and i−2i-2. As it is large enough, the state qnq_{n} will be written at time t1∈ℕt_{1}\in\mathbb{N}. Then it will spread and reach cell 0 before time t1+max⁡(|i−(S+2)|,|i−2|)t_{1}+\max(|i-(S+2)|,|i-2|) or t0t_{0} if the inner border of a counter slows it down. This is illustrated by Figure 7. Hence there exists t2∈ℕt_{2}\in\mathbb{N} such that ∀t≥t2,ℱMt​(c)∈[s]⇔s=qn\forall t\geq t_{2},\mathcal{F}_{M}^{t}(c)\in[s]\Leftrightarrow s=q_{n}. Thus ω~​(ℱM)⊆{qn}ℤ\tilde{\omega}(\mathcal{F}_{M})\subseteq\{q_{n}\}^{\mathbb{Z}}. As ω~​(ℱM)\tilde{\omega}(\mathcal{F}_{M}) cannot be empty, we have ω~​(ℱM)={qn}ℤ=ω~​(ℱ0)\tilde{\omega}(\mathcal{F}_{M})=\{q_{n}\}^{\mathbb{Z}}=\tilde{\omega}(\mathcal{F}_{0}) and ω~​(ℱM)∈𝒫\tilde{\omega}(\mathcal{F}_{M})\in\mathcal{P}.

Refer to caption
Figure 7: The word vv (in blue) is supposed to enable state ss. Then for a good choice of uu (in red), a segment will simulate a computation of MM that eventually halts and produces qnq_{n}. This state spreads (in yellow) and eventually reaches coordinate 0.

∎

Lemma 4.5.

If MM never halts on the empty input, then ω~​(ℱM)=ω~​(ℱ1)∉𝒫\tilde{\omega}(\mathcal{F}_{M})=\tilde{\omega}(\mathcal{F}_{1})\notin\mathcal{P}.

Proof.

Suppose now that MM never halts on the empty input. We will show that ω~​(ℱ1)=ω~​(ℱM)\tilde{\omega}(\mathcal{F}_{1})=\tilde{\omega}(\mathcal{F}_{M}).

First, we show that:

Claim 4.6.

ω~​(ℱM)⊆ω~​(ℱ1)\tilde{\omega}(\mathcal{F}_{M})\subseteq\tilde{\omega}(\mathcal{F}_{1})

  • Proof:

    Let ss be a word that occurs in ω~​(ℱM)\tilde{\omega}(\mathcal{F}_{M}). According to Lemma 2.6, there exists a word vv that enables ss when placed at coordinate ii. As any word containing vv as a factor also enables ss, we can choose vv such that i<0i<0 and i+|v|>|s|i+|v|>|s|.

    We prove that v′=ϕ​(v)v^{\prime}=\phi(v) at coordinate ii enables ss for ℱ1\mathcal{F}_{1}. To do so, we will use Lemma 2.6. Take u′,w′∈Σ1∗u^{\prime},w^{\prime}\in\Sigma_{1}^{*} and denote u=([Uncaptioned image]​_|u′|−1,u′)u=(\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt\_^{|u^{\prime}|-1},u^{\prime}) and w=(_|w′|−1​[Uncaptioned image],w′)w=(\_^{|w^{\prime}|-1}\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt,w^{\prime}). Denote n=|u​v​w|n=|uvw|, T≥max⁡(sb​n,f​(n)+n)T\geq\max(s_{b}n,f(n)+n) (where sbs_{b} is the speed of inner borders of counters), z1=i−|u|z_{1}=i-|u| and z2=i+|v​w|z_{2}=i+|vw|. Apply Lemma 2.6 with ℱM\mathcal{F}_{M}, vv, uu and ww. For infinitely many times tt, there exist a configuration c∈[u​v​w]i−|u|c\in[uvw]_{i-|u|} such that ℱMt​(c)∈[s]\mathcal{F}_{M}^{t}(c)\in[s]. Using Claim 4.3 with cells at coordinates z1z_{1} and z2z_{2} containing state [Uncaptioned image]  , we get that for any t>Tt>T,

    ∀z1≤j≤z2,π2​(ℱMt​(c)j)∈{ℱ1t​(ϕ​(c))j,qn}\forall z_{1}\leq j\leq z_{2},\pi_{2}\left(\mathcal{F}_{M}^{t}(c)_{j}\right)\in\left\{\mathcal{F}_{1}^{t}(\phi(c))_{j},q_{n}\right\}

    That is : π2​(s)=π2​(ℱMt​(c)[0,|u|−1])∈{ℱ1t​(ϕ​(c))[0,|u|−1],qn|u|}\pi_{2}(s)=\pi_{2}\left(\mathcal{F}_{M}^{t}(c)_{[0,|u|-1]}\right)\in\left\{\mathcal{F}_{1}^{t}(\phi(c))_{[0,|u|-1]},q_{n}^{|u|}\right\}.

    Due to the [Uncaptioned image]   states placed at coordinates z1z_{1} and z2z_{2}, we can also apply Claim 4.2 and we get that the computation is finished in any segment between coordinates z1z_{1} and z2z_{2} at time f​(n)f(n). After nn more steps, the potential abortion signals have reached the borders and every cell between coordinates z1z_{1} and z2z_{2} contains a state in Σ1∪{qn}\Sigma_{1}\cup\{q_{n}\}. Moreover, as these cells belonged to a segment in the protected area, and since MM never halts on the empty input, this state cannot be qnq_{n}. Hence s∈Σ∗s\in\Sigma^{*} and as π2\pi_{2} is the identity on Σ\Sigma, necessarily s=π2​(s)=ℱ1t​(ϕ​(c))[0,|u|−1]s=\pi_{2}(s)=\mathcal{F}_{1}^{t}(\phi(c))_{[0,|u|-1]}.

    As ϕ​(c)∈[u′​v′​w′]i−|u′|\phi(c)\in[u^{\prime}v^{\prime}w^{\prime}]_{i-|u^{\prime}|} and as ℱ1t​(ϕ​(c))[0,|u|−1]=s\mathcal{F}_{1}^{t}(\phi(c))_{[0,|u|-1]}=s for infinitely many times tt, Lemma 2.6 allows to conclude that v′v^{\prime} enables ss that is v′v^{\prime} occurs in ω~​(ℱ1)\tilde{\omega}(\mathcal{F}_{1}).

Then we prove the opposite:

Claim 4.7.

ω~​(ℱ1)⊆ω~​(ℱM)\tilde{\omega}(\mathcal{F}_{1})\subseteq\tilde{\omega}(\mathcal{F}_{M})

  • Proof: Let ss be a word that occurs in ω~​(ℱ1)\tilde{\omega}(\mathcal{F}_{1}). According to Lemma 2.6, there exists a word vv that enables it when placed at coordinate ii. We prove that v′=(_|i|​[Uncaptioned image]|v|​_|i|+|s|,x0|i|​v​x0|i|+|s|)v^{\prime}=(\_^{|i|}\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt^{|v|}\_^{|i|+|s|},x_{0}^{|i|}vx_{0}^{|i|+|s|}) at coordinate i−|i|i-|i| enables ss for ℱM\mathcal{F}_{M}.

    For any u′,w′∈Σ∗u^{\prime},w^{\prime}\in\Sigma^{*}, denote n=|u′​v′​w′|n=|u^{\prime}v^{\prime}w^{\prime}|. Let T≥max⁡(sb​n,f​(n)+n)T\geq\max(s_{b}n,f(n)+n) (where sbs_{b} is still the speed of inner borders of counters) and denote

    • –

      u=ϕ​(π2​(u′))​x0|i|u=\phi(\pi_{2}(u^{\prime}))x_{0}^{|i|};

    • –

      w=x0|i|+|s|​ϕ​(π2​(w′))w=x_{0}^{|i|+|s|}\phi(\pi_{2}(w^{\prime})).

    As vv enables ss for ℱ1\mathcal{F}_{1}, there exists c∈[u​v​w]i−|u|c\in[uvw]_{i-|u|} and t≥Tt\geq T such that ℱ1t​(c)∈[s]\mathcal{F}_{1}^{t}(c)\in[s]. We can write cc as c−​u​v​w​c+c_{-}uvwc_{+} where c−c_{-} and c+c_{+} are semi-infinite configuration in Σ1ω{}^{\omega}\Sigma_{1} and Σ1ω\Sigma_{1}^{\omega} respectively. Define c′=(ω[Uncaptioned image],c−)u′v′w′([Uncaptioned image],ωc+)∈[u′v′w′]i−|i|−|u′|c^{\prime}=(^{\omega}\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt{},c_{-})u^{\prime}v^{\prime}w^{\prime}(\vbox to7.0pt{\hbox{\includegraphics{sti}}}\hskip 1.00006pt{}^{\omega},c_{+})\in[u^{\prime}v^{\prime}w^{\prime}]_{i-|i|-|u^{\prime}|}, we will prove that ℱMt​(c′)∈[s]\mathcal{F}_{M}^{t}(c^{\prime})\in[s]. First, note that c=ϕ​(π2​(c′))c=\phi(\pi_{2}(c^{\prime})). Then using Claim 4.3, we have that for every j∈[|i−|i|,i+|i|+|s|]j\in[|i-|i|,i+|i|+|s|]:

    π2​(ℱMt​(c′)j)∈{ℱ1t​(c)j,qn}\pi_{2}\left(\mathcal{F}_{M}^{t}(c^{\prime})_{j}\right)\in\left\{\mathcal{F}_{1}^{t}(c)_{j},q_{n}\right\}

    As t≥T≥sb​nt\geq T\geq s_{b}n and MM does not halt on the empty input, π2​(ℱMt​(c′))j≠qn\pi_{2}\left(\mathcal{F}_{M}^{t}(c^{\prime})\right)_{j}\neq q_{n}. And as t≥T≥f​(n)+nt\geq T\geq f(n)+n, the computation is aborted in every segment fully located between coordinates |i−|i||i-|i| and i+|i|+|s|i+|i|+|s| before step f​(n)f(n). After nn more steps, the first layer of these segments is erased, in particular for coordinates jj with 0≤j<|s|0\leq j<|s|. Hence ℱMt​(c′)[0,|s|−1]=π2​(ℱMt​(c′))[0,|s|−1]=ℱ1t​(c)[0,|s|−1]=s\mathcal{F}_{M}^{t}(c^{\prime})_{[0,|s|-1]}=\pi_{2}\left(\mathcal{F}_{M}^{t}(c^{\prime})\right)_{[0,|s|-1]}=\mathcal{F}_{1}^{t}(c)_{[0,|s|-1]}=s and s∈ω~​(ℱM)s\in\tilde{\omega}(\mathcal{F}_{M}).

∎

The last two lemmas show that M↦ℱMM\mapsto\mathcal{F}_{M} is a reduction from the Halting problem of Turing machines on empty input to the problem of decision of 𝒫\mathcal{P}.

5 Conclusion and perspectives

We proved Rice’s theorem for generic limit sets of CA, which means that for example generic nilpotency is undecidable. In the case of limit sets and μ\mu-limit sets, the nilpotency problem has the lowest complexity in the arithmetical hierarchy amongst properties of limit or μ\mu-limit sets (Σ10\Sigma_{1}^{0}-complete for limit sets and Π30\Pi_{3}^{0}-complete for μ\mu-limit sets). It may be the case once more for generic limit sets. Lemma 2.6 gives a Π30\Pi_{3}^{0} upper bound on the complexity of generic nilpotency and Törmä suggests in [12] that the exact complexity could be obtained using a construction close to the one presented in [1] or in the present paper. One might think that another version of Rice’s theorem could be deduced where the lower bound of complexity on non trivial properties of generic limit sets is higher than Σ10\Sigma_{1}^{0}.

Using again constructions of [1], one can certainly prove properties similar to the ones obtained on μ\mu-limit sets in the same paper, but also build examples to show that the languages of μ\mu-limit set and generic limit set can have totally distinct complexities like Σ30\Sigma_{3}^{0}-complete versus a full-shift.

References

  • [1] Laurent Boyer, Martin Delacourt, Victor Poupet, Mathieu Sablik, and Guillaume Theyssier. μ\mu-limit sets of cellular automata from a computational complexity perspective. Journal of Computer and System Sciences, 81, 09 2013.
  • [2] Benjamin Hellouin de Menibus and Mathieu Sablik. Characterisation of sets of limit measures after iteration of a cellular automaton on an initial measure. CoRR, abs/1301.1998, 2013.
  • [3] Martin Delacourt. Rice’s theorem for μ\mu-limit sets of cellular automata. In ICALP (2), pages 89–100, 2011.
  • [4] Saliha Djenaoui and Pierre Guillon. The generic limit set of cellular automata. working paper or preprint, August 2018.
  • [5] Gustav Arnold Hedlund. Endomorphisms and automorphisms of the shift dynamical systems. Mathematical Systems Theory, 3(4):320–375, 1969.
  • [6] Karel Culik II, Jan Pachl, and Sheng Yu. On the limit sets of cellular automata. SIAM Journal on Computing, 18(4):831–842, 1989.
  • [7] Jarkko Kari. The nilpotency problem of one-dimensional cellular automata. SIAM Journal on Computing, 21:571–586, 1992.
  • [8] Jarkko Kari. Rice’s theorem for the limit sets of cellular automata. Theoretical Computer Science, 127:229–254, 1994.
  • [9] Jarkko Kari. Theory of cellular automata: A survey. Theoretical Computer Science, 334(1):3–33, 2005.
  • [10] Petr Kůrka and Alejandro Maass. Limit sets of cellular automata associated to probability measures. Journal of Statistical Physics, 100(5-6):1031–1047, 2000.
  • [11] John Milnor. On the concept of attractor. Communications in Mathematical Physics, 99(2):177 – 195, 1985.
  • [12] Ilkka Törmä. Complexity of generic limit sets of cellular automata. In Hector Zenil, editor, Cellular Automata and Discrete Complex Systems, pages 126–138, Cham, 2020. Springer International Publishing.
  • [13] John von Neumann. Theory of Self-Reproducing Automata. University of Illinois Press, Champaign, IL, USA, 1966.