Revisiting the validity of the Stokes-Einstein relation
Abstract
The Stokes-Einstein (SE) relation has been widely applied to quantitatively describe the Brownian motion. Notwithstanding, here we show that even for a simple fluid, the SE relation may not be completely applicable. Namely, although the SE relation could be a good approximation for a large enough Brownian particle, we find that it induces significant error for a smaller Brownian particle, and the error increases with the decrease of the Brownian particle’s size, till the SE relation fails completely when the size of Brownian particle is comparable with that of a fluid molecule. The cause is rooted in the fact that the kinetic and the hydrodynamic effects depend on the size of the Brownian particle differently. By excluding the kinetic contribution to the diffusion coefficient, we propose a revised Stokes-Einstein relation and show that it expands significantly the applicable range.
The Stokes-Einstein (SE) relation,
| (1) |
establishes a connection between the diffusion coefficient, , of a Brownian particle and the shear viscosity, , of the fluid it is immersed in. Here is the radius of the Browinan particle, is the Boltzmann constant, is the fluid temperature, and is a constant depending on the boundary conditions. It makes the Einstein relation [1], , a quantitative law. Although the SE relation has been found invalid in certain extreme situations, such as in supercooled liquids[2, 3], in glass-forming liquids [4, 5, 6, 7], and in dense complex medias [8, 9, 10, 11, 12], it has been a long-standing and well acknowledged belief that for a simple fluid the SE relation applies well even when the size of the Brownian particle decreases down to the molecular level [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]. Consequently, this law is routinely used to compute via the measurement of , or to estimate the radius of molecules with measured and .
However, a comprehensive testing of the SE relation is still insufficient though over a century has passed. Previous verifications, experimentally [2, 18, 17, 16, 3, 4, 5, 7] or numerically [21, 18, 22, 24, 20, 19, 23], have focused on the special case where a tagged fluid molecule is adopted as the Brownian particle. Moreover, what these studies have checked is only the linear relationship between and of the SE relation with a fixed . Whether and under what conditions is independent of the size and mass of the Brownian particle for a given fluid have not been systematically studied, to our knowledge. Note that the size and mass dependence are of importance for applications, since in practice the radiuses of a Brownian particle can range from nanometer to millimeter [25, 26] and the mass may vary in a wide range as well.
In this paper, we study the size and mass dependence of the SE relation in the hard-sphere fluid model. A key step is to decompose into the kinetic and the hydrodynamic part, i.e. and . In doing so, we find that but . The scaling behavior of indicates that the product does not remain -independent when cannot be neglected, which provides a key evidence that the SE relation is not an accurate law. On the other hand, the scaling behavior of inspires us to modify the SE relation as
| (2) |
We perform large-scale numerical simulations to examine Eqs. (1) and (2). The results suggest that Eq. (1) is applicable for a Brownian particle over a few hundred times larger than the fluid molecules, while Eq. (2) is accurate for a Brownian particle down to only several times larger than the fluid molecules. These results are in clear contrast with the common belief that the SE relation is applicable at the molecular level.
Methodologically we emphasize the necessity of the decomposition in applying particle diffusion laws. The fact that Eq. (2) holds instead indicates that to apply hydrodynamic laws, it is appropriate to exclude contributions from kinetic effects. Similarly, laws established on the basis of pure kinetic effects should be applied after excluding the hydrodynamic contributions. To support this proposition, we examine the Chapman-Enskog theory of the diffusion coefficient. It is a kinetic theory that accounts for only the binary collisions mutually uncorrelated [27, 10]. Excluding the hydrodynamic effect, we find that the theoretical prediction agrees perfectly with the simulated over the entire fluid regime.
Model and algorithm. We employ the hard-sphere fluid model [28, 29, 27] to perform our tasks. It consists of a sphere Brownian particle of mass and radius , and fluid molecules. Each molecule has a unit mass and a sphere shape of radius . The packing fraction of fluid with radius is given by , where the number density of fluid molecules is fixed at in our study. Note that with and , the Brownian particle reduces to a fluid molecule. Initially, all the entities are placed evenly in a cubic box of side length with periodic boundary conditions, and assigned a random velocity sampled from the equilibrium velocity distributions corresponding to temperature ( is set to be unity) with the restriction that the total momentum is zero. Next, the system is evolved for a sufficiently long time to ensure that it has fully relaxed to the equilibrium state, then the velocity autocorrelation function (VACF), defined as , is calculated, where is the velocity of the Brownian particle at time . The collision between any two constituent entities are completely elastic.
To evolving the system numerically, an event-driven molecular dynamics algorithm is adopted [28, 29, 30]. As it is challenging to compute the VACF of a Brownian particle, the maximum number of fluid molecules and the maximum radius of the Brownian particle are set to be and , respectively. For more details of the simulations, see the Supplemental Materials.
The hard-sphere model has an essential advantage for our purposes here, i.e., the radius of the Brownian particle is definitely defined. As a result, once is shown to vary with radius or mass in a given fluid (thus and are fixed), the violation of the SE relation can be concluded. To this end, only the diffusion coefficient needs to be calculated. The viscosity of the fluid is required only when we want to determine the exact value of .
Results
Decomposition of the diffusion coefficient. The diffusion coefficient can be calculated by the Green-Kubo formula based on the VACF:
| (3) |
Earlier studies have shown that the diffusion of a particle is governed by both kinetics and hydrodynamics [28, 29, 31, 32, 33, 34, 35]. Consequently, the VACF can be decomposed as .
The kinetic approach to the VACF is pioneered by Einstein [1]. The key insight is that the decay of the VACF is induced by random collisions with surrounding fluid molecules, by which the Brownian particle loses its initial momentum exponentially. The collisions are considered to be uncorrelated, which leads to [27]
| (4) |
where .
It has been known since the 1960s that the VACF also includes a hydrodynamic contribution: The momentum transferred to the fluid can feedback to the Brownian particle through velocity vortex field [28, 29, 32, 35, 34] or, equally, through ring collisions [33, 31]. The feedbacked momentum gives rise to . This effect can also be approximately formulated by the extended Langevin equation by involving a memory factor in the collisions [36, 37]. These studies have established that has a power-law tail at the long-time limit [27], i.e.,
| (5) |
where is the kinematic shear viscosity.
Our method for separating from is as following. In a short time, the momentum transferred from the Brownian particle to the fluid is little due to few collisions; moreover, this part of transferred momentum does not contribute to the VACF of the Brownian particle, because a collision ring has not formed. A collision ring forms only when the momentum of the Brownian particle transferred to the fluid molecules comes back at a later moment to the Brownian particle itself through a collision chain of fluid molecules. Therefore, before the collision ring forms, is identical to . In practice, we fit by a proper with Eq. (4) in a given short time interval . The hydrodynamic effect is regarded to play no role if the fitting result does not change by decreasing further.
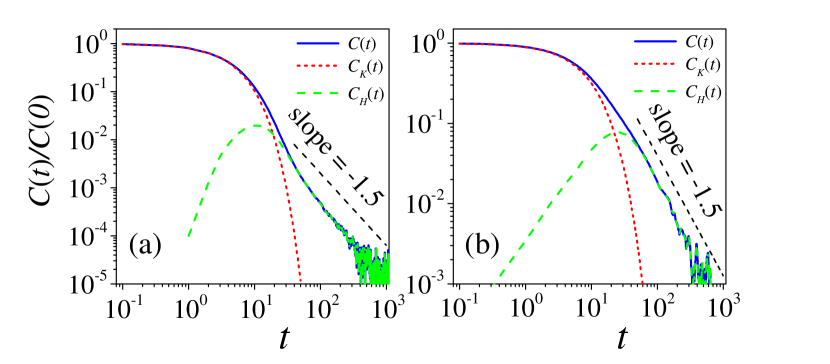
Figure 1(a) and 1(b) show the VACF of the Brownian particle when it is identical with and different from the fluid molecules, respectively. With determined by the best fitting introduced above, we obtain and () in the entire time window, shown in Fig. 1 as well. We see that the hydrodynamic effect of the Brownian particle is significantly larger when it has a bigger mass and a bigger size than a fluid molecule. At large times, the VACFs converge to the long-time tail of .
| 1(0.004) | 2(0.034) | 3(0.11) | 4(0.27) | 4.5(0.39) | 4.7(0.44) | |
| 52.3 | 12.1 | 4.35 | 1.50 | 0.763 | 0.552 | |
| 53.5 | 12.6 | 4.93 | 2.06 | 1.04 | 0.519 |
Testing the Chapman-Enskog kinetic theory based on the decomposition. The diffusion coefficient of identical hard spheres is predicted by the Chapman-Enskog theory in the first Sonine approximation [27], that is, with and . In Tab. I, obtained with this formula for different packing fraction is given, together with of identical hard spheres calculated by the decomposition method. Surprisingly, agrees with the theoretical prediction perfectly over the entire fluid regime. However, in previous studies for testing the Chapman-Enskog theory [21, 29, 38], is compared with , which may gives rise to ambiguous interpretation. To show this, in the Table we also provide calculated by the Green-Kubo formula with the integral time being truncated at (this truncation time is adopted throughout. The finite-size effect induced by such a truncation will be discussed later). We see that the deviation of from may exceed in the high packing fraction region. Deviation of the same level have been encountered in previous studies [38]. Calculating with a small may result in the decrease of the deviations and leads to be closer to [21, 29, 38]. Based on the comparison between and one may conclude that the Chapman-Enskog theory is effective for small systems and in a short time period. But in contrast, the accurate agreement between and suggests that, independent of the system size and the evolution time, predicts accurately, implying that the Chapman-Enskog theory should be interpreted properly as a pure kinetic theory where the hydrodynamical contribution is not taken into account.
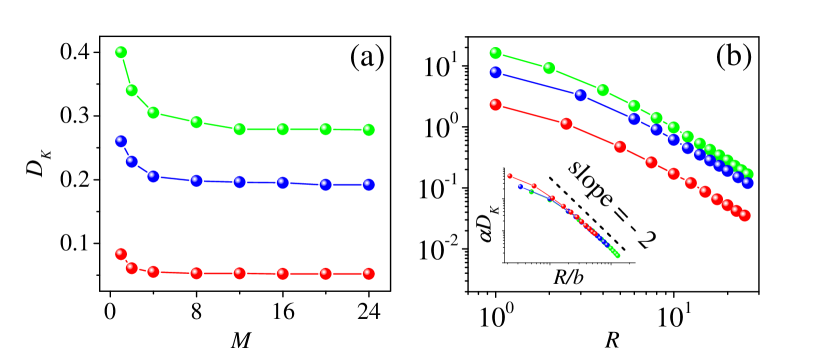
Examining the original and revised SE relations. In Fig. 2 we show of the Brownian particle as a function of with [Fig. 2(a)] and as a function of with [Fig. 2(b)] for three packing fractions, , , and , respectively. Numerical errors, throughout this paper, are suppressed within the size of symbols by collecting a sufficient amount of ensemble samples. In Fig. 2(a), it shows that at a fixed , converges to a mass-independent constant as increases, while in Fig. 2(b) it indicates that at a fixed mass, decreases as
| (6) |
when is large. Moreover, the behavior of versus can be re-scaled to fall on a universal function (i.e., multiplying it by a depenednt constant and plotting it as a function of , see the inset in Fig. 2(b)). This is a key evidence that the left-hand-side of the original SE relation Eq. (1) should depend on the Brownian particle’s size, since it leads to , where is a fitting parameter.
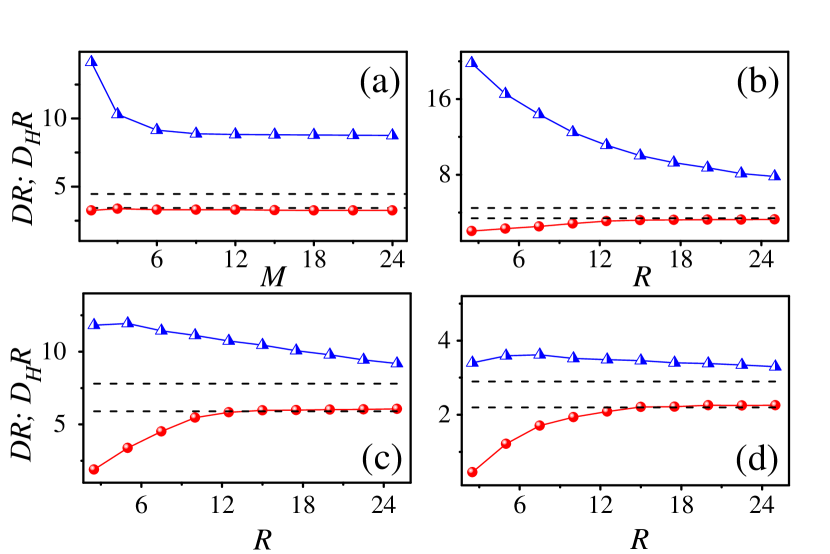
We then examine the mass and size dependent behavior of . Figure 3(a) reveals the -dependence of and in the fluid of . The size of the Brownian particle is fixed at . We see that varies at small masses and converges at large masses, while keeps mass independent. Therefore, light Brownian particles do not obey the original SE relation. Since is mass independent, the mass-dependent behavior of should be ascribed to the consequence of .
Figure 3(b) shows the -dependence in the fluid of . The mass of the Brownian particle is fixed at . We see that decreases as increases, while turns out to be size-independent for . Note that the converged value of in Fig. 3(b) is the same as that in Fig. 3(a). Therefore, is neither mass nor size dependent for about , indicating that the revised SE relation is applicable in this range. This fact also implies that for large Brownian particles and the size dependence of is caused by .
Figure 3(c) and 3(d) show the -dependence in higher packing fractions. The mass of the Brownian particle is fixed also at . We see that they give the qualitatively similar results as in the Fig. 3(b). Note that usually is considered as the boundary between gas and liquid phases [23]. Thus, our studies here cover both the gas and liquid regime. Therefore, in the range of we have investigated, the original SE relation is obviously violated but the revised SE relation is respected for about .
As , is expected to become approximately size independent at large enough when and as a result, . As shown in Fig. 3, at , the deviation between and is about , , and for the three packing fractions. These differences should disappear eventually with the further increase of . Fitting the data shown in Fig. 2(b) we obtain with , , and for the three packing fractions. Then we can infer that when is larger than about and , respectively, the deviation between and will be smaller than . As an estimation for real systems, we set the water molecule diameter (about nanometer) to be the unit length in our model, the remarkable size-dependent effect may disappear for Brownian particles up to a micron in gas, and to hundreds of nanometers in liquid. Note that, though keeping decrease continuous, the rate of decrease of via should become much smaller in liquid than in gas since is much smaller in the former case, as Fig. 3 shown.
In Tab. I, and for the particular case of and are listed. We find that, for example, in the fluid of , we have and , which are remarkably different from the results of large Brownian particles shown in Fig. 3. Therefore, neither the original nor the revised SE relations can stand the size-dependent test when the size of a Brownian particle decreases down to the molecular level.
The kinematic shear viscosity can be calculated following the method in Refs. [21, 39], which gives , and for the three packing fractions, respectively. Then, we can determine the parameter in the SE relation. In Fig. 3, the dashed lines represent . Those with corresponds to the slipping boundary conditions. We see that the converged value does not agree with the predictions with . Instead, they are close to the predictions with .
The finite-size effects may contribute a remarkable correction to and . When the Brownian particle is identical with the fluid molecules, there is a well-known empirical formula [40], , for estimating the diffusion coefficient of infinite large system from that of a finite system, . It gives a lifting to for fluid molecules of , which is slight. There is no empirical formula for a general Brownian particle; in this case, we estimate the correction as following. Due to the computation complexity we have truncated the upper limit of integral of Eq. (3) at . Within such an interval, we can verify that the system size of is large enough, since the VACF obtained with this size overlaps with that obtained with a much larger (see the Supplemental Materials). However, the truncated tail of the VACF may contribute a significant correction. For example, fitting the tail of we obtain for a Brownian particle of and in the fluid of , which may lift and about and , respectively. The latter makes close to the prediction with . Meanwhile, the finite-size effect of has not been considered. Due to the computation complexity we have to leave the accurate value of an open problem. For a more detailed discussion of the finite-size effects, see the Supplemental Materials.
The underlying mechanisms. We propose a phenomenological understanding why the revised SE relation works well for large Brownian particles while becomes also size dependent for small ones. Our reasoning is similar to that for the long-time tail in Ref. [27] (p. 246), but with the key difference that we take the delay effect into account. Suppose that at , the Brownian particle resides at . Then, its initial momentum gradually transfers to the surrounding fluid molecules by collisions, and spreads out by the viscosity and sound modes. The momentum density carried by the viscosity mode relaxes diffusively as . This mode feeds the momentum back to the Brownian particle and contributes to the hydrodynamic component . The characteristic radius of the pack region of expands as . Assuming the Brownian particle floats at the average velocity of fluid molecules in this region, Eq. (5) is derived [27]. Based on this reasoning, we further emphasize that for a Brownian particle of radius , the viscosity mode is physically meaningless for since in this time period. In other words, the feedback begins to play a role only after . Then, plugging Eq. (5) into Eq. (3), the lower limit of integral should be larger than . With this consideration we obtain an estimation of , i.e., . This result explains, on one hand, is size-independent for relatively large Brownian particles when can be neglected comparing with . Extrapolating based on the scaling laws of , we get that , and can assure for the three packing fractions, respectively. These results agree in order with the simulation results of Fig. 3, where no remarkable deviations of can be recognized for . On the other hand, it indicates that must be size dependent for small enough Brownian particles when , where also contributes a dependent component. This feature implies that a full exclusion of the kinetic effect fails.
Though may also be size dependent for small Brownian particles, the threshold of above which it becomes size independent is much smaller than that of . For , whether is negligible should be determined by comparison with (which is usually far smaller than ).
Summary and discussion
Diffusion theories of a Brownian particle are usually established either in the kinetics or in the hydrodynamics framework, and therefore they should be applied on the basis of the decomposition. Excluding the hydrodynamic effect, we find that the Chapman-Enskog theory of the kinetic diffusion coefficient is perfectly accurate over the entire fluid regime. Excluding the kinetic contribution, we find that the SE relation can be extended to Brownian particles down to the size only several times larger than the fluid molecules; otherwise it depends significantly on the size of the Brownian particle till it is several hundred times the size of the fluid molecules, and depends obviously on the mass of the Brownian particle till it is over tenfold the mass of the fluid molecules. When the size of the Brownian particle is comparable with a fluid molecule, a full exclusion of the kinetic effect fails, and neither the original nor the revised SE relation is applicable. Efforts based on the structural entropy of fluids for finding a universal model different from the SE relation [8, 9, 10, 11, 12] may provide a possible way to model the diffusion of fluid molecules.
We would like to point out that a fine experimental test of the size and mass dependence of the SE relation is becoming possible. Indeed, traditional experimental techniques [14, 13, 41, 15, 42, 43] have already allowed one to measure the trajectory of a single Brownian particle of hundreds of nanometers. In recent years, thanks to the state-of-the-art experimental developments, the measurements of displacement as well as instant velocity of a single Brownian particle have been available [44, 45, 46, 47, 48, 49, 50], and thus make it possible to obtain an accurate experimentally and to decompose and . We look forward to the experimental investigations in the near future.
References
- [1] A. Einstein. Un the movement of small particles suspended in statiunary liquids required by the molecular-kinetic theory of heat. Annalen der Physik, 17:549–560, 1905.
- [2] E Rössler. Indications for a change of diffusion mechanism in supercooled liquids. Physical Review Letters, 65(13):1595, 1990.
- [3] Mikhail Dzugutov, Sergei I Simdyankin, and Fredrik HM Zetterling. Decoupling of diffusion from structural relaxation and spatial heterogeneity in a supercooled simple liquid. Physical Review Letters, 89(19):195701, 2002.
- [4] Stephen R Becker, Peter H Poole, and Francis W Starr. Fractional stokes-einstein and debye-stokes-einstein relations in a network-forming liquid. Physical Review Letters, 97(5):055901, 2006.
- [5] Marco G Mazza, Nicolas Giovambattista, H Eugene Stanley, and Francis W Starr. Connection of translational and rotational dynamical heterogeneities with the breakdown of the stokes-einstein and stokes-einstein-debye relations in water. Physical Review E, 76(3):031203, 2007.
- [6] Limei Xu, Francesco Mallamace, Zhenyu Yan, Francis W Starr, Sergey V Buldyrev, and H Eugene Stanley. Appearance of a fractional stokes–einstein relation in water and a structural interpretation of its onset. Nature Physics, 5(8):565–569, 2009.
- [7] Amine Dehaoui, Bruno Issenmann, and Frédéric Caupin. Viscosity of deeply supercooled water and its coupling to molecular diffusion. Proceedings of the National Academy of Sciences, 112(39):12020–12025, 2015.
- [8] Yaakov Rosenfeld. A quasi-universal scaling law for atomic transport in simple fluids. Journal of Physics: Condensed Matter, 11(28):5415, 1999.
- [9] Mikhail Dzugutov. addendum: A universal scaling law for atomic diffusion in condensed matter. Nature, 411(6838):720–720, 2001.
- [10] Jean-Louis Bretonnet. Self-diffusion coefficient of dense fluids from the pair correlation function. the Journal of Chemical Physics, 117(20):9370–9373, 2002.
- [11] Charanbir Kaur, Upendra Harbola, and Shankar P Das. Nature of the entropy versus self-diffusivity plot for simple liquids. the Journal of Chemical Physics, 123(3):034501, 2005.
- [12] Luhui Ning, Peng Liu, Yiwu Zong, Rui Liu, Mingcheng Yang, and Ke Chen. Universal scaling law for colloidal diffusion in complex media. Physical Review Letters, 122(17):178002, 2019.
- [13] TG Mason, K Ganesan, JH Van Zanten, Denis Wirtz, and Scot C Kuo. Particle tracking microrheology of complex fluids. Physical Review Letters, 79(17):3282, 1997.
- [14] Suliman Barhoum, Swomitra Palit, and Anand Yethiraj. Diffusion nmr studies of macromolecular complex formation, crowding and confinement in soft materials. Progress in Nuclear Magnetic Resonance Spectroscopy, 94:1–10, 2016.
- [15] Swomitra Palit, Lilin He, William A Hamilton, Arun Yethiraj, and Anand Yethiraj. Combining diffusion nmr and small-angle neutron scattering enables precise measurements of polymer chain compression in a crowded environment. Physical Review Letters, 118(9):097801, 2017.
- [16] Frank H Stillinger and Jennifer A Hodgdon. Translation-rotation paradox for diffusion in fragile glass-forming liquids. Physical Review E, 50(3):2064, 1994.
- [17] D J Wilbur, T DeFries, and J Jonas. Self-diffusion in compressed liquid heavy water. the Journal of Chemical Physics, 65(5):1783–1786, 1976.
- [18] HJ Parkhurst Jr and J Jonas. Dense liquids. ii. the effect of density and temperature on viscosity of tetramethylsilane and benzene. the Journal of Chemical Physics, 63(6):2705–2709, 1975.
- [19] Kenneth R Harris. Scaling the transport properties of molecular and ionic liquids. Journal of Molecular Liquids, 222:520–534, 2016.
- [20] Kenneth R Harris. The fractional stokes–einstein equation: Application to lennard-jones, molecular, and ionic liquids. the Journal of Chemical Physics, 131(5):054503, 2009.
- [21] BJ Alder, DM Gass, and TE Wainwright. Studies in molecular dynamics. viii. the transport coefficients for a hard-sphere fluid. the Journal of Chemical Physics, 53(10):3813–3826, 1970.
- [22] Shuang Tang, Glenn T Evans, Carl P Mason, and Michael P Allen. Shear viscosity for fluids of hard ellipsoids: a kinetic theory and molecular dynamics study. the Journal of Chemical Physics, 102(9):3794–3811, 1995.
- [23] Norikazu Ohtori, Hikaru Uchiyama, and Yoshiki Ishii. The stokes-einstein relation for simple fluids: From hard-sphere to lennard-jones via wca potentials. the Journal of Chemical Physics, 149(21):214501, 2018.
- [24] Bin Liu, J Goree, and OS Vaulina. Test of the stokes-einstein relation in a two-dimensional yukawa liquid. Physical Review Letters, 96(1):015005, 2006.
- [25] Ron AM Fouchier, Sander Herfst, and Albert DME Osterhaus. Restricted data on influenza h5n1 virus transmission. Science, 335(6069):662–663, 2012.
- [26] Drew Shindell and Christopher J Smith. Climate and air-quality benefits of a realistic phase-out of fossil fuels. Nature, 573(7774):408–411, 2019.
- [27] J. P. Hansen and I. R. McDonald. Theory of Simple Liquids. Academic Press, 2006.
- [28] B. J. Alder and T. E. Wainwright. Velocity autocorrelations for hard spheres. Physical Review Letters, 18(23):988, 1967.
- [29] B. J. Alder and T. E. Wainwright. Decay of the velocity autocorrelation function. Physical Review A, 1(1):18, 1970.
- [30] M Marín. Event-driven hard-particle molecular dynamics using bulk-synchronous parallelism. Computer Physics Communications, 102(1-3):81–96, 1997.
- [31] J. R. Dorfman and E. G. D. Cohen. Velocity correlation functions in two and three dimensions. Physical Review Letters, 25(18):1257, 1970.
- [32] M. H. Ernst, E. H. Hauge, and J. M. J. Van Leeuwen. Asymptotic time behavior of correlation functions. i. kinetic terms. Physical Review A, 4(5):2055, 1971.
- [33] J. R. Dorfman and E. G. D. Cohen. Velocity-correlation functions in two and three dimensions: Low density. Physical Review A, 6(2):776, 1972.
- [34] Y. Pomeau and P. Resibois. Time dependent correlation functions and mode-mode coupling theories. Physics Reports, 19(2):63–139, 1975.
- [35] M. H. Ernst, E. H. Hauge, and J. M. J. Van Leeuwen. Asymptotic time behavior of correlation functions. ii. kinetic and potential terms. Journal of Statistical Physics, 15(1):7–22, 1976.
- [36] R. Zwanzig and M. Bixon. Hydrodynamic theory of the velocity correlation function. Physical Review A, 2(5):2005, 1970.
- [37] W. B. Russel. Brownian motion of small particles suspended in liquids. Annual Review of Fluid Mechanics, 13(1):425–455, 1981.
- [38] H Sigurgeirsson and DM Heyes. Transport coefficients of hard sphere fluids. Molecular Physics, 101(3):469–482, 2003.
- [39] R. García-Rojo, S. Luding, and J. J. Brey. Transport coefficients for dense hard-disk systems. Physical Review E, 74(6):061305, 2006.
- [40] In-Chul Yeh and Gerhard Hummer. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. The Journal of Physical Chemistry B, 108(40):15873–15879, 2004.
- [41] Detlef Dürr and Herbert Spohn. Brownian motion and microscopic chaos. Nature, 394(6696):831–833, 1998.
- [42] Neil YC Lin, Matthew Bierbaum, and Itai Cohen. Determining quiescent colloidal suspension viscosities using the green-kubo relation and image-based stress measurements. Physical Review Letters, 119(13):138001, 2017.
- [43] Hyoungsoo Kim, Koen Muller, Orest Shardt, Shahriar Afkhami, and Howard A Stone. Solutal marangoni flows of miscible liquids drive transport without surface contamination. Nature Physics, 13(11):1105–1110, 2017.
- [44] Yilong Han, AM Alsayed, Maurizio Nobili, Jian Zhang, Tom C Lubensky, and Arjun G Yodh. Brownian motion of an ellipsoid. Science, 314(5799):626–630, 2006.
- [45] Tongcang Li, Simon Kheifets, David Medellin, and Mark G Raizen. Measurement of the instantaneous velocity of a brownian particle. Science, 328(5986):1673–1675, 2010.
- [46] Rongxin Huang, Isaac Chavez, Katja M Taute, Branimir Lukić, Sylvia Jeney, Mark G Raizen, and Ernst-Ludwig Florin. Direct observation of the full transition from ballistic to diffusive brownian motion in a liquid. Nature Physics, 7(7):576–580, 2011.
- [47] Thomas Franosch, Matthias Grimm, Maxim Belushkin, Flavio M Mor, Giuseppe Foffi, László Forró, and Sylvia Jeney. Resonances arising from hydrodynamic memory in brownian motion. Nature, 478(7367):85–88, 2011.
- [48] Simon Kheifets, Akarsh Simha, Kevin Melin, Tongcang Li, and Mark G Raizen. Observation of brownian motion in liquids at short times: instantaneous velocity and memory loss. Science, 343(6178):1493–1496, 2014.
- [49] Ignacio A Martínez, Artyom Petrosyan, David Guéry-Odelin, Emmanuel Trizac, and Sergio Ciliberto. Engineered swift equilibration of a brownian particle. Nature Physics, 12(9):843–846, 2016.
- [50] Xuewen Fu, Bin Chen, Jau Tang, Mohammed Th Hassan, and Ahmed H Zewail. Imaging rotational dynamics of nanoparticles in liquid by 4d electron microscopy. Science, 355(6324):494–498, 2017.
Acknowledgements
This work is supported by the NSFC (Grants No. 11335006).