Revisiting -meson twist-2, 3 distribution amplitudes
Abstract
Due to the significant difference between the experimental measurements and the theoretical predictions of standard model (SM) for the value of of the semileptonic decay , people speculate that it may be the evidence of new physics beyond the SM. Usually, the -meson twist-2, 3 distribution amplitudes (DAs) , and are the main error sources when using perturbative QCD factorization and light-cone QCD sum rules to study . Therefore, it is important to get more reasonable and accurate behaviors for those DAs. Motivated by our previous work [Phys. Rev. D 104, no.1, 016021 (2021)] on pionic leading-twist DA, we revisit -meson twist-2, 3 DAs , and . New sum rules formulae for the -moments of these three DAs are suggested to obtain more accurate values. The light-cone harmonic oscillator models for those DAs are improved, and whose model parameters are determined by fitting the values of -moments with the least squares method.
pacs:
12.38.-t, 12.38.Bx, 14.40.AqI introduction
Since 2012, semileptonic decay has been considered as one of the processes most likely to prove the existence of new physics beyond the standard model (SM). The reason is well known, that is, the significant difference between the experimental measurements of the ratio and its theoretical predictions of SM. The latest statistics given by Heavy Flavor Average Group website HFLAV:2019otj shows that the experimental average value of is , while its average value of SM predictions is FlavourLatticeAveragingGroup:2019iem . The former comes from the experimental measurements for semileptonic decay by BaBar Collaboration in 2012 BaBar:2012obs and 2013 BaBar:2013mob , by Belle Collaboration in 2015 Belle:2015qfa and 2019 Belle:2019rba . The later is obtained by combining two lattice calculations by MILC Collaboration MILC:2015uhg and HPQCD Collaboration Na:2015kha . The authors of Ref. Bigi:2016mdz fit experimental and lattice results for to give . Within the framework of the Heavy-Quark Expansion, Ref. Bordone:2019vic gives . By fitting the experimental data, lattice QCD and QCD sum rules (SRs) results for , Ref. Bernlochner:2017jka predicts . Along with the experimental data, Ref. Jaiswal:2017rve use the lattice predictions MILC:2015uhg ; Na:2015kha for the form factors of as inputs, the prediction for with the Caprini-Lellouch-Neubert parameterization Caprini:1997mu of the form factors is given by , while using Boyd-Grinstein-Lebed parameterization Boyd:1997kz , the authors obtain . Earlier, based on the heavy quark effective theory (HQET), Refs. Tanaka:2010se ; Fajfer:2012vx predict . By using light-cone sum rules (LCSRs) approach with -meson distribution amplitudes (DAs) in HQET, Ref. Wang:2017jow gives in 2017. Based on the -meson DAs Zhang:2017rwz ; Zhong:2018exo obtained by QCD SRs in the framework of background field theory (BFT) Huang:1989gv ; Zhong:2014jla , our previous work gets Zhong:2018exo with LCSRs.
In semileptonic decay and other -meson related processes, -meson twist-2 DA , twist-3 DAs and are usually the key input parameters and the main error sources. Among them, there are relatively more studies on leading-twist DA , such as, earlier, the Kurimoto-Li-Sanda (KLS) model Kurimoto:2002sb based on the expansion of the Gegenbauer polynomials, the Li-Lü-Zou (LLZ) model Li:2008ts by considering a sample harmonic-like -dependence on the basis of KLS model, the Gaussian-type Li-Melic (LM) model Li:1999kna by employing the solution of a relativistic scalar harmonic oscillator potential for the orbital part of the wavefunction (WF), the light-cone harmonic oscillator (LCHO) model Guo:1991eb ; Zuo:2006re based on the Brodsky-Huang-Lepage (BHL) prescription BHL , etc. Recently, in 2019, Ref. Dhiman:2019ddr studied -meson twist-2 DA with the light-front quark model (LFQM) by adopting the Coulomb plus exponential-type confining potential, and given the values of whose first six -moments. Our research on -meson twist-2 DA is in 2018 Zhang:2017rwz . We studied by combining phenomenological LCHO model and non-perturbative QCD SRs approach. By introducing longitudinal WF , we improved the LCHO model of proposed in Refs. Guo:1991eb ; Zuo:2006re . The behavior of our DA is determined by the first four Gegenbauer moments. Those Gegenbauer moments were calculated with QCD SRs in the framework of BFT. Subsequently, in the same year, we used the same method to study -meson twist-3 DAs and and further studied transition form factors (TFFs) with LCSRs and calculated Zhong:2018exo .
Last year we proposed a new scheme to study pionic leading-twist DA in Ref. Zhong:2021epq . Firstly, we suggested a new sum rule formula for -moment of based on the fact that the sum rule of zeroth moment can not be normalized in entire Borel parameter region. Secondly, we adopted the least squares method to fit the values of the first ten -moments to determine the behavior of . In fact, there are several other approaches, such as traditional QCD sum rules Ball:2003sc , Dyson-Schwinger equation Chang:2013pq , lattice calculation RQCD:2019osh ; LatticeParton:2022zqc , etc., to be adopted in the study of the DAs of mesons especially light mesons. By comparison, the scheme suggested in Ref. Zhong:2021epq has its own unique advantages. In which, the new sum rule formula of -moment can reduce the system uncertainties caused222The numerical results in Ref. Zhong:2021epq show that this improves the accuracy of -moments by at least . by the truncation of the high-dimensional condensates as well as the simple parametrization of quark-hadron daulity for continuum states, and this improves the prediction accuracy of QCD SRs and its prediction ability for higher moments; The least squares method is used to fit the -moments to determine DA, which avoids the extremely unreliable high-order Gegenbauer moments, and can absorb as much information of DA carried by high-order -moments as possible to give more accurate behavior of DA Zhong:2022lmn . Very recently, this scheme has been used to study the kaon leading-twist DA by considering the symmetry breaking effect Zhong:2022ecl , the axial-vector -meson longitudinal twist-2 DA Hu:2021lkl , the scaler and -meson leading-twist DAs Huang:2022xny ; Wu:2022qqx . Inspired by these works in Refs. Zhong:2021epq ; Zhong:2022ecl , we will restudy -meson twist-2, 3 DAs , and in this work.
The rest of the paper are organized as follows. In Sec. II, we will present new sum rule formulae for the -moments of , and , and briefly describe and improve the LCHO models of those DAs. In Sec. III, we will analyze the behavior of those DAs based on the new values of -moments in detail. Section IV is reserved for a summery.
II Theoretical framework
II.1 New sum rule formulae for the -moments of -meson twist-2,3 DAs
As discussion in Ref. Zhong:2021epq , the new sum rule formula for the -moments is based on that the sum rule of zeroth moment can not be normalized in entire Borel parameter region. Therefore, the discussion of this paper begins with the sum rule formulae for the -moments of -meson twist-2 DA obtained in Ref. Zhang:2017rwz and twist-3 DAs , obtained in Ref. Zhong:2018exo .
By giving up the priori setting for zeroth -moment normalization, Eq. (28) in Ref. Zhang:2017rwz should be modified as
| (1) |
for the th -moment of . Eq. (27) in Ref. Zhong:2018exo should be modified as
| (2) |
for the th -moment of . Eq. (28) in Ref. Zhong:2018exo should be modified as
| (3) |
for the th -moment of . In Eqs. (1), (2) and (3), is the -meson mass, is the current charm-quark mass, is the decay constant of -meson, is the continuum threshold, indicates Borel transformation operator with the Borel parameter . and are the normalization constants of DAs and respectively. Usually, in literature by employing the equations of motion of on-shell quarks in the meson. However, as discussed in Refs. Huang:2004tp ; Huang:2005av , the quarks inside the bound state are not exactly on-shell. Then and are taken as undetermined parameters in this paper and will be determined via the sum rules of zeroth -moments of DAs and following the idea of Refs. Zhong:2018exo ; Huang:2004tp ; Huang:2005av . In addition, in sum rules (1), (2) and (3), the subscript “pert” stands for the terms coming from the contribution of perturbative part in operator product expansion, subscripts , , , and stand for the terms proportional to double-quark condensate, double-gluon condensate, quark-gluon mixing condensate, four-quark condensate and triple-gluon condensate, respectively. For the expressions of those terms in Eqs. (1), (2) and (3), one can refer to the appendixes in Refs. Zhang:2017rwz ; Zhong:2018exo . By taking in Eq. (1) and (2), one can obtain the sum rules for the zeroth -moments and . As the functions of the Borel parameter, the zeroth -moments in Eq. (1) and in Eqs. (2) and (3) obviously can not be normalized in entire region. Therefore, more reasonable and accurate sum rules should be
| (4) | |||||
| (5) |
and
| (6) |
for , and , respectively.
II.2 LCHO models for -meson twist-2, 3 DAs
In Refs. Zhang:2017rwz ; Zhong:2018exo , we have suggested LCHO models for -meson twist-2, 3 DAs. In this subsection, we first propose a brief review for those models, then we will improve them by reconstructing whose longitudinal distribution functions.
The -meson leading-twist DA can be obtained by integrating out the transverse momentum component in its WF , i.e.,
| (7) |
Based on the BHL description BHL , the LCHO model for the -meson leading-twist WF consists of the spin-space WF and spatial WF , i.e., . The spin-space WF . In which, with the constituent charm-quark mass and light-quark mass . In this paper, we take and Zhong:2022ecl . As discussed in Ref. Zhang:2017rwz , we take approximately due to that . Then, the -meson leading-twist WF reads
where , is the normalization constant, is a harmonious parameter that dominates the WF’s transverse distribution, dominates the WF’s longitudinal distribution.
Substituting Eq. (LABEL:psiR2D) into (7), the expression of -meson leading-twist DA can be obtained, i.e.,
| (9) | |||||
Following the way for constructing the -meson leading-twist DA, the LCHO models for -meson twist-3 DAs and read,
| (10) | |||||
and
| (11) | |||||
respectively.
For the longitudinal distribution functions , and , we used to take the first five terms of Gegenbauer expansions for the corresponding DAs in Refs. Zhang:2017rwz ; Zhong:2018exo . As discussed in Ref. Zhong:2021epq ; Zhong:2022ecl , higher order Gegenbauer polynomials will introduce spurious oscillations Chang:2013pq , while those corresponding coefficients obtained by directly solving the constraints of Gegenbauer moments or -moments are not reliable. Then we improve these three longitudinal distribution functions as following,
By considering the normalization conditions for -meson twist-2, 3 DAs , and , that is,
| (15) | |||||
there are three undetermined parameters in the LCHO models for DAs , and respectively, and which will be taken as the fitting parameters to fit the first ten -moments333In our previous work Zhong:2022lmn , based on the pionic leading-twist DA, we analyzed in detail the influence of different number of -moments included in the fitting, and found that when the order of -moments is not more than ten, the change of the number of -moments has an obvious impact on the fitting results. When the order of -moments is more than ten, the change of the number of -moments has a very small impact on the fitting results. Therefore, we only use the first ten -moments of -meson DAs , and for fitting in this work. of corresponding DAs by adopting the least squares method in next section.
It should be noted that, -meson twist-2, 3 DAs are the universal non-perturbative parameters in essence, and non-perturbative QCD should be used to study them in principle. However, due to the difficulty of non-perturbative QCD, those DAs are studied in this paper by combining the phenomenological model, that is, the LCHO model, and the non-perturbative QCD SRs in the framework of BFT. Otherwise, the improvement of the LCHO model of DAs , and , that is, to reconstruct their longitudinal distribution functions, is only based on mathematical considerations. The rationality of this improvement can be judged by the goodness of fit.
| Continue | Dimension-six | Continue | Dimension-six | ||
|---|---|---|---|---|---|
| Contribution () | Contribution () | Contribution () | Contribution () | ||






III numerical analysis
III.1 Inputs
To do the numerical calculation for the -moments of -meson twist-2, 3 DAs, we take the scale as usual, and take for the number of quark flavors , respectively Zhong:2021epq ; Zhong:2022ecl . For other inputs, we take Workman:2022ynf
| (16) |
and Zhong:2021epq ; Zhong:2014jla ; Colangelo:2000dp
| (17) |
The renormalization group equations of those inputs are Zhong:2021epq
| (18) |
with . For the continuum threshold, we used to take in Ref. Zhang:2017rwz ; Zhong:2018exo . This value comes from the square of the mass of -meson’s first exciting state, i.e., , as suggested by Refs. BaBar:2010zpy ; Li:2012gr . In Refs. Zhong:2021epq ; Zhong:2022ecl , we take the continuum threshold parameters and by requiring that there are reasonable Borel windows to normalize the zeroth -moments of the pion and kaon leading-twist DAs. In this paper, we follow the suggestion in Refs. Zhong:2021epq ; Zhong:2022ecl , and get .
III.2 -moments and behaviors of -meson twist-2, 3 DAs
Then we can calculate the values of the -moments of -meson twist-2, 3 DAs with the sum rules (4), (5) and (6). First, one need to determine the appropriate Borel windows for those -moments by following usual criteria, such as the contributions of continuum state and dimension-six condensate are as small as possible, and the values of those -moments are stable in corresponding Borel windows. Table 1 exhibits the limits to the continuum state’s contributions and the dimension-six condensate’s contributions for the first ten -moments of -meson twist-2, 3 DAs. In which, the symbol “” indicates that corresponding continuum state’s contribution is smaller than or dimension-six condensate’s contribution is much smaller than in a wide Borel parameter region. This is reasonable because both continuum state’s contribution and dimension-six condensate’s contribution are depressed by the sum rules of zeroth -moments in the denominator of the new sum rule formulae (4), (5) and (6). By comparing with the criteria listed in Table 1 and Table 4 in Ref. Zhong:2018exo , the criteria listed in Table 1 are much stricter, which reflects one of the advantages of the new sum rule formulae (4), (5) and (6), that is, they reduce the system uncertainty of the sum rule itself. Then, for those -moments, only the upper or lower limits of the corresponding Borel windows is clearly determined. In order to get complete Borel windows, we directly take their lengths as . Figure 1 shows the -meson twist-2, 3 DA -moments , and with versus the Borel parameter . In this figure, the uncertainties caused by the errors of input parameters is not drawn to clearly show the curves of different -moments. Meanwhile, the Borel windows are also shown with the shaded bands. By taking all error sources, such as -meson mass and decay constant, - and -quark masses, as well as vacuum condensates, etc., shown in Eqs. (16) and (17), into consideration, and adding the uncertainties in quadrature, the values of the first ten -moments of -meson twist-2, 3 DAs are shown in Table 2. Here, we give the first two Gegenbauer moments of -meson twist-2, 3 DAs for reference, that is,
| (19) |
at scale .
In the above work, in order to calculate the -moments of -meson twist-3 DAs and , one should calculate the normalization constants and first. Under the assumption that the sum rules of zeroth -moments and can be normalized in appropriate Borel windows, the sum rules of and can be obtained by taking in Eqs. (5) and (6) and substituting into these two sum rules. We require the continuum state’s contributions are less than and dimension-six condensate’s contributions are not more than and to determine the Borel windows for and , respectively. By adding the uncertainties derived from all error sources in quadrature, we have,
| (20) |
at scale . Compared with the values in Ref. Zhong:2018exo , in (20) increases by about , and decreases by about . The former is caused by the update of input parameters, while the latter is also caused by the new sum rule formula, i.e., Eq. (6), in addition to the update of input parameters.


Then we can determine the model parameters of our LCHO models for -meson twist-2 DA and twist-3 DAs and by using the -moments exhibited in Table 2 with the least squares method following the way suggested in Refs. Zhong:2021epq ; Zhong:2022ecl . Take the -meson leading-twist DA as an example, we first take the fitting parameters as the undetermined LCHO model parameters , and , i.e., , as discussed in Sec. II.2. By minimizing the likelihood function
| (21) |
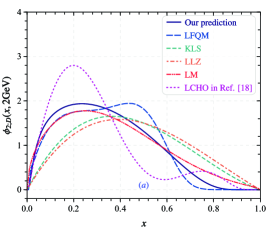
the optimal values of the fitting parameters we are looking for can be obtained. In Eq. (21), is taken to be the order of the -moments of ; the central values of -moments with their errors exhibited in Table 2 are regarded as the independent measurements and the corresponding variance . One can intuitively judge the goodness of fit through the magnitude of probability with the probability density function of , i.e., , where indicates the number of degrees of freedom. The obtained optimal values of the model parameters , and at scale and the corresponding goodness of fit are shown in Table 3. Following the same procedure, the LCHO model parameters for -meson twist-3 DAs and at scale and the corresponding goodness of fits can be obtained and are shown in Table 3 too. Then the corresponding behaviors of DAs , and are determined. In order to intuitively show the behaviors of these three DAs, we plot and exhibit their curves in Fig. 2. As a comparison, the models in literature for -meson leading-twist DA such as KLS model Kurimoto:2002sb , LLZ model Li:2008ts , LM model Li:1999kna , the form with LFQM Dhiman:2019ddr , and our previous research results Zhang:2017rwz ; Zhong:2018exo for , and based on the LCHO model are also shown in Fig. 2. From Fig. 2, one can find that our present prediction for is closes to LM model. Compared with the KLS model and LLZ model, our is narrower, and supports a large momentum distribution of valence quark in . Compared with our previous work in Refs. Zhang:2017rwz ; Zhong:2018exo , our new predictions for , and in this paper is smoother, and effectively eliminating the spurious oscillations introduced by the high-order Gegenbauer moments in old LCHO model.
IV summary
In this paper, we restudied the -meson leading-twist DA , twist-3 DAs and with QCD SRs in the framework of BFT by adopting a new scheme suggested in our previous work Zhong:2021epq . The new sum rule formula for the -moments , and , i.e., Eqs. (4), (5) and (6), were proposed and used to calculate whose values. Those values have been exhibited in Table 2. The LCHO models for DAs , and were improved. By fitting the values of -moments , and shown in Table 2 with the least squares method, the model parameters were determined and shown in Table 3. Then the predicted curves for -meson leading-twist DA , twist-3 DAs and are shown in Fig. 2.
The criteria adopted to determine the Borel windows for -moments of -meson leading-twist DA , twist-3 DAs and exhibited in Table 1 imply that the new sum rule formula (4), (5) and (6) can reduce the system uncertainties and propose more accurate predictions for -moments , and , respectively. The goodness of fits for , and are , and , respectively, which indicate our improved LCHO models shown in Sec. II.2 with the model parameters in Table 3 can well prescribe the behaviors of those three DAs. The predicted DAs’ curves shown in Fig. 2 indicate the improved LCHO models in this work can eliminate the spurious oscillations introduced by the high-order Gegenbauer moments in old LCHO models obtained in Refs. Zhang:2017rwz ; Zhong:2018exo . Otherwise, in order to simply investigate the influence of the new meson twist-2, 3 DAs in this work on the relevant physical quantities, the TFFs and are calculated. For the relevant formulae, one can refer to Ref. Zhong:2018exo . We find that the new DAs can bring about and changes to and respectively. In order to obtain a more accurate TFFs and , it is necessary to consider the next-to-leading order corrections for the contributions of meson twist-3 DAs, which will be our next step.
V Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant No.12265009 and No.12265010, the Project of Guizhou Provincial Department of Science and Technology under Grant No.ZK[2021]024 and No.ZK[2023]142, the Project of Guizhou Provincial Department of Education under Grant No.KY[2021]030, and by the Chongqing Graduate Research and Innovation Foundation under Grant No. ydstd1912.
References
- (1) Y. S. Amhis et al. [HFLAV], Averages of b-hadron, c-hadron, and -lepton properties as of 2018, Eur. Phys. J. C 81, no.3, 226 (2021). [arXiv:1909.12524] Updated results and plots available at https://hflav.web.cern.ch/
- (2) S. Aoki et al. [Flavour Lattice Averaging Group], FLAG Review 2019: Flavour Lattice Averaging Group (FLAG), Eur. Phys. J. C 80, no.2, 113 (2020). [arXiv:1902.08191]
- (3) J. P. Lees et al. [BaBar], Evidence for an excess of decays, Phys. Rev. Lett. 109, 101802 (2012). [arXiv:1205.5442]
- (4) J. P. Lees et al. [BaBar], Measurement of an Excess of Decays and Implications for Charged Higgs Bosons, Phys. Rev. D 88, no.7, 072012 (2013). [arXiv:1303.0571]
- (5) M. Huschle et al. [Belle], Measurement of the branching ratio of relative to decays with hadronic tagging at Belle, Phys. Rev. D 92, no.7, 072014 (2015). [arXiv:1507.03233]
- (6) G. Caria et al. [Belle], Measurement of and with a semileptonic tagging method, Phys. Rev. Lett. 124, no.16, 161803 (2020). [arXiv:1910.05864]
- (7) J. A. Bailey et al. [MILC], form factors at nonzero recoil and from 2+1-flavor lattice QCD, Phys. Rev. D 92, no.3, 034506 (2015). [arXiv:1503.07237]
- (8) H. Na et al. [HPQCD], form factors at nonzero recoil and extraction of , Phys. Rev. D 92, no.5, 054510 (2015) [erratum: Phys. Rev. D 93, no.11, 119906 (2016)]. [arXiv:1505.03925]
- (9) D. Bigi and P. Gambino, Revisiting , Phys. Rev. D 94, no.9, 094008 (2016). [arXiv:1606.08030]
- (10) M. Bordone, M. Jung and D. van Dyk, Theory determination of form factors at , Eur. Phys. J. C 80, no.2, 74 (2020). [arXiv:1908.09398]
- (11) F. U. Bernlochner, Z. Ligeti, M. Papucci and D. J. Robinson, Combined analysis of semileptonic decays to and : , , and new physics, Phys. Rev. D 95, no.11, 115008 (2017) [erratum: Phys. Rev. D 97, no.5, 059902 (2018)]. [arXiv:1703.05330]
- (12) S. Jaiswal, S. Nandi and S. K. Patra, Extraction of from and the Standard Model predictions of , JHEP 12, 060 (2017). [arXiv:1707.09977]
- (13) I. Caprini, L. Lellouch and M. Neubert, Dispersive bounds on the shape of form-factors, Nucl. Phys. B 530, 153-181 (1998). [hep-ph/9712417]
- (14) C. G. Boyd, B. Grinstein and R. F. Lebed, Precision corrections to dispersive bounds on form-factors, Phys. Rev. D 56, 6895-6911 (1997). [hep-ph/9705252]
- (15) M. Tanaka and R. Watanabe, Tau longitudinal polarization in and its role in the search for charged Higgs boson, Phys. Rev. D 82, 034027 (2010). [arXiv:1005.4306]
- (16) S. Fajfer, J. F. Kamenik and I. Nisandzic, On the Sensitivity to New Physics, Phys. Rev. D 85, 094025 (2012). [arXiv:1203.2654]
- (17) Y. M. Wang, Y. B. Wei, Y. L. Shen and C. D. Lü, Perturbative corrections to form factors in QCD, JHEP 06, 062 (2017). [arXiv:1701.06810]
- (18) Y. Zhang, T. Zhong, X. G. Wu, K. Li, H. B. Fu and T. Huang, Uncertainties of the transition form factor from the D-meson leading-twist distribution amplitude, Eur. Phys. J. C 78, no.1, 76 (2018). [arXiv:1709.02226]
- (19) T. Zhong, Y. Zhang, X. G. Wu, H. B. Fu and T. Huang, The ratio and the -meson distribution amplitude, Eur. Phys. J. C 78, no.11, 937 (2018). [arXiv:1807.03453]
- (20) T. Huang and Z. Huang, Quantum Chromodynamics in Background Fields, Phys. Rev. D 39, 1213-1220 (1989).
- (21) T. Zhong, X. G. Wu, Z. G. Wang, T. Huang, H. B. Fu and H. Y. Han, Revisiting the Pion Leading-Twist Distribution Amplitude within the QCD Background Field Theory, Phys. Rev. D 90, no.1, 016004 (2014). [arXiv:1405.0774]
- (22) T. Kurimoto, H. n. Li and A. I. Sanda, form-factors in perturbative QCD, Phys. Rev. D 67, 054028 (2003). [hep-ph/0210289]
- (23) R. H. Li, C. D. Lu and H. Zou, The and decays in the perturbative QCD approach, Phys. Rev. D 78, 014018 (2008). [arXiv:0803.1073]
- (24) H. n. Li and B. Melic, Determination of heavy meson wave functions from B decays, Eur. Phys. J. C 11, 695-702 (1999). [hep-ph/9902205]
- (25) X. H. Guo and T. Huang, Hadronic wave functions in D and B decays, Phys. Rev. D 43, 2931-2938 (1991).
- (26) F. Zuo and T. Huang, form-factors in light-cone sum rules and the meson distribution amplitude, Chin. Phys. Lett. 24, 61-64 (2007). [hep-ph/0611113]
- (27) S. J. Brodsky, T. Huang, and G. P. Lepage, in Particles and Fields-2, Proceedings of the Banff Summer Institute, Ban8; Alberta, 1981, edited by A. Z. Capri and A. N. Kamal (Plenum, New York, 1983), p. 143; G. P. Lepage, S. J. Brodsky, T. Huang, and P. B.Mackenize, ibid. , p. 83; T. Huang, in Proceedings of XXth International Conference on High Energy Physics, Madison, Wisconsin, 1980, edited by L. Durand and L. G Pondrom, AIP Conf. Proc. No. 69 (AIP, New York, 1981), p. 1000.
- (28) N. Dhiman, H. Dahiya, C. R. Ji and H. M. Choi, Twist-2 Pseudoscalar and Vector Meson Distribution Amplitudes in Light-Front Quark Model with Exponential-type Confining Potential, Phys. Rev. D 100, no.1, 014026 (2019). [arXiv:1902.09160]
- (29) T. Zhong, Z. H. Zhu, H. B. Fu, X. G. Wu and T. Huang, Improved light-cone harmonic oscillator model for the pionic leading-twist distribution amplitude, Phys. Rev. D 104, no.1, 016021 (2021). [arXiv:2102.03989]
- (30) P. Ball and M. Boglione, breaking in and distribution amplitudes, Phys. Rev. D 68, 094006 (2003). [arXiv:hep-ph/0307337]
- (31) L. Chang, I. C. Cloet, J. J. Cobos-Martinez, C. D. Roberts, S. M. Schmidt and P. C. Tandy, Imaging dynamical chiral symmetry breaking: pion wave function on the light front, Phys. Rev. Lett. 110 (2013) 132001. [arXiv:1301.0324]
- (32) G. S. Bali et al. [RQCD], Light-cone distribution amplitudes of pseudoscalar mesons from lattice QCD, JHEP 08, 065 (2019). [arXiv:1903.08038]
- (33) J. Hua et al. [Lattice Parton], Pion and Kaon Distribution Amplitudes from Lattice QCD, Phys. Rev. Lett. 129, no.13, 132001 (2022). [arXiv:2201.09173]
- (34) T. Zhong, Z. H. Zhu and H. B. Fu, Constraint of -moments calculated with QCD sum rules on the pion distribution amplitude models, Chin. Phys. C 47, no.1,013111 (2023). [arXiv:2209.02493]
- (35) T. Zhong, H. B. Fu and X. G. Wu, Investigating the ratio of CKM matrix elements from semileptonic decay and kaon twist-2 distribution amplitude, Phys. Rev. D 105, no.11, 116020 (2022). [arXiv:2201.10820].
- (36) D. D. Hu, H. B. Fu, T. Zhong, Z. H. Wu and X. G. Wu, -meson longitudinal twist-2 distribution amplitude and the decay processes, Eur. Phys. J. C 82, no.7, 603 (2022). [arXiv:2107.02758]
- (37) D. Huang, T. Zhong, H. B. Fu, Z. H. Wu, X. G. Wu and H. Tong, Twist-2 Distribution Amplitude and Transition Form Factors, [arXiv:2211.06211].
- (38) Z. H. Wu, H. B. Fu, T. Zhong, D. Huang, D. D. Hu and X. G. Wu, -meson twist-2 distribution amplitude within the QCD sum rules and investigation of , [arXiv:2211.05390].
- (39) T. Huang, X. H. Wu and M. Z. Zhou, Twist three distribute amplitudes of the pion in QCD sum rules, Phys. Rev. D 70, 014013 (2004). [hep-ph/0402100]
- (40) T. Huang, M. Z. Zhou and X. H. Wu, Twist-3 distribution amplitudes of the pion and kaon from the QCD sum rules, Eur. Phys. J. C 42, 271-279 (2005). [hep-ph/0501032]
- (41) R. L. Workman [Particle Data Group], Review of Particle Physics, PTEP 2022, 083C01 (2022).
- (42) P. Colangelo and A. Khodjamirian, QCD sum rules, a modern perspective, [hep-ph/0010175].
- (43) P. del Amo Sanchez et al. [BaBar], Observation of new resonances decaying to and in inclusive collisions near 10.58 GeV, Phys. Rev. D 82, 111101 (2010). [arXiv:1009.2076]
- (44) Z. H. Li, N. Zhu, X. J. Fan and T. Huang, Form Factors and in and Determination of and , JHEP 05, 160 (2012). [arXiv:1206.0091]