Department of Physics, Peking University, No.5 Yiheyuan Rd, Beijing 100871, P.R. China
Revisiting 3D Flat Holography: Causality Structure and Modular Flow
Abstract
Flat space holography is an open and hard problem existing several different approaches, which may finally turn out to be consistent with each other, in the literature to tackle it. Focusing on how bulk emergent spacetime is encoded in quantum information of null boundaries, we choose a specific toy model called the flat3/BMSFT model, which conjectures the duality between boundary BMS3 invariant field theory and bulk quantum gravity in 3D asymptotic flat spacetimes (AFS), to explore. Aiming to find an entanglement wedge like quantity for single interval and a connected entanglement wedge for multi-intervals in flat3/BMSFT model, we explore the bulk causality structures related to the holographic swing surface proposal through both boundary and bulk local modular flow, make a corresponding decomposition of the global Minkowski spacetime and look at the entanglement phase transition. As a byproduct, we solve the problem about the existence of partial entanglement entropy (PEE) correspondence in this model which is a bit nontrivial due to the unusual behavior of boundary modular flow in BMS3 field theory. Among the literature considering quantum information aspects of flat3/BMSFT model, there are several substantial, unusual but overlooked phenomena which need to be emphasized and revisited to gain more deserved attention. Thus another motivation of this paper is to find where these unusual phenomena come from, and physically show in a manifest way what they may imply. After reading we hope readers can feel sincerely what we present about the above mentioned second aim is more valuable than the mathematical results in the present paper.
1 Introduction
The principle of holography Maldacena:1997re ; Witten:1998qj ; Gubser:1998bc has been successfully used to understand theories of quantum gravity in AdS spacetime and strongly coupled field theory for more than twenty years. Starting from the proposal of Ryu-Takayanagi formula Ryu:2006bv ; Hubeny:2007xt ; Nishioka:2009un ; Lewkowycz:2013nqa , there has been profound progress in exploring how spacetime and gravitational dynamics can emerge from boundary quantum information theory Harlow:2018fse ; Almheiri:2020cfm ; Bousso:2022ntt . There are also mixed state entanglement measures generalization of the holographic entanglement entropy, for example the correspondence of entanglement wedge cross section (EWCS) with the reflected entropy Dutta:2019gen , entanglement negativity Kusuki:2019zsp and balanced partial entanglement entropy (BPE) Wen:2021qgx . At the heart of these developments is the entanglement wedge reconstruction, i.e., subregion-subregion duality Faulkner:2013ana ; Jafferis:2015del ; Dong:2016eik , which states that bulk operators in the entanglement wedge can be decoded from the operator algebra in the causal domain of the dual CFT. Another important approach highlighting the emergence of bulk locality and causality is the concept of modular flow Faulkner:2017vdd ; Witten:2018zxz ; Faulkner:2018faa . Operator reconstruction with modular flow allow one to reach everywhere inside of entanglement wedge , which can reach far beyond the causal horizons. For the entanglement wedge , there are two equivalent definitions in AdS/CFT holography Headrick:2014cta . One is the bulk domain of dependence of homology surface (defined in (4.20)) which interpolates between boundary interval and corresponding HRT surface. Another definition is the bulk region bounded by bifurcating horizons of HRT surface on one side and boundary causal domain on the other side. Whether these properties are universal to general holographic theories beyond AdS/CFT? One motivation of the paper is exploring the story of entanglement wedge like quantity in a toy model of 3D flat holography, i.e., the flat3/BMSFT model, using mainly modular flow and other refined tools due to the complications and subtleties here.
Although people face both practical and philosophical difficulties in formulating flat version of AdS holography, there has been interesting work on understanding holography in asymptotically flat spacetimes at the early days of AdS/CFT Susskind:1998vk ; Polchinski:1999ry ; Giddings:1999jq ; Arcioni:2003td ; deBoer:2003vf . In recent years, there is a delightful re-booming about this problem. One key role in this re-booming is the bottom-up approach called celestial holography Strominger:2017zoo ; Pasterski:2021raf , which proposes a correspondence between 4D gravity theories in asymptotically flat spacetimes (AFS) and 2D celestial conformal field theories (CCFT) living on the celestial sphere at null infinity due to advances in understanding the soft theorems and asymptotic structure of AFSHe:2014laa ; He:2015zea ; Cheung:2016iub ; Pasterski:2016qvg ; Pasterski:2017kqt . Bulk S-matrix elements, when written in boost eigenstate basis, can be reinterpreted as correlation functions in 2D conformal field theory. Thus very powerful CFT techniques, such as operator product expansion Fotopoulos:2019tpe ; Pate:2019lpp ; Banerjee:2020kaa ; Costello:2022upu ; Hu:2022bpa , conformal block decomposition Atanasov:2021cje ; Fan:2021isc , crossing symmetry Mizera:2022sln , can all be used to explore properties of celestial CFT. Also using this kind of language lead people find new symmetries Strominger:2021lvk . However it is rather vague at this stage that how much and in which aspects the 2D CCFT would differ from the usual 2D Virasoro CFT. Moreover, the emergence of bulk flat spacetime from boundary degree of freedom of celestial CFT seems to be at least complicated. However viewing recent fascinating developments of understanding how bulk spacetime emerge from boundary and the nature of holographic map as a quantum error correction code Almheiri:2014lwa , it is very attractive to see whether similar nature of holographic duality in AdS hold true in flat case. The most important object underlying this kind of story in AdS/CFT is the entanglement wedge dual to specific boundary subregion, and we would like to find similar objects in flat holography. With this curiosity, we turn to another bottom-up approach called Carrollian holography, which is more similar to the usual AdS/CFT set up. Due to the matter or gravitational radiation, the gravitational charge defined at null infinity would be non-conserved Barnich:2011mi ; Trautman:1958zdi ; Donnay:2022wvx . Thus we focus on 3D flat bulk with pure Einstein action, more specifically, the flat3/BMSFT model. The analysis in this paper are special to 3D AFS, and we make a first but essential step in this direction. Our explorations are complementary to the main trend in literature on flat holography focusing on S-matrix elements, ward identities as well as asymptotic symmetry, and focus more on dynamical gravity aspects of holographic duality. Note another more information theoretic approach about flat holography Laddha:2020kvp explores how quantum information is stored at null infinity by using boundary operator algebra. Also there are interesting and illuminating works trying to link Carrollian holography approach with celestial holography approach in 4D flat spacetime Bagchi:2022emh ; Donnay:2022aba .


The Carrollian holography has been proved to be successful in 3D case, and we would like to link its story to the limiting problem of AdS/CFT. Whether flat holography can be understood as a limiting case of AdS/CFT is still an open problem. Although there are plenty of research working on extracting perturbative S-matrix elements from AdS correlators Penedones:2010ue ; Fitzpatrick:2011ia ; deGioia:2022fcn , they are limited to very special state in the Hilbert space of quantum gravity in AFS (if it exists!). At the level of asymptotic symmetry algebra (ASA) in the machinery of holography, Bagchi:2010zz ; Bagchi:2012cy made an interesting observation that ASA of 3D AFS, i.e., the BMS3 algebra Bondi:1962px ; Sachs:1962wk , can be obtained as a ultra-relativistic limit of 2D conformal algebra. Starting from these works, flat3/BMSFT model go through several non-trivial checks, such as reproducing thermal entropy in the bulk from a Cardy-like formula at the boundary Barnich:2012xq ; Bagchi:2012xr , reproducing characters of the BMS3 group from one loop partition function of 3D flat gravity Barnich:2015mui , reproducing BMS3 blocks from bulk geodesic Feynman diagrams Hijano:2018nhq and reproducing boundary entanglement entropy from bulk swing surface Jiang:2017ecm . Considering the holographic entanglement entropy, Apolo:2020bld ; Apolo:2020qjm updated the generalized Rindler method used in Jiang:2017ecm for limited regions and states to more general cases using approximated modular flow method and a general swing surface proposal. Note that in flat3/BMSFT model, the vacuum state in the Hilbert space of quantum gravitational theory of AFS is assumed to be unique. This may contradict with the lessons learned from celestial holography and soft theorems that the vacuum state of 4D AFS is infinitely degenerated due to supertranslation and soft gravitons Bagchi:2016bcd .
In purpose of exploring how boundary information are related to bulk subregion, similar to the aim of Laddha:2020kvp but working in a more concrete model, we use various tools developed in AdS/CFT to try to find the analogue of the entanglement wedge in flat holography. In the literature there are some checks about matching of holographic reflected entropy and balanced partial entanglement entropy (BPE) Basu:2021awn ; Basak:2022cjs ; Camargo:2022mme in flat3/BMSFT model, however the calculations and physical conclusions need to be reconsidered. The necessity of this revisiting originates from the following facts: 1). The flat3/BMSFT model has a Lorentzian bulk spacetime and no Euclidean path integral apply here. So we should consult to a coordinate invariant codimension zero bulk region to define the entanglement wedge not a coordinate non-invariant codimension one bulk surface, which should be different from the usual AdS/CFT case; 2). Also in the literature, they only studied very limited symmetric boundary two intervals, which gave them an unrealistic illusion about their results. Although these works are interesting, actually no well defined connected entanglement wedge has ever been established in works Basu:2021awn ; Basak:2022cjs ; Camargo:2022mme and the related ones. It turns out that for generic boundary non-symmetric two intervals the entanglement wedge cross section (EWCS) can totally locate outside the naive expected connected entanglement wedge, see Figure 5, although the numerical values can mysterious match with each other. Then the natural question is what’s the entanglement wedge related to single boundary interval? What’s the connected entanglement wedge related to multi-boundary intervals? If we can not specify the parameter range of intervals related to the connected entanglement wedge, what is the meaning of bulk EWCS we compute? Actually according to the results obtained in this paper, finding accurate answers to the above questions are a rather non-trivial task. Even the existence of normal entanglement wedge should be reasonably questioned because of the existence of negative holographic entanglement entropy noticed already in Apolo:2020bld . Actually not only can the holographic entanglement entropy be negative, all entanglement measures calculated in flat3/BMSFT model including the holographic reflected entropy, holographic entanglement negativity and balanced partial entanglement entropy (BPE) can have negative values. This is in fact a general and unique property of flat3/BMSFT model, which has not been given sufficient attention in the literature. Viewing from field theory, the negative value may come from non-unitary property. From bulk side, we make the key observation that the negativeness is just a reflection about the unique structure of local modular flow of BMS3 field theory. More intuitively we can see from Figure 1, the modular evolution along local modular flow of BMS field theory are quite different from the modular evolution of CFT which is consistent with the global time defined on the whole 2D plane. Part of the results in this paper can be viewed as the bulk manifestation of this unusual boundary modular flow behavior.
Another tool we use to find the analogue of entanglement wedge in flat holography is the PEE (partial entanglement entropy) correspondence Wen:2018whg , which proposes to give a fine version of RT formula. We don’t comment on the physical foundation of this proposal, but rather view it as a useful tool to manifest various aspects of holographic duality when we have a local modular flow. From PEE correspondence, people can derive the balanced partial entanglement entropy (BPE) and EWCS correspondence Wen:2021qgx . However in literature Camargo:2022mme ; Basu:2022nyl people just observed the match of BPE and EWCS without giving a more basic proof about PEE correspondence in flat3/BMSFT model. The reason can again be traced back to the curious behavior of modular flow of BMS3 field theory, which makes the finding of corresponding bulk point from modular flow method rather unclear with less physical intuition. As a byproduct, we solve the existence of PEE correspondence in flat3/BMSFT model by using the intersection of swing surfaces (first method) and rewriting the original modular flow correspondence (second method). We find exact match between these two methods and these are solid mathematical results in this paper. The way we solve the above existing problem on modular flow method in flat3/BMSFT model is to explicitly manifest the degree of freedom using our rewriting, and this is also a good place to see the subtlety in flat3/BMSFT model.
Although we find more structures of the correspondence between boundary and bulk modular flow, as well as make a bulk decomposition of global flat3 related to single boundary interval , we fail to specify which bulk subregion is the most natural entanglement wedge in this model. Especially in two intervals case considering the connected entanglement wedge, the confirmed results are only made on the field side. Also we can’t integrate the implications of general lesson learned from negative entanglement entropy and swing surface penetrating phenomena into the exploration of entanglement wedge. We hope that bringing these fundamental issues to researchers in a clearer and more obvious way is more valuable than the mathematical results presented in this paper. This is our second motivation for writing this paper.
The structure of the paper is organized as follows. In section 2, we review the flat3/BMSFT model, the general prescription of swing surface proposal for single interval holographic entanglement entropy and the PEE correspondence in AdS/CFT with useful comments at the end of each subsection. In section 3, we explicitly draw the Penrose diagram of the quotient manifolds, i.e., the zero mode solutions, in AFS and show a subtle issue of the order of taking infinite limit. Then we show where the bulk negative sign of holographic entanglement entropy come from using Noether charge formalism. Finally we present observations about EWCS for general boundary intervals which manifest the loopholes of arguments in the literature. In section 4, we mathematically and pictorially analyze the behavior of bifurcating horizons related to both finite bench and the infinite bifurcating surface . Then we decompose the global flat3 spacetime into four disconnected parts using both the past and future bifurcating horizons. Intersection of swing surface method and bulk boundary modular flow correspondence method for deriving the PEE correspondence in flat3/BMSFT model are presented. In the last by comparing with the entanglement wedge in AdS/CFT case, we show the subtleties of the flat3/BMSFT model. In section 5, we analyze the entanglement phase transition of two intervals on the boundary side and entanglement wedge nesting (EWN) property in the bulk side. In section 6, we discuss two important open questions unique to flat3/BMSFT model which are observed in section 2. We collect several additional results in Appendices. In Appendix A, we give a complete derivation of two disjoint interval reflected entropy in BMS3 field theory with explicit calculations about the three point coefficient. This is a necessary but missing part of the calculations about reflected entropy in Basak:2022cjs , which sincerely pointed out by Basu:2022nyl . Appendix B repeat the analytic analysis of the Poincaré vacuum for the zero mode backgrounds including the bifurcating horizon in Penrose diagram and the entanglement phase transition.
2 flat3/BMSFT model and PEE correspondence
In 3D asymptotically flat spacetimes (AFS) Einstein gravity admits consistent boundary conditions at future null infinity , where the finite dimensional Poincaré isometry group is enhanced to infinite dimensional asymptotic symmetry group, i.e., the BMS3 group Bondi:1962px ; Sachs:1962wk . These facts lead people to conjecture that there is a toy model of flat holography, dubbed flat3/BMSFT model, which maps between Einstein gravity in 3D AFS and BMS invariant field theories at 2D conformal boundary. Intuitively the topology of the null boundary of 3D AFS is with the null direction. And BMS3 group include super-translation which is coordinate dependent translation along the null direction and super-rotation which is the diffeomorphism of . This section includes a self-contained review of 2D BMS3 invariant field theory with more emphasize on entanglement entropy, the development of the general swing surface proposal and the PEE correspondence in AdS/CFT holography. At the end of each subsection, useful comments on the subtleties are presented.
2.1 BMS3 invariant field theory
BMS invariant field theory is a class of 2D ultra relativistic quantum field theories invariant under following spacetime reparametrizations Bagchi:2010zz ; Barnich:2012xq ,
| (2.1) |
where and are arbitrary functions, and are coordinates of the plane the field theory lives. The infinitesimal BMS transformations are generated by following Fourier modes,
| (2.2) |
Under Lie bracket they form the BMS3 algebra without the centrally extension term. While the generators and implementing local coordinate transformations (2.2) on quantum fields form the centrally extended BMS3 algebra,
| (2.3) |
where and are the central charges. The Einstein-Hilbert gravity in flat holography are expected to be dual to a BMS field theory with central charges , while the field theory with more general value of central charges could be constructed by adding a Chern-Simons term to the Einstein-Hilbert action.
The generators and are also called BMS charges on the plane, which are the Fourier modes of the conserved currents and ,
| (2.4) | ||||
| (2.5) |
where can be seen as the contour integral of the complexified coordinates. The conserved currents and generating the coordinate transformations (2.1) transform under the transformations as
| (2.6) | ||||
where denotes the ordinary Schwarzian derivative and the last term denotes the BMS Schwarzian derivative
| (2.7) | |||
| (2.8) |
The infinite dimensional BMS3 algebra not only have the singlet version of the highest weight representation (HWR), but also the multiplet version of the HWR Hao:2021urq . In the singlet version of HWR, a local primary operator at the origin is labelled by the eigenvalues of generators and which are the center of the BMS3 symmetry algebra (2.3),
| (2.9) |
where denotes the conformal weight and denotes the boost charge. The HWR respect the following conditions,
| (2.10) |
The singlet primary operators transform under finite transformation (2.1) as follows,
| (2.11) |
By requiring the vacuum to be invariant under the global symmetry of BMS3 field theory, the correlation functions on the plane have the following form,
| (2.12) | ||||
| (2.13) | ||||
| (2.14) |
where two point function of primary operators are properly normalized, is the coefficient of three-point function encoding dynamical information of the BMS3 field theory and
| (2.15) |
The and appearing in function are BMS invariant cross ratios
| (2.16) |
Entanglement entropy of BMS3 field theory was first considered in Bagchi:2014iea using algebraic twist operator method Calabrese:2009qy . By generalizing the Rindler method to BMS3 invariant field theory, Jiang:2017ecm not only gets the consistent entanglement entropy through an explicitly local modular flow expression, but also extends the calculation into the bulk getting the swing surface picture. We list some results related to entanglement entropy here for later convenience. BMS3 field theory is not Lorentz invariant, thus a general spatial interval instead of an equal time interval is need to show the dependence of entanglement entropy on the choice of frame. In the plane vacuum state, the conformal weight and boost charge in cyclic orbifold are,
| (2.17) |
Then the partition function of the replica manifold and the entanglement entropy of single interval are,
| (2.18) | |||
| (2.19) |
where is the direction UV regulator introduced by relating to the regularization of the divergent partition function . We can see from (2.19) that for the bulk correspondence of Einstein gravity with , the entanglement entropy can be negative due to possible different sign of and . When considering the finite temperature state on the plane, we use the following general thermal periodicity,
| (2.20) |
where denote the coordinates on the thermal cylinder. We can use the BMS conformal transformation to map from plane to cylinder Jiang:2017ecm ,
| (2.21) |
The two point function of twist operators evaluated on this cylinder then is given by
Thus the entanglement entropy of single interval in the thermal state is,
| (2.22) |
Comments: A key assumption in the above calculations is that the twist operators and belong to the singlet version of HWR of the BMS3 algebra. It was noticed and proved in Hao:2021urq that primary fields can also be organized in a Jordan chain and form a multiplet which is a reducible but indecomposable module together with their descendants. Cyclic Orbifold theory of BMS field on replicated Carrollian geometry is a much unexplored area and could go beyond the usual expectations. For example, see Chen:2022fte for the subtleties about the Orbifold theory of 2D WCFT living in Newton-Cartan geometry. It is possible that the twist operators in BMS orbifold theory belong to the multiplet version of HWR, thus affect the final answer of entanglement entropy (2.19) and (2.22).
2.2 Swing Surface Proposal
Instead of directly extend the HRT formula into the flat3/BMSFT model, Jiang:2017ecm derive the swing surface configuration by the exact correspondence between boundary local modular flow generators and bulk killing vector fields. The advantage of this method is the holographic dictionary of the entanglement entropy is automatically consistent. While the disadvantage of this method is that the local modular flow can only exist for special entangled regions and special states. Due to the above reasons, Apolo:2020bld ; Apolo:2020qjm update the above method and propose a more general prescription to get the swing surface for holographic entanglement entropy by using the approximate modular flow in both the boundary and the bulk. Let us summarize the main steps of these developments in flat3/BMSFT model following Apolo:2020bld ; Apolo:2020qjm closely.
For an interval on the vacuum state of BMS3 field theory, which is dual to a spacetime in the bulk invariant under the same set of symmetries, we can find a consistent boundary flow generator and the corresponding bulk Killing field ,
| (2.23) |
where are parameters depending on the entangling region , are boundary and bulk Rindler time respectively satisfying periodicity conditions
| (2.24) |
are the vacuum symmetry generators defined on the boundary, and are the corresponding bulk Killing vectors under the dictionary of flat3/BMSFT holography satisfying . The boundary modular flow generator need satisfy following conditions: 1). The transformation is a symmetry of the field theory where the domain of is the causal domain ; 2). The transformation is invariant under a pure imaginary (thermal) identification ; 3). The one parameter flow generated by through the exponential map leave the causal domain and its boundary invariant when is real.
The periodicity (2.24) is considered as a thermal identification, which implies that the bulk modular flow generator features bifurcating Killing horizons with surface gravity . We denote the bifurcating surface as and two Killing horizons as , which satisfy
| (2.25) | |||
| (2.26) | |||
| (2.27) | |||
| (2.28) |
where is the unit vector binormal to . (2.25) follows from the fact that is an extremal surface; (2.26) shows that is the boost generator in the local Rindler frame near ; (2.27) means the surface gravity is indeed a constant value ; (2.28) is the Frobenius’ theorem guaranteeing the vector field is hypersurface orthogonal. Finally in this special case, the ropes of the swing surface are null geodesics generated by bulk modular flow while the bench of the swing surface is the set of fixed points of bulk modular flow generator that extremizes the distance between the ropes.
For more general states and boundary configurations, we need to consult to the approximate modular flow , which on the 2D boundary can be obtained from the expressions for single intervals on the vacuum by sending the other endpoint to infinity. For each end point of interval, it is possible to find the null geodesic whose tangent vector is an asymptotic Killing vector reducing to at the conformal boundary. Then the general swing surface is the minimal extremal surface bounded by these null geodesics. One major difference compared to standard HRT surface in AdS/CFT is that, in flat3/BMSFT model the fixed points of the boundary modular flow are not the fixed points of the bulk modular flow meaning the bifurcating surface is not attached to the interval at the boundary.
comments:
-
•
In Apolo:2020bld the authors propose that the holographic dictionary of entanglement entropy in flat3/BMSFT model is the area of swing surface (or bench )
(2.29) However as also been noticed by the same paper, the problem is how can the area term have negative value (2.19). In the next section, we would find that the holographic dictionary of need more elements not just the pure gravity area property.
-
•
The descriptions of bifurcating horizons 111Note our notations are different from those in Apolo:2020bld . in section of Apolo:2020bld are not precise. According to the results in section 3, the bifurcating horizons connected to boundary interval are both future directed and the killing horizons emitted from the finite bench only touch the future null infinity at two single points. Note that these unusual features seem to be unique for flat3/BMSFT model, which is not due to the swing surface construction, see Chen:2022fte ; Wen:2018whg for comparison.
2.3 PEE correspondence


Since in this paper we just take the partial entanglement entropy (PEE) correspondence as a useful tool, so we only present the most basic elements of them. Please see Wen:2018whg ; Wen:2021qgx for more physical interpretations.
In Wen:2018whg , the author made two proposals about the holographic dictionary (PEE correspondence) for the entanglement contour of a single interval in the context of AdS3/CFT2. The first proposal states that the partial entanglement entropy , see Figure 2, is given by a linear combination of entanglement entropies of relevant subsets inside interval for general 2D theories
| (2.30) |
The second proposal is a fine structure analysis about the entanglement wedge through boundary and bulk modular flow, which is used in this paper as a way to explore the ”entanglement wedge” of flat3/BMSFT model. This bulk and boundary one-to-one correspondence can also be obtained by intersection of RT surfaces, see Figure 2. Finally the holographic dictionary about PEE says that
| (2.31) |
Comments: As rigorously said by Wen:2021qgx the bulk modular flows exactly settle at the boundary when they approach the boundary, so there are no orbits in the bulk. Thus to really find a boundary and bulk correspondence through local modular flow method, we should choose a cut-off surface, see Figure 2. Then there is a degree of freedom in choosing which modular flow line in the chosen cut-off surface correspond to a specific modular flow line at the asymptotic boundary. This freedom not only can affect the bulk point of PEE correspondence, i.e., in Figure 2, but also can affect the shape of the line between boundary and bulk corresponding points. Wen:2018whg make a good proposal on how to fix this freedom in AdS3/CFT2, but how to fix this freedom in flat3/BMSFT model is not clear. As a byproduct in this paper, we find there is a consistent way to fix the d.o.f. in flat case although the underlying physical reasons need further study. In any case, this is not the focus of this paper and the intersection of RT like surfaces way turn out to be more general and less uncertain.
3 Quotient manifolds and observations
After a summary of the phase space of Einstein gravity solutions under the consistent asymptotic boundary conditions (3.1) in flat3/BMSFT model, we give the exact Penrose diagrams (not cartoon pictures) of the zero mode solutions, which are quotient manifolds of global Minkowski spacetime (the global flat3). To gain more intuition, a subtle issue about drawing boundary causal domain on compact Penrose diagram of the covering global flat3 is shown. Then two key observations about holographic entanglement entropy (swing surface) and holographic reflected entropy related (EWCS) are presented. One is about how to derive the ”negative” sign of holographic entanglement entropy and reflected entropy in the bulk, the other one is about whether the finite bench or the infinite bifurcating surface is more fundamental, or at least more useful, in finding the ”entanglement wedge” of this model. The first two subsections are preliminary to understand the explorations in this paper, the last two subsections are a revisit of the results in Apolo:2020bld ; Basu:2021awn . We try to extract some general lessons from these new observations about flat holography.
More precisely, the above mentioned asymptotic boundary conditions near future null infinity Barnich:2010eb in the retarded Bondi coordinates is
| (3.1) |
where . The phase space of solutions to pure Einstein’s equations in Bondi gauge is parametrized by two periodic functions and such that
| (3.2) |
where the null infinity is located at . The zero mode solutions with constant and describe some classical backgrounds of spacetime and are our main interest. With the convention , the parameters and correspond to the canonical energy and the angular momentum of the spacetime. In particular, the solution corresponds to the global Minkowski vacuum, the solutions correspond to the conical defect geometries, and the solution, called the null orbifold, is supposed to be the analogue of zero temperature BTZ. Solutions with is usually referred to as flat cosmological solutions (FSC) and have Cauchy horizons. This fact can be seen clearly in the ADM form Barnich:2012aw of the zero mode metric
| (3.3) |
which implies that the Cauchy horizon is located at
| (3.4) |
We are also interested in the vacuum state in flat Poincaré coordinates with metric
| (3.5) |
which can be obtained by decompactify the angular direction of null orbifold solution. This is the flat limit of the Poincaré patch of AdS3.
3.1 Boundaries and Horizons
In 3D pure Einstein gravity, there is no propagating degree of freedom. The only way to construct different solutions is by taking quotient. Like the BTZ black holes are the discrete quotient manifolds of global AdS3, the above mentioned zero mode backgrounds, i.e., the (the Poincaré vacuum), (FSC) and (including global Minkowski) zero mode backgrounds, are also the discrete quotient manifolds of global flat3.



For each case we first give the coordinate transformations Apolo:2020bld that map that zero mode background to the global flat3 with coordinates , then point out the corresponding boundaries or horizons of these quotient manifolds.
-
•
The Poincaré vacuum The coordinate transformations 222Note the transformations here are different with Apolo:2020bld ; Jiang:2017ecm , which depend on the boundary interval . are,
(3.6) for any value of and . Without loss of generality we choose in this paper. In order to see the boundary of spacetime clearly, we need an inverse coordinate transformations
(3.7) So the Poincaré vacuum cover only the part of the global Minkowski spacetime, see Figure 3 .
-
•
zero mode backgrounds The coordinate transformations are:
(3.8) So we have the relation , which leads to the boundary location , See Figure 3. Note that if we have , i.e., the whole Minkowski spacetime, then the codimension one boundary in Figure 3 would shrink to one dimensional line with excluding nothing from the global flat3 and consistent with the expectation.
-
•
zero mode backgrounds The coordinate transformations are:
(3.9) The spacetime region with exterior to Cauchy horizon locating at cover the parameter range
(3.10) while the interior of the Cauchy horizon cover the parameter range
(3.11) In Figure 3, the exterior of Cauchy horizon is above both the green and blue surfaces, and the interior of Cauchy horizon is the right part of the region enclosed by both the green and blue surfaces.
Note that if we draw the swing surface in the above compact Penrose diagrams, the finite bench would always penetrate the boundaries or horizons of the original spacetime. This curious phenomena is discussed in the last section.
3.2 Order of taking the Infinity Limit
The order of taking the infinite limit is a subtle issue in mathematics. Here is a good example due to the infinite range of both and coordinates in Bondi gauge. For the above coordinate transformations, if we take the limit of Bondi coordinate, which is equivalent to keep coordinate a finite but arbitrary value and taking to infinity, the BMS field theory would always live on the future null infinity for all , and cases. However, we know that the global Minkowski spacetime with contain not only the future null infinity but also the past null infinity , which actually comes from another limit 333For simplicity in this subsection, we omit the mathematical proof of the statements, which can be obtained by following the same route as (4.11) and (4.18). . With the above observation, we explore the following limits
| (3.12) |
in , and solutions separately and summarize the new phenomena.




-
•
For the usual limit, we have the expected Penrose diagram as 4 for all the zero mode solutions.
- •
-
•
zero mode backgrounds New phenomena happen in both limits of (3.12). When the go around the spacelike infinity as in the case of the Poincaré vacuum; when the go through the timelike infinity , see 4, to a similar configuration symmetric about axis. Thus the causal domain contains two disconnected parts, which is quite unusual.
-
•
zero mode backgrounds New phenomena happen only in the first limit of (3.12). As shown in 4, the part of the would plot a similar configuration on past null infinity as the one on future null infinity . This is the only case that the field theory can touch which is consistent with boundary of zero mode backgrounds in the last subsection.
If we consider the configurations of boundary interval or the corresponding swing surface in the unusual limits (3.12), they are the limiting ones of the usual cases and do not affect our main conclusions.
3.3 Negative pure and mixed state entanglement measures
We already observed that the entanglement entropy can be negative (2.19) in flat3/BMSFT model. From the BMS field theory point of view, the reason and meaning of negative entanglement entropy need further solid explorations. However from the Einstein gravity point of view, the negative holographic entanglement entropy is already annoying enough and may ruin the correspondence of swing surface proposal. In this subsection, we give the mathematical derivation of negative sign of holographic entanglement entropy by identifying the entanglement entropy as a Noether surface charge 444Thank Wei Song for pointing out this viewpoint to us and Boyang Yu for early cooperation on this subsection. and explicitly using the swing surface construction. Also we would give the physical intuition about why the situations in flat3/BMSFT model are different from the ones in AdS/CFT.
The holographic entanglement entropy can be viewed as an Noether surface charge evaluated along the HRT surface in AdS/CFT Faulkner:2013ica ,
| (3.13) |
where denotes the unit vector along the HRT surface, and denotes the bulk modular flow vector. We used the fact (2.26) in the third equality. The surface charge (3.13) is actually a line integral in 3D bulk, and to do the computation we should embed it into a specific coordinate system. Take the Poincaré coordinate of AdS/CFT as an example. If we fix the sign of in Poincaré coordinates and integrate from the left endpoint of interval to the right one, we would always have the following formulas
| (3.14) |
In CFT the modular flow of a general boundary interval always have positive component along the positive direction of ordinate. While in BMS3 field theory when fixing the abscissa, we can change the coordinate of the boundary interval to change the relative sign of the modular flow to the positive direction of ordinate. This global degree of freedom of boundary interval in flat3/BMSFT model is the key to understand the negative sign of holographic entanglement entropy. Mathematically, using (4.49) we can get the parametrization equations of the bifurcating surface in Bondi coordinates of the Poincaré vacuum 555Note there are typos in (3.38) and (3.39) of Apolo:2020bld .
| (3.15) |
then the normalized directional vector along the bench can be obtained as
| (3.16) |
where we can see explicitly the sign of depend on the relative value of when we fix the values of ,. The vector can also be computed using (4.49)
| (3.17) |
thus we have
| (3.18) |
which is indeed the expected form of holographic entanglement entropy in the Poincaré vacuum of the flat3/BMSFT model Apolo:2020qjm ,
| (3.19) |
where and .
We emphasize that not only the entanglement entropy Apolo:2020bld , but also the reflected entropy Basak:2022cjs , entanglement negativity Basu:2021awn and PEE in flat3/BMSFT model all can be negative. These key observations imply us that this is actually a general character of flat3/BMSFT model. Although for the mixed state entanglement measures we do not have a local modular flow to mathematically prove the above statement.
In flat3/BMSFT model the bulk theory is pure Einstein gravity, however we need other property of swing surface to match the expectation of being holographic entanglement entropy and have to consult to the Noether charge formalism. This is unusual to what we learned in AdS/CFT. We leave the discussion in the last section.
3.4 Finite bench or Infinity bifurcating surface?
Due to the phenomena that swing surface always penetrate the boundary or horizon of the original spacetime, in the following we explore the causality structure in global flat3 and overlook the quotient manifolds stuff momentarily. In order to specify which bulk region in global flat3 have similar properties of entanglement wedge in AdS/CFT holography, we are facing two unavoidable questions. The first one is whether this region is a closed co-dimension zero bulk region. The other one is which part of the bifurcating surface is more fundamental, or at least more useful, the finite bench or the infinite bifurcating surface .


Due to the non-local property in direction of boundary BMS field theory, which can be seen from the two point correlation function (2.12), it’s rather unclear that a closed bulk region related to the swing surface would exist. One example is the AdS3/WCFT holographic model, the ”pre-entanglement wedge” is not closed in the direction due to the non-local feature in direction of boundary WCFT Chen:2022fte .
Related to the second question, there are two special bulk surfaces that we could grow null normal congruence from to construct the boundaries of a bulk region. One is the whole bifurcating surface which is unbounded and invariant under the bulk modular flow . Another one is the finite bench which is a bounded portion of . Due to the homology condition between swing surface and boundary interval as well as the Noether charge formalism (3.13), the finite bench may be more basic.
The above mentioned questions turn out to be closely related to each other in flat3/BMSFT model. We approach these problems from more practical ways rather than the more philosophical homology condition. To be consistent with the presentation style of this section, we just show the observations.
The existing literature Basak:2022cjs ; Basu:2021awn only consider the symmetric two intervals on the boundary, where the EWCS would end on the finite bench . However when considering more general configurations of boundary two intervals, we observed that the endpoints of EWCS can exceed . We plot several new situations in Figure 5, where the usual expected entanglement wedge Apolo:2020bld ; Basak:2022cjs and true EWCS are plotted. We can see from the pictures that the not carefully defined connected entanglement wedge would lead to big problems.
Due to these observations, we see that the whole modular invariant bifurcating horizon may be more basic. We would provide more evidence along this perspective through PEE, BPE and bulk modular flow in the next section.
4 Bulk Causality related to single interval
In this section we give a detailed analysis about causality structures related to finite bench and infinite bifurcating surface of a single boundary interval . We use PEE as a useful tool to explore fine correspondence between boundary and bulk modular flow. When familiar with the subtleties in flat3/BMSFT model during the process, we go to the question of finding ”entanglement wedge” in flat3/BMSFT model. As a by product, we solve the problem of PEE in flat3/BMSFT model stated in section 1. For simplicity and without loss of generality we present all the detailed analysis in the Poincaré Vacuum.
Let us slightly generalize the parametrization in Apolo:2020bld of swing surface in the Poincare vacuum (3.5). Considering a general boundary field interval with endpoints
| (4.1) |
The boundary conditions of the null ropes emanating from endpoints are simply
| (4.2) |
The length of the spacelike geodesic connected between two null ropes is given by
| (4.3) |
where are radial coordinates of the points on . The extreme of (4.3) is found at
| (4.4) |
From here we can see a necessity to analytically continuate the original Poincare vacuum spacetime with only to the one that also includes negative values of in order to include just the single interval swing surface . The bench is just a straight line going through the points parametrized by
| (4.5) |
where the left and right endpoints of have following expressions,
| (4.6) |
4.1 Bifurcating horizons
There are several coordinate systems that we would go back and forth when trying to clearly show the causal relations between boundary field theory and bulk gravity theory.
-
•
Bondi coordinates of the original Poincare vacuum:
(4.7) -
•
Cartesian coordinates and Penrose coordinates of the covering global Minkowski spacetime:
(4.8) which are related by the standard textbook transformations,
(4.9)
From boundary to boundary
we first deal with the image of field interval on the future null infinity 666This is a choice of us, which means that we can also choose to map boundary field theory to the past null infinity by putting minus signs in coordinate transformations (3.6). of Penrose diagram with coordinates . There are several facts about this map:
-
•
constant line of field theory would be mapped to constant line on of the Penrose diagram. So a strip like region which is the causal domain of field interval would map to a corner region on the boundary null cone. In particular, the axis would be mapped to line. This can be seen from the following transformation,
(4.10) When goes from to , would go from to . Because (4.10) is a monotonic decreasing function when , then the map is one to one.
-
•
A symmetric interval about the origin would map to a symmetric interval about the point on of the Penrose diagram. This can be seen as follows:
(4.11)
bench and bifurcating surface
we choose the symmetric boundary interval in (4.1) for convenience,
| (4.12) |
putting them into (4.5), we get the parametrization of the finite bench
| (4.13) |
When the parameter has parameter range in (4.13), the parameter equations denote the whole bifurcating surface . In the Penrose diagram, always end on the spacelike infinity with coordinates , which are the results of .
bifurcating Killing horizon
The bifurcating Killing horizon are composed of null congruence emitted from the bifurcating surface . Locally each null generator of is perpendicular to at the intersection point. They could be parametrized as,
| (4.14) |
where and denotes the sign function of parameter . parametrize similar to (4.5), and parametrize the null congruence emitted from . When take values in , two future Killing horizons where two null ropes sit appear with plus and minus sign in coordinates of (4.14). When take values in , two past Killing horizons would appear.


From equations (4.9) and (4.14) we can draw the Killing horizons in the compact Penrose diagram, see Figure 6 and 6. In accordance with our intuition that the non-local property of BMS field theory would destroy the closeness, the two null surfaces related to the finite bench suspend in the Lorentzian Minkowski spacetime with only two points touching the null infinity, so no closed region is formed. We have
| (4.15) |
Unlike the AdS3/WCFT case Chen:2022fte , the Killing horizons related to touch the boundary of Minkowski spacetime on the whole spacelike infinity and two lines on future null infinity , so a closed region is formed. We have
| (4.16) |
where represent part of boundary of which start from endpoints and end on the spacelike infinity . So a special region, we call it , bounded by bifurcating Killing horizons and asymptotic boundaries of Minkowski spacetime are formed
| (4.17) |
where denote the bulk causal future of . There are two important features about the Figure 6, both are related to the limiting behaviors of the null congruence emitted from
- •
-
•
The null congruence emitted from the endpoints of locating on the spacelike infinity would first go around until it touches the boundary of causal domain , then it would go up following this boundary line until touches the endpoint of field interval, see the orange lines in Figure 6. Clearly there is a critical point for its different behaviors on the Penrose diagram. Actually when , the first part of parametrization in (4.14) would dominate and the effect of this term is changing the angle. When , the second part, which shows more explicitly its lightlike property, of parametrization in (4.14) would dominate. The competition of first part and second part in (4.14) tell us where the turning point sit.
4.2 Decomposition of bulk spacetime
In this subsection we analyze the decomposition of the global flat3 in terms of both the future and past bifurcating horizons of , and make a comparison with AdS/CFT to show the unusual features in flat3/BMSFT model.
Viewing from the global coordinates of AdS/CFT, the four null Killing horizons of HRT surface related to single interval together would separate the whole Lorentzian AdS spacetime into four non-intersection parts, which nicely match with the boundary causal structure Headrick:2014cta .



Mathematically, we can decompose boundary spacetime as follows:
| (4.19) |
where is the boundary causal domain of interval and denote the causal future and past of point on . This tells us that the full boundary spacetime would decompose into four causally non-overlapping regions: the causal domain of the region and its complement , and the causal future and past of the entangling surface . For the bulk spacetime we have the decomposition,
| (4.20) |
where the tilde of corresponding notation denote the bulk one, for example is the bulk causal domain and is the spacelike homology surface interpolating between boundary subregion and bulk HRT surface . The causal split of the bulk into two spacelike and two timelike separated regions from the perspective of precisely match the boundary causal decomposition (4.19) when restrict (4.21) to the boundary due to the following relations
| (4.21) |
To facilitate the discussion about AdS and flat spacetime in a unified way, we define the following notations, see Figure 7 and 8
-
•
bulk Region (I): Causal future of bifurcating horizon :
-
•
bulk Region (II): Causal past of bifurcating horizon :
-
•
bulk Region (III), (IV): Two spacelike region which contain all the points spacelike separated from
For flat3/BMSFT model, mathematically we have following relations on the boundary,
| (4.22) |
where denote the spacetime where BMS field theory lives and
| (4.23) |
which satisfy
| (4.24) |
where denotes part of the spacelike infinity with parameter range , denotes part of the spacelike infinity with parameter range . Although regions (III) and (IV) can be defined as the bulk causal domains
| (4.25) |
of the spacelike homology surface and with properties
| (4.26) |
where is a bulk Cauchy surface of the whole Minkowski spacetime , we can not find special meaning of , and the corresponding homology surface and . Also we have no good idea about how to make physical distinctions between and . we summarize main features of causality structures in flat3/BMSFT model by comparisons with AdS/CFT
-
•
Both global AdS and global flat3 can be decomposed into four regions according to (I) (IV). In AdS spacetime, (III) is identified as the entanglement wedge , and the homology surface is a spacelike surface in (III). Boundary interval is a spacelike interval and spacelike separated from the HRT surface. In flat spacetime, (I) is the special region we called (4.17). is a interval viewed from the bulk and locate in the causal future of bifurcating horizon .
-
•
For AdS/CFT the bulk decomposition of spacetime precisely match the boundary one (4.21). The entanglement wedge of and its complement have no overlap. While in flat3/BMSFT model, the bulk decomposition have no relation with the boundary one (4.24). In addition, the special region is exactly the same as the one of the complement interval .
4.3 PEE: intersection of swing surface
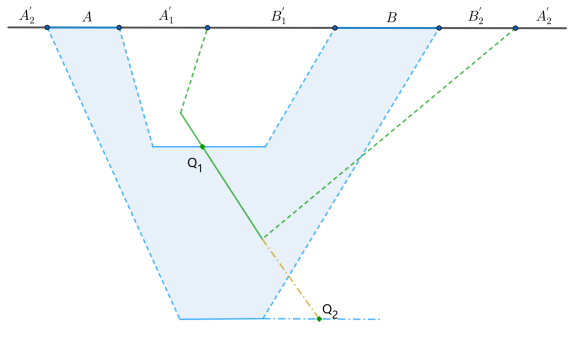
In the following two subsections, we study the PEE correspondence in flat3/BMSFT model using two ways. One is similar to the intersection of HRT surfaces, the other one is the correspondence between boundary and bulk modular flow. This quantity not only provides us more bulk quantities other than swing surface and EWCS to explore, but also gives us a chance to be familiar with the structures of bulk modular flow. As a byproduct, we solve the PEE problem in flat3/BMSFT model, thus giving the foundations about the observed match of BPE Camargo:2022mme ; Basu:2022nyl .


On the field side without loss of generality, we choose the boundary interval to be straight line between two points with coordinates and , see Figure 9. Then the PEE for subinterval with endpoints
| (4.27) |
in interval is given by
| (4.28) |
We can see that if two points of subinterval lie on the same modular flow line, the PEE of this subinterval would be zero. This implies that points on the same modular flow line correspond to exactly one point on the bifurcating surface , and different modular flow lines correspond to different points on . In other words, boundary modular flow lines are in one to one correspondence with points on the bifurcating surface . This is exactly what happens in the bulk.
On the bulk side to find the specific point on the bifurcating surface which corresponds to the boundary point , we need choose another boundary point , see Figure 9, and demand that the bifurcating surface related to intersect the one related to , see Figure 9. Using the parametrization (4.5), we find that when have coordinates (4.27), the above intersection condition need us to have
| (4.29) |
where is the coordinates of point, and are the parameters in (4.5) related to intervals and separately. Putting (4.29) into (4.5) we can see that the intersection point is
| (4.30) |
Thus we proved our above statement about the one to one correspondence between modular flow line denoted by and bulk point on bifurcating horizon (4.30), which is consistent with modular flow invariant property of PEE Wen:2018whg . Two features need to be emphasized. One is that the two corresponding points and can both run on the same modular flow line independently, the specific bulk point would not change. This is not the same as AdS/CFT case, where the two points should run synchronously. Another feature is that the intersection point seldom lie on the finite bench of swing surface, which can be seen from the value of in (4.29). The second feature provides us more evidence that only the information about the finite bench is not enough.
Because from PEE we can intuitively derive BPE correspondence Wen:2021qgx , so we have proved from a more basic step the observations in Camargo:2022mme ; Basu:2022nyl . We list several unconventional configurations in Figure 10 related to adjacent and non-adjacent BPE for completeness. Again we plot the usual expected connected entanglement wedge to show its problem.



4.4 PEE: boundary and bulk modular flow
In this subsection we use modular flow method to explore the PEE correspondence. Subtleties appear in flat3/BMSFT model compared to AdS/CFT case, which is another manifestation of modular flow property of BMS3 field theory stated in section 1.
We first revisit the modular flow method in standard AdS3/CFT2 case using our notations. This rewriting manifests a freedom of bulk and boundary correspondence as mentioned in section 3, which is needed for the success of this method in flat3/BMSFT model 777Thank Qiang Wen for discussion about this point.. We can obtain the modular flow generator for a general interval
| (4.31) |
in CFT by the coordinate transformations Casini:2011kv
| (4.32) |
from Rindler spacetime which have local flow generator
| (4.33) |
to the causal domain of this interval. Then we get the the modular flow generator of symmetric interval lying in timeslice as follows,
| (4.34) | ||||
where are the boundary conformal generators: t direction translation, x direction translation, t-component special conformal transformation and x-component special conformal transformation. The explicit expressions of these conformal generators are
| (4.35) | ||||
The corresponding bulk killing vector fields are
| (4.36) | ||||
Using the holographic dictionary between (4.35) and (4.36) we can obtain the exact bulk modular flow generator as
| (4.37) | ||||
We can see that when taking the boundary limit, the bulk killing vector field (4.37) reduces to the boundary modular flow generator (4.34). In the following we choose the interval to lie on the constant time slice withe in (4.31). Then from (4.37) we can easily derive the location of bifurcating surface and bifurcating Killing horizon,
-
•
bifurcating Killing horizon:
(4.38) -
•
bifurcating surface:
(4.39) (4.40)
For explicit manifestation take in (4.31), we can derive the corresponding parametrization equations of boundary modular flow from (4.34),
| (4.41) |
where parametrize one modular flow line and distinct different modular flow lines. and together manifest the degree of freedom of 2d plane. Similarly from (4.37) we get the trajectory of bulk modular flow,
| (4.42) | ||||
where parameters together manifest the degree of freedom of 3d bulk. The plus and minus sign in (4.41) and (4.42) denote different branches that we need. When the above mentioned parameters have the relation
| (4.43) |
the bulk modular flow line reduce to the boundary one respectively. When they have the relation
| (4.44) |
the bulk modular flow line sit on the bifurcating horizons. Choosing a specific co-dimension one plane in 3d bulk by fixing the value of 888Note the plane defined here is not the same as the modular plane in Wen:2018whg , which is an explicit manifestation of the freedom mentioned above., we can get the boundary and bulk correspondence of PEE,
| (4.45) |
which is consistent with the results in Wen:2018whg .
While for the Poincaré vacuum of flat3/BMSFT model, the exact boundary modular flow generator and the corresponding bulk Killing vector field are Apolo:2020qjm as follows,
| (4.46) | ||||
| (4.47) | ||||
The final expressions for and are
| (4.48) |
and
| (4.49) |
From (4.46), (4.47) and (4.48), (4.49) we can see the existence of a consistent boundary limit . Again without loss of generality, we set the interval to be in (4.12). Then the parametrization equations for boundary and bulk modular flow are
| (4.50) | |||
| (4.51) |
where we have
| (4.52) |
A careful analysis tell us that when we have relations
| (4.53) |
bulk modular flow trajectory (4.51) would reduce to the boundary one (4.50), where in (4.51) goes to that is the boundary limit. When we have relations
| (4.54) |
bulk modular trajectories lie on the bifurcating horizons, and intersect the bifurcating surface at the point
| (4.55) |
Thus when the parameters satisfy
| (4.56) |
we can get the bulk corresponding point (4.30). Note that in flat3/BMSFT model we need to change the values of both bulk modular flow parameters and simultaneously to go from the asymptotic boundary to PEE corresponding point on the bifurcating surface .
4.5 Entanglement wedge ?



In our parametrization (4.41) and (4.42), there are two features of bulk modular flow in entanglement wedge which distinct from those out of entanglement wedge. One is that for both branches the modular time has parameter range for both boundary and bulk modular flow. Within this finite range of modular time, bulk modular flows reach the bifurcating surface. Out of this range out of the entanglement wedge. Another one is that when exceed (4.44), the continuous bulk modular flow line will break apart and at the same time go beyond the entanglement wedge of this interval. See figure 11 for a gradual change with fixed and varying from to .
One complication of the flat3/BMSFT model is that bulk modular flow hit the bifurcating surface out of the range of boundary modular time , which can be seen from (4.56). Apart from this subtlety, similar situations happen as in AdS/CFT case. As we grow parameter from and at the same time from , the bulk modular trajectories go from the asymptotic boundary to the bifurcating surface. When exceed the value , the modular lines disconnected into two parts, see Figure 11 and 11 for explicitly shown of the process. It turns out that in flat3/BMSFT model the connected bulk modular flow lines can grow from boundary causal domain and go through every point in defined in (4.17), especially the boundary causal domain of the complement interval .
A confusing feature of bulk modular flows in flat3/BMSFT model is that all flow lines are spacelike trajectories, which have spacelike modular time viewing from the global flat3. A related question is how to define the homology surface in this case. They are quantum algebraically and information theoretically related to the semiclassical problems in gravity side. Algebraically the bulk modular Hamiltonian can map the algebra of operators localized in a region to the algebra of operators in the region ,
| (4.57) |
along the bulk modular flow lines. When the modular evolution is spacelike from bulk point of view, what is its meaning? Quantum informationally the first quantum correction to holographic entanglement entropy,
| (4.58) |
need homology surface to compute the reduced density matrix . How to define it in this case? We hope more solid study on these key open problems in the future.
5 Two interval entanglement phase transition and EWN
In order to compute the reflected entropy, entanglement negativity, odd entropy or other mixed state entanglement measures from bulk side, we need to have a connected entanglement wedge. When changing the relative configurations of two boundary intervals, there is a phase transition between disconnected entanglement wedge and the connected one. Without specifying clearly what is the connected entanglement wedge from gravity side, all previous calculations regarding the EWCS Basak:2022cjs ; Camargo:2022mme , including the ones in this paper, are problematic. We give criterion for two intervals phase transition from field theory point of view, which is not trivial already. From the gravity theory point of view, the situations are rather vague.
5.1 Entanglement phase transition

In this part we consider the entanglement phase transition for two disjoint boundary intervals using formula (2.19) with . Compared to the usual CFT case, here we should consider three different pairs rather than two to finally get the minimal one, see Figure 12. If we connect points , and , the corresponding holographic entanglement entropy is given by
| (5.1) |
Similarly, we define
| (5.2) |
The difference between them are
| (5.3) |
where are cross ratios defined in (2.16) with identifications . Therefore we get
-
•
is the minimal one when:
(5.4) -
•
is the minimal one when:
(5.5) -
•
is the minimal one when:
(5.6)
Taking symmetric configurations for an example,
| (5.7) |
with . This configuration ensures that , which means that can never be the minimal one. Fixing and , there is a critical value
| (5.8) |
for such that . When , is the minimal one and vice verse. we can check the difference between the slope of the critical interval with and that of interval is
| (5.9) |
When is the minimal one, we think the configuration have a connected entanglement wedge like the case of AdS/CFT.
5.2 Entanglement wedge nesting




Entanglement wedge nesting (EWN) is a prerequisite of existing a connected entanglement wedge in AdS/CFT. EWN states that nested boundary regions should be dual to nested bulk regions, which clearly consistent with subregion duality Casini:2017vbe ; Akers:2017ttv in AdS hologrpahy. According to the last section, region defined in (4.17) is a special region owing many similar properties of the entanglement wedge in AdS/CFT. However when considering the EWN property of two boundary intervals, this special region failed. Actually, no special region can be found due to our limited capabilities, see figure 13. This is really a big problem in the flat3/BMSFT model, which puts all the previous calculations about EWCS into a dangerous situation.
6 Conclusions and Open Questions
Until now, we have showed the usual and unusual features related to causality structure of bifurcating surface in flat3/BMSFT model using the tools from modular flow and various entanglement measures (mainly Reflected entropy and PEE). We studied the two intervals phase transition as well as EWN problem from both field side and gravity side. However due to the observations presented in Section 3, there are still two big problems special to flat3/BMSFT model intentionally hidden by us.
The existence of Entanglement wedge?
In flat3/BMSFT model the holographic entanglement entropy does not own just the properties of pure gravity, i.e., the length, but also contains the ”direction” character even in pure Einstein gravity. This phenomena appear in all the information measures, reflected entropy, entanglement negativity, odd entropy and PEE. Actually as we argued in subsection 3.3, this is a general property of flat3/BMSFT model, which physically puts a question mark on the existence or the meaning of entanglement wedge in this model. Historically the success of ”It from qubit” program, for example, the subregion-subregion duality Dong:2016eik , in Einstein gravity of AdS/CFT holography root in the fact that people can totally geometrize the boundary entanglement entropy . The mathematical object of bulk dual of boundary entanglement entropy is just an area functional with no correction term and no additional character. Maybe the fact that we can’t totally geometrize in flat3/BMSFT model imply us that there is no well defined and useful notion about entanglement wedge in this toy model. Let us make an analogy to make this point clearer. Take ”Topological Massive gravity/anomalous CFT” correspondence as an example, the holographic entanglement entropy contain corrections due to the Chern Simons term Castro:2014tta , but the position of RT surface is the same as pure gravity case. There are spacetimes, for example the vacuum AdS3, that are the solutions of both pure Einstein gravity theory and topological massive gravity theory. In these kind of spacetimes, the positions of RT surfaces and related null bifurcating horizons are the same. However the boundary dual CFTs are rather different. How can the same bulk region encoded different boundary information? Actually there are no solid results of entanglement wedge and bulk reconstruction in this duality. Another possibility would be to find more fine structures of the special bulk region in (4.17). We hope more solid works on this problem due to its substantial role in flat3/BMSFT holography.


Flat holography: which boundary?
Flat spacetime has more complicated asymptotic boundaries than AdS spacetime, thus an important question about flat holography is where the dual boundary field theory lives. Flat3/BMSFT model provides us a vague but unexpected implication on this question.
We made the observation in subsection 3.1 and proved it in (4.4) that the bench always penetrate beyond the boundary of original spacetime, see Figure 14. In other words, we have to analytically continuate the original spacetime to include just the finite bench . Viewing from gravity, analytic continuation of spacetime is quite normal. However from holographic point of view, no similar things happened before. For example in AdS/CFT holography, RT surface always totally lie within the quotient spacetime, no matter for the Poincaré patch or BTZ black holes. This may imply that although field theory live just on the future null infinity , we also need information on other asymptotic boundaries especially the past null infinity .
Let’s make an analogy with the standard eternal black hole case which is dual to the thermofield double state (TFD state) in AdS/CFT holography Maldacena:2001kr , see Figure 14. The Left and right boundaries are spacelike separated with each other, and their CFT Hamiltonians have no coupling. In TFD state, any interval located within left(right) boundary has RT surface totally sit in left(right) exterior and would not penetrate through horizon999If the interval is the whole left (right) boundary, then the RT surface is just the bifurcating horizon.. Only when the boundary interval contains part of both left and right CFTs can the RT surface behave like the green curve in Figure 14. The flat holography case has similar things to some extent, but is more subtle due to the fact that the future null infinity and the past one are timelike separated, which may communicate or contain same but modulated information.
Appendix A Reflected Entropy
In this appendix, we give a complete derivation about the reflected entropy of two disjoint intervals in BMS field theory. For the steps to be self-contained, we have to show some similar calculations with those in Basak:2022cjs . The new thing that is not shown in Basak:2022cjs is the step of deriving three point coefficient in the OPE of twist operators (A.5), which affects the final results up to a constant Basu:2022nyl . See Chen:2022fte for the notations, figures and detailed introduction of reflected entropy.
A.1 The BMS Semi-classical Block
The function in (2.14) can be decomposed into BMS conformal blocks ,
| (A.1) |
In the semi-classical limit a closed form for , which is also consistent with the ultra-relativistic limit of the Virasoro block, is obtained by the null vectors of the BMS algebra as well as the monodromy method Hijano:2018nhq ,
| (A.2) |
where , are the conformal weight and boost charge (2.9) related to external light/heavy operators and are the ones related to internal operators in the OPE expansion. This Heavy-Heavy-Light-Light correlator need heavy operators scale freely with the central charge and light operators obey . Analytically continuing the quantum numbers of heavy operators to the light one, we get the BMS block of four same dimension light operators
| (A.3) |
A.2 OPE coefficient and Twist operator dimension
We assume the primary twist operators in orbifold BMSFT all belong to the singlet version of the highest weight representation of BMS algebra Hao:2021urq . Then the twist operators , and have the following dimensions,
-
•
, , , :
(A.4) -
•
:
(A.5)
For the three point OPE coefficients important for the final results of reflected entropy, we claim that
| (A.6) |
This can be proved by using the same method in CFT Dutta:2019gen and WCFT Chen:2022fte . We show the main steps here:
| (A.7) |
the first equality comes from a BMS symmetry transformation
| (A.8) |
which maps the replica sheets to a replica sheets. The twist operators , have quantum numbers and due to their -cyclic monodromy conditions getting from the above map (A.8), and the explicit values of are
| (A.9) |
From the result (A.7) we can directly see the OPE coefficient as claimed.
A.3 Reflected entropy of vacuum and thermal state on the plane
In the holographic BMS field theory we assume that the single block dominance work in the semi-classical limit, and the dominant BMS block in the block expansion of the four point function (A.1) is the one with lowest quantum dimensions. For -channel OPE of twist operator , the dominant one is related to the primary twist operator . By taking the Von-Neumann limit , the external twist operators and the internal one all become light operators, then (A.3) can be used to evaluate the reflected entropy,
| (A.10) | |||
| (A.11) |
after the cancellation of several factors explicitly shown in (A.11) between numerator and denominator in the evaluation of reflected entropy, the final result of vacuum state on the BMS plane turn out to be
| (A.12) |
For the thermal state reflected entropy, we need the correlator of four point twist operators on the thermal cylinder using (2.11) and (2.20),
| (A.13) |
The first line of (A.13) would again cancel out between enumerator and denominator, and the second line of (A.13) contributes to the final answer. Thus the thermal state reflected entropy can be obtained by the same formula (A.12), but with the cross ratios getting from the map (2.21). Finally we have
| (A.14) | ||||
| (A.15) | ||||
Appendix B Zero Mode Background
In this appendix we work in the zero mode background. After a similar analysis of the bifurcating horizon behavior and the entanglement phase transition in this solution, we will see the conclusions get in the main context from the analysis of the Poincaré vacuum are universal.
B.1 Bifurcating horizon
The zero mode backgrounds which can be regarded as the flat limit of BTZ black hole of asymptotically AdS3 spacetime Barnich:2012xq ; Bagchi:2012xr have metric in Bondi coordinates,
| (B.1) |
For the general interval with The length of spacelike geodesic between the two null ropes satisfying
| (B.2) |
is not illuminating, so we choose to not present it. The extreme of can be found at
| (B.3) |
where is the Cauchy horizon (3.4) and . The parameter equations for the Killing horizon of the bifurcating surface are
| (B.4) | |||
where are the endpoints of the bench that can be obtained by using (B.3) and (3.9). When , (B.4) would reduce to the parametrization of the bifurcating surface for and the bench for . When , (B.4) denote two future bifurcating horizons with two null ropes sitting on; while for these equations parametrize the two corresponding past horizons. Similarly these four bifurcating horizons, which together decompose the global flat3 into four non-intersecting causal regions, would converge to four single points on the future/past null infinity separately in the Penrose diagram. Mathematically, we can map boundary in Bondi coordinates to boundary in Penrose coordinates using (4.9):
| (B.5) |
B.2 Entanglement phase transition
We consider thermal state entanglement phase transition of BMS field theory using formula (2.22) with for the same configurations in Figure 12. The boundary intervals are
| (B.6) |
Similarly we can define
| (B.7) | ||||
The difference between them are
| (B.8) |
where are finite temperature cross ratios. Therefore we get
-
•
is the minimal one when:
(B.9) -
•
is the minimal one when:
(B.10) -
•
is the minimal one when:
(B.11)
Taking symmetric configurations,
| (B.12) |
with . This configuration ensures that , which means that can never be the minimal one. Fixing and , there is a critical value
| (B.13) |
for such that . When , is the minimal one and vice verse. we can check the difference between the slope of the critical interval with and that of interval is
| (B.14) |
Since , we always have . Therefore, the sign of (B.14) only depends on the sign of .
Acknowledgements.
We thank Bin Chen, Wei Song, Qiang Wen, Boyang Yu and Luis Apolo for useful discussions. The work is in part supported by NSFC Grant No. 12275004, 11735001.References
- (1) J.M. Maldacena, The Large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2 (1998) 231 [hep-th/9711200].
- (2) E. Witten, Anti-de Sitter space and holography, Adv. Theor. Math. Phys. 2 (1998) 253 [hep-th/9802150].
- (3) S.S. Gubser, I.R. Klebanov and A.M. Polyakov, Gauge theory correlators from noncritical string theory, Phys. Lett. B 428 (1998) 105 [hep-th/9802109].
- (4) S. Ryu and T. Takayanagi, Holographic derivation of entanglement entropy from AdS/CFT, Phys. Rev. Lett. 96 (2006) 181602 [hep-th/0603001].
- (5) V.E. Hubeny, M. Rangamani and T. Takayanagi, A Covariant holographic entanglement entropy proposal, JHEP 07 (2007) 062 [0705.0016].
- (6) T. Nishioka, S. Ryu and T. Takayanagi, Holographic Entanglement Entropy: An Overview, J. Phys. A 42 (2009) 504008 [0905.0932].
- (7) A. Lewkowycz and J. Maldacena, Generalized gravitational entropy, JHEP 08 (2013) 090 [1304.4926].
- (8) D. Harlow, TASI Lectures on the Emergence of Bulk Physics in AdS/CFT, PoS TASI2017 (2018) 002 [1802.01040].
- (9) A. Almheiri, T. Hartman, J. Maldacena, E. Shaghoulian and A. Tajdini, The entropy of Hawking radiation, Rev. Mod. Phys. 93 (2021) 035002 [2006.06872].
- (10) R. Bousso, X. Dong, N. Engelhardt, T. Faulkner, T. Hartman, S.H. Shenker et al., Snowmass White Paper: Quantum Aspects of Black Holes and the Emergence of Spacetime, 2201.03096.
- (11) S. Dutta and T. Faulkner, A canonical purification for the entanglement wedge cross-section, JHEP 03 (2021) 178 [1905.00577].
- (12) Y. Kusuki, J. Kudler-Flam and S. Ryu, Derivation of holographic negativity in AdS3/CFT2, Phys. Rev. Lett. 123 (2019) 131603 [1907.07824].
- (13) Q. Wen, Balanced Partial Entanglement and the Entanglement Wedge Cross Section, JHEP 04 (2021) 301 [2103.00415].
- (14) T. Faulkner, A. Lewkowycz and J. Maldacena, Quantum corrections to holographic entanglement entropy, JHEP 11 (2013) 074 [1307.2892].
- (15) D.L. Jafferis, A. Lewkowycz, J. Maldacena and S.J. Suh, Relative entropy equals bulk relative entropy, JHEP 06 (2016) 004 [1512.06431].
- (16) X. Dong, D. Harlow and A.C. Wall, Reconstruction of Bulk Operators within the Entanglement Wedge in Gauge-Gravity Duality, Phys. Rev. Lett. 117 (2016) 021601 [1601.05416].
- (17) T. Faulkner and A. Lewkowycz, Bulk locality from modular flow, JHEP 07 (2017) 151 [1704.05464].
- (18) E. Witten, APS Medal for Exceptional Achievement in Research: Invited article on entanglement properties of quantum field theory, Rev. Mod. Phys. 90 (2018) 045003 [1803.04993].
- (19) T. Faulkner, M. Li and H. Wang, A modular toolkit for bulk reconstruction, JHEP 04 (2019) 119 [1806.10560].
- (20) M. Headrick, V.E. Hubeny, A. Lawrence and M. Rangamani, Causality & holographic entanglement entropy, JHEP 12 (2014) 162 [1408.6300].
- (21) L. Susskind, Holography in the flat space limit, AIP Conf. Proc. 493 (1999) 98 [hep-th/9901079].
- (22) J. Polchinski, S matrices from AdS space-time, hep-th/9901076.
- (23) S.B. Giddings, Flat space scattering and bulk locality in the AdS / CFT correspondence, Phys. Rev. D 61 (2000) 106008 [hep-th/9907129].
- (24) G. Arcioni and C. Dappiaggi, Holography in asymptotically flat space-times and the BMS group, Class. Quant. Grav. 21 (2004) 5655 [hep-th/0312186].
- (25) J. de Boer and S.N. Solodukhin, A Holographic reduction of Minkowski space-time, Nucl. Phys. B 665 (2003) 545 [hep-th/0303006].
- (26) A. Strominger, Lectures on the Infrared Structure of Gravity and Gauge Theory, 1703.05448.
- (27) S. Pasterski, M. Pate and A.-M. Raclariu, Celestial Holography, in Snowmass 2021, 11, 2021 [2111.11392].
- (28) T. He, V. Lysov, P. Mitra and A. Strominger, BMS supertranslations and Weinberg’s soft graviton theorem, JHEP 05 (2015) 151 [1401.7026].
- (29) T. He, P. Mitra and A. Strominger, 2D Kac-Moody Symmetry of 4D Yang-Mills Theory, JHEP 10 (2016) 137 [1503.02663].
- (30) C. Cheung, A. de la Fuente and R. Sundrum, 4D scattering amplitudes and asymptotic symmetries from 2D CFT, JHEP 01 (2017) 112 [1609.00732].
- (31) S. Pasterski, S.-H. Shao and A. Strominger, Flat Space Amplitudes and Conformal Symmetry of the Celestial Sphere, Phys. Rev. D 96 (2017) 065026 [1701.00049].
- (32) S. Pasterski and S.-H. Shao, Conformal basis for flat space amplitudes, Phys. Rev. D 96 (2017) 065022 [1705.01027].
- (33) A. Fotopoulos and T.R. Taylor, Primary Fields in Celestial CFT, JHEP 10 (2019) 167 [1906.10149].
- (34) M. Pate, A.-M. Raclariu, A. Strominger and E.Y. Yuan, Celestial operator products of gluons and gravitons, Rev. Math. Phys. 33 (2021) 2140003 [1910.07424].
- (35) S. Banerjee, S. Ghosh and R. Gonzo, BMS symmetry of celestial OPE, JHEP 04 (2020) 130 [2002.00975].
- (36) K. Costello and N.M. Paquette, Associativity of One-Loop Corrections to the Celestial Operator Product Expansion, Phys. Rev. Lett. 129 (2022) 231604 [2204.05301].
- (37) Y. Hu and S. Pasterski, Celestial recursion, JHEP 01 (2023) 151 [2208.11635].
- (38) A. Atanasov, W. Melton, A.-M. Raclariu and A. Strominger, Conformal block expansion in celestial CFT, Phys. Rev. D 104 (2021) 126033 [2104.13432].
- (39) W. Fan, A. Fotopoulos, S. Stieberger, T.R. Taylor and B. Zhu, Conformal blocks from celestial gluon amplitudes, JHEP 05 (2021) 170 [2103.04420].
- (40) S. Mizera and S. Pasterski, Celestial geometry, JHEP 09 (2022) 045 [2204.02505].
- (41) A. Strominger, w(1+infinity) and the Celestial Sphere, 2105.14346.
- (42) A. Almheiri, X. Dong and D. Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 04 (2015) 163 [1411.7041].
- (43) G. Barnich and C. Troessaert, BMS charge algebra, JHEP 12 (2011) 105 [1106.0213].
- (44) A. Trautman, Radiation and Boundary Conditions in the Theory of Gravitation, Bull. Acad. Pol. Sci. Ser. Sci. Math. Astron. Phys. 6 (1958) 407 [1604.03145].
- (45) L. Donnay, A. Fiorucci, Y. Herfray and R. Ruzziconi, Bridging Carrollian and celestial holography, Phys. Rev. D 107 (2023) 126027 [2212.12553].
- (46) A. Laddha, S.G. Prabhu, S. Raju and P. Shrivastava, The Holographic Nature of Null Infinity, SciPost Phys. 10 (2021) 041 [2002.02448].
- (47) A. Bagchi, S. Banerjee, R. Basu and S. Dutta, Scattering Amplitudes: Celestial and Carrollian, Phys. Rev. Lett. 128 (2022) 241601 [2202.08438].
- (48) L. Donnay, A. Fiorucci, Y. Herfray and R. Ruzziconi, Carrollian Perspective on Celestial Holography, Phys. Rev. Lett. 129 (2022) 071602 [2202.04702].
- (49) J. Penedones, Writing CFT correlation functions as AdS scattering amplitudes, JHEP 03 (2011) 025 [1011.1485].
- (50) A.L. Fitzpatrick, J. Kaplan, J. Penedones, S. Raju and B.C. van Rees, A Natural Language for AdS/CFT Correlators, JHEP 11 (2011) 095 [1107.1499].
- (51) L.P. de Gioia and A.-M. Raclariu, Eikonal approximation in celestial CFT, JHEP 03 (2023) 030 [2206.10547].
- (52) A. Bagchi, Correspondence between Asymptotically Flat Spacetimes and Nonrelativistic Conformal Field Theories, Phys. Rev. Lett. 105 (2010) 171601 [1006.3354].
- (53) A. Bagchi and R. Fareghbal, BMS/GCA Redux: Towards Flatspace Holography from Non-Relativistic Symmetries, JHEP 10 (2012) 092 [1203.5795].
- (54) H. Bondi, M.G.J. van der Burg and A.W.K. Metzner, Gravitational waves in general relativity. 7. Waves from axisymmetric isolated systems, Proc. Roy. Soc. Lond. A 269 (1962) 21.
- (55) R.K. Sachs, Gravitational waves in general relativity. 8. Waves in asymptotically flat space-times, Proc. Roy. Soc. Lond. A 270 (1962) 103.
- (56) G. Barnich, Entropy of three-dimensional asymptotically flat cosmological solutions, JHEP 10 (2012) 095 [1208.4371].
- (57) A. Bagchi, S. Detournay, R. Fareghbal and J. Simón, Holography of 3D Flat Cosmological Horizons, Phys. Rev. Lett. 110 (2013) 141302 [1208.4372].
- (58) G. Barnich, H.A. Gonzalez, A. Maloney and B. Oblak, One-loop partition function of three-dimensional flat gravity, JHEP 04 (2015) 178 [1502.06185].
- (59) E. Hijano, Semi-classical BMS3 blocks and flat holography, JHEP 10 (2018) 044 [1805.00949].
- (60) H. Jiang, W. Song and Q. Wen, Entanglement Entropy in Flat Holography, JHEP 07 (2017) 142 [1706.07552].
- (61) L. Apolo, H. Jiang, W. Song and Y. Zhong, Swing surfaces and holographic entanglement beyond AdS/CFT, JHEP 12 (2020) 064 [2006.10740].
- (62) L. Apolo, H. Jiang, W. Song and Y. Zhong, Modular Hamiltonians in flat holography and (W)AdS/WCFT, JHEP 09 (2020) 033 [2006.10741].
- (63) A. Bagchi, R. Basu, A. Kakkar and A. Mehra, Flat Holography: Aspects of the dual field theory, JHEP 12 (2016) 147 [1609.06203].
- (64) D. Basu, A. Chandra, V. Raj and G. Sengupta, Entanglement wedge in flat holography and entanglement negativity, SciPost Phys. Core 5 (2022) 013 [2106.14896].
- (65) J.K. Basak, H. Chourasiya, V. Raj and G. Sengupta, Reflected entropy in Galilean conformal field theories and flat holography, Eur. Phys. J. C 82 (2022) 1169 [2202.01201].
- (66) H.A. Camargo, P. Nandy, Q. Wen and H. Zhong, Balanced partial entanglement and mixed state correlations, SciPost Phys. 12 (2022) 137 [2201.13362].
- (67) Q. Wen, Fine structure in holographic entanglement and entanglement contour, Phys. Rev. D 98 (2018) 106004 [1803.05552].
- (68) D. Basu, Balanced Partial Entanglement in Flat Holography, 2203.05491.
- (69) P.-x. Hao, W. Song, X. Xie and Y. Zhong, A BMS-invariant free scalar model, 2111.04701.
- (70) A. Bagchi, R. Basu, D. Grumiller and M. Riegler, Entanglement entropy in Galilean conformal field theories and flat holography, Phys. Rev. Lett. 114 (2015) 111602 [1410.4089].
- (71) P. Calabrese and J. Cardy, Entanglement entropy and conformal field theory, J. Phys. A 42 (2009) 504005 [0905.4013].
- (72) B. Chen, Y. Liu and B. Yu, Reflected entropy in AdS3/WCFT, JHEP 12 (2022) 008 [2205.05582].
- (73) G. Barnich and C. Troessaert, Aspects of the BMS/CFT correspondence, JHEP 05 (2010) 062 [1001.1541].
- (74) G. Barnich, A. Gomberoff and H.A. Gonzalez, The Flat limit of three dimensional asymptotically anti-de Sitter spacetimes, Phys. Rev. D 86 (2012) 024020 [1204.3288].
- (75) T. Faulkner, M. Guica, T. Hartman, R.C. Myers and M. Van Raamsdonk, Gravitation from Entanglement in Holographic CFTs, JHEP 03 (2014) 051 [1312.7856].
- (76) H. Casini, M. Huerta and R.C. Myers, Towards a derivation of holographic entanglement entropy, JHEP 05 (2011) 036 [1102.0440].
- (77) H. Casini, E. Testé and G. Torroba, Markov Property of the Conformal Field Theory Vacuum and the a Theorem, Phys. Rev. Lett. 118 (2017) 261602 [1704.01870].
- (78) C. Akers, V. Chandrasekaran, S. Leichenauer, A. Levine and A. Shahbazi Moghaddam, Quantum null energy condition, entanglement wedge nesting, and quantum focusing, Phys. Rev. D 101 (2020) 025011 [1706.04183].
- (79) A. Castro, S. Detournay, N. Iqbal and E. Perlmutter, Holographic entanglement entropy and gravitational anomalies, JHEP 07 (2014) 114 [1405.2792].
- (80) J.M. Maldacena, Eternal black holes in anti-de Sitter, JHEP 04 (2003) 021 [hep-th/0106112].