Revealing hidden standard tripartite nonlocality by local filtering

Nonlocal quantum correlations are the essential nature of quantum physics EPRnonlocal . For bipartite systems the Bell nonlocality BellNonlocal ; Wiseman ; StrongNonlocal gives rise to stronger quantum correlations than quantum entanglement HHHH2009entangle ; LS2019 ; CG2005 and EPR steering steer2020 . As a fascinating counterintuitive phenomenon related to the foundation of quantum mechanics Bell1966 , nonlocality is understood as a resource in quantum information process ranging form quantum computation Liang2020 ; Liang2022 , quantum key distributed AK1991 and random numbers certification Nature2010 . It is significant to detect the nonlocality of given quantum systems.

A bipartite quantum state $\rho_{AB}$ is said to be locally correlated if the joint probability distributions satisfies Wiseman ,

where $p_{\lambda}$ is the probability distribution over the hidden variables $\lambda$, $p_{\lambda}\geq 0$, $\sum_{\lambda}p_{\lambda}=1$, $P(a,b|A_{x},B_{y})$ denotes the joint probability distribution that Alice performs measurement $A_{x}$ on subsystem $A$ with outcome $a$, and Bob performs measurement $B_{y}$ on subsystem $B$ with outcome $b$, $P(a|A_{x},\lambda)$ denotes the conditional probability of getting outcome $a$ when Alice performs the measurement $A_{x}$ on her subsystem, $P(b|B_{y},\lambda)$ is similarly defined. The bipartite nonlocality can be detected by the violation of a kind of Bell inequality, the CHSH inequality CHSH1969 .

The maximal violation of a Bell inequality can be enhanced by local filtering operations CHSHviolate . In filterCHSH the authors presented a class of two-qubit entangled states admitting local hidden variable models, and shew that these states violate a Bell inequality after the local filtering. Namely, there exist entangled states whose so called hidden non-locality can be revealed by using a sequence of measurements. In fact, local filtering operations can not only reveal hidden quantum nonlocality, but also hidden quantum steerability FilterSteer .

For tripartite systems, the Mermin inequality Mermin1990 is a natural generalization of the CHSH inequality, which can be violated by not only genuine tripartite nonlocal states but also by standard tripartite nonlocal states. The upper bound on the maximal expectation value of the Mermin operator has been nicely derived in QIP2019 , though not always tight. Similar to the enhanced maximal violation of Bell inequalities, it is interesting to study the enhancement of the maximal violation of the Mermin inequality under local filtering.

In this work, we investigate the maximal violation of the Mermin inequality under local filtering. We first analyze and obtain the tight upper bounds on the maximal expected value of the Mermin operator under local filtering. Then applying our results to some special quantum states, the isotropic states and the noisy GHZ states, we show that local filtering can reveal the hidden standard nonlocality. Moreover, it is shown that the local filtering can transform the initial noisy state to a state with stronger tripartite nonlocality.

A tripartite state $\rho_{ABC}$ is fully locally correlated if the joint probability distribution admits a local hidden variable (LHV) model Wiseman , namely,

for all $x,y,z,a,b$ and $c$, where $P(a,b,c|A_{x},B_{y},C_{z})$ is the joint probability when Alice, Bob and Charlie perform local measurements $A_{x}$, $B_{y}$ and $C_{z}$ with outcomes $a$, $b$ and $c$, respectively, $p_{\lambda}\geq 0$ is the probability distribution over the hidden variable $\lambda$, $\sum_{\lambda}p_{\lambda}=1$, $P(a|A_{x},\lambda)$ denotes the conditional probability of obtaining outcome $a$ when Alice performs the measurement $A_{x}$ on her subsystem, $P(b|B_{y},\lambda)$ and $P(c|C_{z},\lambda)$ are similarly defined.

The tripartite non-locality of arbitrary 3-qubit states $\rho$ can be detected by the violation of the Mermin inequality $|\langle\mathcal{M}\rangle_{\rho}|\equiv|\textrm{Tr}[\mathcal{M}\rho]|\leq 2$. The Mermin operator $\mathcal{M}$ has the form Mermin1990 ,

where $A_{0}$, $A_{1}$, $B_{0}$, $B_{1}$, $C_{0}$ and $C_{1}$ are quantum mechanical observables of the form $K=\vec{k}\cdot\vec{\sigma}=\sum\limits^{3}_{i=1}k_{i}\sigma_{i}$, with a unit vector $\vec{k}\in\{\vec{a},\vec{a}^{\prime},\vec{b},\vec{b}^{\prime},\vec{c},\vec{c}^{\prime}\}$, the standard Pauli matrices $\sigma_{i}$, $K\in\{A_{0},A_{1},B_{0},B_{1},C_{0},C_{1}\}$.

In a recent work QIP2019 it has been shown that the maximal expectation value of the Mermin operator for arbitrary 3-qubit state $\rho$ is given by $\mathcal{Q}_{\mathcal{M}}:=\max|\langle\mathcal{M}\rangle_{\rho}|\leq 2\sqrt{2}\lambda_{\max}$, where $\lambda_{\max}$ is the largest singular value of matrix $C$, $C=(C_{j,ik})$ is the correlation matrix of $\rho$ with entries given by $C_{ijk}=\textrm{Tr}[\rho(\sigma_{i}\otimes\sigma_{j}\otimes\sigma_{k})]$, $i,j,k=1,2,3$. This upper bound is tight if the degeneracy with respect to the largest singular value $\lambda_{\max}$ is more than 1, and the two degenerate nine-dimensional singular vectors corresponding to $\lambda_{\max}$ take the forms of $\vec{a}\otimes\vec{c}-\vec{a}^{\prime}\otimes\vec{c}^{\prime}$ and $\vec{a}\otimes\vec{c}^{\prime}+\vec{a}^{\prime}\otimes\vec{c}$.

Next, we investigate the violations of the Mermin inequality under local filtering, by computing the maximal expectation values of the Mermin operators with respect to the locally filtered 3-qubit states. For any 3-qubit state $\rho$, after local filtering one gets filterCHSH ,

where $F_{A}$, $F_{B}$ and $F_{C}$ are positive operators acted locally on the three subsystems respectively, $F=\textrm{Tr}[(F_{A}\otimes F_{B}\otimes F_{C})\rho(F_{A}\otimes F_{B}\otimes F_{C})^{{\dagger}}]$ is the normalization constant. Suppose the filter operators $F_{A}$, $F_{B}$ and $F_{C}$ have the following spectral decompositions,

where $U$, $V$ and $W$ are unitary operators. Set

for $i,j,k=1,2,3$. Without loss of generality, we assume that the singular matrices have the forms,

with $l,m,n\geq 0$.

We have the following theorem which provides a tight upper bound on the maximal violation value of the Mermin inequality.

Remark The normalization factor $F$ has the following form

where $\tilde{\rho}$ and $\rho$ are local unitary equivalent. They have the same maximal violation value of the Mermin inequality.

Note that the inequality (5) saturates if the degeneracy of $\lambda^{\prime}_{\max}$ is more than 1, and the two nine-dimensional singular vectors corresponding to $\lambda_{\max}$ take the forms of $\vec{a}\otimes\vec{c}-\vec{a}^{\prime}\otimes\vec{c}^{\prime}$ and $\vec{a}\otimes\vec{c}{{}^{\prime}}+\vec{a}{{}^{\prime}}\otimes\vec{c}$, respectively.

To illustrate the theorem let us consider the following examples.

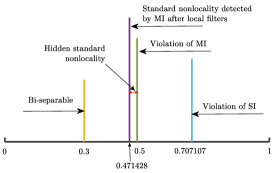
Example 1. Consider the 3-qubit mixed Greenberger-Horne-Zeilinger (GHZ) state EX12015 ,

where $0\leq p\leq 1$, $|GHZ\rangle=\frac{|000\rangle+|111\rangle}{\sqrt{2}}$, $I_{2}$ is the $2\times 2$ identity matrix and $\tilde{I}=$diag$(1,0,0,1)$. The state $\rho_{GHZ}$ is shown to be genuine multipartite entangled for $\frac{1}{3}<p\leq 1$, and it admits bilocal hidden model for $0\leq p\leq 0.41667$ EX12015 . Later, Li et al. pointed out that $\rho_{GHZ}$ is genuine multipartite nonlocal GN2013 ; LM2017 for $0.707107<p\leq 1$, namely, it violates the Svetlichny inequality (SI) Svetlichny1987 when $0.707107<p\leq 1$. The maximal violation of the Svetlichny inequality under local filtering has been also calculated FOP . Recently, the upper bound of the Mermin operator has been studied in QIP2019 , which shows that the state violates the Mermin inequality if $\frac{1}{2}<p\leq 1$, i.e., the state is standard nonlocal for $\frac{1}{2}<p\leq 1$.

By direct calculation, we have the correlation matrix of $\rho_{GHZ}$,

and

where $D=(D_{j,ik})$, $D_{ijk}=\textrm{Tr}[\rho_{GHZ}(\alpha_{i}\otimes\beta_{j}\otimes\gamma_{k})]$. The singular values of $D$ are $\sqrt{2}plmn$, $\sqrt{2}plmn$ and $T=\frac{(l^{2}-1)(m^{2}n^{2}+1)}{4}+\frac{(l^{2}+1)(m^{2}n^{2}-1)}{4}p$. $\tilde{\rho}_{GHZ}$ is locally unitary equivalent to $\rho_{GHZ}$. Then we have that $\frac{\sqrt{2}plmn}{F}$, $\frac{\sqrt{2}plmn}{F}$ and $\frac{T}{F}$ are the singular values of the matrix $\frac{\tilde{D}}{F}$, where

The maximal singular value is $\lambda^{{}^{\prime}}_{\max}=\frac{\sqrt{2}plmn}{F}$ for given $p$ with $\frac{\sqrt{2}plmn}{F}>\frac{T}{F}$. Then the upper bound of the maximal value of the Mermin operator is $2\sqrt{2}\lambda{{}^{\prime}}_{\max}=\frac{4plmn}{F}$. Two singular vectors corresponding to the singular value $\lambda{{}^{\prime}}_{\max}$ with degeneracy 2 can be chosen as $\vec{v}_{1}=(-1,0,0,0,1,0,0,0,0)^{T}$ and $\vec{v}_{2}=(0,1,0,1,0,0,0,0,0)^{T}$, which can be further written as

By taking $\vec{a}=(1,0,0)^{T}$, $\vec{a}^{\prime}=(0,-1,0)^{T}$, $\vec{c}=(-1,0,0)^{T}$, $\vec{c}^{\prime}=(0,1,0)^{T}$, $\vec{b}$ and $\vec{b}^{\prime}$ some suitable unit vectors, the upper bound $\frac{4plmn}{F}$ of $\rho_{GHZ}$ is attained. Therefore, the state violates the Mermin inequality if $\frac{4plmn}{F}>2$ under the restriction $\frac{\sqrt{2}plmn}{F}>\frac{T}{F}$. As a result, the standard nonlocality of the state $\rho^{\prime}_{GHZ}$ can be detected by the Mermin inequality for $0.471428<p\leq 1$. However, the state violates the Mermin inequality if $\frac{1}{2}<p\leq 1$ QIP2019 . Hence, the hidden standard nonlocality of $\rho_{GHZ}$ is revealed by local filtering operation for $0.471428\leq p\leq 0.5$, see FIG. 1.

Example 2. Consider the following state given in EX22007 ,

where $0\leq p\leq 1$, $|\Psi\rangle=\cos\frac{\pi}{8}|000\rangle+\sin\frac{\pi}{8}|111\rangle$. Under local filtering we have

The singular values of $D$ are $plmn$, $plmn$ and $T=\frac{l^{2}m^{2}(n^{2}-1)}{2}+\frac{-2+\sqrt{2}+2l^{2}m^{2}+\sqrt{2}l^{2}m^{2}n^{2}}{4}p$. Since $\tilde{\rho}$ is locally unitary equivalent to $\rho$, the singular value of the matrix $\frac{\tilde{D}}{F}$ are $\frac{plmn}{F}$, $\frac{plmn}{F}$ and $\frac{T}{F}$, where

The maximal singular value is $\lambda^{\prime}_{\max}=\frac{plmn}{F}$ for given $p$ with $\frac{plmn}{F}>\frac{T}{F}$. Then the upper bound of the maximal value of the Mermin operator is $2\sqrt{2}\lambda^{\prime}_{\max}=\frac{2\sqrt{2}plmn}{F}$. This bound can be attained by selecting the two singular vectors, corresponding to the singular value $\lambda^{\prime}_{\max}$ with degeneracy 2, to be $\vec{v}_{1}=(-1,0,0,0,1,0,0,0,0)^{T}$ and $\vec{v}_{2}=(0,1,0,1,0,0,0,0,0)^{T}$, which can be decomposed to

Let $\vec{a}=(1,0,0)^{T}$, $\vec{a}^{\prime}=(0,-1,0)^{T}$, $\vec{c}=(-1,0,0)^{T}$, $\vec{c}^{\prime}=(0,1,0)^{T}$. Together with some suitable unit vectors $\vec{b}$ and $\vec{b}^{\prime}$, the upper bound $\frac{2\sqrt{2}plmn}{F}$ is attained. Therefore, the state violates the Mermin inequality if $\frac{2\sqrt{2}plmn}{F}>2$ under the restriction $\frac{plmn}{F}>\frac{T}{F}$, namely, the state $\rho$ violates the Mermin inequality if $0.318675<p\leq 1$, for which the standard nonlocality of the state $\rho^{\prime}$ is detected. The maximal violation of the Mermin inequality is shown in FIG. 2.

Based on the protocol introduced in QIP2019 , $\rho$ is standard tripartite nonlocal for $0.707107<p\leq 1$. Therefore, the state $\rho$ shows hidden standard tripartite nonlocality for $0.318675\leq p\leq 0.707107$, see FIG. 3.

Example 3. The interaction between a quantum system and its environment may reduce the entanglement and nonlocality of the system. The GHZ state is a genuine tripartite nonlocal state as violates the Svetlichny inequality. Let us consider that the GHZ state goes through the amplitude damping(AD) noise channel which maps a qubit state $\rho$ to $\mathcal{E}_{AD}(\rho)=E_{0}\rho E^{{\dagger}}_{0}+E_{1}\rho E^{{\dagger}}_{1}$, where the Kraus operators are given by Nielsen ,

$\gamma\in(0,1)$ is the damping rate.

When each qubit of the GHZ state $\rho_{G}$ undergoes the amplitude damping noise channel, one gets

The corresponding correlation matrix is

where $s=(1-\gamma)^{\frac{3}{2}}$ and $t=\gamma(3-6\gamma+4\gamma^{2})$. The singular values of $C$ are $\sqrt{2(1-\gamma)^{\frac{3}{2}}}$, $\sqrt{2(1-\gamma)^{\frac{3}{2}}}$ and $\gamma(4\gamma^{2}-6\gamma+3)$. We choose the two nine-dimension vectors to be $\vec{v}_{1}=(-1,0,0,0,1,0,0,0,0)^{T}$ and $\vec{v}_{2}=(0,1,0,1,0,0,0,0,0)^{T}$, which can be decomposed into

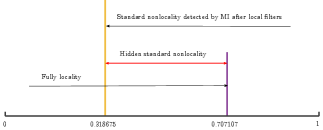
Let $\vec{a}=(1,0,0)^{T}$, $\vec{a}^{\prime}=(0,-1,0)^{T}$, $\vec{c}=(-1,0,0)^{T}$, $\vec{c}^{\prime}=(0,1,0)^{T}$. Together with suitable unit vectors $\vec{b}$ and $\vec{b}^{\prime}$, the upper bound of the maximal expectation of the Mermin operator is $4\sqrt{(1-\gamma)^{\frac{3}{2}}}$ based on Mermin1990 . Hence, the state is standard tripartite nonlocal for $\gamma\in(0,0.370039)$.

Now consider the filtering. The correlation matrix of the filtered state is

where $S=lmn(1-\gamma)^{\frac{3}{2}}$. The singular values of $D$ are $\sqrt{2(1-p)^{3}l^{2}m^{2}n^{2}}$, $\sqrt{2(1-p)^{3}l^{2}m^{2}n^{2}}$ and

As $\tilde{\rho}^{AD}_{G}$ is locally unitary equivalent to $\rho^{AD}_{G}$, the singular values of the matrix $\frac{\tilde{D}}{F}$ are $\frac{\sqrt{2(1-p)^{3}l^{2}m^{2}n^{2}}}{F}$, $\frac{\sqrt{2(1-p)^{3}l^{2}m^{2}n^{2}}}{F}$ and $\frac{T}{F}$, where

The maximal violation value of the Mermin operator is $\frac{4\sqrt{(1-\gamma)^{3}l^{2}m^{2}n^{2}}}{F}$, with the restriction $\frac{\sqrt{2(1-p)^{3}l^{2}m^{2}n^{2}}}{F}\geq\frac{T}{F}$. Therefore, the filtered state violates the Mermin inequality for $\gamma\in(0,0.394752)$. That is to say, for the state with $0.370069\leq\gamma\leq 0.394752$, the state $\rho^{AD}_{G}$ is not a standard nonlocal state. FIG. 4 shows that for $\gamma\in(0,0.394752)$, the filtered state violates the Mermin inequality, i.e., it is a standard tripartite nonlocal state.

In summary, we have investigated the maximal violation of the Mermin inequality under local filtering for any 3-qubit states. We have presented a tight upper bound for the maximal expectation value of the Mermin operator after local filtering. Furthermore, for the 3-qubit GHZ state, the standard tripartite nonlocal be revealed for $0.471428\leq p\leq 0.5$ by local filtering. Similarly, although the amplitude damping GHZ state is fully local for $0.370069\leq\gamma\leq 0.394752$, the filtered one is standard nonlocal. The local filtering process may reveal certain hidden quantum correlations including nonlocality filterCHSH ; FOP and steerability FilterSteer . In order to improve the efficiency of quantum information process, a number of scheme have been put froward purify ; ErrorCorrection ; EntanglementConcentration ; QuantumRepeaters . The filter operations can also be used to improve the fidelity between quantum states and efficiency of information processing with noisy entangled state FilterNoise . Our approach presented in this article can also be used to deal with other Bell-type inequalities for tripartite or multipartite systems.