Requirement analysis for dE/dx measurement and PID performance at the CEPC baseline detector

The TOF of a given particle can be calculated based on its momentum and its flight distance along its trajectory. In magnetic field, the trajectory of a charged particle would be a helix that can interact with the barrel region or the end-cap region of ECAL, depending on the four-momentum of the incident particle. The inner radius of ECAL is represented by R and the radius of the helix is derived as

where $P_{t}$, $q$, and B are the transverse momentum in GeV/c, the charge of the incident particle, and the magnetic field strength in the TPC in T, respectively. Once the incident particle interacts with the barrel of the ECAL, the length of the trajectory of the incident particle can be described by $arc=2\pi r\cdot\frac{\phi}{2\pi}$, and the corresponding arc angle is represented by $\phi=2\cdot arcsin(\frac{R}{2r})$. The velocity of the particle perpendicular/parallel to the B-field is represented by $v_{t}$/$v_{l}$, and the length between the Interaction Point (IP) and the ECAL end cap is represented by $L$. At the CEPC, $L=2.35\,$m and $R=1.8\,$m. If $2\cdot r$ $>$ R & $L/v_{l}>arc/v_{t}$, the helix would interact with the barrel of ECAL, $TOF=arc/v_{t}$. Otherwise, the helix would interact with the end cap of ECAL, $TOF=L/v_{l}$.

The $K^{\pm}/\pi^{\pm}$ separation power as a function of momentum and polar angle $\theta$ is shown in Fig. 3. The separation power is peaking around $cos\theta=0.8$ corresponding to the maximum drift length.

The measured dE/dx of a track follows a Landau distribution with a large tail caused by high-energy $\delta$-electrons. The average dE/dx for a track, denoted $I$, is estimated using the usual “truncated mean” method, where the truncation ratio of 90% is determined to obtain the optimal dE/dx resolution, denoted $\sigma_{I}$. For ${K}^{\pm}$/${\pi}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ , the distributions of $I$ as a function of momentum are shown in Fig. 4. The distributions of the absolute difference of $I$ for ${K}^{\pm}$/${\pi}^{\pm}$ and ${K}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ are shown in Fig. 4. The $K^{\pm}$ and $\pi^{\pm}$ with the same dE/dx at $1\,$GeV/c ($K^{\pm}$ and ( ) [-.7ex] $\kern-1.79993ptp$ at $2.5\,$GeV/c) have no separation power.

The predictive power of the dE/dx method depends on precise knowledge of the dE/dx energy loss parameterization and its resolution. The resolution induced by the design of the TPC and the momentum of the incident particle, including the number of pad rings $n$, the pad height along the radial direction $h$, the density of the working gas $\rho$, the relativistic velocity $\beta\gamma$, and the polar angle $\theta$ of the particle trajectory, is named “intrinsic dE/dx resolution”. While in real experiments, the dE/dx resolution could be deteriorated by the detector effects arising in the processes of electron drift, signal amplification and readout in TPC. We name the dE/dx resolution in real experiments as “actual dE/dx resolution”.

The differential of the dE/dx resolution, denoted $\sigma_{I}/I$, to the parameters of the TPC and the incident particle is shown in Fig. 5. The default values for the parameters of the TPC at the baseline CEPC detector are $n=222$, $h=6\,$mm, and $\rho=\rho_{0}=1.73\,$mg/cm³, which are represented by the solid star markers in Fig. 5. The dE/dx resolution is a power function of $n$/$h$/$\rho$/$\beta\gamma$, while dE/dx resolution is a constant in the barrel region and becomes better with the increase of particle drift distance. However, due to the relatively low physics performance of the end cap, the dE/dx resolution becomes worse in the end-cap region ($|cos\theta|>0.85$), see Fig. 5. It can be seen that dE/dx resolution for ${K}^{\pm}$/${\pi}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ can be better than 2.5% when $\beta\gamma>10$ in the barrel region. In real experiments, the dE/dx resolution in the barrel region is pursued to be better than 3%. This means that the degradation of the dE/dx resolution caused by the electronics and the detector effects must be controlled to be less than 1/5 of the intrinsic dE/dx resolution in the barrel region. The parameterization of dE/dx resolution can be factorized as

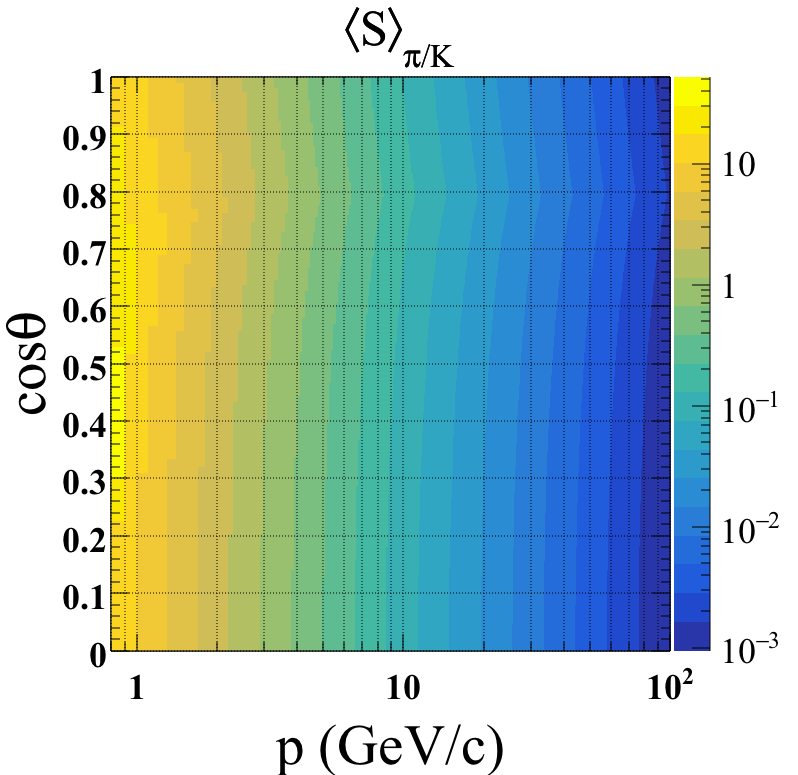
where $h$ and $\rho$ are in mm and mg/cm³, respectively. The distribution of dE/dx resolution as a function of momentum and polar angle for ${K}^{\pm}$/${\pi}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ is shown in Fig. 6. The separation power as a function of momentum and polar angle is shown in Fig. 7 for ${K}^{\pm}$/${\pi}^{\pm}$ and Fig. 7 for ${K}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ . The regions with separation power higher than 3 are shown in warm colors.

The above analyses investigate the separation power of ${K}^{\pm}$/${\pi}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ with TOF and dE/dx information independently. When the polar angle is $\pi/4$, the separation power as a function of momentum for ${K}^{\pm}$/${\pi}^{\pm}$ and ${K}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ is shown in Fig. 8. The TOF information can enhance the separation power of dE/dx information at about $1\,$GeV/c for ${K}^{\pm}$/${\pi}^{\pm}$ separation and about $2.5\,$GeV/c for ${K}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ separation. After combining dE/dx and TOF, the separation power as a function of momentum and polar angle for ${K}^{\pm}$/${\pi}^{\pm}$ and ${K}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ is shown in Fig. 9. The regions with separation power higher than 3 are shown in warm colors.

As demonstrated in Fig. 9, the separation power has a strong dependence on the polar angle and momentum of the particles. Therefore, for a given reference of momentum and polar angle range, we can optimize the cuts to select candidates with maximal efficiency times purity. For example, Fig. 10 shows the distribution of the variable $(R-R_{K})/\sigma_{R}$, where $R$ is the experimental measurement either by dE/dx alone or by the combination of dE/dx and TOF, $R_{k}$ is the expected value for the $K^{\pm}$ hypothesis, and $\sigma_{R}$ denotes the experimental resolution for ${K}^{\pm}$/${\pi}^{\pm}$/ ( ) [-.7ex] $\kern-1.79993ptp$ in a given range of momentum and polar angle. The two vertical lines indicate $K^{\pm}$ selection with maximal efficiency times purity. The $K^{\pm}$ identification efficiency and purity are defined as

where $N_{K}$ is the total number of $K^{\pm}$ produced, $N_{K\to K}$ is the number of $K^{\pm}$ correctly identified, and $N_{\pi(p)\to K}$ is the number of $\pi^{\pm}$( ( ) [-.7ex] $\kern-1.79993ptp$ ) incorrectly identified as $K^{\pm}$.

By combining dE/dx and TOF with intrinsic dE/dx resolution and $50\,$ps TOF resolution, Fig. 10 shows the maximal efficiency times purity of $K^{\pm}$ identification at different ranges of momentum and polar angle. The overall efficiency and purity of $K^{\pm}$ identification is calculated as

where $\sum_{bin}$ means summation over momentum in the range of 0 to $40\,$GeV/c and cosine polar angle in the range of 0 to 1, $\epsilon_{k}$, $p_{k}$ and $N_{k}$ represents the $K^{\pm}$ identification efficiency, purity and the number of $K^{\pm}$, respectively, in a given momentum and polar angle range. With above convention, the overall efficiency and purity in Fig. 10 is 98.43% and 97.89%, respectively.

In reality, the dE/dx resolution is affected by detector effects and readout electronics. With the definition $\sigma_{actual}=factor\cdot\sigma_{intrinsic}$, where $\sigma_{actual}$ is the actual dE/dx resolution and $\sigma_{intrinsic}$ is the intrinsic dE/dx resolution, the performance of $K^{\pm}$ identification under different factors with/without combining TOF information are shown in Table 3. The factors are selected according to Table 1 in Ref. [11], which shows several detectors from other high energy experiments have the actual dE/dx resolution decreased by 15% to 50% relative to the intrinsic ones. The results in Table 3 prove that worse dE/dx resolution leads to worse $K^{\pm}$ identification performance, while TOF information can improve $K^{\pm}$ identification performance on top of dE/dx information. The Ref. [11] performs the same analysis, but the results differ from those in Table 3. There are two reasons for this: First, the Ref. [11] selects candidates based on the intersections of the spectra shown in Fig. 10, which is different from this analysis, and second, the momentum ranges for these two analyzes are different.

$D^{0}$ mesons can be abundantly produced in the CEPC, especially in the Z-pole operating mode, and $D^{0}$ mesons are important research objects for the study of CP violation. It is important to understand the reconstruction performance of $D^{0}$ in the baseline design of the CEPC detector. Using the inclusive $Z\to q\overline{q}$ sample and under the condition of intrinsic dE/dx resolution, the reconstruction performance of $D^{0}\to\pi^{+}K^{-}$ in the baseline CEPC detector is investigated in this subsection.

The method for reconstructing the $D^{0}\to\pi^{+}K^{-}$ is described below.

1. 1.

   Match all pairs of reconstructed oppositely charged tracks.

2. 2.

   To suppress the significant combinatorial backgrounds, the absolute mass difference between two oppositely charged tracks and $D^{0}$ is set to less than $10\,$MeV/c².

3. 3.

   The impact parameter (IMP), which equivalent to the perpendicular distance between IP and the path of a track, is larger than $0.02\,$mm for each track.

4. 4.

   The $\chi^{2}$ of the secondary vertex fit [12] is less than 5.15.

5. 5.

   The distance of the secondary vertex to IP is greater than $0.305\,$mm.

6. 6.

   The identified PID of a positively charged particle is a $\pi^{+}$ and a negative $K^{-}$.

The efficiency and purity of the candidate $D^{0}$ selection are defined in Eq. 6. To maximize the value of the efficiency times the purity of the signal selection, scans of the selection parameters were performed in the determination of the selection criteria. The details of event selection can be found in Table 4.

After applying the above selection criteria, the distribution of the invariant mass of the track pair is shown in Fig. 11. The signal distribution is modeled with a Breit-Wigner theory model convolving a Gaussian detector response function, and the background distribution is modeled with a one order Chebyshev polynomial. The mean value of fitted $D^{0}$ mass is $1864.259\pm 0.025\,$MeV/c².

$D^{0}\to\pi^{+}K^{-}$ reconstruction performance as a function of dE/dx resolution is shown in Fig. 12, which proves that better dE/dx resolution leads to better $D^{0}\to\pi^{+}K^{-}$ reconstruction performance. The red/blue/green line corresponds to 0%/20%/50% degradation of dE/dx resolution. It can be seen that 20% degradation of dE/dx resolution would not significantly degrade the $D^{0}\to\pi^{+}K^{-}$ reconstruction performance.

The $\phi$ plays a central role in the reconstruction of many high-level objects, especially at $B_{s}\to\phi\nu\overline{\nu}$, where $\phi$ is the only visible component. This subsection investigates the performance of $\phi\to K^{+}K^{-}$ reconstruction with the inclusive hadronic Z-pole samples. The reconstruction chain is given below.

1. 1.

   Match all pairs of reconstructed oppositely charged tracks.

2. 2.

   Set the absolute difference between the invariant mass of two tracks and the $\phi$ mass to less than $8\,$MeV/c².

3. 3.

   Use the kinematic fitting package to reconstruct the vertex of the two matched tracks and set the value of the vertex $\chi^{2}$ to less than 9.95.

4. 4.

   The identified positively charged particle must be a $K^{+}$ and a negative $K^{-}$.

Notably, $\phi$ could come from QCD directly or from a decay of other hadrons. Since there is no requirement to identify these two sources, the selection conditions are not applied in a further step. The event selection process is shown in Table 5, where the definition of efficiency and purity is similar to that in the $D^{0}$ reconstruction. The effects of dE/dx resolution on $\phi$ reconstruction performance are shown in Fig. 13.