Representations of a quantum-deformed Lorentz algebra, Clebsch-Gordan map, and Fenchel-Nielsen representation of quantum complex flat connections at level- $\bm{k}$

Muxin Han

Abstract

A family of infinite-dimensional irreducible $\star$ -representations on $\mathcal{H}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ is defined for a quantum-deformed Lorentz algebra $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ , where $\mathbf{q}=\exp[\frac{2\pi i}{k}(1+b^{2})]$ and $\tilde{\mathbf{q}}=\exp[\frac{2\pi i}{k}(1+b^{-2})]$ with $k\in\mathbb{Z}_{+}$ and $|b|=1$ . The representations are constructed with the irreducible representation of quantum torus algebra at level- $k$ , which is developed from the quantization of $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory. We study the Clebsch-Gordan decomposition of the tensor product representation, and we show that it reduces to the same problem as diagonalizing the complex Fenchel-Nielson length operators in quantizing $\mathrm{SL}(2,\mathbb{C})$ flat connections on 4-holed sphere. Finally, the spectral decomposition of the complex Fenchel-Nielson length operators results in the direct-integral representation of the Hilbert space $\mathcal{H}$ , which we call the Fenchel-Nielson representation.

1 Introduction

This work is partly inspired by the early results on the relations between the modular double of $U_{q}(sl(2,\mathbb{R}))$ and quantum Teichmüeller theory [1, 2, 3, 4, 5, 6, 7]. As has been shown in the literature, the representation of the modular double of $U_{q}(sl(2,\mathbb{R}))$ can be defined on $L^{2}(\mathbb{R})$ , where the representations of the generators relate to the representation of quantum torus algebra (composed by the generators of Weyl algebra). For the tensor product representation, the Clebsch-Gordan decomposition is equivalent to the spectral decomposition of certain Fenchel-Nielsen (FN) length operator in quantum Teichmüeller theory. These results find their generalizations in this paper.

The quantum Teichmüeller theory closely relates to the $\mathrm{SL}(2,\mathbb{R})$ Chern-Simons theory [8, 9]. There has been recent generalization in [10, 11, 12] to the Teichmüeller TQFT of integer level, which relates to the quantization of Chern-Simons theory with complex gauge group $\mathrm{SL}(2,\mathbb{C})$ . The quantum $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory has the complex coupling constant $\hbar=\frac{2\pi i}{k}(1+b^{2}),\ \tilde{\hbar}=\frac{2\pi i}{k}(1+b^{-2})$ with $k\in\mathbb{Z},\ |b|=1$ (for one of the unitary branch [13]). The integer $k$ is called the level of Chern-Simons theory and relates to the integer level of the Teichmüeller TQFT. The quantization of $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory results in the Weyl algebra and quantum torus algebra at level- $k$ , motivated by quantizing the Chern-Simon symplectic structure [12, 10]. The Weyl algebra has $\mathbf{q}=\exp(\hbar)$ and $\tilde{\mathbf{q}}=\exp(\tilde{\hbar})$ , and the level- $k$ quantum torus algebra has $q=\exp(\hbar/2)$ and $\tilde{q}=\exp(\tilde{\hbar}/2)$ . The Hilbert space carrying the representation is $\mathcal{H}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ , and the representation reduces to the representation in quantum Teichmüeller theory [5, 14] when $k=1$ . The representation of quantum torus algebra at level- $k$ is reviewed in Section 2.

Based on the representation of the quantum torus algebra, we construct a family of irreducible representation of $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ on $\mathcal{H}$ . The star-structure on $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ is represented by the hermitian conjugate on $\mathcal{H}$ . As the tensor product of two Hopf algebras, $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ has a well-defined Hopf algebra structure and can be understood as a quantum deformation of the Lorentz algebra. In particular, it is a generalization of the quantum Lorentz group with real $\mathbf{q}$ that is well-studied in the literature (see e.g.[15, 16]). The irreducible representations are parametrized by a continuous parameter $\mu_{L}\in\mathbb{R}$ and a discrete parameter $m_{L}\in\mathbb{Z}/k\mathbb{Z}$ . They may be viewed as analog with the principle-series unitary representation of $\mathrm{SL}(2,\mathbb{C})$ , although they are periodic in $m_{L}$ .

We study the Clebsch-Gordan decomposition of the tensor product representation (of $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ ) on $\mathcal{H}\otimes\mathcal{H}$ , and we show that the result is a direct-integral of irreducible representations (see Section 3.2). The direct-integral is given by the spectral decomposition of the Casimir operator $Q_{21}$ of the tensor product representation, and we find the unitary transformation $\mathcal{U}_{21}$ as the Clebsch-Gordan map representing the co-multiplication.

Interestingly $Q_{21}$ relates to the quantization of complex FN lengths for $\mathrm{SL}(2,\mathbb{C})$ flat connections on 4-holed sphere (see Section 4). As resulting from quantizing the $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory, the quantization of $\mathrm{SL}(2,\mathbb{C})$ flat connections on 4-holed sphere can be constructed based on the level- $k$ representation of quantum torus algebra. We focus on the case that $k=2N$ is even ( $N$ is odd). In this case, we have the decomposition $\mathcal{H}\simeq\mathcal{H}_{+}\oplus\mathcal{H}_{-}$ where each of $\mathcal{H}_{\pm}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{N}$ carries the irreducible representation of the quantum algebra from quantizing the Fock-Goncharov (FG) coordinates of flat connections. The complex FN length that relates to $Q_{21}$ is given by the trace of holonomies around two holes. It turns out that the quantization of the complex FN length leads to the normal operators $\bm{L},\tilde{\bm{L}}=\bm{L}^{\dagger}$ , and $\mathrm{id}_{\mathcal{H}}\otimes\bm{L}$ is represented the same as $Q_{21}$ on $\mathcal{H}\otimes\mathcal{H}$ up to a unitary transformation. Moreover, we show that the traces of S-cycle (enclosing the 1st and 2nd holes) and T-cycle (enclosing the 2nd and 3rd holes) holonomies are related by a unitary transformation, which is a realization of the A-move in the Moore-Seiberg groupoid (as a generalizaton from [6]).

We show in Section 5 that the spectral decomposition of $\bm{L},\tilde{\bm{L}}$ endows to $\mathcal{H}$ the direct-integral representation, which we call the FN representation:

\displaystyle\mathcal{H}\simeq\sum_{m_{r}\in\mathbb{Z}/k\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\rho(\mu_{r},m_{r})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}},

(1.1)

where $\mathrm{d}\mu_{r}\rho(\mu_{r},m_{r})^{-1}$ is the spectral measure and each $\mathcal{H}_{\mu_{r},m_{r}}$ is 1-dimensional. The spectra of $\bm{L},\tilde{\bm{L}}$ are respectively $\ell(r)=r+r^{-1}$ and $\ell(r)^{*}$ , where $r=\exp[\frac{2\pi i}{k}(-ib\mu_{r}-m_{r})]$ . Due to the relation between $\bm{L}$ and $Q_{12}$ , the direct-integral representation (1.1) also gives the Clebsch-Gordan decomposition for the tensor product representation of $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ .

The results from this work should have impact on the complex Chern-Simons theory at level- $k$ and its relation to quantum group and quantum Teichmüeller theory. For instance, although the quantum Lorentz group with real deformation and the representation theory has been widely studied, the generalization to complex $\mathbf{q}$ has not been studied in the literature before. We show in this paper that this generalization closely relates to the $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory with level- $k$ ¹¹1The quantum Lorentz group with real deformation relates to the $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory with $k=0$ [17].. As another aspect, given the relation between quantum Teichmüeller theory and Liouville conformal field theory, our study might point toward certain generalization of Liouville conformal field theory relating to the level-k, and this generalization might also relate to the boundary field theory of the $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory.

In addition to the above, another motivation of this work is the potential application to the spinfoam model with cosmological constant in Loop Quantum Gravity [18, 19, 20]. The spinfoam model is formulated with $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory ( $1/k$ is proportional to the absolute value of cosmological constant) with the special boundary condition called the simplicity constraint, which restricts the flat connections on 4-holed sphere to be SU(2) up to conjugation. Classically, the simplicity constraint is conveniently formulated in terms of the complex FN variables [21]. Therefore, it may be convenient to formulate the quantization of the simplicity constraint in the FN representation of quantum flat connections. The investigation on this perspective will be reported elsewhere.

The structure of this paper is as follows: In Section 2, we review briefly the representation of quantum torus algebra at level- $k$ and set up some notations. In section 3, we construct the representations of $U_{\mathbf{q}}(sl_{2})\otimes U_{\tilde{\mathbf{q}}}(sl_{2})$ and discussion the Clebsch-Gordan decomposition of tensor product representation. In Section 4, we discuss the quantization of $\mathrm{SL}(2,\mathbb{C})$ flat connections on 4-holed sphere with a certain ideal triangulation, and we discuss the S-cycle and T-cycle trace operators and their unitary transformations. In Section 5, we compute the eigenvalue and distributional eigenstates of the trace operators and prove the direct-integral decomposition of the Hilbert space. In Section 6, we discuss the unitary transformation induced by changing ideal triangulation of the 4-holed sphere.

2 Quantum torus algebra and the representation at level- $k$

The quantum torus algebra $\mathcal{O}_{q}(\mathbb{T}^{2})$ is spanned by Laurent polynomials of the symbols $\bm{x}_{\alpha,\beta}$ with $\alpha,\beta\in\mathbb{Z}$ , satisfying the following relation

\bm{x}_{\alpha,\beta}\bm{x}_{\gamma,\delta}=q^{\alpha\delta-\beta\gamma}\bm{x}_{\alpha+\gamma,\beta+\delta},\qquad q=e^{\hbar/2}.

(2.1)

where $\hbar\in\mathbb{C}$ is the quantum deformation parameter. We associated to $\mathcal{O}_{q}(\mathbb{T}^{2})$ the “anti-holomorphic counterpart” $\mathcal{O}_{\tilde{q}}(\mathbb{T}^{2})$ generated by $\tilde{\bm{x}}_{\alpha,\beta}$ with $\alpha,\beta\in\mathbb{Z}$ , satisfying

\tilde{\bm{x}}_{\alpha,\beta}\tilde{\bm{x}}_{\gamma,\delta}=\tilde{q}^{\alpha\delta-\beta\gamma}\tilde{\bm{x}}_{\alpha+\gamma,\beta+\delta},\qquad\tilde{q}=e^{\tilde{\hbar}/2},\qquad\tilde{\hbar}=-\hbar^{*},

(2.2)

and $\mathcal{O}_{\tilde{q}}(\mathbb{T}^{2})$ commutes with $\mathcal{O}_{q}(\mathbb{T}^{2})$ . The entire algebra is denoted by $\mathcal{A}_{\hbar}(\mathbb{T}^{2})=\mathcal{O}_{q}(\mathbb{T}^{2})\otimes\mathcal{O}_{\tilde{q}}(\mathbb{T}^{2})$ . We can endow the algebra a $\star$ -structure by

\star\left(\bm{x}_{\alpha,\beta}\right)=\tilde{\bm{x}}_{\alpha,\beta},\qquad\star\left(\tilde{\bm{x}}_{\alpha,\beta}\right)=\bm{x}_{\alpha,\beta}.

which interchanges the holomorphic and antiholomorphic copies.

In this paper, we use the following parametrizations of $\hbar$ and $\tilde{\hbar}$

\hbar=\frac{2\pi i}{k}\left(1+b^{2}\right),\qquad\tilde{\hbar}=\frac{2\pi i}{k}\left(1+b^{-2}\right),

where $k,b$ satsifies

k\in\mathbb{Z}_{+},\qquad|b|=1,\qquad\mathrm{Re}(b)>0,\qquad\mathrm{Im}(b)>0.

As we are going to see in Section 4, $k$ relates to the integer level of the $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory.

It has been proposed in [12, 11] an infinite-dimensional unitary irreducible representation of $\mathcal{A}_{\hbar}(\mathbb{T}^{2})$ as the quantization of complex Chern-Simons theory. The Hilbert space carrying the representation is $\mathcal{H}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ , where a state is denoted by $f(\mu,m),$ $\mu\in\mathbb{R},$ $m\in\mathbb{Z}/k\mathbb{Z}$ . The following operators are defined on $\mathcal{H}$

	$\displaystyle\bm{\mu}f(\mu,m)$	$\displaystyle=\mu f(\mu,m),\qquad\bm{\nu}f(\mu,m)=-\frac{k}{2\pi i}\frac{\partial}{\partial\mu}f(\mu,m)$
	$\displaystyle e^{\frac{2\pi i}{k}\bm{m}}f(\mu,m)$	$\displaystyle=e^{\frac{2\pi i}{k}m}f(\mu,m),\qquad e^{\frac{2\pi i}{k}\bm{n}}f(\mu,m)=f(\mu,m+1).$

They satisfy

\displaystyle[\bm{\mu},\bm{\nu}]=\frac{k}{2\pi i},\qquad e^{\frac{2\pi i}{k}\bm{n}}e^{\frac{2\pi i}{k}\bm{m}}=e^{\frac{2\pi i}{k}}e^{\frac{2\pi i}{k}\bm{m}}e^{\frac{2\pi i}{k}\bm{n}},\qquad[\bm{\nu},e^{\frac{2\pi i}{k}\bm{m}}]=[\bm{\mu},e^{\frac{2\pi i}{k}\bm{n}}]=0

(2.3)

The representation of $\bm{x},\bm{y},\tilde{\bm{x}},\tilde{\bm{y}}$ in the quantum torus algebra are represented by

	$\displaystyle\bm{y}$	$\displaystyle=\exp\left[\frac{2\pi i}{k}(-ib\boldsymbol{\mu}-\bm{m})\right],$	$\displaystyle\qquad\tilde{\bm{y}}=\exp\left[\frac{2\pi i}{k}\left(-ib^{-1}\boldsymbol{\mu}+\bm{m}\right)\right],$		(2.4)
	$\displaystyle\bm{x}$	$\displaystyle=\exp\left[\frac{2\pi i}{k}(-ib\boldsymbol{\nu}-\bm{n})\right],$	$\displaystyle\qquad\tilde{\bm{x}}=\exp\left[\frac{2\pi i}{k}\left(-ib^{-1}\boldsymbol{\nu}+\bm{n}\right)\right].$		(2.5)

Their actions on states $f(\mu,m)$ are given by

	$\displaystyle\bm{y}f(\mu,m)$	$\displaystyle=e^{\frac{2\pi i}{k}(-ib{\mu}-{m})}f(\mu,m),\qquad$	$\displaystyle\bm{x}f(\mu,m)=f(\mu+ib,m-1),$		(2.6)
	$\displaystyle\tilde{\bm{y}}f(\mu,m)$	$\displaystyle=e^{\frac{2\pi i}{k}(-ib^{-1}{\mu}+{m})}f(\mu,m),\qquad$	$\displaystyle\tilde{\bm{x}}f(\mu,m)=f(\mu+ib^{-1},m+1).$		(2.7)

These operators form the $\mathbf{q},\tilde{\mathbf{q}}$ -Weyl algebra with $\mathbf{q}=q^{2}=e^{\hbar}$ , and $\tilde{\mathbf{q}}=\tilde{q}^{2}=e^{\tilde{\hbar}}$ :

\bm{x}\bm{y}=\mathbf{q}\bm{y}\bm{x},\qquad\tilde{\bm{x}}\tilde{\bm{y}}=\tilde{\mathbf{q}}\tilde{\bm{y}}\tilde{\bm{x}},\qquad\bm{x}\tilde{\bm{y}}=\tilde{\bm{y}}\bm{x},\qquad\tilde{\bm{x}}{\bm{y}}={\bm{y}}\tilde{\bm{x}}.

The tilded and untilded operators are related by the Hermitian conjugate

\bm{x}^{\dagger}=\tilde{\bm{x}},\qquad\bm{y}^{\dagger}=\tilde{\bm{y}},

and they are normal operators. It is often convenient to use the following formal notation

\bm{x}=e^{\bm{X}},\qquad\bm{y}=e^{\bm{Y}};\qquad\tilde{\bm{x}}=e^{\tilde{\bm{X}}},\qquad\tilde{\bm{y}}=e^{\tilde{\bm{Y}}}

where

	$\displaystyle\bm{Y}$	$\displaystyle=\frac{2\pi i}{k}(-ib\boldsymbol{\mu}-\bm{m}),\qquad\tilde{\bm{Y}}=\frac{2\pi i}{k}\left(-ib^{-1}\boldsymbol{\mu}+\bm{m}\right),$
	$\displaystyle\bm{X}$	$\displaystyle=\frac{2\pi i}{k}(-ib\boldsymbol{\nu}-\bm{n}),\qquad\tilde{\bm{X}}=\frac{2\pi i}{k}\left(-ib^{-1}\boldsymbol{\nu}+\bm{n}\right),$

satisfy the canonical commutation relation

[\bm{X},\bm{Y}]=\hbar,\qquad[\tilde{\bm{X}},\tilde{\bm{Y}}]=\tilde{\hbar},\qquad[\bm{X},\tilde{\bm{Y}}]=[\tilde{\bm{X}},{\bm{Y}}]=0.

The operators $\bm{x},\tilde{\bm{x}},\bm{y},\tilde{\bm{y}}$ are unbounded operators. The common domain $\mathfrak{D}$ of their Laurent polynomials contains $f(\mu,m)$ being entire functions in $\mu$ and satisfying

e^{\alpha\frac{2\pi}{k}b\mu}f(\mu,m)\in L^{2}(\mathbb{R}),\qquad f(\mu+ib\alpha,m)\in L^{2}(\mathbb{R}),\qquad\forall\,m\in\mathbb{Z}/k\mathbb{Z},\quad\alpha\in\mathbb{Z}.

The Hermite functions $e^{-\mu^{2}/2}H_{n}(\mu)$ , $n=1,\cdots,\infty$ satisfy all the requirements and span a dense domain in $L^{2}(\mathbb{R})$ , so $\mathfrak{D}$ is dense in $\mathcal{H}$ .

We denote by $\mathcal{L}(\mathfrak{D})$ the space of linear operators on $\mathfrak{D}$ . The representation $\rho$ : $\mathcal{A}_{\hbar}(\mathbb{T}^{2})\to\mathcal{L}(\mathfrak{D})$ is given by

	$\displaystyle\rho:\$	$\displaystyle\bm{x}_{\alpha,\beta}\mapsto e^{\alpha\bm{X}+\beta\bm{Y}}=q^{-\alpha\beta}\bm{x}^{\alpha}\bm{y}^{\beta},$		(2.8)
		$\displaystyle\tilde{\bm{x}}_{\alpha,\beta}\mapsto e^{\alpha\tilde{\bm{X}}+\beta\tilde{\bm{Y}}}=\tilde{q}^{-\alpha\beta}\tilde{\bm{x}}^{\alpha}\tilde{\bm{y}}^{\beta}.$		(2.9)

The relations (2.1) and (2.2) are obtained by appyling the $(\mathbf{q},\tilde{\mathbf{q}})$ -Weyl algebra. In the following, we often denote $\rho(\bm{x}_{\alpha,\beta}$ ) by $\bm{x}_{\alpha,\beta}$ for simplifying notations. The $\star$ -stucture is represened by the Hermitian conjugate

\bm{x}_{\alpha,\beta}^{\dagger}=\tilde{q}^{\alpha\beta}\tilde{\bm{y}}^{\beta}\tilde{\bm{x}}^{\alpha}=\tilde{q}^{-\alpha\beta}\tilde{\bm{x}}^{\alpha}\tilde{\bm{y}}^{\beta}=\tilde{\bm{x}}_{\alpha,\beta}.

3 Representation of a q-deformed Lorentz algebra

3.1 The representation

Based on the representation $(\mathcal{H},\rho)$ of the quantum torus algebra and by the linear combinations of the operators $\bm{x}_{\alpha\beta}$ , we obtain a representation of $U_{{\bf q}}(sl_{2})$ on $\mathcal{H}$ . Indeed, we define a family of operators $E_{\lambda},F_{\lambda},K_{\lambda},K_{\lambda}^{-1}$ by

	$\displaystyle K_{\lambda}$	$\displaystyle=\bm{x}_{-1,0},\qquad K_{\lambda}^{-1}=\bm{x}_{1,0},\qquad E_{\lambda}=-\frac{1}{{\bf q}-{\bf q}^{-1}}\bm{x}_{-1,1},$		(3.1)
	$\displaystyle F_{\lambda}$	$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}\left[\left(\lambda+\lambda^{-1}\right)\bm{x}_{1,-1}+\bm{x}_{3,-1}+\bm{x}_{-1,-1}\right],$		(3.2)

where the parameter $\lambda\in\mathbb{C^{\times}}$ . It is straight-forward to check that $E_{\lambda},F_{\lambda},K_{\lambda},K_{\lambda}^{-1}$ satisfy the commutation relation of $U_{{\bf q}}(sl_{2})$ ²²2See the convention in [4] up to an inverse of $\mathbf{q}$ .:

\displaystyle K_{\lambda}E_{\lambda}={\bf q}^{-1}E_{\lambda}K_{\lambda}

\displaystyle,\qquad K_{\lambda}F_{\lambda}={\bf q}F_{\lambda}K_{\lambda},\qquad\left[E_{\lambda},F_{\lambda}\right]=\frac{K_{\lambda}^{2}-K_{\lambda}^{-2}}{{\bf q}-{\bf q}^{-1}}.

Similarly, we define the tilded operators

	$\displaystyle\tilde{K}_{\lambda}$	$\displaystyle=\tilde{\bm{x}}_{-1,0},\qquad\tilde{K}_{\lambda}^{-1}=\tilde{\bm{x}}_{1,0},\qquad\tilde{E}_{\lambda}=-\frac{1}{\tilde{{\bf q}}-\tilde{{\bf q}}^{-1}}\tilde{\bm{x}}_{-1,1},$
	$\displaystyle\tilde{F}_{\lambda}$	$\displaystyle=-\frac{1}{\tilde{{\bf q}}-\tilde{{\bf q}}^{-1}}\left[\left(\tilde{\lambda}+\tilde{\lambda}^{-1}\right)\tilde{\bm{x}}_{1,-1}+\tilde{\bm{x}}_{3,-1}+\tilde{\bm{x}}_{-1,-1}\right],$

They satisfy the commutation relation of $U_{\tilde{{\bf q}}}(sl_{2})$ :

\displaystyle\tilde{K}_{\lambda}\tilde{E}_{\lambda}=\tilde{{\bf q}}^{-1}\tilde{E}_{\lambda}\tilde{K}_{\lambda},\qquad\tilde{K}_{\lambda}\tilde{F}_{\lambda}=\tilde{{\bf q}}\tilde{F}_{\lambda}\tilde{K}_{\lambda}

\displaystyle,\qquad\left[\tilde{E}_{\lambda},\tilde{F}_{\lambda}\right]=\frac{\tilde{K}_{\lambda}^{2}-\tilde{K}_{\lambda}^{-2}}{\tilde{{\bf q}}-\tilde{{\bf q}}^{-1}}.

It shows that $\mathcal{H}$ carries a $\star$ -representation of $U_{{\bf q}}(sl_{2})\otimes U_{\tilde{{\bf q}}}(sl_{2})$ labelled by the parameters $(\lambda,\tilde{\lambda})$ with $\lambda,\tilde{\lambda}\in\mathbb{C^{\times}}$ . When $\lambda^{*}=\tilde{\lambda}$ , the tilded operators and untilded operator are related by the Hermitian conjugate

\tilde{K}_{\lambda}=K_{\lambda}^{\dagger},\qquad\tilde{E}_{\lambda}=-E_{\lambda}^{\dagger},\qquad\tilde{F}_{\lambda}=-F_{\lambda}^{\dagger},

as the representation of the $\star$ -structure. The minus sign is due to $\bf{q}^{*}=\tilde{\bf{q}}^{-1}$ . The representation is irreducible because the representation of the Weyl algebra is irreducible³³3The generators of the Weyl algebra relate to the $U_{{\bf q}}(sl_{2})$ generators by $\bm{x}=\bm{x}_{1,0}=K_{\lambda}^{-1}$ , $\bm{y}=\bm{x}_{0,1}=q^{-1}\bm{x}_{1,0}\bm{x}_{-1,1}=-(\mathbf{q}-\mathbf{q}^{-1})q^{-1}K_{\lambda}^{-1}E_{\lambda}$ . . We denote this representation by $\pi_{\lambda,\tilde{\lambda}}$ ⁴⁴4 The above representation is motivated by generalizing the representations studied in e.g. [2, 3, 1] for the modular double of ${U}_{q}(\mathrm{SL}(2,\mathbb{R}))$ , although here $(\mathbf{q},\tilde{\mathbf{q}})\to(e^{2\pi ib^{2}},e^{2\pi ib^{-2}})$ when $k=1$ or $(\mathbf{q},\tilde{\mathbf{q}})\to(-e^{\pi ib^{2}}$ and $-e^{\pi ib^{-2}})$ when $k=2$ , whereas the modular deformation parameter there is $q=e^{\pi ib^{2}}$ and $\tilde{q}=e^{\pi ib^{-2}}$ ..

The comultiplication $\Delta$ of $U_{{\bf q}}(sl_{2})\otimes U_{\tilde{{\bf q}}}(sl_{2})$ is defined by

	$\displaystyle\Delta K$	$\displaystyle=K\otimes K,\qquad\Delta E=E\otimes K+K^{-1}\otimes E,\qquad\Delta F=F\otimes K+K^{-1}\otimes F,$
	$\displaystyle\Delta\tilde{K}$	$\displaystyle=\tilde{K}\otimes\tilde{K},\qquad\Delta\tilde{E}=\tilde{E}\otimes\tilde{K}+\tilde{K}^{-1}\otimes\tilde{E},\qquad\Delta\tilde{F}=\tilde{F}\otimes\tilde{K}+\tilde{K}^{-1}\otimes\tilde{F}.$

The Casimir operators defined by

	$\displaystyle Q_{\lambda}$	$\displaystyle=\left({\bf q}-{\bf q}^{-1}\right)^{2}F_{\lambda}E_{\lambda}-\mathbf{q}^{-1}K_{\lambda}^{2}-{\bf q}K_{\lambda}^{-2}$
	$\displaystyle\tilde{Q}_{\lambda}$	$\displaystyle=\left(\tilde{{\bf q}}-{\bf\tilde{q}}^{-1}\right)^{2}\tilde{F}_{\lambda}\tilde{E}_{\lambda}-\tilde{\mathbf{q}}^{-1}K_{\lambda}^{2}-\tilde{{\bf q}}K_{\lambda}^{-2}$

are constant on $\mathcal{H}$ : $Q_{\lambda}=\left(\lambda+\lambda^{-1}\right)\mathrm{id}_{\mathcal{H}}$ and $\tilde{Q}_{\lambda}=\left(\tilde{\lambda}+\tilde{\lambda}^{-1}\right)\mathrm{id}_{\mathcal{H}}$ . Then $Q_{\lambda}^{\dagger}=\tilde{Q}_{\lambda}$ is equivalent to $\lambda^{*}=\tilde{\lambda}$ if we fix the “Weyl refection” $\lambda\to\lambda^{-1}$ .

Alternatively, we may define

K_{\lambda}^{\prime}=\tilde{K}_{\lambda},\qquad K_{\lambda}^{\prime-1}=\tilde{K}_{\lambda}^{-1},\qquad F_{\lambda}^{\prime}=-\tilde{E}_{\lambda},\qquad E_{\lambda}^{\prime}=-\tilde{F}_{\lambda},

They satisfy the commutation relation of $U_{{\bf q}^{*}}(sl_{2})$

K_{\lambda}^{\prime}F_{\lambda}^{\prime}={\bf q}^{*}F_{\lambda}^{\prime}K_{\lambda}^{\prime},\qquad K_{\lambda}^{\prime}E_{\lambda}^{\prime}={\bf q}^{*-1}E_{\lambda}^{\prime}K_{\lambda}^{\prime},\qquad\left[F_{\lambda}^{\prime},E_{\lambda}^{\prime}\right]=-\frac{\tilde{K}_{\lambda}^{2}-\tilde{K}_{\lambda}^{-2}}{{\bf q^{*}}-{\bf q}^{*-1}}.

This shows that $\mathcal{H}$ also carries a $\star$ -representation of $U_{{\bf q}}(sl_{2})\otimes U_{{\bf q}^{*}}(sl_{2})$ with

K_{\lambda}^{\prime}=K_{\lambda}^{\dagger},\qquad E_{\lambda}^{\prime}=F_{\lambda}^{\dagger},\qquad E_{\lambda}^{\prime}=F_{\lambda}^{\dagger}.

We may view $U_{{\bf q}}(sl_{2})\otimes U_{{\bf q}^{*}}(sl_{2})$ and $U_{{\bf q}}(sl_{2})\otimes U_{\tilde{\bf q}}(sl_{2})$ as two versions of the quantum deformation of Lorentz Lie algebra $sl_{2}\oplus sl_{2}$ . $K,E,F$ and $\tilde{K},\tilde{E},\tilde{F}$ (or ${K}^{\prime},{E}^{\prime},{F}^{\prime}$ ) are q-deformed analogs of the self-dual and anti-self-dual generators in the Lorentz algebra. The representation $(\mathcal{H},\rho)$ of the quantum torus algebra with (3.1) and (3.2) define a family of representations of these two version of q-deformed Lorenz algebra. All the representations are infinite-dimensional and parametrized by $\lambda\in\mathbb{C}^{\times}$ .

When $\mathbf{q}$ is real, $U_{{\bf q}}(sl_{2})\otimes U_{{\bf q}^{*}}(sl_{2})$ reduces to the quantum Lorentz group widely studied earlier e.g. [15, 16]. In this sense, the q-deformed Lorentz algebra considered here generalizes the quantum Lorentz group to complex $\mathbf{q}$ . However, we introduce $s\in\mathbb{R}$ for parametrizing $\mathbf{q}$ by

\displaystyle\mathbf{q}=\exp\left[\frac{2\pi i}{k}(1+b^{2})\right]=\exp\left[\frac{4\pi i}{k+is}\right],\qquad is=k\frac{1-b^{2}}{1+b^{2}}\ \ \text{or}\ \ b^{2}=\frac{k-is}{k+is}.

(3.3)

The real $\mathbf{q}$ for the quantum Lorentz group corresponds to the limit $k\to 0$ and $b^{2}\to-1$ such that $s$ is finite. The representation discussed above is singular in this limit, so it is not clear how to compare the above representation with the representation of quantum Lorentz group.

3.2 The Clebsch-Gordan decomposition

The tensor product representation of $U_{{\bf q}}(sl_{2})\otimes U_{\tilde{{\bf q}}}(sl_{2})$ on $\mathcal{H}\otimes\mathcal{H}$ is given by $(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}})\circ\Delta$ . In the following, we often use the notation e.g. $K_{1}\equiv K_{\lambda_{1}}\equiv\pi_{\lambda_{1},\tilde{\lambda}_{1}}(K)$ and similar for other generators. We only focus on the represesentation of untilded operator, while the tilded operator can be analyzed in the same way.

The representation of Casimir $Q_{21}=(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}})\circ\Delta Q$ is expressed as

	$\displaystyle Q_{21}=$	$\displaystyle K_{2}^{-2}Q_{1}+Q_{2}K_{1}^{2}+\left({\bf q}+{\bf q}^{-1}\right)K_{2}^{-2}K_{1}^{2}+K_{2}^{-1}\left({\bf q}^{-1}K_{2}^{2}+{\bf q}K_{2}^{-2}+Q_{2}\right)E_{2}^{-1}E_{1}K_{1}$
		$\displaystyle+K_{2}^{-1}E_{2}\left({\bf q}^{-1}K_{1}^{2}+{\bf q}K_{1}^{-2}+Q_{1}\right)E_{1}^{-1}K_{1}.$

where $Q_{1}$ and $Q_{2}$ are proprtional to identity operator on $\mathcal{H}$ . Our task is to find the unitary transformation $C_{12}$ to diagonalize $Q_{21}$ .

It turns out that we can use a few elementary unitary transformations to simplify $Q_{21}$ :

•

Firstly, given $f(\mu_{2},m_{2}\mid\mu_{1},m_{1})\in\mathcal{H}\otimes\mathcal{H}$ , the unitary transformation $\mathcal{S}_{2}$ shift $\mu_{1},m_{1}$ by $-\mu_{2},-m_{2}$

	$\displaystyle\mathcal{S}_{2}f(\mu_{2},m_{2}\mid\mu_{1},m_{1})=$	$\displaystyle e^{\frac{2\pi i}{k}\left(\mu_{2}\bm{\nu}_{1}-m_{2}\bm{n}_{1}\right)}f(\mu_{2},m_{2}\mid\mu_{1},m_{1})$
	$\displaystyle=$	$\displaystyle f(\mu_{2},m_{2}\mid\mu_{1}-\mu_{2},m_{1}-m_{2}).$

•

The unitary transformation $t_{12}$ is defined by the quantum dilogarithm:

t_{21}=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}},e^{\tilde{\bm{Y}}_{1}-\tilde{\bm{Y}}_{2}+2\tilde{\bm{X}}_{2}}\right),

where $\varphi(y,\tilde{y})$ is the quantum dilogarithm function (see Appendix A for details)

\varphi(y,\tilde{y})=\left[\frac{\prod_{j=0}^{\infty}\left(1+{\bf q}^{2j+1}y\right)}{\prod_{j=0}^{\infty}\left(1+\tilde{{\bf q}}^{-2j-1}\tilde{y}\right)}\right]^{-1}.

To understand the action of $t_{21}$ on $\mathcal{H}\otimes\mathcal{H}$ , we consider the Weil transformation $\mathcal{V}_{2}$ representing the following symplectic transformation:

	$\displaystyle\qquad\left(\begin{array}[]{c}Y_{2}\\ X_{2}\end{array}\right)\mapsto\left(\begin{array}[]{c}Y_{2}-2X_{2}\\ X_{2}\end{array}\right)=\begin{pmatrix}1&-2\\ 0&1\end{pmatrix}\left(\begin{array}[]{c}Y_{2}\\ X_{2}\end{array}\right)=\begin{pmatrix}0&1\\ -1&0\end{pmatrix}\begin{pmatrix}1&0\\ 2&1\end{pmatrix}\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\left(\begin{array}[]{c}Y_{2}\\ X_{2}\end{array}\right),$		(3.12)
	$\displaystyle\mathcal{V}_{2}f(\mu_{2},m_{2}\mid\mu_{1},m_{1})=\frac{1}{k^{2}}\sum_{n,m\in\mathbb{Z}/k\mathbb{Z}}\int d\nu d\mu\,e^{\frac{2\pi i}{k}\left(\mu_{2}\nu-m_{2}n\right)}e^{\frac{2\pi i}{k}\left(\nu^{2}-n^{2}\right)}e^{-\frac{2\pi i}{k}\left(\mu\nu-mn\right)}f(\mu,m\mid\mu_{1},m_{1}),$

for all $f\in\mathfrak{D}\otimes\mathfrak{D}$ . $\mathcal{V}_{2}$ diagonalizes $e^{-\bm{Y}_{2}+2\bm{X}_{2}}$ and $e^{-\tilde{\bm{Y}}_{2}+2\tilde{\bm{X}}_{2}}$ by

e^{-\bm{Y}_{2}+2\bm{X}_{2}}\mathcal{V}_{2}f=\mathcal{V}_{2}e^{-\bm{Y}_{2}}f,\qquad e^{-\tilde{\bm{Y}}_{2}+2\tilde{\bm{X}}_{2}}\mathcal{V}_{2}f=\mathcal{V}_{2}e^{-\tilde{\bm{Y}}_{2}}f,

for any $f\in\mathfrak{D}\otimes\mathcal{H}$ . Therefore

t_{21}=\mathcal{V}_{2}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}},e^{\tilde{\bm{Y}}_{1}-\tilde{\bm{Y}}_{2}}\right)\mathcal{V}_{2}^{-1},

where $\varphi(e^{\bm{Y}_{1}-\bm{Y}_{2}},e^{\tilde{\bm{Y}}_{1}-\tilde{\bm{Y}}_{2}})$ simply multiplies the quantum dilogarithm function $\varphi(y_{1}y_{2}^{-1},\tilde{y}_{1}\tilde{y}_{2}^{-1})$ to $f(\mu_{2},m_{2}\mid\mu_{1},m_{1})$ .

•

The unitary transformation $C_{1}$ is defined by

C_{1}^{-1}=\varphi\left(e^{\bm{Y}_{1}-L_{2}},e^{\tilde{\bm{Y}}_{1}-\tilde{L}_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}},e^{-2\tilde{\bm{X}}_{1}+\tilde{L}_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}},e^{2\tilde{\bm{X}}_{1}+\tilde{L}_{1}}\right)}

where $L_{a}=\log(\lambda_{a})$ , $a=1,2$ .

Lemma 3.1.

The unitary transfromation $t_{12}\mathcal{S}_{2}$ transforms $Q_{21}$ to act only on the second factor of $\mathcal{H}\otimes\mathcal{H}$ . Namely $Q_{21}=t_{21}\mathcal{S}_{2}Q_{1}^{\prime}\mathcal{S}_{2}^{-1}t_{21}^{-1}$ where

Q_{1}^{\prime}=e^{\bm{Y}_{1}-2\bm{X}_{1}}+e^{-\bm{Y}_{1}+2\bm{X}_{1}}+e^{-\bm{Y}_{1}}Q_{1}+e^{-2\bm{X}_{1}}Q_{2}+e^{-2\bm{X}_{1}-\bm{Y}_{1}}.

(3.13)

Proof.

Since $\mathcal{S}_{2}e^{\bm{Y}_{1}}\mathcal{S}_{2}^{-1}=e^{\bm{Y}_{1}-\bm{Y}_{2}}$ and $\mathcal{S}_{2}e^{\bm{X}_{1}}\mathcal{S}_{2}^{-1}=e^{\bm{X}_{1}}$ , we have

\mathcal{S}_{2}Q_{1}^{\prime}\mathcal{S}_{2}^{-1}=e^{\bm{Y}_{1}-\bm{Y}_{2}-2\bm{X}_{1}}+e^{-\bm{Y}_{1}+\bm{Y}_{2}+2\bm{X}_{1}}+e^{-\bm{Y}_{1}+\bm{Y}_{2}}Q_{1}+e^{-2\bm{X}_{1}}Q_{2}+e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}.

Since $[\bm{Y}_{1}-\bm{Y}_{2}-2\bm{X}_{1},\,\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}]=[-\bm{Y}_{2},2\bm{X}_{2}]+[-2\bm{X}_{1},\,\bm{Y}_{1}]=0$ , ther first two terms commute with $t_{21}=\varphi(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}},e^{\tilde{\bm{Y}}_{1}-\tilde{\bm{Y}}_{2}+2\tilde{\bm{X}}_{2}})$ . In the following, we often suppress the tilded entry of $\varphi$ when it is not involved in the manipulation. We check the following relation by using the recursion relation of $\varphi(y,\tilde{y})$ :

	$\displaystyle t_{21}e^{-\bm{Y}_{1}+\bm{Y}_{2}}t_{21}^{-1}$	$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{Y}_{1}+\bm{Y}_{2}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}$
		$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)\varphi\left({\bf q}^{-2}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}e^{-\bm{Y}_{1}+\bm{Y}_{2}}$
		$\displaystyle=\left(1+{\bf q}^{-1}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{Y}_{1}+\bm{Y}_{2}}$
		$\displaystyle=e^{-\bm{Y}_{1}+\bm{Y}_{2}}+e^{2\bm{X}_{2}}$

	$\displaystyle t_{21}e^{-2\bm{X}_{1}}t_{21}^{-1}$	$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-2\bm{X}_{1}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}$
		$\displaystyle=e^{-\bm{X}_{1}}\varphi\left({\bf q}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)\varphi\left({\bf q}^{-1}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}e^{-\bm{X}_{1}}$
		$\displaystyle=e^{-\bm{X}_{1}}\left(1+e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{X}_{1}}$
		$\displaystyle=e^{-2\bm{X}_{1}}+e^{\bm{Y}_{1}-2\bm{X}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}$

	$\displaystyle t_{21}e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}t_{21}^{-1}$	$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}$
		$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)\varphi\left({\bf q}^{-4}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}$
		$\displaystyle=\left(1+{\bf q}^{-3}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)\left(1+{\bf q}^{-1}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}$
		$\displaystyle=\left[1+\left({\bf q}^{-1}+{\bf q}^{-3}\right)e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}+{\bf q}^{-4}e^{2\bm{Y}_{1}-2\bm{Y}_{2}+4\bm{X}_{2}}\right]e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}$
		$\displaystyle=e^{-2\bm{X}_{1}-\bm{Y}_{1}+\bm{Y}_{2}}+\left({\bf q}+{\bf q}^{-1}\right)e^{-2\bm{X}_{1}+2\bm{X}_{2}}+e^{\bm{Y}_{1}-\bm{Y}_{2}-2\bm{X}_{1}+4\bm{X}_{2}}$

We obtain that

	$\displaystyle t_{21}\mathcal{S}_{2}Q_{1}^{\prime}\mathcal{S}_{2}^{-1}t_{21}^{-1}=$	$\displaystyle\bm{x}_{0,-1}^{(2)}\bm{x}_{-2,1}^{(1)}+\bm{x}_{0,1}^{(2)}\bm{x}_{2,-1}^{(1)}+Q_{1}\left(\bm{x}_{0,1}^{(2)}\bm{x}_{0,-1}^{(1)}+\bm{x}_{2,0}^{(2)}\right)+Q_{2}\left(\bm{x}_{-2,0}^{(1)}+\bm{x}_{2,-1}^{(2)}\bm{x}_{-2,1}^{(1)}\right)$
		$\displaystyle+\bm{x}_{0,1}^{(2)}\bm{x}_{-2,-1}^{(1)}+\left({\bf q}+{\bf q}^{-1}\right)\bm{x}_{2,0}^{(2)}\bm{x}_{-2,0}^{(1)}+\bm{x}_{4,-1}^{(2)}\bm{x}_{-2,1}^{(1)}.$

It is the same as the expression of $Q_{21}$ in terms of $\bm{x}_{\alpha,\beta}$ . ∎

Lemma 3.2.

The unitary transformation $C_{1}$ further simplifies $Q_{1}^{\prime}$ :

{Q}_{1}^{\prime\prime}=C_{1}Q_{1}^{\prime}C_{1}^{-1}=e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+e^{-\bm{Y}_{1}-L_{1}}.

Proof.

For the 1st, 4th, and 5th terms of $Q_{1}^{\prime}$ in (3.13),

		$\displaystyle C_{1}\left(e^{\bm{Y}_{1}-2\bm{X}_{1}}+e^{-2\bm{X}_{1}}Q_{2}+e^{-2\bm{X}_{1}-\bm{Y}_{1}}\right)C_{1}^{-1}$
	$\displaystyle=$	$\displaystyle\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\varphi\left(e^{\bm{Y}_{1}-L_{2}}\right)^{-1}e^{-\bm{X}_{1}}\left(e^{\bm{Y}_{1}}+e^{-\bm{Y}_{1}}+e^{L_{2}}+e^{-L_{2}}\right)e^{-\bm{X}_{1}}\varphi\left(e^{\bm{Y}_{1}-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}$
	$\displaystyle=$	$\displaystyle e^{-\bm{X}_{1}}\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\varphi\left({\bf q}e^{\bm{Y}_{1}-L_{2}}\right)^{-1}e^{-\bm{Y}_{1}}\left(1+e^{\bm{Y}_{1}-L_{2}}\right)\left(1+e^{\bm{Y}_{1}+L_{2}}\right)\varphi\left({\bf q}^{-1}e^{\bm{Y}_{1}-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{X}_{1}}$
	$\displaystyle=$	$\displaystyle e^{-\bm{X}_{1}}\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{Y}_{1}}\left(1+e^{\bm{Y}_{1}+L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{X}_{1}}$
	$\displaystyle=$	$\displaystyle\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{X}_{1}}e^{-\bm{Y}_{1}}e^{-\bm{X}_{1}}\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}+e^{-2\bm{X}_{1}+L_{2}}.$

For the 2nd term of $Q_{1}^{\prime}$ ,

		$\displaystyle C_{1}e^{-\bm{Y}_{1}+2\bm{X}_{1}}C_{1}^{-1}$
	$\displaystyle=$	$\displaystyle\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\varphi\left(e^{\bm{Y}_{1}-L_{2}}\right)^{-1}e^{\bm{X}_{1}}e^{-\bm{Y}_{1}}e^{\bm{X}_{1}}\varphi\left(e^{\bm{Y}_{1}-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}$
	$\displaystyle=$	$\displaystyle e^{\bm{X}_{1}}\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\varphi\left({\bf q}^{-1}e^{\bm{Y}_{1}-L_{2}}\right)^{-1}e^{-\bm{Y}_{1}}\varphi\left({\bf q}e^{\bm{Y}_{1}-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}e^{\bm{X}_{1}}$
	$\displaystyle=$	$\displaystyle e^{\bm{X}_{1}}\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{Y}_{1}}\left(1+e^{\bm{Y}_{1}-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}e^{\bm{X}_{1}}$
	$\displaystyle=$	$\displaystyle e^{\bm{X}_{1}}\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\left(e^{-\bm{Y}_{1}}+e^{-L_{2}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}e^{\bm{X}_{1}}$
	$\displaystyle=$	$\displaystyle\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}e^{\bm{X}_{1}}e^{-\bm{Y}_{1}}e^{\bm{X}_{1}}\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}+e^{2\bm{X}_{1}-L_{2}}.$

For the 3rd term,

\displaystyle C_{1}e^{-\bm{Y}_{1}}Q_{1}C_{1}^{-1}=

\displaystyle\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{Y}_{1}}\left(e^{L_{1}}+e^{-L_{1}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}.

Inserting these results, we obtain

		$\displaystyle C_{1}Q_{1}^{\prime}C_{1}^{-1}$
	$\displaystyle=$	$\displaystyle e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\left({\bf q}^{-1}e^{-2\bm{X}_{1}}e^{-\bm{Y}_{1}}+{\bf q}e^{2\bm{X}_{1}}e^{-\bm{Y}_{1}}+e^{-\bm{Y}_{1}+L_{1}}+e^{-\bm{Y}_{1}-L_{1}}\right)\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}$
	$\displaystyle=$	$\displaystyle e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\left({\bf q}^{-1}e^{-2\bm{X}_{1}+L_{1}}+{\bf q}e^{2\bm{X}_{1}+L_{1}}+e^{2L_{1}}+1\right)e^{-\bm{Y}_{1}-L_{1}}\frac{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}$
	$\displaystyle=$	$\displaystyle e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+\frac{\varphi\left(e^{2\bm{X}_{1}+L_{1}}\right)}{\varphi\left(e^{-2\bm{X}_{1}+L_{1}}\right)}\left(1+{\bf q}e^{2\bm{X}_{1}+L_{1}}\right)\left(1+{\bf q}^{-1}e^{-2\bm{X}_{1}+L_{1}}\right)\frac{\varphi\left({\bf q}^{-2}e^{-2\bm{X}_{1}+L_{1}}\right)}{\varphi\left({\bf q}^{2}e^{2\bm{X}_{1}+L_{1}}\right)}e^{-\bm{Y}_{1}-L_{1}}$
	$\displaystyle=$	$\displaystyle e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+e^{-\bm{Y}_{1}-L_{1}}.$

∎

If we define the unitary transformation $\mathcal{U}_{21}^{-1}=t_{21}\mathcal{S}_{2}C_{1}^{-1}:\,\mathcal{H}\otimes\mathcal{H}\to\mathcal{H}\otimes\mathcal{H}$ , the Casimir operator is simplified by

Q_{1}^{\prime\prime}=\mathcal{U}_{21}Q_{21}\mathcal{U}_{21}^{-1}=e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+e^{-\bm{Y}_{1}-L_{1}}.

A similar computation gives for the tilded operator

\tilde{Q}_{1}^{\prime\prime}=\mathcal{U}_{21}\tilde{Q}_{21}\mathcal{U}_{21}^{-1}=e^{-2\tilde{\bm{X}}_{1}+\tilde{L}_{2}}+e^{2\tilde{\bm{X}}_{1}-\tilde{L}_{2}}+e^{-\tilde{\bm{Y}}_{1}-\tilde{L}_{1}}.

$Q_{1}^{\prime\prime}$ and $\tilde{Q}_{1}^{\prime\prime}=Q_{1}^{\prime\prime\dagger}$ commute, so they are normal operators. $Q_{1}^{\prime\prime}$ and $\tilde{Q}_{1}^{\prime\prime}$ only acting on the second copy of $\mathcal{H}\otimes\mathcal{H}$ , and their spectral decomposition gives a direct integral decomposition $\mathcal{H}\simeq\int_{\mathbb{C}}^{\oplus}d\mu\left(\ell,\ell^{*}\right)\,\mathcal{H}\left(\ell,\ell^{*}\right)$ where $\mu$ is the spectral measure.

\mathcal{U}_{21}:\ \mathcal{H}\otimes\mathcal{H}\to\int_{\mathbb{C}}^{\oplus}d\mu\left(\ell,\ell^{*}\right)\,\bm{\mathcal{H}}\left(\ell,\ell^{*}\right),\qquad\bm{\mathcal{H}}\left(\ell,\ell^{*}\right)=\mathcal{H}\otimes\mathcal{H}\left(\ell,\ell^{*}\right).

The unitary transformation $\mathcal{U}_{21}$ gives a Clebsch-Gordan decomposition of the tensor product representation by the following result:

Lemma 3.3.

If $\dim\mathcal{H}\left(\ell,\ell^{*}\right)=1$ , each $\bm{\mathcal{H}}\left(\ell,\ell^{*}\right)$ is a irreducible representation of $(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}})\circ\Delta$ .

Proof.

$F_{2},E_{2},K_{2},K_{2}^{-1}$ and their tilded relatives are represented irreducibly on the first factor in $\bm{\mathcal{H}}\left(\ell,\ell^{*}\right)=\mathcal{H}\otimes\mathcal{H}\left(\ell,\ell^{*}\right)$ , and they are explicitly given by

	$\displaystyle K_{2}$	$\displaystyle=e^{-\bm{X}_{2}},\qquad K_{\lambda}^{-1}=e^{\bm{X}_{2}},\qquad E_{2}=-\frac{1}{{\bf q}-{\bf q}^{-1}}e^{-\bm{X}_{2}+\bm{Y}_{2}},$
	$\displaystyle F_{2}$	$\displaystyle=\frac{1}{\left({\bf q}-{\bf q}^{-1}\right)^{2}}\left({\bf q}^{-1}K_{2}^{2}+{\bf q}K_{2}^{-2}+Q_{1}^{\prime\prime}\right)E_{2}^{-1},\qquad Q_{1}^{\prime\prime}=\ell\mathrm{id}_{\mathcal{H}}$

and similarly for the tilded operators. The representaion is unitarily equivalent to the tensor production representation:

	$\displaystyle\mathcal{U}_{21}^{-1}K_{2}\mathcal{U}_{21}$	$\displaystyle=t_{21}\mathcal{S}_{2}e^{-\bm{X}_{2}}\mathcal{S}_{2}^{-1}t_{21}^{-1}=t_{21}e^{-\bm{X}_{2}-\bm{X}_{1}}t_{21}^{-1}$
		$\displaystyle=\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{X}_{2}-\bm{X}_{1}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}$
		$\displaystyle=e^{-\bm{X}_{2}-\bm{X}_{1}}=K_{2}K_{1}=\left(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}}\right)\circ\Delta(K)$

	$\displaystyle\mathcal{U}_{21}^{-1}E_{2}\mathcal{U}_{21}$	$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}t_{21}\mathcal{S}_{2}e^{-\bm{X}_{2}+\bm{Y}_{2}}\mathcal{S}_{2}^{-1}t_{21}^{-1}$
		$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{X}_{1}-\bm{X}_{2}+\bm{Y}_{2}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}$
		$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}\varphi\left(e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)\varphi\left({\bf q}^{-2}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)^{-1}e^{-\bm{X}_{1}-\bm{X}_{2}+\bm{Y}_{2}}$
		$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}\left(1+{\bf q}^{-1}e^{\bm{Y}_{1}-\bm{Y}_{2}+2\bm{X}_{2}}\right)e^{-\bm{X}_{1}-\bm{X}_{2}+\bm{Y}_{2}}$
		$\displaystyle=-\frac{1}{{\bf q}-{\bf q}^{-1}}\left(e^{-\bm{X}_{1}-\bm{X}_{2}+\bm{Y}_{2}}+e^{\bm{Y}_{1}-\bm{X}_{1}+\bm{X}_{2}}\right)=E_{2}K_{1}+K_{2}^{-1}E_{1}$
		$\displaystyle=\left(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}}\right)\circ\Delta(E)$

Combining the above result $\mathcal{U}_{21}^{-1}Q_{1}^{\prime\prime}\mathcal{U}_{21}=Q_{21}=(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}})\circ\Delta Q$ ,

	$\displaystyle\left(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}}\right)\circ\Delta(F)$	$\displaystyle=\left(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}}\right)\circ\Delta\frac{\left({\bf q}^{-1}K^{2}+{\bf q}K^{-2}+Q\right)E^{-1}}{\left({\bf q}-{\bf q}^{-1}\right)^{2}}$
		$\displaystyle=\mathcal{U}_{21}^{-1}\frac{\left({\bf q}^{-1}K_{2}^{2}+{\bf q}K_{2}^{-2}+Q_{1}^{\prime\prime}\right)E_{2}^{-1}}{\left({\bf q}-{\bf q}^{-1}\right)^{2}}\mathcal{U}_{21}=\mathcal{U}_{21}^{-1}F_{2}\mathcal{U}_{21}.$

∎

The above shows that if If $\dim\mathcal{H}\left(\ell,\ell^{*}\right)=1$ holds, the unitary transformation $\mathcal{U}_{21}$ is a Clebsch-Gordan map intertwining three representations $\lambda_{1},\lambda_{2},\lambda_{3}$ :

\displaystyle\mathcal{U}_{21}\left[\left(\pi_{\lambda_{2},\tilde{\lambda}_{2}}\otimes\pi_{\lambda_{1},\tilde{\lambda}_{1}}\right)\circ\Delta(X)\right]\mathcal{U}_{21}^{-1}=\pi_{\lambda_{3},\tilde{\lambda}_{3}}(X)

(3.14)

where $\lambda_{3}+\lambda_{3}^{-1}=\ell$ and $\tilde{\lambda}_{3}+\tilde{\lambda}_{3}^{-1}=\ell^{*}$ .

The property $\dim\mathcal{H}\left(\ell,\ell^{*}\right)=1$ can be derived if we assume $\lambda_{a}=e^{L_{a}}$ , $a=1,2$ , is quantized

\displaystyle\lambda_{a}=\exp\left[\frac{2\pi i}{k}(-ib\mu_{L_{a}}-m_{L_{a}})\right],\qquad\mu_{L_{a}}\in\mathbb{R},\ m_{L_{a}}\in\mathbb{Z}/k\mathbb{Z}.

(3.15)

Then we can further apply a unitary shift operator

\displaystyle\mathcal{S}_{L_{1}}=\exp\left[\frac{2\pi i}{k}\left(\mu_{L_{1}}\bm{\nu}_{1}-m_{L_{1}}\bm{n}_{1}\right)\right],\qquad\mathcal{S}_{L_{1}}e^{-\bm{Y}_{1}-L_{1}}\mathcal{S}_{L_{1}}^{-1}=e^{-\bm{Y}_{1}}.

(3.16)

We obtain

	$\displaystyle\mathcal{Q}_{1}^{\prime\prime}=\mathcal{S}_{L_{1}}Q_{1}^{\prime\prime}\mathcal{S}_{L_{1}}^{-1}$	$\displaystyle=$	$\displaystyle e^{-2\bm{X}_{1}+L_{2}}+e^{2\bm{X}_{1}-L_{2}}+e^{-\bm{Y}_{1}},$		(3.17)
	$\displaystyle\tilde{\mathcal{Q}}_{1}^{\prime\prime}=\mathcal{S}_{L_{1}}\tilde{Q}_{1}^{\prime\prime}\mathcal{S}_{L_{1}}^{-1}$	$\displaystyle=$	$\displaystyle e^{-2\tilde{\bm{X}}_{1}+\tilde{L}_{2}}+e^{2\tilde{\bm{X}}_{1}-\tilde{L}_{2}}+e^{-\tilde{\bm{Y}}_{1}}.$		(3.18)

The spectral decomposition of $\mathcal{Q}_{1}^{\prime\prime},\tilde{\mathcal{Q}}_{1}^{\prime\prime}$ will be discussed in detail in Section 5. The analysis shows that $\dim\mathcal{H}(\ell,\ell^{*})=1$ indeed holds.

4 Quantum flat connections on 4-holed sphere

4.1 Fock-Goncharov coordinates and quantization

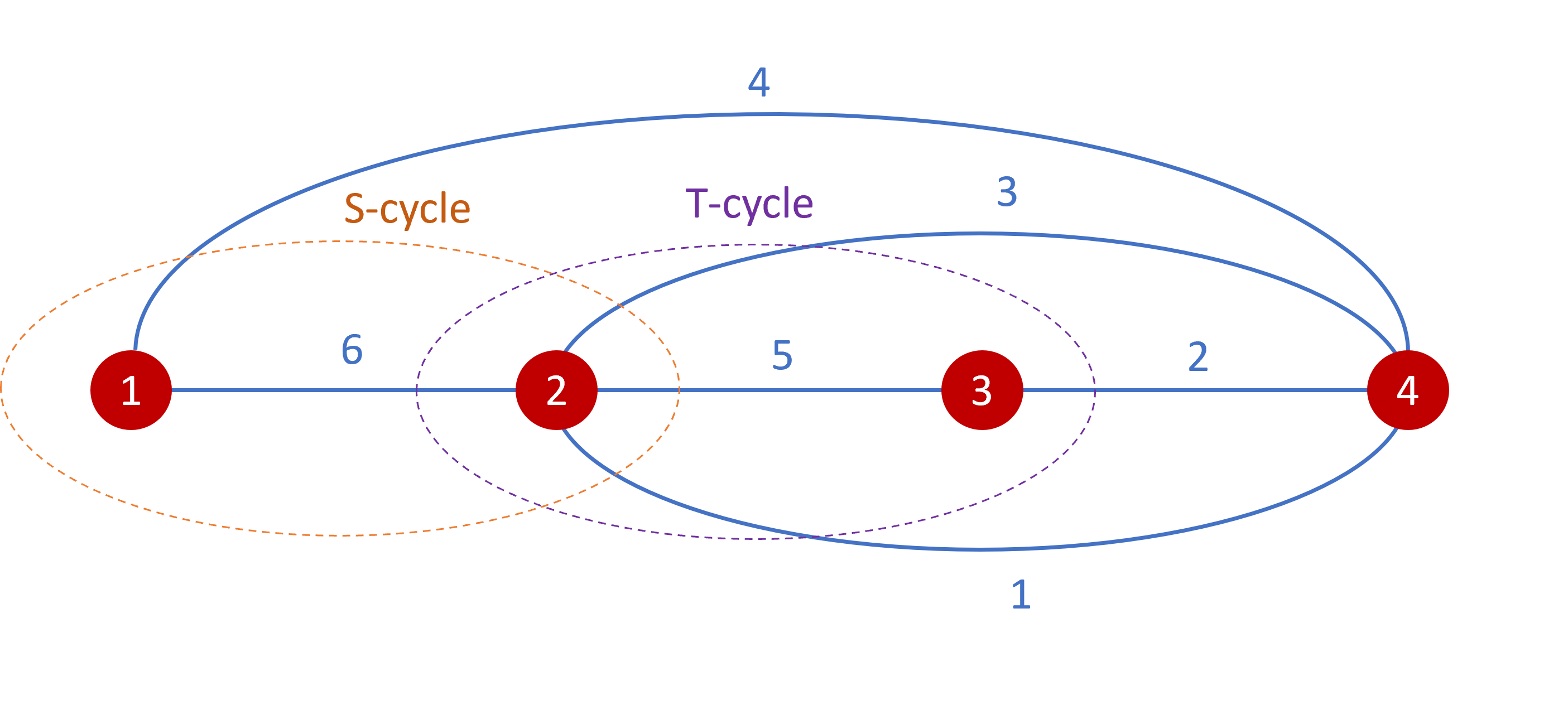
In this section, we study the quantization of $\rm{SL}(2,\mathbb{C})$ flat connections on 4-holed sphere. The moduli space of $\rm{SL}(2,\mathbb{C})$ flat connections on $n$ -holed sphere is a Poisson manifold. A set of useful coordinates are known as the Fock-Goncharov (FG) coordinates, each of which associate to an edge in an ideal triangulation of the $n$ -holed sphere. See Appendix B for details. FIG.1 is an example of the ideal triangulation of 4-holed sphere. Given any ideal triangulation on $n$ -holed sphere, we denote the FG coordinate by $z_{e}=e^{Z_{e}},\ \tilde{z}_{e}=e^{\tilde{Z}_{e}}$ , $e=1,\cdots,|E|$ ( $|E|$ is the number of edges), where $Z_{e},\tilde{Z}_{e}$ are lifts of $\log(z_{e}),\log(\tilde{z}_{e})$ . We define their classical Poisson bracket by $\{z_{e},z_{e^{\prime}}\}=2\varepsilon_{e,e^{\prime}}z_{e}z_{e^{\prime}},\ \{\tilde{z}_{e},\tilde{z}_{e^{\prime}}\}=2\varepsilon_{e,e^{\prime}}\tilde{z}_{e}\tilde{z}_{e^{\prime}}$ . Their quantization $[\bm{O},\bm{O}^{\prime}]=\hbar\{O,O^{\prime}\}$ and $[\tilde{\bm{O}},\tilde{\bm{O}}^{\prime}]=\tilde{\hbar}\{\tilde{O},\tilde{O}^{\prime}\}$ leads to the operator algebra

\displaystyle\bm{z}_{e}\bm{z}_{e^{\prime}}=\mathbf{q}^{2\varepsilon_{e,e^{\prime}}}\bm{z}_{e^{\prime}}\bm{z}_{e},\qquad\tilde{\bm{z}}_{e}\tilde{\bm{z}}_{e^{\prime}}=\tilde{\mathbf{q}}^{2\varepsilon_{e,e^{\prime}}}\tilde{\bm{z}}_{e^{\prime}}\tilde{\bm{z}}_{e},\qquad\bm{z}_{e}\tilde{\bm{z}}_{e^{\prime}}=\tilde{\bm{z}}_{e^{\prime}}\bm{z}_{e}

(4.1)

$\varepsilon_{e,e^{\prime}}=0,\pm 1,\pm 2$ counts the number of oriented triangles shared by edges $e,e^{\prime}$ , The contribution from each triangle is $+1$ ( $-1$ ) if $e$ rotates to $e^{\prime}$ counterclockwisely (clockwisely) in the triangle. $\varepsilon_{e,e^{\prime}}$ for the triangulation in FIG.1 reads

\displaystyle\varepsilon=\left(\begin{array}[]{cccccc}0&-1&0&1&1&-1\\ 1&0&-1&0&0&0\\ 0&1&0&-1&-1&1\\ -1&0&1&0&0&0\\ -1&0&1&0&0&0\\ 1&0&-1&0&0&0\\ \end{array}\right).

(4.8)

Similar as the above, we often write $z_{e}=e^{\bm{Z}_{e}}$ and $\tilde{\bm{z}}_{e}=e^{\tilde{\bm{Z}}_{e}}$ . The algebra has centers given by

\displaystyle\prod_{e}\bm{z}_{e},\qquad\prod_{e}\tilde{\bm{z}}_{e}

(4.9)

where the products are over edges adjacent to a given hole. This quantization can be applied to all ideal triangulations, and different triangulation are associated with different data $(\{e\},\varepsilon_{e,e^{\prime}})$ .

These Poisson bracket defined above can be derived from the Poisson bracket of $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory at level $k$ . Therefore the operator algebra (4.1) relates to the quantization of $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory on 4-holed sphere.

Refer to caption — Figure 1: An ideal triangulation of a 4-holed sphere, the S-cycle (orange) and T-cycle (purple).

Let us focus on the triangulation in FIG.1. The representation of (4.1) on $\mathcal{H}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ can be constructed as the following: Firstly, we relate $\bm{X},\bm{Y}$ to $\bm{Z}_{1},\bm{Z}_{5}$ by

-\bm{X}+i\pi=\bm{Z}_{1},\qquad-2\bm{Y}+i\pi=\bm{Z}_{5},\quad\text{i.e.}\quad\bm{z}_{1}=-\bm{x}^{-1},\qquad\bm{z}_{5}=-\bm{y}^{-2}.

where the representations of $\bm{x},\bm{y}$ are the same as the above.

\displaystyle\bm{y}=\exp\left[\frac{2\pi i}{k}(-ib\bm{\mu}-\bm{m})\right],\qquad\bm{x}=\exp\left[\frac{2\pi i}{k}(-ib\bm{\nu}-\bm{n})\right].

For the triangulation in FIG.1, the center of the algebra is given by $\lambda_{a}^{2}=e^{2L_{a}}$ , where

	$\displaystyle-L_{1}$	$\displaystyle=$	$\displaystyle\frac{1}{2}\left(\bm{Z}_{4}+\bm{Z}_{6}-2\pi i\right),\qquad-L_{2}=\frac{1}{2}\left(\bm{Z}_{1}+\bm{Z}_{3}+\bm{Z}_{5}+\bm{Z}_{6}-4\pi i\right),$
	$\displaystyle-L_{3}$	$\displaystyle=$	$\displaystyle\frac{1}{2}\left(\bm{Z}_{2}+\bm{Z}_{5}-2\pi i\right),\qquad-L_{4}=-\frac{1}{2}\left(\bm{Z}_{1}+\bm{Z}_{2}+\bm{Z}_{3}+\bm{Z}_{4}-4\pi i\right).$		(4.10)

We may express $\bm{Z}_{1},\cdots,\bm{Z}_{6}$ in terms of $\bm{X},\bm{Y},L_{1},\cdots,L_{4}$

$\displaystyle\bm{Z}_{1}$	$\displaystyle=-\bm{X}+i\pi,\qquad\bm{Z}_{2}=-2L_{3}+2\bm{Y}+i\pi,$
$\displaystyle\bm{Z}_{3}$	$\displaystyle=L_{1}-L_{2}+L_{3}+L_{4}+\bm{X}+i\pi,$
$\displaystyle\bm{Z}_{4}$	$\displaystyle=-L_{1}+L_{2}+L_{3}+L_{4}-2\bm{Y}+i\pi,\qquad\bm{Z}_{5}=-2\bm{Y}+i\pi,$
$\displaystyle\bm{Z}_{6}$	$\displaystyle=-L_{1}-L_{2}-L_{3}-L_{4}+2\bm{Y}+i\pi$	(4.11)

We find the representation of all $\bm{z}_{e}$ by

	$\displaystyle\bm{z}_{1}$	$\displaystyle=-\bm{x}^{-1},\qquad\bm{z}_{2}=-\lambda_{3}^{-2}\bm{y}^{2},\qquad\bm{z}_{3}=-\frac{\lambda_{1}\lambda_{3}\lambda_{4}}{\lambda_{2}}\bm{x},$		(4.12)
	$\displaystyle\bm{z}_{4}$	$\displaystyle=-\frac{\lambda_{2}\lambda_{3}\lambda_{4}}{\lambda_{1}}\bm{y}^{-2},\qquad\bm{z}_{5}=-\bm{y}^{-2},\qquad\bm{z}_{6}=-\frac{1}{\lambda_{1}\lambda_{2}\lambda_{3}\lambda_{4}}\bm{y}^{2}.$		(4.13)

$\lambda_{1},\cdots,\lambda_{6}\in\mathbb{C}^{\times}$ are constants labelling the representation, and they relate to the centers of the operators algebra of $\bm{z}_{e}$ , $e=1,\cdots,6$ , by

\displaystyle\bm{z}_{4}\bm{z}_{6}=\lambda_{1}^{-2},\qquad\bm{z}_{1}\bm{z}_{3}\bm{z}_{5}\bm{z}_{6}=\lambda_{2}^{-2},\qquad\bm{z}_{2}\bm{z}_{5}=\lambda_{3}^{-2},\qquad\bm{z}_{1}\bm{z}_{3}\bm{z}_{2}\bm{z}_{4}=\lambda_{4}^{2},

(4.14)

The tilded operator can be defined similarly

	$\displaystyle\tilde{\bm{z}}_{1}$	$\displaystyle=-\tilde{\bm{x}}^{-1},\qquad\tilde{\bm{z}}_{2}=-\tilde{\lambda}_{3}^{-2}\tilde{\bm{y}}^{2},\qquad\tilde{\bm{z}}_{3}=-\frac{\tilde{\lambda}_{1}\tilde{\lambda}_{3}\tilde{\lambda}_{4}}{\tilde{\lambda}_{2}}\tilde{\bm{x}},$		(4.15)
	$\displaystyle\tilde{\bm{z}}_{4}$	$\displaystyle=-\frac{\tilde{\lambda}_{2}\tilde{\lambda}_{3}\tilde{\lambda}_{4}}{\tilde{\lambda}_{1}}\tilde{\bm{y}}^{-2},\qquad\tilde{\bm{z}}_{5}=-\tilde{\bm{y}}^{-2},\qquad\tilde{\bm{z}}_{6}=-\frac{1}{\tilde{\lambda}_{1}\tilde{\lambda}_{2}\tilde{\lambda}_{3}\tilde{\lambda}_{4}}\tilde{\bm{y}}^{2}.$		(4.16)

where $\tilde{x},\tilde{y}$ are represented by

\displaystyle\tilde{\bm{y}}=\exp\left[\frac{2\pi i}{k}(-ib^{-1}\bm{\mu}+\bm{m})\right],\qquad\tilde{\bm{x}}=\exp\left[\frac{2\pi i}{k}(-ib^{-1}\bm{\nu}+\bm{n})\right].

(4.17)

and $\tilde{\lambda}_{1},\cdots,\tilde{\lambda}_{6}\in\mathbb{C}^{\times}$ are also constants and label the representation. We set $\tilde{\lambda}_{a}=\lambda_{a}^{*}$ so that

\displaystyle\bm{z}_{e}^{\dagger}=\tilde{\bm{z}}_{e}

(4.18)

representing the star structure. The above representation on $\mathcal{H}$ of the quantum FG coordinates may be denoted by $\varrho_{\{\lambda,\tilde{\lambda}\}}$ , which is labelled by $\{\lambda,\tilde{\lambda}\}\equiv\{\lambda_{a},\tilde{\lambda}_{a}\}_{a=1}^{4}$ .

In the following, we mainly focus on the case that $k=2N$ is an even number and $N$ is odd. In this case, we may decompose $\mathcal{H}$ into orthogonal subspaces

\displaystyle\mathcal{H}\simeq\mathcal{H}_{+}\oplus\mathcal{H}_{-}

(4.19)

where $\mathcal{H}_{\pm}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{N}$ contains $\phi_{\pm}\in\mathcal{H}_{\pm}$ satisfying

\displaystyle\phi_{\pm}(\mu,m+N)=\pm\phi_{\pm}(\mu,m).

(4.20)

$\mathcal{H}_{\pm}$ is the eigenspace of $e^{\pi i\bm{n}}$ with eigenvalue $\pm 1$ . The quantization of FG coordinates relates to $\bm{x},\bm{y}^{2},\tilde{\bm{x}},\tilde{\bm{y}}^{2}$ , which act irreducibly on each of $\mathcal{H}_{+}$ and $\mathcal{H}_{-}$ . The full $\mathcal{H}$ is not irreducible with respect to the quantization of FG coordinates, although it is irreducible with respect to $\bm{x},\bm{y},\tilde{\bm{x}},\tilde{\bm{y}}$ . Note that the action of $\bm{y}$ or $\tilde{\bm{y}}$ maps from $\mathcal{H}_{+}$ to $\mathcal{H}_{-}$ and vice versa.

4.2 S-cycle trace operator

We define the S-cycle to be the loop enclosing the 1st and 2nd holes (see FIG. 1). Classically, the trace of holonomy along the S-cycle can be written as a function of FG coordinates

	$\displaystyle L_{s}$	$\displaystyle=$	$\displaystyle e^{-\frac{Z_{1}}{2}-\frac{Z_{3}}{2}-\frac{Z_{4}}{2}-\frac{Z_{5}}{2}}-e^{-\frac{Z_{1}}{2}+\frac{Z_{3}}{2}-\frac{Z_{4}}{2}-\frac{Z_{5}}{2}}+e^{-\frac{Z_{1}}{2}+\frac{Z_{4}}{2}+\frac{Z_{3}}{2}-\frac{Z_{5}}{2}}+e^{-\frac{Z_{1}}{2}+\frac{Z_{5}}{2}+\frac{Z_{3}}{2}+\frac{Z_{4}}{2}}$		(4.21)
			$\displaystyle-\,e^{-\frac{Z_{1}}{2}+\frac{Z_{4}}{2}+\frac{Z_{5}}{2}+\frac{Z_{3}}{2}}+e^{\frac{Z_{1}}{2}+\frac{Z_{3}}{2}+\frac{Z_{4}}{2}+\frac{Z_{5}}{2}}.$		(4.21)

This is derived by using the ”snake rule” outlined in Appendix B. In the language of Teichmüeller theory, $L_{s}$ is the complexification of the FN length of the S-cycle, along which the 4-holed sphere is cut into two pairs of pants.

The quantization of the S-cycle trace by $Z_{a}\to\bm{Z}_{a}$ and inserting (4.1) leads to the operator

	$\displaystyle\bm{L}_{s}$	$\displaystyle=$	$\displaystyle e^{-2\bm{Y}_{s}}+e^{2\bm{Y}_{s}}+e^{L_{1}-L_{2}+L_{3}+L_{4}+2\bm{Y}_{s}+\bm{X}}+e^{L_{1}-L_{2}+\bm{X}}+e^{L_{3}+L_{4}+\bm{X}}+e^{-2\bm{Y}_{s}+\bm{X}},$		(4.22)
		$\displaystyle=$	$\displaystyle e^{-2\bm{Y}_{s}}+e^{2\bm{Y}_{s}}+e^{L_{3}+L_{4}}e^{-2\bm{Y}}{\bf q}^{-1}\left(e^{L_{1}-L_{2}-L_{3}-L_{4}}{\bf q}e^{2\bm{Y}}+1\right)\left(1+e^{2\bm{Y}}{\bf q}\right)e^{\bm{X}},$		(4.22)

where $2\bm{Y}_{s}=2\bm{Y}-L_{3}-L_{4}$ . Its tilded counter-part $\tilde{\bm{L}}_{s}=\bm{L}_{s}^{\dagger}$ is obtained analogously

\displaystyle\tilde{\bm{L}}_{s}

\displaystyle=

\displaystyle e^{-2\tilde{\bm{Y}}_{s}}+e^{2\tilde{\bm{Y}}_{s}}+e^{\tilde{L}_{3}+\tilde{L}_{4}}e^{-2\tilde{\bm{Y}}}{\tilde{\mathbf{q}}}^{-1}\left(e^{\tilde{L}_{1}-\tilde{L}_{2}-\tilde{L}_{3}-\tilde{L}_{4}}{\tilde{\mathbf{q}}}e^{2\tilde{\bm{Y}}}+1\right)\left(1+e^{2\tilde{\bm{Y}}}{\tilde{\mathbf{q}}}\right)e^{\tilde{\bm{X}}}.

(4.23)

The trace operator $\bm{L}_{s}$ can be simplified by the unitary transformation

\displaystyle\bm{U}^{\prime}_{s}=\varphi\left(y^{2}e^{L_{1}-L_{2}-L_{3}-L_{4}},\tilde{y}^{2}e^{\tilde{L}_{1}-\tilde{L}_{2}-\tilde{L}_{3}-\tilde{L}_{4}}\right)\varphi\left(y^{2},\tilde{y}^{2}\right).

(4.24)

Indeed, the recursion relation of the quantum dilogarithm implies the following relation:

\displaystyle\bm{U}^{\prime}_{s}\left[e^{L_{3}+L_{4}}e^{-2\bm{Y}}{\bf q}^{-1}\left(e^{L_{1}-L_{2}-L_{3}-L_{4}}{\bf q}e^{2\bm{Y}}+1\right)\left(1+e^{2\bm{Y}}{\bf q}\right)e^{\bm{X}}\right]\bm{U}_{s}^{\prime-1}=e^{-2\bm{Y}_{s}+\bm{X}}.

(4.25)

Thereore, we obtain

\displaystyle\bm{U}^{\prime}_{s}\bm{L}_{s}\bm{U}_{s}^{\prime-1}=e^{-2\bm{Y}_{s}}+e^{2\bm{Y}_{s}}+e^{-2\bm{Y}_{s}+\bm{X}}.

(4.26)

The operator can be further simplified by the Weil representation $\bm{T}$ of the T-type symplectic transformation ⁵⁵5We refer to [12] for a general discussion of T-type symplectic transformation and its Weil representation as unitary operator.

\displaystyle\left(\begin{array}[]{c}Y\\ X\end{array}\right)\to\begin{pmatrix}1&0\\ -2&1\end{pmatrix}\left(\begin{array}[]{c}Y\\ X\end{array}\right),\qquad\bm{T}=e^{\frac{2\pi i}{k}\left(\bm{\mu}^{2}-\bm{m}^{2}\right)}.

(4.31)

The unitary operator $\bm{T}$ satisfies

\displaystyle\bm{T}e^{\bm{X}-2\bm{Y}}\bm{T}^{-1}=e^{\bm{X}}.

(4.32)

As a result, we obtain

\displaystyle\bm{L}_{s}^{\prime}=\bm{U}_{s}\bm{L}_{s}\bm{U}_{s}^{-1}=e^{-2\bm{Y}_{s}}+e^{2\bm{Y}_{s}}+e^{\bm{X}_{s}},\qquad\bm{U}_{s}=\bm{U}_{s}^{\prime}\bm{T},

(4.33)

where $\bm{X}_{s}=\bm{X}+L_{3}+L_{4}$ . A similar computation shows that $\bm{U}_{s}$ also simplify $\tilde{\bm{L}}_{s}$ :

\displaystyle\tilde{\bm{L}}_{s}^{\prime}=\bm{U}_{s}\tilde{\bm{L}}_{s}\bm{U}_{s}^{-1}=e^{-2\tilde{\bm{Y}}_{s}}+e^{2\tilde{\bm{Y}}_{s}}+e^{\tilde{\bm{X}}_{s}}.

(4.34)

$\bm{L}_{s},\tilde{\bm{L}}_{s}$ can relate to the Casimir operator $\mathcal{Q}_{1}^{\prime\prime},\tilde{\mathcal{Q}}_{1}^{\prime\prime}$ in the representation theory of quantum group (recall (3.17) and (3.18)) by unitary transformations. Indeed, we further make a Fourier transform

\mathcal{F}f(\mu,m)=\frac{1}{k}\sum_{m^{\prime}\in\mathbb{Z}/k\mathbb{Z}}\int d\mu^{\prime}\>e^{\frac{2\pi i}{k}\left(\mu\mu^{\prime}-mm^{\prime}\right)}{f}(\mu^{\prime},m^{\prime}),\qquad\forall\,f\in\mathfrak{D},

such that

\displaystyle\mathcal{F}^{-1}e^{\bm{Y}}\mathcal{F}=e^{\bm{X}},\qquad\mathcal{F}^{-1}e^{\bm{X}}\mathcal{F}=e^{-\bm{Y}}.

(4.35)

Then

\displaystyle\mathcal{F}^{-1}\bm{L}_{s}^{\prime}\mathcal{F}=e^{-2{\bm{X}}+L_{3}+L_{4}}+e^{2{\bm{X}}-L_{3}-L_{4}}+e^{-{\bm{Y}}+L_{3}+L_{4}}.

(4.36)

Here we assume both $e^{L_{3}},e^{L_{4}}$ can be parametrized by

\displaystyle e^{L_{3}}=\exp\left[\frac{2\pi i}{k}\left(-ib\mu_{3}-m_{3}\right)\right],\qquad e^{L_{4}}=\exp\left[\frac{2\pi i}{k}\left(-ib\mu_{4}-m_{4}\right)\right]

(4.37)

where $\mu_{3},\mu_{4}\in\mathbb{R}$ and $m_{3},m_{4}\in\mathbb{Z}$ . For this paper, the purpose of this assumption is to simplify some analysis in the following. However, when we consider the quantization of $\mathrm{SL}(2,\mathbb{C})$ Chern-Simons theory on 3-manifold whose boundary is a closed 2-surface containing the 4-holed sphere as a part of the geodesic boundary (see e.g. [22, 18]), $\{L_{a}\}_{a=1}^{4}$ are part of the Darboux coordinate of the phase space, so $\{e^{L_{a}}\}_{a=1}^{4}$ should be quantized in the same way as $e^{\bm{Y}}$ .

We apply the unitary shift operator

\displaystyle\mathcal{S}_{34}=\exp\left[-\frac{2\pi i}{k}\left((\mu_{3}+\mu_{4})\bm{\nu}-(m_{3}+m_{4})\bm{n}\right)\right]

(4.38)

which gives

\displaystyle\mathcal{S}_{34}e^{-{\bm{Y}}+L_{3}+L_{4}}\mathcal{S}_{34}^{-1}=e^{-{\bm{Y}}}

(4.39)

similar to (3.16). We obtain

\displaystyle\mathcal{S}_{34}\mathcal{F}^{-1}\bm{L}_{s}^{\prime}\mathcal{F}\mathcal{S}_{34}^{-1}=e^{-2{\bm{X}}+L_{3}+L_{4}}+e^{2{\bm{X}}-L_{3}-L_{4}}+e^{-{\bm{Y}}},

(4.40)

which relates to $\mathcal{Q}_{1}^{\prime\prime}$ by identifying $L_{3}+L_{4}$ here to $L_{2}$ in $\mathcal{Q}_{1}^{\prime\prime}$ . The relation between $\tilde{\bm{L}}_{s}^{\prime}$ and $\tilde{\mathcal{Q}}_{1}^{\prime\prime}$ is obtained analogously.

If we further assume $m_{3}+m_{4}\in 2\mathbb{Z}$ , we can use another unitary shift operator

\displaystyle\mathcal{D}_{34}=\exp\left[-\frac{2\pi i}{k}\left(\frac{\mu_{3}+\mu_{4}}{2}\bm{\mu}-\frac{m_{3}+m_{4}}{2}\bm{m}\right)\right]

(4.41)

to give

\displaystyle\mathcal{D}_{34}^{-1}e^{2\bm{X}-L_{3}-L_{4}}\mathcal{D}_{34}=e^{2\bm{X}},\qquad\mathcal{D}_{34}^{-1}e^{-2\bm{X}+L_{3}+L_{4}}\mathcal{D}_{34}=e^{-2\bm{X}}.

(4.42)

As a result, the sequence of unitary transformation gives a relatively simple expression of S-cycle trace operator

	$\displaystyle\bm{L}_{s}^{\prime\prime}=\mathcal{D}_{34}^{-1}\mathcal{S}_{34}\mathcal{F}^{-1}\bm{L}_{s}^{\prime}\mathcal{F}\mathcal{S}_{34}^{-1}\mathcal{D}_{34}=e^{-2{\bm{X}}}+e^{2{\bm{X}}}+e^{-{\bm{Y}}}$		(4.43)
	$\displaystyle\tilde{\bm{L}}_{s}^{\prime\prime}=\mathcal{D}_{34}^{-1}\mathcal{S}_{34}\mathcal{F}^{-1}\tilde{\bm{L}}_{s}^{\prime}\mathcal{F}\mathcal{S}_{34}^{-1}\mathcal{D}_{34}=e^{-2{\tilde{\bm{X}}}}+e^{2\tilde{\bm{X}}}+e^{-\tilde{\bm{Y}}}.$		(4.44)

In summary, we have made a sequence of unitary transformations

\displaystyle\mathfrak{U}_{s}=\mathcal{D}_{34}^{-1}\mathcal{S}_{34}\mathcal{F}^{-1}\bm{U}_{s}

(4.45)

so that

\displaystyle\bm{L}_{s}^{\prime\prime}=\mathfrak{U}_{s}\bm{L}_{s}\mathfrak{U}_{s}^{-1},\qquad\tilde{\bm{L}}_{s}^{\prime\prime}=\mathfrak{U}_{s}\tilde{\bm{L}}_{s}\mathfrak{U}_{s}^{-1}.

(4.46)

4.3 T-cycle trace operator

The operator quantizing the trace of T-cycle enclosing the 2nd and 3rd holes is given by

	$\displaystyle\bm{L}_{t}$	$\displaystyle=$	$\displaystyle e^{-2\bm{Y}_{t}}+e^{2\bm{Y}_{t}}+e^{-L_{1}+L_{2}-L_{3}-L_{4}-\bm{X}+2\bm{Y}_{t}}+e^{-L_{1}-L_{4}-\bm{X}}+e^{L_{2}-L_{3}-\bm{X}}+e^{-\bm{X}-2\bm{Y}_{t}}$		(4.47)
		$\displaystyle=$	$\displaystyle e^{-2\bm{Y}_{t}}+e^{2\bm{Y}_{t}}+e^{L_{2}+L_{3}}{\bf q}e^{-2\bm{Y}}\left(1+e^{-2L_{3}}e^{2\bm{Y}}{\bf q}^{-1}\right)\left(1+e^{-\left(L_{1}+L_{2}+L_{3}+L_{4}\right)}e^{2\bm{Y}}{\bf q}^{-1}\right)e^{-\bm{X}}$		(4.47)

where $2\bm{Y}_{t}=2\bm{Y}-L_{2}-L_{3}$ . We obtain the tilded operator by $\tilde{\bm{L}}_{t}=\bm{L}_{t}^{\dagger}$ . We apply the unitary transformation

\displaystyle\bm{U}^{\prime}_{t}\bm{L}_{t}\bm{U}^{\prime-1}_{t}

\displaystyle=

\displaystyle e^{-2\bm{Y}+L_{2}+L_{3}}+e^{2\bm{Y}-L_{2}-L_{3}}+e^{-2\bm{Y}-\bm{X}+L_{2}+L_{3}},

(4.48)

where

\displaystyle\bm{U}^{\prime}_{t}

\displaystyle=

\displaystyle\varphi\left(e^{-\left(L_{1}+L_{2}+L_{3}+L_{4}\right)}y^{2},e^{-\left(\tilde{L}_{1}+\tilde{L}_{2}+\tilde{L}_{3}+\tilde{L}_{4}\right)}\tilde{y}^{2}\right)^{-1}\varphi\left(e^{-2L_{3}}y^{2},e^{-2\tilde{L}_{3}}\tilde{y}^{2}\right)^{-1}.

(4.49)

The further simplification can be made by the Weil transformation representing the following symplectic transformation

\displaystyle\left(\begin{array}[]{c}Y\\ X\end{array}\right)\to\begin{pmatrix}-1&0\\ -2&-1\end{pmatrix}\left(\begin{array}[]{c}Y\\ X\end{array}\right)=\begin{pmatrix}1&0\\ 2&1\end{pmatrix}\begin{pmatrix}-1&0\\ 0&-1\end{pmatrix}\left(\begin{array}[]{c}Y\\ X\end{array}\right)

(4.56)

We define the unitary operator $\bm{V}$ by $\bm{V}f(\mu,m)=f(-\mu,-m)$ and obtain

\displaystyle\bm{L}_{t}^{\prime}=\bm{U}_{t}\bm{L}_{t}\bm{U}_{t}^{-1}=e^{-2\bm{Y}-L_{2}-L_{3}}+e^{2\bm{Y}+L_{2}+L_{3}}+e^{\bm{X}+L_{2}+L_{3}},\qquad\bm{U}_{t}=\bm{T}^{-1}\bm{V}\bm{U}^{\prime}_{t}.

(4.57)

Similar to $\bm{L}_{s}$ , we further make the Fourier transform:

\displaystyle\mathcal{F}^{-1}\bm{L}_{t}^{\prime}\mathcal{F}=e^{-2{\bm{X}}-L_{2}-L_{3}}+e^{2{\bm{X}}+L_{2}+L_{3}}+e^{-{\bm{Y}}+L_{2}+L_{3}}.

(4.58)

If both $e^{L_{2}},e^{L_{3}}$ can be parametrized by

\displaystyle e^{L_{2}}=\exp\left[\frac{2\pi i}{k}\left(-ib\mu_{2}-m_{2}\right)\right],\qquad e^{L_{3}}=\exp\left[\frac{2\pi i}{k}\left(-ib\mu_{3}-m_{3}\right)\right]

(4.59)

where $\mu_{2},\mu_{3}\in\mathbb{R}$ and $m_{2},m_{3}\in\mathbb{Z}$ . Apply the shift operator

\displaystyle\mathcal{S}_{23}=\exp\left[-\frac{2\pi i}{k}\left((\mu_{2}+\mu_{3})\bm{\nu}-(m_{2}+m_{3})\bm{n}\right)\right]

(4.60)

which gives

\displaystyle\mathcal{S}_{23}\mathcal{F}^{-1}\bm{L}_{t}^{\prime}\mathcal{F}\mathcal{S}_{23}^{-1}=e^{-2{\bm{X}}-L_{2}-L_{3}}+e^{2{\bm{X}}+L_{2}+L_{3}}+e^{-{\bm{Y}}},

(4.61)

which relates to $\mathcal{Q}_{1}^{\prime\prime}$ by identifying $-L_{2}-L_{3}$ here to $L_{2}$ in $\mathcal{Q}_{1}^{\prime\prime}$ .

If we assume $m_{2}+m_{3}\in 2\mathbb{Z}$ , we can define another shift operator

\displaystyle\mathcal{D}_{23}=\exp\left[-\frac{2\pi i}{k}\left(\frac{\mu_{2}+\mu_{3}}{2}\bm{\mu}-\frac{m_{2}+m_{3}}{2}\bm{m}\right)\right]

(4.62)

which gives

\displaystyle\mathcal{D}_{23}e^{2\bm{X}+L_{2}+L_{3}}\mathcal{D}_{23}^{-1}=e^{2\bm{X}},\qquad\mathcal{D}_{23}e^{-2\bm{X}-L_{2}-L_{3}}\mathcal{D}_{23}^{-1}=e^{-2\bm{X}}.

(4.63)

As a result, the sequence of unitary transformation gives same expression as (4.43) for the S-cycle trace operator

	$\displaystyle\bm{L}_{t}^{\prime\prime}=\mathcal{D}_{23}\mathcal{S}_{23}\mathcal{F}^{-1}\bm{L}_{t}^{\prime}\mathcal{F}\mathcal{S}_{23}^{-1}\mathcal{D}_{23}=e^{-2{\bm{X}}}+e^{2{\bm{X}}}+e^{-{\bm{Y}}}=\bm{L}_{s}^{\prime\prime}$		(4.64)
	$\displaystyle\tilde{\bm{L}}_{t}^{\prime\prime}=\mathcal{D}_{23}^{-1}\mathcal{S}_{23}\mathcal{F}^{-1}\tilde{\bm{L}}_{t}^{\prime}\mathcal{F}\mathcal{S}_{23}^{-1}\mathcal{D}_{23}^{-1}=e^{-2{\tilde{\bm{X}}}}+e^{2\tilde{\bm{X}}}+e^{-\tilde{\bm{Y}}}=\tilde{\bm{L}}_{s}^{\prime\prime}$		(4.65)

We denote by

\displaystyle\mathfrak{U}_{t}=\mathcal{D}_{23}\mathcal{S}_{23}\mathcal{F}^{-1}\bm{U}_{t},

(4.66)

so that

\displaystyle\bm{L}_{t}^{\prime\prime}=\mathfrak{U}_{t}\bm{L}_{t}\mathfrak{U}_{t}^{-1},\qquad\tilde{\bm{L}}_{t}^{\prime\prime}=\mathfrak{U}_{t}\tilde{\bm{L}}_{t}\mathfrak{U}_{t}^{-1}.

(4.67)

Then $\bm{L}_{t}^{\prime\prime}=\bm{L}_{s}^{\prime\prime}$ , $\tilde{\bm{L}}_{t}^{\prime\prime}=\tilde{\bm{L}}_{s}^{\prime\prime}$ implies that there is a unitary transformation relating $(\bm{L}_{t},\tilde{\bm{L}}_{t})$ and $(\bm{L}_{s},\tilde{\bm{L}}_{s})$ .

\displaystyle\bm{L}_{s}=\mathfrak{U}_{s}^{-1}\mathfrak{U}_{t}\bm{L}_{t}\mathfrak{U}_{t}^{-1}\mathfrak{U}_{s},\qquad\tilde{\bm{L}}_{s}=\mathfrak{U}_{s}^{-1}\mathfrak{U}_{t}\tilde{\bm{L}}_{t}\mathfrak{U}_{t}^{-1}\mathfrak{U}_{s}.

(4.68)

Finally, an additional Fourier transform gives the final expression of the trace operator that is studied extensively in the next section

	$\displaystyle\bm{L}=\mathcal{F}\bm{L}_{s}^{\prime\prime}\mathcal{F}^{-1}=e^{-2{\bm{Y}}}+e^{2{\bm{Y}}}+e^{{\bm{X}}},$		(4.69)
	$\displaystyle\tilde{\bm{L}}=\mathcal{F}\tilde{\bm{L}}_{s}^{\prime\prime}\mathcal{F}^{-1}=e^{-2\tilde{\bm{Y}}}+e^{2\tilde{\bm{Y}}}+e^{\tilde{\bm{X}}}.$		(4.70)

The operators $\bm{L},\tilde{\bm{L}}$ are generalizations of of the Dehn twist operator of quantum Teichmüller theory studied in [1, 3, 5]. The unitary transformation relating $(\bm{L}_{s},\tilde{\bm{L}}_{s})$ and $(\bm{L}_{t},\tilde{\bm{L}}_{t})$ can be seen as realizing the A-move of Moore-Seiberg groupoid on $\mathcal{H}$ , as a generalization from the result from quantum Teichmüller theory in [6].

The following S-cycle and T-cycle trace operators and their tilded partners are also useful in the following discussion

	$\displaystyle\bm{L}_{s}^{(aux)}=e^{-2{\bm{Y}}+L_{3}+L_{4}}+e^{2{\bm{Y}}-L_{3}-L_{4}}+e^{{\bm{X}}},$		(4.71)
	$\displaystyle\bm{L}_{t}^{(aux)}=e^{-2{\bm{Y}}-L_{2}-L_{3}}+e^{2{\bm{Y}}+L_{2}+L_{3}}+e^{{\bm{X}}}.$		(4.72)

They are Fourier transforms of (4.40) and (4.61). The derivation of these operator does not rely on the assumption $m_{3}+m_{4}\in 2\mathbb{Z}$ or $m_{2}+m_{3}\in 2\mathbb{Z}$ , in contrast to $\bm{L}$ .

5 Eigenstates of the trace operators

The unbounded operator $\bm{L}$ is defined on the domain $\mathfrak{D}(\bm{L})\subset\mathcal{H}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ . Any functions $f(\mu,m)$ in $\mathfrak{D}(\bm{L})$ should satisfy

e^{\frac{4\pi}{k}b\mu}f(\mu,m)\in L^{2}(\mathbb{R}),\qquad e^{-\frac{4\pi}{k}b\mu}f(\mu,m)\in L^{2}(\mathbb{R}),\qquad f(\mu+ib,m)\in L^{2}(\mathbb{R}),\qquad\forall m\in\mathbb{Z}/k\mathbb{Z}.

Recall that $\mathrm{Re}(b)>0$ , the conditions are satisfied for $f(\mu,m)$ decaying as fast as $e^{\mp\frac{4\pi}{k}\left[\mathrm{Re}(b)+\epsilon\right]\mu}$ ( $\epsilon>0$ ) when $\mu\to\pm\infty$ and holomorpic in the strip $\left\{\mu\in\mathbb{C}\mid\mathrm{Im}(\mu)\in\left[0,\mathrm{Re}(b)\right]\right\}$ satisfying $f(\mu+ib,m)\in L^{2}(\mathbb{R})$ . The Hermite functions $e^{-\mu^{2}/2}H_{n}(\mu)$ , $n=1,\cdots,\infty$ satisfy the requirements and make a densed domain in $L^{2}(\mathbb{R})$ . Therefore the domain $\mathfrak{D}(\bm{L})$ is dense in $L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ . Similarly, the adjoint $\tilde{\bm{L}}=\bm{L}^{\dagger}$ is also densely defined on $L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ . ${\bm{L}}$ and its adjoint $\tilde{\bm{L}}$ are commutative.

We would like to solve the eigen-equations:

\displaystyle\bm{L}\alpha_{r}(\mu,m)=\ell(r)\alpha_{r}(\mu,m),\qquad\tilde{\bm{L}}\alpha_{r}(\mu,m)=\ell(r)^{*}\alpha_{r}(\mu,m),\qquad\ell(r)\in\mathbb{C}.

for some eigenstates $\alpha_{r}$ . We can always make the following parametrization of any $\ell\in\mathbb{C}$ ,

\ell=r+r^{-1},

where $r\in\mathbb{C}^{\times}$ is determined by $\ell$ up to a “Weyl refection” $r\to r^{-1}$ .

We consider the following ansatz

\displaystyle\alpha_{r}(\mu,m)=\frac{\varphi\left(-{\bf q}^{-1}y^{2}r,-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{r}\right)}{\varphi\left(-{\bf q}y^{-2}r,-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{r}\right)}f_{r}(\mu,m),

(5.1)

where $r,\tilde{r}$ are parametrized as the following

\displaystyle r=\exp\left[\frac{2\pi i}{k}(-ib\mu_{r}-m_{r})\right],\qquad\tilde{r}=\exp\left[\frac{2\pi i}{k}(-ib^{-1}\mu_{r}+m_{r})\right]\qquad\mu_{r}\in\mathbb{R},\quad m_{r}\in\mathbb{Z}/k\mathbb{Z}.

(5.2)

The eigen-equations implies the following recursion relations of $f_{r}(\mu,m)$ :

\displaystyle rf_{r}(\mu+ib,m-1)=f_{r}(\mu,m),\qquad\tilde{r}f_{r}(\mu+ib^{-1},m+1)=f_{r}(\mu,m),

(5.3)

and we find that

\displaystyle f_{r}(\mu,m)=e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m_{r}m\right)},

(5.4)

is a solution for any $r$ . Note that in the above, we have restrict $r$ to satisfy $m_{r}\in\mathbb{Z}/k\mathbb{Z}$ so that $f_{r}(\mu,m)$ is single-valued. As a result, up to a constant rescaling independent of $\mu,m$ , the following function

\displaystyle\alpha_{r}(\mu,m)=e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m_{r}m\right)}\frac{\varphi\left(-{\bf q}^{-1}y^{2}r,-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{r}\right)}{\varphi\left(-{\bf q}y^{-2}r,-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{r}\right)}

(5.5)

is the eigenstate of $\bm{L}$ and $\tilde{\bm{L}}$ corresponding to the eigenvalues $r+r^{-1}$ and $\tilde{r}+\tilde{r}^{-1}$ .

A similar computation shows that the eignstates of $\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s}$ and $\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t}$ are given respectively by

	$\displaystyle\alpha_{r}^{(s)}(\mu,m)$	$\displaystyle=$	$\displaystyle e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m_{r}m\right)}\frac{\varphi\left(-{\bf q}^{-1}y^{2}\lambda_{3}^{-1}\lambda_{4}^{-1}r,-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{\lambda}_{3}^{-1}\tilde{\lambda}_{4}^{-1}\tilde{r}\right)}{\varphi\left(-{\bf q}y^{-2}\lambda_{3}\lambda_{4}r,-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{\lambda}_{3}\tilde{\lambda}_{4}\tilde{r}\right)}\ ,$		(5.6)
	$\displaystyle\alpha_{r}^{(t)}(\mu,m)$	$\displaystyle=$	$\displaystyle e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m_{r}m\right)}\frac{\varphi\left(-{\bf q}^{-1}y^{2}\lambda_{2}\lambda_{3}r,-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{\lambda}_{2}\tilde{\lambda}_{3}\tilde{r}\right)}{\varphi\left(-{\bf q}y^{-2}\lambda_{2}^{-1}\lambda_{3}^{-1}r,-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{\lambda}_{2}^{-1}\tilde{\lambda}_{3}^{-1}\tilde{r}\right)}\ .$		(5.7)

Theorem 5.1.

For $k=2N$ with odd $N$ , the spectral decomposition of $(\bm{L},\tilde{\bm{L}})$ , $(\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s})$ , or $(\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t})$ gives the following direct integral representation

\displaystyle\mathcal{H}\simeq\sum_{m_{r}\in\mathbb{Z}/k\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}}.

(5.8)

where each $\mathcal{H}_{\mu_{r},m_{r}}$ is 1-dimensional, and

\displaystyle\rho(\mu_{r},m_{r})

\displaystyle=

\displaystyle N^{2}\left[\sin\left(\frac{\pi}{N}(ib\mu_{r}+m_{r})\right)\sin\left(\frac{\pi}{N}(-ib^{-1}\mu_{r}+m_{r})\right)\right]^{-1}

(5.9)

Any $f\in\mathcal{H}$ can be represented by $f(\mu_{r},m_{r})$ where $\mu_{r}\in\mathbb{R}_{+}$ and $m_{r}\in\mathbb{Z}/k\mathbb{Z}$ , such that $\bm{L},\tilde{\bm{L}}$ are represented as the multiplication operators

\displaystyle\bm{L}f(\mu_{r},m_{r})=\ell(r)f(\mu_{r},m_{r}),\qquad\tilde{\bm{L}}f(\mu_{r},m_{r})=\ell(r)^{*}f(\mu_{r},m_{r}).

(5.10)

The same holds for $(\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s})$ or $(\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t})$ . For any pair of states $f,f^{\prime}\in\mathcal{H}$

\displaystyle\langle f\mid f^{\prime}\rangle=\sum_{m_{r}\in\mathbb{Z}/k\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}f(\mu_{r},m_{r})^{*}f^{\prime}(\mu_{r},m_{r}).

(5.11)

We call this direction integral representation the FN representation of $S$ -cycle or $T$ -cycle, since the corresponding trace operator is diagonalized.

For $k=2N$ with odd $N$ , we have the decomposition $\mathcal{H}=\mathcal{H}_{+}\oplus\mathcal{H}_{-}$ , where $f_{\pm}(\mu,m+N)=\pm f_{\pm}(\mu,m)$ for $f_{\pm}\in\mathcal{H}_{\pm}$ . On each of $\mathcal{H}_{\pm}$ , $\bm{x},\bm{y}^{2}$ are represented as

	$\displaystyle\bm{y}^{2}f_{\pm}(\mu,m)=e^{\frac{2\pi i}{N}(-ib\mu-m)}f_{\pm}(\mu,m),$		$\displaystyle\quad\bm{x}f_{\pm}(\mu,m)=f_{\pm}(\mu+ib,m-1),$
	$\displaystyle\tilde{\bm{y}}^{2}f_{\pm}(\mu,m)=e^{\frac{2\pi i}{N}(-ib^{-1}\mu+m)}f_{\pm}(\mu,m),$		$\displaystyle\quad\tilde{\bm{x}}f_{\pm}(\mu,m)=f_{\pm}(\mu+ib^{-1},m+1)$		(5.12)

where $f_{\pm}\in\mathcal{H}_{\pm}$ respectively and $m\in\mathbb{Z}/N\mathbb{Z}$ . $\bm{L},\tilde{\bm{L}}$ leave each of $\mathcal{H}_{+},\mathcal{H}_{-}$ invariant. Correspondingly, the eigenstate $\alpha_{r}$ satisfy

\displaystyle\alpha_{r}(\mu,m+N)=(-1)^{m_{r}}\alpha_{r}(\mu,m),

(5.13)

i.e. it is $N$ -periodic as $f_{+}$ (anti-periodic as $f_{-}$ ) when $m_{r}$ is even (odd).

$\mathcal{H}_{\pm}$ as subspaces of $\mathcal{H}$ have the inner products inherited from $\mathcal{H}$ . Since $\mathcal{H}_{\pm}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{N}$ It is also helpful to consider a different inner product on $\mathcal{H}_{\pm}$ :

\displaystyle\langle f_{\pm}\mid f^{\prime}_{\pm}\rangle_{N}=\sum_{m\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}\mu\,f_{\pm}(\mu,m)^{*}f^{\prime}_{\pm}(\mu,m)=\frac{1}{2}\langle f_{\pm}\mid f^{\prime}_{\pm}\rangle.

(5.14)

Since all $\bm{L},\tilde{\bm{L}}$ , $(\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s})$ , and $(\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t})$ leave each of $\mathcal{H}_{+},\mathcal{H}_{-}$ invariant, we prove Theorem 5.1 by studying the spectral decompostion in $\mathcal{H}_{+}$ and $\mathcal{H}_{-}$ separately. The following proof mainly focuses on the spectral decomposition of $\bm{L},\tilde{\bm{L}}$ . The proof for $\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s}$ and $\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t}$ can be obtained analogously.

5.1 Periodic states

We firstly restrict to the subset of eigenstates $\alpha_{r}$ with even $m_{r}$ . In this case, we can express $\alpha_{r}$ in terms of $\gamma(x,n)={\rm D}_{b}(-x,n)$ , where ${\rm D}_{b}$ is the quantum dilogarithm function studied in [11, 10] (see Appendix A for some useful properties):

	$\displaystyle\gamma(-x,n)$	$\displaystyle=$	$\displaystyle{\rm D}_{b}(x,n)=\prod_{j=0}^{\infty}\frac{1-{\bf q}^{2j+1}\exp\left[\frac{2\pi i}{N}\left(-ibx\sqrt{N}+n\right)\right]}{1-\tilde{{\bf q}}^{-2j-1}\exp\left[\frac{2\pi i}{N}\left(-ib^{-1}x\sqrt{N}-n\right)\right]},$		(5.15)
	$\displaystyle{\bf q}$	$\displaystyle=$	$\displaystyle e^{\frac{\pi i}{N}(1+b^{2})},\qquad\tilde{{\bf q}}=e^{\frac{\pi i}{N}(1+b^{-2})},$		(5.16)

and $\mathrm{D}_{b}$ relates to $\varphi$ by

\displaystyle\varphi\left(-y^{2},-\tilde{y}^{2}\right)=\mathrm{D}_{b}\left(\frac{\mu}{\sqrt{N}},-m\right)^{-1}=\gamma\left(-\frac{\mu}{\sqrt{N}},-m\right)^{-1}.

(5.17)

The expression of $\alpha_{r}$ is given by

\displaystyle\alpha_{r}(\mu,m)=e^{-\frac{\pi i}{N}\left[m_{r}m-\mu_{r}\mu\right]}\frac{\gamma\left(-\frac{\mu_{r}/2-\mu+c_{b}}{\sqrt{N}},m-m_{r}/2\right)}{\gamma\left(-\frac{\mu_{r}/2+\mu-c_{b}}{\sqrt{N}},-m-m_{r}/2\right)},\qquad c_{b}=\frac{i}{2}(b+b^{-1}).

(5.18)

$\alpha_{r}$ has poles along the real $\mu$ axis, so we propose a regularization by shifting $\mu\to\mu+i\epsilon\sqrt{N}$ with $\epsilon>0$ inside $\gamma$ . Moreover, if we multiply $\alpha_{r}$ by a factor $\beta_{r}$ independent of $\mu,m$

\displaystyle\psi_{r}=\beta_{r}\alpha_{r},\qquad\beta_{r}=\exp\left(-\frac{i\pi c_{b}^{2}}{3N}-\frac{i\pi c_{b}\mu_{r}}{N}+\frac{i\pi m_{r}}{2}+\frac{i\pi\mu_{r}^{2}}{4N}-\frac{i\pi N}{6}\right),

(5.19)

$\psi_{r}$ is manifestly invariant under the Weyl reflection $r\to r^{-1}$ (recall that the eigenvalue is invariant under the reflection ):

\displaystyle\psi_{r}=\psi_{r^{-1}}.

(5.20)

Indeed, we introduce some short-hand notations ⁶⁶6These notations are inspired by [7].

\displaystyle\omega=\frac{i}{2b\sqrt{N}},\quad\omega^{\prime}=\frac{ib}{2\sqrt{N}},\quad\omega^{\prime\prime}=\frac{c_{b}}{\sqrt{N}},\quad x=\frac{\mu}{\sqrt{N}},\quad\lambda=\frac{\mu_{r}}{2\sqrt{N}}.

(5.21)

and apply the inverse relation $\gamma(x,n)\gamma(-x,-n)=\exp(-\frac{i\pi n^{2}}{N}-i\pi n-\frac{i\pi N}{6}+i\pi x^{2}-\frac{1}{3}i\pi\omega^{\prime\prime}{}^{2})$ to $\alpha_{r}$ , and we obtain

	$\displaystyle\psi_{r}(\mu,m)$	$\displaystyle=$	$\displaystyle e^{\frac{i\pi m^{2}}{N}+\frac{i\pi m_{r}^{2}}{4N}-i\pi m-i\pi\left(x+i\epsilon-\omega^{\prime\prime}\right)^{2}}$		(5.22)
			$\displaystyle\gamma\left(-\lambda+x-\omega^{\prime\prime}+i\epsilon,m-\frac{m_{r}}{2}\right)\gamma\left(\lambda+x-\omega^{\prime\prime}+i\epsilon,m+\frac{m_{r}}{2}\right)$		(5.22)

which is manifestly invariant under $(\lambda,m_{r})\to(-\lambda,-m_{r})$ ⁷⁷7A similar computation re-scales $\alpha_{r}^{(s)},\alpha_{r}^{(t)}$ to $\psi_{r}^{(s)},\psi_{r}^{(t)}$ , where $\displaystyle\psi_{r}^{(s)}$ $\displaystyle=$ $\displaystyle e^{\frac{i\pi m_{r}^{2}}{4N}+\frac{i\pi\left(m-\frac{m_{3}}{2}-\frac{m_{4}}{2}\right){}^{2}}{N}-i\pi\left(m-\frac{m_{3}}{2}-\frac{m_{4}}{2}\right)-i\pi\left(x-\omega^{\prime\prime}+i\epsilon\right)^{2}}$ (5.23) $\displaystyle\gamma\left(-\lambda+x-\omega^{\prime\prime}+i\epsilon,-\frac{m_{r}}{2}+m-\frac{m_{3}}{2}-\frac{m_{4}}{2}\right)\gamma\left(\lambda+x-\omega^{\prime\prime}+i\epsilon,\frac{m_{r}}{2}+m-\frac{m_{3}}{2}-\frac{m_{4}}{2}\right)$ up to a constant shift of $x$ , and $\psi_{r}^{(t)}$ is given by $m_{3}\to-m_{2},\ m_{4}\to-m_{3}$ . Both $\psi_{r}^{(s)}$ and $\psi_{r}^{(t)}$ are invariant under $(\lambda,m_{r})\to(-\lambda,-m_{r})$ .. We often fix the symmetry by requiring $\lambda\geq 0$ ( $\mu_{r}\geq 0$ ).

The following two lemmas state that $\psi_{r}$ for even $m_{r}$ form a complete distributional orthogonal basis for $\mathcal{H}_{+}$ .

Lemma 5.2.

The eigenstates with even $m_{r}$ satisfy the following orthogonality

\displaystyle\left\langle\psi_{r}\mid\psi_{r^{\prime}}\right\rangle_{N}=\frac{1}{2}\left\langle\psi_{r}\mid\psi_{r^{\prime}}\right\rangle=\frac{1}{2}\rho(\mu_{r},m_{r})\delta_{r,r^{\prime}}.

(5.24)

where

\displaystyle\delta_{r,r^{\prime}}

\displaystyle=

\displaystyle\frac{1}{2}\left[\delta(\mu_{r}-\mu_{r^{\prime}})\delta_{m_{r},m_{r^{\prime}}}+\delta(\mu_{r}+\mu_{r^{\prime}})\delta_{m_{r},-m_{r^{\prime}}}\right].

(5.25)

Proof.

First of all, by the periodicity of $\psi_{r}$ , we have

\displaystyle\sum_{m\in\mathbb{Z}/k\mathbb{Z}}\int\mathrm{d}\mu\,\psi_{r}(\mu,m)^{*}\psi_{r^{\prime}}(\mu,m)=2\sum_{m\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}\mu\,\psi_{r}(\mu,m)^{*}\psi_{r^{\prime}}(\mu,m).

(5.26)

The integrand $\psi_{r}(\mu,m)^{*}\psi_{r^{\prime}}(\mu,m)$ is given by

\displaystyle e^{-\frac{i\pi(m_{r}^{2}-m_{r^{\prime}}^{2})}{4N}+4i\pi x(\omega^{\prime\prime}-i\epsilon)}\frac{\gamma\left(-\lambda^{\prime}+x-\omega^{\prime\prime}+i\epsilon,m-\frac{m_{r^{\prime}}}{2}\right)\gamma\left(\lambda^{\prime}+x-\omega^{\prime\prime}+i\epsilon,m+\frac{m_{r^{\prime}}}{2}\right)}{\gamma\left(-\lambda+x+\omega^{\prime\prime}-i\epsilon,m-\frac{m_{r}}{2}\right)\gamma\left(\lambda+x+\omega^{\prime\prime}-i\epsilon,\frac{m_{r}}{2}+m\right)},

(5.27)

where $\lambda^{\prime}={\mu_{r^{\prime}}}/{2\sqrt{N}}$ . We use the integration identity (A.17) to transform the ratio of two $\gamma$ ’s ⁸⁸8The variables involved in (A.17) are given by $t=x$ , $\alpha=\lambda^{\prime}-\omega^{\prime\prime}+i\epsilon,\ \beta=\lambda^{\prime}+\omega^{\prime\prime}-i\epsilon$ , $d=m$ , $a=m_{r}^{\prime}/2$ , and $p=m_{r}/2$ . We have $\mathrm{Im}\left(\alpha+\frac{c_{b}}{\sqrt{N}}\right)=\epsilon>0,\ \mathrm{Im}\left(\frac{c_{b}}{\sqrt{N}}-\beta\right)=\epsilon>0,\ \mathrm{Im}(\alpha-\beta)=2\epsilon-\frac{b+b^{-1}}{\sqrt{N}}<0$ for sufficiently small $\epsilon>0$ . Therefore there exist an integration contour of $s$ with $\mathrm{Im}(\alpha-\beta)<\mathrm{Im}(s)<0$ allowing (A.17) to hold.

			$\displaystyle\frac{\gamma\left(\lambda^{\prime}+x-\omega^{\prime\prime}+i\epsilon,m+\frac{m_{r^{\prime}}}{2}\right)}{\gamma\left(\lambda+x+\omega^{\prime\prime}-i\epsilon,\frac{m_{r}}{2}+m\right)}$		(5.28)
		$\displaystyle=$	$\displaystyle\frac{\zeta_{0}}{\sqrt{N}}\sum_{c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}s\frac{e^{\frac{2i\pi c(m+m_{r^{\prime}}/2)}{N}+2i\pi s(x+\lambda^{\prime})}\gamma\left(-\lambda^{\prime}+\lambda+s+\omega^{\prime\prime}-2i\epsilon,-c-\frac{m_{r^{\prime}}}{2}+\frac{m_{r}}{2}\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma\left(-\lambda^{\prime}+\lambda+\omega^{\prime\prime}-2i\epsilon,\frac{m_{r}}{2}-\frac{m_{r^{\prime}}}{2}\right)},$		(5.28)

where $\zeta_{0}=e^{-\frac{1}{12}i\pi\left(N-4c_{b}^{2}/N\right)}$ .

Inserting (5.28) in (5.27), we check that the integrand of $\int\mathrm{d}\mu\mathrm{d}s$ is a Schwarz function on $\mathbb{R}^{2}$ ⁹⁹9The integrand suppresses exponentially fast as $\mu,\mathrm{Re}(s)\to\infty$ , as can be shown by using ${\rm D}_{b}(\frac{c_{b}}{\sqrt{N}}+x,n)\sim\exp\left[i\pi\left(x+\frac{c_{b}}{\sqrt{N}}\right)^{2}+O(1)\right]$ as $\mathrm{Re}(x)\to\infty$ and ${\rm D}_{b}(\frac{c_{b}}{\sqrt{N}}+x,n)\sim O(1)$ as $\mathrm{Re}(x)\to-\infty$ [12]. , so we can interchange the order of integration. Then we compute the integral and sum of $\mu=x\sqrt{N},m\in\mathbb{Z}/N\mathbb{Z}$ by applying (A.15) ¹⁰¹⁰10 We replace the variables in (A.15) by $t\to x,\ \alpha\to-\lambda^{\prime}-\omega^{\prime\prime}+2i\epsilon,\ \beta\to-\lambda+\omega^{\prime\prime}-2i\epsilon,\ s\to-s+2i\epsilon-2\omega^{\prime\prime},\ a\to-m_{r}^{\prime}/2,\ p\to-m_{r}/2,\ c\to-c$ (the left-hand sides are variables in (A.15), while the right-hand sides are variables in (5.28)). We have $\mathrm{Im}\left(\alpha+\frac{c_{b}}{\sqrt{N}}\right)\to\epsilon>0,\ \mathrm{Im}\left(\frac{c_{b}}{\sqrt{N}}-\beta\right)\to\epsilon>0,\ \mathrm{Im}(\alpha-\beta)\to 2\epsilon-\frac{b+b^{-1}}{\sqrt{N}}<0$ for sufficiently small $\epsilon>0$ , and $\mathrm{Im}(s)\to 2\epsilon-\frac{b+b^{-1}}{\sqrt{N}}-\mathrm{Im}(s)$ . Therefore for sufficiently small $\epsilon>0$ , $\mathrm{Im}(s)<0$ and small $|\mathrm{Im}(s)|$ in (5.28) implies $\mathrm{Im}(\alpha-\beta)<\mathrm{Im}(s)<0$ in (A.15), ensuring the validity of (A.15). then using the inverse formula and recusion relation of $\gamma$ . We obtain that as $\epsilon\to 0$

	$\displaystyle\sum_{m\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}\mu\,\psi_{r}(\mu,m)^{*}\psi_{r^{\prime}}(\mu,m)$	$\displaystyle=$	$\displaystyle\frac{1}{2\sqrt{N}}\rho(\mu_{r},m_{r})\sum_{c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}s\,e^{-\frac{2\pi i}{N}c\left(\frac{m_{r^{\prime}}}{2}+\frac{m_{r}}{2}\right)+2i\pi s\left(\lambda^{\prime}+\lambda\right)}$		(5.29)
		$\displaystyle=$	$\displaystyle\frac{1}{2}\rho(\mu_{r},m_{r})\delta(\mu_{r}+\mu_{r^{\prime}})\delta_{m_{r}+m_{r^{\prime}},0}\ .$		(5.29)

This equation holds in the sense of tempered distribution¹¹¹¹11The result of $s$ -integral is understood as a tempered distribution, which makes sense only when interring another integral, say, over $\mu_{r}=2\sqrt{N}\lambda_{r}$ . For finite $\epsilon$ , the integrand of $\int\mathrm{d}s$ is $e^{-\frac{2\pi i}{N}c\left(\frac{m_{r^{\prime}}}{2}+\frac{m_{r}}{2}\right)+2i\pi s\left(\lambda^{\prime}+\lambda\right)}$ multiply a Schwarz function in $s$ . Consider the following integral: $\int\mathrm{d}x\mathrm{d}k\ e^{2\pi ik(x-x^{\prime})}f_{\epsilon}(k)F(x)$ with both $f_{\epsilon},F$ Schwarz functions and $\lim_{\epsilon\to 0}f_{\epsilon}(k)=1$ . This integral equals $\int\mathrm{d}k\,e^{-2\pi ikx^{\prime}}f_{\epsilon}(k)\widetilde{F}(k)=f(x^{\prime})$ as $\epsilon\to 0$ , where the limit and integral can be interchanged by the dominant convergence. The computation in (5.29) is the same.. Finally, using the reflection symmetry of $\psi_{r}$

	$\displaystyle\sum_{m\in\mathbb{Z}/k\mathbb{Z}}\int\mathrm{d}\mu\,\psi_{r}(\mu,m)^{*}\psi_{r^{\prime}}(\mu,m)$	$\displaystyle=$	$\displaystyle\frac{1}{2}\sum_{m\in\mathbb{Z}/k\mathbb{Z}}\int\mathrm{d}\mu\,\psi_{r}(\mu,m)^{*}\left[\psi_{r^{\prime}}(\mu,m)+\psi_{r^{\prime}{}^{-1}}(\mu,m)\right]$		(5.30)
		$\displaystyle=$	$\displaystyle\rho(\mu_{r},m_{r})\,\delta_{r,r^{\prime}}$		(5.30)

∎

Lemma 5.3.

The eigenstates satisfy the following resolution of identity on $\mathcal{H}_{+}$

\displaystyle 2\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\psi_{r}(\mu^{\prime},m^{\prime})\,\psi_{r}(\mu,m)^{*}=\delta(\mu,\mu^{\prime})\,\delta_{m,m^{\prime}}.

(5.31)

for $\mu,\mu^{\prime}\in\mathbb{R}$ and $m,m^{\prime}\in\mathbb{Z}/N\mathbb{Z}$ .

Proof.

Firstly we define $\sigma(\mu_{r},m_{r})$ such that $\rho(\mu_{r},m_{r})^{-1}=\sigma(\mu_{r},m_{r})+\sigma(-\mu_{r},-m_{r})$ :

\displaystyle\sigma(\mu_{r},m_{r})=\frac{e^{-4i\pi\lambda\omega^{\prime\prime}}e^{-\frac{i\pi m_{r}}{N}+4i\pi m_{r}\omega^{\prime}{}^{2}-4i\pi m_{r}\omega^{\prime}{}\omega^{\prime\prime}}-e^{-4i\pi\lambda(\omega^{\prime\prime}-2\omega^{\prime}{})}e^{\frac{i\pi m_{r}}{N}+4i\pi m_{r}\omega^{\prime}{}^{2}-4i\pi m_{r}\omega^{\prime}{}\omega^{\prime\prime}}}{4N^{2}},

(5.32)

so that

\displaystyle\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{-\infty}^{\infty}\mathrm{d}\mu_{r}\,\sigma(\mu_{r},m_{r})\,\psi_{r}(\mu^{\prime},m^{\prime})\,\psi_{r}(\mu,m)^{*}

\displaystyle=

\displaystyle\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\psi_{r}(\mu^{\prime},m^{\prime})\,\psi_{r}(\mu,m)^{*}.

We consider the integral

$\displaystyle I$	$\displaystyle=$	$\displaystyle\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{-\infty}^{\infty}\mathrm{d}\mu_{r}\,\sigma(\mu_{r},m_{r})\,\psi_{r}(\mu^{\prime},m^{\prime})\,\psi_{r}(\mu,m)^{*}$	(5.33)
	$\displaystyle=$	$\displaystyle 2\sqrt{N}\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{-\infty}^{\infty}\mathrm{d}\lambda\,\sigma\,e^{-\frac{i\pi\left(m^{2}-{m^{\prime}}^{2}\right)}{N}+i\pi(m-{m^{\prime}})+i\pi\left(x^{2}-y^{2}\right)+2i\pi(x+y)\omega^{\prime\prime}}$
		$\displaystyle\frac{\gamma\left(-\lambda-\omega^{\prime\prime}+y+i\epsilon,m^{\prime}-\frac{m_{r}}{2}\right)\gamma\left(\lambda-\omega^{\prime\prime}+y+i\epsilon,\frac{m_{r}}{2}+m^{\prime}\right)}{\gamma\left(-\lambda+x+\omega^{\prime\prime}-i\epsilon,m-\frac{m_{r}}{2}\right)\gamma\left(\lambda+x+\omega^{\prime\prime}-i\epsilon,\frac{m_{r}}{2}+m\right)},$

and we make the following change of variables

\displaystyle-t=\lambda,\qquad\alpha=-\omega^{\prime\prime}+y+i\epsilon,\qquad\beta=x+\omega^{\prime\prime}-i\epsilon,\qquad a=m^{\prime},\qquad p=m,\qquad-d=\frac{m_{r}}{2}.

(5.34)

Then we apply (A.17) for $\mathrm{Im}(\alpha+\frac{c_{b}}{\sqrt{N}})=\mathrm{Im}(-\beta+\frac{c_{b}}{\sqrt{N}})=\epsilon>0$ and $\mathrm{Im}(\alpha-\beta)=2\epsilon-\frac{2\mathrm{Im}(c_{b})}{\sqrt{N}}<\mathrm{Im}(s)<0$ . The result is

\displaystyle I=I_{1}+I_{2}

(5.35)

where $I_{1},I_{2}$ correspond to two terms in $\sigma(\mu_{r},m_{r})$ ,

	$\displaystyle I_{1}$	$\displaystyle=$	$\displaystyle\frac{\zeta_{0}}{2N^{2}}\sum_{d,c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}t\mathrm{d}s\,e^{-i\pi\left(\alpha^{2}-\beta^{2}\right)+\frac{i\pi\left(a^{2}+2ac-p^{2}\right)}{N}-i\pi(a-p)-\frac{2i\pi}{N}dc}$		(5.36)
			$\displaystyle e^{2i\pi s\left(\alpha+\omega^{\prime\prime}\right)-2i\pi t(s-2\omega^{\prime\prime})}\frac{\gamma(\alpha+t,a+d)\gamma\left(-\alpha+\beta+s-\omega^{\prime\prime},-a-c+p\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma(\beta+t,d+p)\gamma\left(-\alpha+\beta-\omega^{\prime\prime},p-a\right)},$		(5.36)

and

	$\displaystyle I_{2}$	$\displaystyle=$	$\displaystyle-\frac{\zeta_{0}}{2N^{2}}\sum_{d,c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}t\mathrm{d}s\,e^{-i\pi\left(\alpha^{2}-\beta^{2}\right)+\frac{i\pi\left(a^{2}+2ac-p^{2}\right)}{N}-i\pi(a-p)-\frac{2i\pi}{N}d\left(c+2\right)}$		(5.37)
			$\displaystyle e^{2i\pi s\left(\alpha+\omega^{\prime\prime}\right)-2i\pi t\left(s-2\omega+2\omega^{\prime}\right)}\frac{\gamma(\alpha+t,a+d)\gamma\left(-\alpha+\beta+s-\omega^{\prime\prime},-a-c+p\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma(\beta+t,d+p)\gamma\left(-\alpha+\beta-\omega^{\prime\prime},p-a\right)}.$		(5.37)

We insert a regularization $\int\mathrm{d}t\to\int\mathrm{d}t\,e^{2\pi t\delta}$ in $I_{1}$ . This may also be understood as a modification of the integration measure by inserting a factor $e^{-2\pi\lambda\delta}$ to the first term in $\sigma(\mu_{r},m_{r})$ . We requiring $2\epsilon-\delta<\mathrm{Im}(s)<0$ . This condition implies $\mathrm{Im}(\alpha-\beta)<\mathrm{Im}(s+i\delta-2\omega^{\prime\prime})<0$ and ensures that the integrand is a Schwarz function of $t,s$ . Then we can interchange the order of integration and apply (A.15) to carry out the integration and sum of $t,d$

	$\displaystyle I_{1}$	$\displaystyle=$	$\displaystyle\frac{\zeta_{0}^{2}}{2N^{3/2}}\sum_{c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}s\,e^{\frac{4i\pi cm^{\prime}{}}{N}-\frac{i\pi\left(m^{2}-m^{\prime}{}^{2}\right)}{N}+i\pi(m-m^{\prime}{})+4i\pi sy+i\pi\left(x^{2}-y^{2}\right)+2i\pi(x-y)\omega^{\prime\prime}-2\pi\delta y}$		(5.38)
			$\displaystyle\frac{\gamma\left(s+x+\omega^{\prime\prime}-y-2i\epsilon,-c+m-m^{\prime}{}\right)\gamma\left(i\delta+s+x-\omega^{\prime\prime}-y-2i\epsilon,-c+m-m^{\prime}{}\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma\left(i\delta+s-\omega^{\prime\prime},-c\right)\gamma\left(x+\omega^{\prime\prime}-y-2i\epsilon,m-m^{\prime}{}\right)^{2}}.$		(5.38)

In $I_{2}$ , the integrand is already a Schwarz function of $t,s$ , and we have $\mathrm{Im}(s-2\omega+2\omega^{\prime})=\mathrm{Im}(s)<0$ , so (A.15) can be applied without any regularization.

	$\displaystyle I_{2}$	$\displaystyle=$	$\displaystyle-\frac{\zeta_{0}^{2}}{2N^{3/2}}\sum_{c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}s\,e^{\frac{2i\pi(2cm^{\prime}{}+2m^{\prime}{})}{N}-\frac{i\pi\left(m^{2}-m^{\prime}{}^{2}\right)}{N}+i\pi(m-m^{\prime}{})+4i\pi sy+i\pi\left(x^{2}-y^{2}\right)+2i\pi(x+3y)\omega^{\prime}+2i\pi\omega(x-y)}$		(5.39)
			$\displaystyle\frac{\gamma\left(s+x-y+\omega^{\prime\prime}-2i\epsilon,-c+m-m^{\prime}{}\right)\gamma\left(s+x+3\omega^{\prime}-y-\omega-2i\epsilon,-c+m-m^{\prime}{}-2\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma\left(s+3\omega^{\prime}-\omega,-c-2\right)\gamma\left(x-y+\omega^{\prime\prime}-2i\epsilon,m-m^{\prime}{}\right)^{2}}.$		(5.39)

The integrand of $I_{1}$ is suppressed asymptotically as $e^{\mp 4\pi\epsilon s}$ as $s\to\pm\infty$ .

The poles and zeros of $D_{b}(x,n)=\gamma(-x,n)$ ( $\mathrm{Im}(b)>0$ ) is respectively at $x=\frac{1}{\sqrt{N}}({c_{b}}+ib^{-1}l+ibm)$ for $n=m-l+N\mathbb{Z}$ and $x=-\frac{1}{\sqrt{N}}({c_{b}}+ib^{-1}l+ibm)$ for $n=l-m+N\mathbb{Z}$ , where $l,m\geq 0$ for both [11]. The integrand of $I_{1}$ has the following poles ( $l,m\geq 0$ for below):

•

$\gamma\left(s+x+\omega^{\prime\prime}-y-2i\epsilon,-c+m-m^{\prime}{}\right)=\mathrm{D}_{b}\left(-\frac{c_{b}}{\sqrt{N}}-s-x+y+2i\epsilon,-c+m-m^{\prime}\right)$ has poles at

\displaystyle s_{\rm pole}=-\frac{il}{b\sqrt{N}}-\frac{ibm}{\sqrt{N}}-\frac{i}{b\sqrt{N}}-\frac{ib}{\sqrt{N}}-x+y+2i\epsilon,\qquad n=m-l+N\mathbb{Z}.

(5.40)

These poles satisfy $\mathrm{Im}(s_{\rm pole})\leq-2\mathrm{Re}(b)/\sqrt{N}+2\epsilon$ and are below the integration contour of (5.38).

•

$\gamma\left(i\delta+s+x-\omega^{\prime\prime}-y-2i\epsilon,-c+m-m^{\prime}{}\right)=\mathrm{D}_{b}\left(\frac{c_{b}}{\sqrt{N}}-i\delta-s-x+y+2i\epsilon,-c+m-m^{\prime}\right)$ has poles

\displaystyle s_{\rm pole}=-\frac{il}{b\sqrt{N}}-\frac{ibm}{\sqrt{N}}-i\delta-x+y+2i\epsilon,\qquad n=m-l+N\mathbb{Z}.

(5.41)

These poles satisfy $\mathrm{Im}(s_{\rm pole})\leq 2\epsilon-\delta$ and are below the integration contour of (5.38), since the contour of (5.38) satisfy $2\epsilon-\delta\leq\mathrm{Im}(s)<0$ .

•

$\gamma\left(s+\omega^{\prime\prime},-c\right)^{-1}=\mathrm{D}_{b}\left(-\frac{c_{b}}{\sqrt{N}}-s,-c\right)^{-1}$ has poles

$\displaystyle s_{\rm pole}=\frac{il}{b\sqrt{N}}+\frac{ibm}{\sqrt{N}},\qquad n=l-m+N\mathbb{Z}.$ (5.42)

It contains the pole at the origin $s_{\rm pole}=0$ only when $c=0$ , while other poles satisfy $\mathrm{Im}(s_{\rm pole})\geq\mathrm{Re}(b)/\sqrt{N}$ .

•

$\gamma\left(i\delta+s-\omega^{\prime\prime},-c\right)^{-1}=\mathrm{D}_{b}\left(\frac{c_{b}}{\sqrt{N}}-i\delta-s,-c\right)^{-1}$ has poles

\displaystyle s_{\rm pole}=\frac{il}{b\sqrt{N}}+\frac{ibm}{\sqrt{N}}+\frac{i}{b\sqrt{N}}+\frac{ib}{\sqrt{N}}-i\delta,\qquad n=l-m+N\mathbb{Z}.

(5.43)

These poles satisfy $\mathrm{Im}(s_{\rm pole})\geq 2\mathrm{Re}(b)/\sqrt{N}+\delta$

We deform the integration contour of $I_{1}$ to $s\to s+2\omega^{\prime}=s+\frac{ib}{\sqrt{N}}$ and a circle around $s_{\rm pole}=0$ only when $c=0$ . The integration along $s+2\omega^{\prime}$ cancels with $I_{2}$ as $\delta\to 0$ ¹²¹²12It is shown by applying some recursion relations of $\gamma$ ’s and $c\to c+1$ . $I_{1}$ along $s+2\omega^{\prime}$ converges absolutely. The limit $\delta\to 0$ is taken by the dominant convergence. . Therefore, the nonvanishing contribution to $I$ is the residue at $s=0$ only coming from $c=0$ in $\sum_{c\in\mathbb{Z}/N\mathbb{Z}}$ . The residue of ${\rm D}_{b}\left(\frac{c_{b}}{\sqrt{N}}+s,0\right)$ is

\displaystyle-\frac{\sqrt{N}}{2\pi b^{-1}}\frac{\left({\bf q}^{2},{\bf q}^{2}\right)_{\infty}}{\left(\tilde{{\bf q}}^{-2},\tilde{{\bf q}}^{-2}\right)_{\infty}}

(5.44)

and ${\rm D}_{\mathrm{b}}\left(-\frac{c_{b}}{\sqrt{N}}+s,0\right)\sim-\frac{2\pi b}{\sqrt{N}}s(\mathbf{q}^{2},\mathbf{q}^{2})_{\infty}/(\tilde{\mathbf{q}}^{-2},\tilde{\mathbf{q}}^{-2})_{\infty}$ as $s\to 0$ . The residue of $I_{1}$ at $s_{\rm pole}=0$ vanishes as $\delta\to 0$ unless $m=m^{\prime}$ . As a result, for $\delta,\epsilon\to 0$ with $\delta>2\epsilon$ , we obtain

\displaystyle I=\delta_{m,m^{\prime}}\frac{\delta}{4\pi\sqrt{N}(x-y-2i\epsilon)(i(\delta-2\epsilon)+x-y)}\to\frac{1}{2}\delta(\mu-\mu^{\prime})\delta_{m,m^{\prime}}.

(5.45)

∎

The result indicates that for any $f_{+}\in\mathcal{H}_{+}$ , we can find the spectral representation $f(\mu_{r},m_{r})$ with $\mu_{r}\in\mathbb{R}_{+}$ , $m_{r}/2\in\mathbb{Z}/N\mathbb{Z}$ ,

	$\displaystyle\mid f_{+}\rangle$	$\displaystyle=$	$\displaystyle\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}f_{+}(\mu_{r},m_{r})\mid\psi_{r}\rangle,$
	where		$\displaystyle\quad f_{+}(\mu_{r},m_{r})=\langle\psi_{r}\mid f_{+}\rangle=2\langle\psi_{r}\mid f_{+}\rangle_{N}$		(5.46)

and

\displaystyle\langle f_{+}\mid f_{+}^{\prime}\rangle=\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}f_{+}(\mu_{r},m_{r})^{*}f^{\prime}_{+}(\mu_{r},m_{r}).

(5.47)

$\bm{L},\tilde{\bm{L}}$ are represented as the multiplication operators

\displaystyle\bm{L}f_{+}(\mu_{r},m_{r})=\ell(r)f_{+}(\mu_{r},m_{r}),\qquad\tilde{\bm{L}}f_{+}(\mu_{r},m_{r})=\ell(r)^{*}f_{+}(\mu_{r},m_{r}).

(5.48)

The spectral decomposition can be conveniently represented as the direct integral decomposition

\displaystyle\mathcal{H}_{+}\simeq\sum_{m_{r}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}}.

(5.49)

where each $\mathcal{H}_{\mu_{r},m_{r}}$ is 1-dimensional.

When deriving the spectral decomposition for $\bm{L}^{(aux)}_{s},\tilde{\bm{L}}^{(aux)}_{s}$ (or $\bm{L}^{(aux)}_{t},\tilde{\bm{L}}^{(aux)}_{t}$ ), we should instead require $m_{r}+m_{3}+m_{4}\in 2\mathbb{Z}$ (or $m_{r}+m_{2}+m_{3}\in 2\mathbb{Z}$ ), then the above computation generalizes straight-forwardly, and the result (5.49) is modified by changing the sum to $\sum_{\frac{m_{r}+m_{3}+m_{4}}{2}\in\mathbb{Z}/N\mathbb{Z}}$ (or $\sum_{\frac{m_{r}+m_{2}+m_{3}}{2}\in\mathbb{Z}/N\mathbb{Z}}$ ).

5.2 Anti-periodic states

The unitary transformation maps between $\mathcal{H}_{+}$ and $\mathcal{H}_{-}$ is given by $e^{i\pi\bm{m}}$ :

\displaystyle f_{\pm}(\mu,m)\in\mathcal{H}_{\pm}\quad\mapsto\quad e^{i\pi{m}}f_{\pm}(\mu,m)\in\mathcal{H}_{\mp}.

(5.50)

$e^{i\pi\bm{m}}$ commutes with $\bm{y}^{2},\tilde{\bm{y}}^{2}$ but flips signs of $\bm{x},\tilde{\bm{x}}$ : $e^{i\pi\bm{m}}\bm{x}e^{-i\pi\bm{m}}=-\bm{x}$ and $e^{i\pi\bm{m}}\tilde{\bm{x}}e^{-i\pi\bm{m}}=-\tilde{\bm{x}}$ .

Secondly, given that $\mathcal{H}_{+}\simeq L^{2}(\mathbb{R})\otimes\mathbb{C}^{N}$ , for any $f\in\mathcal{H}_{+}$ and for any $\mu\in\mathbb{R}$ , $\{f(\mu,m)\}_{m=1}^{N}$ can be seen as a vector in $\mathbb{C}^{N}$ , and it has the discrete Fourier transform

\displaystyle f\left(\mu,m\right)=\frac{1}{\sqrt{N}}\sum_{n=0}^{N-1}f_{n}(\mu)e^{\frac{2\pi i}{N}mn}.

(5.51)

We define a unitary map $O:\mathcal{H}_{+}\to\mathcal{H}_{+}$ by

\displaystyle f_{n}(\mu)\mapsto(-1)^{n}f_{n}(\mu),\qquad\forall\ n=0,\cdots,N-1.

(5.52)

The unitary map may also be written formally as $\bm{O}f(\mu,m)=f(\mu,m+N/2)$ . $O$ is unitary since $\langle Of,Of^{\prime}\rangle=\sum_{n=0}^{N-1}\int\mathrm{d}\mu f_{n}(\mu)^{*}f_{n}^{\prime}(\mu)=\langle f,f^{\prime}\rangle$ . $O$ commutes with $\bm{x},\tilde{\bm{x}}$ but flips signs of $\bm{y}^{2},\tilde{\bm{y}}^{2}$ : $O\bm{y}^{2}O^{-1}=-\bm{y}^{2}$ and $O\tilde{\bm{y}}^{2}O^{-1}=-\tilde{\bm{y}}^{2}$ . $O$ shows that the two representations of Weyl algebra $\bm{x}\bm{y}^{2}=\mathbf{q}^{2}\bm{y}^{2}\bm{x}$ on $L^{2}(\mathbb{R})\otimes\mathbb{C}^{N}$ with flipping $\bm{y}^{2}\to-\bm{y}^{2}$ are unitary equivalent.

By composing these unitary maps, we have $Oe^{i\pi\bm{m}}:\mathcal{H}_{-}\to\mathcal{H}_{+}$ , and since $\bm{L},\tilde{\bm{L}}$ leave $\mathcal{H}_{\pm}$ invariant, we have

\displaystyle Oe^{i\pi\bm{m}}\bm{L}e^{-i\pi\bm{m}}O^{-1}=-\bm{L}\qquad Oe^{i\pi\bm{m}}\tilde{\bm{L}}e^{-i\pi\bm{m}}O^{-1}=-\tilde{\bm{L}}.

(5.53)

where the right-hand sides acting on $\mathcal{H}_{+}$ . This shows that the spectral decomposition of $\bm{L},\tilde{\bm{L}}$ on $\mathcal{H}_{-}$ is unitary equivallent to the spectral decomposition of $-\bm{L},-\tilde{\bm{L}}$ on $\mathcal{H}_{+}$ . Therefore, we obtain the same direction integral decomposition as (5.49) for $\mathcal{H}_{-}$

\displaystyle\mathcal{H}_{-}\simeq\sum_{m_{r}^{\prime}/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r}^{\prime})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}^{\prime}}.

(5.54)

But the representation of $\bm{L},\tilde{\bm{L}}$ is different from (5.48) by a minus sign

\displaystyle\bm{L}f_{-}(\mu_{r},m_{r}^{\prime})=-\ell(r^{\prime})f_{-}(\mu_{r},m_{r}^{\prime}),\qquad\tilde{\bm{L}}f_{-}(\mu_{r},m_{r}^{\prime})=-\ell(r^{\prime})^{*}f_{-}(\mu_{r},m_{r}^{\prime}).

(5.55)

where $r^{\prime}=\exp[\frac{\pi i}{N}(-ib\mu_{r}-m_{r}^{\prime})]$ . In these two formulae, $m_{r}^{\prime}/2\in\mathbb{Z}/N\mathbb{Z}$ , i.e. $m_{r}^{\prime}$ is even. We may define the shift $m_{r}=m_{r}^{\prime}+N$ , where $m_{r}$ is odd, and $F_{-}(\mu_{r},m_{r})=f_{-}(\mu_{r},m_{r}^{\prime})$ , then

\displaystyle\bm{L}F_{-}(\mu_{r},m_{r})=\ell(r)F_{-}(\mu_{r},m_{r}),\qquad\tilde{\bm{L}}F_{-}(\mu_{r},m_{r})=\ell(r)^{*}F_{-}(\mu_{r},m_{r}).

(5.56)

where $r=\exp[\frac{\pi i}{N}(-ib\mu_{r}-m_{r})]$ . By relabeling $\mathcal{H}_{\mu_{r},m_{r}^{\prime}}\simeq\mathcal{H}_{\mu_{r},m_{r}}$ , (5.54) can be written as

\displaystyle\mathcal{H}_{-}\simeq\sum_{(m_{r}+N)/2\in\mathbb{Z}/N\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}}.

(5.57)

From the perspective of eigenstates $\alpha_{r}$ , we find for odd $m_{r}$ ,

	$\displaystyle Oe^{i\pi\bm{m}}\alpha_{r}$	$\displaystyle=$	$\displaystyle e^{i\pi(m+N/2)}e^{-\frac{i\pi}{N}m_{r}\frac{N}{2}}e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m_{r}m\right)}\frac{\varphi\left(-{\bf q}^{-1}y^{2}r^{\prime},-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{r}^{\prime}\right)}{\varphi\left(-{\bf q}y^{-2}r^{\prime},-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{r}^{\prime}\right)}$		(5.58)
		$\displaystyle=$	$\displaystyle e^{i\pi\frac{m_{r}^{\prime}}{2}}e^{-\frac{2\pi i}{k}\left(-\mu_{r}\mu+m^{\prime}_{r}m\right)}\frac{\varphi\left(-{\bf q}^{-1}y^{2}r^{\prime},-\tilde{{\bf q}}^{-1}\tilde{y}^{2}\tilde{r}^{\prime}\right)}{\varphi\left(-{\bf q}y^{-2}r^{\prime},-\tilde{{\bf q}}\tilde{y}^{-2}\tilde{r}^{\prime}\right)}=(-1)^{m_{r}^{\prime}/2}\alpha_{r^{\prime}}$		(5.58)

where $m_{r}^{\prime}=m_{r}-N$ is even and $r^{\prime}=\exp[\frac{\pi i}{N}(-ib\mu_{r}-m_{r}^{\prime})]$ , $\tilde{r}^{\prime}=\exp[\frac{\pi i}{N}(-ib^{-1}\mu_{r}+m_{r}^{\prime})]$ . The unitary transformation maps $\alpha_{r}$ with odd $m_{r}$ to $\alpha_{r^{\prime}}$ (up to a constant phase) with even $m_{r}^{\prime}$ . Then all the results in Section 5.1 follows for $\alpha_{r^{\prime}}$ .

Combining (5.49) and (5.57), we obtain the spectral decompostion of the full Hilbert space

\displaystyle\mathcal{H}=\mathcal{H}_{+}\oplus\mathcal{H}_{-}\simeq\sum_{m_{r}\in\mathbb{Z}/k\mathbb{Z}}\int_{0}^{\infty}\mathrm{d}\mu_{r}\,\rho(\mu_{r},m_{r})^{-1}\,\mathcal{H}_{\mu_{r},m_{r}}.

(5.59)

containing both even and odd $m_{r}$ . This completes the proof of Theorem 5.1.

6 Changing triangulation

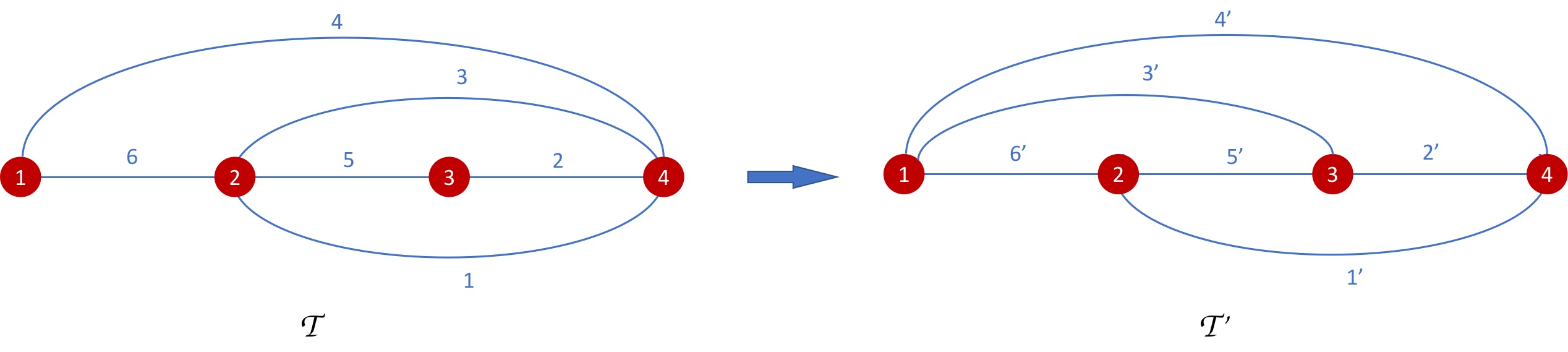
The above discussion is based on the ideal triangulation FIG.1. Changing ideal triangulation results in unitary equivalent quantization of FG coordinates. Let us denote the triangulation in FIG.1(a) by $\mathcal{T}$ and consider the change of triangulation from $\mathcal{T}$ to the tetrahedral triangulation $\mathcal{T}^{\prime}$ shown in FIG.2. The change is made by flipping the edge $3$ in the quadrilateral bounded by edges $4,6,5,2$ . Other changes of triangulations have similar result. The edges in $\mathcal{T}^{\prime}$ are labelled by $1^{\prime},\cdots,6^{\prime}$ , and their associated FG coordinates are denoted by $z_{e}^{\prime}=\exp(Z_{e}^{\prime})$ , ( $e=1,\cdots,6$ ). We may identify the triangulation and the associated data i.e. $\mathcal{T}=(\{e\},\varepsilon_{e_{1},e_{2}})$ and $\mathcal{T}^{\prime}=(\{e^{\prime}\},\varepsilon^{\prime}_{e^{\prime}_{1},e^{\prime}_{2}})$ .

Classically, changing triangulation results in a change of FG coordinate. Taking $\mathcal{T}\to\mathcal{T}^{\prime}$ as an example, $z_{e}^{\prime}$ relates to $z_{e}$ by the following tranformation

$\displaystyle{z}_{1}^{\prime}$	$\displaystyle=$	$\displaystyle{z}_{1},\qquad{z}_{3}^{\prime}={z}_{3}^{-1},$	(6.1)
$\displaystyle{z}_{2}^{\prime}$	$\displaystyle=$	$\displaystyle{z}_{2}\left(1-{z}_{3}\right),\qquad{z}_{4}^{\prime}{}^{-1}=(1-{z}_{3}^{-1}){z}_{4}^{-1},$	(6.2)
$\displaystyle{z}_{6}^{\prime}$	$\displaystyle=$	$\displaystyle{z}_{6}\left(1-{z}_{3}\right),\qquad{z}_{5}^{\prime}{}^{-1}=(1-{z}_{3}^{-1}){z}_{5}^{-1}.$	(6.3)

where we denote $e^{\prime}_{a}$ simply by $a$ . The transformation preserves the Poisson bracket in a nontrivial manner, namely we have $\{z_{a}^{\prime},z_{b}^{\prime}\}={2}\varepsilon_{a,b}^{\prime}z_{a}^{\prime}z_{b}^{\prime},\ \{\tilde{z}_{a}^{\prime},\tilde{z}_{b}^{\prime}\}={2}\varepsilon_{a,b}^{\prime}\tilde{z}_{a}^{\prime}\tilde{z}_{b}^{\prime}$ from the Poisson bracket of $z_{a},\tilde{z}_{a}$ , whereas $\varepsilon_{a,b}\neq\varepsilon^{\prime}_{a,b}$ . $\varepsilon^{\prime}_{ab}$ is given by

\displaystyle\varepsilon^{\prime}=\left(\begin{array}[]{cccccc}0&-1&0&1&1&-1\\ 1&0&1&-1&-1&0\\ 0&-1&0&1&1&-1\\ -1&1&-1&0&0&1\\ -1&1&-1&0&0&1\\ 1&0&1&-1&-1&0\\ \end{array}\right).

(6.10)

The quantization on $\mathcal{T}$ has been studied in the above. The quantization of the FG coordinates on $\mathcal{T}^{\prime}$ gives the quantum algebra

\displaystyle\bm{z}^{\prime}_{a}\bm{z}^{\prime}_{b}=\mathbf{q}^{2\varepsilon^{\prime}_{ab}}\bm{z}^{\prime}_{b}\bm{z}^{\prime}_{a},\qquad\tilde{\bm{z}}^{\prime}_{a}\tilde{\bm{z}}^{\prime}_{b}=\tilde{\mathbf{q}}^{2\varepsilon^{\prime}_{ab}}\tilde{\bm{z}}^{\prime}_{b}\tilde{\bm{z}}^{\prime}_{a},\qquad\bm{z}^{\prime}_{a}\tilde{\bm{z}}^{\prime}_{b}=\tilde{\bm{z}}^{\prime}_{b}\bm{z}^{\prime}_{a}

(6.11)

The representation of this algebra relates to the representation of (4.1) (of $\mathcal{T}$ ) by a unitary transformation known as the quantum cluster transformation, generalizing the results in [23, 5]. Firstly, we define the map $i_{3}$ acting on the logarithmic coordinate

\displaystyle i_{3}:\ \bm{Z}_{a}\mapsto\begin{cases}-\bm{Z}_{3}+2\pi i,&a=3\\ \bm{Z}_{a}+\mathrm{Max}(\{\varepsilon_{a,3},0\})(\bm{Z}_{3}-i\pi),&a\neq 3\end{cases},

(6.12)

or explicitly,

$\displaystyle i_{3}\left(\bm{Z}_{1}\right)$	$\displaystyle=$	$\displaystyle-\bm{X}+i\pi,\qquad i_{3}\left(\bm{Z}_{2}\right)\to-2L_{3}+2\bm{Y}+i\pi,$
$\displaystyle i_{3}\left(\bm{Z}_{3}\right)$	$\displaystyle=$	$\displaystyle-L_{1}+L_{2}-L_{3}-L_{4}-\bm{X}+i\pi,$
$\displaystyle i_{3}\left(\bm{Z}_{4}\right)$	$\displaystyle=$	$\displaystyle 2L_{3}+2L_{4}+\bm{X}-2\bm{Y}+i\pi,\qquad i_{3}\left(\bm{Z}_{5}\right)=L_{1}-L_{2}+L_{3}+L_{4}+\bm{X}-2\bm{Y}+i\pi,$
$\displaystyle i_{3}\left(\bm{Z}_{6}\right)$	$\displaystyle=$	$\displaystyle-L_{1}-L_{2}-L_{3}-L_{4}-2\bm{Y}+i\pi$	(6.13)

and the same for $\tilde{\bm{Z}}_{a}$ . They satisfy

	$\displaystyle i_{3}\left(Z_{3}\right)+i_{3}\left(Z_{4}\right)+i_{3}\left(Z_{6}\right)-3\pi i=-2L_{1},\qquad i_{3}\left(Z_{1}\right)+i_{3}\left(Z_{5}\right)+i_{3}\left(Z_{6}\right)-3\pi i=-2L_{2},$		(6.14)
	$\displaystyle i_{3}\left(Z_{2}\right)+i_{3}\left(Z_{3}\right)+i_{3}\left(Z_{5}\right)-3\pi i=-2L_{3},\qquad i_{3}\left(Z_{1}\right)+i_{3}\left(Z_{2}\right)+i_{3}\left(Z_{4}\right)-3\pi i=2L_{4}$		(6.15)

$i_{3}$ induces the monomial transformation of $\bm{z}_{a}$ .

	$\displaystyle i_{3}\left(\bm{z}_{1}\right)$	$\displaystyle=$	$\displaystyle-\bm{x}^{-1},\qquad i_{3}\left(\bm{z}_{2}\right)=-{\lambda_{3}^{-2}}\bm{y}^{2},\qquad i_{3}\left(\bm{z}_{3}\right)=-\lambda_{1}^{-1}\lambda_{2}\lambda_{3}^{-1}\lambda_{4}^{-1}\bm{x}^{-1},$
	$\displaystyle i_{3}\left(\bm{z}_{4}\right)$	$\displaystyle=$	$\displaystyle-\mathbf{q}{\lambda_{3}^{2}\lambda_{4}^{2}}\bm{x}\bm{y}^{-2},\qquad i_{3}\left(\bm{z}_{5}\right)=-\mathbf{q}\lambda_{2}^{-1}\lambda_{1}\lambda_{3}\lambda_{4}\bm{x}\bm{y}^{-2},\qquad i_{3}\left(\bm{z}_{6}\right)=-{(\lambda_{1}\lambda_{2}\lambda_{3}\lambda_{4})^{-1}}\bm{y}^{2}.$		(6.16)

The image of $i_{3}$ gives operators on $\mathcal{H}$ with the following commutation relation

\displaystyle\left[i_{3}(\bm{Z}_{a}),i_{3}(\bm{Z}_{b})\right]=2\hbar\varepsilon^{\prime}_{ab},\qquad\left[i_{3}(\tilde{\bm{Z}}_{a}),i_{3}(\tilde{\bm{Z}}_{b})\right]=2\tilde{\hbar}\varepsilon^{\prime}_{ab}.

(6.17)

Therefore, the set of $i_{3}(\bm{z}_{a})$ , $i_{3}(\tilde{\bm{z}}_{a})$ satisfies the same operator algebra as (6.11). Then we define the unitary transformation

\displaystyle\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3}):\ \mathcal{H}\to\mathcal{H}^{\prime}

(6.18)

where $\mathcal{H}^{\prime}$ carries the representation of (6.11). Both $\mathcal{H}$ and $\mathcal{H}^{\prime}$ as Hilbert spaces are isomorphic to $L^{2}(\mathbb{R})\otimes\mathbb{C}^{k}$ . $\varphi$ is the quantum dilogarithm and $\bm{z}_{3}=-\frac{\lambda_{1}\lambda_{3}\lambda_{4}}{\lambda_{2}}\bm{x}$ . Explicitly, for any state $f\in\mathcal{H}$ , $f$ can be represented as $\widetilde{f}(\nu,n)$ as the Fourier transform of $f(\mu,\nu)$ . $\bm{x}$ acts on $\widetilde{f}(\nu,n)$ as the multiplication of $x=\exp[\frac{2\pi i}{k}(-ib\nu-n)]$ . Then

\displaystyle\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})\widetilde{f}(\nu,n)=\varphi\left(\frac{\lambda_{1}\lambda_{3}\lambda_{4}}{\lambda_{2}}x,\frac{\tilde{\lambda}_{1}\tilde{\lambda}_{3}\tilde{\lambda}_{4}}{\tilde{\lambda}_{2}}\tilde{x}\right)\widetilde{f}(\nu,n)

(6.19)

Then the representation of $\bm{z}^{\prime}_{a},\tilde{\bm{z}}_{a}^{\prime}$ is given by

\displaystyle\bm{z}^{\prime}_{a}=\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})i_{3}(\bm{z}_{a})\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})^{-1},\qquad\tilde{\bm{z}}^{\prime}_{a}=\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})i_{3}(\tilde{\bm{z}}_{a})\varphi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})^{-1}.

(6.20)

We may compute (6.20) explicitly

$\displaystyle\bm{z}_{1}^{\prime}$	$\displaystyle=$	$\displaystyle\bm{z}_{1},\qquad\bm{z}_{3}^{\prime}=\bm{z}_{3}^{-1},$
$\displaystyle\bm{z}_{2}^{\prime}$	$\displaystyle=$	$\displaystyle\bm{z}_{2}\left(1-\mathbf{q}\bm{z}_{3}\right),\qquad\bm{z}_{4}^{\prime}{}^{-1}=(1-\mathbf{q}\bm{z}_{3}^{-1})\bm{z}_{4}^{-1},$
$\displaystyle\bm{z}_{6}^{\prime}$	$\displaystyle=$	$\displaystyle\bm{z}_{6}\left(1-\mathbf{q}\bm{z}_{3}\right),\qquad\bm{z}_{5}^{\prime}{}^{-1}=(1-\mathbf{q}\bm{z}_{3}^{-1})\bm{z}_{5}^{-1},$	(6.21)

and similar for $\tilde{\bm{z}}^{\prime}_{a}$ . As $\mathbf{q}\to 1$ , these transformations reduce to the classical transformation of FG coordinate under the flip.

If we denote by $V_{s}$ the unitary transformation from $\mathcal{H}$ to the direct integral representation in (5.59) for the S-cycle trace, the composition $V_{s}\circ\phi(-\bm{z}_{3},-\tilde{\bm{z}}_{3})^{-1}$ maps from $\mathcal{H}^{\prime}$ to the direct integral representation.

Acknowledgements

M.H. acknowledges Chen-Hung Hsiao and Qiaoyin Pan for helpful discussions. M.H. receives supports from the National Science Foundation through grant PHY-2207763 and the College of Science Research Fellowship at Florida Atlantic University. M.H. also receives support from the visiting professorship at FAU Erlangen-Nürnberg at the early stage of this work.

Appendix A Quantum dilogarithm

The quantum dilogarithm function is defined by

\displaystyle\varphi\left(y,\tilde{y}\right)

\displaystyle\equiv\varphi_{\bf{q},\tilde{\bf q}}\left(y,\tilde{y}\right)=\left[\prod_{j=0}^{\infty}\frac{1+\mathbf{q}^{2j+1}y}{1+\tilde{\mathbf{q}}^{-2j-1}\tilde{y}}\right]^{-1}\equiv\phi(\mu,m)

(A.1)

where $y=\exp[\frac{2\pi i}{k}(-ib\mu-m)]$ and $\tilde{y}=\exp[\frac{2\pi i}{k}(-ib^{-1}\mu+m)]$ . The quantum dilogarithm function satisfies the following recursion relations:

	$\displaystyle\varphi\left(\mathbf{q}^{2}y,\tilde{y}\right)=\left(1+\mathbf{q}y\right)\varphi\left(y,\tilde{y}\right),\qquad\varphi\left(y,\tilde{\mathbf{q}}^{2}\tilde{y}\right)=\left(1+\tilde{\mathbf{q}}\tilde{y}\right)\varphi\left(y,\tilde{y}\right),$		(A.2)
	$\displaystyle\varphi\left(\mathbf{q}y,\tilde{y}\right)=\left(1+y\right)\varphi\left(\mathbf{q}^{-1}y,\tilde{y}\right),\qquad\varphi\left(y,\tilde{\mathbf{q}}\tilde{y}\right)=\left(1+\tilde{y}\right)\varphi\left(y,\tilde{\mathbf{q}}^{-1}\tilde{y}\right),$		(A.3)
	$\displaystyle\varphi\left(y,\tilde{y}\right)=\left(1+\mathbf{q}^{-1}y\right)\varphi\left(\mathbf{q}^{-2}y,\tilde{y}\right),\qquad\varphi\left(y,\tilde{y}\right)=\left(1+\tilde{\mathbf{q}}^{-1}\tilde{y}\right)\varphi\left(y,\tilde{\mathbf{q}}^{-2}\tilde{y}\right).$		(A.4)

We also use an alternative convention of the quantum dilogarithm

\mathcal{D}_{b}(x,n)=\frac{\left(\chi^{+}\left(x+\frac{C_{b}}{\sqrt{k}},n\right);\mathfrak{q}^{2}\bm{w}\right)_{\infty}}{\left(\chi^{-}\left(x-\frac{C_{b}}{\sqrt{k}},n\right);\tilde{\mathfrak{q}}^{2}\bar{\bm{w}}\right)_{\infty}},

where

	$\displaystyle\mathfrak{q}=e^{2i\pi b^{2}/k},\qquad\tilde{\mathfrak{q}}=e^{-2i\pi b^{-2}/k},\qquad\bm{w}=e^{4\pi i/k},\qquad C_{b}={i}\left(b+b^{-1}\right)=2c_{b}$
	$\displaystyle\chi^{\pm}(x,n)=\exp\left[\frac{2\pi i}{k}\left(-ib^{\pm 1}x\sqrt{k}\pm n\right)\right]$		(A.5)

and we have $\mathfrak{q}^{2}\bm{w}=e^{4i\pi\left(b^{2}+1\right)/k}=\mathbf{q}^{2}$ and $\mathfrak{\tilde{q}}^{2}\bar{\bm{w}}=e^{-4i\pi\left(b^{-2}+1\right)/k}=\tilde{\mathbf{q}}^{-2}$ . Our convention of $q$ -Pochammer symbol is $(x;q)_{\infty}=\prod_{j=0}^{\infty}\left(1-q^{j}x\right)$ . So

\displaystyle\mathcal{D}_{b}(x,n)=\prod_{j=0}^{\infty}\frac{1-{\bf q}^{2j+1}\exp\left[\frac{2\pi i}{k}\left(-ibx\sqrt{k}+n\right)\right]}{1-\tilde{{\bf q}}^{-2j-1}\exp\left[\frac{2\pi i}{k}\left(-ib^{-1}x\sqrt{k}-n\right)\right]}

(A.6)

relates to $\varphi(y,\tilde{y})$ by

\displaystyle\varphi\left(-y,-\tilde{y}\right)=\mathcal{D}_{b}\left(\frac{\mu}{\sqrt{k}},-m\right)^{-1}

(A.7)

When $k=2N$ is even ( $N\in\mathbb{Z}$ ), the quantum dilogarithm ${\rm D}_{b}(x,n)$ used in [10, 11] is related by

\displaystyle{\rm D}_{b}(x,n)=\mathcal{D}_{b}(\sqrt{2}x,2n),\qquad\varphi\left(-y^{2},-\tilde{y}^{2}\right)={\rm D}_{b}\left(\frac{\mu}{\sqrt{N}},-m\right)^{-1}.

(A.8)

We also introduce ¹³¹³13This notation is inspired by [7].

\displaystyle\gamma(x,n)=\mathrm{D}_{b}(-x,n).

(A.9)

The quantum dilogarithm functions satisfy the unitarity

\displaystyle\phi\left(\mu,m\right)^{*}=\phi\left(\mu^{*},m\right)^{-1},\qquad\mathcal{D}_{b}(x,n)^{*}=\mathcal{D}_{b}(x^{*},n)^{-1},\qquad\gamma(x,n)^{*}=\gamma(x^{*},n)^{-1}.

(A.10)

We introduce some notations $\omega,\omega^{\prime},\omega^{\prime\prime}$ by

\displaystyle\omega=\frac{i}{2b\sqrt{N}},\quad\omega^{\prime}=\frac{ib}{2\sqrt{N}},\quad\omega^{\prime\prime}=\frac{c_{b}}{\sqrt{N}}\ .

(A.11)

The following summarizes some useful properties of $\gamma(x,n)$ :

•

The inverse relation:

\displaystyle\gamma(x,n)\gamma(-x,-n)=\exp\left(-\frac{i\pi n^{2}}{N}-i\pi n-\frac{i\pi N}{6}+i\pi x^{2}-\frac{1}{3}i\pi\omega^{\prime\prime}{}^{2}\right).

(A.12)

•

The recursion relation:

	$\displaystyle\gamma(x\pm 2\omega^{\prime},n\mp 1)$	$\displaystyle=$	$\displaystyle\left(1+e^{\frac{2i\pi n}{N}\pm\frac{i\pi(N-1)}{N}+4i\pi x\omega^{\prime}\pm 4i\pi\omega^{\prime}{}^{2}}\right)^{\pm 1}\gamma(x,n),$		(A.13)
	$\displaystyle\gamma(x\pm 2\omega,n\pm 1)$	$\displaystyle=$	$\displaystyle\left(1+e^{-\frac{2i\pi n}{N}\pm\frac{i\pi(N-1)}{N}+4i\pi x\omega\pm 4i\pi\omega^{2}}\right)^{\pm 1}\gamma(x,n).$		(A.14)

•

The integration identity:

			$\displaystyle\frac{1}{\sqrt{N}}\sum_{d\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}t\frac{\gamma(t+\alpha,a+d)}{\gamma(t+\beta,p+d)}e^{-2i\pi st}e^{-\frac{2i\pi cd}{N}}$		(A.15)
		$\displaystyle=$	$\displaystyle\zeta_{0}\,e^{\frac{2i\pi ac}{N}+2i\pi s\left(\alpha+\omega^{\prime\prime}\right)}\frac{\gamma\left(-\alpha+\beta+s-\omega^{\prime\prime},-a-c+p\right)}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma\left(-\alpha+\beta-\omega^{\prime\prime},p-a\right)},$		(A.15)

where $\zeta_{0}=e^{-\frac{1}{12}i\pi\left(N-\frac{4c_{b}^{2}}{N}\right)}$ and $\alpha,\beta,s$ satisfy

\displaystyle\mathrm{Im}(\alpha+\frac{c_{b}}{\sqrt{N}})>0,\qquad\mathrm{Im}(-\beta+\frac{c_{b}}{\sqrt{N}})>0,\qquad\mathrm{Im}(\alpha-\beta)<\mathrm{Im}(s)<0.

(A.16)

The inverse of the identity:

			$\displaystyle\frac{\gamma(\alpha+t,a+d)}{\gamma(\beta+t,d+p)}$		(A.17)
		$\displaystyle=$	$\displaystyle\frac{\zeta_{0}}{\sqrt{N}}\sum_{c\in\mathbb{Z}/N\mathbb{Z}}\int\mathrm{d}s\frac{\gamma\left(-\alpha+\beta+s-\omega^{\prime\prime},-a-c+p\right)e^{\frac{2i\pi(a+d)c}{N}+2i\pi s\left(\alpha+\omega^{\prime\prime}\right)+2i\pi st}}{\gamma\left(s+\omega^{\prime\prime},-c\right)\gamma\left(-\alpha+\beta-\omega^{\prime\prime},p-a\right)}.$		(A.17)

Appendix B Fock-Goncharov coordinate and holonomies

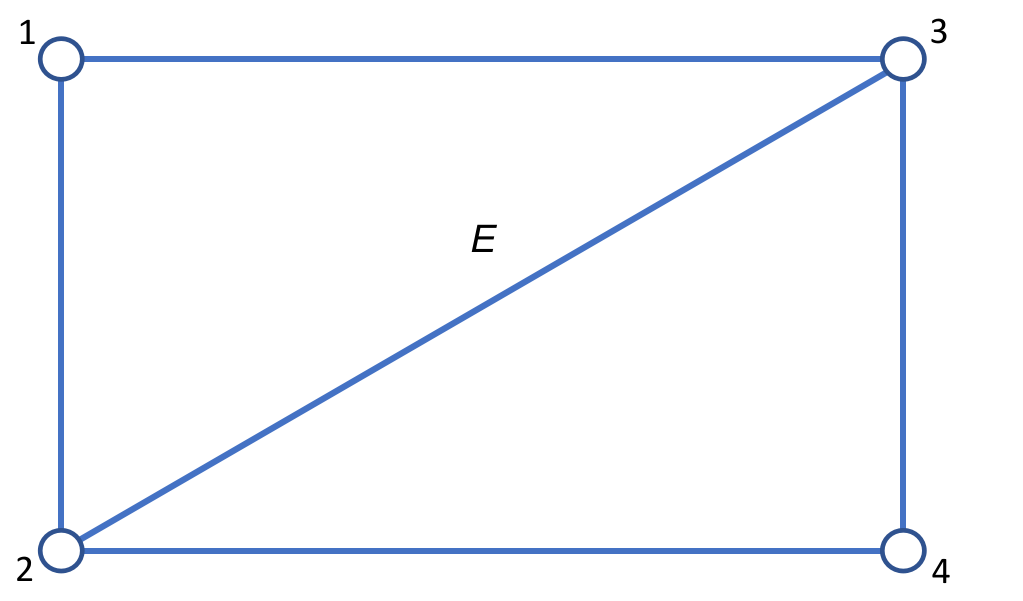
A 2-sphere in which $n$ discs are removed is a $n$ -holed sphere. We make a 2d ideal triangulation of the $n$ -holed sphere such that edges in the triangulation end at the boundary of the holes. For example, the boundary of the ideal tetrahedron is an ideal triangulation of the 4-holed sphere. The 2d ideal triangulation has $3(n-2)$ edges on the $n$ -holed sphere. Each edge $E$ associates to a coordinate $z_{E}$ of the moduli space of framed $\mathrm{SL}(2,\mathbb{C})$ flat connections. A framed flat connection on is a standard flat connection with a choice of $\mathbb{CP}^{1}$ flat section $s_{i}$ for each hole $i$ . The section $s_{i}$ obeying the condition $\nabla s_{i}=0$ ( $\nabla$ is the flat connection) and is the eigenvector of monodromy around the hole $i$ . $s_{i}$ associates to the eigenvalue $\lambda_{i}=e^{L_{i}}$ of the monodromy matrix. Given a framed flat connection, $z_{E}$ is a cross-ratio of 4 flat section $s_{1},s_{2},s_{3},s_{4}$ associated to the vertices of the quadrilateral containing $E$ as the diagonal (see FIG.3),

\displaystyle z_{E}=\frac{\left\langle s_{1}\wedge s_{2}\right\rangle\left\langle s_{3}\wedge s_{4}\right\rangle}{\left\langle s_{1}\wedge s_{3}\right\rangle\left\langle s_{2}\wedge s_{4}\right\rangle}

(B.1)

where $\left\langle s_{i}\wedge s_{j}\right\rangle$ is an $\mathrm{SL}(2,\mathbb{C})$ invariant volume on $\mathbb{C}^{2}$ , and is computed by parallel transporting $s_{1},\cdots,s_{4}$ to a common point inside the quadrilateral by the flat connection. The coordinates $z_{E}$ for all $E$ are the Fock-Goncharov (FG) coordinates. Our convention is the same as [24, 9]. We often consider a lift of $z_{E}$ to the logarithmic coordinate $Z_{E}$ such that $z_{E}=e^{Z_{E}}$ . At any hole $i$ , $z_{E}$ on the adjacent edges $E$ satisfy

\displaystyle\prod_{E\ \text{at}\ i}(-z_{E})=\lambda_{i}^{2}.

(B.2)

We often use the lift of this relation

\displaystyle\sum_{E\ \text{at}\ i}(Z_{E}-\pi i)=2L_{i}.

(B.3)

Note that $L_{1,\cdots,3}$ in (4.10) are defined with flipped sign.

$\mathrm{SL}(2,\mathbb{C})$ holonomy along any closed path on the $n$ -holed sphere can be expressed as $2\times 2$ matrices whose entries are functions of $\{Z_{E}\}$ by using the “snake rule” [22]: There are three rules for transporting a snake – an arrow pointing from one vertex of the triangle to another with a fin facing inside the triangle, each corresponds to a matrix as follows. (The inverse transportation of each type corresponds to the inverse of the relevant matrix.

\displaystyle\includegraphics[width=110.57327pt]{snake_rule1.pdf}\quad\qquad\includegraphics[width=110.57327pt]{snake_rule2.pdf}\quad\qquad\includegraphics[width=132.68929pt]{snake_rule3}\,.

(B.4)

A snake represents a projective basis $(v_{1},v_{2})$ given by $v_{1}\in\mathbb{C}$ at the tail of the snake and $v_{2}\in\mathbb{C}$ at the head of the snake, such that either $v_{1}+v_{2}$ (type I: blue) or $v_{1}-v_{2}$ (type I: red) at the third vertex of the triangle. Type I and II correspond to transporting a snake within a triangle and III correspond to moving a snake from one triangle to its adjacent triangle. The transformation matrix acts on the projective basis $(v_{1},v_{2})^{T}$ by left multiplication. Any holonomy $H(\gamma)$ of a closed loop $\gamma$ can be calculated by multiplying the matrices from right to left corresponding to moving a snake along the loop. The holonomy resulting from the snake rule is not $\mathrm{SL}(2,\mathbb{C})$ . The $\mathrm{SL}(2,\mathbb{C})$ holonomy is obtained up to a $\pm$ sign by a lift that can conveniently chosen by normalizing the Type III matrix

\displaystyle\text{Type III:}\qquad\left(\begin{array}[]{cc}e^{-\frac{Z_{E}-\pi i}{2}}&0\\ 0&e^{\frac{Z_{E}-\pi i}{2}}\end{array}\right)\equiv E[Z_{E}].

(B.7)

For any closed path $\gamma_{i}$ around a single hole $i$ , the $\pm$ sign of $H(\gamma_{i})$ can be determined by requiring the trace of $H(\gamma_{i})$ to be

\displaystyle\mathrm{Tr}(H(\gamma_{i}))=e^{\frac{1}{2}\sum_{E\ \text{at}\ i}(Z_{E}-i\pi)}+e^{-\frac{1}{2}\sum_{E\ \text{at}\ i}(Z_{E}-i\pi)}=e^{L_{i}}+e^{-L_{i}}.

(B.8)

This requirements is consistent with (B.3) and the eigenvalue of the monodromy matrix when discussing $s_{i}$ . The fundamental group of the $n$ -holed sphere is generated by $\{\gamma_{i}\}_{i=1,\dots,n}$ , so $\{H(\gamma_{i})\}_{i=1,\dots,n}$ determine all holonomies of closed paths.

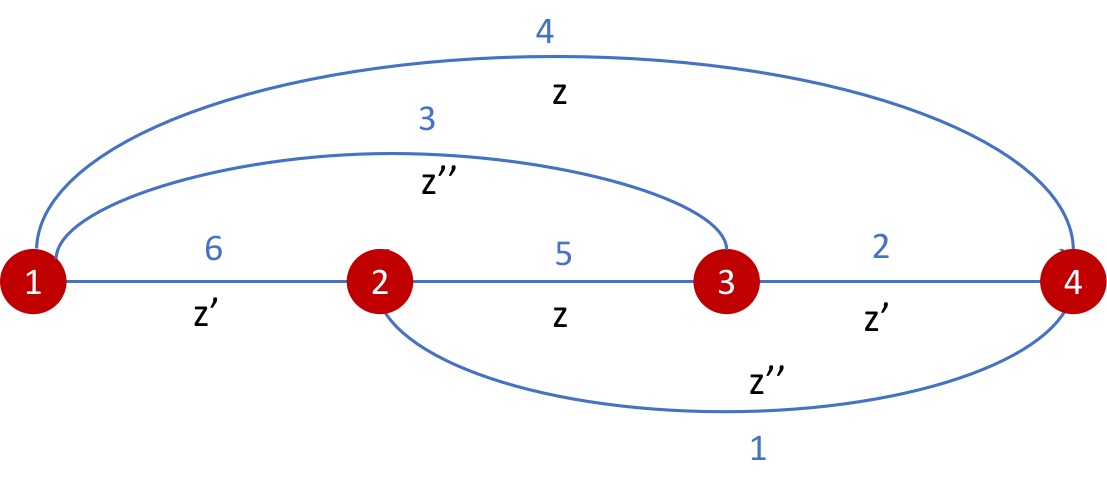
We consider the 4-holed sphere and the ideal triangulation in FIG.4 as an example. The ideal triangulation is tetrahedral since it is the boundary of an ideal tetrahedron. We denote by $\gamma_{i}$ a loop around the hole $i$ oriented counter-clockwisely. All $\gamma_{i}$ share the same base point represented by a snake pointing from the 4th hole to the 2nd hole along the edge 1 with the fin inside the triangle with vertices $2,3,4$ .

$\displaystyle H(\gamma_{4})$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{2}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{4}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{1}\right),$	(B.15)
$\displaystyle H(\gamma_{3})$	$\displaystyle=$	$\displaystyle-\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)^{-1}\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)E\left(Z_{5}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{3}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)^{-1}E\left(Z_{2}\right)^{-1}\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)^{-1},$	(B.30)
$\displaystyle H(\gamma_{2})$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)E\left(Z_{1}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{6}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{5}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)^{-1},$	(B.41)
$\displaystyle H(\gamma_{4})$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)E\left(Z_{1}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)^{-1}\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{4}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{3}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)E\left(Z_{6}\right)$	(B.61)
		$\displaystyle\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)\left(\begin{array}[]{cc}1&0\\ 1&1\\ \end{array}\right)^{-1}E\left(Z_{1}\right){}^{-1}\left(\begin{array}[]{cc}0&1\\ -1&0\\ \end{array}\right)^{-1}.$	(B.61)

They satisfy $\mathrm{Tr}(H(\gamma_{i}))=e^{L_{i}}+e^{-L_{i}}$ and

\displaystyle H(\gamma_{1})H(\gamma_{2})H(\gamma_{3})H(\gamma_{4})=1.

(B.62)

When the 4-holed sphere is the boundary of an ideal tetrahedron, all $H(\gamma_{i})$ are constrained to the identity matrix, since the connection is flat inside the tetrahedron. In this case, all $L_{i}$ vanishes, i.e.

\displaystyle Z_{1}+Z_{2}+Z_{4}=Z_{3}+Z_{4}+Z_{6}=Z_{1}+Z_{5}+Z_{6}=Z_{2}+Z_{3}+Z_{5}=3\pi i

(B.63)

so we can parametrize $z_{e}$ by calling the FG coordinates $z,z^{\prime},z^{\prime\prime}$ occurring in the same counter-clockwise order around any hole, equal on opposite edges, and satisfying ¹⁴¹⁴14We relabel $z_{1}=z_{3}=z^{\prime\prime},\ z_{2}=z_{6}=z^{\prime},\ z_{4}=z_{5}=z$ .

\displaystyle zz^{\prime}z^{\prime\prime}=-1.

(B.64)

The off-diagonal vanishes implies

\displaystyle z^{\prime\prime}+z^{-1}-1=0.

(B.65)

$z,z^{\prime\prime}$ are the symplectic coordinates of the phase space (of flat connections) on the boundary of ideal tetrahedron, with the poisson bracket given by $\{Z^{\prime\prime},Z\}=\{Z,Z^{\prime}\}=\{Z^{\prime},Z^{\prime\prime}\}=2$ . Eq.(B.65) defines the Lagrangian submanifold $\mathcal{L}_{\Delta}$ of the flat connections that can be extended to interior of the tetrahedron.

References

[1] R. M. Kashaev, On the spectrum of Dehn twists in quantum Teichmuller theory, math/0008148.
[2] A. G. Bytsko and J. Teschner, R operator, coproduct and Haar measure for the modular double of U(q)(sl(2,R)), Commun. Math. Phys. 240 (2003) 171–196, [math/0208191].
[3] I. Nidaiev and J. Teschner, On the relation between the modular double of $U_{q}(sl(2,R))$ and the quantum Teichmueller theory, arXiv:1302.3454.
[4] B. Ponsot and J. Teschner, Clebsch-Gordan and Racah-Wigner coefficients for a continuous series of representations of U(q)(sl(2,R)), Commun. Math. Phys. 224 (2001) 613–655, [math/0007097].
[5] J. Teschner, An Analog of a modular functor from quantized teichmuller theory, math/0510174.
[6] J. Teschner, On the relation between quantum Liouville theory and the quantized Teichmuller spaces, Int. J. Mod. Phys. A 19S2 (2004) 459–477, [hep-th/0303149].
[7] S. E. Derkachov and L. D. Faddeev, 3j-symbol for the modular double of $SL_{q}(2,\mathbb{R})$ revisited, J. Phys. Conf. Ser. 532 (2014) 012005, [arXiv:1302.5400].
[8] T. P. Killingback, Quantization of SL(2,R) Chern-Simons theory, Commun. Math. Phys. 145 (1992) 1–16.
[9] J. Teschner, Supersymmetric gauge theories, quantisation of moduli spaces of flat connections, and Liouville theory, arXiv:1412.7140.
[10] J. Ellegaard Andersen and R. Kashaev, Complex Quantum Chern-Simons, ArXiv e-prints (Sept., 2014) [arXiv:1409.1208].
[11] J. E. Andersen and S. Marzioni, Level n teichmüller tqft and complex chern-simons theory, arXiv:1612.06986.
[12] T. Dimofte, Complex Chern-Simons Theory at Level k via the 3d-3d Correspondence, Commun. Math. Phys. 339 (2015), no. 2 619–662, [arXiv:1409.0857].
[13] E. Witten, Quantization of chern-simons gauge theory with complex gauge group, Communications in Mathematical Physics 137 (1991), no. 1 29–66.
[14] A. Goncharov and L. Shen, Quantum geometry of moduli spaces of local systems and representation theory, 2022.
[15] P. Podleś and S. L. Woronowicz, Quantum deformation of Lorentz group, Comm. Math. Phys. 130 (1990), no. 2 381–431.
[16] E. Buffenoir and P. Roche, Harmonic analysis on the quantum Lorentz group, Commun.Math.Phys. 207 (1999) 499–555, [q-alg/9710022].
[17] E. Buffenoir, K. Noui, and P. Roche, Hamiltonian quantization of Chern-Simons theory with SL(2,C) group, Class.Quant.Grav. 19 (2002) 4953, [hep-th/0202121].
[18] M. Han, Four-dimensional spinfoam quantum gravity with a cosmological constant: Finiteness and semiclassical limit, Phys. Rev. D 104 (2021), no. 10 104035, [arXiv:2109.00034].
[19] H. M. Haggard, M. Han, W. Kaminski, and A. Riello, SL(2,C) Chern-Simons Theory, a non-Planar Graph Operator, and 4D Loop Quantum Gravity with a Cosmological Constant: Semiclassical Geometry, Nucl. Phys. B900 (2015) 1–79, [arXiv:1412.7546].
[20] H. M. Haggard, M. Han, W. Kaminski, and A. Riello, Four-dimensional Quantum Gravity with a Cosmological Constant from Three-dimensional Holomorphic Blocks, Phys. Lett. B752 (2016) 258–262, [arXiv:1509.00458].
[21] M. Han and Q. Pan, Melonic Radiative Correction in Four-Dimensional Spinfoam Model with Cosmological Constant, arXiv:2310.04537.
[22] T. Dimofte, D. Gaiotto, and R. van der Veen, RG Domain Walls and Hybrid Triangulations, Adv.Theor.Math.Phys. 19 (2015) 137–276, [arXiv:1304.6721].
[23] V. V. Fock and A. B. Goncharov, The quantum dilogarithm and representations of quantum cluster varieties, Inventiones Mathematicae 175 (Sept., 2008) 223–286, [math/0702397].
[24] D. Gaiotto, G. W. Moore, and A. Neitzke, Wall-crossing, Hitchin Systems, and the WKB Approximation, arXiv:0907.3987.

Representations of a quantum-deformed Lorentz algebra, Clebsch-Gordan map, and Fenchel-Nielsen representation of quantum complex flat connections at level-𝒌\bm{k}

Abstract

1 Introduction

2 Quantum torus algebra and the representation at level-kk

3 Representation of a q-deformed Lorentz algebra

3.1 The representation

3.2 The Clebsch-Gordan decomposition

Lemma 3.1.

Proof.

Lemma 3.2.

Proof.

Lemma 3.3.

Proof.

4 Quantum flat connections on 4-holed sphere

4.1 Fock-Goncharov coordinates and quantization

4.2 S-cycle trace operator

4.3 T-cycle trace operator

5 Eigenstates of the trace operators

Theorem 5.1.

5.1 Periodic states

Lemma 5.2.

Proof.

Lemma 5.3.

Proof.

5.2 Anti-periodic states

6 Changing triangulation

Acknowledgements

Appendix A Quantum dilogarithm

Appendix B Fock-Goncharov coordinate and holonomies

References

Representations of a quantum-deformed Lorentz algebra, Clebsch-Gordan map, and Fenchel-Nielsen representation of quantum complex flat connections at level- $\bm{k}$

2 Quantum torus algebra and the representation at level- $k$