Representation Magnitude has a Liability to Privacy Vulnerability
Abstract
The privacy-preserving approaches to machine learning (ML) models have made substantial progress in recent years. However, it is still opaque in which circumstances and conditions the model becomes privacy-vulnerable, leading to a challenge for ML models to maintain both performance and privacy. In this paper, we first explore the disparity between member and non-member data in the representation of models under common training frameworks. We identify how the representation magnitude disparity correlates with privacy vulnerability and address how this correlation impacts privacy vulnerability. Based on the observations, we propose Saturn Ring Classifier Module (SRCM), a plug-in model-level solution to mitigate membership privacy leakage. Through a confined yet effective representation space, our approach ameliorates models’ privacy vulnerability while maintaining generalizability. The code of this work can be found here: https://github.com/JEKimLab/AIES2024˙SRCM
Introduction
Machine learning has a profound impact on society, touching various aspects of our lives. It has gained significant influence in many fields, such as medical care, logistics, and knowledge dissemination. However, uncertainty in machine learning, which brings new risks and challenges to our society, disturbs its positive impact in more fields. Among many, we focus on privacy vulnerability. The public and related researchers’ concerns about the privacy security of machine learning have increased as the ML technique plays an increasingly important role in our lives. Undoubtedly, safe and trustworthy data privacy preservation can build trust among the public and stakeholders, fostering the responsible and ethical use of machine learning technologies.
Despite the great advancement of machine learning, recent works (Chen et al. 2020; Zhang et al. 2020; Yang, Gohari, and Topcu 2023) have shown a risk of privacy leakage in applications of machine learning models. Some studies (Shokri et al. 2017; Salem et al. 2019; Del Grosso et al. 2022) have successfully developed a proxy attacker to steal the membership privacy of a victim model by imitating the training process of the victim model. Besides, some other studies (Tramèr et al. 2016; Kariyappa, Prakash, and Qureshi 2021; Truong et al. 2021; Sanyal, Addepalli, and Babu 2022) explored how to steal a well-trained model’s information even without training data and knowing the model’s architectural information. Despite the modern models’ great performance, such potential risks make them difficult to apply in privacy-sensitive applications.
In particular, membership inference attack (MIA) is widespread due to its simple prerequisites that usually require only prediction probabilities or even final predictions. In contrast, other privacy attacks are harder to deploy in the real world because of their more restricted prerequisites (e.g., gradient-based data reconstruction attacks (Chen and Campbell 2021; Zhu and Blaschko 2021)). The fundamentals of the membership inference attacks lie in the ability to distinguish the ML models’ behaviors between on training and testing data that are also called ‘in’ and ‘out’ membership, or ‘member’ and ‘non-member’ data, respectively. For instance, the prediction confidence is significantly higher on ‘in’ data than ‘out’ data. Behavioral inconsistencies exist in different aspects, such as prediction confidence, robustness, etc. Based on such discrepancies, an attacker can determine whether a sample is ‘in’ membership or not.
Many existing defense mechanisms for ML models put lots of preconditions on the training procedure, such as oversaturated data or multiplying model costs. They have achieved privacy protection ability from different perspectives, e.g., unlearning partial data, aligning ‘in’ and ‘out’ predictions, and reducing the degree of fitting members. However, they still have some limitations. For example, some studies (Nasr, Shokri, and Houmansadr 2018; Shejwalkar and Houmansadr 2021) require a lot of additional data, which directly leads to a loss of models’ generalizability. Or, some others (Abadi et al. 2016; Wang et al. 2021; Yuan and Zhang 2022; Tang et al. 2022) require significantly more computational cost during the inference or training phases. The other group of work (Jia et al. 2019) is not effective on every MIAs (Choquette-Choo et al. 2021).
The recent non-model-internal privacy defense approaches (Jia et al. 2019; Tang et al. 2022; Yang et al. 2023) using external modules to wrap the model and regenerate or decorate predictions, and they show promising competitiveness. However, from a long-term view, the defense that directly impacts the model’s prediction distribution is worth exploring. On one hand, obfuscation-based defense solutions (Jia et al. 2019; Tang et al. 2022; Yang et al. 2023) can provide effective privacy protection capabilities against certain types of attacks while the direct-model-impact solutions are general for MIAs since they consider the model distribution rather than specific attacks. On the other hand, the direct-model-impact solution could lead to a better model design standard or training paradigm. Besides, they could also be combined with any model-external privacy defense approaches to achieve better privacy-preserving ability.
Hence, in this paper, we propose a model-level plug-in solution against membership privacy attack, called Saturn Rings Classifier Module (SRCM). The module focuses on the model’s representation space itself so that it can directly affect the final prediction of both ‘in’ and ‘out’ data. The main idea is to make ‘in’ and ‘out’ data indistinguishable by directly transforming the magnitude of hidden feature vectors of the two groups of data to specific ranges. By limiting the classification model’s representation space, SRCM can significantly improve the model’s privacy protection ability while maintaining generalizability. In summary, we make the following contributions:
-
•
To the best of our knowledge, our work is the first to study how the representation magnitude affects membership privacy leakage.
-
•
Based on the observation, we propose Saturn Rings Classifier Module that mitigates the privacy vulnerability with no loss of generalizability.
-
•
We extensively evaluate SRCM and show that it not only can improve the privacy-preserving ability but also can be combined with non-model-internal level approaches (common existing approaches) to boost privacy protection.



Related Work
Membership Inference Attacks
(Shokri et al. 2017) proposed the shadow model technique to simulate the prediction distribution of the target model. (Salem et al. 2019) proposed three kinds of attack approaches with lower-cost or less-preconditions. (Yuan and Zhang 2022) tried to add adversarial samples to enhance the MIAs. Besides NN-based technique mentioned above that relies upon machine learning techniques to develop a proxy as the attacker, (Choquette-Choo et al. 2021) designed several label-only MIAs to reduce the attack requirements. (Song and Mittal 2021) proposed modified cross-entropy (Mentr.) as a more sensitive attack metric. (Del Grosso et al. 2022) introduced adversarial attacks into MIAs via the difference of the model predictions to a sample and its adversarial version.
Privacy Defense with Direct Impact on Models
Adversarial regularization (Nasr, Shokri, and Houmansadr 2018) is one of the earliest studies that tried defense for MIAs via simulating the offensive behavior. (Salem et al. 2018) proposed dropout and model stacking approaches to defend from MIAs. Distillation for membership privacy (DMP) defense method (Shejwalkar and Houmansadr 2021) selects ‘reference’ data and generates proper labels to train a protected model. (Hu et al. 2022) tried to protect privacy by producing synthetic data through GAN. (Yuan and Zhang 2022) explored pruning and found that it does not help the membership privacy, while (Wang et al. 2021) concluded a contradiction. (Chen, Yu, and Fritz 2022) were aware of the fitting priority problem and proposed RelaxLoss to help the model keep a trade-off between privacy and generalizability. (Fang and Kim 2024) proposed an approach to discriminate features among classes in the representation space while relaxing the model. (Zhou, Nezhadarya, and Ba 2022) tried to select the most valuable training data to help the model avoid memorizing the entire training set. (Tarun et al. 2023) made the model unlearn the data in forgetting needs via alignment between models trained with and without sensitive data. (Chundawat et al. 2023) tried to make the student network forget specific sub-datasets through two differently trained teacher networks.
Prior studies have achieved great progress in privacy preservation via novel training diagrams or external decorators. However, discussion on the impact of architectures of neural networks remains insufficient. Hence, we study factors of modules in neural network architectures that impact privacy leakages in this paper.
Problem Formulation
In our study, we take into account classification tasks. In a scenario of membership inference attacks, an attacker basically tries to determine if a sample is a member of the training dataset by querying the target model (a.k.a., victim model). The membership inference attacks to a target model, , where and respectively denote the number of input features and task classes, can be formulated as:
| (1) |
where denotes a binary classification where the attacker outputs when the input is predicted as a member of the training set used for the target model , and otherwise. The MIAs function varies a lot according to the attack schemes. For NN-based MIAs, is an ML model that uses the predictions of the target model as inputs. In contrast, when the attack scheme is based on some other metrics (such as threshold-based MIAs), the MIAs function is a manual set function that computes the corresponding metrics and compares them with the threshold selected by statistical results via some techniques, such as using shadow models.
Methodology
From Representation Space to Privacy
To begin with, we ought to ask what makes the MIAs successful to gain the training membership information of the target model (a.k.a victim model.) One consensus is that models behave differently on the members and non-members. However, the causes of the inconsistent behavior can vary. One of the causes can be attributed to the confidence gap. (Yuan and Zhang 2022) found out that class-level prediction confidence gaps often exist between member and non-member data in all classes. In a machine learning model, the degree of prediction confidence directly depends on how distant the sample’s represented position of the logits in the model’s representation space is from the decision boundary.
Then, does the disparity in the prediction results only come from the final classification layer? Clearly, the answer is no since if the classification layer receives similar inputs produced by the prior layers, then the prediction results should be similar. Due to logits being directly correlated to probabilities, their inevitable consistency makes it difficult to separate irrelevant and relevant factors for our goal. Another reason why the bottleneck layer matters is that it is effective in showing the overall distribution, and most network architectures have common bottleneck layers, naturally improving the universality of the empirical conclusion. Therefore, we move our attention to the deep features extracted from a bottleneck layer - usually the 2nd or 3rd last layer. A feature vector can be decomposed into magnitude (the distance to the origin) and direction (a.k.a. angle). The angle, which directly determines if a sample is located within a class’ decision area, has been widely explored as an important factor in classification models (Liu et al. 2016; Wang et al. 2018b). Unlike them, we question if the representation magnitude has such a significant relationship between decision boundaries and privacy.
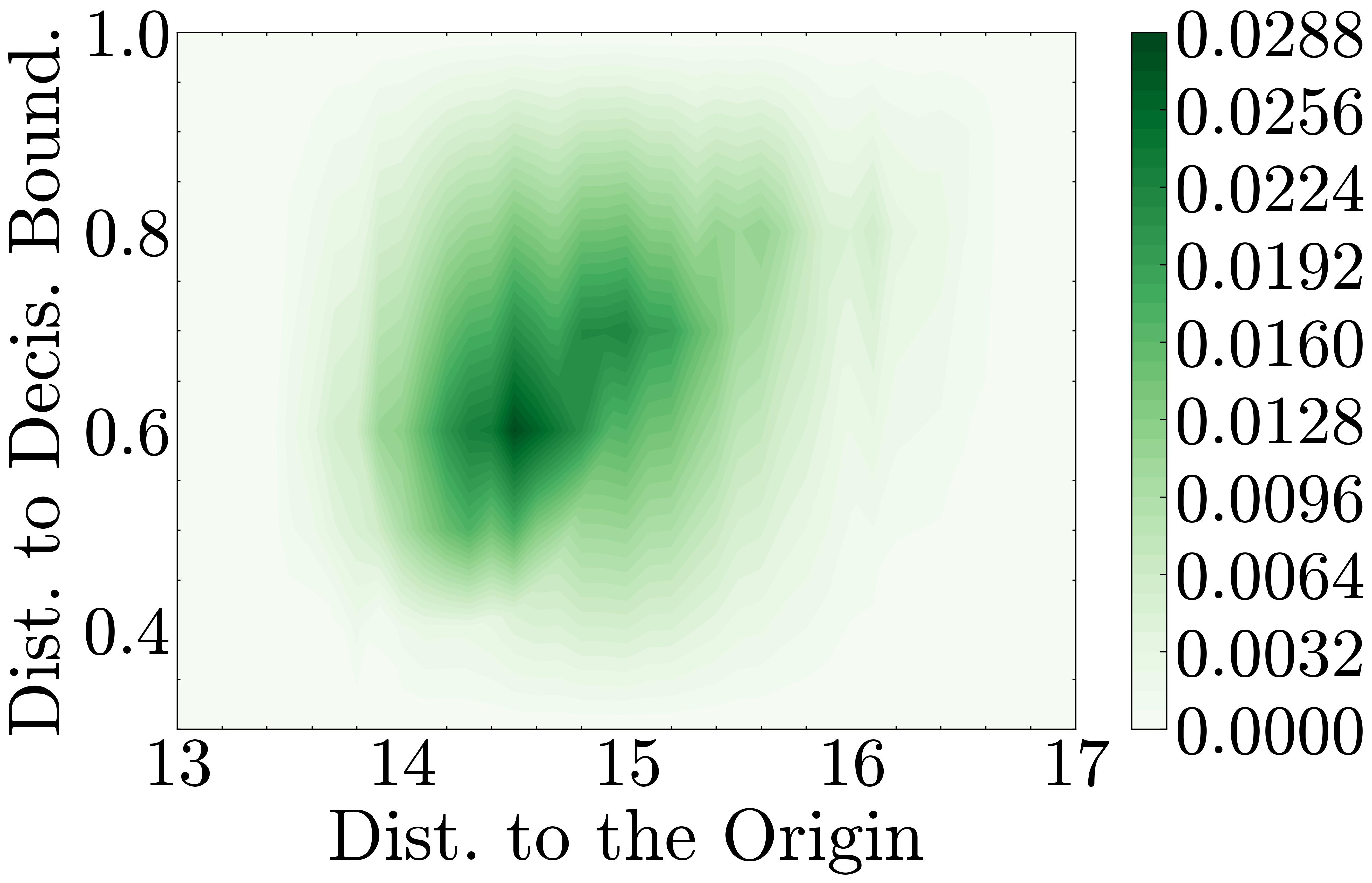
To further explore the relationship between distance to the decision boundary and MIAs accuracy, we visualize the sample-level distribution of the training and test sets. Fig. 1 shows the sample-level prediction results of MIAs accuracy vs. distance to the decision boundary, and distance to the origin vs. decision boundary. Trained with vanilla cross-entropy loss, the model’s prediction and attack distributions differ on members and non-members. On members, the model and the attacker are highly confident in all data. However, on non-members, the MIAs accuracy decreases when the sample becomes farther from the decision boundary, which indicates that the samples become closer to the training data. In Fig. 1(c), we find that the distance to the origin is uncorrelated to the distance to the decision boundary in members, while they are positively correlated (although not linearly) in non-member data as shown in Fig. 1(d).
We conjecture it is mainly due to the model using magnitude to take shortcuts in order to easily classify the members during training. Therefore, it is necessary to restrict the way of representation to guide the model to better representation in training and evaluation. To achieve it, we propose Saturn Rings Classifier Module (SRCM) in the next section.
Saturn Rings Classifier Module
Traditional activation functions (e.g., ReLU family (Agarap 2019; Clevert, Unterthiner, and Hochreiter 2016)) and normalization layers (Ioffe and Szegedy 2015; Ba, Kiros, and Hinton 2016; Ulyanov, Vedaldi, and Lempitsky 2017; Wu and He 2018) are mainly for solving overfitting and underfitting problems. However, they cannot avoid the occurrence of privacy leakage since they do not consider prediction alignment on the train and test sets. Unlike them, we propose the Saturn Rings Classifier Module (SRCM) to help the model’s behavioral alignment in this section.

Saturn Rings Activation Function (SR)
To solve the under-confidence problem of non-member data, we designed the Saturn Rings Activation Function (SR). As depicted in Fig. 2, the SR is composed of two n-sphere (2D in the figure) boundaries with radiuses and (), respectively. The gap . These boundaries delimit the representation space to the non-intersecting closed region they enclose, forming an annulus when . SR can be formulated as follows:
| (2) |
where is the norm function. The boundary is intuitive that there should be a low boundary to guarantee that all samples, especially the non-members, stay far enough from the origin so that they are more likely to be predicted with higher confidence during evaluation. However, the single boundary is practically ineffective when the model is in a high computational complexity (i.e., many more parameters or more complex connections.) Due to the huge computation requirement of these days’ neural networks, models tend to push the training samples further away from the origin during training, leading to enlarging the gap between members and non-members. Therefore, for an outer boundary is encouraged to construct a closed representation space.
To further explain the correlation relationship between the capacity of representation space ( denotes the dimension of the vector space), we discuss its relationship between the inner boundary radius, , and the outer boundary radius, . We first establish their relationship within a 2D vector space and then generalize it to an n-dimensional vector space. For a 2D vector space, can be formulated as follows:
| (3) |
Similarly, in 4D vector space,
| (4) |
Accordingly, we find that the would be always proportional to the difference of powers between and . Using the ‘Difference of Powers Formula,’ we can obtain their relationship in n-dimensional space:
| (5) |
Due to the constraint that SR is supposed to limit the distance to the origin, should not be too large. Therefore, the capacity of the representation space is primarily determined by . This indicates that, to maintain the representation space capacity, when we significantly reduce , we only need to slightly increase , and vice versa.
Magnitude Normalized Linear Layer (LinearNorm)
Although some studies (Liu et al. 2016; Wang et al. 2018a, b; Deng et al. 2019; Sun et al. 2020; Meng et al. 2021; Kim, Jain, and Liu 2022) were aware that the classification layer’s weights’ magnitude and direction have different impacts on the model’s generalization ability in the training phase, research on the bottleneck layer’s magnitude’s impact on member and non-member data during training and evaluation is still unexplored. Here, we discuss how the bottleneck layer’s outputs’ magnitude interacts with the classification layer’s weights.
There are two potential placements for SR: after or before the classification linear layer. If placed after the classification layer, SR can work individually, as it directly affects the magnitude of the logits. In contrast, if we simply apply SR prior to the standard classification layer, the classification layer may rescale the magnitude during training, resulting in SR being ineffective. To avoid this situation, we propose Magnitude Normalized Linear Layer (LinearNorm) (also see Algorithm 1). For the sake of notational simplicity, we use to denote the classification model’s last 2nd layer’s output of an input , to denote the logits, and to denote the weights matrix, and to denote a bias of the classification layer. Therefore, the logits can be computed as follows:
| (6) |
If is a vector in dimensions, then is a matrix for a -class classification task. The can be decomposed to , where is a vector with elements. Then, for the -th class, we can obtain its corresponding logit as follows:
| (7) |
where is the angle between vector and , and is the -th element of . Therefore, the logits depend on two factors: the magnitude and the direction. Although the magnitude of is constrained by and in Eq. 2, a learnable magnitude could render this restriction ineffective, particularly for large models. Hence, a model with SR before the classification layer must normalize all s. Accordingly,
| (8) |
where is a unit vector with the same direction of . To simplify the computation, we use = instead of . Therefore, the LinearNorm layer can be represented as follows:
| (9) |
An additional advantage using rather than is that it can achieve less accuracy loss since the module does not indicate all feature dimensions with the same importance (i.e., larger weights are regarded to carry more important features) while the fairness always requires trade-offs at the cost of accuracy (Wang, Wang, and Liu 2022).

Three Structural Designs
We design three different structures as shown in Fig. 3. The comparison between Fig. 3 (a) and (b) can justify where SR should be placed. Comparison between Fig. 3 (b) and (c) can determine whether LinearNorm works in the evaluation stage. Note that there is an additional linear layer in Fig. 3 (b) and (c) to mitigate the impact of existing various activation functions in various architectures. For Fig. 3 (b) and (c), a dual mode LinearNorm is implemented incorporating a switch shown in Algorithm 1.
Experimental Setups
Datasets and Model Architectures
Our approaches and others are evaluated on CIFAR-10, CIFAR-100 (Krizhevsky, Hinton et al. 2009), and Purchase100 (DMDave 2014). CIFAR-10 and CIFAR-100 contain RGB images with a size of . They have 10 and 100 classes, respectively. Purchase100 is a shopping dataset aiming to make appropriate discounts to attract shoppers to buy new products. Derived from a Kaggle challenge called ‘acquire valued shopper,’ Purchase100 contains individuals’ shopping records data. A simplified version in which each individual contains 600 binary features (every feature stands for a product) is applied in our study. All customers’ records are labeled into classes.
In CIFAR-10, we normalize the original training and testing data as the common existing studies did. In CIFAR-100, data normalization, random flipping, and random cropping are applied to enhance the models’ generalization ability and evaluate all approaches under these augmentations. In Purchase100, we directly feed the original data into the models. In all datasets, we first merge training and testing sets. Then, the whole dataset is split into two halves of equal quantity as target and shadow sets. To further make the results fair, all other settings, such as the optimizer and the way of splitting the dataset, remain the same throughout the experiments in each dataset. All experimental results are repeated five times or more (unless stated otherwise.) The default random seed is set to 0 for reproducibility.
As for target models, we evaluate our approaches using VGG11 (Simonyan and Zisserman 2015), ResNet18 (He et al. 2016), and MobileNetV3 (large version) (Howard et al. 2019) on CIFAR. For Purchase100, we apply a small multilayer perceptron (MLP) composed of four linear layers with hidden size and Tanh activation function.
Membership Inference Attacks
In all MIAs approaches, the shadow model technique (Shokri et al. 2017) is applied. Some studies (He et al. 2017; Athalye, Carlini, and Wagner 2018) state that a perfect performance against attacks under ordinary conditions (a.k.a. non-adaptive attacks) is not sufficient to claim that the defense approach is effective. Hence, in this paper, adaptive attacks, which means the target model’s training configurations and defense mechanisms are all known by the attacker, are also applied to evaluate various defense mechanisms’ performance more accurately and conservatively. Besides the settings above, a neural network of four linear layers with hidden layer sizes [128, 64, 64] is applied when using NN-based MIAs. ReLU activation function and dropout technique are also applied to the attack model. Besides NN-based MIAs, we apply metric-based approaches, including Entropy-based method (Entropy) (Salem et al. 2018), Modified Entropy-based method (M-Entropy) (Song and Mittal 2021), and Gradient-based method with regularization (Grad- ) (Rezaei and Liu 2021).
Defense Mechanism for MIA
We compare our approach with a recent approach RelaxLoss (Chen, Yu, and Fritz 2022), and a well-known approach, Adversarial regularization (AdvReg) (Nasr, Shokri, and Houmansadr 2018). Additionally, some other approaches, including Early-stopping, Label-smoothing (Guo et al. 2017; Müller, Kornblith, and Hinton 2019), and Confidence-penalty (Pereyra et al. 2017) are also included in our evaluation for comparison. When using AdvReg approach, the settings follow the original paper to produce the inference attack model.
Common Configurations
For all target and shadow models, stochastic gradient descent (SGD) optimizer with momentum and weight decay is applied to the three datasets. To study the impact of magnitude in deep features, the last global average pooling layer or the 2nd last fully connected layer is chosen.
| CIFAR-10 | CIFAR-100 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Train Tech. | Train | Test | NN | Entr. | M-Entr. | Grad- | Train | Test | NN | Entr. | M-Entr. | Grad- |
| CE (baseline) | 100.00 | 74.83 | 80.26 | 72.53 | 73.62 | 73.52 | 93.98 | 54.48 | 75.57 | 64.94 | 72.40 | 72.21 | |
| AdvReg | 82.13 | 62.51 | 62.76 | 54.19 | 60.67 | 60.37 | 94.70 | 50.70 | 77.88 | 66.58 | 75.60 | 75.29 | |
| RelaxLoss | 79.84 | 71.43 | 59.80 | 55.77 | 57.56 | 58.92 | 83.40 | 54.47 | 69.54 | 60.32 | 67.60 | 68.08 | |
| - (Large) | SCRM (Ours) | 100.00 | 74.63 | 77.10 | 70.32 | 71.78 | 71.74 | 91.91 | 54.39 | 71.41 | 63.14 | 71.06 | 70.64 |
| MobileNetV3 | + RelaxLoss | 84.44 | 73.58 | 60.33 | 56.40 | 58.08 | 58.69 | 83.97 | 54.71 | 67.61 | 58.45 | 66.49 | 67.74 |
| CE (baseline) | 100.00 | 70.31 | 88.09 | 85.91 | 86.44 | 86.31 | 100.00 | 58.06 | 86.88 | 82.96 | 84.04 | 84.20 | |
| AdvReg | 99.95 | 61.89 | 81.58 | 74.99 | 78.74 | 77.57 | 94.24 | 47.94 | 76.11 | 72.36 | 81.45 | 72.06 | |
| RelaxLoss | 91.56 | 69.25 | 77.32 | 71.51 | 72.25 | 73.50 | 91.78 | 57.97 | 78.22 | 73.04 | 75.38 | 76.13 | |
| SCRM (Ours) | 100.00 | 71.43 | 80.35 | 82.17 | 82.78 | 82.67 | 92.86 | 57.91 | 50.00 | 71.65 | 73.38 | 77.05 | |
| ResNet18 | + RelaxLoss | 92.00 | 70.52 | 74.28 | 69.77 | 70.53 | 71.89 | 92.22 | 58.58 | 58.84 | 61.48 | 70.38 | 76.89 |
| CE (baseline) | 100.00 | 76.46 | 76.31 | 74.15 | 74.90 | 75.33 | 99.97 | 53.75 | 85.18 | 81.67 | 83.08 | 83.46 | |
| AdvReg | 99.28 | 69.52 | 72.43 | 64.96 | 69.22 | 69.84 | 99.91 | 50.08 | 89.20 | 87.11 | 89.19 | 77.00 | |
| RelaxLoss | 94.44 | 75.88 | 69.64 | 66.87 | 66.87 | 68.12 | 91.77 | 53.42 | 76.94 | 72.27 | 76.08 | 76.03 | |
| SCRM (Ours) | 100.00 | 75.69 | 57.09 | 72.96 | 73.37 | 74.35 | 98.81 | 53.67 | 82.90 | 76.95 | 80.37 | 81.52 | |
| VGG11 | + RelaxLoss | 95.70 | 75.07 | 61.46 | 66.14 | 66.62 | 67.66 | 89.55 | 52.79 | 75.16 | 69.81 | 73.07 | 75.29 |




Empirical Study



Comparison between Three Designs
We verify our design of SRCM with other variational designing options for proof of concept - one without LinearNorm and the other with a Linear layer in the evaluation phase. Firstly, we design multiple sets of hyper-parameters and show the relationship between testing accuracy and MIAs accuracy. Shown in Fig. 4, we show the impacts of three designs on testing accuracy and MIAs accuracy. It shows that SRCM can preserve privacy best, meaning that the common computing process in the training and testing phase helps the protection of privacy. The results in Fig. 4 are based on the grid search of hyper-parameters combinations. The three structures show the effectiveness of SR and LinearNorm. Omitting LinearNorm layer from SRCM may not be sufficiently effective on ResNet18 because placing it on the end of the model will fully lose its adaptive ability to adjust the magnitude of logits. Meanwhile, it also verifies the effectiveness and necessity of LinearNorm.
The SRCM has been validated as an effective way for privacy preservation. Then, we explore how it changes with various hyper-parameter combinations (radius and radius gap ). As shown in Fig. 5, we explore the relationship between performance (privacy and accuracy) and hyper-parameters (inner radius and radius gap ). We find that a model’s representation space capacity impacts its generalizability and memorizing ability. All three figures of Fig. 5 agree that training, testing, and MIAs accuracy are all positively correlated with . This is aligned with our expectation that the larger the capacity of the feature space is, the greater the degree of representation freedom of the model itself.
From Fig. 5(a) and Fig. 5(b), we note that, unlike network pruning, reducing network capacity by SRCM has a more consistent impact across training and testing accuracy. (In network pruning, either in unstructured magnitude or structured pruning, there is a discrepancy in training and testing accuracy.) This indicates that changing the representation space’s capacity and shape significantly affects the model’s memorizing ability. Since the computation capacity of the other hidden layers is not directly reduced (while network pruning directly reduces the compute capacity), the model can still maintain generalizability. Combined with Fig. 5(c), we can find that a proper range of magnitude can maintain a better accuracy and privacy trade-off. In particular, we empirically found that a ‘sweet spot’ (that is shown in the following subsection) exists in a model’s representation space, allowing the model to gain more privacy with no or little accuracy loss. In other words, this means that a larger range of representation magnitude may achieve limited accuracy improvement while resulting in a significant loss of privacy-preserving ability. It suggests that further reducing the range will result in a greater loss of accuracy with insignificant privacy improvement. It also verifies that a model requires sufficient computational capacity to support its generalizability.
| Model | Train Tech. | Train Acc. | Test Acc. | NN | Entr. | M-Entr. | Grad- |
|---|---|---|---|---|---|---|---|
| CE (baseline) | 99.98 | 91.70 | 51.94 | 56.00 | 56.73 | 56.75 | |
| Early-Stopping | 95.50 | 86.68 | 51.23 | 54.11 | 55.45 | 55.33 | |
| Label-Smoothing | 97.94 | 90.71 | 51.83 | 53.65 | 54.72 | 53.65 | |
| Confidence-Penalty | 97.04 | 90.91 | 50.14 | 53.41 | 54.47 | 52.02 | |
| AdvReg | 99.96 | 88.59 | 51.66 | 56.59 | 58.05 | 58.07 | |
| RelaxLoss | 97.24 | 88.86 | 55.71 | 56.50 | 57.17 | 57.36 | |
| SCRM(Ours) | 98.80 | 90.18 | 52.04 | 55.62 | 57.75 | 57.12 | |
| MLP | +Confidence-Penalty | 96.97 | 90.28 | 50.14 | 53.43 | 54.54 | 52.63 |
More Results and Discussion
In CIFAR-10, as shown in Table. 1, the combination of SRCM and RelaxLoss achieves significant improvement over others. Through experiments on MobileNetV3, SRCM has achieved significant improvements in privacy preservation with minimal accuracy loss. Also, combining with RelaxLoss provides further improvement. Experiments on ResNet18 also show a similar trend. However, trends slightly changed when we conducted the experiments on VGG11. The effect of SRCM becomes less effective than that on other larger neural networks. We attribute it to the insufficient computation capacity of the model, which is verified by the experiments with Purchase100 in Fig. 8. Additional experiments on ResNet18 are shown in Fig. 6. In the figure, Label-smoothing and Confidence-Penalty have a significantly negative impact on the model under NN-Base and two Entropy-based attacks. Interestingly, Confidence-Penalty has a strong defensive effect against Grad- attacks. Label-Smoothing does not have a positive effect in all four MIAs setups. EarlyStopping, AdvReg, and RelaxLoss perform better than the other approaches. In particular, RelaxLoss outperforms the other two approaches. With the combination of RelaxLoss, our approach is even further enhanced since SRCM and RelaxLoss optimize privacy from different perspectives.
In CIFAR-100, similar trends are observed. Compared to that in CIFAR-10, the effectiveness of all methods diminishes as task difficulty increases. As shown in Fig. 7, the impact of AdvReg becomes more limited, especially on NN-Base and M-Entropy. Both SCRM and the combination of SCRM and RelaxLoss achieve outstanding results. One thing to note is that SCRM becomes less effective if the method significantly degrades the model performance (the model must not lose its learnability).
In Purchase100, the trends significantly change. As shown in Table 2, the MIAs AUC scores become significantly lower due to the smaller gap between testing and training sets. As a lightweight network with much fewer parameters than other networks in this study, it achieves significant improvement with Confidence-Penalty and Label-Smoothing over other approaches. This reflects the difference between shallow neural networks and DNN. Due to the weaker fitting ability of the model compared to DNN, RelaxLoss has little effect in this scenario. AdvReg’s regularization mechanism is similar to the Confidence-Penality and starts to achieve the effect after losing some accuracy caused by splitting the training set. Additional results are presented in Fig. 8. Unlike the results in CIFAR, RelaxLoss exhibits a discontinuous trend, which makes it less effective in privacy preservation. Aligned with our hypothesis, SRCM does not achieve significant performance enhancement on such a small model due to the low computation capacity.
| Classifier | ResNet18 | VGG11 | MobileNetV3-Large |
|---|---|---|---|
| Vanilla | 17.80(0.07) | 5.23(0.00) | 8.65(0.10) |
| SRCM | 17.81(0.10) | 5.35(0.02) | 8.83(0.20) |
For efficiency evaluation, we measure a series of models with and without SRCM to show the computational cost of our approach. Seen in Table. 3, SRCM shows minor inference time increase. Compared with the model’s original inference cost, the difference is insignificant.
In summary, SRCM has a significant privacy-preserving impact on the models with sufficient computing capacity and can incorporate many existing methods to achieve cooperative privacy enhancement. Its effectiveness in those models suggests that redundant computing capacity can potentially be converted into privacy-preserving capabilities to some extent.
Conclusion
We explored the privacy-leaking factors and presented a lightweight yet effective neural network component, SRCM, which mitigates the privacy vulnerability of over-parameterized classification models by restricting models’ representation capacity. The insight of this work is that privacy vulnerability can be mitigated by aligning the factors that are in disparities between members and non-members. Through experiments, we validated our hypothesis and the effectiveness and ease of use of our approach. Importantly, we found new possibilities for making use of the models’ oversaturated computation capacity.
References
- Abadi et al. (2016) Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H. B.; Mironov, I.; Talwar, K.; and Zhang, L. 2016. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC conference on computer and communications security, 308–318.
- Agarap (2019) Agarap, A. F. 2019. Deep Learning using Rectified Linear Units (ReLU). arXiv:1803.08375.
- Athalye, Carlini, and Wagner (2018) Athalye, A.; Carlini, N.; and Wagner, D. 2018. Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples. In Proceedings of the 35th International Conference on Machine Learning. PMLR.
- Ba, Kiros, and Hinton (2016) Ba, J. L.; Kiros, J. R.; and Hinton, G. E. 2016. Layer Normalization. arXiv:1607.06450.
- Chen and Campbell (2021) Chen, C.; and Campbell, N. D. F. 2021. Understanding Training-Data Leakage from Gradients in Neural Networks for ImageClassifications. In NeurIPS Workshop Privacy in Machine Learning.
- Chen, Yu, and Fritz (2022) Chen, D.; Yu, N.; and Fritz, M. 2022. RelaxLoss: Defending Membership Inference Attacks without Losing Utility. In International Conference on Learning Representations.
- Chen et al. (2020) Chen, D.; Yu, N.; Zhang, Y.; and Fritz, M. 2020. Gan-leaks: A taxonomy of membership inference attacks against generative models. In Proceedings of the 2020 ACM SIGSAC conference on computer and communications security, 343–362.
- Choquette-Choo et al. (2021) Choquette-Choo, C. A.; Tramer, F.; Carlini, N.; and Papernot, N. 2021. Label-Only Membership Inference Attacks. In Proceedings of the 38th International Conference on Machine Learning.
- Chundawat et al. (2023) Chundawat, V. S.; Tarun, A. K.; Mandal, M.; and Kankanhalli, M. 2023. Can bad teaching induce forgetting? Unlearning in deep networks using an incompetent teacher. In Proceedings of the AAAI Conference on Artificial Intelligence.
- Clevert, Unterthiner, and Hochreiter (2016) Clevert, D.; Unterthiner, T.; and Hochreiter, S. 2016. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). In Bengio, Y.; and LeCun, Y., eds., 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, May 2-4, 2016, Conference Track Proceedings.
- Del Grosso et al. (2022) Del Grosso, G.; Jalalzai, H.; Pichler, G.; Palamidessi, C.; and Piantanida, P. 2022. Leveraging adversarial examples to quantify membership information leakage. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 10399–10409.
- Deng et al. (2019) Deng, J.; Guo, J.; Xue, N.; and Zafeiriou, S. 2019. Arcface: Additive angular margin loss for deep face recognition. In CVPR.
- DMDave (2014) DMDave, W. C., Todd B. 2014. Acquire Valued Shoppers Challenge.
- Fang and Kim (2024) Fang, X.; and Kim, J.-E. 2024. Center-Based Relaxed Learning Against Membership Inference Attacks. In The 40th Conference on Uncertainty in Artificial Intelligence.
- Guo et al. (2017) Guo, C.; Pleiss, G.; Sun, Y.; and Weinberger, K. Q. 2017. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning.
- He et al. (2016) He, K.; Zhang, X.; Ren, S.; and Sun, J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778.
- He et al. (2017) He, W.; Wei, J.; Chen, X.; Carlini, N.; and Song, D. 2017. Adversarial example defense: Ensembles of weak defenses are not strong. In 11th USENIX workshop on offensive technologies (WOOT 17).
- Howard et al. (2019) Howard, A.; Sandler, M.; Chen, B.; Wang, W.; Chen, L.-C.; Tan, M.; Chu, G.; Vasudevan, V.; Zhu, Y.; Pang, R.; Adam, H.; and Le, Q. 2019. Searching for MobileNetV3. In 2019 IEEE/CVF International Conference on Computer Vision (ICCV), 1314–1324.
- Hu et al. (2022) Hu, L.; Li, J.; Lin, G.; Peng, S.; Zhang, Z.; Zhang, Y.; and Dong, C. 2022. Defending against membership inference attacks with high utility by GAN. IEEE Transactions on Dependable and Secure Computing.
- Ioffe and Szegedy (2015) Ioffe, S.; and Szegedy, C. 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning - Volume 37, ICML’15, 448–456. JMLR.org.
- Jia et al. (2019) Jia, J.; Salem, A.; Backes, M.; Zhang, Y.; and Gong, N. Z. 2019. Memguard: Defending against black-box membership inference attacks via adversarial examples. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security, 259–274.
- Kariyappa, Prakash, and Qureshi (2021) Kariyappa, S.; Prakash, A.; and Qureshi, M. K. 2021. Maze: Data-free model stealing attack using zeroth-order gradient estimation. In CVPR, 13814–13823.
- Kim, Jain, and Liu (2022) Kim, M.; Jain, A. K.; and Liu, X. 2022. Adaface: Quality adaptive margin for face recognition. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 18750–18759.
- Krizhevsky, Hinton et al. (2009) Krizhevsky, A.; Hinton, G.; et al. 2009. Learning multiple layers of features from tiny images.
- Liu et al. (2016) Liu, W.; Wen, Y.; Yu, Z.; and Yang, M. 2016. Large-Margin Softmax Loss for Convolutional Neural Networks. In International Conference on Machine Learning, 507–516. PMLR.
- Meng et al. (2021) Meng, Q.; Zhao, S.; Huang, Z.; and Zhou, F. 2021. Magface: A universal representation for face recognition and quality assessment. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 14225–14234.
- Müller, Kornblith, and Hinton (2019) Müller, R.; Kornblith, S.; and Hinton, G. E. 2019. When does label smoothing help? In Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc.
- Nasr, Shokri, and Houmansadr (2018) Nasr, M.; Shokri, R.; and Houmansadr, A. 2018. Machine learning with membership privacy using adversarial regularization. In 2018 ACM SIGSAC conference on computer and communications security.
- Pereyra et al. (2017) Pereyra, G.; Tucker, G.; Chorowski, J.; Łukasz Kaiser; and Hinton, G. 2017. Regularizing Neural Networks by Penalizing Confident Output Distributions. arXiv:1701.06548.
- Rezaei and Liu (2021) Rezaei, S.; and Liu, X. 2021. On the difficulty of membership inference attacks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 7892–7900.
- Salem et al. (2018) Salem, A.; Zhang, Y.; Humbert, M.; Berrang, P.; Fritz, M.; and Backes, M. 2018. ML-Leaks: Model and Data Independent Membership Inference Attacks and Defenses on Machine Learning Models. arXiv:1806.01246.
- Salem et al. (2019) Salem, A.; Zhang, Y.; Humbert, M.; Berrang, P.; Fritz, M.; and Backes, M. 2019. ML-Leaks: Model and Data Independent Membership Inference Attacks and Defenses on Machine Learning Models.
- Sanyal, Addepalli, and Babu (2022) Sanyal, S.; Addepalli, S.; and Babu, R. V. 2022. Towards data-free model stealing in a hard label setting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 15284–15293.
- Shejwalkar and Houmansadr (2021) Shejwalkar, V.; and Houmansadr, A. 2021. Membership privacy for machine learning models through knowledge transfer. In Proceedings of the AAAI conference on artificial intelligence, volume 35, 9549–9557.
- Shokri et al. (2017) Shokri, R.; Stronati, M.; Song, C.; and Shmatikov, V. 2017. Membership inference attacks against machine learning models. In IEEE symposium on security and privacy (SP).
- Simonyan and Zisserman (2015) Simonyan, K.; and Zisserman, A. 2015. Very Deep Convolutional Networks for Large-Scale Image Recognition. In 3rd International Conference on Learning Representations, ICLR.
- Song and Mittal (2021) Song, L.; and Mittal, P. 2021. Systematic evaluation of privacy risks of machine learning models. In 30th USENIX Security Symposium (USENIX Security 21), 2615–2632.
- Sun et al. (2020) Sun, Y.; Cheng, C.; Zhang, Y.; Zhang, C.; Zheng, L.; Wang, Z.; and Wei, Y. 2020. Circle loss: A unified perspective of pair similarity optimization. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition.
- Tang et al. (2022) Tang, X.; Mahloujifar, S.; Song, L.; Shejwalkar, V.; Nasr, M.; Houmansadr, A.; and Mittal, P. 2022. Mitigating Membership Inference Attacks by Self-Distillation Through a Novel Ensemble Architecture. In 31st USENIX Security Symposium.
- Tarun et al. (2023) Tarun, A. K.; Chundawat, V. S.; Mandal, M.; and Kankanhalli, M. 2023. Deep Regression Unlearning. In Proceedings of the 40th International Conference on Machine Learning, 33921–33939.
- Tramèr et al. (2016) Tramèr, F.; Zhang, F.; Juels, A.; Reiter, M. K.; and Ristenpart, T. 2016. Stealing Machine Learning Models via Prediction APIs. In 25th USENIX Security Symposium. ISBN 978-1-931971-32-4.
- Truong et al. (2021) Truong, J.-B.; Maini, P.; Walls, R. J.; and Papernot, N. 2021. Data-free model extraction. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 4771–4780.
- Ulyanov, Vedaldi, and Lempitsky (2017) Ulyanov, D.; Vedaldi, A.; and Lempitsky, V. 2017. Instance Normalization: The Missing Ingredient for Fast Stylization. arXiv:1607.08022.
- Wang et al. (2018a) Wang, F.; Cheng, J.; Liu, W.; and Liu, H. 2018a. Additive margin softmax for face verification. IEEE Signal Processing Letters, 25(7): 926–930.
- Wang et al. (2018b) Wang, H.; Wang, Y.; Zhou, Z.; Ji, X.; Gong, D.; Zhou, J.; Li, Z.; and Liu, W. 2018b. Cosface: Large margin cosine loss for deep face recognition. In CVPR.
- Wang, Wang, and Liu (2022) Wang, J.; Wang, X. E.; and Liu, Y. 2022. Understanding Instance-Level Impact of Fairness Constraints. In Proceedings of the 39th International Conference on Machine Learning, 23114–23130.
- Wang et al. (2021) Wang, Y.; Wang, C.; Wang, Z.; Zhou, S.; Liu, H.; Bi, J.; Ding, C.; and Rajasekaran, S. 2021. Against Membership Inference Attack: Pruning is All You Need. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI-21, 3141–3147.
- Wu and He (2018) Wu, Y.; and He, K. 2018. Group Normalization. arXiv:1803.08494.
- Yang, Gohari, and Topcu (2023) Yang, Y.; Gohari, P.; and Topcu, U. 2023. On the Privacy Risks of Deploying Recurrent Neural Networks in Machine Learning Models. Proceedings on Privacy Enhancing Technologies, 1: 68–84.
- Yang et al. (2023) Yang, Z.; Wang, L.; Yang, D.; Wan, J.; Zhao, Z.; Chang, E.-C.; Zhang, F.; and Ren, K. 2023. Purifier: Defending Data Inference Attacks via Transforming Confidence Scores. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, 10871–10879.
- Yuan and Zhang (2022) Yuan, X.; and Zhang, L. 2022. Membership inference attacks and defenses in neural network pruning. In 31st USENIX Security Symposium (USENIX Security 22), 4561–4578.
- Zhang et al. (2020) Zhang, J.; Zhang, J.; Chen, J.; and Yu, S. 2020. Gan enhanced membership inference: A passive local attack in federated learning. In IEEE International Conference on Communications (ICC), 1–6.
- Zhou, Nezhadarya, and Ba (2022) Zhou, Y.; Nezhadarya, E.; and Ba, J. 2022. Dataset Distillation using Neural Feature Regression. In Advances in Neural Information Processing Systems, volume 35, 9813–9827. Curran Associates, Inc.
- Zhu and Blaschko (2021) Zhu, J.; and Blaschko, M. B. 2021. R-{GAP}: Recursive Gradient Attack on Privacy. In International Conference on Learning Representations.