Renormalons beyond the Borel plane

E. Cavalcanti [email protected] Centro Brasileiro de Pesquisas Físicas/MCTI, 22290-180 Rio de Janeiro, RJ, Brazil

Abstract

The renormalon singularities are a known source of the divergent behavior of asymptotic perturbative series from field theoretical models. These singularities live in the Borel plane and are responsible for ambiguities in the physical plane. We propose that field theories can have renormalons beyond the usual first Borel plane. We show an example with a scalar field theory where, considering a chain of cat’s eyes diagrams, the model develops a Gevrey-3 asymptotic series.

I Introduction

The renormalon phenomenon is known since the ‘70s; it was initially proposed by ’t Hooft, who noted it as one source of divergence for the perturbative asymptotic series of quantum field theories. The renormalon shows up as a singularity in the Borel plane. Initially, the exact definition of the renormalon singularity was a matter of discussion, with some debate whether it was a simple pole, a $n$ -th order pole, or rather a branch cut on the Borel plane Beneke (1999). Although new perspectives have draw attention in the past two decades Loewe and Valenzuela (2000); Kneur and Reynaud (2003); Guralnik and Guralnik (2010); Unsal and Yaffe (2008); Argyres and Unsal (2012a, b); Dunne and Unsal (2012); Dunne and Ünsal (2013); Poppitz et al. (2013); Cherman et al. (2014); Shifman (2015a); Dabrowski and Dunne (2013); Cherman et al. (2015); Shifman (2015b); Anber and Sulejmanpasic (2015); Sulejmanpasic and Ünsal (2018); Sulejmanpasic (2017); Dunne and Ünsal (2016); Buividovich and Valgushev (2017); Caprini et al. (2017); Aniceto et al. (2019); Cherman et al. (2019); Aniceto et al. (2019); Cherman et al. (2019); Maiezza and Vasquez (2018); Cavalcanti et al. (2018); Fujimori et al. (2019); Mariño and Reis (2019, 2020a, 2020b); Correa et al. (2019); Ishikawa et al. (2020a, b); Ashie et al. (2020a); Correa et al. (2019); Borinsky and Dunne (2020); Cavalcanti (2020); Dondi et al. (2020); Ashie et al. (2020b); Borinsky and Dunne (2020); Ünsal (2020); Costin and Dunne (2020), the seminal report from Beneke, see ref. Beneke (1999), is still a useful reference on state of the art regarding the formal discussion.

Nowadays, the renormalon problem is understood as a component of the broader context of the resurgence program Anber and Sulejmanpasic (2015); Dunne and Ünsal (2016); Maiezza and Vasquez (2018); Mariño and Reis (2019, 2020a, 2020b); Ishikawa et al. (2020a); Dondi et al. (2020). The singularity is an indication that the original perturbative series requires a transseries contribution. Also, the renormalon singularity, which arose as a formal aspect from quantum field theory, is seen as a useful guide to phenomenological predictions Cvetič (2020); Hadjimichef et al. (2020); Takaura (2019); Hayashi and Sumino (2019); Corcella (2019); Maiezza and Vasquez (2019); Nason (2019a); Cvetič (2019); Ortega et al. (2018); Kataev and Molokoedov (2018a); Mateu et al. (2019); Boito et al. (2019, 2018); Ferrario Ravasio et al. (2019); Brambilla et al. (2018a); Braun et al. (2019); Kataev and Molokoedov (2018b); Bell et al. (2019); Takaura et al. (2019a, b); Suzuki and Takaura (2019); Del Debbio et al. (2018); Kataev and Molokoedov (2018c); Peset et al. (2018); Bazavov et al. (2018); Brambilla et al. (2018b); Nason (2019b); Ortega and Mateu (2018); Mateu and Ortega (2018); Hoang et al. (2017); Ahmadov et al. (2017); Steinhauser (2016); Jamin and Miravitllas (2016); Ayala et al. (2016); Mishima et al. (2017).

It is usual in the literature to consider a large- $N$ expansion when one is interested in exploring the existence of renormalons inside the theory. That occurs because, in this limit, the relevant contributions are planar diagrams, more commonly chains of bubble diagrams. For example, for quantum chromodynamics (QCD) this produces the usual contribution to the Adler function. However, the large- $N$ expansion hides other singularities, as the instanton problem, because the poles get far away from the origin in this approximation. Due to historical reasons – as pointed by ref. Beneke (1999) – it is very common to relate renormalons and bubble-chain diagrams, although the renormalon singularity might appear at different subsets of Feynman diagrams. Once we consider a quantum field theory in general (outside the large- $N$ approximation), we have no guarantee that the usual planar diagrams are the most relevant ones, and other scenarios might appear.

Another common relationship is that the renormalon singularities live in the Borel plane. To our knowledge, every report so far is still considering that renormalons are singularities that lives in the first Borel plane and produce a Gevrey-1 asymptotic series Marino and Reis (2020); Mariño and Reis (2020b, a); Ishikawa et al. (2020a, b); Cavalcanti et al. (2018); Cavalcanti (2020); Ashie et al. (2020b). Here we propose a new perspective, where we suppose a generic chain and show that new kinds of singularities occur that might live in a $q$ -Borel plane instead of the typical Gevrey-1 case of the Borel plane. Therefore, we propose an extension on the definition of the renormalon singularity, asserting that they live in a Gevrey- $q$ plane, thus extending the Gevrey-order of the perturbative series.

We aim to identify scenarios where a renormalon singularity might occur. Notice that we do not intend to discuss at which order in some perturbative expansions these contributions appear. The relevant point here is that the contributions considered are subsets of the full perturbative expansion and shall appear. Following this chain of thought, we also do not apply any procedure to circumvent the renormalon problem and give the nonperturbative solution, as we are mostly interested in studying the existence or not of renormalons singularities.

As our main interest lies in the formal aspect of quantum field theory, it suffices to consider as a toy model a massless scalar field theory. This model is known to possess ultraviolet (UV) renormalons produced by a sum of bubble-chain diagrams, and – more importantly – we show that this model reveals one novel scenario with cat’s eyes chain diagrams. The sum over these chains produces a Gevrey-3 series, therefore extending the definition of the renormalon singularity beyond the usual Borel plane.

II $q$ -Borel series

In many scenarios, perturbative series diverge and only make sense as an asymptotic series. A rather simple example of divergence occurs when the perturbative series has a factorial growth, as

A\sim\sum_{k=0}^{\infty}(k!)^{q}(s)^{k}g^{k},

(1)

where $g$ is the expansion parameter (the coupling constant), $q$ is the power of the factorial growth, and $s$ is the sign ( $s=\pm 1$ ) of the coefficients.

A well-stablished procedure is to consider an extension of the Borel sum Bender and Orszag (2013). The usual Borel sum occurs for $q=1$ and relates to the conventional asymptotic power series (in the sense of Poincaré). In this extension we consider $q$ factorials to control the growth, which is well established in the studies of $q$ -summability and Gevrey- $q$ series. First we transport the usual sum to a summation in the $q$ -Borel plane

A\rightarrow B_{q}[A](u)\sim\sum_{k=0}^{\infty}(su)^{k}=\frac{1}{1-su}.

(2)

Then, if this new infinite sum is summable in the $q$ -Borel plane we proceed to implement a $q$ -Borel inverse transform

\widetilde{A}[g]=\int_{0}^{\infty}du_{1}\ldots du_{q}e^{-(u_{1}+\cdots+u_{q})}B_{q}[A](gu_{1}\ldots u_{q}).

(3)

In the following, we denote the physical plane as 0-Borel (Gevrey-0), the usual Borel plane as 1-Borel (Gevrey-1), and so on.

Let us consider, as an example, $q=1$ and $q=2$ in the most simple scenario. For $s=-1$ ,

	$\displaystyle-\frac{e^{\frac{1}{g}}}{g}\text{Ei}\left(-\frac{1}{g}\right),$	$\displaystyle\quad q=1;$
	$\displaystyle\frac{\pi}{g}\text{G}^{1,1}_{3,1}\left\lparen\,-\frac{1}{g}\middle\|\begin{smallmatrix}0,\frac{1}{2}\\ 0,0,0,\frac{1}{2}\end{smallmatrix}\right\rparen,$	$\displaystyle\quad q=2;$

where Ei is the exponential integral function and $\text{G}^{mn}_{pq}$ is the Meijer- $G$ function. Therefore, we can relate the asymptotic sum to a well-defined function through $q$ -summability.

On the other hand, if we take $s=1$ , we find a pole in the positive real axis of the $q$ -Borel plane. This singularity introduces an ambiguity due to the choice of the integration path.

Few known physical models produce a Gevrey- $q$ series and discuss $q$ -summability. For example, a scenario with Gevrey-2 is the sextic anharmonic oscillator, while for Gevrey-3 there is the octic anharmonic oscillator Shalaby (2020); Weniger (1996).

In sec. III, we propose with some degree of generality that there can be Gevrey- $q$ series in field theoretical models. This is shown both for UV and IR renormalons. In sec. IV, we take a toy model and show explicitly the existence of a Gevrey-3 series when considering the subset of cat’s eyes chain diagrams.

III Renormalons from chains

Renormalons are singularities that arise due to low/large momenta of integration (IR/UV renormalons) in the summing of a particular subset of Feynman diagrams. The usual understanding is that they live in the first Borel plane. In this section, we argue that they can occur in the $q$ -Borel plane, meaning that we are not considering the Gevrey-1 asymptotic series as usual, but that the asymptotic series can be of the Gevrey- $q$ type.

In the following we consider the sum over a subset of Feynman diagrams that produce a “chain”, $R_{k}(\alpha)$ (fig. 2). The chain is built by the successive introduction of “chain-links”, $g(\ell)$ (fig. 1). The chain link is some simple structure as a bubble diagram, a sunset diagram, a cat’s eye diagram or other possibilities. Formally, we can write the sum over all chain diagrams of some particular chain link as

R(\alpha)=\sum_{k}\int d\ell f(\ell)\left[\alpha g(\ell)\right]^{k},

(4)

where $\alpha$ is related to the coupling of the theory, and $f(\ell)$ contains all additional contribution for the chain diagram. The momentum $\ell$ is integrated over the whole chain.

This representation is very general and contains all possibilities for a one-chain scenario. We remark that we do not deal here with the multi-chain scenario.

To determine the structure of $R(\alpha)$ we are mainly interested in the asymptotic behavior with respect fo the internal momentum $\ell$ (this translates to consider the large $k$ behavior. The behavior of both $f(\ell)$ and $g(\ell)$ depends on the particular scenario under interest. However, it is known from the expression of Feynman amplitudes in the complete Mellin representation Bergere et al. (1978); Smirnov (1995); Linhares et al. (2008), that the asymptotic expansion with respect to the external momentum behaves as

I_{G}\sim\ell^{p}\ln^{q}\ell,

(5)

where $p\in\mathbb{Z}$ , $q\in\mathbb{Z}^{+}$ .

Therefore, we can say without loss of generality¹¹1In a recent article, ref. Mariño and Reis (2020b) considered a scenario that behaves as $\ln x/(x+1)$ . That produces renormalon poles in scenarios prohibited here. However, this expression is “unstable”, a small perturbation in the asymptotic approximation ( $\ln x\rightarrow\ln 1+x$ ) destroys the renormalon pole. that both $f(\ell)$ and $g(\ell)$ behaves asymptotically as a transmonomial²²2The transmonomial is an extension of the usual monomial structure and is related to the definition of a transseries. $\ell^{p}\ln^{q}\ell$ .

III.1 UV renormalons

We have to split the investigation into the IR and UV scales, as the asympototic behavior is different in each case. First, let us consider the UV scale


$\displaystyle f(\ell)$	$\displaystyle=\ell^{-a}\ln^{b}\ell,\quad g(\ell)=\ell^{-c}\ln^{d}\ell,$	(6a)
$\displaystyle R_{UV}(\alpha)$	$\displaystyle\sim\sum_{k}\int_{1}^{\infty}d\ell f(\ell)\left[\alpha g(\ell)\right]^{k}$
	$\displaystyle=\sum_{k}\alpha^{k}\int_{1}^{\infty}d\ell\;\ell^{-a-ck}\ln^{b+dk}\ell,$	(6b)

here $a\geq 0,c\geq 0$ such that the integration does not require any new subtraction and is well behaved for $\ell\rightarrow\infty$ .

Making the change of variables $\ell=e^{t}$ and identifying the gamma function,

R_{UV}(\alpha)\sim\sum_{k}\alpha^{k}\frac{\Gamma(dk+b+1)}{(a+ck-1)^{dk+b+1}}.

(7)

We obtain the large $k$ behavior using the Stirling approximation for the gamma function,

R_{UV}(\alpha)\sim\sum_{k}\alpha^{k}\left(\frac{dk+b}{e(a+ck-1)}\right)^{dk+b}\frac{\sqrt{2\pi(dk+b)}}{a+ck-1}.

In the scenario with $c\neq 0$ the $k^{k}$ behaviour related to the factorial growth is cancelled out and the function is well defined,

R_{UV}(\alpha)\sim\sum_{k}\alpha^{k}\left(\frac{d}{ec}\right)^{dk+b}\frac{\sqrt{2\pi d}}{c\sqrt{k}}\\ =\frac{\sqrt{2\pi d}}{c}\left(\frac{d}{ec}\right)^{b}\text{Li}_{1/2}\left(\left(\frac{d}{ec}\right)^{d}\alpha\right).

The relevant scenario occurs only if $c=0$ and $d>1$ , at large $k$ we obtain

R_{UV}(\alpha)\sim\frac{1}{(2\pi)^{\frac{d-1}{2}}}\frac{d^{b+\frac{1}{2}}}{(a-1)^{b+1}e^{b}}\times\\ \sum_{k}\frac{k^{b}k!^{d}}{(2\pi k)^{\frac{d-1}{2}}}\left[\alpha\left(\frac{d}{a-1}\right)^{d}\right]^{k}.

(8)

This expression reveals that in the UV regime the sum over the set of chain diagrams behaves as a Gevrey- $d$ series. The special case of $d=1$ produces the usual Grevrey-1 scenario of the Borel sum. In this approximation the sum of chains is $d$ -Borel summable and produces a polylogarithm of order $(d-1)/2-b$ ,

R_{UV}(\alpha)\rightarrow B_{d}[R_{UV}](u)\sim\frac{1}{(2\pi)^{\frac{d-1}{2}}}\frac{d^{b+\frac{1}{2}}}{(a-1)^{b+1}e^{b}}\times\\ \sum_{k}\left[\left(\frac{d}{a-1}\right)^{d}\text{sign}(\alpha)u\right]^{k}\frac{k^{b}}{k^{\frac{d-1}{2}}}\\ =\frac{d^{b+\frac{1}{2}}\text{Li}_{\frac{d-1}{2}-b}\left[\left(\frac{d}{a-1}\right)^{d}\text{sign}(\alpha)u\right]}{(2\pi)^{\frac{d-1}{2}}(a-1)^{b+1}e^{b}}.

(9)

The polylogarithm function of order $\nu$ , $\text{Li}_{\nu}(x)$ , has a branch point at $x=1$ if $\nu>0$ , or a pole of order $1-\nu$ if $\nu\leq 0$ . Therefore, if $\frac{d-1}{2}-b>0$ we have a branch point at $u=u_{0}=\text{sign}(\alpha)\left(\frac{a-1}{d}\right)^{d}$ . And, if $\frac{d-1}{2}-b\leq 0$ this point is a pole of order $1+b+\frac{1-d}{2}$ .

For example, at perturbative QCD, see ref. Beneke (1999), $\alpha=-|\alpha|$ and in UV region (for the chain of fermionic bubbles at $1/N_{f}$ , where $N_{f}$ is the number of flavors) we have $a=2,b=1,c=0,d=1$ This means that $\nu=1$ and we obtain a Gevrey-1 UV renormalon located at $u=-1$ as a double pole (as expected).

III.2 IR renormalons

To take into account the IR scale we use a slightly different choice of $f(\ell)$ and $g(\ell)$ ,


$\displaystyle f(\ell)$	$\displaystyle=\ell^{a}\ln^{b}\ell,\quad g(\ell)=\ell^{c}\ln^{d}\ell,$	(10a)
$\displaystyle R_{IR}(\alpha)$	$\displaystyle\sim\sum_{k}\int_{0}^{1}d\ell\;f(\ell)\left[\alpha g(\ell)\right]^{k}$
	$\displaystyle=\sum_{k}\alpha^{k}\int_{0}^{1}d\ell\;\ell^{a+ck}\ln^{b+dk}\ell.$	(10b)

Note that the power dependence with $\ell$ is in the numerator instead of the denominator as in the UV scale. This choice is to guarantee that $R_{IR}$ is well behaved in the IR scale and does not require any new subtraction.

We can employ the substitution $\ell=1/v$ ,

R_{IR}(\alpha)\sim\sum_{k}\alpha^{k}\int_{1}^{\infty}dv\;\frac{1}{v^{2}}v^{-a-ck}(-\ln v)^{b+dk}\\ =\sum_{k}(-1)^{b}\left((-1)^{d}\alpha\right)^{k}\int_{1}^{\infty}dv\;\frac{1}{v^{2}}v^{-a-ck}(\ln v)^{b+dk},

the integral assumes the same form as $R_{UV}$ , see eq. (6b), with the little shift $a\rightarrow a+2$ . Following the same steps as before we obtain that – requiring $c=0$ and $d>1$ – in the IR regime the sum of chains also behaves as a Gevrey- $d$ series. At large $k$ it produces

R_{IR}(\alpha)\sim\frac{1}{(2\pi)^{\frac{d-1}{2}}}\frac{(-1)^{b}d^{b+\frac{1}{2}}}{(a+1)^{b+1}e^{b}}\times\\ \sum_{k}\frac{k^{b}k!^{d}}{(2\pi k)^{\frac{d-1}{2}}}\left[\alpha\left(-\frac{d}{a+1}\right)^{d}\right]^{k},

(11)

which is $d$ -Borel summable, producing a polylogarithm of order $(d-1)/2-b$ with a singularity at

u=\left(-\text{sign}(\alpha)\frac{a+1}{d}\right)^{d},

once again this singularity is a pole of order $1+b+(1-d)/2$ in the scenario where $(d-1)/2-b\leq 0$ , or a branch point if $(d-1)/2-b>0$ .

At perturbative QCD, see ref. Beneke (1999), $\alpha=-|\alpha|$ and in IR region we have $a=1,b=0,c=0,d=1$ for the chain of fermionic bubbles at $1/N_{f}$ , where $N_{f}$ is the number of flavors. Also $\nu=1$ , so $u=2$ is the first IR renormalon and is a simple pole (as expected).

III.3 Discussion

In the last sections, we indicate that the existence of renormalons is directly related to the logarithm behavior of the chain links. This relationship is commonly assumed, although not explicitly formulated. Therefore we propose to conjecture that:

•

the sum of a set of chains can have a renormalon only if the chain-link behaves as $\ln\ell$ .

About the renormalon singularity, we also claim that:

•

The renormalon “lives” in the $d$ -Borel plane, where $\ln^{d}\ell$ is the behavior of each “insertion”/chain-link.
•

The renormalon is a pole of order $1+b+(1-d)/2$ , where $b$ is the logarithm contribution, $\ln^{b}\ell$ , outside the insertions. It can also be a branch point if $b+(1-d)/2<0$ .
•

The location of the UV/IR pole depends only on $a$ and $d$ , where $a$ is the power contribution ( $\ell^{a}$ for IR renormalons, $\ell^{-a}$ for UV renormalons) outside the insertions.

With this, it becomes clear that renormalons do not need to be singularities in the first Borel plane; this is just a particular case.

In what follows, we exhibit a simple example where a Gevrey-3 renormalon appears.

IV cat’s eyes chain

Let us consider a flavorless and massless scalar field theory with quartic interaction $\lambda\phi^{4}/4!$ . We propose to build a chain diagram where each chain link is given by a cat’s eye diagram. Each insertion is

G(\ell)=(-g)^{3}I(\ell),

(12)

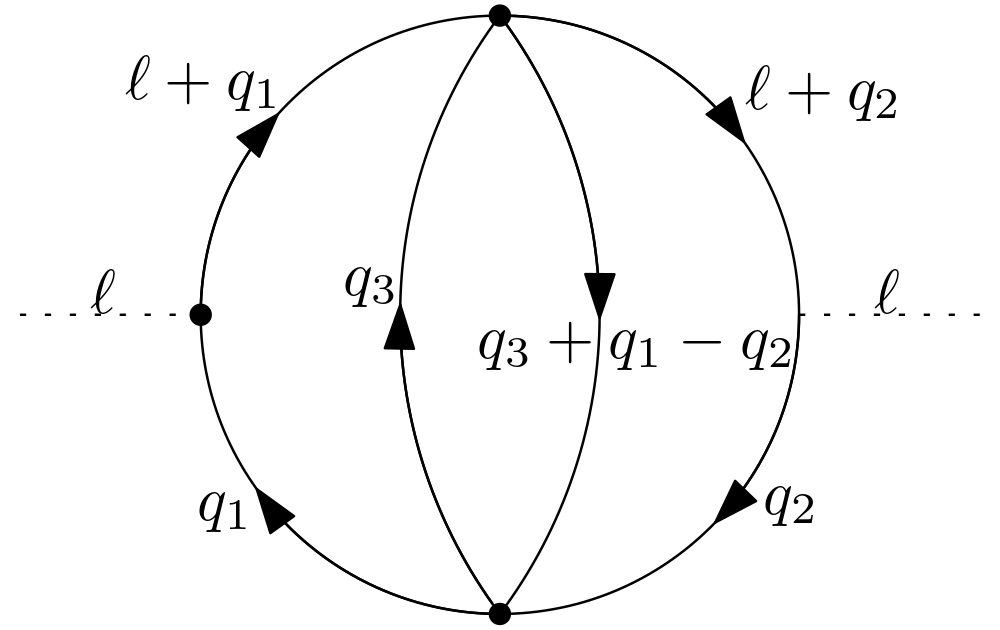
Refer to caption — Figure 1: Eye-cat–link diagram

where $I(\ell)$ is the cat’s eye diagram, see fig. 1, whose amplitude is given by

I(\ell)=\int\frac{d^{D}q_{1}}{(2\pi)^{D}}\int\frac{d^{D}q_{2}}{(2\pi)^{D}}\int\frac{d^{D}q_{3}}{(2\pi)^{D}}\frac{1}{(q_{1}+\ell)^{2}}\frac{1}{q_{1}^{2}}\times\\ \frac{1}{(q_{2}+\ell)^{2}}\frac{1}{q_{2}^{2}}\frac{1}{(q_{3}+q_{1}-q_{2})^{2}}\frac{1}{q_{3}^{2}}.

(13)

After some manipulations, see app. A, we can obtain that the solution of cat’s eye diagram at $D=4-2\varepsilon$ is

	$I(\ell)=\frac{\Gamma\left[3\varepsilon\right]}{(4\pi)^{6-3\varepsilon}\ell^{6\varepsilon}}\Bigg{(}-c_{1}+c_{2}+\frac{1}{8\varepsilon^{2}}+\mathcal{O}(\varepsilon)\Bigg{)},$		(14a)
with

	$\displaystyle c_{1}$	$\displaystyle=0.822\,467\,029\,8\ldots$	(14b)
	$\displaystyle c_{2}$	$\displaystyle=0.822\,467\,033\,4\ldots$	(14c)

Or, after applying a minimal subtraction scheme and keeping only the finite components

	$\widehat{I}(\ell)=a_{0}+a_{1}\ln\ell^{2}+a_{2}\ln^{2}\ell^{2}+a_{3}\ln^{3}\ell^{2},$		(15a)
with constants

	$\displaystyle a_{3}$	$\displaystyle=-\frac{3}{4^{8}\pi^{6}}=-4.761\,481\,354\times 10^{-8},$	(15b)
	$\displaystyle a_{2}$	$\displaystyle=-\frac{3\gamma}{4^{8}\pi^{6}}=-2.748\,401\,625\times 10^{-7},$	(15c)
	$\displaystyle a_{1}$	$\displaystyle=5.886\,714\,656\times 10^{-9},$	(15d)
	$\displaystyle a_{0}$	$\displaystyle=7.074\,471\,170\times 10^{-7}.$	(15e)

We can already expect that this will generate a Gevrey-3 series due to the $\ln^{3}$ behavior.

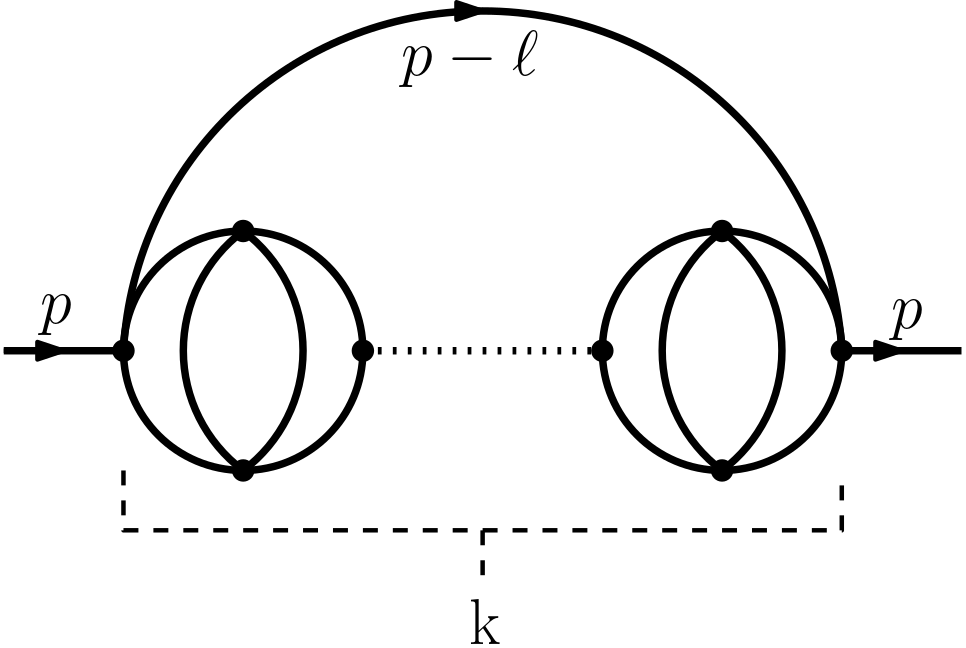
We produce the chain diagram by adding the chain-links. At fig. 2 we show the scenario with $k$ chain links. The amplitude, before regularization, is

R_{k}(p)=-gS_{k}\int\frac{d^{D}\ell}{(2\pi)^{D}}\frac{(-g^{3}{I}(\ell))^{k}}{(p-\ell)^{2}},

(16)

where $S_{k}=\left[(k+1)2^{k}\right]^{-1}$ is the symmetry factor for the diagram with $k$ eye-cat–links. We calculate the symmetry factor using a general expression for symmetry factors of the scalar theory, by ref. Palmer and Carrington (2002).

At $D=4$ the function $I$ behaves asymptotically as a logarithm and by power counting $R_{k}$ has a quadratic divergence. We can make a subtraction as a BPHZ procedure Itzykson and Zuber (1980) ( $R_{k}(p)-R_{k}(0)-p^{2}\partial_{p^{2}}R_{k}(p)|_{0}$ ), which produces at low $p$

\widehat{R}_{k}(p)\sim-\frac{gp^{4}}{8\pi^{2}}\frac{1}{k+1}\left(-\frac{1}{2}g^{3}\right)^{k}\int_{0}^{\infty}\frac{d\ell}{\ell^{3}}\;\widehat{I}^{k}(\ell).

(17)

To investigate the asymptotic UV behavior, we can consider $\ell\in[1,\infty[$ and make the change of variables $\ell=e^{t}$ such that,

\widehat{R}_{k}(p)\sim-\frac{gp^{4}}{8\pi^{2}}\frac{1}{k+1}\left(-\frac{1}{2}g^{3}\right)^{k}\times\\ \int_{0}^{\infty}dt\;e^{-2t}(a_{0}+2a_{1}t+4a_{2}t^{2}+8a_{3}t^{3})^{k}.

(18)

As $k\in\mathbb{N}$ we can use the multinomial representation and integrate over $t$ ,

\widehat{R}_{k}(p)\sim-\frac{gp^{4}}{16\pi^{2}}\frac{1}{k+1}\left(-\frac{1}{2}g^{3}\right)^{k}\times\\ \sum_{j_{0}+j_{1}+j_{2}+j_{3}=k}a_{0}^{j_{0}}a_{1}^{j_{1}}a_{2}^{j_{2}}a_{3}^{j_{3}}\frac{k!\Gamma\left(1+j_{1}+2j_{2}+3j_{3}\right)}{j_{0}!j_{1}!j_{2}!j_{3}!}.

(19)

The dominant contribution comes from $\mathbf{j}=(0,0,0,k)$ (accuracy of ${\approx 70}\%$ , it can be checked numerically for large values of $k$ ). The second contribution comes from $\mathbf{j}=(0,0,1,k-1)$ (with an accuracy of more than $90\%$ ). That way, we can write

\widehat{R}_{k}(p)\sim-\frac{gp^{4}}{16\pi^{2}}\left(1+\frac{a_{2}}{3a_{3}}\right)\left(-\frac{g^{3}a_{3}}{2}\right)^{k}\frac{\Gamma\left(1+3k\right)}{k+1},

(20)

and it is clear that these coefficients produce a divergent series. Taking the Stirling approximation for large values of $k$ the sum over all cat’s eyes chains produce

	$R\sim\sum_{k=1}^{\infty}\widehat{R}_{k}(p)\sim\kappa\sum_{k=1}^{\infty}\left(\frac{\widetilde{g}}{e^{3}}\right)^{k}k^{3k-\frac{1}{2}},$		(21a)
with $\kappa$ and $\widetilde{g}$ given by

	$\displaystyle\kappa$	$\displaystyle=-\sqrt{6\pi}\frac{gp^{4}}{16\pi^{2}}\left(1+\frac{a_{2}}{3a_{3}}\right),$	(21b)
	$\displaystyle\widetilde{g}$	$\displaystyle=-\frac{3^{3}}{2}g^{3}a_{3}.$	(21c)

This expression for $R$ is not summable in the first Borel plane. The Borel transform introduces a $k!$ damping that behaves just as $k^{k}$ . We can control the divergent behavior only with a 3-Borel transform, that introduces a $k!^{3}$ , meaning a $k^{3k}$ damping, sufficient to obtain a summable expression. Therefore, this is a Gevrey-3 asymptotic series.

If we transport eq. (20) into the 3-Borel plane we obtain a hypergeometric function,

B_{3}[R]\sim-\frac{gp^{4}}{16\pi^{2}}\left(1+\frac{a_{2}}{3a_{3}}\right)\Bigg{[}-1+\,{}_{2}F_{1}\left(\frac{1}{3},\frac{2}{3};2;\widetilde{g}u\right)\Bigg{]},

(22)

it has a branch point at $u=1/\widetilde{g}$ . This cut lies in the integration path of the 3-Borel plane, therefore we have a singularity that blocks the inverse Borel transform.

If we try to get back into the physical plane we obtain an imaginary ambiguity due to the choice of the integration path from the 3-Borel to the 2-Borel plane. However, there are no new poles in the 2-Borel plane, neither in the 1-Borel plane. Meaning that the only ambiguity appears when passing the Gevrey-3 series to the 2-Borel plane.

The fact that the only singularity comes from the 3-Borel plane is a consequence of the previous approximation to consider the most dominant divergent behavior. In the full scenario, one would expect renormalon singularities at Gevrey-1,2 and 3. Note, for example, that at eq. (19) one of the contributions is $j_{0}=j_{1}=j_{3}=0,j_{2}=k$ which produces a Gevrey-2 series,

\sum_{k=1}^{\infty}\frac{(-g^{3}a_{2}/2)^{k}}{k+1}\Gamma(1+2k),

This new series has a branch point in the 2-Borel plane located at $u=-1/(2a_{2}g^{3})<0$ , which does not lie in the integration path. If we keep investigating, we find other singularities produced by eq. (19). In fact, the sum over the cat’s eyes chain diagrams produces more then one asymptotic series, each with a different Gevrey order. However, the relevant behavior is already revealed: the highest degree is Gevrey-3 and there is a renormalon singularity that lives in the 3-Borel plane.

V Conclusion

We exhibited that the renormalon problem goes beyond the first Borel plane. It seems that the renormalon singularities are in some different category when compared to the instanton-like singularities, only known to occur at the Gevrey-1 level. Although we did not discuss a realistic theory nor considered the phenomenological influence, it is beyond doubt that we have a new singularity that lives in the 3-Borel plane. We remark that our report poses a new difficulty for the program to cure all renormalon ambiguities. Furthermore, there are some aspects open to future investigations. We need to determine how the Gevrey- $q$ renormalon impacts the asymptotic series or the resurgence program. Also, we must check whether a Gevrey- $d$ series (with $d>1$ ) also appear for realistic theories.

Acknowledgements.

The author thanks the Brazilian agency Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for financial support.

Appendix A Cat’s eye diagram

In this section, we consider for completeness a step-by-step computation of the cat’s eye diagram, as this evaluation is not easily found in textbooks.

Let us start from the original amplitude,

I(\ell)=\int\frac{d^{D}q_{1}}{(2\pi)^{D}}\int\frac{d^{D}q_{2}}{(2\pi)^{D}}\int\frac{d^{D}q_{3}}{(2\pi)^{D}}\frac{1}{(q_{1}+\ell)^{2}}\frac{1}{q_{1}^{2}}\times\\ \frac{1}{(q_{2}+\ell)^{2}}\frac{1}{q_{2}^{2}}\frac{1}{(q_{3}+q_{1}-q_{2})^{2}}\frac{1}{q_{3}^{2}},

(23)

and then introduce Schwinger parameters $\alpha_{i}$ for each propagator,

I(\ell)=\int\frac{d^{D}q_{1}}{(2\pi)^{D}}\int\frac{d^{D}q_{2}}{(2\pi)^{D}}\int\frac{d^{D}q_{3}}{(2\pi)^{D}}\int_{0}^{\infty}\prod_{i=1}^{6}d\alpha_{i}\\ e^{-\alpha_{1}(q_{1}+\ell)^{2}-\alpha_{2}q_{1}^{2}}e^{-\alpha_{3}(q_{2}+\ell)^{2}-\alpha_{4}q_{2}^{2}}e^{-\alpha_{5}(q_{3}+q_{1}-q_{2})^{2}-\alpha_{6}q_{3}^{2}}.

(24)

After some algebraic manipulations on these expressions, we obtain that

I(\ell)=\int\frac{d^{D}q_{1}}{(2\pi)^{D}}\int\frac{d^{D}q_{2}}{(2\pi)^{D}}\int\frac{d^{D}q_{3}}{(2\pi)^{D}}\int_{0}^{\infty}\prod_{i=1}^{6}d\alpha_{i}\\ e^{-\alpha_{125}\left(q_{1}+\frac{\ell\alpha_{1}+q_{3}\alpha_{5}}{\alpha_{125}}\right)^{2}}e^{-\alpha_{346}\left(q_{2}+\frac{\ell\alpha_{3}+q_{3}\alpha_{6}}{\alpha_{346}}\right)^{2}}\times\\ e^{-\frac{U}{\alpha_{125}\alpha_{346}}\left[q_{3}-\ell\frac{\alpha_{1}\alpha_{5}\alpha_{346}+\alpha_{3}\alpha_{6}\alpha_{125}}{U}\right]^{2}}e^{-\frac{V\ell^{2}}{U}},

(25)

where


$\displaystyle\alpha_{i_{1}i_{2}\ldots i_{k}}$	$\displaystyle=\alpha_{i_{1}}+\alpha_{i_{2}}+\cdots+\alpha_{i_{k}},$	(26a)
$\displaystyle U$	$\displaystyle=\alpha_{12}\alpha_{5}\alpha_{346}+\alpha_{34}\alpha_{6}\alpha_{125},$	(26b)
$\displaystyle V$	$\displaystyle=\alpha_{1}\alpha_{2}(\alpha_{34}\alpha_{56}+\alpha_{5}\alpha_{6})+\alpha_{3}\alpha_{4}(\alpha_{12}\alpha_{56}+\alpha_{5}\alpha_{6})$
	$\displaystyle+\alpha_{5}\alpha_{6}(\alpha_{1}\alpha_{4}+\alpha_{2}\alpha_{3}).$	(26c)

We can make a shift in the momenta,

I(\ell)=\int\frac{d^{D}q_{1}}{(2\pi)^{D}}\int\frac{d^{D}q_{2}}{(2\pi)^{D}}\int\frac{d^{D}q_{3}}{(2\pi)^{D}}\int_{0}^{\infty}\prod_{i=1}^{6}d\alpha_{i}\\ e^{-\alpha_{125}q_{1}^{2}}e^{-\alpha_{346}q_{2}^{2}}e^{-\frac{U}{\alpha_{125}\alpha_{346}}q_{3}^{2}}e^{-\frac{V\ell^{2}}{U}},

(27)

and then compute the integration of the internal momenta

I(\ell)=\frac{1}{(4\pi)^{\frac{3D}{2}}}\int_{0}^{\infty}\prod_{i=1}^{6}d\alpha_{i}\frac{e^{-\ell^{2}\frac{V}{U}}}{U^{\frac{D}{2}}}.

(28)

Let us reparametrize defining the new sectors

	$\displaystyle\alpha_{1}$	$\displaystyle=st_{1}\cdots t_{5},$
	$\displaystyle\alpha_{2}$	$\displaystyle=st_{1}\cdots t_{4}(1-t_{5}),$
	$\displaystyle\alpha_{3}$	$\displaystyle=st_{1}t_{2}t_{3}(1-t_{4}),$
	$\displaystyle\alpha_{4}$	$\displaystyle=st_{1}t_{2}(1-t_{3}),$
	$\displaystyle\alpha_{5}$	$\displaystyle=st_{1}(1-t_{2}),$
	$\displaystyle\alpha_{6}$	$\displaystyle=s(1-t_{1}),$

such that $\alpha_{1}+\ldots+\alpha_{6}=s$ . This change of variables produce the Jacobian

d\alpha_{1}\cdots d\alpha_{6}=s^{5}t_{1}^{4}t_{2}^{3}t_{3}^{2}t_{4}dsdt_{1}\cdots dt_{5},

and after some manipulation we obtain that


$\displaystyle\alpha_{12}$	$\displaystyle=st_{1}\cdots t_{4},$	(29a)
$\displaystyle\alpha_{34}$	$\displaystyle=st_{1}t_{2}(1-t_{3}t_{4}),$	(29b)
$\displaystyle\alpha_{125}$	$\displaystyle=st_{1}(1-t_{2}+t_{2}t_{3}t_{4}),$	(29c)
$\displaystyle\alpha_{346}$	$\displaystyle=s\left(1-t_{1}+t_{1}t_{2}(1-t_{3}t_{4})\right),$	(29d)
$\displaystyle U$	$\displaystyle=s^{3}t_{1}^{2}t_{2}\overline{U},$	(29e)
$\displaystyle V$	$\displaystyle=s^{4}t_{1}^{3}t_{2}^{2}t_{3}\overline{V},$	(29f)

with $\overline{U}$ and $\overline{V}$ given by

\overline{U}=(1-t_{2})t_{3}t_{4}(1-t_{1}+t_{1}t_{2}(1-t_{3}t_{4}))\\ +(1-t_{2}+t_{2}t_{3}t_{4})(1-t_{3}t_{4})(1-t_{1}),

(30)

\overline{V}=(1-t_{1})(1-t_{2})(1-t_{4}+t_{4}t_{5})(1-t_{3}+t_{3}t_{4}(1-t_{5}))\\ +t_{2}t_{3}t_{4}(1-t_{1}t_{2})\left((1-t_{3})(1-t_{4})+(1-t_{3}t_{4})(1-t_{5})t_{4}t_{5}\right).

(31)

Substituting this back into the integral $I$ , eq. (28), we obtain

I(\ell)=\frac{1}{(4\pi)^{\frac{3D}{2}}}\int_{0}^{1}\prod_{i=1}^{5}dt_{i}\frac{t_{1}^{4-D}t_{2}^{3-\frac{D}{2}}t_{3}^{2}t_{4}}{\overline{U}^{\frac{D}{2}}(\boldsymbol{t})}\\ \int_{0}^{\infty}ds\;s^{\left(6-\frac{3D}{2}\right)-1}e^{-st_{1}t_{2}t_{3}\ell^{2}\frac{\overline{V}}{\overline{U}}}.

(32)

This expression can be directly integrated over $s$ ,

I(\ell)=\frac{\Gamma\left[6-\frac{3D}{2}\right]}{(4\pi)^{\frac{3D}{2}}}\int_{0}^{1}\prod_{i=1}^{5}dt_{i}\frac{t_{1}^{-2+\frac{D}{2}}t_{2}^{-3+D}t_{3}^{-4+\frac{3D}{2}}t_{4}}{\overline{U}^{2D-6}\overline{V}^{6-\frac{3D}{2}}\ell^{12-3D}},

(33)

and taking that $D=4-2\varepsilon$ ,

I(\ell)=\frac{\Gamma\left[3\varepsilon\right]}{(4\pi)^{6-3\varepsilon}\ell^{6\varepsilon}}\int_{0}^{1}\prod_{i=1}^{5}dt_{i}\frac{t_{1}^{-\varepsilon}t_{2}^{1-2\varepsilon}t_{3}^{2-3\varepsilon}t_{4}}{\overline{U}^{2-4\varepsilon}\overline{V}^{3\varepsilon}}.

(34)

Although at this point we do not know the behavior of the remaining integral with respect to $\varepsilon$ , we can already see that the pure logarithmic behavior of $\ell$ can only occur at $\varepsilon=0$ , which reinforces the perception that the existence of renormalons is an aspect related to the dimension where the theory is renormalizable.

Let us take $t_{1}^{-\varepsilon}\overline{V}^{-3\varepsilon}$ as a subdominant contribution ( $1+\mathcal{O}(\varepsilon)$ ). And as the polynomial $\overline{U}$ is independent of $t_{5}$ this variable can be integrated out. Also we can rewrite $\overline{U}$ as

\overline{U}=(1-t_{2}+t_{2}t_{3}t_{4}(1-t_{3}t_{4}))\\ -t_{1}(1-t_{2}+t_{2}^{2}t_{3}t_{4}(1-t_{3}t_{4}))=A_{1}-t_{1}A_{2},

(35)

to integrate over $t_{1}$

\int_{0}^{1}dt_{1}\frac{1}{(A_{1}-t_{1}A_{2})^{2-4\varepsilon}}=\int_{A_{1}}^{A_{1}-A_{2}}\frac{dy}{-A_{2}}\frac{1}{y^{2-4\varepsilon}}\\ =\frac{1}{1-4\varepsilon}\left[\frac{1}{(A_{1}-A_{2})^{1-4\varepsilon}A_{2}}-\frac{1}{A_{1}^{1-4\varepsilon}A_{2}}\right].

(36)

At this point, eq. (34) becames

I(\ell)=\frac{\Gamma\left[3\varepsilon\right](1+\mathcal{O}(\varepsilon))}{(4\pi)^{6-3\varepsilon}\ell^{6\varepsilon}}J_{1}-\frac{\Gamma\left[3\varepsilon\right](1+\mathcal{O}(\varepsilon))}{(4\pi)^{6-3\varepsilon}\ell^{6\varepsilon}}J_{2},

(37)

where $J_{1}$ and $J_{2}$ are given by

J_{1}=\int_{0}^{1}dt_{2}dt_{3}dt_{4}\frac{t_{2}^{1-2\varepsilon}t_{3}^{2-3\varepsilon}t_{4}}{1-t_{2}+t_{2}^{2}t_{3}t_{4}(1-t_{3}t_{4})}\times\\ \frac{1}{\left[t_{2}t_{3}t_{4}(1-t_{2})(1-t_{3}t_{4})\right]^{1-4\varepsilon}},

(38)

J_{2}=\int_{0}^{1}dt_{2}dt_{3}dt_{4}\frac{t_{2}^{1-2\varepsilon}t_{3}^{2-3\varepsilon}t_{4}}{1-t_{2}+t_{2}^{2}t_{3}t_{4}(1-t_{3}t_{4})}\times\\ \frac{1}{\left[1-t_{2}+t_{2}t_{3}t_{4}(1-t_{3}t_{4})\right]^{1-4\varepsilon}}.

(39)

The second integral, $J_{2}$ , is finite and gives

J_{2}=0.822\,467\,029\,8\ldots=c_{1}.

(40)

The integral $J_{1}$ has a divergent contribution from the $t_{2}$ integration. We can reorganize it and compute the other integrals

J_{1}=\int_{0}^{1}dt_{2}\frac{t_{2}^{2\varepsilon}}{(1-t_{2})^{1-4\varepsilon}}\int_{0}^{1}dt_{3}\int_{0}^{1}dt_{4}\times\\ \frac{1}{1-t_{2}+t_{2}^{2}t_{3}t_{4}(1-t_{3}t_{4})}\frac{t_{3}}{(1-t_{3}t_{4})^{1-4\varepsilon}}\\ =\int_{0}^{1}dt\,t^{2\varepsilon-1}(1-t)^{4\varepsilon-1}\frac{2\ln(1-t)}{t-2}.

Note that we can rewrite it as a derivative of a function of $\mu$ and $\nu$ (and later identify $\mu=2\varepsilon$ , $\nu=4\varepsilon$ )

	$\displaystyle G(\mu,\nu)=-\int_{0}^{1}dt\,t^{\mu-1}(1-t)^{\nu-1}\left(1-\frac{t}{2}\right)^{-1},$		(41)
	$\displaystyle\partial_{\nu}G(\mu,\nu)=\int_{0}^{1}dt\,t^{\mu-1}(1-t)^{\nu-1}\frac{2\ln(1-t)}{t-2}.$		(42)

Where is $G(\mu,\nu)$ is known, see eq. 3.197(3) from ref. Gradshteyn and Ryzhik (2007),

	$\displaystyle G(\mu,\nu)$	$\displaystyle=-B(\mu,\nu){}_{2}F_{1}\left(1,\mu;\mu+\nu;\frac{1}{2}\right)$
		$\displaystyle=-\sum_{k=0}^{\infty}\frac{\Gamma(\mu+k)\Gamma(\nu)}{\Gamma(\mu+\nu+k)}\frac{1}{2^{k}},$		(43)

where $B(\mu,\nu)$ is the Beta function and ${}_{2}F_{1}$ is the hypergeometric function. We use the representation as a infinite sum of gamma functions, to make manipulations easier.

Making the derivative with respect to $\nu$ and substituting $\mu=2\varepsilon,\nu=4\varepsilon$ ,

J_{1}=G^{(0,1)}(2\varepsilon,4\varepsilon)=-\sum_{k=0}^{\infty}\frac{\Gamma(2\varepsilon+k)}{2^{k}\Gamma(6\varepsilon+k)}\Bigg{(}\Gamma^{\prime}(4\varepsilon)\\ -\frac{\Gamma(4\varepsilon)\Gamma^{\prime}(6\varepsilon+k)}{\Gamma(6\varepsilon+k)}\Bigg{)}=\left(\frac{1}{16\varepsilon^{2}}+\frac{\pi^{2}}{6}+\mathcal{O}(\varepsilon)\right)\\ +\Bigg{[}\left(\frac{1}{16\varepsilon^{2}}-\frac{\pi^{2}}{12}-\frac{\gamma^{2}}{2}\right)\sum_{k=1}^{\infty}\frac{1}{2^{k}}-\gamma\sum_{k=1}^{\infty}\frac{\psi^{(0)}(k)}{2^{k}}\\ -\frac{1}{2}\sum_{k=1}^{\infty}\frac{\left(\psi^{(0)}(k)\right)^{2}}{2^{k}}+\frac{1}{2}\sum_{k=1}^{\infty}\frac{\psi^{(1)}(k)}{2^{k}}+\mathcal{O}(\varepsilon)\Bigg{]}=\\ \frac{1}{8\varepsilon^{2}}+\frac{\pi^{2}}{8}+\frac{\gamma^{2}}{2}-\gamma\ln 2+\frac{1}{4}\ln^{2}2-\frac{1}{2}\sum_{k=1}^{\infty}\frac{\left(\psi^{(0)}(k)\right)^{2}}{2^{k}}+\mathcal{O}(\varepsilon)=\\ \frac{1}{8\varepsilon^{2}}+\underbrace{0.822\,467\,033\,4\ldots}_{c_{2}}+\mathcal{O}(\varepsilon)

(44)

Finally, we obtain

I(\ell)=\frac{\Gamma\left[3\varepsilon\right]}{(4\pi)^{6-3\varepsilon}\ell^{6\varepsilon}}\Bigg{(}-c_{1}+c_{2}+\frac{1}{8\varepsilon^{2}}+\mathcal{O}(\varepsilon)\Bigg{)}.

(45)

We can expand with respect to $\varepsilon\rightarrow 0$ to make the poles evident,

I(\ell)=\frac{1}{(4\pi)^{6}}\left(\frac{1}{3\varepsilon}-\gamma+\frac{\varepsilon}{4}\left(6\gamma^{2}+\pi^{2}\right)+\mathcal{O}(\varepsilon^{2})\right)\\ \left(1-3\varepsilon\ln\frac{\ell^{2}}{4\pi}+\frac{9}{2}\varepsilon^{2}\ln^{2}\frac{\ell^{2}}{4\pi}-\frac{9}{2}\varepsilon^{3}\ln^{3}\frac{\ell^{2}}{4\pi}+\mathcal{O}(\varepsilon^{4})\right)\times\\ \Bigg{(}\frac{1}{8\varepsilon^{2}}-c_{1}+c_{2}+\mathcal{O}(\varepsilon)\Bigg{)}.

(46)

After some algebraic manipulations it produces

I(\ell)=\frac{1}{(4\pi)^{6}}\Bigg{[}\frac{1}{8\varepsilon^{3}}+\frac{1}{\varepsilon^{2}}\left(-\frac{\gamma}{8}-\frac{1}{8}\ln\frac{\ell^{2}}{4\pi}\right)\\ +\frac{1}{\varepsilon}\left(\frac{c_{2}-c_{1}}{3}+\frac{\pi^{2}+6\gamma^{2}}{32}-\frac{9\gamma}{16}\ln\frac{\ell^{2}}{4\pi}+\frac{3}{16}\ln^{2}\frac{\ell^{2}}{4\pi}\right)\\ -3\ln\frac{\ell^{2}}{4\pi}\left(\frac{c_{2}-c_{1}}{3}+\frac{\pi^{2}+6\gamma^{2}}{32}\right)\\ -\frac{3\gamma}{16}\ln^{2}\frac{\ell^{2}}{4\pi}-\frac{3}{16}\ln^{3}\frac{\ell^{2}}{4\pi}+a_{0}+\mathcal{O}(\varepsilon)\Bigg{]}

(47)

We consider a $\overline{MS}$ subtraction, such that the poles ( $\varepsilon^{-3},\varepsilon^{-2},\varepsilon^{-1}$ ) are removed and the amplitude becames

	$\widehat{I}(\ell)=a_{0}+a_{1}\ln\ell^{2}+a_{2}\ln^{2}\ell^{2}+a_{3}\ln^{3}\ell^{2},$	(48a)
where the constants are

	$\displaystyle a_{3}=-\frac{3}{4^{8}\pi^{6}}=-4.761\,481\,354\times 10^{-8},$	(48b)
	$\displaystyle a_{2}=-\frac{3\gamma}{4^{8}\pi^{6}}=-2.748\,401\,625\times 10^{-7},$	(48c)
	$\displaystyle a_{1}=5.886\,714\,656\times 10^{-9}.$	(48d)

The correct determination of $a_{0}$ requires one more term in the $\varepsilon$ -expansion in eq. (46). After some computations one finds $a_{0}=7.074\,471\,170\times 10^{-7}.$

Therefore, the chain of cat’s eyes has the $\ln^{3}\ell$ behavior that can produce a Gevrey-3 divergent series. This logarithmic behavior is a property of $D=4$ and is responsible for the renormalon divergence. If we consider the same diagram in any other dimension we will obtain something like $\ell^{a}\ln^{b}\ell$ that does not produce a renormalon divergence.

References

Beneke (1999) M. Beneke, Phys. Rept. 317, 1 (1999), arXiv:hep-ph/9807443 .
Loewe and Valenzuela (2000) M. Loewe and C. Valenzuela, Mod. Phys. Lett. A 15, 1181 (2000), arXiv:hep-th/9911151 .
Kneur and Reynaud (2003) J. Kneur and D. Reynaud, JHEP 01, 014 (2003), arXiv:hep-th/0111120 .
Guralnik and Guralnik (2010) G. Guralnik and Z. Guralnik, Annals Phys. 325, 2486 (2010), arXiv:0710.1256 [hep-th] .
Unsal and Yaffe (2008) M. Unsal and L. G. Yaffe, Phys. Rev. D 78, 065035 (2008), arXiv:0803.0344 [hep-th] .
Argyres and Unsal (2012a) P. C. Argyres and M. Unsal, JHEP 08, 063 (2012a), arXiv:1206.1890 [hep-th] .
Argyres and Unsal (2012b) P. Argyres and M. Unsal, Phys. Rev. Lett. 109, 121601 (2012b), arXiv:1204.1661 [hep-th] .
Dunne and Unsal (2012) G. V. Dunne and M. Unsal, JHEP 11, 170 (2012), arXiv:1210.2423 [hep-th] .
Dunne and Ünsal (2013) G. V. Dunne and M. Ünsal, Phys. Rev. D 87, 025015 (2013), arXiv:1210.3646 [hep-th] .
Poppitz et al. (2013) E. Poppitz, T. Schäfer, and M. Ünsal, JHEP 03, 087 (2013), arXiv:1212.1238 [hep-th] .
Cherman et al. (2014) A. Cherman, D. Dorigoni, G. V. Dunne, and M. Ünsal, Phys. Rev. Lett. 112, 021601 (2014), arXiv:1308.0127 [hep-th] .
Shifman (2015a) M. Shifman, Int. J. Mod. Phys. A 30, 1543001 (2015a), arXiv:1310.1966 [hep-th] .
Dabrowski and Dunne (2013) R. Dabrowski and G. V. Dunne, Phys. Rev. D 88, 025020 (2013), arXiv:1306.0921 [hep-th] .
Cherman et al. (2015) A. Cherman, D. Dorigoni, and M. Unsal, JHEP 10, 056 (2015), arXiv:1403.1277 [hep-th] .
Shifman (2015b) M. Shifman, J. Exp. Theor. Phys. 120, 386 (2015b), arXiv:1411.4004 [hep-th] .
Anber and Sulejmanpasic (2015) M. M. Anber and T. Sulejmanpasic, JHEP 01, 139 (2015), arXiv:1410.0121 [hep-th] .
Sulejmanpasic and Ünsal (2018) T. Sulejmanpasic and M. Ünsal, Comput. Phys. Commun. 228, 273 (2018), arXiv:1608.08256 [hep-th] .
Sulejmanpasic (2017) T. Sulejmanpasic, Phys. Rev. Lett. 118, 011601 (2017), arXiv:1610.04009 [hep-th] .
Dunne and Ünsal (2016) G. V. Dunne and M. Ünsal, Ann. Rev. Nucl. Part. Sci. 66, 245 (2016), arXiv:1601.03414 [hep-th] .
Buividovich and Valgushev (2017) P. Buividovich and S. Valgushev, (2017), arXiv:1706.08954 [hep-lat] .
Caprini et al. (2017) I. Caprini, J. Fischer, G. Abbas, and B. Ananthanarayan, (2017), arXiv:1711.04445 [hep-ph] .
Aniceto et al. (2019) I. Aniceto, G. Basar, and R. Schiappa, Phys. Rept. 809, 1 (2019), arXiv:1802.10441 [hep-th] .
Cherman et al. (2019) A. Cherman, M. Shifman, and M. Ünsal, Phys. Rev. D 99, 105001 (2019), arXiv:1812.04642 [hep-th] .
Maiezza and Vasquez (2018) A. Maiezza and J. C. Vasquez, Annals Phys. 394, 84 (2018), arXiv:1802.06022 [hep-th] .
Cavalcanti et al. (2018) E. Cavalcanti, J. A. Lourenço, C. A. Linhares, and A. P. C. Malbouisson, Phys. Rev. D 98, 045013 (2018), arXiv:1804.10708 [hep-th] .
Fujimori et al. (2019) T. Fujimori, S. Kamata, T. Misumi, M. Nitta, and N. Sakai, JHEP 02, 190 (2019), arXiv:1810.03768 [hep-th] .
Mariño and Reis (2019) M. Mariño and T. Reis, (2019), 10.1088/1742-5468/ab4802, arXiv:1905.09569 [hep-th] .
Mariño and Reis (2020a) M. Mariño and T. Reis, JHEP 04, 160 (2020a), arXiv:1909.12134 [hep-th] .
Mariño and Reis (2020b) M. Mariño and T. Reis, JHEP 07, 216 (2020b), arXiv:1912.06228 [hep-th] .
Correa et al. (2019) M. Correa, M. Loewe, D. Valenzuela, and R. Zamora, Phys. Rev. D 99, 096024 (2019), arXiv:1901.06426 [hep-ph] .
Ishikawa et al. (2020a) K. Ishikawa, O. Morikawa, K. Shibata, H. Suzuki, and H. Takaura, PTEP 2020, 013B01 (2020a), arXiv:1909.09579 [hep-th] .
Ishikawa et al. (2020b) K. Ishikawa, O. Morikawa, A. Nakayama, K. Shibata, H. Suzuki, and H. Takaura, PTEP 2020, 023B10 (2020b), arXiv:1908.00373 [hep-th] .
Ashie et al. (2020a) M. Ashie, O. Morikawa, H. Suzuki, H. Takaura, and K. Takeuchi, PTEP 2020, 023B01 (2020a), arXiv:1909.05489 [hep-th] .
Borinsky and Dunne (2020) M. Borinsky and G. V. Dunne, Nucl. Phys. B 957, 115096 (2020), arXiv:2005.04265 [hep-th] .
Cavalcanti (2020) E. Cavalcanti, (2020), arXiv:2011.04099 [hep-th] .
Dondi et al. (2020) N. A. Dondi, G. V. Dunne, M. Reichert, and F. Sannino, Phys. Rev. D 102, 035005 (2020), arXiv:2003.08397 [hep-th] .
Ashie et al. (2020b) M. Ashie, O. Morikawa, H. Suzuki, and H. Takaura, PTEP 2020, 093B02 (2020b), arXiv:2005.07407 [hep-th] .
Ünsal (2020) M. Ünsal, (2020), arXiv:2007.03880 [hep-th] .
Costin and Dunne (2020) O. Costin and G. V. Dunne, Phys. Lett. B 808, 135627 (2020), arXiv:2003.07451 [hep-th] .
Cvetič (2020) G. Cvetič, Nucl. Part. Phys. Proc. 309-311, 87 (2020), arXiv:1909.13593 [hep-ph] .
Hadjimichef et al. (2020) D. Hadjimichef, E. Luna, and M. Peláez, Phys. Lett. B 804, 135350 (2020), arXiv:1907.07577 [hep-ph] .
Takaura (2019) H. Takaura, PoS ALPHAS2019, 025 (2019).
Hayashi and Sumino (2019) Y. Hayashi and Y. Sumino, Phys. Lett. B 795, 107 (2019), arXiv:1904.02563 [hep-ph] .
Corcella (2019) G. Corcella, Front. in Phys. 7, 54 (2019), arXiv:1903.06574 [hep-ph] .
Maiezza and Vasquez (2019) A. Maiezza and J. C. Vasquez, Annals Phys. 407, 78 (2019), arXiv:1902.05847 [hep-th] .
Nason (2019a) P. Nason, in 11th International Workshop on Top Quark Physics (2019) arXiv:1901.04737 [hep-ph] .
Cvetič (2019) G. Cvetič, Phys. Rev. D 99, 014028 (2019), arXiv:1812.01580 [hep-ph] .
Ortega et al. (2018) P. G. Ortega, V. Mateu, D. R. Entem, and F. Fernández, PoS Confinement2018, 121 (2018), arXiv:1811.12191 [hep-ph] .
Kataev and Molokoedov (2018a) A. Kataev and V. Molokoedov, JETP Lett. 108, 777 (2018a), arXiv:1811.02867 [hep-ph] .
Mateu et al. (2019) V. Mateu, P. G. Ortega, D. R. Entem, and F. Fernández, Eur. Phys. J. C 79, 323 (2019), arXiv:1811.01982 [hep-ph] .
Boito et al. (2019) D. Boito, P. Masjuan, and F. Oliani, SciPost Phys. Proc. 1, 049 (2019), arXiv:1811.01601 [hep-ph] .
Boito et al. (2018) D. Boito, P. Masjuan, and F. Oliani, JHEP 08, 075 (2018), arXiv:1807.01567 [hep-ph] .
Ferrario Ravasio et al. (2019) S. Ferrario Ravasio, P. Nason, and C. Oleari, JHEP 01, 203 (2019), arXiv:1810.10931 [hep-ph] .
Brambilla et al. (2018a) N. Brambilla, H. S. Chung, and J. Komijani, Phys. Rev. D 98, 114020 (2018a), arXiv:1810.02586 [hep-ph] .
Braun et al. (2019) V. M. Braun, A. Vladimirov, and J.-H. Zhang, Phys. Rev. D 99, 014013 (2019), arXiv:1810.00048 [hep-ph] .
Kataev and Molokoedov (2018b) A. Kataev and V. Molokoedov, EPJ Web Conf. 191, 04005 (2018b), arXiv:1809.04395 [hep-ph] .
Bell et al. (2019) G. Bell, A. Hornig, C. Lee, and J. Talbert, JHEP 01, 147 (2019), arXiv:1808.07867 [hep-ph] .
Takaura et al. (2019a) H. Takaura, T. Kaneko, Y. Kiyo, and Y. Sumino, Phys. Lett. B 789, 598 (2019a), arXiv:1808.01632 [hep-ph] .
Takaura et al. (2019b) H. Takaura, T. Kaneko, Y. Kiyo, and Y. Sumino, JHEP 04, 155 (2019b), arXiv:1808.01643 [hep-ph] .
Suzuki and Takaura (2019) H. Suzuki and H. Takaura, PTEP 2019, 103B04 (2019), arXiv:1807.10064 [hep-ph] .
Del Debbio et al. (2018) L. Del Debbio, F. Di Renzo, and G. Filaci, Eur. Phys. J. C 78, 974 (2018), arXiv:1807.09518 [hep-lat] .
Kataev and Molokoedov (2018c) A. Kataev and V. Molokoedov, (2018c), arXiv:1807.05406 [hep-ph] .
Peset et al. (2018) C. Peset, A. Pineda, and J. Segovia, JHEP 09, 167 (2018), arXiv:1806.05197 [hep-ph] .
Bazavov et al. (2018) A. Bazavov et al. (Fermilab Lattice, MILC, TUMQCD), Phys. Rev. D 98, 054517 (2018), arXiv:1802.04248 [hep-lat] .
Brambilla et al. (2018b) N. Brambilla, J. Komijani, A. Kronfeld, and A. Vairo (TUMQCD), Phys. Rev. D 97, 034503 (2018b), arXiv:1712.04983 [hep-ph] .
Nason (2019b) P. Nason, “The Top Mass in Hadronic Collisions,” in From My Vast Repertoire …: Guido Altarelli’s Legacy, edited by A. Levy, S. Forte, and G. Ridolfi (2019) pp. 123–151, arXiv:1712.02796 [hep-ph] .
Ortega and Mateu (2018) P. G. Ortega and V. Mateu, PoS Hadron2017, 031 (2018), arXiv:1711.09998 [hep-ph] .
Mateu and Ortega (2018) V. Mateu and P. G. Ortega, JHEP 01, 122 (2018), arXiv:1711.05755 [hep-ph] .
Hoang et al. (2017) A. H. Hoang, C. Lepenik, and M. Preisser, JHEP 09, 099 (2017), arXiv:1706.08526 [hep-ph] .
Ahmadov et al. (2017) A. Ahmadov, C. Aydin, and O. Uzun, J. Phys. Conf. Ser. 804, 012001 (2017).
Steinhauser (2016) M. Steinhauser, PoS DIS2016, 148 (2016).
Jamin and Miravitllas (2016) M. Jamin and R. Miravitllas, JHEP 10, 059 (2016), arXiv:1606.06166 [hep-ph] .
Ayala et al. (2016) C. Ayala, G. Cvetic, and A. Pineda, J. Phys. Conf. Ser. 762, 012063 (2016), arXiv:1606.01741 [hep-ph] .
Mishima et al. (2017) G. Mishima, Y. Sumino, and H. Takaura, Phys. Rev. D 95, 114016 (2017), arXiv:1612.08711 [hep-ph] .
Marino and Reis (2020) M. Marino and T. Reis, (2020), arXiv:2006.05131 [hep-th] .
Bender and Orszag (2013) C. M. Bender and S. A. Orszag, Advanced mathematical methods for scientists and engineers I: Asymptotic methods and perturbation theory (Springer Science & Business Media, 2013).
Shalaby (2020) A. M. Shalaby, Phys. Rev. D 101, 105006 (2020), arXiv:2004.08711 [hep-th] .
Weniger (1996) E. J. Weniger, Ann. Phys. 246, 133 (1996).
Bergere et al. (1978) M. Bergere, C. de Calan, and A. Malbouisson, Commun. Math. Phys. 62, 137 (1978).
Smirnov (1995) V. A. Smirnov, Mod. Phys. Lett. A 10, 1485 (1995), arXiv:hep-th/9412063 .
Linhares et al. (2008) C. Linhares, A. Malbouisson, and I. Roditi, Rev. Math. Phys. 20, 933 (2008), arXiv:0711.4972 [hep-th] .
Palmer and Carrington (2002) C. Palmer and M. Carrington, Can. J. Phys. 80, 847 (2002), arXiv:hep-th/0108088 .
Itzykson and Zuber (1980) C. Itzykson and J. Zuber, Quantum Field Theory, International Series In Pure and Applied Physics (McGraw-Hill, New York, 1980).
Gradshteyn and Ryzhik (2007) I. Gradshteyn and J. Ryzhik, Table of Integrals, Series, and Products, 7th ed., edited by A. Jeffrey and D. Zwillinger (Elsevier, Amsterdam, 2007).