Relay synchronization and control of dynamics in multiplex networks with unidirectional inter layer coupling
Abstract
Multiplex networks provide a proper framework for understanding the dynamics of complex systems with different types of interactions. In this study, we consider the occurrence of different dynamical states in a multiplex network of nonlinear oscillators, with a drive layer and two identical response layers where the interlayer interactions are unidirectional. We report how the directionality in coupling can lead to relay synchronization with amplification in the two response layers, through the middle drive layer. Moreover, we find that the dynamics of the response layers can be controlled by adjusting the strength of interlayer coupling or tuning the dynamical time scale of the drive layer. With nonidentical parameters between the drive and response layers, the response layers get completely synchronized, with a functional relation with the drive, indicating generalized synchronization between the drive and response networks.
keywords:
Multiplex network , Relay Synchronization , Unidirectional coupling , Time scale mismatch[first]Indian Institute of Science Education and Research Tirupati, Tirupati-517 619, India
[second]Indian Institute of Science Education and Research Thiruvananthapuram, Thiruvananthapuram-695 551, India
1 Introduction
The emergent dynamics of several real-world complex systems, having many interacting subsystems, can be effectively modeled using the framework of complex networks. When the subsystems are not identical in the dynamics or nature of their interactions, we can model them using multilayer networks such that the different layers can take care of the dissimilarities [1]. Multiplex networks are a special case of multilayer networks, where all layers have the same number of nodes and the node of each layer is connected only to the nodes of the corresponding layers [2]. This framework can be especially useful for studying different types of emergent dynamics [3, 4, 5, 6, 7, 8, 7, 9] in nervous systems at different organizational levels [10, 11], social interaction networks with varying interactions [12], and power grid networks having different loads for connections [13] etc . Additionally, this can add an extra layer of controllability to the system such that a desired state can be achieved in one of the layers by tuning the parameters of the other [14].
Among the possible dynamical states in complex systems, synchronization is the most relevant and well-studied collective phenomenon due to its theoretical , biological and technological significance. Thus, in both single and multilayer networks, achieving synchronization is important[15, 16, 17, 18] and a variety of synchronous behavior, such as frequency, in/anti phase [19], complete, cluster [20, 21], explosive [22, 23, 24], intralayer [25, 26], and interlayer [27, 28, 29] synchronization are reported.
Distinct from these, is the concept of relay synchronization in multilayer network where two distant networks, which are not directly connected, can synchronize with each other with the help of an intermediate network acting as the relay[30, 31, 32, 33]. One specific application in this context is the human brain network [34, 35, 36, 37], where the thalamus acts as a relay between distant cortical areas through the thalamocortical pathways. In recent studies, researchers have looked at the effects of network topology [38], edge weights [39], intralayer coupling [40] and even repulsive coupling [41] in achieving relay synchronization. Also, the relay synchronization of chimeras [42] occur, where synchronization of the coherent domains of chimera states in the first layer occurs with their counterparts in the third layer, whereas the incoherent domains either remain desynchronized or synchronized. In a specific context, relay synchronization is found to improve when the distant layers have positive coupling while the relay layer has repulsive coupling [41].
We note most of the reported studies on relay synchronization till now is with bidirectional coupling in intra layer and inter layer regimes, and hence the effects of directionality of interlayer links in relay synchronization are much less explored. There are, in fact, many real world complex systems like the brain that function with its component networks having unidirectional connectivity. As an example, we note two-layer neuronal network with unidirectional interlayer connections is found to have interesting patterns like non stationary and imperfect chimera states. [43].
We also note that most of the complex real world systems have constituents that often evolve under non-identical time scales [44]. In such cases also, the framework of multiplex networks would be a good approach to model them, with the interacting units separated into multiple layers depending on their time scales. Some such real-world scenarios with multiple time scales are temporal neural dynamics [45, 46], chemical reactions [47], hormonal regulation [48], and population dynamics [49]. In some of the recent studies, the time scale mismatch between the layers is found to generate dynamical states such as amplitude death [50], cluster synchronization [51], and frequency synchronization [52] and even revival of synchronized oscillations [14].
In this study we explore the role of uni directional coupling in achieving relay synchronization in a three layer multiplex network. In this framework, the middle layer (L2) acts as the drive with inter layer unidirectional coupling with two other layers L1 and L3. Using the Stuart Landau oscillator with periodic limit cycle as nodal dynamics, we study the onset of relay synchronisation in the system. We find, when the interlayer coupling is of feedback type, the drive layer L2 induces relay synchronisation in L1 and L3 with amplification of oscillations and in phase synchronisation with the drive layer. We show how the amplitude of oscillations in the response layers can be controlled by tuning the dynamical time scale mismatch between the drive and the responses. This mismatch between layers can also be tuned to control the nature of dynamics induced in the response layers, giving rise to interesting patterns like quasi periodic states in response layers. When the inter layer coupling is of diffusive type, drive layer L2 induces complete synchronization of all the three layers in the network.
In recent times, few studies related to generalized synchronization (GS) of complex networks have been reported where a functional relation is achieved between pairs of nodes in the network [53, 54, 55]. The framework we use in the study can serve as the auxiliary system approach to study GS when there is a parameter mismatch between the systems in the drive and response layers. This is then an extension of generalized synchronization to networks of systems, since here one network is driving two other similar networks that get synchronized but with a functional relation with the drive.
2 Relay synchronization in three layer multiplex network with unidirectional inter layer coupling
We start with a three-layer multiplex network of Stuart-Landau (SL) oscillators with ring topology, where each layer has bidirectional intralayer diffusive coupling. The oscillators in first (L1) and third layers (L3) are connected to the corresponding ones in the second layer (L2) via interlayer coupling of the feedback type to form a multiplex network. The interlayer coupling is directional in nature, indicating that L1 and L3 receive feedback from L2 through both and variables without any feedback input to L2, as shown in Fig. 1.

The dynamical equation for such a three layer multiplex network is as shown below.
where the variables and for i = 1, 2,…, N define the dynamics of SL oscillators in all three layers and is the inherent frequency of their limit cycle oscillations. The intralayer coupling strength, and , and the coupling range, and , control the interactions between the SL oscillators in the response layers (L1 and L3), whereas and control the interactions in the drive layer (L2). In this scenario, represents the number of nearest neighbours in each direction; hence, , where for local connections and for a global coupling; and is for nonlocal coupling. The unidirectional feedback coupling from drive to response governs the inter-layer interactions and we take their strengths to be equal as . We also introduce a parameter that can decide the dynamical time scale mismatch between the drive and response layers, such that the response layers L1 and L3 can be made to evolve on a slower time scale than the drive layer L2 by choosing a value of .
Initially, we keep so that the three layers evolve under identical time scales. We set the intra layer coupling strength and coupling range of each individual network with parameters chosen as , , , for systems in each layer. Then for random initial condition between (-1, 1) and for , the response layers do not have intra layer synchronization, while the drive layer has intra layer synchronized oscillations. As the inter layer coupling strength () between the drive and response is increased, the response layers achieve both intra and interlayer synchronization with amplification with respect to the drive. To detect intralayer and interlayer synchronization, we define the corresponding synchronization errors as in Eq. 2 and 3 where represents the average over time, indicates the variable of the node in the layer and is the mean value of in the layer.
| (2) |
| (3) |
Clearly, for complete intralayer synchronization, while for complete interlayer synchronization, . These measures are computed for varying and plotted in Fig. 2. As is increased, as seen in Fig. 2 (a1), the intralayer synchronization error of both the response layers (red for L1 and green for L3) drops to zero, indicating the onset of synchronization. Fig. 2 (a2) shows the variation in the inter layer synchronization error as is increased. Here, the synchronization error between L1 and L2 is indicated in red, that between L2 and L3 in green and between L3 and L1 in blue. It is clear that as is increased, both the response layers get synchronized to each other achieving relay synchronization as shown in the Fig. 2(a2) while the synchronization error between the drive and response first decreases and then gradually increases with due to the amplification induced by the directional coupling.

To study the amplification of the response layers due to the directional coupling, we compute the average amplitude, defined as,
| (4) |
We show in Fig. 3 (a1) the variation in the average amplitude of intralayer synchronized oscillations in the drive and response layers for . We observe that as the strength of interlayer coupling () is increased, the amplitude of oscillations in both the response layers increases while that of the drive remains the same due to the directional nature of the coupling. In this state, the response layers are phase synchronized with the drive, as is clear from Fig. 3 (a2) where the variation in the phase difference between the drive and the responses is shown as is increased.
We repeat the above analysis for the case where the inter layer coupling is of diffusive type. For this in Eq. LABEL:eq1, replace the feedback coupling term by ) and ) for the x and y variables respectively, where . Then we find that the response layers do not show amplification but on adjusting , they get synchronized with the drive resulting in complete synchronization in the entire multiplex network.

3 Effects of tuning dynamical time scales between layers
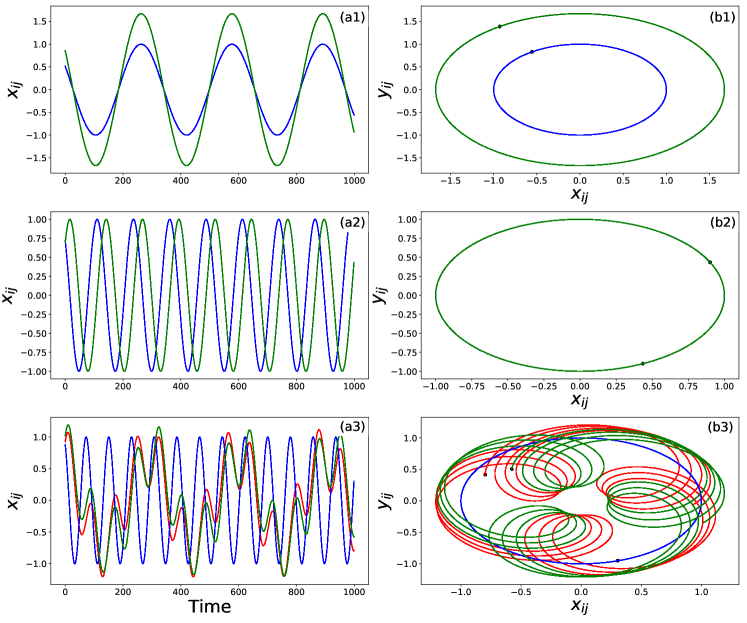
In this section we present the effect of mismatch in dynamical time scales between the drive and response layers. For this we introduce a time scale difference between the layers by increasing the parameter in Eqn 1 and study the resulting changes in dynamics of the response layers. We observe that the amplitude of oscillations in the response layers can be controlled by increasing and even made equal to that of the drive. With further increase in the value of , the dynamics of the response layers changes and quasi periodic oscillations set in, with only frequency synchronization between the responses layers. We illustrate this scenario for chosen values of and in Fig. 4.
For and , in Fig. 4 (a1),we see the response layers are perfectly synchronized to each other, indicating relay synchronization and are phase synchronized with the drive layer. The phase portrait of the three layers in Fig. 4 (b1) clearly indicates the amplification of oscillations for the response layers. As the drive layer is made to evolve on faster time scale, with and , we observe that the amplitude of the oscillations in the response and drive layers are equal but frequency synchronized with constant phase difference between them as shown in Fig. 4 (a2). This is clear from Fig. 4 (b2) where the phase portraits of the three layers overlap. With further increase of , multiple frequencies are observed in the response layers and the oscillations are quasi-periodic in nature, as shown in Fig. 4 (a3, b3) for and . Then, relay synchronization between the responses is lost and they are frequency synchronized to each other.
We indicate the possible dynamical states induced in the response layers in the parameter plane vs in Fig. 5. We keep the other parameter values as , , and and study the nature of dynamics on varying and by computing average amplitude and synchronization errors. The region marked as (i) indicates parameter values for which there is amplification in the response layer with respect to the drive. The average amplitudes of oscillations in the drive and the response layers are equal for the range of parameter values lying in region (ii). In region (iii) the average amplitude of the response is less than that of the drive and in region (iv), quasi periodic states are observed in the response layers.
The variation in the average amplitude of L1 and L3 with is depicted in Fig. 6. For when both the drive and the response layers have the same time scales, the average amplitude of the response is greater than the drive due to the directional feedback coupling. As a time scale difference is introduced between the response and the drive (both and ), the average amplitude of the responses decreases, becoming equal at .

In the case of diffusive inter layer coupling, as the drive layer is made faster () or slower () the response layers show relay synchronization with decreased average amplitude when compared to the drive as depicted in Fig. 6 (black). So, introducing a dynamical time scale difference between the drive and response in this case can make the system go from complete synchronization to relay synchronization.

In addition to the time scale mismatch between layers, we also consider mismatch in the parameters of the intrinsic dynamics, , of SL oscillators between layers. With , , , , , and , for feedback type of inter layer coupling, we observe relay synchronization with amplification of the response layers but they have only frequency synchronization with the drive unlike the previous case where phase synchronization is observed. As is varied for a fixed epsilon, , similar to the above observations, tuning of the oscillations of the response to that of the drive is possible. This is then followed by quasi periodic behavior for very high values. In the case of diffusive coupling, with the same set of parameters, we observe relay synchronization of the responses instead of complete synchronization due to parameter mismatch and the amplitude of oscillations of the response layers can be controlled by tuning just like the case without intrinsic parameter mismatch.
4 Conclusion
While relay synchronization is one of the active research areas in the context of complex networks, most of the works till now consider bidirectional coupling in the multilayer framework. In this study, we explore the effects of uni directional inter layer coupling in a three layer multiplex network of Stuart Landau oscillators, with the middle layer L2 being the drive and the remote layers L1 and L3 being the responses. We analyze how different coupling strategies affect the development of relay synchronization on the response networks.
When all the layers evolve at the same dynamical time scale and with identical systems, the unidirectional feedback from the drive causes amplification of oscillations in the response layers along with relay synchronization that is in phase with the drive. We show that the amplification can be controlled by adjusting the strength of inter layer coupling.
By introducing appropriate time scale difference between the layers using the mismatch parameter , we can control the amplitude of oscillations in the response layers and they can be made equal to that of the drive with a phase difference. With further increase in , the amplitude of oscillations of the response becomes smaller than the drive, finally leading to quasi periodic behavior in the response layers. But as quasi periodic behavior emerges, relay synchronization is lost with only frequency synchronization between the response layers.
In the case of unidirectional diffusive coupling between identical layers, we obtain synchronization between the drive and responses leading to complete synchronization of the entire network. When a time scale miss match is introduced, the amplitude of oscillations of the response decreases.
We also study the dynamics on the response networks when there is a parameter mismatch in the response compared to the drive layer. In this case, for both feedback and diffusive inter layer coupling, the response layers get completely synchronized, with a functional relation with drive layer. This can be interpreted as generalized synchronization between the drive and response networks since the framework used corresponds to the auxiliary system approach.
The study provides an understanding of the occurrence and control of collective behavior in multiplex networks with unidirectional inter layer interactions. It can lead to possible mechanisms for remotely controlling the dynamics to desired states on complex networks by adjusting the strength of driving and parameters of another accessible network. This will have applications in controlling layers of networks in smart grids as well as in modeling remote synchronization in neuronal networks. The study can be extended further to multiple response layers with different dynamics and topology that can induce various levels of synchronous dynamics and spatio temporal patterns.
References
- Kivela et al. [2014] M. Kivela, A. Arenas, M. Barthelemy, J. P. Gleeson, Y. Moreno, M. A. Porter, Multilayer networks, J. Complex. Netw. 2 (2014) 203–271.
- Wang et al. [2024] Y. Wang, O. Zhao, L. Zhang, Multiplex networks in resilience modeling of critical infrastructure systems: A systematic review, Reliab. Eng. Syst. Saf. 250 (2024) 110300.
- Strogatz [2003] S. Strogatz, Synchronization: A universal concept in nonlinear sciences, Phys. Today. 56 (2003) 47–47.
- Saxena et al. [2012] G. Saxena, A. Prasad, R. Ramaswamy, Amplitude death: The emergence of stationarity in coupled nonlinear systems, Phys. Rep. 521 (2012) 205–228.
- Pranesh and Gupta [2023] S. Pranesh, S. Gupta, Explosive death transitions in complex networks of limit cycle and chaotic systems, Chaos Solit. Fractals 168 (2023) 113112.
- Koseska et al. [2013] A. Koseska, E. Volkov, J. Kurths, Transition from amplitude to oscillation death via turing bifurcation, Phys. Rev. Lett. 111 (2013) 024103.
- Zakharova et al. [2014] A. Zakharova, M. Kapeller, E. Schöll, Chimera death: Symmetry breaking in dynamical networks, Phys. Rev. Lett. 112 (2014) 154101.
- Sethia and Sen [2014] G. C. Sethia, A. Sen, Chimera states: The existence criteria revisited, Phys. Rev. Lett. 112 (2014) 144101.
- Banerjee [2015] T. Banerjee, Mean-field-diffusion–induced chimera death state, Europhys. Lett. 110 (2015) 60003.
- Boccaletti et al. [2009] S. Boccaletti, V. Latora, Y. Moreno, Handbook on Biological Networks, volume 10, WORLD SCIENTIFIC, 2009.
- Makovkin et al. [2020] S. Y. Makovkin, I. V. Shkerin, S. Y. Gordleeva, M. V. Ivanchenko, Astrocyte-induced intermittent synchronization of neurons in a minimal network, Chaos Solit. Fractals 138 (2020) 109951.
- Deville et al. [2016] P. Deville, C. Song, N. Eagle, V. D. Blondel, A. L. Barabasi, D. Wang, Scaling identity connects human mobility and social interactions, Proc. Natl. Acad. Sci 113 (2016) 7047–7052.
- Pagani and Aiello [2013] G. A. Pagani, M. Aiello, The power grid as a complex network: A survey, Physica A 392 (2013) 2688–2700.
- Vadakkan et al. [2024] A. T. Vadakkan, U. K. Verma, G. Ambika, Recovery of synchronized oscillations on multiplex networks by tuning dynamical time scales, Phys. Lett. A 525 (2024) 129842.
- Khanra [2021] P. Khanra, SYNCHRONIZATION IN MULTILAYER NETWORKS, Ph.D. thesis, 2021.
- Belykh et al. [2019] I. Belykh, D. Carter, R. Jeter, Synchronization in multilayer networks: When good links go bad, SIAM J. Appl. Dyn. Syst 18 (2019) 2267–2302.
- Makovkin et al. [2021] S. Makovkin, T. Laptyeva, S. Jalan, M. Ivanchenko, Synchronization in multiplex models of neuron–glial systems: Small-world topology and inhibitory coupling, Chaos 31 (2021) 113111.
- Anwar et al. [2023] M. S. Anwar, S. Rakshit, J. Kurths, D. Ghosh, Synchronization induced by layer mismatch in multiplex networks, Entropy 25 (2023) 1083.
- Verma and Ambika [2021] U. K. Verma, G. Ambika, Emergent dynamics and spatio temporal patterns on multiplex neuronal networks, Front. Comput. Neurosci 15 (2021).
- Jalan and Singh [2016] S. Jalan, A. Singh, Cluster synchronization in multiplex networks, Europhys. Lett. 113 (2016) 30002.
- Rossa et al. [2020] F. D. Rossa, L. Pecora, K. Blaha, A. Shirin, I. Klickstein, F. Sorrentino, Symmetries and cluster synchronization in multilayer networks, Nature Communications 11 (2020) 3179.
- Zhang et al. [2015] X. Zhang, S. Boccaletti, S. Guan, Z. Liu, Explosive synchronization in adaptive and multilayer networks, Phys. Rev. Lett. 114 (2015) 038701.
- Verma and Ambika [2022] U. K. Verma, G. Ambika, Explosive synchronization in coupled nonlinear oscillators on multiplex network, Phys. Lett. A 450 (2022) 128391.
- Kumar et al. [2020] A. Kumar, S. Jalan, A. D. Kachhvah, Interlayer adaptation-induced explosive synchronization in multiplex networks, Phys. rev. res. 2 (2020) 023259.
- Gambuzza et al. [2015] L. V. Gambuzza, M. Frasca, J. Gómez-Gardeñes, Intra-layer synchronization in multiplex networks, Europhys. Lett. 110 (2015) 20010.
- Rakshit et al. [2020] S. Rakshit, B. K. Bera, E. M. Bollt, D. Ghosh, Intralayer synchronization in evolving multiplex hypernetworks: Analytical approach, SIAM J. Appl. Dyn. Syst 19 (2020) 918–963.
- Sevilla-Escoboza et al. [2016] R. Sevilla-Escoboza, I. Sendiña-Nadal, I. Leyva, R. Gutiérrez, J. M. Buldú, S. Boccaletti, Inter-layer synchronization in multiplex networks of identical layers, Chaos 26 (2016).
- Leyva et al. [2017] I. Leyva, R. Sevilla-Escoboza, I. Sendiña-Nadal, R. Gutiérrez, J. Buldú, S. Boccaletti, Inter-layer synchronization in non-identical multi-layer networks, Sci. Rep. 7 (2017) 45475.
- Pitsik et al. [2018] E. Pitsik, V. Makarov, D. Kirsanov, N. Frolov, M. Goremyko, X. Li, Z. Wang, A. Hramov, S. Boccaletti, Inter-layer competition in adaptive multiplex network, New J. Phys. 20 (2018) 075004.
- Kuptsov and Kuptsova [2015] P. V. Kuptsov, A. V. Kuptsova, Variety of regimes of starlike networks of hénon maps, Phys. Rev. E 92 (2015) 042912.
- Bergner et al. [2012] A. Bergner, M. Frasca, G. Sciuto, A. Buscarino, E. J. Ngamga, L. Fortuna, J. Kurths, Remote synchronization in star networks, Phys. Rev. E 85 (2012) 026208.
- Fischer et al. [2006] I. Fischer, R. Vicente, J. M. Buldú, M. Peil, C. R. Mirasso, M. C. Torrent, J. García-Ojalvo, Zero-lag long-range synchronization via dynamical relaying, Phys. Rev. Lett. 97 (2006) 123902.
- Banerjee et al. [2012] R. Banerjee, D. Ghosh, E. Padmanaban, R. Ramaswamy, L. M. Pecora, S. K. Dana, Enhancing synchrony in chaotic oscillators by dynamic relaying, Phys. Rev. E 85 (2012) 027201.
- Guillery and Sherman [2002] R. Guillery, S. Sherman, Thalamic relay functions and their role in corticocortical communication, Neuron 33 (2002) 163–175.
- Sherman [2007] S. M. Sherman, The thalamus is more than just a relay, Curr. Opin. Neurobiol. 17 (2007) 417–422.
- Mitchell et al. [2014] A. S. Mitchell, S. M. Sherman, M. A. Sommer, R. G. Mair, R. P. Vertes, Y. Chudasama, Advances in understanding mechanisms of thalamic relays in cognition and behavior, J. Neurosci. 34 (2014) 15340–15346.
- Vlasov and Bifone [2017] V. Vlasov, A. Bifone, Hub-driven remote synchronization in brain networks, Sci. Rep. 7 (2017) 10403.
- Drauschke et al. [2020] F. Drauschke, J. Sawicki, R. Berner, I. Omelchenko, E. Schöll, Effect of topology upon relay synchronization in triplex neuronal networks, Chaos 30 (2020).
- Anwar et al. [2021] M. S. Anwar, D. Ghosh, N. Frolov, Relay synchronization in a weighted triplex network, Mathematics 9 (2021) 2135.
- Leyva et al. [2018] I. Leyva, I. Sendiña-Nadal, R. Sevilla-Escoboza, V. P. Vera-Avila, P. Chholak, S. Boccaletti, Relay synchronization in multiplex networks, Sci. Rep. 8 (2018) 8629.
- Wei et al. [2024] Z. Wei, G. Sriram, K. Rajagopal, S. Jafari, Enhancing relay synchronization in multiplex networks by repulsive relay layer, Europhys. Lett. 145 (2024) 21003.
- Sawicki et al. [2018] J. Sawicki, I. Omelchenko, A. Zakharova, E. Schöll, Delay controls chimera relay synchronization in multiplex networks, Phys. Rev. E 98 (2018) 062224.
- Li et al. [2019] X. Li, T. Xu, J. Li, Synchronization and chimera states in a multilayer neuronal network with unidirectional interlayer links, Eur. Phys. J. Spec. Top. 228 (2019) 2419–2427.
- Feudel [2023] U. Feudel, Rate-induced tipping in ecosystems and climate: the role of unstable states, basin boundaries and transient dynamics, Nonlinear Process. Geophys. 30 (2023) 481–502.
- Samek et al. [2016] W. Samek, D. A. Blythe, G. Curio, K.-R. Müller, B. Blankertz, V. V. Nikulin, Multiscale temporal neural dynamics predict performance in a complex sensorimotor task, NeuroImage 141 (2016) 291–303.
- Boyden et al. [2005] E. S. Boyden, F. Zhang, E. Bamberg, G. Nagel, K. Deisseroth, Millisecond-timescale, genetically targeted optical control of neural activity, Nat. Neurosci. 8 (2005) 1263–1268.
- Das and Ray [2013] D. Das, D. S. Ray, Multiple time scale based reduction scheme for nonlinear chemical dynamics, Eur. Phys. J. Spec. Top. 222 (2013) 785–798.
- Radovick et al. [1992] S. Radovick, M. Nations, Y. Du, L. A. Berg, B. D. Weintraub, F. E. Wondisford, A mutation in the pou-homeodomain of pit-1 responsible for combined pituitary hormone deficiency, Science 257 (1992) 1115–1118.
- Bena et al. [2007] I. Bena, M. Droz, J. Szwabiński, A. Pekalski, Complex population dynamics as a competition between multiple-time-scale phenomena, Phys. Rev. E 76 (2007) 011908.
- Gupta and Ambika [2019] K. Gupta, G. Ambika, Role of time scales and topology on the dynamics of complex networks, Chaos 29 (2019).
- Yang et al. [2017] W. Yang, Y.-W. Wang, Y. Shen, L. Pan, Cluster synchronization of coupled delayed competitive neural networks with two time scales, Nonlinear. Dyn. 90 (2017) 2767–2782.
- Kachhara and Ambika [2021] S. Kachhara, G. Ambika, Frequency chimera state induced by differing dynamical timescales, Phys. Rev. E 104 (2021) 064214.
- Shang et al. [2009] Y. Shang, M. Chen, J. Kurths, Generalized synchronization of complex networks, Phys. Rev. E 80 (2009) 027201.
- Guan et al. [2010] S. Guan, X. Gong, K. Li, Z. Liu, C.-H. Lai, Characterizing generalized synchronization in complex networks, New J. Phys. 12 (2010) 073045.
- Guan et al. [2009] S. Guan, X. Wang, X. Gong, K. Li, C.-H. Lai, The development of generalized synchronization on complex networks, Chaos 19 (2009).