OCU-PHYS 558
AP-GR 179
NITEP 132
Relativistic Nontopological Soliton Stars
in a U(1) Gauge Higgs Model
Abstract
We study spherically symmetric nontopological soliton stars (NTS stars) numerically in the coupled system of a complex scalar field, a U(1) gauge field, a complex Higgs scalar field, and Einstein gravity, where the symmetry is broken spontaneously. The gravitational mass of NTS stars is limited by a maximum mass for a fixed breaking scale, and the maximum mass increases steeply as the breaking scale decreases. In the case of the breaking scale is much less than the Planck scale, the maximum mass of NTS stars becomes the astrophysical scale, and such a star is relativistically compact so that it has the innermost stable circular orbit.
The first author contributed with a part of numerical calculations. The second did with planning and conducting the research, and the third did with all numerical calculations and finding new properties of the system.
I Introduction
Nontopological solitons (NTSs) are localized solutions carrying a Noether charge in nonlinear field theories that have a continuous global symmetry. Rosen Rosen:1968mfz , in his pioneering work, showed that a self-interacting complex scalar field theory admits particlelike NTS solutions, and Coleman Coleman:1985ki proved the existence theorem of spherically symmetric NTS solutions with a conserved charge, he called them ‘Q-balls’ , in nonlinearly self-coupling complex scalar field theories with some conditions. Friedberg, Lee, and Sirlin Friedberg:1976me studied a coupled system of a complex scalar field and a real scalar field with a double-well potential, and showed the existence of the NTS solutions (see e.g. reviews Lee:1991ax ; Nugaev:2019vru and textbooks Shnir:2018yzp ). The NTS solutions in extended field theories including a gauge field were also studied in the works Lee:1988ag ; Shi:1991gh ; Gulamov:2015fya . The NTSs are interested as a possible candidate of dark matter Kusenko:1997si ; Kusenko:2001vu ; Fujii:2001xp ; Enqvist:2001jd ; Kusenko:2004yw , and as sources for baryogenesis Enqvist:1997si ; Kasuya:1999wu ; Kawasaki:2002hq .
Recently, NTS solutions were constructed in the theory that consists of a complex scalar field, a U(1) gauge field, and a complex Higgs scalar field with a Mexican hat potential which causes the spontaneous symmetery breaking Ishihara:2018rxg ; Ishihara:2019gim ; Ishihara:2021iag 111 NTSs in a generalized model are discussed in Refs.Forgacs:2020vcy ; Forgacs:2020sms . . In this model, there are interesting properties: the charges carried by two scalar fields are screening each other; and NTS solutions with infinitely large mass can exist Ishihara:2021iag . These would suggest that NTSs with astrophysical scale in this model can play important roles in cosmology. However, infinite mass should be prohibited if we take gravity produced by the NTS into account, namely, the mass should be limited by a maximum mass for self-gravitaing NTSs.
It is also investigated that localized objects made by self-gravitating complex scalar fields, so-called boson stars. In the model of a free massive complex scalar field with gravity, the gravitational mass of the localized solutions is quite small then the solutions are called mini boson stars Kaup:1968zz ; Ruffini:1969qy , while if the complex scalar field has nonlinear self-coupling, the mass of solution can be large Colpi:1986ye . Boson stars in various field models are studied in Refs.Jetzer:1989av ; Henriques:1989ar ; Henriques:1989ez (see also Jetzer:1991jr ; Schunck:2003kk ; Liebling:2012fv for review). Furthermore, self-gravity of the NTS is also studied in the Colman’s model Lynn:1988rb and the Friedberg-Lee-Sirlin’s model Lee:1986ts ; Friedberg:1986tq ; Lee:1986tr ; Kunz:2021mbm .
In this paper, we consider the coupled system of two complex scalar fields and a U(1) gauge field, which is studied in Refs.Ishihara:2018rxg ; Ishihara:2019gim ; Ishihara:2021iag , with Einstein gravity. The local U(1) symmetry of the system is spontaneously broken in a vacuum state where one of the scalar field has an expectation value. The system has two dimensionful parameters, the symmetry breaking scale, , and the Plank scale, , then the dimensionless parameter is an important quantity that characterizes the model.
Assuming spherically symmetry, stationary rotation of the phase of complex scalar fields, and static geometry, we derive a set of coupled ordinary differential equations. We obtain numerical solutions that describe self-gravitating objects, we call them ‘nontopological soliton stars (NTS stars)’ in this paper, and investigate properties of the solutions, especially, mass and radius that depend on . It is interesting that NTS stars with mass of astrophysical scale are possible, e.g., the solar mass is possible for 1GeV, and the NTS stars can be so compact that they have the innermost stable circular orbits for .
The paper is organized as follows. In Sec.II, we present the model that has a symmetry breaking scale, and derive basic equations on the assumptions of the geometrical symmetries of the fields. In Sec.III, we solve the basic equations numerically, and present NTS star solutions. In Sec.IV, we investigate internal structures of the NTS stars: energy density, pressure, and charge density. In Sec.V, we study mass and radius of the NTS stars, and see that the maximum mass appears for each breaking scale. Paying attention to the NTS stars with maximum mass in various breaking scales, we investigate scale dependence of the maximum mass and the compactness in Sec.VI. Section VII is devoted to conclusions.
II Basic Model
We consider the action
| (1) |
where is the scalar curvature with respect to a metric, , , and is the gravitational constant. The matter Lagrangian, , is given by
| (2) | ||||
| (3) |
where it consists of a complex matter scalar field , the field strength of a U(1) gauge field , and a complex Higgs scalar field . The gauge field couples to the scalar fields through the gauge covariant derivative, . The parameter is the charge of the fields and , the Higgs-self coupling, the Higgs-scalar coupling, and the Higgs vacuum expectation value determining the scale of the symmetry breaking.
The Lagrangian (3) has local U(1) global U(1) symmetry under the gauge transformation given by
| (4) | |||
| (5) | |||
| (6) |
where is an arbitrary function that depends on spacetime coordinate, and is an arbitrary constant. Concering to this invariance, conserved currents,
| (7) |
and conserved charges
| (8) |
are defined, where and are charge densities induced by the complex scalar field and , respectively. The integrations in (8) are performed on a timeslice
Owing to the potential term of the complex Higgs scalar field in (3), takes a nonzero vacuum expectation value in a vacuum state. As a result, the symmetry is spontaneously broken, then, the scalar field and the U(1) gauge field acquire masses, and , respectively, through interactions with the complex Higgs field. Simultaneously, a real scalar field as a fluctuation of the amplitude of around also acquires the mass .
From the action (1), we can derive field equations
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
where is the Einstein tensor and is the energy-momentum tensor given by
| (13) | ||||
| (14) |
Here, we assume stationary and spherically symmetric fields in the form:
| (15) |
where we use a spherical coordinate . The parameters and are constant angular frequencies of the complex scalar fields. Owing to the gauge transformation (4)-(6), we can fix the variables as
| (16) |
where is the parameter which characterizes the solution, and takes a positive value without loss of generality.
We also take static and spherically symmetric spacetime assumptions in the form
| (17) |
where and are functions of . Note that is dimensionless, and has dimension of length. The Einstein equations reduce to
| (18) |
Substituting assumptions (16) and (17) into (9)(11), we obtain equations for the fields and to be solved in the form:
| (19) | |||
| (20) | |||
| (21) | |||
| (22) |
where the prime denotes the derivative with respect to . Here and hereafter, , , , , , and are normalized by .
As for the Einstein equations, we solve the time-time component of (18) and the combination
| (23) |
The rests are guaranteed by the Bianchi identity. Explicit forms of the energy-momentum tensor and the charge densities are given in Appendix. Then, we have
| (24) | ||||
| (25) |
and
| (26) | ||||
| (27) |
The dimensionless parameter represents the symmetry breaking scale with respect to the Planck mass, . In the limiting case of , the gravitational field decouples with the matter fields, where the matter system (19)-(22) with and are studied in Refs.Ishihara:2018rxg ; Ishihara:2019gim ; Ishihara:2021iag .
We require regularity of the spherically symmetric fields at the origin described by
| (28) |
In addition, we assume that the solutions are localized in finite regions. Therefore, for the matter fields, we assume
| (29) |
at spatial infinity. The energy-momentum tensor of the matter fields satisfying (28) and (29) is localized in a neighborhood of the origin with a quick radial decay, then we require that the gravitational fields satisfy
| (30) |
at spatial infinity.
III Numerical Calculations
In this section, we obtain solutions by solving the set of equations (19), (21), (22), (25), and (27), numerically, and study properties of the numerical soutions. In this article, we fix the coupling constants as , , and , for an example. On the other hand, we consider various symmetry breaking scales. For the Planck breaking scale, , we have , and for the lower breaking scale, , , respectively.
At a large distance, should decrease quickly so that the energy is localized in a compact region. The boundary conditions at the spatial infinity, (29) and (30), require , and , then the equation (19) for reduces to
| (31) |
Then, is bounded above by . There is also the lower bound , which depends on , for existence of a solution, and, as is seen later, the solution has the maximum mass for near . We can find numerical solutions for the parameter in the range
| (32) |
Typical behaviors of the fields obtained by numerical calculations are shown as functions of in Fig.1 for the Planck breaking scale case, and in Fig.2 for the lower breaking scale case. They show that the matter fields and the gravitational field are localized in a finite region in each case. Thus, they represent nontopological solitons with self-gravity, we call them nontopological soliton star (NTS star) solutions.
|
Planck breaking scale:
|
(a)   (b)
(b)   (c)
(c)  
|
|
Lower breaking scale:
|
(d)   (e)
(e)   (f)
(f)  
|
In the cases (a) and (b) in the Planck breaking scale, and (d) in the lower breaking scale, the function has Gaussian forms, while and almost everywhere. In these cases, the scalar field and the gauge field are not excited anywhere, and only the scalar field , which has the mass by the Higgs mechanism, becomes a source of gravity. The behavior that the massive scalar field with gravity yields compact objects is just the same as ‘mini boson star’ solutions Kaup:1968zz ; Ruffini:1969qy . On the other hand, in the cases (e) and (f) in the lower breaking scale, , and are exited inside the stars. In these cases, interaction between the scalar fields and the gauge field plays an important role for appearance of solutions Ishihara:2018rxg ; Ishihara:2019gim ; Ishihara:2021iag .
As for the gravity, in the cases (a), (b), (d), and (e), the lapse function, , is almost constant. It means that the gravity is weak so that the the Newtonian description is possible. In contrast, in the cases (c) and (f), varies significantly from to infinity, i.e., it means the gravity requires relativistic description. Paying attention to the scale of horizontal axises, we see the size of the NTS stars depend on . The dependence is discussed later in detail.
IV Energy density, Pressure, and Charge densities
IV.1 Energy density and pressure
The energy density and the pressure, defined by (43)-(47) in Appendix A, are plotted in Fig.3 for numerical solutions. We see that the pressures can be ignored compared to the energy density in the cases (a), (b) in the Planck breaking scale case, and in the cases (d), (e) in the lower breaking scale case. Then, NTS stars in these cases behave as ‘gravitating dust balls’. On the other hand, in the cases (c) and (f), the radial and tangential pressures become large in the central regions.
IV.2 Charge distribution
We plot the charge density of , , and charge density of , , and total one of the NTS stars in Fig.4. In all cases except (c), is compensated by then charge screening occurs everywhere Ishihara:2018rxg . In the case (c), is positive in the central region, and negative surround the region. Total charge, integration of from to the large , vanishes. Namely, the charge is totally screened. This fact is consistent with that the gauge field, , becomes massive, and decays quickly as .
|
Planck breaking scale:
|
(a)  (b)
(b)  (c)
(c) 
|
|
Lower breaking scale:
|
(d)  (e)
(e)  (f)
(f) 
|
|
Planck breaking scale:
|
(a)  (b)
(b)  (c)
(c) 
|
|
Lower breaking scale:
|
(d)  (e)
(e)  (f)
(f) 
|
V Mass and radius
We see in Figs.1, 2, 3, that the size of NTS solutions much depend on the parameter . We study total mass and radius of the solutions in this section.
V.1 Gravitational Mass
The gravitational mass of the NTS star, , is given by
| (33) |
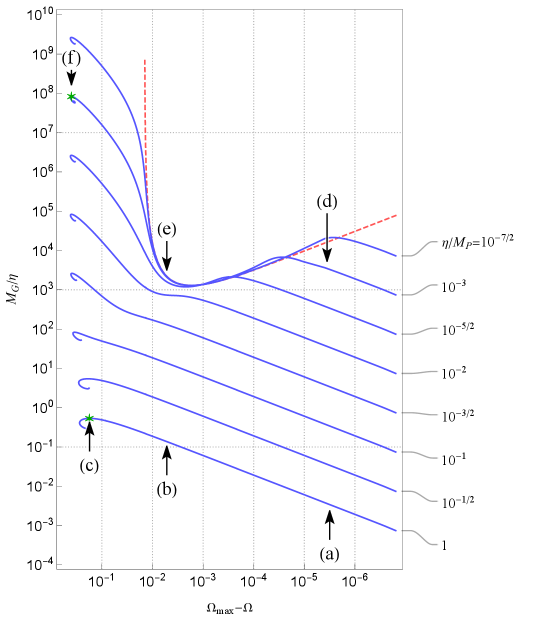
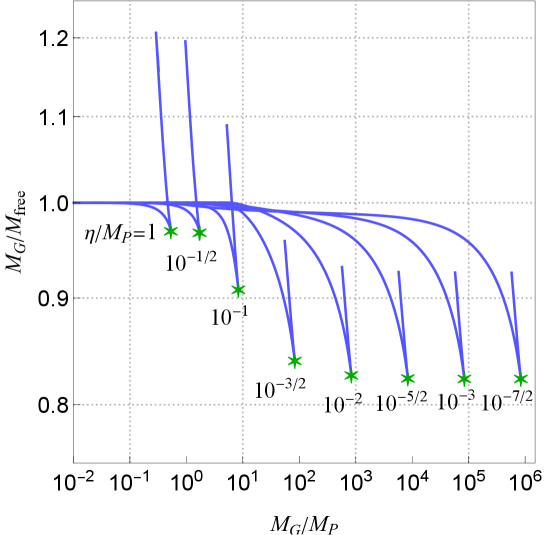
For a fixed , we have a NTS star solution for each , then is a function of . In Fig.5, curves represent as functions of for various breaking scales . We find each curve has a spiral shape at the left end. Then there appears lower limit of , , for existence of NTS star solutions. Numerically, we have for , while for . The gravitational mass is multi-valued in near a region . For a fixed , there exists maximum of near . We call the NTS star with the maximum mass ‘maximum NTS star’. The maximum NTS stars for and are marked by asterisks in Fig.5. In Fig.3, the central pressure in the maximum NTS star cases, (c) and (f), become large in the order of times the central energy density. The pressure gradient balances to the gravitational force by the large mass.
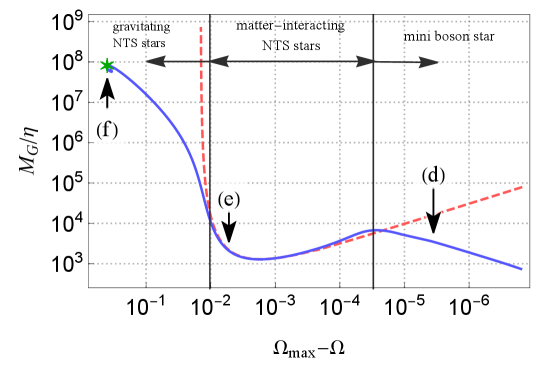
For , the curves are shifted upward, as a whole, as decreases, while for , the curves are modified, and middle part of the curves converge to the limiting curve of . Let us pay attention to the curve of , for example (see Fig.6). The curve is divided into three parts: the middle segment that lies on the limiting curve , the right segment apart downward from the limiting curve, the left segment apart leftward. Firstly, solutions on the right segment are ‘mini boson stars’ as mentioned before. Secondly, solutions on the middle are NTS stars whose gravity can be neglected, while the interaction of the scalar fields and the gauge field is important, then we call them ‘matter-interacting NTS stars’. Thirdly, solutions on the left segment are NTS stars whose gravity is important, then we call them ‘gravitating NTS stars’. In the family of the gravitating NTS stars, the mass quickly increases as approaches . The points (a) - (f) on the curves in Fig.5 correspond to the solutions shown in Figs.1 and 2, respectively.
V.2 Surface Radius
We define the surface radius of the numerical solutions, say , by
| (34) |
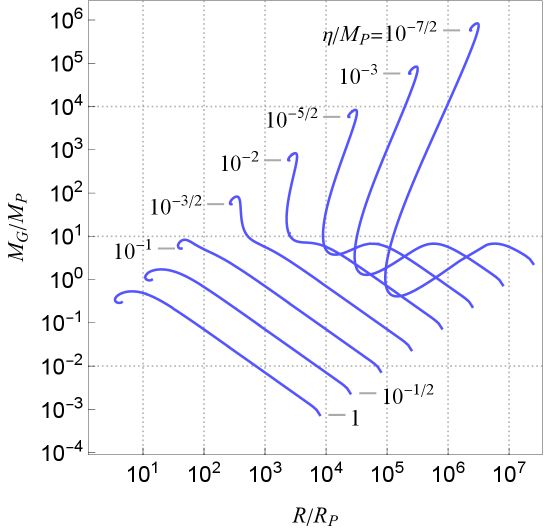
Namely, of total mass of the NTS stars includes within the surface radius . We plot gravitational mass of the NTS stars normalized by as a function of dimensionful radius for various breaking scales in Fig.7. For a fixed breaking scale in the range , increases toward the maximum mass as decreases, while in the range , depends on in a complicated way: in the region , local maximum and local minimum appear and in the region , increases toward the maximum mass as increases.
V.3 Compactness
Next, we investigate the compactness, , defined by
| (35) |
In the Schwarzschild geometries, which are exterior of NTS stars, if there exists the photon sphere and if the innermost stable circular orbit (ISCO) appears.
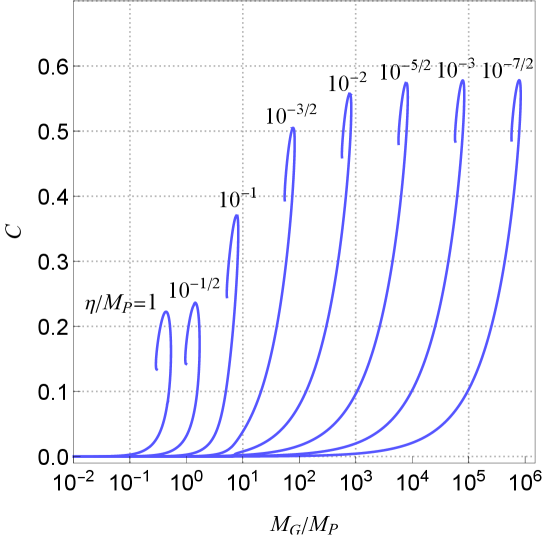
In Fig.8, we show the compactness of the NTS stars as a function of the gravitational mass for various breaking scales. For a fixed breaking scale, increases monotonically toward the maximum value as increases. The maximum value of depends on the breaking scale: for , and for . In the latter case a NTS star can be so compact that the star has ISCO around it.
V.4 Binding Energy
Here, we consider stability of the NTS stars in terms of the binding energy defined by , where is sum of mass of free particles that carry totally the same charge of the NTS stars. A NTS star with , , would disperse into free particles, i.e., the NTS star is energetically unstable, while a NTS star with , , is stable against dispersion.
In Fig.9, we plot the mass ratio, , as a function of for various breaking scales. The asterisk marks represent the maximum NTS solutions. It shows that the maximum NTS stars in all breaking scales have maximum negative binding energies where , then solutions near the maximum NTS stars are stable in all breaking scales.
VI Breaking Scale Dependence
As shown in the previous section, in each breaking scale, there exists the maximum NTS star that has maximum gravitational mass. The mass, the surface radius, and the compactness of the maximum NTS star much depend on the breaking scale. Here, we show how these properties of the maximum NTS star depend on the breaking scale.
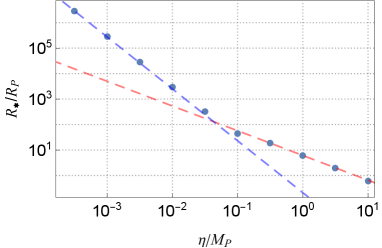
In Fig.10, we plot the mass, , and the surface radius, , of the maximum NTS stars for the various values of the breaking scale . We observe that the both and obey power laws of with two different power indices as
| (36) |
and
| (37) |
where the critical values and are order of , and the ratio is . The power index in is the same as mini boson stars studied in Kaup:1968zz ; Ruffini:1969qy , and the one in is the same as soliton stars studied in Friedberg:1986tq ; Lee:1986tr .
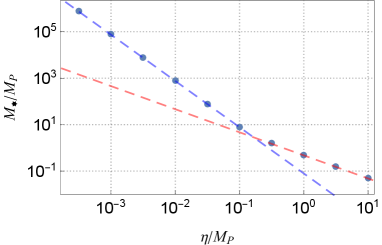
We consider simple model formulae for and shown in Fig.10 as
| (38) | ||||
| (39) |
where and are constants. If we can extrapolate (38) and (39) for much lower breaking scale than the cases calculated in the present paper, typical scales of and for the maximum NTS stars are listed in Table.1. We see that the maximum NTS star would be an astrophysical scale for 100GeV.
| Symmetry Breaking Scale | ||
|---|---|---|
| GeV | ||
| GeV | ||
| GeV | ||
| GeV | ||
| MeV | ||
| keV | ||
| eV |
According to the model functions (38) and (39), we have
| (40) |
then takes the different constant values for and , respectively, and the ratio of them becomes
| (41) |
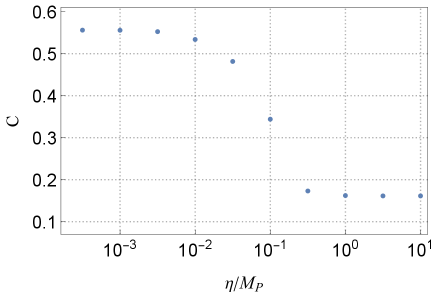
In Fig.11, we depict the compactness of the maximum NTS stars, , by the use of the numerical values of and as a function of the breaking scale. From numerical results we see for and for . Therefore, the maximum NTS stars in are relativistic self-gravitating objects that have innermost stable circular orbits while no photon sphere.
VII Conclusions
We studied the coupled system of field theory that consists of a complex scalar field, a U(1) gauge field, a complex Higgs scalar field that causes a spontaneous symmetry breaking, and Einstein gravity. The system has a dimensionless parameter, , which represents the ratio of the symmetry breaking scale to the Plank scale. We obtained numerical solutions that describe nontopological soliton stars, parametrized by the angular phase velocity of the complex scalar field, . The solutions have a variety of properties depending on the parameters and .
In the case of the large breaking scale, , the solutions are almost determined by the gravitational field and a scalar field that acquires its mass by the Higgs mechanism. Then, the solutions are almost same as the mini boson stars obtained in the system of the gravitational field and a massive complex scalar field. On the other hand, in the case of small breaking scale, , the solutions are classified into three types: mini boson stars, matter-interacting NTS stars, and gravitating NTS stars. For the first type, gravity and a scalar field contribute the solutions as same as the large breaking scale case. In the second type, interactions between matter fields are important as in the case of nontopological solitons discussed in Refs.Ishihara:2018rxg ; Ishihara:2019gim ; Ishihara:2021iag . In the last one, the both matter interaction and self-gravity are important, and NTS star solutions in this type can have much larger mass than other types. In the cases of mini boson stars and matter-interacting NTS stars, the gravity is weak because the lapse function is almost constant everywhere, while in the case of gravitating NTS stars, gravity requires relativistic description where the lapse varies significantly.
We found that the maximum mass, which depend on the breaking scale, obeys a double power law: for and for , where . If we can extrapolate this for much lower breaking scale, the maximum mass of the NTS star can be astrophysical scale, the solar mass for 1GeV and the claster of galaxies scale for 1eV.
We studied the compactness, the gravitational radius over the radius of the NTS stars. The compactness of NTS stars with maximum mass, , takes the value for and for , and change in its value quickly around . It means the NTS stars with maximum mass in the lower breaking scale are relativistically compact object that have the innermost stable circular orbits. Therefore, the NTS stars in the case can be seeds of supermassive black holes.
It is an important issue to clarify the stability of the NTS stars. We would expect that the NTS stars with maximum mass evolve to black holes if they become unstable. Linear perturbation of the NTS stars would be our next work.
In this paper, we construct NTS star solutions whose internals are filled by kinetic energy of the scalar fields. These are self-gravitating solutions of dust balls Ishihara:2021iag . There are other types of NTSs, potential balls and shell balls, in the model without gravity Ishihara:2021iag . If we take gravity into account, a self-gravitating potential ball would be a ‘gravastar’ Mazur:2001fv ; Mazur:2004fk that join de Sitter and Scwarzshild spacetimes by a spherical shell, and a self-gravitating shell ball would join Minkowski and Scwarzshild spacetimes Kleihaus:2009kr . It is also interesting to construct these solutions.
Acknowledgements
We would like to thank K.-i. Nakao, H. Yoshino, and M. Minamitsuji for valuable discussion. This work was partly supported by Osaka City University Advanced Mathematical Institute: MEXT Joint Usage/Research Center on Mathematics and Theoretical Physics JPMXP0619217849.
Appendix A Energy-momentum tensor and charge censities
On the assumptions of the scalar and the gauge field forms, we can reduce the energy-momentum tensor (14) as
| (42) | ||||
| (43) | ||||
| (44) | ||||
| (45) | ||||
| (46) | ||||
| (47) |
where represents an energy density of the fields, and denote pressure in the direction of and . We have the charge densities as
| (48) | |||
| (49) |
References
- (1) G. Rosen, J. Math. Phys. 9, 996 (1968) doi:10.1063/1.1664693
- (2) S. R. Coleman, Nucl. Phys. B262, 263 (1985) Erratum: [B269, 744(E) (1986)].
- (3) R. Friedberg, T. D. Lee and A. Sirlin, Phys. Rev. D 13, 2739 (1976).
- (4) T. D. Lee and Y. Pang, Phys. Rep. 221, 251 (1992)
- (5) E. Y. Nugaev and A. V. Shkerin, J. Exp. Theor. Phys. 130, no.2, 301 (2020)
- (6) Y. M. Shnir, Topological and Non-Topological Solitons in Scalar Field Theories (Cambridge University Press, Cambridge, England 2018).
- (7) K. M. Lee, J. A. Stein-Schabes, R. Watkins and L. M. Widrow, Phys. Rev. D 39, 1665 (1989).
- (8) X. Shi and X. Z. Li, J. Phys. A 24, 4075 (1991).
- (9) I. E. Gulamov, E. Y. Nugaev, A. G. Panin and M. N. Smolyakov, Phys. Rev. D 92, no. 4, 045011 (2015).
- (10) A. Kusenko and M. E. Shaposhnikov, Phys. Lett. B 418, 46 (1998).
- (11) A. Kusenko and P. J. Steinhardt, Phys. Rev. Lett. 87, 141301 (2001).
- (12) M. Fujii and K. Hamaguchi, Phys. Lett. B 525, 143 (2002).
- (13) K. Enqvist, A. Jokinen, T. Multamaki and I. Vilja, Phys. Lett. B 526, 9 (2002).
- (14) A. Kusenko, L. Loveridge and M. Shaposhnikov, Phys. Rev. D 72, 025015 (2005).
- (15) K. Enqvist and J. McDonald, Phys. Lett. B 425, 309 (1998).
- (16) S. Kasuya and M. Kawasaki, Phys. Rev. D 61, 041301 (2000).
- (17) M. Kawasaki, F. Takahashi and M. Yamaguchi, Phys. Rev. D 66, 043516 (2002).
- (18) H. Ishihara and T. Ogawa, PTEP 2019, no.2, 021B01 (2019)
- (19) H. Ishihara and T. Ogawa, Phys. Rev. D 99, no.5, 056019 (2019)
- (20) H. Ishihara and T. Ogawa, Phys. Rev. D 103, no.12, 123029 (2021)
- (21) P. Forgács and Á. Lukács, Phys. Rev. D 102, no.7, 076017 (2020)
- (22) P. Forgács and Á. Lukács, Eur. Phys. J. C 81, no.3, 243 (2021).
- (23) D. J. Kaup, Phys. Rev. 172, 1331-1342 (1968).
- (24) R. Ruffini and S. Bonazzola, Phys. Rev. 187, 1767-1783 (1969).
- (25) M. Colpi, S. L. Shapiro and I. Wasserman, Phys. Rev. Lett. 57, 2485-2488 (1986).
- (26) P. Jetzer and J. J. van der Bij, Phys. Lett. B 227, 341-346 (1989).
- (27) A. B. Henriques, A. R. Liddle and R. G. Moorhouse, Phys. Lett. B 233, 99 (1989).
- (28) A. B. Henriques, A. R. Liddle and R. G. Moorhouse, Nucl. Phys. B 337, 737-761 (1990).
- (29) P. Jetzer, Phys. Rept. 220, 163-227 (1992).
- (30) F. E. Schunck and E. W. Mielke, Class. Quant. Grav. 20, R301-R356 (2003).
- (31) S. L. Liebling and C. Palenzuela, Living Rev. Rel. 15, 6 (2012).
- (32) B. W. Lynn, Nucl. Phys. B 321, 465 (1989).
- (33) T. D. Lee, Phys. Rev. D 35, 3637 (1987).
- (34) R. Friedberg, T. D. Lee and Y. Pang, Phys. Rev. D 35, 3658 (1987).
- (35) T. D. Lee and Y. Pang, Phys. Rev. D 35, 3678 (1987).
- (36) J. Kunz, V. Loiko and Y. Shnir, [arXiv:2112.06626 [gr-qc]].
- (37) P. O. Mazur and E. Mottola, [arXiv:gr-qc/0109035 [gr-qc]].
- (38) P. O. Mazur and E. Mottola, Proc. Nat. Acad. Sci. 101, 9545-9550 (2004).
- (39) B. Kleihaus, J. Kunz, C. Lammerzahl and M. List, Phys. Lett. B 675, 102-115 (2009).