Relative Equilibria of Magnetic Micro-Swimmers

The configuration of an arbitrary rigid body is given by its position $\bm{x}$ and its orientation, represented by a right-handed, orthonormal and material frame $R=\begin{bmatrix}\bm{d}_{1}&\bm{d}_{2}&\bm{d}_{3}\end{bmatrix}$ - the body frame. The kinematic of the body is specified by $\bm{v}$ and $\bm{\omega}$ which are respectively its linear and angular velocities:

$\displaystyle\dot{\bm{x}}$

$\displaystyle=\bm{v},$

$\displaystyle\dot{R}$

$\displaystyle=\left[\bm{\omega}\times\right]R.$

(1)

Note that the second equation in (1) can also be casted in the form $\dot{\bm{d}}_{i}=\bm{\omega}\times\bm{d}_{i}$ for $i=1,2,3$.

The linear $\bm{p}$ and angular $\bm{L}$ momenta about the centre of mass are

$\displaystyle\bm{p}$

$\displaystyle=k\bm{v},$

$\displaystyle\bm{L}$

$\displaystyle=I_{\mathrm{cm}}\bm{\omega},$

(2)

where $k$ is the mass of the body and $I_{\mathrm{cm}}=I_{\mathrm{cm}}^{T}>0$ its inertia tensor with respect to the centre of mass; it is constant in the body frame.

The rigid body dynamic is governed by the balance of linear and angular momenta

$\displaystyle\dot{\bm{p}}$

$\displaystyle=\bm{f},$

$\displaystyle\dot{\bm{L}}$

$\displaystyle=\bm{\tau},$

(3)

where $\bm{f}$ and $\bm{\tau}$ are respectively the resultant force and torque acting upon the body. In our case, $\bm{f}$ and $\bm{\tau}$ arise from hydrodynamic drag, applied magnetic field, gravity and buoyancy. We first focus on the role played by the drag.

We make the assumption that the body is in an unbounded fluid at low Reynolds number. This implies in particular that the loads due to hydrodynamic drag depend linearly on the velocities:

$$\begin{bmatrix}\bm{f}^{\left(d\right)}\\ \bm{\tau}^{\left(d\right)}\end{bmatrix}=-\mathbb{D}\begin{bmatrix}\bm{v}\\ \bm{\omega}\end{bmatrix}=-\begin{bmatrix}D_{11}\bm{v}+D_{12}\bm{\omega}\\ D_{12}^{T}\bm{v}+D_{22}\bm{\omega}\end{bmatrix},$$

(4)

where $\mathbb{D}\in\mathbb{R}^{6\times 6}$ is the symmetric and positive definite drag tensor the components of which are constant in the body frame (Happel and Brenner, 1983).

We gather all forces and torques from effects other than drag respectively in $\bm{f}^{\left(\text{ext}\right)}$ and $\bm{\tau}^{\left(\text{ext}\right)}$ and expand (3) in the body frame:

	$\displaystyle\dot{\bm{\mathsf{p}}}+\mathbf{\omega}\times\bm{\mathsf{p}}=$	$\displaystyle-\mathsf{D}_{11}\bm{\mathsf{v}}-\mathsf{D}_{12}\mathbf{\omega}+\bm{\mathsf{f}}^{\left(\text{ext}\right)}$		(5)
	$\displaystyle\dot{\bm{\mathsf{L}}}+\mathbf{\omega}\times\bm{\mathsf{L}}=$	$\displaystyle-\mathsf{D}_{12}^{T}\bm{\mathsf{v}}-\mathsf{D}_{22}\mathbf{\omega}+\mathbf{\tau}^{\left(\text{ext}\right)}$

where the sans-serif letter $\bm{\mathsf{p}}$ denotes the triple $\left(\bm{p}\cdot\bm{d}_{i}\right)_{i=1,2,3}$, the entries of $\mathsf{D}_{11}$ are $\left(\bm{d}_{i}\cdot D_{11}\bm{d}_{j}\right)_{i,j=1,2,3}$, and so on. In particular, the matrices $\mathsf{D}_{ij}$ appearing in (5) are constant.

We will later focus on the specific case where the loads $\bm{\mathsf{f}}^{\left(\text{ext}\right)}$ and $\mathbf{\tau}^{\left(\text{ext}\right)}$ arise from gravity, buoyancy, and an interplay between a magnetic moment of the body and an external magnetic field. Note however that (5) is valid for arbitrary external loads and so is the dimensional analysis carried out in section 2.2.

The relevant scales for our problem are a characteristic body length $\ell$, mass $k$ and volume $V$, the dynamic viscosity of the fluid $\eta$, its mass density $\rho_{f}$, and the magnitude of the applied force $N$. The characteristic time scale for the resulting settling phenomenon is then $t_{c}=\frac{\eta\,\ell^{2}}{N}$ (see Gonzalez et al. (2004) for a discussion).

Accordingly, we non-dimensionalise according to

$\displaystyle\overline{t}$

$\displaystyle=\frac{t}{t_{c}},$

$\displaystyle\overline{\bm{\mathsf{v}}}$

$\displaystyle=\frac{t_{c}}{\ell}\bm{\mathsf{v}},$

$\displaystyle\overline{\mathbf{\omega}}$

$\displaystyle=t_{c}\mathbf{\omega},$

$\displaystyle\overline{\bm{\mathsf{f}}}^{\left(\text{ext}\right)}$

$\displaystyle=\frac{1}{N}\bm{\mathsf{f}}^{\left(\text{ext}\right)},$

$\displaystyle\overline{\mathbf{\tau}}^{\left(\text{ext}\right)}$

$\displaystyle=\frac{1}{\ell\,N}\mathbf{\tau}^{\left(\text{ext}\right)}$

$\displaystyle\overline{\bm{\mathsf{p}}}$

$\displaystyle=\frac{t_{c}}{k\,\ell}\bm{\mathsf{p}},$

$\displaystyle\overline{\bm{\mathsf{L}}}$

$\displaystyle=\frac{t_{c}}{k\,\ell^{2}}\bm{\mathsf{L}},$

$\displaystyle\overline{\mathsf{D}}_{11}$

$\displaystyle=\frac{1}{\ell\,\eta}\mathsf{D}_{11},$

$\displaystyle\overline{\mathsf{D}}_{12}$

$\displaystyle=\frac{1}{\ell^{2}\eta}\mathsf{D}_{12},$

$\displaystyle\overline{\mathsf{D}}_{22}$

$\displaystyle=\frac{1}{\ell^{3}\eta}\mathsf{D}_{22}.$

The equations (5) then become

		$\displaystyle\frac{k\,\ell}{t_{c}^{2}}\left(\dot{\overline{\bm{\mathsf{p}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{p}}}\right)$	$\displaystyle=$	$\displaystyle-\frac{\eta\,\ell^{2}}{t_{c}}\left(\overline{\mathsf{D}}_{11}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{12}\overline{\mathbf{\omega}}\right)$		$\displaystyle+N\,\overline{\bm{\mathsf{f}}}^{\left(\text{ext}\right)}$		(6)
		$\displaystyle\frac{k\,\ell^{2}}{t_{c}^{2}}\left(\dot{\overline{\bm{\mathsf{L}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{L}}}\right)$	$\displaystyle=$	$\displaystyle-\frac{\eta\,\ell^{3}}{t_{c}}\left(\overline{\mathsf{D}}_{12}^{T}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{22}\overline{\mathbf{\omega}}\right)$		$\displaystyle+\ell\,N\,\overline{\mathbf{\tau}}^{\left(\text{ext}\right)}.$

We made the assumption that the Reynolds number $\mathrm{Re}=\rho_{f}\ell^{2}/\eta\,t_{c}\ll 1$; accordingly, $\varepsilon:=V\mathrm{Re}/\ell^{3}$ is small and we can rewrite (6) as

		$\displaystyle\frac{\varepsilon}{1+\varepsilon_{b}}\left(\dot{\overline{\bm{\mathsf{p}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{p}}}\right)$	$\displaystyle=$	$\displaystyle-\left(\overline{\mathsf{D}}_{11}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{12}\overline{\mathbf{\omega}}\right)$		$\displaystyle+\overline{\bm{\mathsf{f}}}^{\left(\text{ext}\right)}$		(7)
		$\displaystyle\frac{\varepsilon}{1+\varepsilon_{b}}\left(\dot{\overline{\bm{\mathsf{L}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{L}}}\right)$	$\displaystyle=$	$\displaystyle-\left(\overline{\mathsf{D}}_{12}^{T}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{22}\overline{\mathbf{\omega}}\right)$		$\displaystyle+\overline{\mathbf{\tau}}^{\left(\text{ext}\right)},$

where $\varepsilon_{b}=\rho_{f}V/k-1$. Note that the limit $\varepsilon\to 0$ corresponds to the Stokes flow limit $\mathrm{Re}\to 0$. The limit $\varepsilon\to 0$ could also be satisfied without $\mathrm{Re}\to 0$, in a thin rod for example. However, hydrodynamic loads defined by equation (4) require $\mathrm{Re}\ll 1$ to be valid.

The parameter $\varepsilon_{b}$ is defined such that if the external loads arise solely from buoyancy, the body sinks if $\varepsilon_{b}<0$, floats if $\varepsilon_{b}>0$, and is neutrally buoyant if $\varepsilon_{b}=0$. In principle, the limit $\varepsilon_{b}\to-1$ could be studied, and the inertial effects would then need to be taken into account. In practice however, even for swimmers made of a metallic alloy, i.e. swimmers that have a high density compared to the density of the fluid, the order of magnitude of the swimmer’s density $\rho_{s}$ will not exceed about $10\,\rho_{f}$, so that $1+\varepsilon_{b}$ is of order $10^{-1}$. Then, one must require $\varepsilon\ll 10^{-1}$ to ensure that $\varepsilon/(1+\varepsilon_{b})\ll 1$ so that inertial effects can be neglected.

Note that $\frac{\varepsilon}{1+\varepsilon_{b}}=\frac{k\,N}{l^{3}\,\eta^{2}}$ consistently with the small parameter expressed in Gonzalez et al. (2004). In writing it this way, we implicitly aim at comparing the impact of loads arising from gravity and buoyancy in comparison to other external loads.

The system of differential equation (7) is singular. Standard singular perturbation techniques (Hinch, 1991) are used to find a uniform leading order solution:

$$\begin{bmatrix}\overline{\bm{\mathsf{p}}}\left(\overline{t}\right)\\ \overline{\bm{\mathsf{L}}}\left(\overline{t}\right)\end{bmatrix}=\exp\left(-\left(1+\varepsilon_{b}\right)\frac{\overline{t}}{\varepsilon}G\right)\left(\begin{bmatrix}\overline{\bm{\mathsf{p}}}_{0}\\ \overline{\bm{\mathsf{L}}}_{0}\end{bmatrix}-G^{-1}\begin{bmatrix}\overline{\bm{\mathsf{f}}}^{(ext)}\left(0\right)\\ \overline{\mathbf{\tau}}^{(ext)}\left(0\right)\end{bmatrix}\right)+G^{-1}\begin{bmatrix}\overline{\bm{\mathsf{f}}}^{(ext)}\left(\overline{t}\right)\\ \overline{\mathbf{\tau}}^{(ext)}\left(\overline{t}\right)\end{bmatrix},$$

(8)

where $G:=\overline{\mathbb{D}}\begin{bmatrix}\mathbf{I}&0\\ 0&\overline{\mathsf{I}_{\mathrm{cm}}}\end{bmatrix}$, and $\overline{\bm{\mathsf{p}}}_{0}$, $\overline{\bm{\mathsf{L}}}_{0}$ are the initial conditions to (7). This solution is valid as long as the loadings $\overline{\bm{\mathsf{f}}}^{(ext)}$ and $\overline{\mathbf{\tau}}^{(ext)}$ vary slowly compared to the timescale $\varepsilon$ of the initial layer. That is we assume $||d\overline{\bm{\mathsf{f}}}/d\overline{t}||\ll\frac{1}{\varepsilon}$ and $||d\overline{\mathbf{\tau}}/\overline{t}||\ll\frac{1}{\varepsilon}$.

System (5) was studied by Gonzalez et al. (2004) for the particular case where the external loads arise from a constant force, namely the resultant of gravity and buoyancy. Here we treat a complementary case where the external force is $\mathbf{0}$ and the external torque is periodic and has a simple expression: the loads are due to a spatially uniform magnetic field $\bm{B}$ rotating at constant angular velocity $\alpha$ about a fixed axis of rotation in the lab frame, and the body subjected to it is a permanent magnet so that its magnetic moment $\bm{m}$ is constant in the body frame. The force and torque are then

$\displaystyle\bm{f}^{\left(m\right)}$

$\displaystyle=\mathbf{0},$

$\displaystyle\bm{\tau}^{\left(m\right)}$

$\displaystyle=\bm{m}\times\bm{B}.$

(9)

Without loss of generality, we can choose the lab frame so that the basis vector $\bm{e}_{3}$ corresponds with the axis of rotation of the magnetic field and that $\bm{B}$ lies in the $\left(\bm{e}_{1},\bm{e}_{3}\right)$-plane at time $t=0$, so that $\bm{B}$ can be explicitly written as

$$\bm{B}=R_{3}\left(\alpha t\right)\bm{B}_{0},\qquad\text{where }R_{3}\left(s\right)=\begin{bmatrix}\cos s&-\sin s&0\\ \sin s&\cos s&0\\ 0&0&1\end{bmatrix}\text{ and }\bm{B}_{0}=B\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix},$$

(10)

where $B$ is the magnitude of the magnetic field, and $\psi$ is the angle between $\bm{B}$ and its axis of rotation $\bm{e}_{3}$. Note that the lab frame is chosen so that $\bm{e}_{3}$ is the axis of rotation of the magnetic field, and not the direction of gravity.

We non-dimensionalise by substituting $N=m\,B/\ell$, where $m$ is the magnitude of the magnetic moment. The torque due to magnetism is then rewriten in the body frame as

$$\overline{\mathbf{\tau}}^{\left(m\right)}\left(\overline{t}\right)=\overline{\bm{\mathsf{m}}}\times\overline{\bm{\mathsf{B}}}\left(\overline{t}\right)=\overline{\bm{\mathsf{m}}}\times\left(R^{T}\left(\overline{t}\right)R_{3}\left(\mathrm{Ma}\,\overline{t}\right)\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix}\right),$$

(11)

where all the dependencies in $\overline{t}$ are written explicitly, and $\mathrm{Ma}$ is the Mason number (Man and Lauga, 2013) given by

$$\mathrm{Ma}=\alpha\,t_{c}=\frac{\alpha\,\eta\,\ell^{3}}{m\,B}\,.$$

(12)

We define the magnetic frame so that it is aligned with the lab frame at $\overline{t}=0$ and rotates with the magnetic field. Namely, the magnetic frame is given by the columns of the matrix $R_{3}\left(\mathrm{Ma}\,t\right)$. We observe in (11) that the torque $\overline{\mathbf{\tau}}$ applied by the field on the swimmer depends on the rotation matrix

$$Q\left(t\right):=R^{T}(t)\leavevmode\nobreak\ R_{3}(\mathrm{Ma}\,t)$$

(13)

that applies the body frame onto the magnetic frame: $\overline{\mathbf{\tau}}^{\left(m\right)}=\overline{\bm{\mathsf{m}}}\times Q\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix}$.

This rotation matrix $Q$ will prove to be more practical than the original matrix $R$. Note that $R$ can be recovered at any point by inverting (13). This, in turn, can be substituted in (1) to find an equivalent form for Q:

$$\dot{Q}=\left[\left(\mathrm{Ma}\,\bm{\mathsf{e}}_{3}-\mathbf{\omega}\right)\times\right]Q,\qquad Q\left(0\right)=Q_{0},$$

(14)

where $\bm{\mathsf{e}}_{3}=Q\begin{bmatrix}0\\ 0\\ 1\end{bmatrix}$ is the third basis vector of the lab frame expressed in the body frame.

Our study will focus on neutrally buoyant bodies. Nevertheless, this assumption is never strictly achieved in experiments. Therefore, we pause to discuss under which conditions this assumption can be expected to hold. Let $-\bm{\mathsf{g}}$ be the force due to gravity (constant in the lab frame) and $\mathbf{{\Delta}}$ the misalignment between the centre of mass and the centre of volume (constant in the body frame). We can then write the loads due to gravity and buoyancy as

$\displaystyle\bm{\mathsf{f}}^{\left(b\right)}$

$\displaystyle=\varepsilon_{b}\bm{\mathsf{g}},$

$\displaystyle\mathbf{\tau}^{\left(b\right)}$

$\displaystyle=\left(1+\varepsilon_{b}\right)\mathbf{{\Delta}}\times\bm{\mathsf{g}}.$

(15)

The corresponding non-dimensionalised quantities in the body frame are $\overline{\bm{\mathsf{g}}}=\frac{1}{k\,g}\bm{\mathsf{g}}$, and $\overline{\mathbf{{\Delta}}}=1/\ell\,\mathbf{{\Delta}}$, where $g$ is the gravitational acceleration on earth. Defining the constant $\gamma:=\rho_{f}V\,\ell\,g/m\,B$, we rewrite (7) as

		$\displaystyle\frac{\varepsilon}{1+\varepsilon_{b}}\left(\dot{\overline{\bm{\mathsf{p}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{p}}}\right)$	$\displaystyle=$	$\displaystyle-\left(\overline{\mathsf{D}}_{11}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{12}\overline{\mathbf{\omega}}\right)$		$\displaystyle+\gamma\,\frac{\varepsilon_{b}}{1+\varepsilon_{b}}\overline{\bm{\mathsf{g}}}$				(16)
		$\displaystyle\frac{\varepsilon}{1+\varepsilon_{b}}\left(\dot{\overline{\bm{\mathsf{L}}}}+\overline{\mathbf{\omega}}\times\overline{\bm{\mathsf{L}}}\right)$	$\displaystyle=$	$\displaystyle-\left(\overline{\mathsf{D}}_{12}^{T}\overline{\bm{\mathsf{v}}}+\overline{\mathsf{D}}_{22}\overline{\mathbf{\omega}}\right)$		$\displaystyle+\overline{\bm{\mathsf{m}}}\times\overline{\bm{\mathsf{B}}}$		$\displaystyle+\gamma\,\overline{\mathbf{{\Delta}}}\times\overline{\bm{\mathsf{g}}}.$

In the following, we focus on the case of a neutrally buoyant body whose centre of mass and centre of buoyancy coincide, that is $\varepsilon_{b}=0$ and $\overline{\mathbf{{\Delta}}}=\mathbf{0}$. These strict equalities cannot be achieved experimentally; however we expect our conclusions to be a good approximation when $|\varepsilon_{b}|,\left|\overline{\mathbf{{\Delta}}}\right|\ll 1/\gamma$. See Rüegg-Reymond (2019) for a study of cases where these hypotheses are relaxed.

Assuming that the swimmer is neutrally buoyant, we substitute $\varepsilon_{b}=0$ and $\overline{\mathbf{{\Delta}}}=\mathbf{0}$ in (16). Gathering (1, 2, 14) and dropping the overbars, we obtain the full system of differential equations for our problem

$\displaystyle\begin{aligned} \dot{\bm{x}}&=\bm{v},\\ \dot{Q}&=[\mathrm{Ma}\,\bm{\mathsf{e}}_{3}-\mathbf{\omega}]^{\times}\,Q,\\ \varepsilon\left(\dot{\bm{\mathsf{p}}}+\mathbf{\omega}\times\bm{\mathsf{p}}\right)&=-\left(\mathsf{D}_{11}\bm{\mathsf{v}}+\mathsf{D}_{12}\mathbf{\omega}\right)\\ \varepsilon\,\left(\dot{\bm{\mathsf{L}}}+\mathbf{\omega}\times\bm{\mathsf{L}}\right)&=-\left(\mathsf{D}_{12}^{T}\bm{\mathsf{v}}+\mathsf{D}_{22}\mathbf{\omega}\right)+\bm{\mathsf{m}}\times\bm{\mathsf{B}},\end{aligned}$

(17)

together with the relations

$$\bm{\mathsf{p}}=\bm{\mathsf{v}},\qquad\qquad\bm{\mathsf{L}}=\mathsf{I}_{\mathrm{cm}}\mathbf{\omega},\qquad\qquad\bm{\mathsf{B}}\left(t\right)=Q\left(t\right)\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix}.$$

(18)

In the particular case of the problem (17, 18), the solution (8) becomes

$$\begin{bmatrix}\bm{\mathsf{p}}\left(t\right)\\ \bm{\mathsf{L}}\left(t\right)\end{bmatrix}=\exp\left(-\frac{t}{\varepsilon}G\right)\begin{bmatrix}\bm{\mathsf{p}}_{0}-\mathsf{M}_{12}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(0\right)\\ \bm{\mathsf{L}}_{0}-\mathsf{I}_{\mathrm{cm}}\mathsf{M}_{22}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(0\right)\end{bmatrix}+\begin{bmatrix}\mathsf{M}_{12}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(t\right)\\ \mathsf{I}_{\mathrm{cm}}\mathsf{M}_{22}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(t\right)\end{bmatrix}$$

(19)

where $\mathsf{M}_{12}$ and $\mathsf{M}_{22}$ are 3-by-3 blocks of the mobility matrix

$\displaystyle\mathbb{M}=\mathbb{D}^{-1}=\begin{bmatrix}\mathsf{M}_{11}&\mathsf{M}_{12}\\ \mathsf{M}_{12}^{T}&\mathsf{M}_{22}\end{bmatrix}\,,$

which is constant in the body frame.

In order for (19) to be a valid leading order solution, we need $\mathrm{Ma}\ll 1/\varepsilon$. We expect that it represents accurately the dynamics of our system in the outer layer, i.e. for $t\gg\varepsilon$, in the limit $\varepsilon\to 0$. In the inner layer however, the leading-order solution may be inaccurate for any $\varepsilon\neq 0$ (see Gonzalez et al. (2004) and Kim and Karrila (2013)).

In the outer layer, the first term in (19) can be neglected and substituting the first two equations of  (18) therein, the problem (17, 18) becomes

	$\displaystyle\dot{\bm{x}}$	$\displaystyle=\bm{v},$		(20)
	$\displaystyle\dot{Q}$	$\displaystyle=[\mathrm{Ma}\,\bm{\mathsf{e}}_{3}-\mathbf{\omega}]^{\times}\,Q,$

where

		$\displaystyle\bm{\mathsf{v}}\left(t\right)=\mathsf{M}_{12}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(t\right),$		$\displaystyle\mathbf{\omega}\left(t\right)=\mathsf{M}_{22}\left[\bm{\mathsf{m}}\times\right]\bm{\mathsf{B}}\left(t\right),$		(21)
		$\displaystyle\bm{\mathsf{B}}\left(t\right)=Q\left(t\right)\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix},$		$\displaystyle\bm{\mathsf{e}}_{3}\left(t\right)=Q\left(t\right)\begin{bmatrix}0\\ 0\\ 1\end{bmatrix}.$

Finally, substituting (21) in (20), we find the following closed form system of ODEs

	$\displaystyle\dot{\bm{x}}=R_{3}(\mathrm{Ma}\,t)\,Q(t)\,\mathsf{M}_{12}\,\left[\bm{\mathsf{m}}\times\right]\,Q\,\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix},$		$\displaystyle\bm{x}(0)=\bm{x}_{0},$		(22)
	$\displaystyle\dot{Q}=\left[\left(\mathrm{Ma}\,Q\begin{bmatrix}0\\ 0\\ 1\end{bmatrix}-\mathsf{P}\,Q\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix}\right)\times\right]Q,$		$\displaystyle Q\left(0\right)=Q_{0},$		(23)

where $\mathsf{P}:=\mathsf{M}_{22}\left[\bm{\mathsf{m}}\times\right]$ is a constant matrix that only depends on the shape and the magnetisation of the swimmer. Propositions 3.1 and 3.2 of Gonzalez et al. (2004) can be straightforwardly adapted to show that the solutions of (22, 23) completely determine the long-time behaviour of the leading-order solution of (17, 18).

Much of our subsequent analysis will consist in studying the set of solutions of (22, 23). We readily note that (23) decouples from (22) so that for any solution of the $\dot{Q}$ equation, $\bm{x}$ can be recovered by quadrature. Accordingly most of what follows will be focused on (23).

The swimmer is at relative equilibrium when $Q$ is a steady state solution of the differential equation in (23): the orientation of the swimmer is fixed in the magnetic frame. Accordingly, relative equilibria occur if and only if

$$\mathrm{Ma}\,Q\,\begin{bmatrix}0\\ 0\\ 1\end{bmatrix}=\mathsf{P}\,Q\,\begin{bmatrix}\sin\psi\\ 0\\ \cos\psi\end{bmatrix}.$$

(24)

Instead of working directly with the rotation matrix $Q$, we will work with the body frame components of two vectors: $\bm{\mathsf{e}}_{3}$ and $\bm{\mathsf{B}}$. In this picture, finding relative equilibria (i.e. $Q$ respecting (24)) amounts to finding pairs $\left(\bm{\mathsf{e}}_{3},\bm{\mathsf{B}}\right)$ such that

$\displaystyle\mathrm{Ma}\,\bm{\mathsf{e}}_{3}$

$\displaystyle=\mathsf{P}\,\bm{\mathsf{B}},$

$\displaystyle\bm{\mathsf{e}}_{3}\cdot\bm{\mathsf{B}}$

$\displaystyle=\cos\psi,$

$\displaystyle\bm{\mathsf{e}}_{3}\cdot\bm{\mathsf{e}}_{3}$

$\displaystyle=1,$

$\displaystyle\bm{\mathsf{B}}\cdot\bm{\mathsf{B}}$

$\displaystyle=1,$

(25)

for given parameters $\mathrm{Ma}$ and $\psi$. Note that an equivalent set of equations can be found in Meshkati and Fu (2014); Fu et al. (2015) where they were solved numerically. The version that we propose here enables the determination of all solutions analytically.

Although experimentally, one wants to fix $\mathrm{Ma}$ and $\psi$ and then find all the $(\bm{\mathsf{e}}_{3},\bm{\mathsf{B}})$ solutions of (25) for these parameters, it is mathematically expedient to consider (25) as a system of 6 equations of the 8 unknown $(\mathrm{Ma},\cos\psi,\,\bm{\mathsf{e}}_{3},\,\bm{\mathsf{B}})$. We will show that the complete set of solutions is then a two dimensional surface that can be parameterised by a single map. That is, each pair of values of the parameters to be described here under corresponds to a single equilibrium of the system. This is in contrast with the experimental viewpoint where for a given $\mathrm{Ma}$ and $\psi$ there can be up to 8 different solutions of (25).

We first consider the singular value decomposition of the matrix $\mathsf{P}=\mathsf{M}_{22}\left[\bm{\mathsf{m}}\times\right]$. Let $\sigma_{0}=0<\sigma_{2}<\sigma_{1}$ be the singular values of $\mathsf{P}$ with corresponding right-singular vectors $\mathbf{\beta}_{0}=\bm{\mathsf{m}}$, $\mathbf{\beta}_{1}$, and $\mathbf{\beta}_{2}$ and left-singular vectors $\mathbf{\eta}_{0}=\mathsf{M}_{22}^{-1}\bm{\mathsf{m}}/\left\|\mathsf{M}_{22}^{-1}\bm{\mathsf{m}}\right\|$, $\mathbf{\eta}_{1}$, and $\mathbf{\eta}_{2}$. Recall that we have the relations

$\displaystyle\mathsf{P}\mathbf{\beta}_{i}$

$\displaystyle=\sigma_{i}\mathbf{\eta}_{i},$

$\displaystyle\mathsf{P}^{T}\mathbf{\eta}_{i}=\sigma_{i}\mathbf{\beta}_{i},$

(26)

and that the two sets of singular vectors can be chosen so that they each form a right-handed and orthonormal basis.

The first equilibrium condition in (25) constrains $\bm{\mathsf{e}}_{3}$ to lie in the span of $\mathsf{P}$, that is in the $\left(\mathbf{\eta}_{1},\mathbf{\eta}_{2}\right)$-plane. Therefore, an angle $\theta\in\left(-\pi,\pi\right]$ exists such that

$$\bm{\mathsf{e}}_{3}=\cos\theta\,\mathbf{\eta}_{1}+\sin\theta\,\mathbf{\eta}_{2}.$$

(27)

Next, we expand $\bm{\mathsf{B}}$ in the $\left\{\mathbf{\beta}_{i}\right\}$-basis as $\bm{\mathsf{B}}=\cos\phi\,\mathbf{\beta}_{0}+\sin\phi\left(\cos\xi\,\mathbf{\beta}_{1}+\sin\xi\,\mathbf{\beta}_{2}\right)$ for $\phi\in\left[0,\pi\right]$ and $\xi\in\left[0,2\pi\right)$. Substituting in (25) and using (26), we find that

• •

  there is a one-to-one correspondence between $\xi$ and $\theta$ so that $\bm{\mathsf{B}}$ rewrites as

  $$\bm{\mathsf{B}}=\cos\phi\,\mathbf{\beta}_{0}+\sin\phi\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}+\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)^{-1/2}\,\left(\frac{\cos\theta}{\sigma_{1}}\,\mathbf{\beta}_{1}+\frac{\sin\theta}{\sigma_{2}}\,\mathbf{\beta}_{2}\right),$$

  (28)

  and

• •

  $\mathrm{Ma}$ and $\cos\psi$ are also fixed by $\theta$ and $\phi$:

	$\displaystyle\mathrm{Ma}=$	$\displaystyle\sin\phi\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}+\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)^{-1/2},$		(29a)
	$\displaystyle\cos\psi=$	$\displaystyle\cos\phi\left(c_{01}\,\frac{\cos\theta}{\sigma_{1}}+c_{02}\,\frac{\sin\theta}{\sigma_{2}}\right)$		(29b)
		$\displaystyle+\sin\phi\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}+\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)^{-1/2}\,\left(c_{11}\,\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}-\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)+c_{12}\,\frac{\cos\theta\,\sin\theta}{\sigma_{1}\,\sigma_{2}}\right)\,,$

where $c_{01}=\mathbf{\beta}_{0}\cdot\mathsf{P}\,\mathbf{\beta}_{1}$, $c_{02}=\mathbf{\beta}_{0}\cdot\mathsf{P}\ \mathbf{\beta}_{2}$, $c_{11}=\mathbf{\beta}_{1}\cdot\mathsf{P}\,\mathbf{\beta}_{1}=-\mathbf{\beta}_{2}\cdot\mathsf{P}\,\mathbf{\beta}_{2}$, and $c_{12}=\mathbf{\beta}_{1}\cdot(\mathsf{P}+\mathsf{P}^{T})\,\mathbf{\beta}_{2}$.

As a result, the angles $\theta$ and $\phi$ are smooth coordinates on the set of relative equilibria. That is a value $\left(\theta,\phi\right)$ is in one-to-one correspondence with a unique relative equilibrium.

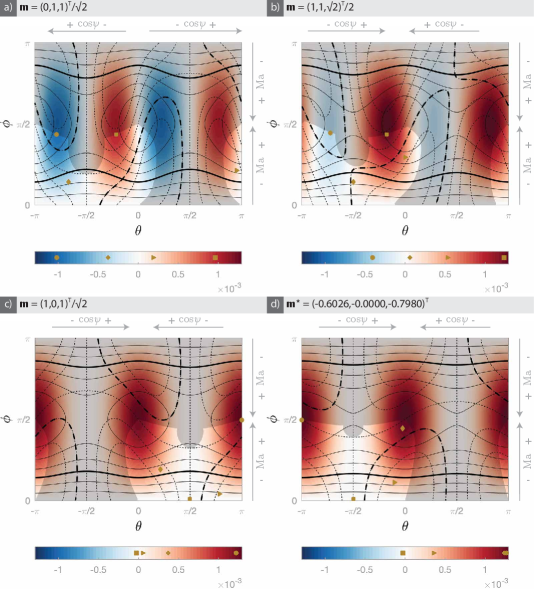
The level sets of $\mathrm{Ma}$ and $\cos\psi$ are shown in figure 1 for the helical swimmer A described in section 4 and shown in figure 6. Figure 1 can be used to find all the equilibria occurring for any given values of the experimental parameters. The arrows indicating increasing values of $\cos\psi$ are valid on the upper border of the figure. The bold curves highlight the particular level sets corresponding to $\mathrm{Ma}=0.015$ and $\cos\psi=0.01$. For these parameter values, the full and dashed lines have 8 intersections corresponding to 8 different relative equilibria at these values of the parameters. Once the pair ($\theta,\phi$) is found for a particular equilibrium, the orientation of the body can be inferred by computing $\bm{\mathsf{e}}_{3}$ and $\bm{\mathsf{B}}$ from (27) and (28). Note that this map also proves that there are relative equilibria for all orientations of $\bm{\mathsf{B}}$ (not all of them stable, more on this in section 3.3) but not for all orientations of $\bm{\mathsf{e}}_{3}$: at equilibrium, the rotation axis is in a plane orthogonal to $\mathsf{M}_{22}^{-1}\bm{\mathsf{m}}$.

The maximal $\mathrm{Ma}$ for which a given swimmer has any relative equilibria is equal to the largest singular value $\sigma_{1}$ of the $\mathsf{P}$ matrix (see equation (29a)). It is straightforward to show that for a swimmer of a given shape, the maximal value of $\sigma_{1}$ is obtained by magnetising the body in a direction perpendicular to the "easy rotation axis" – i.e. perpendicular to the eigenvector of $\mathsf{M}_{22}$ corresponding to its largest eigenvalue.

Finally, note that by definition (27), all functions of $\theta$ can be extended to the real line by imposing periodicity modulo $2\pi$. In particular, it will help to wrap figure 1 on a cylinder by identifying the borders at $\theta=\pm\pi$.

The solutions of the ODE (23) come in symmetric pairs. Indeed, if the function $Q\left(t\right)$ is a solution, then so is

$$\breve{Q}\left(t\right):=Q\left(-t\right)\begin{bmatrix}-1&\phantom{-}0&\phantom{-}0\\ \phantom{-}0&\phantom{-}1&\phantom{-}0\\ \phantom{-}0&\phantom{-}0&-1\end{bmatrix}=:Q\left(-t\right)R_{2}\left(\pi\right).$$

With obvious notations, one finds that in the body frame $\breve{\bm{\mathsf{B}}}\left(t\right)=-\bm{\mathsf{B}}\left(-t\right)$, $\breve{\bm{\mathsf{e}}}_{3}\left(t\right)=-\bm{\mathsf{e}}_{3}\left(-t\right)$, $\breve{\bm{\mathsf{v}}}\left(t\right)=-\bm{\mathsf{v}}\left(-t\right)$ and $\breve{\mathbf{\omega}}\left(t\right)=-\mathbf{\omega}\left(-t\right)$.

In the magnetic frame, the equations of motion are autonomous. At any instant, if the body is oriented according to $Q^{T}$ (w.r.t. the magnetic frame) and has angular velocity $\bm{u}$ with respect to the magnetic frame, then the symmetric solution is rotated by $\pi$ through the axis perpendicular to both $\bm{e}_{3}$ and $\bm{B}$ and the angular velocity $\breve{\bm{u}}$ is the reflection of $\bm{u}$ through the plane containing both $\bm{e}_{3}$ and $\bm{B}$.

At relative equilibria, the body is locked in the magnetic frame ($\bm{u}=\bm{0}$) and symmetric solutions are obtained by rotations through $\pi$ with respect to the axis perpendicular to both $\bm{e}_{3}$ and $\bm{B}$. Accordingly, one finds

$\displaystyle\breve{\phi}$

$\displaystyle=\pi-\phi.$

$\displaystyle\breve{\theta}$

$\displaystyle=(2\pi+\theta\mod 2\pi)-\pi.$

(30)

The corresponding symmetry of figure 1 consists in a reflection through the line at $\phi=\pi/2$ followed by a horizontal translation by $\pi$ (making use of the $\theta$-periodicity).

The linear stability of relative equilibria of (20) is given by the sign of the real part of the eigenvalues of the linearised dynamics matrix

$$A=\mathsf{P}\left[\bm{\mathsf{B}}\times\right]-\mathrm{Ma}\left[\bm{\mathsf{e}}_{3}\times\right],$$

(31)

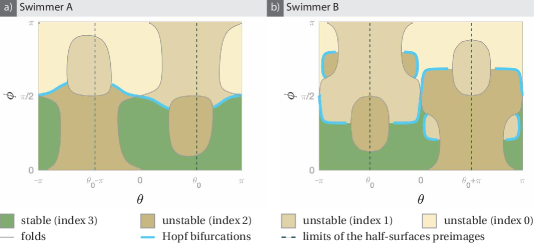
where $\bm{\mathsf{B}}$ and $\bm{\mathsf{e}}_{3}$ are taken at that equilibrium. They are therefore explicit functions of $\theta$ and $\phi$. Each equilibrium is thus associated with an index defined as the number of eigenvalues of $A$ with strictly negative real parts (counting multiplicities). An equilibrium is therefore unstable whenever its index is strictly less than $3$. If the index is 3, it is stable (see figure 2).

We remark that the linearised dynamics matrices $A$ of symmetric pairs of relative equilibria (in the sense of section 3.2) have opposite eigenvalues. So if one equilibrium of the pair is stable, then the other is necessarily unstable with index 0.

As we move on the set of relative equilibria, stability changes only at bifurcation points of the dynamical system (23) (Kuznetsov, 2004). In this system almost all bifurcations are either folds or Hopf bifurcations.

By definition, the trajectory corresponding to a relative equilibrium has constant linear and angular velocities $\bm{\mathsf{v}}$ and $\mathbf{\omega}$ in the body frame and is therefore helical. The axis of the helix is given by $\mathbf{\omega}$ while its pitch and radius are given by (Crenshaw, 1993).

$$p=\frac{2\pi}{\mathrm{Ma}^{2}}\,\mathbf{\omega}\cdot\bm{\mathsf{v}}\quad\text{and}\quad r=\frac{1}{\mathrm{Ma}^{2}}\left|\mathbf{\omega}\times\bm{\mathsf{v}}\right|.$$

(34)

Substituting the equilibrium condition (25) in the equation for the outer layer behaviour (21) yields

$\displaystyle\bm{\mathsf{v}}$

$\displaystyle=\mathrm{Ma}\,\mathsf{M}_{12}\mathsf{M}_{22}^{-1}\,\bm{\mathsf{e}}_{3},$

$\displaystyle\mathbf{\omega}$

$\displaystyle=\mathrm{Ma}\,\bm{\mathsf{e}}_{3}.$

(35)

Further substituting (35) in (34), we obtain

$$p=2\pi\,\bm{\mathsf{e}}_{3}\cdot\mathsf{M}_{12}\mathsf{M}_{22}^{-1}\bm{\mathsf{e}}_{3}\quad\text{and}\quad r=\left|\bm{\mathsf{e}}_{3}\times\mathsf{M}_{12}\mathsf{M}_{22}^{-1}\bm{\mathsf{e}}_{3}\right|.$$

The swimmer evolves along a helix the axis of which is parallel to the axis of rotation of the external field (see eq. (35)). The so called chirality matrix $\textit{Ch}=\mathsf{M}_{12}\mathsf{M}_{22}^{-1}$ is studied in details in Morozov et al. (2017) including a discussion of how the off-diagonal terms of Ch allow some non-chiral objects to nevertheless transform their rotational dynamic into translational motion.

We have seen is section 3.1 that the set of relative equilibria forms a 2-dimensional surface in the eight dimensional space $(\mathrm{Ma},\cos\psi,\,\bm{\mathsf{e}}_{3},\,\bm{\mathsf{B}})$. To visualise it we project it in $\mathbb{R}^{3}$ by considering the function

$$\Sigma:(-\pi,\pi]\times[0,\pi]\mapsto\mathbb{R}^{3}:(\theta,\phi)\mapsto\Big{(}\mathrm{Ma}\left(\theta,\phi\right),\cos\psi\left(\theta,\phi\right),\phi\Big{)},$$

(40)

and defining the surface $\mathcal{S}$ as the image set of $\Sigma$. Furthermore $\Sigma$ is extended to $\mathbb{R}\times[0,\pi]$ by asking that it be $2\pi$-periodic in $\theta$.

The graph of $\Sigma$, or equivalently the surface $\mathcal{S}$, is shown in figure 4 with the colour encoding the stability index (green is stable). Close inspection of equations (29) reveals that $\Sigma$ is not injective (see appendix B for details). One of the self-intersection of $\mathcal{S}$ is found along the coordinate line $(\theta_{0},\phi)$ with $\theta_{0}=\arctan\left(-c_{01}\,\sigma_{2}/(c_{02}\,\sigma_{1})\right)$ where $\Sigma\left(\theta_{0},\phi\right)=\Sigma\left(\theta_{0}+\pi,\phi\right)$ for all $\phi$. Furthermore, the two restrictions

	$\displaystyle\mathcal{S}_{1}$	$\displaystyle:=\left\{\Sigma\left(\theta,\phi\right):\theta\in\left[\theta_{0}-\pi,\theta_{0}\right),\phi\in\left[0,\pi\right]\right\},\quad\textrm{and}$		(41)
	$\displaystyle\mathcal{S}_{2}$	$\displaystyle:=\left\{\Sigma\left(\theta,\phi\right):\theta\in\left[\theta_{0},\theta_{0}+\pi\right),\phi\in\left[0,\pi\right]\right\}.$

are symmetric in the sense of section 3.2: the symmetric equilibrium to a state in $\mathcal{S}_{1}$ is in $\mathcal{S}_{2}$ and vice-versa. This same symmetry also implies that $\mathcal{S}$ has a mirror symmetry about the plane $\phi=\pi/2$.

Because of the mirror symmetry between $\mathcal{S}_{1}$ and $\mathcal{S}_{2}$, the number of relative equilibria for fixed parameters $\mathrm{Ma}$ and $\psi$ is even. We now show that it is generically $0$, $4$, or $8$. Using (29a) to express $\phi$ in terms of $\mathrm{Ma}$ and $\theta$, and substituting in (29b), we find

		$\displaystyle\left(\frac{\mathrm{Ma}}{\sigma_{1}\sigma_{2}}\left(c_{11}\,\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}-\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)+c_{12}\,\frac{\cos\theta\,\sin\theta}{\sigma_{1}\,\sigma_{2}}\right)-\cos\psi\right)^{2}$
	$\displaystyle+$	$\displaystyle\left(\mathrm{Ma}^{2}\left(\frac{\cos^{2}\theta}{\sigma_{1}^{2}}+\frac{\sin^{2}\theta}{\sigma_{2}^{2}}\right)-1\right)\,\left(c_{01}\,\frac{\cos\theta}{\sigma_{1}}+c_{02}\,\frac{\sin\theta}{\sigma_{2}}\right)^{2}=0\,.$

For fixed values of the parameters $\mathrm{Ma}$ and $\psi$, this is a trigonometric polynomial of degree 4 in $\theta$; it has therefore at most 8 roots (Powell, 1981).

$\mathcal{S}_{1}$ does not have boundaries. Indeed, the mapping $(\theta,\phi)\mapsto\Sigma(\theta,\phi)$ is continuous, and therefore any boundary would arise on the borders of the chart $[\theta_{0}-\pi,\theta_{0})\times[0,\pi]$. However $\mathcal{S}_{1}$ has no boundary at $\theta\in\{\theta_{0}-\pi,\theta_{0}\}$: for all $\phi$, we have $\Sigma(\theta_{0}-\pi,\phi)=\Sigma(\theta_{0},\phi)$, and for $\phi$ fixed in $[0,\pi]$, the curve $\{\Sigma(\theta,\phi):\theta\in[\theta_{0}-\pi,\theta_{0})\}$ is closed. Furthermore, $\mathcal{S}_{1}$ has no boundary at $\phi=\{0,\pi\}$: for $\sin\phi=0$, equation (29a) yields $\mathrm{Ma}=0$, so that for $\phi\in\{0,\pi\}$, the closed curve $\{\Sigma(\theta,\phi):\theta\in[\theta_{0}-\pi,\theta_{0})\}$ is reduced to the segment $\{0\}\times[-\max\{|c_{01}/\sigma_{1}|,\,|c_{02}/\sigma_{2}|\},\max\{|c_{01}/\sigma_{1}|,\,|c_{02}/\sigma_{2}|\}]\times\{\phi\}$ travelled twice, thereby sealing the boundaries at $\phi\in\{0,\pi\}$. By symmetry, $\mathcal{S}_{2}$ does not have boundaries either.