Relations between global forcing number and maximum anti-forcing number of a graph111This work is supported by NSFC (Grant No. 11871256)
E-mails: [email protected], [email protected])
Abstract
The global forcing number of a graph is the minimal cardinality of an edge subset discriminating all perfect matchings of , denoted by . For any perfect matching of , the minimal cardinality of an edge subset such that has a unique perfect matching is called the anti-forcing number of , denoted by . The maximum anti-forcing number of among all perfect matchings is denoted by . It is known that the maximum anti-forcing number of a hexagonal system equals the famous Fries number.
We are interested in some comparisons between the global forcing number and the maximum anti-forcing number of a graph. For a bipartite graph , we show that . Next we mainly extend such result to non-bipartite graphs. Let be the set of all graphs with a perfect matching which contain no two disjoint odd cycles such that their deletion results in a subgraph with a perfect matching. For any , we also have by revealing further property of non-bipartite graphs with a unique perfect matching. As a consequence, this relation also holds for the graphs whose perfect matching polytopes consist of non-negative -regular vectors. In particular, for a brick , de Carvalho, Lucchesi and Murty [4] showed that if and only if is solid, and if and only if its perfect matching polytope consists of non-negative -regular vectors.
Finally, we obtain tight upper and lower bounds on . For a connected bipartite graph with vertices, we have that ; For non-bipartite case, .
Keywords: Perfect matching; Perfect matching polytope; Solid brick; Maximum anti-forcing number; Global forcing number.
1 Introduction
In this paper, we only consider finite simple graphs with at least one perfect matching. Let be a graph with vertex set and edge set . We denote the order of by , and the size by . An edge subset of is a perfect matching (1-factor or a Kekulé structure in chemical literature), if every vertex of is incident with exactly one edge in .
In 1987, Klein and Randić [15] introduced the innate degree of freedom of a Kekulé structure, which plays an important role in the resonance theory in chemistry. Harary et al. [13] called it as forcing number: If a subset of a perfect matching in a graph is contained in exactly one perfect matching of , then is a forcing set of . The minimum cardinality over all forcing sets of is called the forcing number of , denoted by . The minimum (resp. maximum) forcing number of is denoted by (resp. ). For a hypercube , Diwan [9] showed that , confirming a conjecture by Pachter and Kim [24]. For a hexagonal system, Xu et al. [32] and Zhou and Zhang [35] showed that the maximum forcing number is equal to its Clar number (resonant number). For polyomino graphs and (4,6)-fullerenes (also called Birkoff-Von Neumann graphs) the same result also holds (cf. [34, 36, 27]).
As early as 1997, Li [19] raised the concept of forcing single edge (i.e. anti-forcing edge). In 2007, Vukičević and Trinajstić [30, 31] introduced the anti-forcing number of a graph . In general, recently Lei et al. [18] and Klein and Rosenfeld [16] independently defined the anti-forcing number of a single perfect matching of a graph . A subset of is an anti-forcing set of if its removal results in a graph with a unique perfect matching. The minimum cardinality of an anti-forcing set of is called the anti-forcing number of in , denoted by . The minimum (resp. maximum) anti-forcing number of is denoted by (resp. ). Lei et al. [18] and Shi et al. [27] respectively showed that the maximum anti-forcing number of hexagonal systems and (4,6)-fullerenes are equal to their Fries numbers. For upper bounds on maximum anti-forcing number of graphs, see [7, 28]
The concept of “global forcing” was introduced by Vukičević [29] to distinguish all perfect matchings of a graph. An edge subset of is called a global forcing set of , if no two distinct perfect matchings of coincide on . The minimum cardinality of a global forcing set of is the global forcing number of , denoted by . Since then, some scholars studied the global forcing numbers of some chemical graphs, see [10, 1, 20, 33, 26, 29].
In this paper, we readily find that for any graph . A relation has been already revealed [18]. Došlić [10] and Deng and Zhang [8] respectively proved that the global forcing number and the maximum forcing number of a graph have the cyclomatic number as a common upper bound. Motivated by the above facts, it is natural to consider relations between the global forcing number and the maximum anti-forcing number of a graph.
For (4,6)-fullerene graph , a plane cubic graph whose faces are hexagons and squares, Cai and Zhang [1] gave a sharp lower bound on global forcing number: , and Shi and Zhang [27] obtained a formula for the maximum anti-forcing number: , where and are the numbers of faces and vertices of respectively. By Euler’s formula we have , which implies that . Accordingly we have that for any (4,6)-fullerene graph .
For a general bipartite graph with vertices, luckily we can prove that by finding a special edge of with and . Moreover, we get that , and equality holds if and only if is isomorphic to .
The next question is whether we can extend the above relation to non-bipartite graphs. In this paper we give a negative answer by constructing a matching covered graph for any positive integer such that . However we can extend such a relation to conformal graphs which has a close connection with classical problems as perfect matching polytope and tight cut decomposition in matching theory of graphs [22, 12, 11, 21].
Let denote the set of graphs with a perfect matching such that contains no two disjoint odd cycles and such that has a perfect matching. We reveal a novel substructure of a graph with a unique perfect matching and the minimum degree larger than , which consists of two disjoint odd cycles and an odd path connecting them such that contains a perfect matching of it. Based on this substructure, we show that for a graph by finding a -degree vertex from a special subgraph of with a unique perfect matching. As a corollary, we have that for a graph whose perfect matching polytope consists of non-negative -regular vectors, and thus .
In particular, for a brick (3-connected bicritical graph), de Carvalho, Lucchesi and Murty [4] showed that if and only if the perfect matching polytope of consists of non-negative -regular vectors, and if and only if is solid (without non-trivial separating cuts). For a general graph, the above three conditions are not necessarily equivalent. For more details on solid bricks, see [2, 23, 12, 3, 6, 5]. In 2013, Kawarabayashi [14] gave a simpler proof for the characterization of the graphs without two disjoint odd cycles.
Finally, for a connected graph , we get tight upper and lower bounds on : , where the second equality holds if is isomorphic to complete graph .
2 Definitions and some preliminary results
For a vertex in , we denote the set of all neighbors of by . And the cardinality of is said to be the degree of , denoted by . Let and denote the maximum and minimum degree of respectively. Lei et al. [18] showed the following relations between the forcing number and the anti-forcing number of a perfect matching of a graph.
Theorem 2.1.
[18] Let be a graph with a perfect matching . Then , and thus .
The cyclomatic number of a connected graph is . In 2017, Deng and Zhang [8] proved that the maximum forcing number of is less than or equal to .
Theorem 2.2.
[8] Let be a connected graph with a perfect matching. Then . If is non-bipartite, then .
For two sets and , the symmetric difference of and is defined by . Let be a graph with at least one perfect matching . We say a subgraph of is nice if has a perfect matching. For convenience, we denote by . An even cycle of is called an M-alternating cycle, if the edges of appear alternately in or not. An even cycle is a nice cycle of if and only if has two perfect matchings and such that . In 2007, Došlić [10] gave the following result.
Theorem 2.3.
[10] Let be a connected graph with a perfect matching. Then , and equality holds if and only if all cycles of are nice.
We denote the set of all perfect matchings of a graph by , and . Došlić gave the following lower bound on the global forcing number.
Theorem 2.4.
[10] Let be a graph with a perfect matching. Then .
The following results give equivalent conditions for forcing sets, anti-forcing sets and global forcing sets of a graph.
Lemma 2.5.
[25] Let be a graph with a perfect matching . Then an edge subset is a forcing set of if and only if contains an edge from every -alternating cycle.
Lemma 2.6.
[7] Let be a graph with a perfect matching . Then an edge subset is an anti-forcing set of if and only if contains at least one edge of every -alternating of .
Lemma 2.7.
[1] Let be a graph with a perfect matching. Then an edge subset is a global forcing set of if and only if intersects each nice cycle of .
From these equivalent definitions, we can find some correlations.
Theorem 2.8.
Let be a graph with a perfect matching. Then .
Proof.
Let be a minimum global forcing set of and let be a perfect matching of with . Then , and intersects every -alternating cycle by Lemma 2.7. If , then is a forcing set of from Lemma 2.5. Thus . Otherwise, for each edge in not in there exists an edge in which is adjacent to . Replacing all edges in with the edges in and the other edges of remaining unchanged we get a new edge subset . Then and intersect every -alternating cycle. So is a forcing set of by Lemma 2.5, and . ∎
Corollary 2.9.
Let be a graph with a perfect matching. Then .
Let be a subgraph of . For any , we denote by .
Lemma 2.10.
[1] An edge subset is a global forcing set of a graph if and only if for each nice subgraph of , is a global forcing set of .
Lemma 2.11.
[1] Let be a connected graph with a perfect matching. Then is a minimum global forcing set of if and only if is a maximum (spanning) connected subgraph of without any nice cycle of .
The lemma gives a characterization for the complement of a minimum global forcing set of . The following result shows that the addition of some edges in to results in a graph with a unique perfect matching.
Lemma 2.12.
Let be a graph with a perfect matching. Then for any minimum global forcing set of , we can find an edge subset such that has a unique perfect matching.
Proof.
Let . Then is a connected spanning subgraph of , containing no nice cycles of by Lemma 2.11. If has a perfect matching, then has exactly one perfect matching and we are done. Otherwise, we can pick two different perfect matchings of , their symmetry difference forms at least one cycle of , a nice cycle in , a contradiction.
So suppose that has no perfect matchings. But we can choose a minimum subset such that has a perfect matching. Next, we will show that has exactly one perfect matching. If not, we can get two different perfect matchings of . Their symmetry difference contains a nice cycle of , which is also a nice cycle of . By Lemma 2.7, there exists an edge in . So and . Let . Then is smaller than but still has a perfect matching, a contradiction. ∎
If has a 1-degree vertex , then is called a pendant vertex and a pendant edge, where is the neighbor of . The deletion of and with their incident edges is called a leaf matching operation (simply operation). Next, we can see that operation has no effect on the minimum global forcing sets of a graph.
Lemma 2.13.
Let be a graph with a perfect matching. If is a graph obtained from by a series of operations, then the minimum global forcing sets of are the same as the ones of .
Proof.
If is a pendant edge of , let . Since belongs to all perfect matchings of , it follows that a cycle of is nice in if and only if it is also nice in . By Lemma 2.7, the minimum global forcing sets of corresponds to that of . When we make repeatedly operations from , the same result holds always. ∎
3 Bipartite graphs
We consider some relations between the global forcing number and the maximum anti-forcing number of graphs by starting bipartite graphs in this section. The following structure of a bipartite graph with a unique perfect matching will play an important role.
Theorem 3.1.
[22] If is a bipartite graph with a unique perfect matching and vertices, then we can label all vertices in and such that . Hence has pendant vertices and , and , equality holds if and only if .
Combining Theorem 3.1 and Lemma 2.12, we can obtain the following critical result that connects a minimum global forcing set of a bipartite graph with anti-forcing sets of a perfect matching of .
Lemma 3.2.
Let be a bipartite graph with at least two perfect matchings. For any perfect matching of , has a minimum global forcing set such that .
Proof.
Let be a graph obtained from by a series of LM operations so that . Then is a perfect matching of . By Lemma 2.13, it suffices to prove that the result holds for and . Let be a minimum global forcing set of . Then is a maximum subgraph of without any nice cycle of by Lemma 2.11. We claim that contains a pendant vertex. From Lemma 2.12, we can find an edge subset such that has a unique perfect matching. By Theorem 3.1, we know that has a pendant vertex . Hence is also a pendant vertex of . Let and be the two edges incident with in ( and may be the same). Then also contains no nice cycles of . Since has the same size as , by Lemma 2.11 we have that is a new minimum global forcing set. Since , has an edge incident with other than in , so . ∎
From the lemma, we can obtain a main result in comparing the global forcing number and the maximum anti-forcing number of a bipartite graph.
Theorem 3.3.
Let be a bipartite graph with a perfect matching. Then .
Proof.
We apply induction on . If , then and we are done. Next we consider bipartite graph with larger size. Suppose that for any bipartite graph with sizes smaller than , the result holds. If has a unique perfect matching, then it is trivial as the initial case. Otherwise, by Lemma 3.2 we have that for any perfect matching of with , has a minimum global forcing set such that . Take an edge in , and let .
We claim that . Since is also a perfect matching of , . Let be a minimum anti-forcing set of in . Since any -alternating cycle in either is contained in or contains , is an anti-forcing set of in by Lemma 2.6. So
which implies that and the claim holds.
From Lemma 2.10, we know that is a global forcing set of , which implies that . By the induction hypothesis, we get that . Thus
∎
Corollary 3.4.
If is a connected graph with , then .
Proof.
Next we will fix the order of a graph, but ignore its size to estimate the difference between the global forcing number and the maximum anti-forcing number of bipartite graphs.
Theorem 3.5.
If is a connected bipartite graph with a perfect matching and vertices, then
and the right equality holds if and only if is isomorphic to .
Proof.
By Theorem 3.3, we directly get the left inequality. So we now consider the right inequality. For any perfect matching of , we can get a maximum subgraph of such that is the unique perfect matching of . So . Let be a maximum subgraph of without nice cycles of . Then and by Lemma 2.11. By Theorem 3.1, we have that . So
| (3.1) | |||||
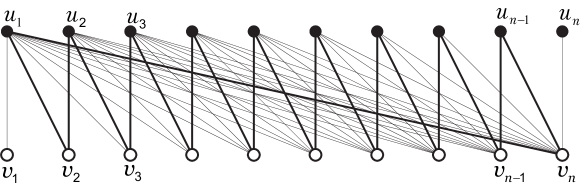
If is isomorphic to , then by Theorem 3.1, for every perfect matching of , we have . Since every cycle of is nice, is a spanning tree of , i.e. . Thus .
Conversely, if , then both equalities in Ineq. (3.1) hold. so we have that and for every perfect matching of , . Next we want to show that is isomorphic to , that is, for each . By Theorem 2.3, every cycle of is nice. By Theorem 3.1, we can label all vertices in such that and . Since is a nice cycle of missing exactly and (see Fig. 1(a)), .
For any , is a nice cycle of missing exactly and (see Fig. 1(b)), which implies that and induces a complete bipartite graph. It remains to show that the degrees of and must be .
We can get a new perfect matching by replacing the edges , by and in . Theorem 3.1 implies that contains an edge not in such that its two end vertices have degree . So contains another -degree vertex except for and , say . Then must have degree , since contains a path from to and missing exactly , and , and a cycle missing exactly and formed by this path adding (see Fig. 1(c)) for any . ∎
Shi et al. [28] gave an upper bound of the maximum anti-forcing number of graphs.
Theorem 3.6.
[28] Let be a graph with a perfect matching . Then .
A perfect matching of is said to be nice, if satisfies all equalities in Theorem 3.6. A characterization for a nice perfect matching of a graph was given as follows [28].
Theorem 3.7.
[28] For a perfect matching of a graph , is nice if and only if for any two edges and in , if and only if , and if and only if .
Corollary 3.8.
Let be a connected graph with a nice perfect matching and vertices. Then .
Proof.
In the following, we will give a graph such that is one less than the upper bound in Theorem 3.5, i.e. . A cycle in a graph is a Hamilton cycle if .
Proposition 3.9.
Let be a connected bipartite graph with vertices. If is isomorphic to for any , then and . Conversely, if , then is isomorphic to .
Proof.
If is isomorphic to for any , let and be nonadjacent vertices in different partite sets of . Then is isomorphic to . We claim that for any cycle in , it is nice in if and only if it is not a Hamilton cycle of . If is a Hamilton cycle of , it is not nice in . If either or belongs to , then is either a null graph or a complete bipartite graph, so is a nice cycle of . Otherwise, neither nor are in , and can be obtained from a complete bipartite with order at least by deleting an edge. Hence has a perfect matching, i.e. is a nice cycle of , and the claim is verified. Let be a maximum subgraph of without any nice cycle of . Since two Hamilton cycles of together contain a shorter cycle, which is a nice cycle of , there is exactly one cycle in , so . By Lemma 2.11, .
Conversely, if , then by Theorem 2.3. Because is bipartite, . If , then is isomorphic to . By Theorem 3.5, , a contradiction. If , then for distinct . Since , by Theorem 2.3, all cycles in are nice. If and are adjacent, then has a Hamilton cycle, not a nice cycle of , a contradiction. So and are not adjacent.
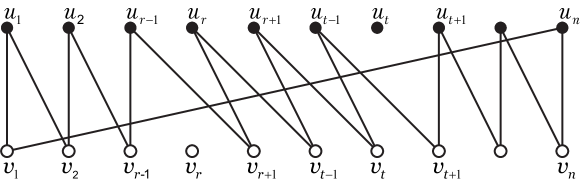
Let and be a bipartite sets of . We can assume and . Let and (see Fig. 2). Obviously, is a cycle of missing exactly and , which is not a nice cycle of , a contradiction. Thus, . ∎
4 Generalizations of Theorem 3.3
A connected graph is called matching covered, if every edge of belongs to a perfect matching of . For a graph , denotes the set of all vectors whose entries are indexed by the edges of . For any perfect matching of , the incidence vector of is denoted by . The perfect matching polytope of is the convex hull of , denoted by . In a landmark paper, Edmonds [11] gave a linear inequality description of . For any and , let . For a nonempty subset , represents for a cut, the set of edges which have exactly one end vertex in . If is a singleton, then is a trivial cut.
Theorem 4.1.
[11] A vector in belongs to if and only if it satisfies the following system of linear inequalities:
A vector in is 1-regular if , for all . For a cut of , we denote the graph obtained from by shrinking the shore to a vertex by . We refer to and as the -contractions of . A cut of a matching covered graph is a separating cut if both of the -contractions of are also matching covered, and is tight if for all . Every tight cut is separating, but the converse is not true. A matching covered graph is solid if all separating cuts of it are tight. A brick is a non-bipartite matching covered graph satisfying that all tight cuts of it are trivial.
Theorem 4.2.
[4]
For a brick , the following three statements are equivalent.
(i) is solid,
(ii) , and
(iii) consists of non-negative -regular vectors.
de Carvalho et al. [4] pointed out that in 2003 Reed and Wakabayashi had already showed that (i) and (ii) are equivalent in Theorem 4.2, and gave a new proof to it and proved the equivalence of (i) and (iii).
In 1959, Kotzig [17] showed the following property of the graphs with a unique perfect matching.
Theorem 4.3.
[17] If is a connected graph with a unique perfect matching, then has a cut-edge belonging to the perfect matching.
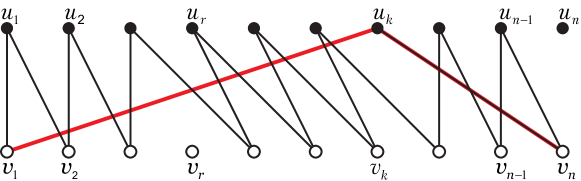
For the graphs with a unique perfect matching, we come to a deeper structure property: contains either a pendant vertex as Theorem 3.1 in the bipartite case or an odd dumbbell (see Fig. 3): two disjoint odd cycles connected by one path of odd length.
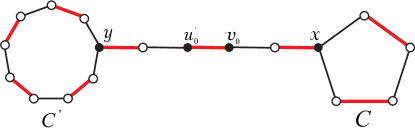
Theorem 4.4.
Let a graph have a unique perfect matching without pendant vertices. Then contains an odd dumbbell as a subgraph so that contains the perfect matching of the subgraph.
Proof.
By Theorem 4.3, has a cut edge . Since , the components and of containing and respectively, must be non-trivial. Consider the longest -alternating path in each component, starting with and , respectively. This must end with an edge in , and the last vertex must be adjacent to some vertex in the path. This must form an odd cycle and gives the required subgraph. ∎
Now we can extend the relation to the class of graphs . First we extend Lemma 3.2 as follows.
Lemma 4.5.
Let have at least two perfect matchings. Then for any perfect matching of , there exists a minimum global forcing set such that .
Proof.
Then by using the above lemma we obtain the following generalization as the proof of Theorem 3.3 .
Theorem 4.6.
If , then .
Corollary 4.7.
If is a solid brick, then .
For general non-bipartite graphs, the three conditions in Theorem 4.2 are not equivalent. However we have the following implication.
Lemma 4.8.
If consists of non-negative -regular vectors, then .
Proof.
Suppose to the contrary that has disjoint odd cycles and such that has a perfect matching . Let be a vector in such that , if ; , if ; , otherwise. Note that is a non-negative and -regular vector. So . But for odd cycle , , contradicting the odd set constraint in Theorem 4.1. ∎
Corollary 4.9.
If consists of non-negative -regular vectors, then .
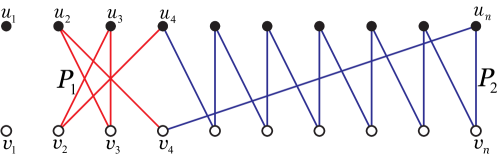
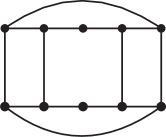
An example in Fig. 4 shows there exists a matching covered graph not in with .
5 The difference
In this section, we will give sharp lower and upper bounds on the difference on general connected graphs .
Theorem 5.1.
[22] If has a unique perfect matching and vertices, then .
Theorem 5.2.
Let be a connected graph with a perfect matching and vertices. Then
and the left equality holds if and only if .
Proof.
() We first prove the left inequality. If , then has a unique perfect matching, so . If , then has at least two perfect matchings. By Theorem 2.4, we have that . Hence, has exactly two perfect matchings, denoted by and . Obviously, . So for the case of , we have that .
Next we consider . Let be a maximum subgraph of without any nice cycle of . By Lemma 2.12, we can find an edge subset such that has a unique perfect matching. From Theorem 5.1, . By Lemma 2.11 and Theorem 3.6, we have
| (5.1) | |||||
Now we verify the equivalence condition for the left equality. If , for all cases of , we can verify that . Conversely, if , then for , we know , which implies that . For , all the equalities in Ineq. (5.1) hold, so and . By Corollary 3.8, . Next we will prove that if , then . For , we have , so , and . By Theorem 3.7, has two cases and as shown in Fig. in the sense of isomorphism, where is a nice perfect matching of .
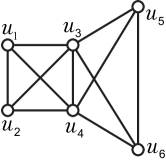
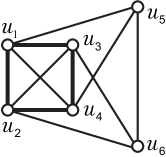
We first consider the graph . Let be a minimum global forcing set of . Then , for the subgraph of induced by , which is isomorphic to . Similarly, the subgraph of induced by satisfies that . Thus we have .
Next we claim that . Since is a global forcing set of , . Suppose to the contrary that . Let be a minimum global forcing set of . Then contains at least three cycles. Note that every even cycle in is nice, with length either or . And any three triangles in must produce a -cycle. So has a pentagon . Let be another cycle in except for . Then . So we can take two consecutive common vertices of and such that there exists three internally disjoint paths between them, which must contain an even cycle, a contradiction. Thus .
() We now prove the right inequality. For any perfect matching of , let be a maximum subgraph of with a unique perfect matching . Then . Corollary 5.1 implies that . Let be a maximum spanning subgraph of without nice cycles of . Then . If , then , and the required result holds.
Next we consider the case . Let , where . By the definition of , the subgraph of induced by can contain at most 4 edges. Consider the subgraphs induced by for . If of these subgraphs contain only 3 edges, the number of edges in is at most , a contradiction. Therefore of these must have 4 edges and give triangles whose edges can not form additional cycles. So we have . It follows that and we are done. ∎
The following discussions will show that the upper bound on in Theorem 5.2 can be achieved.
Proposition 5.3.
and .
Proof.
Let be a maximum spanning subgraph of which contains no any nice cycle of . By Lemma 2.11, . Obviously, every even cycle in is nice. So has no even cycles. We claim that . Let be different cycles in . Then they are pairwise edge-disjoint. Otherwise, there are distinct and sharing an edge. So we can take a path on , which has only two end vertices and no edges in . Then consists of three internally disjoint paths between two vertices, which must contain an even cycle, a contradiction. For any , we have . So
which implies that and . So the claim holds.
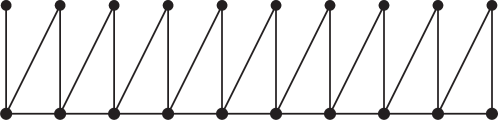
Finally, for any positive integer we will construct a matching covered graph such that . Let be a copy of the triangular prism, where . Let and be two triangles in , and , and are three remaining edges in . We join consecutively with edges and , for each , resulting in a graph (see Fig. 7(a)). Dr. Kai Deng gave . In general we have the following result.
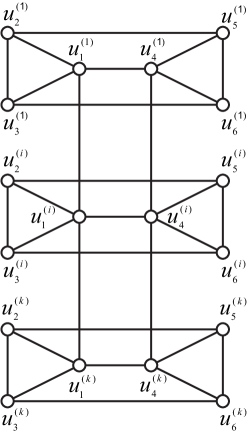
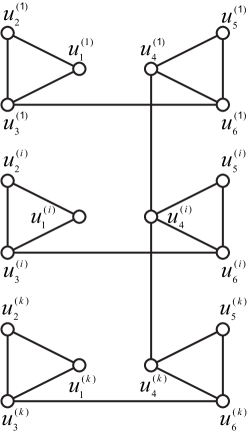
Proposition 5.4.
For any integer , is a matching covered graph, and . Thus, .
Proof.
Take a perfect matching of as . We can see that each edge of belongs to an -alternating cycle in , so is matching covered. From Theorem 3.7, is a nice perfect matching of , so .
Now we consider the global forcing number of . Set
Because all cycles of are triangles (see Fig. 7(b)), it contains no nice cycles of , so .
Next, we prove that by induction on . If , then is a triangular prism. We know . Otherwise, has a global forcing set of a single edge, which belongs to at most two of three nice cycles , and , a contradiction. We now consider with . Suppose that for such graphs with less than triangular prisms, the assertion holds. Let
Then . Let be a minimum global forcing set of . We claim or or for some . Otherwise, , and for all , . In this case, we can construct a nice cycle of not passing through any edge of . Let . By induction hypothesis, . Since is a nice subgraph of , by Lemma 2.10, is a global forcing set of . We have
So , and for all . For , in an analogous argument, we get and . Thus . For and , since , we can take one path in from three edge-disjoint paths between and such that . We can check that such two paths and with two paths and form a nice cycle of , a contradiction. So the claim is verified.
If (similarly for the case ), as before by the induction hypothesis we have
So suppose that there is an integer such that . Then has two components, denoted by and . Using the induction hypothesis to and , . Further,
In conclusion, we get . Thus . ∎
References
- [1] J. Cai, H. Zhang, Global forcing number of some chemical graphs, MATCH Commun. Math. Comput. Chem. 67 (2012) 289-312.
- [2] M. H. de Carvalho, C. L. Lucchesi, U. S. R. Murty, A generalization of Little’s Theorem on Pfaffian orientations, J. Combin. Theory Ser. B 102 (2012) 1241-1266.
- [3] M. H. de Carvalho, C. L. Lucchesi, U. S. R. Murty, On a conjecture of Lovász concerning bricks. I. The characteristic of a matching covered graph, J. Combin. Theory Ser. B 85 (2002) 94-136.
- [4] M. H. de Carvalho, C. L. Lucchesi, U. S. R. Murty, The perfect matching polytope and solid bricks, J. Combin. Theory Ser. B 92 (2004) 319-324.
- [5] M. H. de Carvalho, C. L. Lucchesi, U. S. R. Murty, How to build a brick, Discrete Math. 306 (2006) 2383–2410.
- [6] G. Chen, X. Feng, F. Lu, L. Zhang, Disjoint odd cycles in cubic solid bricks, SIAM J. Discrete Math. 33 (2019) 393–397.
- [7] K. Deng, H. Zhang, Anti-forcing spectra of perfect matchings of graphs, J. Comb. Optim. 33 (2017) 660-680.
- [8] K. Deng, H. Zhang, Extremal anti-forcing numbers of perfect matchings of graphs, Discrete Appl. Math. 224 (2017) 69-79.
- [9] A.A. Diwan, The minimum forcing number of perfect matchings in the hypercube, Discrete Math. 342 (2019) 1060-1062.
- [10] T. Došlić, Global forcing number of benzenoid graphs, J. Math. Chem. 41 (2007) 217-229.
- [11] J. Edmonds, Maximum matching and a polyhedron with (0,1) vertices, J. Res. Nat. Bur. Stand. B 69 (1965) 125-130.
- [12] J. Edmonds, L. Lovász, W.R. Pulleyblank, Brick decomposition and the matching rank of graphs, Combinatorica 2 (1982) 247-274.
- [13] F. Harary, D. J. Klein, T. P. Živković, Graphical properties of polyhexes: perfect matching vector and forcing, J. Math. Chem. 6 (1991) 295-306.
- [14] K. Kawarabayashi and K. Ozeki, A simpler proof for the two disjoint odd cycles theorem, J. Combin. Theory Ser. B 103 (2013) 313-319.
- [15] D. J. Klein, M. Randić, Innate degree of freedom of a graph, J. Comput. Chem. 8 (1987) 516-521.
- [16] D.J. Klein, V. Rosenfeld, Forcing, freedom, and uniqueness in graph theory and chemistry, Croat. Chem. Acta 87 (2014) 49-59.
- [17] A. Kotzig, On the theory of finite graphs with a linear factor II, Mat.-Fyz. Časopis Slovensk. Akad. Vied 9 (1959) 136-159. (Slovak).
- [18] H. Lei, Y.-N. Yeh, H. Zhang, Anti-forcing numbers of perfect matchings of graphs, Discrete Appl. Math. 202 (2016) 95-105.
- [19] X. Li, Hexagonal systems with forcing single edges, Discrete Appl. Math. 72 (1997) 295-301.
- [20] X. Liu, S. Xu, L. Tu, Global forcing numbers of handgun-shaped benzenoid systems, Curr. Nanosci. 10 (2014) 766-771.
- [21] L. Lovász, Matching structure and the matching lattice, J. Combin. Theory Ser. B 43 (1987) 187-222.
- [22] L. Lovász, M. D. Plummer, Matching Theory, Ann. Discrete Math. Vol. 29 (North-Holland, Amsterdam, 1986).
- [23] C. L. Lucchesi, M. H. de Carvalho, N. Kothari, U. S. R. Murty, On two unsolved problems concerning matching covered graphs, SIAM J. Discrete Math. 32 (2018) 1478-1504.
- [24] L. Pachter, P. Kim, Forcing matchings on square grids, Discrete Math. 190 (1998) 287-294.
- [25] M. E. Riddle, The minimum forcing number for the torus and hypercube, Discrete Math. 245 (2002) 283-292.
- [26] J. Sedlar, The global forcing number of the parallelogram polyhex, Discrete Appl. Math. 160 (2012) 2306-2313.
- [27] L. Shi, H. Wang, H. Zhang, On the maximum forcing and anti-forcing numbers of (4, 6)-fullerenes, Discrete Appl. Math. 233 (2017) 187-194.
- [28] L. Shi, H. Zhang, Tight upper bound on the maximum anti-forcing numbers of graphs, Discrete Math. Theor. Comput. Sci. 19 (2017) 9-15.
- [29] D. Vukičević, J. Sedlar, Total forcing number of the triangular grid, Math. Commun. 9 (2004) 169-179.
- [30] D. Vukičević, N. Trinajstić, On the anti-forcing number of benzenoids, J. Math. Chem. 42 (2007) 575-583.
- [31] D. Vukičević, N. Trinajstić, On the anti-Kekulé number and anti-forcing number of cata-condensed bezenoids, J. Math. Chem. 43 (2008) 719-726.
- [32] L. Xu, H. Bian, F. Zhang, Maximum forcing number of hexagonal systems, MATCH Commun. Math. Comput. Chem. 70 (2013) 493-500.
- [33] H. Zhang, J. Cai, On the global forcing number of hexagonal systems, Discrete Appl. Math. 162 (2014) 334-347.
- [34] H. Zhang, X. Zhou, A maximum resonant set of polyomino graphs, Discussiones Mathematicae Graph Theory 36(2) (2016) 323-337
- [35] X. Zhou, H. Zhang, Clar sets and maximum forcing numbers of hexagonal systems, MATCH Commun. Math. Comput. Chem. 74 (2015) 161-174.
- [36] X. Zhou, H. Zhang, A minimax result for perfect matchings of a polyomino graph, Discrete Applied Mathematics 206 (2016) 165-171.