Relational Reactive Programming: miniKanren for the Web

The PutGet law for functional lenses states that the value written to a source should be the value returned by subsequent reads (Fischer et al., 2015). We adapt this law for reactive unification in order to preserve the reorderability of relations—an important property in miniKanren—as follows:

Here, $x_{t+1}\equiv y_{t}$ signifies reactive unification of variable $x$ at timestep $t+1$ with the value of variable $y$ at timestep $t$. $\hat{x}_{t+1}$ and $\hat{y_{t}}$ are the reified values of logic variables $x$ and $y$ at times $t+1$ and $t$, respectively.³³3We disallow free logic variables in the model and view, and so assume for present purposes that all reified values are fully bound. Consequently, simple equality in the host language is sufficient to define equivalence of reified terms without needing to resort to alpha equivalence. This states that the reified value of a variable should be equal to the reified value of the variable or value to which it was set in the previous timestep using reactive unification.

This law, interpreted in a relational context, has several additional implications, such as a significant weakening of the PutPut law. PutPut states that for two consecutive writes to a source, the second write should overwrite the first and be returned by subsequent reads. However, in the relational context the question of which write is second is indeterminate, as goals may be reordered. This yields the weakened form of PutPut:

Which states that if a variable is reactively unified twice, the reified values of the terms to which it is set must be equal. Otherwise, reactive unification fails and the term is unchanged.

An additional implication is that updates must be temporally stratified. Consider the simultaneous swapping of two variables:

If updates happened within a timestep, this would impose an ordering on the updates at odds with the constraints of relational goal reorderability. As such, values at one timestep must be fixed from the perspective of updates in the subsequent timestep.

This property states that all variables that belong to the same equivalence class as defined by mutual unification should be set to the same value at the next timestep if any of them is set through reactive unification. More precisely:

Intuitively, some version of this property is a practical necessity. Goal constructors only receive direct references to the model variable bound to the root value of the model. Any reactive unifications that target subterms of the model must do so indirectly by reactively unifying destructuring variables bound to subterms of the model. Without any version of this property, the only useful left-hand argument for reactive unification would be the root model variable itself, requiring programmers to reconstruct the entire model manually at each timestep in order to update it. With this property, we aim for a more mutational metaphor according to which subterms can be set directly. For example, consider the case of replacing the head of a list x with the string "lorem ipsum":

Because we do not have direct access to the variable bound to the current head of the list, we must bind a fresh variable y and reactively unify that variable with the new string. In order for this operation to make sense, we must be sure that the variable to which y is ultimately bound is updated as well, as it is this original variable that stores the ground truth information about its value.

As an arbitrary miniKanren goal, update goals may return multiple answers. We define the total reactive unification relating one application state to its successor state as the conjunction of all reactive unifications in all answers $A$ returned by a given update goal.

In other words, at the next timestep, the reified value of variable $x$ should be equal to the reified values of all variables $y$ bound to $x$ in any answer. This in turn implies that $y$ must reify to the same value in all states in which it is bound to $x$ lest it violate PutGet.

This definition is one way to reduce the ambiguity of the otherwise unspecified behavior as to how to treat multiple, non-deterministic answers returned by an update goal. Moreover, it has the desirable property that it allows programmers to leverage miniKanren’s search capabilities and reuse existing relations used to derive data in the forward direction to propagate changes backwards without writing a separate class of update relations. For example, consider the case of mapping over a list and duplicating each element:

By leveraging search to nondeterministically reactively unify $y$, it is possible to avoid the need to write a dedicated deterministic relation that walks the list and reactively assigns new values. Moreover, we observe that because the substitution preserves the provenance of all atomic data within the system, it is possible to set any atomic value from any reference to that value no matter how many intervening computations have processed that data. This gives the programmer significant leverage in specifying state transitions without writing dedicated update relations. This enables techniques such as relational joins, where answers may contain data combinatorially composed from a variety of sources (such as by conjoining several membero relations) and reactive unification will be able to overwrite any of those values by tracing them to their respective sources in the substitution.

One final property of potential value is recursive stratification. This property technically conflicts with earlier properties, such as the relational PutGet law, in that it requires cases that would generate failures in the PutGet law to instead return valid answers. Rather than complicate the presentation of earlier properties, we describe it here as an exception.

The intuition behind this property is that if we assign a value to the tail of a list, and then assign a value to the tail of the tail, we would like both operations to succeed rather than fail due to conflicts. Specifically, we would like to support the pattern of using deterministic assignment to modify the structure of a complex structure such as a list. Consider the following code which removes all instances of "lorem" from a list:

tail is bound to each cons pair headed by "lorem," and so by setting those cons pairs to their cdrs, the intent is to locally modify the list to remove each matching pair. Without the present property, if there is more than a single "lorem" in the list, this goal will amount to setting sublists of the tail to conflicting values, resulting in failure. With special handling, however, it is possible to make the above goal work in accordance with the intuition given. This allows "pointers" to structural elements of the model to be bound to logic variables and locally set through reactive unification to change the structure of the model in a somewhat controlled way.

This mutable metaphor avoids some of the traditional problems of such mutability. For instance, structure cannot be shared between model variables due to the normalization described in Section 3.1, so local changes are somewhat protected from interference by other reactive goals. Moreover, because changes are still temporally stratified, there is no risk of changing the list one is iterating over as one iterates. However, further experience is necessary to determine the limits or liabilities of this property.

Before we can define reactive unification, it is necessary to modify ordinary unification slightly so that operations performed by reactive unification remain consistent with the properties proposed in Section 3.2. When miniKanren is used for search, the substitution is typically immutable. In this case, there is no practical difference between two variables happening to be equal and being constrained to be so. Consider, for example, the substitution $x\mapsto 1\land y\mapsto 1$. Unifying $x$ and $y$ in this substitution, in most implementations, yields the same substitution. The information that $x$ and $y$ have been unified is thrown away because for all intents and purposes, it is enough to know that $x$ and $y$ have the same value, regardless of that value’s provenance.

To account for reactive unification, we must record the unification between $x$ and $y$ even if the two are already equal, so that if we later reactively update $x$, we can ensure that $y$ is appropriately updated as well. We capture this information by ensuring that both $x$ and $y$ walk to the same variable. For instance, we could remove the binding for $y$ and rebind it to $x$, yielding the substitution $x\mapsto 1\land y\mapsto x$. To make this intuition more precise, we can define the equivalence class of all mutually unified variables in a given substitution as the set of variables that share a common descendant, with ancestry defined by the walk procedure:

Where the $descendant$ relation is recursively defined as:

We can then modify non-reactive unification to guarantee that each set of mutually unified variables contains one member that is the common descendant of all members of the set. This can be achieved by, each time two variables are unified, replacing the binding of one unified variable with a binding to the other variable, after confirming that they do not conflict. See Appendix A for a full implementation.

With normal unification so defined, we can proceed to define reactive unification. Reactive unification begins with $\mathcal{S}$ and a stream of answers $\mathcal{A}$ produced by the update goal. Each answer $a\in\mathcal{A}$ contains some number of stored reactive unification goals $r\in a$. Each reactive unification goal $r$ possesses a left-hand side variable to which the right-hand side value will be written.

The update goal is not applied directly to $\mathcal{S}$, but to an $\mathcal{S}^{\prime}$ that is the result of applying all of the goals contained in the view tree along the path from the root to the leaf containing the update goal. As such, reactive unification first generates a patch by calculating the diff entailed by the set of reactive unifications $r$ applied to $\mathcal{S}^{\prime}$. The patch takes the form of a list of cons pairs in which the left-hand side is a variable bound in $\mathcal{S}$ and the right-hand side is a ground value. This patch is then applied to $\mathcal{S}$ to calculate the successor state.

In a simple implementation, the left and right hand sides of each reactive unification can simply be walked and reified, respectively, in their corresponding answer state. In order to support the recursive stratification property from Section 3.2.4, however, an additional step is required. Specifically, the reification procedure must be extended such that when reification encounters a variable that is set directly by another reactive update, it must abandon further reification within the answer substitution and proceed with the reified results of that update. Updates that are descendants of other updates are subsequently discarded, as they have already been incorporated into ancestor updates.

Applying the patch is a simple unification-like procedure in which variables and patch values are walked in tandem, with the latter overwriting the former as applicable.

Reactive miniKanren lends itself to an interesting approach to the problem of synchronizing the view tree with the model, which, while its performance characteristics have yet to be tested in a practical environment, nevertheless possesses interesting properties that bear further investigation.

Reactive miniKanren maintains a persistent tree of dynamic view elements and attributes, which corresponds roughly to the structure of the template that generated it. We will refer to as the "view tree." When $\mathcal{S}$ is modified through reactive unification, its successor, $\mathcal{S}^{\prime}$, is passed down the branches of this tree, which re-run goals and update view elements as needed. In particular, goal constructor templates give rise to particularly interesting subtrees in that these subtrees are isomorphic to the structure of the miniKanren search performed by these goal constructors. Consider the following example of a pair of sibling text nodes containing the text "ipsum" and "dolor," respectively, as produced by the following goal constructor applied to $\mathcal{M}$, ("ipsum" "dolor"):

Because the list has two elements, membero will succeed twice at destructuring the list and binding the view to its first and second elements before failing to destructure the empty tail of the list. Reactive miniKanren will therefore render this search as the view subtree in Figure 1.

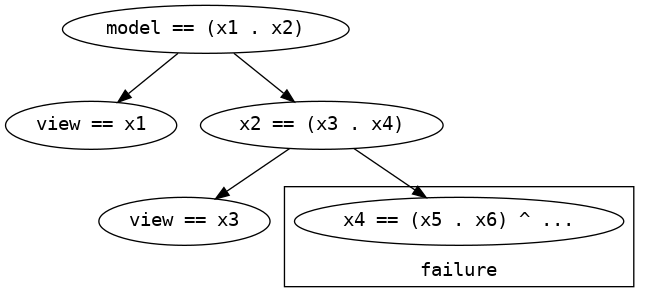
To build this tree representation, reactive miniKanren threads an additional value through the search procedure alongside the substitution that corresponds to a conjunction of all unifications and constraints seen to this point in the search. When the search encounters a conde, it creates a branching node in the view tree, as in Figure 1, containing the first-order conjunction of unifications and constraints seen to this point in the search. It then discards these conjuncts and proceeds with the trivial succeed goal as its new conjunction. Likewise, when successful answers or failures are encountered, nodes are created containing the new current conjunction.

This tree is isomorphic to the miniKanren search, and can be viewed as a first-order representation of that search. The top layer of Figure 1 , for example, can be read as destructuring the head of $\mathcal{M}$ and then, in the second layer, nondeterministically both binding $x1$ to the first element, "ipsum" and destructuring the tail of $\mathcal{M}$. The third layer of the tree then represents the nondeterministic binding of $x2$ to the second element of $\mathcal{M}$ and the failed attempt to destructure the subsequent tail. This isomorphism allows reactive miniKanren to re-run its search with a new $\mathcal{S}^{\prime}$ by passing $\mathcal{S}^{\prime}$ down the branches of this tree and re-applying the stored goals at each node.

The advantage of maintaining and modifying a representation of the search over simply re-running the search in toto is that the first-order search tree representation can store additional information about how its answers are bound to the live view elements that would be lost if the search information was discarded. Rather than producing a new representation of the view and performing potentially expensive diffs, nodes in this tree that transition from failing to succeeding states or vice versa can directly add elements to or remove them from the live DOM. Each answer’s unique position as a node in this view tree, therefore, can be viewed as an implicit "key" in the above sense of keyed iteration that establishes a unique identity that is not dependent on deriving a unique identifier from the data. Because even failures possess such unique positions in the search tree, they preserve their implicit order in the stream of answers and can insert their corresponding view elements at the correct sibling position when they become non-failing, which is information that would be lost in a postprocessing of the answer stream via a diff-based method.

This approach, however, has both strengths and weaknesses due to the fact that the "keys" supplied by the position in the search tree are assigned without regard to the intended usage pattern of the underlying model. For example, the strategy described above excels in cases such as filtering a list according to a search term, which changes which nodes are displayed but does not change the relationship between a given node and its contents. The first node will remain bound to "ipsum" even as it is hidden and shown in response to changes in the filter term. Nodes not affected by visibility changes can remain as they are in the DOM.

This model is much weaker, however, when it comes to cases such as insertion into a list. If an element is inserted at the beginning position of a list that was naively traversed with membero, then the first, second, and all of the rest of the answers returned by the goal will have changed their value, and all nodes will have to be modified even though a more efficient strategy, from the perspective of the DOM, may have been to simply insert one node at the front of the list. Using Figure 1 as an example, if "lorem" was inserted at the head of the list, then due to the mutable metaphor through which reactive unification operates, the entire list would be overwritten in place by new values. Hence, $x1$ becomes "lorem" while $x2$ becomes "ipsum" and so on. Because key identity is derived from position in the search tree, every node will have to be modified in order to bring the view into synchronicity with the model.

To address such shortcomings, we observe that because we are using position in the search tree as a form of identity, we can control the type of key strategy used by the reactive system by changing the dynamics of the search tree. In the case of lists of sibling view nodes, this means that changing the list representation and associated traversal strategy can result in different keying strategies with different performance characteristics.

We introduce here the concept of "insertion lists," which are conceptually related to techniques such as difference lists in which the underlying representation and operations of list structures are modified, with resultant changes to performance and behavior (Hughes, 1986). In particular, an insertion list is a list backed by a binary tree as the underlying representation. List order is defined by an in-order traversal of the tree. membero can be implemented for such lists, then, as a simple tree traversal:

When used as a drop-in replacement for ordinary cons lists and membero, the resulting view remains the same. However, consider the view tree associated with the goal imembero(model, view) when the model is the insertion list ("ipsum" . "dolor"), as depicted in Figure 2.

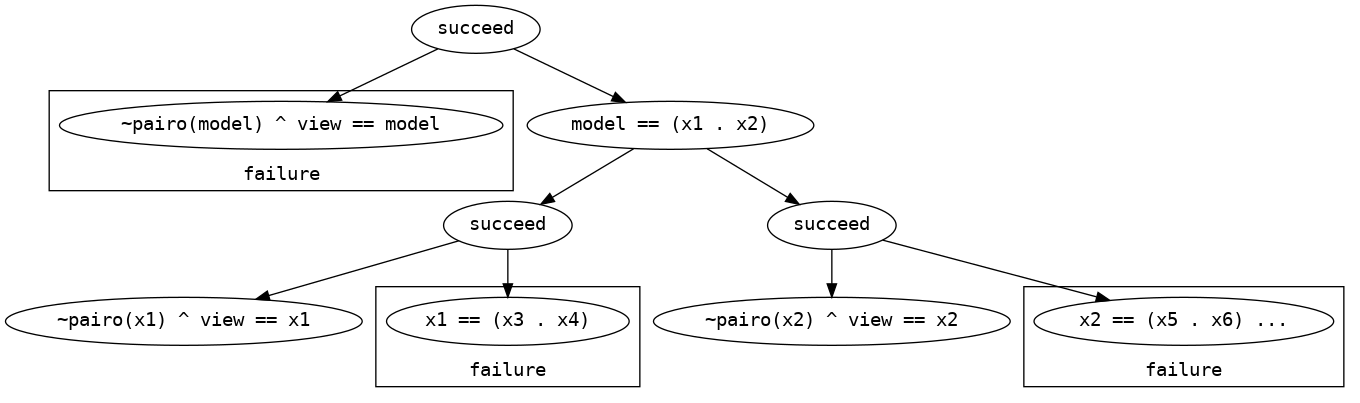
Reading this diagram from top to bottom, the second level corresponds to the nondeterministic choice of whether $\mathcal{M}$ is a displayable non-pair, signified by the failing left hand check, or the right hand check, which destructures the pair. The fourth level likewise nondeterministically checks that the two children of $\mathcal{M}$, "ipsum" corresponding to $x1$ and "dolor" corresponding to $x2$, are displayable non-pairs and binds them to the view variable.

If we now define the insertion procedure as replacing a leaf of the binary tree representation with a binary tree of depth 1, inserting "lorem" at the beginning of the list yields (("lorem" . "ipsum") . "dolor"). After reactive unification, this means that $x1$, previously bound to "ipsum" is now bound to the binary tree ("lorem" . "ipsum"). The view tree will therefore swap the failure statuses of the left-hand grandchildren and further expand the previously failing pair node to account for the new substructure, binding $x3$ and $x4$ in the process.

Note, however, that $x2$ remains unchanged by reactive unification and therefore its corresponding view node does not need to modify the DOM. Likewise, all subsequent elements would be unaffected by this insertion, yielding the same final result as in the membero case, but doing so by removing only one node and replacing it with two new ones, as opposed to changing every node in the list. Note too that the insertion list retains the same rough performance characteristics as the cons list in cases such as list filtering, albeit with the additional base overhead required to perform efficient insertions. It is possible that other list representations or traversal strategies could result in other useful performance profiles. While it is ultimately an empirical question whether these strategies result in net performance gains in a real-world application, because DOM operations tend to be expensive relative to the execution of pure Javascript, we argue that such properties represent a promising line of future inquiry.

One important caveat is that as a result of the isomorphism between the search tree and the view tree, any conde expressions that serve only to select between two possible values for the same view element will produce redundant view elements for each branch of the conde clause, potentially impacting performance. This is analogous to the problem in normal miniKanren of using conde to write constraints, such as checking that a list is a proper list, and paying the performance penalty when that relation generates useless list structures when its arguments are free. It is likely, however, that this problem can be solved in a manner analogous to that of normal miniKanren through the use of non-generative disjunctive constraints, so this may not ultimately pose a great problem (Donahue, 2023).