Reinforced Grounded Action Transformation for Sim-to-Real Transfer

The sim-to-real literature can be broadly divided into two categories of approaches. Methods in the first category seek to learn policies robust to changes in the environment. In applications where the target domain is unknown or non-stationary, these methods can be very useful. Dynamics Randomization adds noise to the environment dynamics, which has led to success in finding robust policies for robotic manipulation tasks [9]. Action Noise Envelope (ane) [10] randomizes the environment by adding noise to the action. While these methods uses noise injected at random to modify the environment, Robust Adversarial Reinforcement Learning (rarl) uses an adversarial agent to modify the environment dynamics [11]. Using a different paradigm, meta-learning attempts to find a meta-policy which can be learned in simulation and then can quickly learn an actual policy on the real environment [12].

Methods in the second category, which we refer to as grounding methods, seek to improve the accuracy of the simulator with respect to the real-world. Unlike the robustness methods, these methods have a particular target real-world domain and usually require collecting data from it. We can think of grounding methods as strategies to correct for simulator bias, whereas the robustness methods only correct for simulator variance. System identification type approaches try to learn the exact physical parameters of the system—either through careful experimentation as done with the Minitaur robot [13] or through more automated methods of system identification like TuneNet [14]. Often, these methods require alternating between improving the simulator and improving the policy as in Grounded Simulation Learning [1]. Our approach follows this basic format, but unlike these methods (and like gat [2]), we do not assume that we have a parameterized simulator that we can modify. Neural-Augmented Simulation (nas) [15] and policy adjustment [16] are similar approaches to gat but use different neural architectures and training procedures.

gat achieved remarkable success on a challenging domain; however, there has not been much work applying it to different domains. Our approach improves upon the gat algorithm to overcome some of its limitations.

Formally, we treat the sim-to-real problem as a reinforcement learning problem [17]. The real environment is a Markov Decision Process (mdp). At each time step, $t$, the environment’s state is described by $s_{t}\in\mathcal{S}$. The agent samples an action, $a_{t}\in\mathcal{A}$, from its policy, $a_{t}\sim\pi(\cdot|s_{t})$. The environment then produces a next state: $s_{t+1}\sim T_{real}(\cdot|s_{t},a_{t})$, where $T_{real}$ is the transition probability distribution. The agent also receives a reward, $r_{t+1}\in\mathbb{R}$, from a known function of the action taken and the next state: $r_{t+1}=R(a_{t},s_{t+1})$. In the controls literature, this is often called a cost function (which is a negative reward function). The discount factor $\gamma\in[0,1]$ controls the relative utility of near-term and long-term rewards. The RL problem is to find a policy, $\pi$, that maximizes the expected sum of discounted rewards: $\Sigma_{t=0}^{\infty}\gamma^{t}R(a_{t},s_{t+1})$

The simulator is an mdp that differs only in the transition probabilities, $T_{sim}$. The sim-to-real objective is to maximize the expected return for the RL problem while minimizing the number of time steps evaluated on the real mdp. The tradeoff between these objectives depends on the specific application.

The GSL framework [1] consists of alternating between two steps, called the grounding step and the policy improvement step. During the grounding step, the target policy, $\pi$, remains frozen while the simulator is improved, and, during the policy improvement step, the grounded simulator is fixed, making this step a standard RL problem. The policy improvement step is done entirely in the grounded simulator. GSL continues alternating between these steps until the policy performs well on the real environment.

gat [2] introduced a particular way of grounding the simulator which treats the simulator as a black box. The grounding step for gat is as follows:

1. 1.

   Evaluate the current policy on both environments and store trajectories, $\{s_{0},a_{0},s_{1},a_{1},...\}$ as $\tau_{real}$ and $\tau_{sim}$.

2. 2.

   Using supervised learning, train a forward model of the dynamics, $f_{real}:\mathcal{S}\times\mathcal{A}\rightarrow\mathcal{S}^{\prime}$, from the data in $\tau_{real}$. This model—usually a neural network—learns a mapping from $(s_{t},a_{t})$ to the maximum likelihood estimate of the next state observation, $\hat{s}_{t+1}$.

3. 3.

   Similarly, train an inverse model, $f^{-1}_{sim}:\mathcal{S}\times\mathcal{S}^{\prime}\rightarrow\mathcal{A}$ from $\tau_{sim}$. This model is a mapping from two states, $(s_{t},s_{t+1})$, to the action, $\hat{a}_{t}$, that is most likely to produce this transition in the simulator.

4. 4.

   Compose the forward and inverse models to form the action transformer, $g(s_{t},a_{t})=f^{-1}_{sim}(s_{t},f_{real}(s_{t},a_{t}))$.

During the policy improvement step, the reward is still computed explicitly as $R(a_{t},s_{t+1})$. A block diagram of the grounded simulator for gat is shown in Fig. 1. When the action transformer is prepended to the simulator, the resulting grounded simulator produces a next state, $s_{t+1}$, that is closer to the next state observed in the real world. Thus, if we learn a policy on a good grounded simulator, the policy will also perform well on the real world.

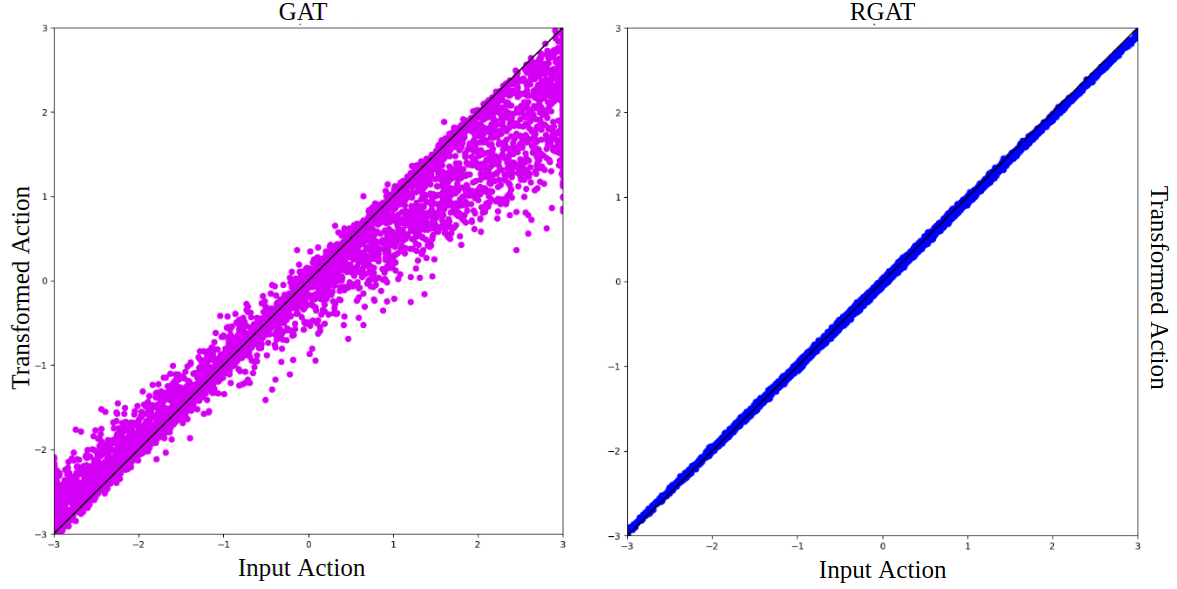
To test the precision of an action transformer, we first apply both the gat and rgat algorithms to settings where the sim and real domains were exactly the same. Ideally, during the grounding step, the action transformer should learn not to transform the actions at all. This effect is easy to visualize for InvertedPendulum, since the action space is one dimensional. Fig. 3 shows the transformed action versus the input action after one grounding step for gat and rgat. The black line shows the points where the transformed action is the same as in the input action. From the figure, we can see that rgat produces a better action transformer, since the dots lie much closer to the black line. The transformer for gat has a wider distribution with a bias toward the black line.

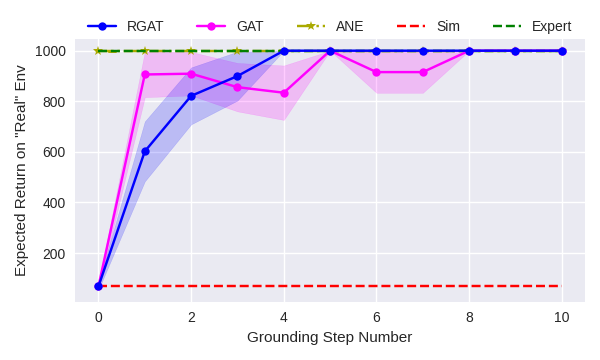
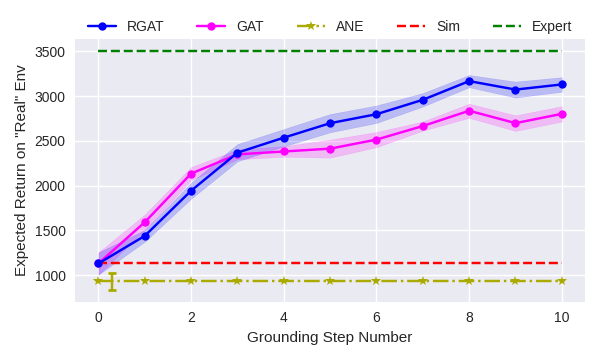
Consistent with Hanna and Stone [2], we find that gat works well on transferring policies where the policy representation is low dimensional. When we use a shallow neural network for the target policy—one hidden layer of four neurons—gat and rgat have very similar performance. We run ten trials of both algorithms, evaluating the performance on the “real” environment after each policy improvement step. Fig. 5(a) shows the mean return over ten grounding steps for both algorithms. For reference, we compare the results to a policy trained only in simulation (red line), and a policy that is allowed to train directly on “real” until convergence (green line).

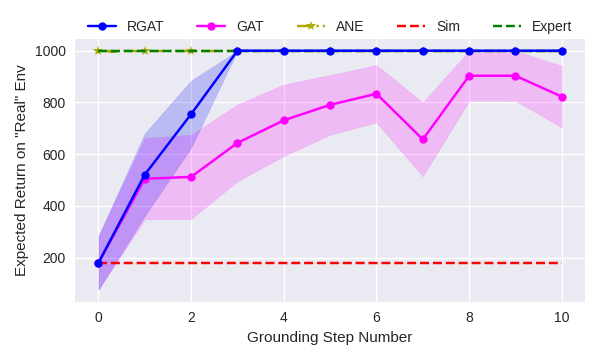
We then repeat that experiment using a deeper network—a fully connected neural network with two hidden layers of 64 neurons. The sim-to-real experiment results on InvertedPendulum is shown in Fig. 5(b). gat fails to transfer a policy from sim to “real”, as was discussed in the previous sections. However, rgat receives close to the optimal reward even with a high-dimensional policy representation.

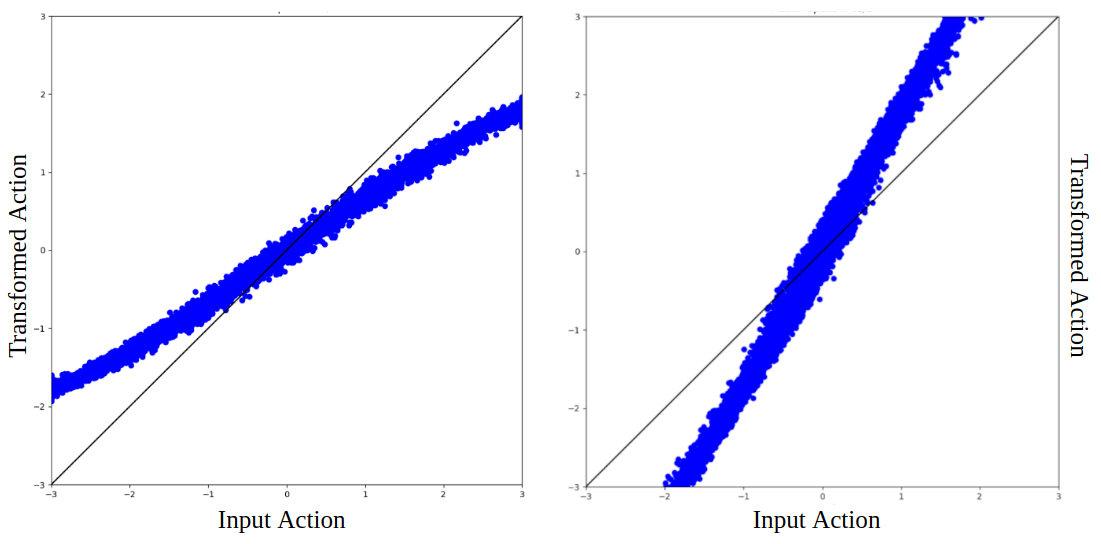
Similar to the action transformation visualizations shown in Section IV-A, we can visualize the transformations for the sim-to-real case. Fig. 4 shows the action transformation graphs for two different InvertedPendulum “real” world environments. On the left, the “real” pendulum has a greater pendulum mass than the simulated pendulum. Therefore, the magnitude of the actions decreases—a weaker force on the lighter pendulum has the same effect as a stronger force on the heavier pendulum. If the real pendulum is lighter, the opposite happens, as is shown in the figure on the right.

Note that the action transformer takes both the state and action as input, so the same input action could be transformed to different output action depending on the state. Thus, this effect accounts for some of the variance in Fig. 4, whereas in Fig. 3 the variance is only due to modeling error.

To further test the effectiveness of rgat, we repeat the experiment from Fig. 5(b) on the HalfCheetah and Hopper domains. The target policy architecture is the same as in Fig. 5(b). For these domains, using shallower networks is not an option, because lower capacity networks fail to learn good policies, even when trained directly on the real domain.

We chose the mass for the “real” environments based on the analysis from the rarl paper [11]. Changing the physical parameters of the robot results in different transition dynamics, which acts as our surrogate for the “real” environment; however in certain cases, it can make the task much easier or harder. We thus verify that an agent trained directly on the modified environment reaches the same optimal return as is expected on the original domain. Therefore, if a policy performs poorly on the modified simulator, we know this is because of poor transfer and not because the task is harder.

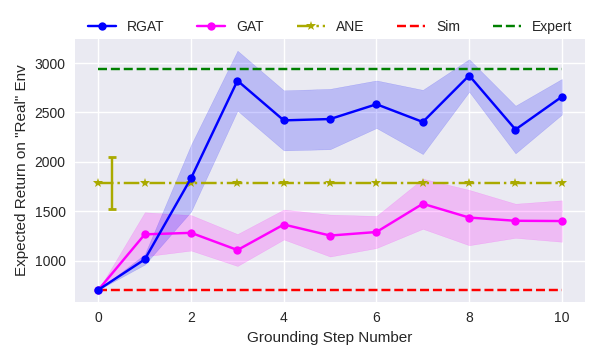
Figs. 5(a), 5(b), 6, and 7 show plots comparing the performance of gat and rgat. Both algorithms use 50 real world trajectories for every grounding step. In all of these experiments, rgat performs significantly better than gat and performs as well as a policy trained directly on the ”real” domain (green line). For comparison, the green lines on these plots show the performance of a policy trained directly on the real environment for up to ten million timesteps of experience.

We also compare against the Action Noise Envelope method [10]. Like gat and rgat, ane is a sim-to-real method that treats the simulator as a black-box. However, ane is not a grounding method—it seeks only to find policies that are robust to a prespecified noise distribution. For a given target domain, this distribution is typically unknown, but we performed experiments for several specified distributions and report only the best results. In the Inverted Pendulum domain, ane does well, but in the more complex domains, it is unable to learn a policy that transfers well. This behavior is expected because robustness methods try to perform well over a variety of environments at the cost of performance on any one particular domain.

Though we use the stable-baselines library hyperparameters for policy improvement, using trpo as the grounding step optimizer introduces a new set of hyperparameters for the algorithm. The parameters we found to be most critical to the success of the algorithm were the maximum KL divergence constraint and the entropy coefficient. We found that if the action transformer policy changed too much during a single grounding step, then the target policy often failed to learn. Thus, the maximum KL divergence should be small, but not so small that the policy cannot change at all. The entropy coefficient should be large enough to ensure exploration. In our experiments, we set the max KL divergence constraint value to 1e-4 and entropy coefficient to 1e-5.

The discount factor for the action transformer, $\gamma_{AT}$, is an additional hyperparamter we can control. Since the action transformer in rgat is an RL agent, it may pick suboptimal actions at the present step to get a higher reward in the future. In this sense, the action transformer tries to match the whole trajectory instead of just individual transitions. Setting $\gamma_{AT}=1$ leads to matching the entire trajectory, and setting $\gamma_{AT}=0$ causes the learner to only look at individual transitions. In our experiments, we set $\gamma_{AT}$ to 0.99.