Refutation of Hilbert Space Fundamentalism
Abstract
According to the “Hilbert Space Fundamentalism” Thesis, all features of a physical system, including the D-space, a preferred basis, and factorization into subsystems, uniquely emerge from the state vector and the Hamiltonian alone. I give a simplified account of the proof from arXiv:2102.08620 showing that such emerging structures cannot be both unique and physically relevant.
Hilbert Space Fundamentalism
Quantum Mechanics (QM) represents the state of any closed system, which may even be the entire universe, as a vector in a complex Hilbert space . The Hamiltonian operator fully specifies its evolution equation,
| (1) |
where is the time evolution operator.
Since QM is invariant to unitary symmetries, this seems to justify the following:
HSF.
The Hilbert-space fundamentalism Thesis (HSF): everything about a physical system, including the D-space, a preferred basis, a preferred factorization of the Hilbert space (needed to represent subsystems, e.g. particles), emerge uniquely from the triple
| (2) |
MQS.
We call minimalist quantum structure.
The HSF Thesis is sometimes assumed more or less explicitly in some versions of various approaches to QM, like information-theoretic, decoherence, and Everett’s Interpretation. The sufficiency of the MQS is claimed, perhaps most explicitly, by Carroll and Singh [4], p. 95:
Everything else–including space and fields propagating on it–is emergent from these minimal elements.
But this goes beyond Everettianism. We read in [3]
The laws of physics are determined solely by the energy eigenspectrum of the Hamiltonian.
Scott Aaronson states in “The Zen Anti-Interpretation of Quantum Mechanics” [2] that a quantum state is
a unit vector of complex numbers […] which encodes everything there is to know about a physical system.
I confess that I think the HSF Thesis makes sense, if we take seriously the unitary symmetry of QM. Why would the position basis of the space be fundamental, when it’s like other bases of ? Just like the reference frames provide convenient descriptions of the D-space with no physical reality, why would and be fundamental among all of the bases of ? And if they play a privileged role, shouldn’t this role emerge from the MQS alone? Unfortunately, we will see that this cannot happen.
Refutation of Hilbert Space Fundamentalism
In [5] I gave a fully general proof that the HSF Thesis is not true: for any MQS, no emerging structure can be both unique and physically relevant. Here I will give a less abstract and less technical version of that proof.
Denote a preferred structure expected to uniquely emerge from the MQS by , to express its dependence on and . Any such structure should be invariant, so it can be defined in terms of tensor objects from [6].
For a structure to be considered “preferred”, it has to consist of tensors that satisfy specific conditions, expressed as invariant tensor equations or inequations. For example, a preferred basis can be given by a set of operators , satisfying the relations , =0, and .
This is generally true, and justifies the following
Definition 1.
The kind of a structure is given by the types of its tensors and the defining tensor (in)equations specific to that structure (more details in [5]).
In every case of interest, a set of Hermitian operators suffices to specify the candidate preferred structure. We already saw this for a preferred basis. The D-space can be given by the number operators for particles of each type at each point in space, . Tensor product structures of can be specified in terms of local algebras of Hermitian operators. Therefore, we can limit to Hermitian operators only, avoiding much of the mathematical framework developed in [5] to include any kind of tensor objects.
Two state vectors and are physically equivalent, if they represent the same physical state, i.e. if they are related by gauge symmetry, space isometries etc. There is a group of unitary or anti-unitary transformations of , so that iff for some . This equivalence extends uniquely to tensors on . The main claim of the HSF Thesis is:
Condition 1 (“Essentially unique”-ness).
For any two -structures and , there is a symmetry transformation so that
| (3) |
Often the symmetry transformation from eq. (3) simply permutes the operators . For example, space isometries permute the position operators.
To be physically relevant, a D-space should be able to distinguish among physically distinct states, e.g., since the density can be different for different values of , the same should be true for any candidate preferred D-space. In particular, it should detect changes that the Hamiltonian cannot detect (the Hamiltonian cannot distinguish from iff there is a unitary so that and , for example , but space should be able to distinguish them). The same applies to the components of in a preferred basis, and to tensor factors of . Otherwise, such structures would have no physical relevance.
Physical equivalence requires that the structure has to distinguish not merely the unit vectors , but any other state vectors and representing the same physical states, for any .
Condition 2 (Physical relevance).
There exist at least two unit vectors representing distinct physical states not distinguished by the Hamiltonian, so that for any symmetry transformations ,
| (4) |
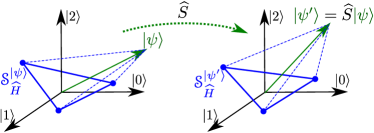
Example 1.
An obvious example satisfying Condition 2 is given by , where , because we expect that space, a preferred basis, and a preferred factorization to detect state changes in time.
I now prove that these two conditions are incompatible.
Theorem 1.
If a -structure is physically relevant, then it is not the only -structure.
Proof.
Fig. 2 illustrates the following construction. The -structure being a tensor object, its defining conditions are invariant to any unitary transformation that commutes with . Then transforms into a -structure for ,
| (5) |
This contradicts Condition 2. ∎
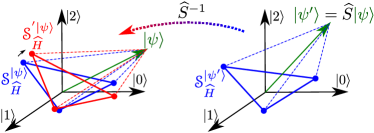
Example 1 gives an infinite family of physically distinct ways to choose the D-space. But in fact there is such an infinite family for each generator commuting with .
Theorem 1 was applied explicitly to various constructions assumed by the HSF Thesis to emerge from the MQS, and showed that, if they are physically relevant, they are not unique [5]. In particular, uniqueness fails for the generalized preferred basis (including for subsystems), the tensor product structure, emergent D-space, emergent classicality etc. Such structures cannot emerge uniquely from the MQS, a choice is always required.
A question stands: what breaks the symmetry of QM?
References
- [1]
- [2] S. Aaronson, The Zen anti-interpretation of Quantum Mechanics, www.scottaaronson.com/blog/?p=5359 (2021).
- [3] S.M. Carroll, Reality as a vector in Hilbert space, Tech. Report CALT-TH-2021-010, Cal-Tech, 2021.
- [4] S.M. Carroll and A. Singh, Mad-dog Everettianism: Quantum Mechanics at its most minimal, What is Fundamental? (A. Aguirre, B. Foster, and Z. Merali, eds.), Springer, 2019, pp. 95–104.
- [5] O.C. Stoica, 3d-space and the preferred basis cannot uniquely emerge from the quantum structure, Preprint arXiv:2102.08620 (2021), 1–18.
- [6] H. Weyl, The classical groups: their invariants and representations, vol. 45, Princeton University Press, 1946.