Reflectance-Oriented Probabilistic Equalization
for Image Enhancement

Given a color image $\mathbf{C}_{\mathrm{in}}$, its grayscale image $\mathbf{A}_{\mathrm{in}}$ is defined as the max of its RGB components and is equal to its value channel in HSV space [18]. Let $\mathbf{A}_{\mathrm{out}}$ be the enhanced image of $\mathbf{A}_{\mathrm{in}}$ in ROPE. Let $\circ$ and $\oslash$ denote element-wise manipulation and division, respectively. The final output $\mathbf{C}_{\mathrm{out}}$ is computed as

Let $\mathbf{A}_{\mathrm{in}}=\{a(q)\}$ and $\mathbf{A}_{\mathrm{out}}=\{\hat{a}(q)\}$, where $a(q)\in[0,K)$ and $\hat{a}(q)\in[0,K)$ are the intensities of the pixels $q$ in the input and output, respectively. $K$ is the total number of possible intensity values (typically 256). Our goal is to find an intensity mapping function $T$ of the form $\hat{a}(q)=T(a(q))$ to produce the enhanced image.

Let $o_{k}$ be the event of $a(q)=k$ (occurrence), where $a(q)\in\mathbf{A}_{\mathrm{in}}$ and $k\in[0,K)$ is an intensity value. Let $p(o_{k})$ be its probability. The 1D histogram of $\mathbf{A}_{\mathrm{in}}$ can then be expressed by $\{p(o_{k})\}$. Let $P(o_{k})$ be the cumulative distribution function of $p(o_{k})$. In HE, the intensity mapping function $T(\cdot)$ is given by $T(k)=KP(o_{k})-1$. The problem is how to properly define $p(o_{k})$.

In ROPE, we define $p(o_{k})$ based on the 2D histogram of $\mathbf{A}_{\mathrm{in}}$. Let $c_{i,j}$ be the event of $a(q)=i$ and $a(q^{\prime})=j$ (co-occurrence), where $q^{\prime}\in\mathcal{N}(q)$ and $\mathcal{N}(q)$ is the set of coordinates in the local window centered on the pixel $q$. Let $p(c_{i,j})$ be its probability. Then the 2D histogram can be written as $\{p(c_{i,j})\}$ with $i,j\in[0,K)$ and $i<j$. The construction of this 2D histogram is discussed in Section 2.3.

In CVC [2], given two intensities $i$ and $j$, their 2D histogram value $p(c_{i,j})$ is voted into the bin of the larger intensity $j$ and added to the 1D histogram value $p(o_{j})$, as illustrated in Fig. 1a. Similarly, CACHE [6, 7] votes $p(c_{i,j})$ into the bins of both intensities (Fig. 1b). These schemes overemphasize $p(o_{i})$ and/or $p(o_{j})$ and thus tend to cause precipitous brightness fluctuation in very dark or bright image areas as shown in Figs. 2b and 2e. Instead, we aim to find a proper method to distribute $p(c_{i,j})$ over all $k\in(i,j]$ for more adequate contrast enhancement (Fig. 1c as well as Figs. 2c and 2f).

Our thinking is as follows. Wu et al. [6, 7] have revealed that in HE, for any $k\in(0,K)$, the degree of contrast enhancement (CE) between $k-1$ and $k$ is ultimately proportional to $p(o_{k})$. Thus, for any $i,j\in[0,K)$, the degree of CE between $i$ and $j$ is proportional to $\sum_{k=i+1}^{j}p(o_{k})$. Meanwhile, related studies [2, 3] suggested that in 2DHE, $p(c_{i,j})$ needs to be defined in such a way that it is positively correlated with the requirement of CE between $i$ and $j$. These two insights lead to the inference that $p(o_{k})$ should be modeled such that $p(c_{i,j})\propto\sum_{k=i+1}^{j}p(o_{k})$. This confirms our motivation above: $p(c_{i,j})$ should not be delegated to $p(i)$ and/or $p(j)$ alone, but should be distributed over all $k\in(i,j]$.

Now, we would like to build a bridge between $p(o_{k})$ and $p(c_{i,j})$. We assume that $o_{k}$ and $c_{i,j}$ are dependent on each other. If we consider $o_{k}$ to be a marginal event, its distribution $p(o_{k})$ can be obtained by marginalizing over $p(c_{i,j})$:

where $p(o_{k}|c_{i,j})$ is the conditional probability of $o_{k}$ given $c_{i,j}$. This formula implies that the 1D histogram value $p(o_{k})$ can be modeled as a weighted average of all 2D histogram values $p(c_{i,j})$. The conditional probabilities $p(o_{k}|c_{i,j})$ act as weights.

Recall that it is necessary to determine $p(o_{k})$ in such a way that $p(c_{i,j})\propto\sum_{k=i+1}^{j}p(o_{k})$. Therefore, it is reasonable to assume that $o_{k}$ and $c_{i,j}$ are dependent on each other, i.e., $p(o_{k}|c_{i,j})\neq 0$, if and only if $k\in(i,j]$; otherwise, $o_{k}$ and $c_{i,j}$ are mutually exclusive and $p(o_{k}|c_{i,j})=0$. In view of this, we introduce a significance factor $s_{k}$ for all $k\in[0,K)$ and define the conditional probabilities by

The intensity value $k$, which requires a greater contrast between $k-1$ and $k$, should have a greater value of $s_{k}$, and vice versa. However, we have no idea which intensity values are more important than others. In this study, we propose to determine $s_{k}$ through an iterative method. Let $t\in[1,\tau]$ be the index of the iteration and $\tau$ be the maximum number of iterations. When $t=1$, we initialize $s^{(1)}_{k}=\nicefrac{{1}}{{K}}$ for all $k\in[0,K)$ and compute $p^{(1)}(o_{k})$ using Eq. 2. For all $t>1$, we update $s^{(t)}_{k}$ with $s^{(t)}_{k}=p^{(t-1)}(o_{k})$ and recalculate $p^{(t)}(o_{k})$ using the updated significance factor. In this way, we can guarantee that $o_{k}$ with a larger probability $p(o_{k})$ tends to have a larger significance factor and thus tends to receive more contribution from the 2D histogram values $p(c_{i,j})$. Empirically, we found that two iterations are sufficient for ROPE to achieve satisfactory performance.

Fig. 2 compares RG-CACHE [7] and our approach. Using RG-CACHE, dark and bright intensity values fluctuated sharply, causing blurred contrast (Fig. 2b) and eerie artifacts (Fig. 2e). In comparison, ROPE achieved more high-quality and reliable enhancement.

Next, we describe how to construct the 2D histogram of the grayscale image $\mathbf{A}_{\mathrm{in}}$. In CVC [2], the histogram value $p(c_{i,j})$ is determined as the co-occurrence frequency of the intensity value $j$ in the local window centered on the pixel of intensity $i$, further weighted by $|i-j|$. RG-CACHE [7] directly constructs a 1D histogram by incorporating the gradient of image reflectance into the density estimation. In this study, we borrow the idea of RG-CACHE to mitigate the negative effect of dark lighting conditions but embed the image reflectance into a 2D histogram instead of a 1D histogram.

Let $\mathbf{I}$ and $\mathbf{R}$ be the illumination and the reflectance components of $\mathbf{A}_{\mathrm{in}}$, respectively. We first use the relative total variation (RTV) approach [19, 15] as an edge-preserving filter [20, 21, 22, 23, 24, 25] to estimate $\mathbf{I}$. We then consider a modified Retinex model as the formation of $\mathbf{A}_{\mathrm{in}}$: $\mathbf{A}_{\mathrm{in}}=\mathbf{I}\circ e^{\mathbf{R}}$ (where $e$ is the Euler number). Thus, the definition of the reflectance becomes

Eq. 4 calculates $\mathbf{R}$ in the logarithmic domain. It reveals much richer objectness information hidden in the dark areas because logarithmic scaling magnifies the difference between small quantities, as shown in Figs. 3a and 3f.

Let $\mathbf{R}=\{r(q)\}$, where $r(q)$ is the reflectance value of the pixel $q\in\mathbf{A}_{\mathrm{in}}$. We calculate the 2D histogram values by

where $\mathcal{N}(q)$ is a $7\times 7$ window centered on $q$ according to CVC, and $\delta_{\cdot,\cdot}$ is the Kronecker delta. In this study, it is assumed that $p(c_{i,j})=p(c_{j,i})$ and $p(c_{i,i})=0$ for all $i,j\in[0,K)$.

Recall that $p(c_{i,j})$ needs to be defined in such a way that it is positively correlated with the requirement of CE between $i$ and $j$ (Section 2.2). Eq. 5 satisfies this condition exactly; the 2D histogram values capture the local pixel value differences in reflectance and are sensitive to the presence of meaningful objects hidden in the dark. As shown in Fig. 3f, most large differences in reflectance are present in the foreground objects, e.g., the plants in the center and on the right and the ColorChecker. These objects obviously require greater brightness and contrast (high CE requirement) than the background. Conversely, the reflectance values of the background, where contrast is of less importance (low CE requirement), are rather smooth. Once the 2D histogram is constructed, it is substituted into Eq. 2 to iteratively calculate the 1D histogram. The input image is then enhanced by HE as described in Section 2.1.

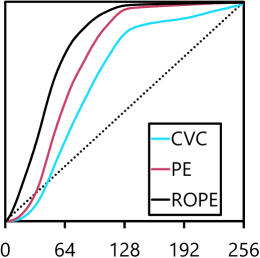
Fig. 3a shows an example of input image $\mathbf{A}_{\mathrm{in}}$. Figs. 3b–3e show the 2D/1D histograms and the intensity mapping function $T$ obtained using CVC, PE, and ROPE (PE indicates our approach proposed in Section 2.2, but with the 2D histogram of CVC used). Compared to CVC, ROPE has more emphasis on darker pixels, especially for important objects, thanks to the incorporation of reflectance. As shown in Fig. 3g, CVC made no significant changes to the input, whereas PE improved the visibility of image detail, thereby demonstrating the effectiveness of Eq. 2. By harnessing the reflectance effectively, ROPE further boosted brightness and contrast for the most satisfying image enhancement.

The enhanced images obtained with the compared approaches are shown in Fig. 4. KIND uses CNNs for image enhancement, but in a broader sense, it is also based on the Retinex model and so has similar performance to LIME, NPIE, and LECARM. Two common disadvantages of the four approaches are 1) a tendency to over-amplify brightness (first row) and 2) excessive saturation if color distortion was previously hidden in the dark areas of the input (second row). In comparison, ROPE does not suffer from these problems. The previous approaches essentially excel at enhancing low-light images, but there are exceptions, as shown in the third row. In this example, ROPE provided the most pleasant brightness, especially for the flowers in the center. All of these examples demonstrate the much greater adaptability and consistency of ROPE; our approach is capable of improving brightness sufficiently for dark images while avoiding excessive enhancement for normal-light images.

We objectively evaluated the image enhancement approaches using five metrics: discrete entropy (DE), EME, PD, and PCQI for contrast enhancement and LOE for naturalness. DE measures the amount of information in an image. EME [31] measures the average local contrast in an image. PD [32] measures the average intensity difference of all pixel pairs in an image. PCQI [33] measures the distortions of contrast strength and structure between input and output. LOE [13] measures the difference in lightness order between the input and enhanced images. The lightness order means the relative order of the intensity values of two pixels. For DE, EME, PD, and PCQI, higher statistics indicate better quality, while LOE is the opposite.

Table 1 shows the statistics averaged over 500 test images of BSDS500. Let us first focus on the contrast enhancement metrics. Since CVC, RG-CACHE, and ROPE are based on HE, they could maximize the range of intensity values and so achieved the highest scores. ROPE showed excellent contrast improvement capabilities, taking first place in EME and PD and second place in DE and PCQI. In comparison, none of the four approaches compared in Section 3.1 showed good performance.

In terms of image naturalness, all the approaches based on HE obtained the best LOE scores. These approaches have an inherent monotonicity constraint on the intensity mapping function $T$, so that the contrast enhancement does not change the order of intensity values in all pixels. In comparison, the approaches based on the Retinex model have poorer scores because they alter or eliminate the illumination component of the image, which results in a large variation in the lightness order.