Recovering a Molecule’s 3D Dynamics from Liquid-phase Electron Microscopy Movies

The primary objective of both cryo-EM and liquid-phase EM is to reconstruct a molecule’s 3D scattering potential (volume) from a collection of its 2D projection images. The formation model of an EM image can be represented as

$$\begin{split}&X(r_{x},r_{y})=g*\int_{\mathbb{R}}V(R^{T}\mathbf{r}+\mathbf{t})dr_{z}+n,\\ &\mathbf{r}=(r_{x},r_{y},r_{z})^{T},\ \mathbf{t}=(t_{x},t_{y},0)^{T}\end{split}$$

(1)

where $X$ denotes the 2D EM image, $V$ denotes the molecule’s 3D volume, $g$ is the microscope’s point spread function caused by electron diffraction, $n$ is the measurement noise, and $R\in SO(3)$ and $\mathbf{t}$ are the unknown orientation and translation of the molecule, respectively.

By taking Fourier transforms ($\mathcal{F}_{2D}$ or $\mathcal{F}_{3D}$) of both sides of Eq. 1, one can derive the image formation model in the frequency domain,

$$\hat{X}(k_{x},k_{y})=\hat{g}S(\mathbf{t})\hat{V}(R^{T}(k_{x},k_{y},0)^{T})+\hat{n}$$

(2)

where $\hat{X}=\mathcal{F}_{2D}\{X\}$ and $\hat{V}=\mathcal{F}_{3D}\{V\}$ represent the Fourier transformed image and volume, $\hat{g}=\mathcal{F}_{2D}\{g\}$ is the microscope’s Contrast Transfer Function (CTF), $S(\mathbf{t})$ is the phase shift operator defined by the spatial domain translation, $\hat{n}=\mathcal{F}_{2D}\{n\}$ is the frequency-dependent measurement noise, and $(k_{x},k_{y})$ is the frequency coordinate. Equation 2 defines a modified version of the Fourier slice theorem, which states that the Fourier transformed 2D projection of a volume equals the central slice from the Fourier transformed 3D volume in the perpendicular direction. This relationship simplifies the connection between the 2D projection measurements and the underlying 3D volume.

Cryo-EM collects images of frozen single particles with unknown poses, denoted as $\mathcal{D}_{\text{cryo}}=\{X_{i};i\in[1,N]\}$, to reconstruct a molecule’s 3D volume(s). Depending on whether different particles share the same structure, we conduct either homogeneous or heterogeneous reconstruction of the molecule’s 3D volume(s).

Homogeneous reconstruction assumes the volumes of all particles are identical, so different EM images are simply projections of a fixed structure from different angles. The volume, $\hat{V}$, and the pose of each particle, $\phi_{i}=\{R_{i},t_{i}\}$, can be jointly solved using a maximum a posteriori (MAP) formulation,

$$\begin{split}\hat{V}^{\star},\phi_{i}^{\star}=\underset{\hat{V},\phi_{i}}{\arg\max}\{\sum_{i=1}^{N}\log p(\hat{X}_{i}|\phi_{i},\hat{V})\\ +\sum_{i=1}^{N}\log p(\phi_{i})+\log p(\hat{V})\},\end{split}$$

(3)

where $p(\hat{X}_{i}|\phi_{i},\hat{V})$ is the probability of observing an image $\hat{X}_{i}$ with pose $\phi_{i}$ from volume $\hat{V}$, $p(\phi_{i})$ is the prior distribution of a particle’s pose, and $p(\hat{V})$ is the prior distribution of a particle’s volume. Since the measurement noise typically satisfies an independent, zero-mean Gaussian distribution, it is straightforward to derive the probabilistic model, $p(\hat{X}_{i}|\phi_{i},\hat{V})$, based on the image formation model in Eq. 2.

Heterogeneous reconstruction relaxes the assumption that different particles share the same structure, allowing for the recovery of multiple independent volumes, $\{\hat{V}_{j}^{\star};j\in[1,M]\}$, from a set of cryo-EM images. This involves optimizing the following expression,

$$\begin{split}\hat{V}_{j}^{\star},\phi_{i}^{\star},\pi_{i,j}^{\star}=\underset{\hat{V}_{j},\phi_{i},\pi_{i,j}}{\arg\max}\{\sum_{i=1}^{N}\log\sum_{j=1}^{M}\pi_{i,j}p(\hat{X}_{i}|\phi_{i},\hat{V}_{j})\\ +\sum_{i=1}^{N}\log p(\phi_{i})+\sum_{j=1}^{M}\log p(\hat{V}_{j})\},\end{split}$$

(4)

where $\pi_{i,j}$ is the probability of image $\hat{X}_{i}$ assigned to volume $\hat{V}_{j}$. In addition to recovering the volumes and poses, this optimization problem also needs to cluster particles into different volume categories. The number of volume categories $M$ is a user-defined hyper-parameter that measures structural heterogeneity in a cryo-EM dataset. The reconstruction problem becomes increasingly challenging as $M$ increases.

Liquid-phase EM captures movies of freely-moving particles, denoted as $\mathcal{D}_{\text{liquid}}=\{X_{i,t};i\in[1,N],t\in[1,T]\}$, to recover the dynamics of a molecule’s 3D volume. A liquid-phase EM dataset typically contains tens to hundreds of movies, where each movie consists of 10-100 frames and represents a sequence of projection images from an evolving particle. Compared to cryo-EM, the total number of images in a liquid-phase EM dataset is two to three orders of magnitude smaller. Moreover, because a particle’s volume varies over time, we need to compute a $\hat{V}_{i,t}$ for each frame of a liquid-phase EM movie $\hat{X}_{i,t}$. This gives rise to a highly ill-posed reconstruction inverse problem, which can be expressed as follows,

$$\begin{split}\hat{V}_{i,t}^{\star},\phi_{i,t}^{\star}=&\underset{\hat{V}_{i,t},\phi_{i,t}}{\arg\max}\{\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{X}_{i,t}|\phi_{i,t},\hat{V}_{i,t})\\ &+\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\phi_{i,t})+\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{V}_{i,t})\}.\end{split}$$

(5)

If we ignore the temporal dependency in a movie, this problem becomes equivalent to a heterogeneous cryo-EM reconstruction task with the same number of volume categories and images. Due to its limited data and massive unknown variables, this problem remains an open challenge in liquid-phase EM, and consequently, current research using liquid-phase EM has rarely explored the 3D structures of a molecule. In the following sections, we will present our proposed solution to this problem and demonstrate its effectiveness through a series of numerical experiments.

A common approach for homogeneous cryo-EM reconstruction is the expectation-maximization algorithm[31], which alternates between solving for the unknown 3D volume or the particles’ poses while fixing the other. This algorithm refines the 3D molecule structure iteratively until the image formation model predicts 2D images that match the EM measurements, hence it is also known as iterative refinement in structural biology. A modified version of iterative refinement algorithm, termed multi-class refinement, can be extended to heterogeneous cryo-EM reconstruction when the number of volume categories is small. Multi-class refinement algorithm loops between expert-guided clustering of cryo-EM images and homogeneous reconstruction of each independent group, finally providing a structure for each cluster of images. Many popular cryo-EM analysis tools, such as FREALIGN[18], CryoSPARC[28] and RELION[22], have been developed using this refinement framework. However, refinement-based approaches struggle to achieve robust reconstruction when the molecule’s structural heterogeneity is complex. Recent heterogeneous reconstruction methods such as CryoDRGN[44, 45, 46] have proposed modeling heterogeneity using a deep generative model with continuous latent states instead of discrete categories. This innovative formulation enables an infinite number of volume categories to be captured, allowing for the recovery of continuous conformational changes from the cryo-EM data. CryoFire[12] and HetEM[3] further enhanced training speed and robustness by upgrading CryoDRGN’s search-based pose estimation to an amortized inference neural network.

Dynamic computed tomography (CT) is a challenging but essential problem in various fields, including security, industry, and healthcare. In dynamic CT, the object’s temporal variation leads to the acquisition of only sparse angular views during CT scanning, making it difficult to reconstruct the object’s structure at each moment. Classical dynamic CT techniques utilize parametric models to suppress periodic motions (e.g., cardiac or respiratory motions in clinical CT) for high-quality volume reconstruction[30, 32, 33]. Advanced dynamic CT methods can handle more complicated non-periodic motions by jointly solving a static scene and a motion field for the recovery of the object’s dynamics[21, 42, 43]. Recent research has proposed using novel deep learning techniques from 3D computer vision to improve the modeling of time-dependent scene and motion fields in dynamic CT[29]. However, most existing dynamic CT techniques require slow object motion and low-noise measurements to generate high-quality results. These limitations make them inapplicable for solving liquid-phase EM reconstruction, which defines a unique dynamic CT problem aiming to reconstruct a 3D volume from every single view despite having very noisy measurements.

Implicit Neural Representation (INR) has proven to be a powerful technique in computer vision and graphics applications. This approach is based on the concept of “coordinate-based” neural networks[19, 20, 24, 34] that learn functions mapping 3D coordinates to physical properties of the scene. INR’s simple network structure enables it to be less prone to overfitting and utilize its inherent function smoothness to regularize unobserved views of scenes. It has achieved remarkable success in graphical rendering of static and dynamic scenes from limited views[5, 13, 25, 26, 27, 36], as well as in scientific imaging applications, including clinical X-ray CT[4], surgical endoscopy[39], optical microscopy[1, 14], and black hole emission tomography[10]. The latest cryo-EM reconstruction algorithms, such as CryoDRGN[44, 45, 46] and Cryo-AI[11], also use INR to model the Fourier domain of a molecule’s 3D structure.

Dynamical variational auto-encoder (DVAE)[6] is a versatile class of deep generative models that has a wide range of applications in spatial-temporal analysis. This type of model inherits the fundamental characteristics of variational auto-encoder (VAE)[7], which transforms high-dimensional data into a low-dimensional latent space. Additionally, it incorporates deep temporal inference models, such as recurrent neural networks and state space models, to capture the temporal dependence of the learned latent states. DVAE has found numerous applications in vision tasks, including human motion estimation[2] and video generation[15, 41], and has also demonstrated remarkable performance in scientific fields such as dynamical system identification in physics[16, 35] and health monitoring in biomedicine[9]. By extracting low-dimensional dynamics from spatial-temporal data in an unsupervised manner, DVAE offers a natural way to analyze the temporal variation of complex systems. In the following context, we will utilize a specific type of DVAE called structured inference network[8, 9] to model the molecule’s temporal variation in a movie.

Liquid-phase EM reconstruction can be formulated as an MAP estimation problem in Eq. 5, which aims to recover a 3D volume, $\hat{V}_{i,t}$, and its pose, $\phi_{i,t}$, for each frame of liquid-phase EM movies, $\mathcal{D}_{\text{liquid}}=\{X_{i,t};i\in[1,N],t\in[1,T]\}$. This reconstruction problem can be denoted as follows,

$$\begin{split}\underset{\hat{V}_{i,t},\phi_{i,t}}{\max}&\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{X}_{i,t}|\hat{V}_{i,t},\phi_{i,t})\\ s.t.\ &\hat{V}_{i,t}\sim p_{\hat{V}}(\cdot),\end{split}$$

(6)

where $p_{\hat{V}}(\cdot)$ is the prior distribution of a molecule’s 3D volume. Given that a molecule’s conformational changes can often be represented using low-dimensional features, it is possible to parameterize the 3D volume distribution using a deep generative model, $G_{\theta}(\cdot)$, with continuous latent states $z_{i,t}$,

$$\begin{split}\underset{\theta,z_{i,t},\phi_{i,t}}{\max}&\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{X}_{i,t}|\hat{V}_{i,t},\phi_{i,t})\\ s.t.\ &\hat{V}_{i,t}=G_{\theta}(z_{i,t}),\\ &z_{i,t}\sim q(\cdot),\end{split}$$

(7)

where $q(\cdot)$ is the prior distribution of the latent states.

Assuming that the latent states and the poses can be computed from the EM images using an amortized inference manner, the reconstruction problem can be rewritten as

$$\begin{split}\underset{\theta,\psi}{\max}&\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{X}_{i,t}|\hat{V}_{i,t},\phi_{i,t})\\ s.t.\ &\hat{V}_{i,t}=G_{\theta}(z_{i,t}),\\ &z_{i,t},\phi_{i,t}\sim q_{\psi}(\cdot|\hat{X}_{i,t})\\ &z_{i,t}\sim\mathcal{N}(0,1).\end{split}$$

(8)

This formulation is in agreement with the state-of-the-art deep learning cryo-EM reconstruction method, CryoDRGN, which employs a standard VAE framework to solve for the heterogeneous particle volumes. The objective function optimized by CryoDRGN is the evidence lower bound (ELBO) of the EM images,

$$\begin{split}\mathcal{L}(\hat{X}_{i,t};,\theta,\psi)&=\sum_{i=1}^{N}\sum_{t=1}^{T}\{-D_{KL}[q_{\psi}(z_{i,t}|\hat{X}_{i,t})\|\mathcal{N}(0,1)]\\ &+\mathbb{E}_{q_{\psi}(z_{i,t},\phi_{i,t}|\hat{X}_{i,t})}[\log p(\hat{X}_{i,t}|G_{\theta}(z_{i,t},\phi_{i,t})]\}.\end{split}$$

(9)

In CryoDRGN, the generator, $G_{\theta}(\cdot)$, is modeled as an INR, which effectively regularizes the heterogeneous volumes in a given dataset to be fundamentally similar, despite low-dimensional conformational changes. Consequently, even though only a single view is observed for each volume, reasonable heterogeneous reconstruction can still be achieved. CryoDRGN provides a baseline approach for liquid-phase EM reconstruction.

However, CryoDRGN neglects the crucial temporal information in liquid-phase EM movies. In contrast to cryo-EM reconstruction, liquid-phase EM data comprise movies of multiple particles. The temporal dependency among these movie frames could provide additional regularization to enhance the reconstruction quality. Given that the number of images in a liquid-phase EM dataset is considerably smaller (two to three orders of magnitude) than a cryo-EM dataset, it becomes extremely important to leverage these temporal information in the reconstruction. Motivated by the structured inference network[8, 9], we reformulate the representation of the latent state distribution as a temporal inference model $E_{\psi_{1}}$. Meanwhile, given the molecule’s Brownian motion has a characteristic time notably shorter than its deformation, the pose estimator is still represented as a time-independent inference model $F_{\psi_{2}}$. Now the liquid-phase EM reconstruction problem can be written as,

$$\begin{split}\underset{\theta,\psi}{\max}&\sum_{i=1}^{N}\sum_{t=1}^{T}\log p(\hat{X}_{i,t}|\hat{V}_{i,t},\phi_{i,t})\\ s.t.\ &\hat{V}_{i,t}=G_{\theta}(z_{i,t}),\\ &z_{i,t}\sim E_{\psi_{1}}(\cdot|z_{i,t-1},\hat{X}_{i,1:T}),\\ &\phi_{i,t}\sim F_{\psi_{2}}(\cdot|\hat{X}_{i,t}),\\ &z_{i,t}\sim\mathcal{N}(0,1),\psi=\{\psi_{1},\psi_{2}\}\end{split}$$

(10)

where each latent state, $z_{i,t}$, depends on its past state, $z_{i,t-1}$, as well as all frames in a particle’s movie, $\hat{X}_{i,1:T}$, but each pose, $\phi_{i,t}$, only depends on a single frame. The objective function of our TEMPOR algorithm for liquid-phase EM reconstruction now becomes

$$\begin{split}&\mathcal{L}(\hat{X}_{i,t};,\theta,\psi)=\\ &\sum_{i=1}^{N}\sum_{t=2}^{T}\{-D_{KL}[E_{\psi}(z_{i,t}|z_{i,t-1},\hat{X}_{i,1:T})\|\mathcal{N}(0,1)]+\\ &\mathbb{E}_{E_{\psi_{1}}(z_{i,t}|z_{i,t-1},\hat{X}_{i,1:T})F_{\psi_{2}}(\phi_{i,t}|\hat{X}_{i,t})}[\log p(\hat{X}_{i,t}|G_{\theta}(z_{i,t},\phi_{i,t}))]\}.\end{split}$$

(11)

Based on the probabilistic model in Eq. 10, the neural network architecture for our TEMPOR algorithm is designed as depicted in Fig. 2.

The volume generator $G_{\theta}(\cdot)$, inspired by CryoDRGN, is modeled as an INR in Fourier domain, which is a multi-layer perceptron (MLP) that takes latent state, $z_{i,t}$, and frequency coordinates $\mathbf{k}=(k_{x},k_{y},k_{z})$ as its inputs and outputs the corresponding frequency components of a volume. Defining the volume generator in Fourier domain significantly improves training efficiency, as we only need to evaluate a 2D slice of coordinates for each movie frame, as suggested by the Fourier slice theorem. Similar to other INR frameworks, the coordinates first pass a positional encoding block before being sent to the generator,

$$\gamma(\mathbf{k})=[\sin(\mathbf{k}),\cos(\mathbf{k}),\cdots,\sin(2^{L-1}\mathbf{k}),\cos(2^{L-1}\mathbf{k})],$$

(12)

where $L$ is the maximum positional encoding degree.

The temporal inference encoder, $E_{\psi_{1}}(\cdot)$, is modeled as a compound architecture that comprises a feature extractor, a bidirectional recurrent neural network (RNN) layer and a combiner function. The bidirectional RNN enables message passing along movie frames, allowing the latent state at each moment to depend on both the past state and the entire sequence of a particle’s movie. For simplicity of computation, we assume that the latent state inferred by the encoder follows a mean field Gaussian distribution. The encoder’s output is split in half, with the first half defining the mean of our latent state and the second half defining the diagonal components of its covariance matrix,

$$E_{\psi_{1}}(\cdot)=\mathcal{N}(E_{\psi_{1}}^{1}(z_{i,t-1},\hat{X}_{i,1:T}),\text{diag}\{E_{\psi_{1}}^{2}(z_{i,t-1},\hat{X}_{i,1:T})\}).$$

(13)

The pose estimation encoder, $F_{\psi_{2}}(\cdot)$, estimates the pose of each frame independently using a similar mean field Gaussian approach,

$$F_{\psi_{2}}(\cdot)=\mathcal{N}(F_{\psi_{1}}^{1}(\hat{X}_{i,t}),\text{diag}\{F_{\psi_{1}}^{2}(\hat{X}_{i,t})\}).$$

(14)

As illustrated in Fig. 2, $E_{\psi_{1}}(\cdot)$ and $F_{\psi_{2}}(\cdot)$ share the same feature extractor.

CryoDRGN and HetEM are used as baseline approaches in the numerical experiments to evaluate our method’s performance. To ensure a fair comparison, our baseline implementation uses many identical building blocks as our TEMPOR algorithm, including an identical volume generator and an identical feature extractor in its latent encoder.

Due to the complex optimization problem defined by our method, we have observed that training our reconstruction network from scratch (ab initio) sometimes fails to converge to the optimal solution. To overcome this challenge, we adopt a pretrain-finetune strategy in which we first train a baseline network that shares multiple identical build blocks with our TEMPOR algorithm. We then initialize our TEMPOR network with baseline’s weights and train it for an extended duration. Empirical evidence has shown that this training strategy leads to higher quality reconstructions. See supplementary material for more implementation details.

Two simulated datasets of different levels of complexity were created for this study. The first dataset, 7bcq, is a simulated protein that undergoes motion primarily in one dimension. A short peptide chain of 7bcq rotates around a chemical bond at a constant speed (9^∘ per frame) within a range of 90 degrees (Fig. 3b). Our 7bcq dataset includes movies of 100 particles, each with 10 continuous frames.

Cas9 is a more complex protein that undergoes non-rigid deformational motion. To generate multiple conformational changes of Cas9, we run molecular dynamics simulations that are initialized with two Cas9 structures from the protein data bank - the free (PDB ID 4CMQ) and RNA-bound (PDB ID 4ZT0) forms. We classify the resulting Cas9 volumes into 19 continuous states and created 500 synthetic movies, with each movie sequentially sampling a conformation from each of the 19 volume categories. In summary, the 7bcq dataset models simple one-dimensional rigid-body motions and contains 100 movies (10 frames each), while the Cas9 dataset models complex flexible structural deformations and contains 500 movies (19 frames each). See supplementary material for more details about the datasets.

Our reconstruction methods are evaluated using two major metrics: the manifold of learned latent space and the Fourier shell correlation (FSC) curves of reconstructed volumes. The latent space manifold serves as a qualitative metric for evaluating the reconstruction performance, as a good reconstruction algorithm typically results in a latent space that well clusters different categories of volumes. On the other hand, the FSC coefficient is a widely accepted quantitative metric in electron microscopy reconstruction[37]. It measures the normalized cross-correlation between the reconstructed and true volumes, $\hat{V}_{1}$ and $\hat{V}_{2}$, as a function of radial shells in Fourier space (frequency radius $k$),

$$FSC(k)=\frac{\sum_{|\mathbf{k_{i}}|=k}\hat{V}_{1}(\mathbf{k_{i}})\cdot\hat{V}_{2}(\mathbf{k_{i}})^{\star}}{\sqrt{\sum_{|\mathbf{k_{i}}|=k}|\hat{V}_{1}(\mathbf{k_{i}})|^{2}\sum_{|\mathbf{k_{i}}|=k}|\hat{V}_{2}(\mathbf{k_{i}})|^{2}}}.$$

(15)

Using FSC, we can also calculate the reconstruction resolution, which is the reciprocal of the maximum frequency radius, $k_{max}$, that yields a cross-correlation coefficient greater than 0.5. FSC and the resulting resolution provide a reliable measure of different algorithms’ performance. For reference, we also report two standard computational imaging metrics of our reconstructed volumes: the Structural Similarity Index Measure (SSIM) and the Peak Signal-to-Noise Ratio (PSNR).

In this section, we evaluate the performance of our method on recovering a linear rigid motion using the 7bcq dataset. As 7bcq’s peptide chain rotation is a one-dimensional motion (Fig. 3b), we set the latent state dimension of both CryoDRGN and our method to one.

Figure 3a displays the reconstructed volumes obtained by our method and CryoDRGN, along with the ground truth 3D structures. This experiment was performed on a dataset with an SNR of 0.1, and the motion shown in Fig. 3a was recovered from a randomly selected 7bcq movie with frames 1, 3, 5, 7, 9, 10 displayed. These results clearly demonstrate that our method produces higher-resolution 3D volumes with fewer errors compared to CryoDRGN, which sometimes exhibits unexpected spikes due to measurement noise. Additionally, we perform statistical analysis by computing the resolution improvement factor ($f_{i,t}$) for each movie frame

$$f_{i,t}=\frac{res_{i,t}^{cryoDRGN}-res_{i,t}^{ours}}{res_{i,t}^{cryoDRGN}},$$

(16)

where $i$ and $t$ are movie and frame indices, and $res_{i,t}^{cryoDRGN}$ and $res_{i,t}^{ours}$ are the reconstruction resolutions obtained by CryoDRGN and our method, respectively. Our method reconstructs a higher resolution volume in 95.1% of movie frames, and on average improves the resolution by 1.5% compared to CryoDRGN (Fig. 4a). The mean FSC curve of all movies (Fig. 4c) indicates that, on average, our method increases the resolution by 0.18 Å. We also evaluate PSNR and SSIM values for volumes recovered by CryoDRGN and TEMPOR after passing a low-pass filter, where TEMPOR also performs better in nearly all the cases.

The peptide-chain angles in the 7bcq movie are uniformly distributed between 0-90 degrees. In Fig. 5, we show the relationship between the true rotational angles and the latent state values estimated by CryoDRGN and our method, respectively. Our method demonstrates a more compact latent space manifold than CryoDRGN, suggesting better discrimination of images projected from volumes with small conformational differences. We further visualize the latent state distribution of movie frames from 10 different intervals of rotational angles ($0-9,9-18,\cdots,81-90$). Our method again reveals a stronger capability to distinguish small angle changes, suggesting its potential to improve the temporal resolution in liquid-phase EM reconstruction.

In this section, we evaluate the performance of our method in recovering a more complex deformational motion using the Cas9 dataset. Biologically, this motion represents the protein’s transformation from a free state to an RNA-bound state, which is more commonly observed in real experiments. To capture the complex conformational changes, we set the latent state dimensions to eight for both our method and CryoDRGN in all Cas9 experiments. Given that known poses simplify volume reconstruction, we use only 100 videos for training in this section.

Figure. 6a compares the 3D reconstruction of a randomly sampled Cas9 movie using CryoDRGN and our method, along with the ground-truth volumes. This experiment was performed on a dataset with an SNR of 0.3. Our method recovers finer structural details, such as the gap between protein domains and the central backbone in the 17th frame shown in Fig. 6b. Statistical metrics in Fig. 4b demonstrate the great advantages of our method in this example with complex deformational motions. It achieves better performance in 99.8% of movie frames and on average improves the reconstruction resolution by 13.5% compared to CryoDRGN. In Fig. 4d the mean FSC curve suggests that the resolution of our method outperforms CryoDRGN’s by around 2 Å. As shown in Fig. 6a, we also find that both PSNR and SSIM have greatly improved by TEMPOR.

In Fig. 7, we visualize the 2-dimensional latent space manifolds obtained through PCA, with different colors representing the 19 conformational states in the Cas9 dataset. Our method shows a more compact manifold than CryoDRGN. As illustrated by both the 2D latent distribution and their 1D projections on each principal component, our method also displays better clustering ability.

In this section, we demonstrate the performance of our method when jointly estimating pose (rotation and translation) parameters and recovering 3D volumes. This experiment is conducted on the Cas9 dataset with SNR=1.0, 500 movies, and we compare the performance of TEMPOR with HetEM, a novel algorithm that considers the pose estimation but disregards temporal information.

As illustrated in Fig. 8a and Fig. 10, our method surpasses HetEM in both reconstruction quality and the compactness of latent state manifolds. Its reconstruction resolution outperforms that of HetEM by around $0.8\AA$ as shown in Fig. 8b. TEMPOR also generated volumes with higher PSNR and SSIM values for most projections.

The previous numerical experiments on 7bcq and Cas9 have demonstrated the superior performance of our method in handling different motion dynamics. In this section, we investigate the robustness of our method under varying noise levels and report several ablation studies on neural network architectures and training strategies, all conducted on the Cas9 dataset.

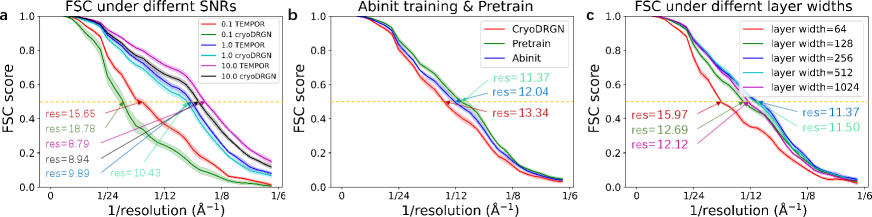
In Fig. 9a, we compare the FSC curves of CryoDRGN and our method under three SNR levels (0.1, 1, 10). While the two algorithms achieve comparable resolution at SNR=10, the gap between the two algorithms widens as SNR decreases, indicating the better robustness of our method in handling low-SNR liquid-phase EM data.

Figure 9b compares the FSC curves of our method with and without the pre-training strategy proposed in Sec. 4.2. Our method outperforms CryoDRGN even without pretraining, but a better training strategy further improves the reconstruction resolution by approximately 0.7 Å. This justifies the necessity of advanced training techniques.

Figure 9c compares the FSC curves obtained by varying neural network architectures. We experiment on INR decoders with different layer widths (number of neurons in each MLP layer). The results show that the reconstruction resolution first improves as the layer width increases, but then deteriorates when the layer width becomes too high. The layer width reflects the model capacity of an INR decoder. As the INR decoder models the prior distribution of the reconstructed volumes, this study suggests that the decoder architecture should not be overly simple or complex to achieve the best results. A careful design is necessary to balance the trade-off between capturing complex deformations and avoiding overfitting.