Recognizing and Embedding
Simple Optimal $2$-Planar Graphs^††thanks: The work of C. Raftopoulou is funded by the National Technical University of Athens research program $\mathrm{\Pi}$EBE 2020. H. Förster and M. Kaufmann are supported by DFG grant KA812-18/2.

In the field of graph drawing beyond planarity, researchers study graphs that admit drawings with crossings only in restrictive local configurations [6, 14, 15, 18, 24]. Mostly studied are 1-planar graphs, which admit drawings where each edge is crossed at most once. Classic results on these graphs concern mostly the density [7, 28], recently, other problems such as generation [29], characterization [20], recognition [2, 9, 10, 11, 13], coloring [8] and page number [3, 16] have been studied. The most natural extension of $1$-planar graphs, is the family of $k$-planar graphs, that is graphs that admit drawings where each edge is crossed at most $k$ times. While there are plenty of results on $1$-planarity, $k$-planarity turns out to be more challenging. The first outstanding results on the density of simple $k$-planar graphs came with the work of Pach and Tóth [27] for $k\leq 4$. In particular, they proved that simple $2$-planar graphs have at most $5n-10$ edges. Later on, improved upper bounds of $5.5n-11$ [26] and $6n-12$ [1] have been shown for simple $3$- and $4$-planar graphs, respectively. The bounds for $2$- and $3$-planar graphs are tight even for non-simple graph without homotopic parallel edges and self-loops [5].

While testing for planarity can be done in linear time, and several classes of beyond-planar graphs have a linear number of edges, the corresponding recognition problems are NP-hard, which impedes the practical application of related results. In particular, it was recently proven that the recognition of $k$-planar graphs is NP-hard for every value of $k\geq 1$  [30]. Still, optimal 1-planar graphs, which form a prominent subclass of $1$-planar graphs, can be recognized in linear time [11], while recognition of maximal $1$-planar graphs and $4$-maps takes cubic time [17, 12]. Previously, efficient recognition algorithms have been developed for more restricted subclasses of $1$-planar graphs, see e.g. [2, 10, 13, 19].

For $k\geq 2$, there are significantly fewer results. A notable result is the linear time recognition algorithm for full outer-2-planar graphs [21], while for $k\geq 3$ the literature still lacks similar results.

The degree of a vertex $v\in V$ is denoted by $d(v)$ and its set of neighbors by $N(v)$. For $u,v\in V$ we write $N(u,v)$ to denote the set of common neighbors of $u$ and $v$, that is $N(u,v)=N(u)\cap N(v)$. A drawing of a graph maps the vertices to points in the plane and the edges to simple open Jordan curves connecting the points corresponding to their endpoints. A drawing is $k$-planar if each curve representing an edge is crossed at most $k$ times by the other edges together. A graph $G$ is $k$-planar if it admits a $k$-planar drawing.

The topology of a planar drawing is described by a rotation scheme. For $k$-planarity, a $k$-planar rotation scheme specifies the counter-clockwise circular order of edges around each vertex and, additionaly, a sequence of at most $k$ crossings along each edge. Hence, a $k$-planar rotation scheme defines an equivalence class of $k$-planar drawings.

For a graph $G$, let $H$ a subgraph of $G$ and let $\mathcal{R}_{H}$ be a ($k$-planar) rotation scheme of $H$. We say that $\mathcal{R}_{H}$ is a partial ($k$-planar) rotation scheme of $G$. We further say that $\mathcal{R}_{H}$ can be extended to a ($k$-planar) rotation scheme $\mathcal{R}$ of $G$ if the restriction of $\mathcal{R}$ on $H$ is $\mathcal{R}_{H}$. Conversely, we say that $\mathcal{R}$ extends $\mathcal{R}_{H}$. Let $C$ be a cycle of graph $G$, whose edges define a simple closed curve in a drawing $\Gamma$ of $G$. We refer to the region to the left of this curve in a counter-clockwise walk along $C$ in $\Gamma$ as the interior of the region bounded by cycle $C$. Note that given drawing $\Gamma$, the interior of a region may be unbounded.

A $2$-planar graph that reaches the upper bound of $5n-10$ edges is called optimal $2$-planar. Note that the value of $5n-10$ edges can be reached only when $n\equiv 2\mod 3$. Each induced subgraph $H$ of a $2$-planar graph $G$ is also 2-planar and thus has at most $5|V(H)|-10$ edges. This implies that if $G$ is 2-planar then it is also 9-degenerate, i.e. there is a vertex ordering $v_{1},\ldots,v_{n}$ such that, for each $i=1,\ldots,n$, vertex $v_{i}$ of the induced subgraph $G_{i}=G[v_{1},\ldots,v_{i}]$ has degree at most 9 in $G_{i}$. We call such a vertex ordering a 9-degenerate sequence of $G$.

In this work, we consider only simple graphs which we assume from now on without explicitly stating it. The structure of simple optimal $2$-planar graphs is well established. Namely, an optimal $2$-planar rotation scheme $\mathcal{R}$ of a simple optimal $2$-planar graph specifies a crossing-free $3$-connected¹¹1The 3-connectivity derives from the fact that the graph is simple. spanning pentangulation $\mathcal{P}$ and a set of crossing edges [4, 5]. The edges around each vertex are cyclically ordered so that every crossing-free edge (belonging to $\mathcal{P}$) is followed by two crossing edges, which are succeeded by one crossing-free edge, and so on. Hence the degree of every vertex is a multiple of three. Moreover, the minimum degree of a simple optimal $2$-planar graph is $9$ since $\mathcal{P}$ is $3$-connected, i.e., every vertex is incident to at least $3$ crossing-free edges. Now, each pentangular face $f$ of $\mathcal{P}$ contains exactly five crossing edges of $\mathcal{R}$ which form a $5$-clique in $G$ with the boundary edges of $f$; we call such a $5$-clique a facial $5$-clique. Note that not all $5$-cliques of $G$ are facial in $\mathcal{R}$. This is a major difficulty for recognizing optimal $2$-planar graphs. We denote a facial $5$-clique of $\mathcal{R}$ with outer cycle $(c_{0},\ldots,c_{4})$ as $\langle c_{0},\ldots,c_{4}\rangle$ and say that the crossing edges $(c_{i},c_{j})$ with $(i-j)\mod 5\in\{2,3\}$ belong to $\langle c_{0},\ldots,c_{4}\rangle$. As $\mathcal{P}$ is $3$-connected, it suffices to detect all facial $5$-cliques to find the optimal $2$-planar rotation scheme of a given input graph, if one exists.

In the following, we state some preliminary observations and properties that we will use in the remainder of the paper. In particular, Properties 2.1–2.4 immediately arise from the combinatorial characterization of simple optimal 2-planar graphs in [5] also summarized above. So, let $G$ be an optimal $2$-planar graph with an optimal $2$-planar rotation scheme $\mathcal{R}$.

Combining the above properties we can further prove the following:

Consider an optimal $2$-planar rotation scheme $\mathcal{R}$ of $G$. If edge $(u,v)$ is crossing-free in $\mathcal{R}$, then by Property 2.4 $u$ and $v$ belong to two facial $5$-cliques. Hence, $|N(u,v)|\geq 6$ holds. Although this condition is not sufficient to conclude that an edge is crossing-free, we can use it to identify some crossing edges:

Our recognition algorithm relies on the identification of crossing edges based on Corollary 2.3. We say that an edge $(u,v)$ is clearly crossing if and only if $|N(u,v)|<6$. Otherwise $(u,v)$ is potentially planar. Note that in an optimal $2$-planar rotation scheme, a potentially planar edge is not necessarily crossing-free. However, every crossing-free edge of any optimal $2$-planar rotation scheme is potentially planar. We define as $G_{p}$ the subgraph of $G$ formed by all potentially planar edges. Graph $G_{p}$ is $3$-connected and spans $G$ as the corresponding crossing-free pentangulation of each optimal $2$-planar rotation scheme is a subgraph of $G_{p}$.

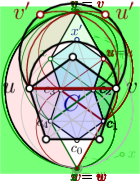
In this section, we study the 3-connected spanning subgraph $G_{p}$ formed by the potentially planar edges of $G$. We want to compute a rotation scheme of $G_{p}$ which is extendable to an optimal $2$-planar rotation scheme of $G$, if it exists. If in each optimal $2$-planar rotation scheme of $G$ subgraph $G_{p}$ is plane, then the rotation scheme of $G_{p}$ is unique and easy to compute. Though we cannot assure this property, we prove that in any optimal $2$-planar rotation scheme of $G$, crossings between edges of $G_{p}$ occur in restricted configurations: A CROSS-BAT instance is an induced subgraph $H$ of $G$ isomorphic to the graph $G_{CB}$ shown in Fig. 2(a), so that (i) for edge $(u_{H},u^{\prime}_{H})$ of $H$ isomorphic to $(u,u^{\prime})$ of $G_{CB}$, it holds that $V(H)=N(u_{H})\cup N(u^{\prime}_{H})$, and (ii) the isomorphism between $H$ and $G_{CB}$ preserves the classification of edges to clearly crossing or potentially planar.

In particular, CROSS-BAT has ten vertices, named as in Fig. 2(a). Vertices $u$ and $u^{\prime}$ have degree $9$ in $G$ and they have $8$ common neighbors (the remaining vertices of CROSS-BAT). The edges of CROSS-BAT form four $5$-cliques that pairwise share two vertices, and are shown as facial $5$-cliques in Fig. 2(a). We call edge $(u,u^{\prime})$ the base edge of CROSS-BAT. No other edges with both endpoints in CROSS-BAT exist, except possibly for edges $(v,v^{\prime})$ and $(w,w^{\prime})$. Fig. 2(a) shows the classification of edges of CROSS-BAT as potentially planar and clearly crossing.

Let $\mathcal{R}$ be an optimal $2$-planar rotation scheme of $G$, such that two potentially planar edges cross each other. These two edges must belong to the same facial $5$-clique and, in particular, also to an instance of CROSS-BAT.

Next, we show that CROSS-BAT has only two rotation schemes:

As it is evident in Figs. 2(b) and 2(c), if an optimal $2$-planar graph $G$ contains an instance of CROSS-BAT as subgraph, then it admits two different optimal $2$-planar rotation schemes $\mathcal{R}$ and $\mathcal{R}^{\prime}$, that only differ in the choice of the rotation scheme of CROSS-BAT. Hence for any instance of CROSS-BAT, we may arbitrarily choose one of its two rotation schemes. Next, we formalize this observation:

Both rotation schemes of a CROSS-BAT instance contain two crossings between potentially planar edges:

Using Lemma 3.2 we can fix a rotation scheme for each instance $H$ of CROSS-BAT identified in $G$ by reclassifying two crossing potentially planar edges of $H$ to clearly crossing edges. After performing this reclassification for all instances, if $G$ is optimal $2$-planar, then the subgraph $G_{p}$ induced by the potentially planar edges is planar. Furthermore, in this case, Lemma 3.3 guarantees that the unique planar embedding of $G_{p}$ is part of an optimal $2$-planar rotation scheme of $G$.

Assume that we have fixed the rotation scheme for every identified instance of CROSS-BAT. Let $G_{p}$ be the spanning subgraph of $G$ formed by all potentially planar edges after the reclassification process. As discussed in Section 3, $G_{p}$ is planar and $3$-connected, i.e. it has a unique planar rotation scheme $\mathcal{R}_{p}$. Furthermore, by Lemma 3.3, if $G$ is optimal $2$-planar, it admits an optimal $2$-planar rotation scheme that extends $\mathcal{R}_{p}$ which we call $\mathcal{R}_{p}$-compliant. For any $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme $\mathcal{R}$, $G_{p}$ contains the corresponding spanning pentangulation $\mathcal{P}$ as a subgraph. Hence each face of $\mathcal{R}_{p}$ has length $3$, $4$ or $5$ and is part of a facial $5$-clique. Hence, we can arbitrarily triangulate them and assume from now on that $G_{p}$ is triangulated. Triangulating a face of $\mathcal{R}_{p}$ corresponds to reclassifying some chords from clearly crossing to potentially planar.

Let $(f_{1},f,f_{2})$ be a path in the dual $G_{p}^{*}$ of $G_{p}$ so that $f_{1}=(u,w_{1},v_{1})$, $f=(u,w_{2},w_{1})$ and $f_{2}=(u,v_{2},w_{2})$, as shown in Fig. 3. If the subgraph induced by the vertices $\{u,v_{2},w_{2},w_{1},v_{1}\}$ is a $5$-clique in $G$, we call $T=\langle f_{1},f,f_{2}\rangle$ a triplet. $T$ contains vertices $u,v_{2},w_{2},w_{1},v_{1}$, faces $f_{1},f,f_{2}$ and the three clearly crossing edges $e_{1}=(v_{1},w_{2})$, $e_{2}=(v_{2},w_{1})$ and $e=(v_{1},v_{2})$, as shown in Fig. 3. We say that $e_{1}$, $e_{2}$ and $e$ belong to triplet $T$.

In any $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme $\mathcal{R}$ (if it exists), faces and clearly crossing edges of $\mathcal{R}_{p}$ are partitioned into triplets, such that every face and clearly crossing edge belongs to exactly one of these triplets. Furthermore, the triplets are in 1-1 correspondence with the facial $5$-cliques of $\mathcal{R}$. We say that $e$, $e_{1}$ and $e_{2}$ are assigned to the triplet $T=\langle f_{1},f,f_{2}\rangle$ w.r.t. $\mathcal{R}$ if $T$ induces a facial $5$-clique in $\mathcal{R}$. Similarly, we say that faces $f_{1}$, $f$ and $f_{2}$ of $T$ are assigned to $T$. If such an assignment is not possible, then $G$ is not optimal $2$-planar.

Let $\mathcal{T}$ be a set of triplets such that any two triplets in $\mathcal{T}$ are face-disjoint and contain different clearly crossing edges. Consider the partial $2$-planar rotation scheme $\mathcal{R}_{\mathcal{T}}$ of $G$ that (i) extends $\mathcal{R}_{p}$, (ii) the clearly crossing edges of each $T\in\mathcal{T}$ are assigned to $T$, and (iii) there is no other assignment of clearly crossing edges. We say that $\mathcal{T}$ is bad if and only if $\mathcal{R}_{\mathcal{T}}$ cannot be extended to a $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme $\mathcal{R}$ of $G$. Our goal is to find an assignment of all clearly crossing edges of $G$ to a set of triplets $\mathcal{T}$ such that $\mathcal{T}$ is not bad if $G$ is optimal 2-planar. We actually prove a stronger result, namely that the set $\mathcal{T}$ is unique. We will use two observations that follow from the simplicity of $G$:

If any of $e_{1}$, $e_{2}$ or $e$ belongs only to one triplet $T$, then $T$ is a facial $5$-clique in any $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme $\mathcal{R}$ and $e_{1}$, $e_{2}$ and $e$ can be assigned to $T$. So, we assume that each of $e_{1}$, $e_{2}$ and $e$ belong to at least one triplet different from $T$. Let $T_{1}$ and $T_{2}$ be two triplets that contain edges $e_{1}$ and $e_{2}$ respectively and are different from $T$. Note that $T_{1}=T_{2}$ might hold. Let $\mathcal{T}=\{T\}$. If for each such pair of triplets $T_{1}$ and $T_{2}$ we can conclude that the set $\mathcal{T}^{\prime}=\{T_{1},T_{2}\}$ is bad, then in any $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme $\mathcal{R}$ of $G$ (if it exists) edges $e_{1}$, $e_{2}$ and $e$ must be assigned to $T$. In the following, we compare $\mathcal{T}$ against all possible sets $\mathcal{T}^{\prime}$ and prove that at least one of $\mathcal{T}$ and $\mathcal{T}^{\prime}$ is bad. This allows to decide, for each triplet $T$, if $T$ forms a facial $5$-clique in every $\mathcal{R}_{p}$-compliant optimal $2$-planar rotation scheme of $G$ or in none. Note that when we write $\mathcal{T}=\{T\}$ and $\mathcal{T}^{\prime}=\{T_{1},T_{2}\}$, we assume that $T=\langle f_{1},f,f_{2}\rangle$ as shown in Fig. 3 and triplets $T_{1}$ and $T_{2}$ contain edges $e_{1}$ and $e_{2}$, respectively.

We first restrict how triplets $T_{1}$ and $T_{2}$ relate to triplet $T$. Observation 4.2 applied to $T_{1}$ implies that if $T_{1}$ shares either $f$ or $f_{1}$ with $T$, then, in the presence of edge $e_{1}$, $T_{1}$ shares both $f$ and $f_{1}$ with $T$. A symmetric argument applies for $T_{2}$. It follows that one of the following cases holds for $\{i,j\}=\{1,2\}$:

1.   C.1

   $T_{i}$ is face-disjoint with $T$, or

2.   C.2

   $T_{i}$ shares only face $f_{j}$ with $T$, or,

3.   C.3

   $T_{i}$ shares only faces $f$ and $f_{i}$ with $T$.

In the next two lemmas, we show that every $\mathcal{T}^{\prime}=\{T_{1},T_{2}\}$ is bad if Case C.1 applies either for none or for both of $T_{1}$ and $T_{2}$.

By Lemmas 4.1 and 4.2, Case C.1 applies for exactly one of the two triplets $T_{1}$ and $T_{2}$ and $T_{1}\neq T_{2}$. Then, the other triplet complies with Case C.2 or with Case C.3. For each possible combination we first prove structural properties arising from the assumption that $\mathcal{T^{\prime}}$ is not bad, and then show that these new restrictions make $\mathcal{T}$ bad. In the next two lemmas, we consider the setting, where one of $T_{1}$ and $T_{2}$ complies with Case C.1 while the other one complies with C.2.

By Lemmas 4.3 and 4.4 it remains to consider the case where one of $T_{1}$ and $T_{2}$ complies with Case C.1 while the other complies with Case C.3. So, we assume w.l.o.g. that $T_{1}$ is face-disjoint with $T$, while $T_{2}$ shares faces $f$ and $f_{2}$ with $T$. Recall that clearly crossing edge $e$ belongs to $T$. If $\mathcal{T}^{\prime}=\{T_{1},T_{2}\}$ is not bad $e$ belongs to a triplet $T_{e}\neq T$ such that $\mathcal{T}^{\prime}\cup\{T_{e}\}$ is not bad. Note that $T_{e}\neq T_{2}$ as otherwise vertex $v_{1}$ belongs to $T_{2}$ and $T_{2}=T$. Hence, either $T_{e}\neq T_{1}$ or $T_{e}=T_{1}$.

The following four lemmas investigate the subcase $T_{e}\neq T_{1}$. Note that $T_{1}$ and $T_{e}$ are face-disjoint as otherwise $\mathcal{T}^{\prime}=\{T_{1},T_{2},T_{e}\}$ is bad. The first two lemmas examine the scenario where $T_{1}$ contains vertex $w_{1}$ or $T_{e}$ contains vertex $u$ of $T$.

The next two lemmas consider the scenario, where $T_{1}$ does not contain vertex $w_{1}$ and $T_{e}$ does not contain vertex $u$ of triplet $T$.

For the second subcase, where $T_{1}=T_{e}$, Property 2.3 assures that $T_{1}$ and $T_{2}$ share only vertices $v_{2}$ and $w_{2}$, as otherwise $\mathcal{T}^{\prime}=\{T_{1}=T_{e},T_{2}\}$ would be bad. As indicated by the next lemma, no further restrictions (imposed by the assumption that $\mathcal{T}^{\prime}$ is not bad) are needed to prove that $\mathcal{T}=\{T\}$ is bad.

In the following two lemmas, we summarize our findings from this section.

Now that we have all required ingredients, we are ready to state our main theorem for the recognition of optimal $2$-planar graphs.

The remainder of this section contains the proof of Theorem 5.1 which is split into two parts. In Section 5.1 we describe our algorithm and prove its correctness, while an efficient implementation is discussed in Section 5.2.

We showed that simple optimal $2$-planar graphs can be recognized and embedded in linear time. It remains open to extend our result also for simple $2$-planar graphs with the maximum number of edges when $n\not\equiv 2\mod 3$, as well as to non-simple optimal $2$-planar graphs. Another reasonable attempt would be recognizing $5$-maps, similarly to [12]. Finally, a natural question would be if a recognition algorithm for non-simple optimal $2$-planar graphs could be adopted for optimal $3$-planar graphs that are non-simple, or if our approach could work for simple optimal $3$-planar graphs.