Realizations of Measurement Based Quantum Computing

Every one-qubit rotation $U_{R}\in$ SU(2) admits a decomposition in Euler angles as [2]

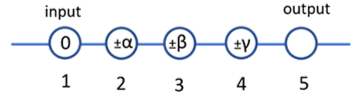
where $U_{X}$ and $U_{Z}$ describe rotations about the Pauli-X and Pauli-Z axis respectively. This can be implemented using a linear chain of 5 qubits on a cluster state with input state on qubit 1 (Fig. 3). Qubits 1$\rightarrow$4 are measured in the following bases [1]

where $s1\dots s4$ are the measurement outcomes. The implemented unitary operation is given by $U_{g}=U_{\Sigma}U_{R}$ where $U_{\Sigma}\equiv X^{s2+s4}Z^{s1+s3}$ describes the correction required based on measurement outcomes.

In order to have a universal set of gates, a universal 2-qubit gate is necessary. Fig. 4 shows a minimal CNOT implementation on a cluster state. The input qubit $t_{in}$ and its neighbor are measured in the Pauli-X basis, thereby implementing a CNOT (up to Pauli corrections) between control qubit $c$ and output qubit $t_{out}$ [1]. In practice, the control and target qubits are teleported to other qubits (Eq. (4)) in the cluster after computation.

A composite circuit such as in Fig. 2 can be created on the cluster which uses arbitrary one qubit rotations and CNOT gates to perform complex unitary operations on the input qubits.

The article [Ref. 4] describes generation of a 2-d cluster state with temporal mode encoding of squeezed photon states in two spatial modes, $A$ and $B$ in Fig. 5. Optical Parametric Oscillators (OPO) are used to generate the squeezed photon states which are interfered in an unbalanced interferometer (delay of $\tau$ in spatial mode B) to generate a 1-d cluster state, also known as a dual rail quantum wire [5]. Each point in this cluster corresponds to a single spatial mode $s\in\{A,B\}$ and temporal mode $k\in\mathbb{N}$. Using a delay line of $N\tau$ for mode $B$ of the 1-d cluster, it is coiled up into a 2-d cylindrical cluster state. High efficiency homodyne detectors are employed for both spatial modes which can make projective measurements in arbitrary quadrature basis $\hat{q}\cos{\theta}+\hat{p}\sin{\theta}$.

In Fig. 5, the gray nodes have $k$ odd and are measured in the quadrature basis $\theta_{c}=(-1)^{(k-1)/2}\pi/4$. This projects the cluster as wires for state teleportation along the length of the 2-d cylinder [4, 5]. These form the logic levels for computation of arbitrary multimode gaussian unitaries. If Gottesman-Kitaev-Preskill (GKP) encoded qubits are available, universal fault-tolerant quantum computation is possible with this framework [6, 4].

A single mode Gaussian unitary is implemented using teleportation on a logic level of the 2-d cluster [4] (Fig. 6).

The unitary that is implemented depends on the measurement bases for the two homodyne detectors (up to a measurement dependent displacement) as [4]

where $w$ is the wire number, $\theta_{\pm}=\theta_{A,k}\pm\theta_{B,k}$ and $\hat{R}\left(\theta\right)$, $\hat{S}(t)$ are the quadrature rotation and squeezing unitaries given by

A cascade of two such unitaries (Eq. (7)) can implement any single mode Gaussian unitary (up to a displacement) by choosing appropriate quadrature measurement bases [5].

To complete the universal set of Gaussian unitaries, an entangling two mode gate must be implemented. The authors demonstrate how entanglement between two logic levels and one pair of control modes can be used to implement a Gaussian unitary with two input modes [4] (Fig. 7).

As with the single mode case, the implemented two mode unitary is determined by the measurement bases of the homodyne detectors for each temporal mode. The two mode controlled phase gate $\hat{C}_{z}\equiv e^{ig(\hat{q}_{1}\otimes\hat{q}_{2})}$ along with the single mode rotation and sqeezing gates (Eq. (8)) form a universal multimode Gaussian gate set [4]. To implement the controlled phase gate (up to known rotations) between the two input modes, choice of measurement bases are determined to be [4, 5]

where $w$ is the wire number of the input mode $B,k$ and the implemented unitary transformation is $\left[\hat{R}(\pi/2)\otimes\hat{R}\left((-1)^{w}\pi/2\right)\right]\hat{C}_{z}$.

The above gate implementations assume infinite squeezing, which would require infinite energy and are therefore unphysical. In practice, one employs finitely squeezed photon states which introduce gate noise in the computation which accumulates as more gates are added. For one and two mode gates, the measured gate noise (after accounting for the gate noise factor of 6 dB) agrees well with the measured squeezing variance of -4.4 dB in the initial momentum quadratures. In order to make this approach scalable, some form of error correction would be required. GKP encoded qubits [6] (albeit not yet experimentally realized in optical spectrum) is one approach which could be used for fault-tolerant quantum computation with this scheme.

The interaction Hamiltonian of a pair of Transmon qubits with same energy gap between ground $\left|0\right\rangle$ and excited $\left|1\right\rangle$ states is of the form [8]

For a 2-d lattice of Transmons, time evolution of interaction is given by $\hat{\mathcal{U}}=e^{-i\hat{H}_{\mathrm{int}}t/\hbar}$. For $g_{\mathrm{eff}}t=\pi$ and initial states $\left|+\right\rangle$, this describes a cluster state of the form

which differs in sign of Pauli-Z operator from Eq. (1). To express this cluster state in terms of $\hat{C}_{z}$ gates, one considers initial state of a qubit to be $\left|+\right\rangle$ for control of even number of qubits and $\left|-\right\rangle$ for control of odd number of qubits (Fig. 8). For a 2-d lattice of Transmon qubits of size $h\times l$, each qubit can be represented by a vector $\vec{p}\equiv(j,k)$, where $(j,k)$ is its coordinate on the lattice [8].

Using this, the cluster (Eq. (11)) is given by

where $\mathcal{L}\equiv\{(j,k)\}$, $\mathcal{L}_{x}\equiv\{(j,l)\}$, $\mathcal{L}_{y}\equiv\{(h,k)\}$, $j=\{1,2\dots h-1\}$, $k=\{1,2\dots l-1\}$ and $\hat{m}\equiv(1,0)$, $\hat{n}\equiv(0,1)$.

Implementation of a CNOT gate using the Transmon cluster state (Eq. (11)) follows the recipe shown in Fig. 4. The initial state of the four qubits is

On applying the three $\hat{C}_{z}$ gates followed by measurement of qubits 1 and 2 in the Pauli-X basis, this state evolves into [8]

where $l,m$ are measurement outcomes of the respective qubits and $\mathcal{F}_{3,4}\equiv\left(\sigma^{3}_{x}\right)^{m}\left(\sigma^{3}_{z}\sigma^{4}_{z}\right)^{l}$ is the measurement based correction. The authors report a $\hat{C}_{z}$ gate fidelity of $99.5\%$ with an evolution time of $\approx 0.05\mu s$ per gate. Also, the readout and measurement process is estimated to have an error of $2\%$ and a processing time of $\approx 2\mu s$ per measurement. Estimated CNOT gate fidelity is therefore $(0.995^{3}-0.04)\times 100\approx 94.5\%$ with an evaluation time of $<5\mu s$, which is much smaller than Transmon coherence times [8].

The authors further discuss an alternative entangling gate $\hat{U}_{Bell}$ for generating cluster states. The action of this gate is given in block matrix form as

With a cluster state made using a $\hat{U}_{Bell}$ and a $\hat{C}_{z}$ gate, CNOT can be implemented with only 3 qubits (Fig. 9).

Qubits 1 and 2 are entangled with the $\hat{U}_{Bell}$ gate (Eq. (15)) and qubits 2 and 3 are entangled with a $\hat{C}_{z}$ gate to form a 3 qubit cluster state to implement CNOT. The initial state of the qubits is

On applying the $\hat{U}_{Bell}$ and $\hat{C}_{z}$ gates, this evolves into

Measurement of qubit 1 in Pauli-X basis followed by Hadamard operation on qubit 2 yields

where $m$ is the measurement outcome and $\mathcal{F}_{2,3}\equiv\left(\sigma^{3}_{z}\sigma^{2}_{x}\sigma^{2}_{z}\right)^{m}$ is the measurement based correction. The authors estimate the fidelity of this CNOT to be $\approx 96.5\%$ for an evaluation time of $2.5\mu s$ which is a significant improvement over the 4 qubit CNOT (Eq. (14)) with a $25\%$ reduction in number of qubits. Beyond CNOT, the cluster state created using only $\hat{U}_{Bell}$ gates has other useful characteristics of being - a) Maximally connected (measuring all but 2 qubits of the cluster results in a Bell state) and b) Maximally persistent (minimal product state decomposition has $2^{N}$ terms for an N qubit cluster state) [8].

The electron states $\left|D_{5/2},m=+3/2\right\rangle$ and $\left|S_{1/2},m=+1/2\right\rangle$ of ${}^{40}\mathrm{Ca}^{+}$ ions are used as qubit states $\left|1\right\rangle$ and $\left|0\right\rangle$ respectively ($\lambda=729$ nm) [9]. The $n$ ionic qubits in a linear Paul trap are initialized in state $\left|1\right\rangle^{\otimes n}$ via optical pumping. The axial center of mass and stretch vibrational modes are initialized in ground state using resolved sideband cooling. The cluster states are created from the ion string using three types of interactions - a) Molmer Sorenson interaction which is a long range qubit-qubit interaction of the form $M(\theta)\equiv\exp{\left(-i\theta\sum_{a<b}X_{a}X_{b}\right)}$, b) Single qubit phase flips $G_{k}(\theta)\equiv\exp{\left(-i\frac{\theta}{2}Z_{k}\right)}$ and c) Hiding pulses (in this case, hiding qubit state $\left|1\right\rangle$ in a different Zeeman level $\left|D_{5/2},m=+5/2\right\rangle$) of the form $F_{h}\equiv\exp{\left(-i\pi/4\sum_{k}X_{k}\right)}$.

Fig. 10 [9] illustrates an equivalent quantum circuit to generate a 4 qubit 1-d cluster state using these interactions as gates. The resultant cluster state, $\left|E_{LC_{4}}\right\rangle$, is equivalent to $\left|{LC_{4}}\right\rangle$ (described by Eq. (1)) up to single qubit unitary operations.

On performing quantum tomography of the cluster state density matrix, authors found its fidelity with respect to ideal state as being $0.841\pm 0.006$.

For implementation of single qubit gates, decomposition into Euler angles and measurements, described by Eq. (5) and (6), is employed with the 1-d cluster state $\left|E_{LC_{n}}\right\rangle$. Using quantum state tomography, the authors obtained an average fidelity of $0.92\pm 0.01$ for single qubit gates.

For illustration of two qubit gates, qubits 1 and 4 of $\left|{LC_{4}}\right\rangle$ act as inputs which are initially in state $\left|++\right\rangle$. Measuring them in bases $\mathcal{B}(\alpha)$ and $\mathcal{B}(\beta)$ (Eq. (6)) results in their rotations about the Pauli-Z axis, followed by Hadamard transformation. These are subjected to the teleported $\hat{C}_{z}$ gate and results are read out from qubits 2 and 3 (Fig. 11). The measurement based correction for this gate is $\mathcal{F}=(\sigma^{2}_{x}\sigma^{3}_{z})^{s1}(\sigma^{3}_{x}\sigma^{2}_{z})^{s4}$, where $s1$ and $s4$ are the measurement outcomes. Using this scheme, an entangled state $(\alpha=\pi/2,\beta=-\pi/2)$ and a separable state $(\alpha=0,\beta=0)$ were generated. Quantum state tomography yielded respective fidelities of $0.88\pm 0.02$ and $0.83\pm 0.01$ [9].

These implementations of a $\hat{C}_{z}$ gate and single qubit rotations form a universal gate set for quantum computation.

Using cluster states, it is possible to implement a phase flip code capable of correcting full phase flips of $(n-1)/2$ of qubits forming the $n$-qubit code-word ($n$ is odd) [9]. The cluster state employed for error correction (Fig. 12) has the form

The input qubit $A$ is measured in the eigenbasis of the state to be encoded. This is followed by a measurement of code-word qubits in the Pauli-X basis which both a) teleports the encoded state to the output qubit $B$ and b) reveals the error syndrome for correction of any phase flip errors before measurement. From Eq. (20), it can be seen that if $>(n-1)/2$ of code-word qubits are measured in $\left|+\right\rangle$ state, no recovery operation is required. If, however, $>(n-1)/2$ of code-word qubits are measured in $\left|-\right\rangle$ state, the output state needs to be corrected by applying a $\sigma^{B}_{x}$ operation on qubit $B$.