Realization of Topological Metal in Single-Crystalline Nickel Deficient NiV2Se4
Abstract
Temperature-dependent electronic and magnetic properties are reported for a topological metal single-crystalline nickel-deficient NiV2Se4. It is found to crystallize in the monoclinic Cr3S4 structure type with space group . From single-crystal x-ray diffraction, we find that there are vacancies on the Ni site, resulting in the composition Ni0.85V2Se4 in agreement with our electron-probe microanalysis. The electrical resistivity shows metallic behavior with a broad anomaly around 150–200 K that is also observed in the heat capacity data. This anomaly indicates a change of state of the material below 150 K. We believe that this anomaly could be due to spin fluctuations or charge-density-wave (CDW) fluctuations, where the lack of long-range order is caused by vacancies at the Ni site of Ni0.85V2Se4. Although we fail to observe any structural distortion in this crystal down to 1.5 K, its electronic and thermal properties are anomalous. The observation of non-linear temperature dependence of resistivity as well as an enhanced value of the Sommerfeld coefficient mJ/molK2 suggests strong electron-electron correlations in this material. The first-principles calculations performed for NiV2Se4, which are also applicable to Ni0.85V2Se4, classify this material as a topological metal with and coexisting electron and hole pockets at the Fermi level. The phonon spectrum lacks any soft phonon mode, consistent with the absence of periodic lattice distortion in the present experiments.
keywords:
Charge-density-wave, Topological metal, Vacancies, Non Fermi liquidSitaram Ramakrishnan* Shidaling Matteppanavar Andreas Schönleber Bikash Patra Birender Singh Arumugam Thamizhavel Bahadur Singh* Srinivasan Ramakrishnan* Sander van Smaalen*
S. Ramakrishnan
Department of Quantum Matter, AdSE,
Hiroshima University,
Higashi-Hiroshima 739-8530, Japan
Email Address: [email protected]
S. Matteppanavar,
B. Patra,
B. Singh,
B. Singh,
A. Thamizhavel,
S. Ramakrishnan
Department of Condensed Matter Physics
and Materials Science,
Tata Institute of Fundamental Research,
Mumbai 400005, India
Email Address: [email protected], [email protected]
A. Schönleber,
S. van Smaalen
Laboratory of Crystallography,
University of Bayreuth, 95447 Bayreuth, Germany
Email Address: [email protected]
1 Introduction
Topological metals such as Dirac and Weyl semimetals represent exotic quantum materials with non-trivial band crossings at the charge neutrality point in the bulk band structure that lead to peculiar quasi-particle excitations and physical properties. There has been a surge of interest in realizing these topological metals, owing to their novelty for fundamental science and device applications [1, 2]. Here, we show that nickel-deficient Ni0.85V2Se4 is a topological metal with based on first-principles calculations. Our bulk measurements on single-crystalline Ni0.85V2Se4 show unusual quasi-particle excitations. The presence of vacancies is a common feature of compounds AT2X4 (A and T are transition metals; X is chalcogenide), which display exotic electronic and magnetic properties.
Cubic thiospinels of the type AT2S4 (A = Cu, Ni; T = V, Rh, Ir) have attracted attention due to the unusual ground states exhibited by them [3, 4, 5, 6, 7, 8]. For instance, superconductivity (e.g. in CuRh2S4) [3], magnetic order in insulators (CuIr2S4) [4, 5] and charge density waves (CDWs; CuV2S4) [6, 7] have been found to exist in this class of compounds. It is worthwhile to recall here that the CDW in CuV2S4 was suppressed in as-grown crystals, because of the presence of defects [9]. In addition, structural studies have shown that phase transitions are accompanied by charge ordering and spin dimerization [8]. The occurrence of spin dimerization in a three-dimensional compound, like CuIr2S4, is unique and not understood at present.
Apart from these cubic spinel compounds, there exists more than 50 chalcogenides with the same stoichiometry AT2X4 (A = Y, Cr, Fe, Co, Ni; T = Ti, Y, Cr; X = S, Se, Te), but crystallizing in the monoclinic defect NiAs structure type (Figure 1) [10], where very little investigations have been made.

When we consider the band structures of compounds with the defect NiAs structure, we find that only octahedral site ions (both Ni and other transition metal) are involved. Unlike spinels, all metal ions are on octahedral sites and, therefore, the levels have the lowest energy. The metallic behavior for the AT2X4 compounds can be ascribed to partially filled bands formed as a result of T–T overlap. The NiAs structure is also known as the Cr3S4 structure type (space group ) with two nonequivalent crystallographic sites for Cr. Chromium atoms occupy Wyckoff positions 2a and 4i, with two and four atoms per unit cell, respectively. These sites can be occupied by different elements [11, 12, 13, 14, 15, 16, 17, 18, 19].
A study on polycrystalline NiV2S4 has indicated a CDW transition at 165 K [20], while another study on NiV2Se4 reported a small anomaly in the resistivity around 160 K [21]. Using the vapor transport method, we have obtained a Ni-deficient single crystal of composition Ni0.85V2Se4, which has the same crystal structure as NiV2Se4. Band structure calculations reveal that it is a topological metal. Our experimental studies on the physical properties of Ni0.85V2Se4 single crystal unfold an unusual electronic ground state of this material with exotic properties.
2 Results and discussion
2.1 Evidence of vacancies and absence of lattice distortion.
Single-crystal x-ray diffraction (SXRD) data were processed by Eval15 [22] and SADABS [23]. All diffraction maxima could be indexed by a single unit cell with lattice parameters Å, Å, Å and deg, similar to the published unit cell of NiV2Se4 [24]. Crystal structure refinements were done with Jana2006 [25] with the monoclinic space group . Table 1 shows the structural analysis for three different models on basis of the occupancy of the Ni site, in order to determine whether there are vacancies on the Ni site or there exists Ni/V disorder.
| Model | I | II | III |
|---|---|---|---|
| Composition | NiV2Se4 | Ni0.4178(143)V2.5822Se4 | Ni0.8524(35)V2Se4 |
| Occ[Ni] | 1 | 0.4178(143) | 0.8524(35) |
| Occ[V] | 1 | 1 | 1 |
| Occ[VNi] | - | 0.5822 | - |
| Unique reflections (obs/all) | 578/685 | 578/685 | 578/685 |
| No. of parameters | 24 | 25 | 25 |
| (obs) | 0.0317 | 0.0213 | 0.0209 |
| (all) | 0.0454 | 0.0253 | 0.0255 |
| GoF (obs/all) | 2.65/2.45 | 1.46/1.37 | 1.43/1.34 |
| , (e Å | -2.87, 1.49 | -1.07, 1.30 | -1.08, 1.28 |
Initially, model I was tested where
the Ni site is completely filled.
The composition is NiV2Se4 and
it leads to a good fit of the
diffraction data with .
In model II, a Vanadium atom (VNi)
was introduced on the Ni site, such that
the sum of the occupancies remains 1,
Occ[Ni] + Occ[VNi] = 1.
Refinement of Occ[VNi] then leads to
a significant improvement of the fit, with
.
However, the chemical composition derived
from model II (Table 1)
is not in agreement with the composition
Ni0.925(9)V2.054(7)Se4 found
by an electron probe micro-analyzer (EPMA).
Such a large difference in the measured
compositions between SXRD and EPMA led us
to believe that the partially filled site
of Ni is not occupied by V.
Therefore, model II is not suitable.
Model III involves vacancies at the Ni site.
Refinement of the occupancy of Ni results in
an even better fit to the data, with .
Moreover the chemical composition of model III
is in agreement with that obtained by EPMA,
with a difference of about 7% deemed
acceptable.
One can also notice the standard uncertainty (su.)
in the refined occupancy of Ni in model III
is four times smaller than in model II.
Our findings from SXRD and EPMA suggest that
there is 15% vacancies on the Ni site.
Table 2 provides the
atomic coordinates and atomic displacement
parameters (ADPs) of model III.
| Atom | Occ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | 0.8524(35) | 0 | 0 | 0 | 0.0158(3) | 0.0019(4) | 0.0017(4) | 0 | 0.0011(3) | 0 | 0.0175(2) |
| V | 1 | -0.0451(1) | 0 | 0.2556(1) | 0.0133(2) | 0.0021(3) | 0.0153(3) | 0 | -0.0006(2) | 0 | 0.0166(2) |
| Se1 | 1 | 0.3373(1) | 0 | 0.3641(1) | 0.0119(2) | 0.0146(1) | 0.0176(2) | 0 | -0.0003(1) | 0 | 0.0015(1) |
| Se2 | 1 | 0.3381(1) | 0 | 0.8924(1) | 0.0138(1) | 0.0153(2) | 0.0163(2) | 0 | -0.0004(1) | 0 | 0.0152(1) |
From the measured diffraction data at 298 K and at 100 K, reciprocal layers were reconstructed for , and (Figure S1, S2 and S3 in the Supplemental Material [26]). They demonstrate that, upon cooling the crystal down to 100 K, there are no superlattice reflections observed and there is no change to the lattice, indicating the absence of a CDW phase transition. Table 3 shows the crystallographic information of the crystal at 298 and 100 K, respectively, as based on model III.
| Temperature (K) | 298 | 100 |
|---|---|---|
| Crystal system | Monoclinic | Monoclinic |
| Space group | ||
| Space group no. | 12 | 12 |
| (Å) | 6.1453(3) | 6.1314(2) |
| (Å) | 3.4327(2) | 3.4174(3) |
| (Å) | 11.5901(4) | 11.5462(3) |
| (deg) | 91.619(3) | 91.741(3) |
| Volume (Å3) | 244.45(3) | 241.83(3) |
| 2 | 2 | |
| Wavelength (Å) | Ag-K | Ag-K |
| Detector distance (mm) | 100 | 100 |
| -offset (deg) | 0 | 0, 30 |
| Rotation per image (deg) | 1 | 1 |
| (Å-1) | 0.683589 | 1.009913 |
| Absorption, (mm-1) | 19.271 | 19.469 |
| Tmin, Tmax | 0.5796, 0.8622 | 0.6018 0.8627 |
| Criterion of observability | ||
| Number of reflections | ||
| measured | 4410 | 8970 |
| unique (obs/all) | 451/470 | 841/1024 |
| (obs/all) | 0.0312/0.0321 | 0.0407/0.0415 |
| Composition | Ni0.8524(35)V2Se4 | Ni0.8488(25)V2Se4 |
| No. of parameters | 25 | 25 |
| Occ[Ni] | 0.8524(35) | 0.8488(25) |
| (obs) | 0.0209 | 0.0196 |
| (all) | 0.0255 | 0.0246 |
| GoF (obs/all) | 1.43/1.34 | 1.32/1.21 |
| , (e Å-3) | -1.08, 1.28 | -1.27, 1.71 |
2.2 Structural stability and electronic structure
We now discuss the stability and nontrivial state of NiV2Se4 with regards to the calculated band structure (Figure 2).

These results also apply to Ni0.85V2Se4, because the major effect of the introduction of vacancies is a shift of the Fermi level, which is presented in Section S3 of the Supporting Information. The results on Ni-deficient material show a 50 meV downward shift of the Fermi level as compared to pristine NiV2Se4. The phonon dispersion curves and associated phonon density of states (PDOS) are shown in Figure 2(a). The absence of imaginary phonon frequency in the full BZ ensures that NiV2Se4 is dynamically stable. Moreover, the absence of a soft phonon mode indicates the absence of a structural instability or a periodic lattice distortion, as it would be expected in CDW materials, in agreement with the experiments. The PDOS suggests that Ni and Se atoms contribute to low-lying phonon modes, whereas the V and Se atoms dominate the high-frequency phonon modes.
The bulk band structure along the high-symmetry directions in the BZ of NiV2Se4 is shown in Figure 2(b) without spin-orbit coupling (SOC). It is metallic, where both the valence and conduction bands cross the Fermi level. Notably, the valence and conduction bands cross along –, –, – directions at generic points close to the Fermi level, as indicated by red circles. The crossing points are stable against band hybridization to realize nodal line crossings. The band structure in presence of SOC is shown in Figure 2(c). Although the system remains metallic, the band crossing points are now gapped, separating the valence and conduction bands locally at each point. The orbital resolved band structure in Figure 2(d) shows that these band crossing points are composed of Ni–, V–, and Se– orbitals. The existence of local band gap allows the computation of the invariants in a manner similar to topological insulators. Since NiV2Se4 crystal respects inversion symmetry, we can calculate the invariants from the parity eigenvalues of the valence bands at each time-reversal-invariant momentum (TRIM) point [28]. The product of the parity eigenvalues of the occupied bands at the eight TRIM points is shown in Figure 2(e). The calculated of indicates that NiV2Se4 is topological metal. The topological phases are immune to the effects of a Hubbard for the Ni and V atoms, as discussed in Section S4 of the Supporting Information.
The nontrivial state is further demonstrated by calculations of the surface electronic structure. They reveal a single Dirac cone topological state present within the energy gap of the bulk band structure (see Section S3 of the Supplemental Material for details [26]). Figure 2(f)-(h) show the calculated Fermi surface of NiV2Se4. Owing to the multiband crossings at the Fermi level, the Fermi surface consists of both electron and hole bands which are shown separately in Figure 2(f) and 2(g), respectively. The metallic behavior is consistent with the experimental measurements.
2.3 Electrical resistivity
The electrical resistivity, , of Ni0.85V2Se4 decreases upon cooling from room temperature down to 1.5 K (Figure 3).

In particular, a broad hump is observed between 150–200 K, which also agrees with Bouchard et al. (1966) [21], who first reported an anomaly at about 160 K in of a polycrystalline sample of NiV2Se4. They suggested that the observed anomaly may be due to either a crystallographic or a magnetic transition. However, we find that the broad anomaly between 150–200 K cannot be ascribed to a structural transition, since our diffraction studies did not find any evidence for it (Section 2.1). Explanations for these features could be the development of spin fluctuations or CDW fluctuations as opposed to long-range magnetic order or CDW ordering. The latter involve structural distortions, like in CuV2S4 [9], BaFe2Al9 [29], and Ir3Si5 ( = Lu, Er) [30, 31].
The metallic behavior of Ni0.85V2Se4 is consistent with the properties of polycrystalline materials of the defect-NiAs structure [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]. Below the broad hump, exhibits an unusual dependence for 15–150 K. Such a behavior is generally observed in spin glasses and amorphous ferromagnets, where a dependence in is the result of a diffusive motion of the charge carriers [32, 33]. Most theories suggest an explanation of the anomalous resistivity by an inhomogeneous magnetic state, through comparison with the resistivity of spin glasses [34]. Since Ni0.85V2Se4 is a single crystal, the diffusive carrier motion has to be intrinsic somewhat similar to the behavior observed in MnSi under pressure [35].
It is well established that the electronic properties of metals on the border of magnetic phase transitions at low temperatures are often found to exhibit temperature dependencies that differ from the predictions of Fermi liquid theory. Early attempts to explore such non-Fermi-liquid behavior have been based on mean-field treatments of the effects of enhanced magnetic fluctuations, as in the self-consistent renormalization (SCR) model [36]. The SCR model seems to explain the temperature dependence of the resistivity of Ni3Al at high pressures, where its ferromagnetism is suppressed, leading to a negligible magnetic correlation vector . In the idealized limit and , the SCR model predicts that in 3D, the quasiparticle scattering rate varies linearly with the quasiparticle excitation energy, rather than quadratically as in the standard Fermi-liquid picture. This form of is similar to that of the marginal Fermi-liquid model [37], which is normally associated with a linear temperature dependence of the resistivity. However, at the border of ferromagnetism, the relevant fluctuations responsible for quasiparticle scattering are of long wavelength and, thus, are ineffective in reducing the current. This leads to a transport relaxation rate that differs from and is not linear in . Instead, it varies as , which was observed in high pressure studies on Ni3Al.
For a metal on the border of metallic antiferromagnetism in three dimensions, the SCR model predicts to vary as in the idealized limit , , where now stands for the correlation wave vector for the staggered magnetization. This simple model for the scattering from antiferromagnetic fluctuations assumes that the scattering rate can be averaged over the Fermi surface. Within the SCR model, this procedure would seem to require the presence of a sufficient level of defects, the latter which might be provided by the chemical disorder due to vacancies at the A-site in Ni0.85V2Se4. This site vacancy is supposed to inhibit the short circuiting caused by the carriers on the cold spots of the Fermi surface, i.e., regions far from the hot spots connected by the antiferromagnetic ordering wave vector and, thus, strongly affected by spin-fluctuation scattering. Such a behavior has been observed in NiSSe [38].
In the case of single crystalline Ni0.85V2Se4, the temperature dependence of the electrical resistivity between 15 and 150 K could be fitted by (upper inset (b) of Figure 3)
| (1) |
where is the residual resistivity and the second term is the contribution from scattering proposed by the SCR model. It is of interest to see that below 15 K, can be described by (lower inset (c) of Figure 3)
| (2) |
which suggests that the anomalous temperature dependence ceases to exist below 15 K. The second term in Equation 2 arises from the scattering of electrons due to localized spin fluctuations [39].
2.4 Magnetic susceptiblity
The temperature dependence of the magnetic susceptibility clearly shows paramagnetic behavior (Figure 4).
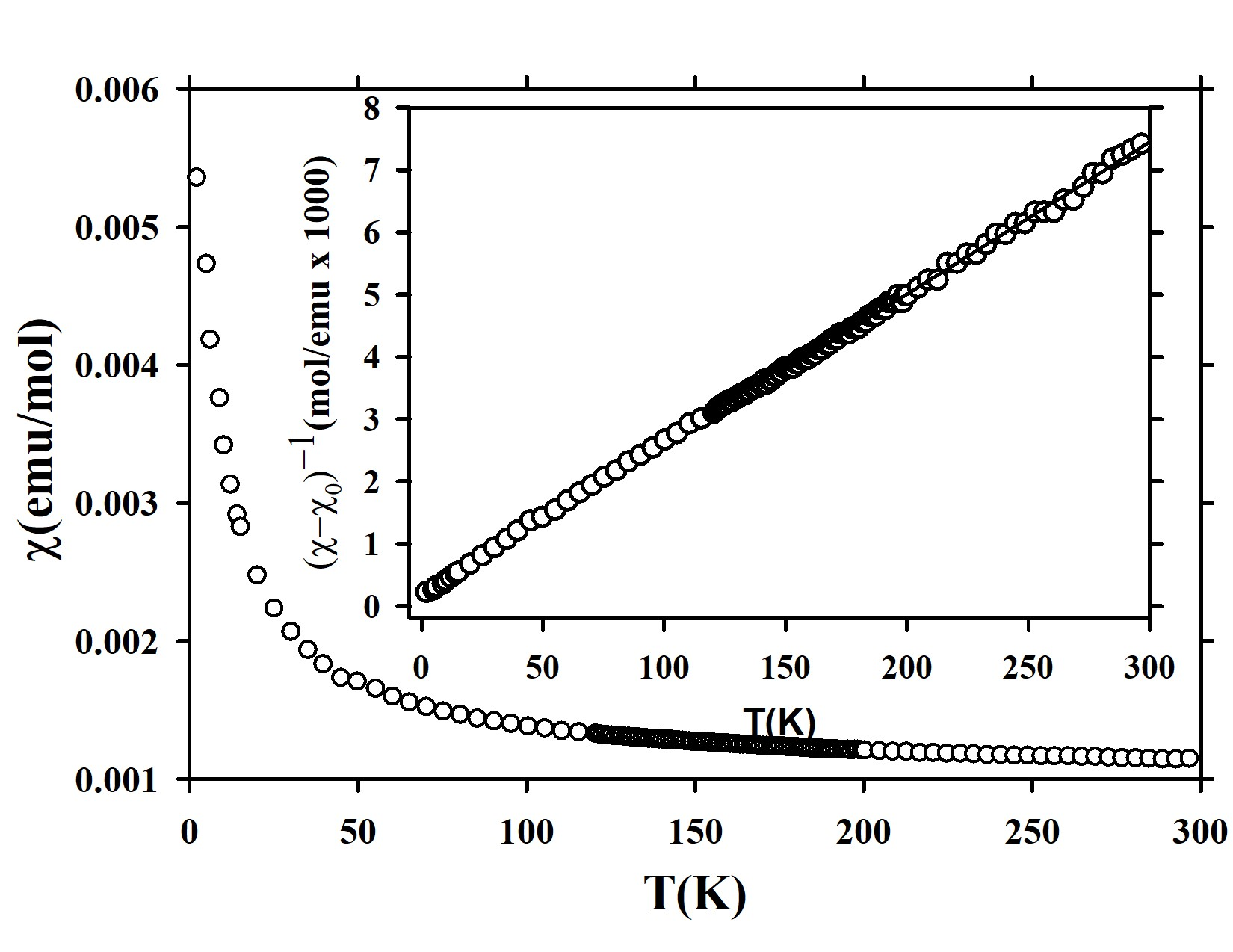
However, it does deviate from a simple Curie-Weiss behaviour, as discussed below. Magnetization measurements performed under field cooled (FC; not shown) and zero-field cooled (ZFC; Figure 4) conditions produced identical results, implying that spin glass phenomena can be ruled out in the case of Ni0.85V2Se4. The high temperature (150–300 K) data can be described by a modified Curie-Weiss law,
| (3) |
where includes the diamagnetic and temperature-independent paramagnetic contributions. From the value of the Curie constant , the effective magnetic moment is estimated as per formula unit. Usually, the Ni ion does not have a magnetic moment in metallic compounds of the type AT2X4, since all valence electrons of Ni are completely delocalized in fully ordered crystal structures. Apparently, this scenario breaks down in Ni0.85V2Se4, which again might be related to the vacancies on the Ni site. The Weiss temperature is found to be K, indicative of weak antiferromagnetic exchange interactions. The inverse susceptibility (Figure 4) shows small deviations from linear behavior below 150 K.
Isothermal magnetization (M–H) curves have been measured at selected temperatures within the range 2–300 K up to magnetic fields of T (Figure 5).

Hysteresis is absent at all temperatures, demonstrating that Ni0.85V2Se4 does not undergo a magnetic phase transition, but remains in the paramagnetic state down to 2 K. At the lowest measured temperatures, the M–H dependence is S-shaped instead of linear at higher temperatures. This might be related to the fact that lower temperatures allow to reach higher values of H/T, thus bringing the M–H relation outside the linear regime. However, attempts failed to bring all data onto a universal H/T dependence. This seems to imply that the crystal does not behave like an usual paramagnet below 15 K.
2.5 Specific heat
The specific heat, , decreases on cooling (Figure 6).

The absence of sharp features and the presence of a broad, weak anomaly at = 150–170 K rule out a possible structural phase transition, which is in agreement with our single-crystal x-ray diffraction data. However, the presence of this anomaly in the specific heat data is in agreement with the anomalies observed in resistivity data. The origin of this anomaly could be attributed to spin or CDW fluctuations. It is important to specify here, that the anomalous temperature dependence of the resistivity () starts below this transition. The low temperature data can be fitted with the model [40],
| (4) |
The first term is the contribution due to conduction electrons, the second term is the contribution from the lattice, and the third term is the contribution from spin fluctuations due to disorder. This model was successfully employed to explain a similar anomaly in the specific heat of Fe1-xV2+xAl in another context [40]. The fit yields mJ/mol K2 and the Debye temperature K. The existence of magnetic fluctuations below 15 K has been corroborated by the isothermal magnetization data, as explained earlier. The presence of such magnetic fluctuations seems to change the anomalous temperature dependence of resistivity behavior below 15 K.
3 Conclusions
The perfectly ordered crystal structure of NiV2Se4 does not have a magnetic moment on Ni. However, our attempted growth of single crystals of NiV2Se4 has resulted in Ni-deficient crystals, where the crystallographic Ni site has 15% vacancies, but full chemical order is preserved at the V and the two Se sites of the AT2Se4 monoclinic structure type. This observation is in agreement with reports in the literature of crystallization attempts, where part or all of the transition metal A can be occupied by defects or V atoms [21, 41].
Single crystalline Ni0.85V2Se4 is found to be a topological metal, that exhibits a cross-over in its physical properties at temperatures around 150 K. All properties, including low-temperature x-ray diffraction data, are in agreement with the absence of phase transitions down to K in the absence of a magnetic field. The temperature dependence of the electrical resistivity of Ni0.85V2Se4 is anomalous in the temperature range from 15–150 K, while the presence of magnetic correlations below 15 K probably leads to T2 dependence of resistivity. It is interesting to compare the present results to the well established topological metal V6Sn6 ( = Gd and Y) [42], containing a kagome network of V ions coordinated by Sn and separated by triangular lattice planes of rare-earth ions. The Gd spins contribute to the observed magnetism of GdV6Sn6 while YV6Sn6 is in a paramagnetic state. Unlike the case of YV6Sn6, minor site disorder of Ni in Ni0.85V2Se4 is responsible for its anomalous low-temperature properties. The broad hump in the resistivity may be related to the anomaly in the specific heat in the temperature range 150–160 K. However, the exact nature of the crossover is not understood at present. These features combine with the gradual build-up of antiferromagnetic fluctuations upon cooling. Isothermal magnetization curves confirm the absence of bulk magnetic order down to 2 K, but attempts have failed to bring all data onto a universal H/T dependence. This seems to imply that the crystal does not behave like a usual paramagnet below 15 K, and it suggests a build-up of antiferromagnetic correlations. We believe that Ni0.85V2Se4 is a is a topological metal that displays unusual electronic properties due to significant electron correlations. However, to understand this system, one needs more investigations, notably on the nature of the anomalous behavior around 160 K and Fermi surface studies using angle-resolved photoemission spectroscopy.
4 Experimental and computational section
Crystal growth and characterization by EPMA
Attempts to synthesize single-crystalline NiV2Se4 resulted in the formation of Ni0.85V2Se4
prepared by solid-state reaction of the elements in evacuated quartz-glass
tubes at a temperature of K, employing stoichiometric amounts of the elements obtained
from Alfa Aesar: nickel (99.996% purity), vanadium (99.5%),
and selenium (99.999%).
Single crystals have been grown by
vapor transport in evacuated quartz-glass tubes, employing
iodine as transport agent and a temperature gradient
of K over 200 mm.
The chemical composition has been determined as
Ni0.925(9)V2.054(7)Se4 by an electron
probe micro-analyzer (EPMA). These values are the
average over 57 points measured on a a flat,
as-grown surface sliced off from the large single crystal
used for the physical-properties measurements. The finding
agrees with the results of x-ray diffraction
(see Section 2.1).
Temperature dependent Single-crystal
x-ray diffraction (SXRD)
SXRD has been measured on a mar345dtb
image plate diffractometer (marXperts, Germany)
with Ag-K radiation from a rotating
anode generator.
Initially, several crystals from
the batch were tested, all showing that they were Ni deficient
similar to what has been found with EPMA.
For the final reported measurement a crystal
of dimensions mm3
was crushed from the large crystal which was used for
physical properties measurements.
A complete set of diffraction images has been measured at temperatures 298 K and 100 K, employing an exposure time such that the strongest Bragg’s reflection was close to the saturation of the detector. A second run was measured with an offset of 30 deg in for obtaining data at high resolution, and employing an eight times longer exposure time, resulting in overexposed strong reflections but allowing for detection of weak scattering effects. Superlattice reflections could not be detected, in agreement with the absence of a CDW at 100 K. Details are given in Section S1 and S2 of the Supplemental Material [26].
Physical property measurements
The electrical resistivity has been measured on cooling
from 300 down to 1.5 K in a standard four-probe configuration,
employing a cryostat and a LR-700 (Linear Research, USA) bridge
with 5 mA current of small AC frequency of 16 Hz. Electrical
contacts have been made using silver paste and gold wires (m diameter).
The magnetic susceptibility has been measured for
temperatures 2–300 K, using a commercial SQUID magnetometer
(MPMS5 by Quantum Design, USA). Measurements have been repeated
in both zero-field-cooled (ZFC) and field-cooled (FC) conditions
for magnetic fields of different strength. The isothermal
magnetization has been measured for magnetic fields
from to +7 Tesla at a few selected temperatures.
The heat capacity has been measured from
2 to 300 K by the thermal relaxation method using a
Physical property measuring system (PPMS, Quantum Design, USA).
Density functional theory calculations
Electronic structure calculations were performed using the Vienna ab
initio simulation package (VASP) [43]
with the projector augmented (PAW) [44]
wave method. Generalized gradient approximation of Perdew,
Burke and Ernzerhof (PBE) [45] was used
to include the exchange-correlation effects. An energy cutoff
of 380 eV was used for the plane wave basis and a
centered k-mesh was employed for
the Brillouin zone (BZ) sampling. Experimental lattice parameters
with fully optimized ionic positions were considered in our computations.
We optimized atomic positions until the residual
forces on each atom were less than 0.0001 eV/Å.
The material-specific tight-binding Hamiltonian [46, 47]
was generated to compute the topological properties using the
WannierTools [48] package.
The Xcrysden program was used to visualize the Fermi surface [49].
The phonon spectrum was obtained using the frozen phonon method as implemented in the
Phonopy [50] code with a supercell.
Supporting Information
Supporting Information is available from the Wiley Online Library or from the author.
Acknowledgements
Single crystals have been grown by Kerstin Küspert at the Laboratory of Crystallography in Bayreuth. We thank Detlef Krauße of the Bavarian Geoinstitute (BGI) in Bayreuth for performing the electron microprobe experiments. This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–265092781. SM thanks the Tata Institute of Fundamental Research Mumbai for providing a postdoctoral fellowship and VGST CESEM GRD-852. The work at TIFR is supported by the Department of Atomic Energy of the Government of India under Project No. 12-R&D-TFR-5.10-0100.
Conflict of interest
The authors declare no conflict of interest
References
- [1] S. Li, Z.-M. Yu, Y. Yao, S. A. Yang, Frontiers of Physics 2020, 15 43201.
- [2] B. Singh, H. Lin, A. Bansil, Adv. Mater. 2022, 2022, n/a 2201058.
- [3] T. Hagino, Y. Seki, N. Wada, S. Tsuji, T. Shirane, K. I. Kumagai, S. Nagata, Phys. Rev. B 1995, 51 12673.
- [4] S. Nagata, T. Hagino, Y. Seki, T. Bioth, Physica B 1994, 194-196 1077.
- [5] T. Furubayashi, T. Matsumoto, T. Hagino, S. Nagata, J. Phys. Soc. Jpn 1994, 63 3333.
- [6] T. Sekine, K. Uchinokura, H. Iimura, R. Yoshizaki, E. Matsuura, Solid State Commun. 1984, 51 187.
- [7] J. Mahy, D. Colatis, D. V. Dyck, S. Amelinck, J. Solid State Chem. 1987, 68 320.
- [8] P. G. Radaelli, Y. Horibe, M. J. Gutmann, M. Ishibashi, C. H. Chen, R. M. Ibberson, M. Koyama, Y. S. Hor, V. Kiryukhin, S. W. Cheong, Nature 2002, 416 155.
- [9] S. Ramakrishnan, A. Schönleber, C. B. Hübschle, C. Eisele, A. M. Schaller, T. Rekis, N. H. A. Bui, F. Feulner, S. van Smaalen, B. Bag, S. Ramakrishnan, M. Tolkiehn, C. Paulmann, Phys. Rev. B 2019, 99 195140.
- [10] A. Wold, K. Dwight, Solid State Chemistry: synthesis, structure, and properties of selected oxides and sulfides, 227–234, Chapman & Hall, New York, 1993.
- [11] R. J. Bouchard, Inorg. chem. 1969, 8 850.
- [12] F. Jellinek, Acta Crystallogr. 1957, 10 620.
- [13] A. V. Powell, D. C. Colgan, C. Ritter, J. Solid State Chem. 1997, 134 110.
- [14] A. V. Powell, C. Ritter, P. Vaqueiro, J. Solid State Chem. 1999, 144 372.
- [15] P. Vaqueiro, A. V. Powell, A. I. Coldea, C. A. Steer, I. M. Marshall, S. J. Blundell, J. Singleton, T. Ohtani, Phys. Rev. B 2001, 64 132402.
- [16] R. H. Plovnick, D. S. Perloff, M. Vlasse, A. Wold, J. Phys. Chem. Solids 1968, 29 1935.
- [17] B. L. Morris, P. Russo, A. Wold, J. Phys. Chem. Solids 1970, 31 635.
- [18] B. L. Morris, R. H. Plovnick, A. Wold, Solid State Commun. 1969, 7 291.
- [19] P. Vaqueiro, M. Bold, A. V. Powell, C. Ritter, Chem. Mater. 2000, 12 1034.
- [20] Y. K. Kuo, K. M. Sivakumar, J. Y. Lin, C. N. Kuo, C. S. Lue, J. Phys.: Condens. Matter 2007, 19 216210.
- [21] R. J. Bouchard, A. Wold, J. Phys. Chem. Solids 1966, 27 591.
- [22] A. M. M. Schreurs, X. Xian, L. M. J. Kroon-Batenburg, J. Appl. Crystallogr. 2010, 43 70.
- [23] G. M. Sheldrick, SADABS, Version 2008/1, Göttingen: University of Göttingen, 2008.
- [24] R. J. Bouchard, W. T. Robinson, A. Wold, Inorg. Chem. 1966, 5 977.
- [25] V. Petricek, M. Dusek, L. Palatinus, Z. Kristallogr. 2014, 229 345.
- [26] See Supplemental Material at [URL will be inserted by publisher] for details on the diffraction experiments, at 100 K and reconstructed reciprocal images.
- [27] T. Hahn, editor, International Tables for Crystallography Vol. A, fifth edition, Kluwer Academic Publishers, Dordrecht, 2006.
- [28] L. Fu, C. L. Kane, Phys. Rev. B 2007, 76 045302.
- [29] W. R. Meier, B. C. Chakoumakos, S. Okamoto, M. A. McGuire, R. P. Hermann, G. D. Samolyuk, S. Gao, Q. Zhang, M. B. Stone, A. D. Christianson, B. C. Sales, Chem. Mater. 2021, 33 2855–2863.
- [30] S. Ramakrishnan, A. Schönleber, J.-K. Bao, T. Rekis, S. R. Kotla, A. M. Schaller, S. van Smaalen, L. Noohinejad, M. Tolkiehn, C. Paulmann, N. S. Sangeetha, D. Pal, A. Thamizhavel, S. Ramakrishnan, Phys. Rev. B 2021, 104 054116.
- [31] S. Ramakrishnan, A. Schönleber, T. Rekis, N. van Well, L. Noohinejad, S. van Smaalen, M. Tolkiehn, C. Paulmann, B. Bag, A. Thamizhavel, D. Pal, S. Ramakrishnan, Phys. Rev. B 2020, 101 060101(R).
- [32] J. A. Hertz, Phys. Rev. B 1976, 14 1165.
- [33] A. J. Millis, Phys. Rev. B 1993, 48 7183.
- [34] J. A. Mydosh, Spin glasses: an experimental introduction, Taylor and Francis, London, 1993.
- [35] C. Pfleiderer, G. J. McMullan, S. R. Julian, G. G. Lonzarich, Phys. Rev. B 1997, 55 8330.
- [36] P. G. Niklowitz, F. Beckers, G. G. Lonzarich, G. Knebel, B. Salce, J. Thomasson, N. Bernhoeft, D. Braithwaite, J. Flouquet, Phys. Rev. B 2005, 72 024424.
- [37] C. M. Varma, P. B. Littlewood, S. Schmitt-Rink, E. Abrahams, A. E. Ruckenstein, Phys. Rev. Lett. 1989, 63 1996.
- [38] S. Miyasaka, H. Takagi, Y. Sekine, H. Takahashi, N. Mori, R. J. Cava, J. Phys. Soc. Jpn 2000, 69 3166.
- [39] A. Kaiser, Phil. Mag. B 1992, 65 1197.
- [40] A. T. Lonchakov, V. V. Marchenkov, V. I. Okulov, K. A. Okulova, T. E. Govorkova, S. M. Podgornykh, H. W. Weber, Journal of Physics: Conference Series 2014, 568, 5 052018.
- [41] K. Kallel, H. Boller, J. Less-Common Met. 1984, 102 213.
- [42] G. Pokharel, S. M. L. Teicher, B. R. Ortiz, P. M. Sarte, G. Wu, S. Peng, J. He, R. Seshadri, S. D. Wilson, Phys. Rev. B 2021, 104 235139.
- [43] G. Kresse, J. Furthmüller, Phys. Rev. B 1996, 54 11169.
- [44] P. E. Blöchl, Phys. Rev. B 1994, 50 17953.
- [45] J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 1996, 77 3865.
- [46] N. Marzari, D. Vanderbilt, Phys. Rev. B 1997, 56 12847.
- [47] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, N. Marzari, Computer Physics Communications 2008, 178, 9 685.
- [48] Q. Wu, S. Zhang, H.-F. Song, M. Troyer, A. A. Soluyanov, Computer Physics Communications 2018, 224 405.
- [49] A. Kokalj, Journal of Molecular Graphics and Modelling 1999, 17, 3 176.
- [50] A. Togo, I. Tanaka, Scripta Materialia 2015, 108 1.
Table of Contents
