Realistic Spin Model for Multiferroic NiI₂

The materials of van der Waals type can potentially be made into two-dimensional (2D) layers, which exhibit exceptional properties, such as massless fermions Novoselov et al. (2005), valleytronics Mak et al. (2012), ferroelectricity Chang et al. (2016) and ferromagnetism Gong et al. (2017); Huang et al. (2017). Recently, electromagnetic couplings were observed in few layers and monolayers of NiI₂, which makes NiI₂ the first established 2D multiferroic Ju et al. (2021); Song et al. (2022).

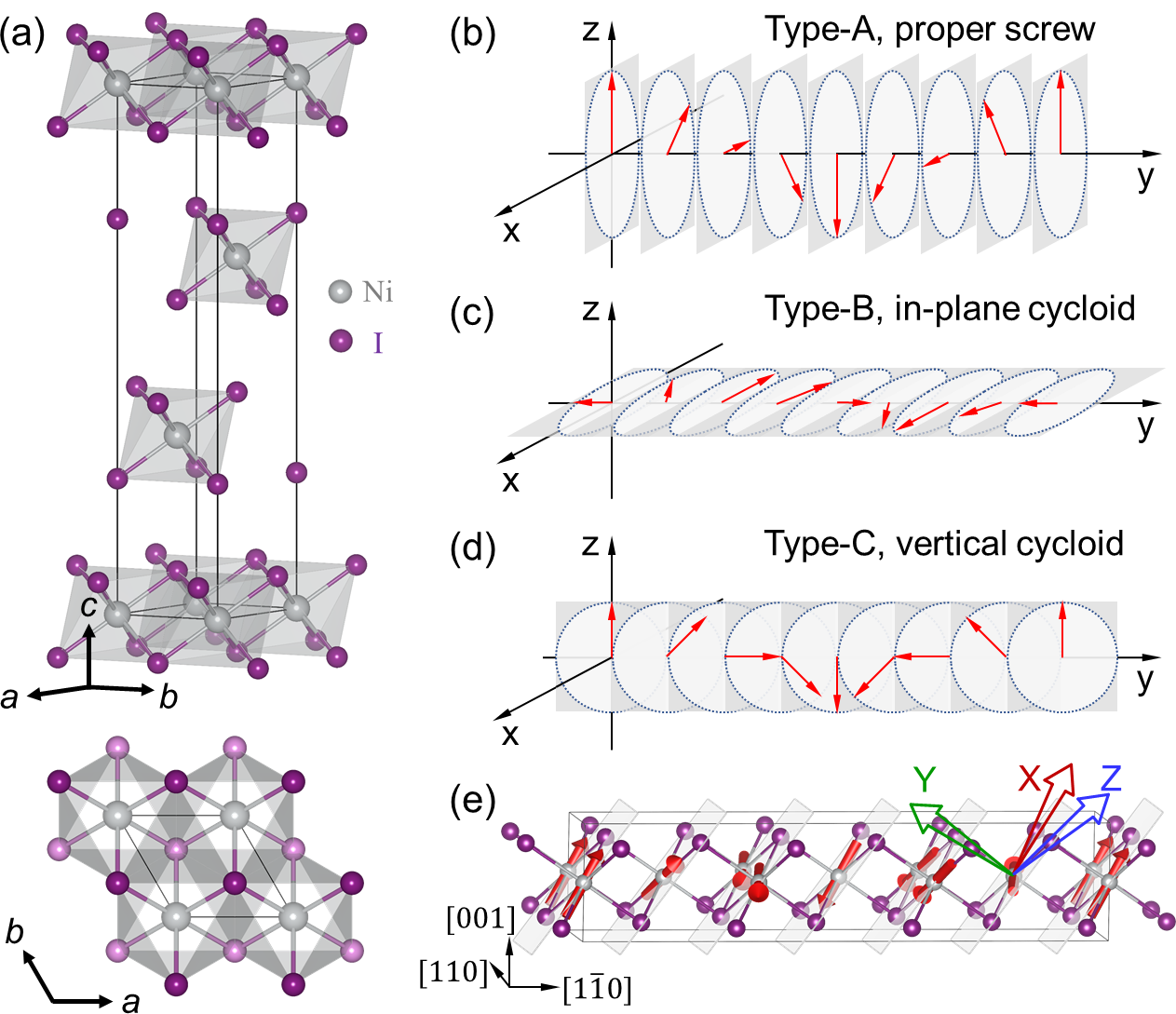
Bulk NiI₂ has been known as a van der Walls layered type-II multiferroic. It crystallizes in a rhombohedral lattice with a space group of $R\bar{3}m$ (point group $D_{3d}$). Each layer of NiI₂ consists of edge-sharing NiI₆ octahedra, yielding a triangular lattice of magnetic Ni²⁺ ions, as shown in Fig. 1a. The Ni²⁺ ion exhibits an electronic configuration of $3d^{8}$, with fully occupied $t_{2g}$ orbits and half-filled $e_{g}$ orbits, resulting in the spin value of $S=1$ and a local moment of 2 $\mu_{B}$ on each Ni²⁺. The ground state was determined to be a proper screw (PS) state, where spins rotate in a plane that is perpendicular to the propagation direction. This proper screw is characterized by ${\bm{q}}\approx(0.138,0,1.457)$ in the bulk system Kuindersma et al. (1981), which indicates in-plane propagation along ${\langle 1\bar{1}0\rangle}$ directions with a period of $\lambda\approx 7.23{\bm{a}}$, and the out-of-plane propagation arises from the interlayer antiferromagnetic (AFM) alignments. As NiI₂ is insulating, such PS state breaks the inversion symmetry and induces an electric polarization along ${\langle 110\rangle}$ directions Kuindersma et al. (1981); Kurumaji et al. (2013).

To understand the specific propagation directions of the PS of NiI₂, analytical results on $J_{1}-J_{2}-J_{3}$ model of triangular lattice indicate that (i) the ${\langle 1\bar{1}0\rangle}$ propagation can be stabilized by FM $J_{1}$ and AFM $J_{2}$ with $J_{2}/J_{1}<-1/3$; while (ii) the ${\langle 110\rangle}$ propagation is favored by FM $J_{1}$ and AFM $J_{3}$ with $J_{3}/J_{1}<-1/4$ Okubo et al. (2012). However, various models extracted from density functional theory (DFT) actually predict a ${\langle 110\rangle}$ propagated ground state, with $J_{1}$ and $J_{2}$ both being FM Amoroso et al. (2020); Riedl et al. (2022); Ni et al. (2021, 2022), implying that the competing $J_{1}-J_{2}$ mechanism is not suitable for NiI₂. Moreover, even though the Heisenberg model can stabilize a ${\langle 1\bar{1}0\rangle}$ propagation, it can not explain why the ground state is PS, instead of other degenerate helical states (see Figs. 1c and 1d).

Another interesting but still elusive point is the canting of the spin rotation plane. Measurements find that the normal of the rotation plane is not along the in-plane ${\langle 1\bar{1}0\rangle}$ propagation direction, but rather forms an angle of 55^∘ with the out-of-plane direction of NiI₂ bulk Kuindersma et al. (1981). Such canting has been believed to be natural, as the presumed PS state should have its rotation plane being perpendicular to its propagation direction and the PS state of NiI₂ does have an out-of-plane propagation component Kurumaji et al. (2011, 2013). However, common mechanisms can not explain such canting, as (i) single ion anisotropy (SIA) does not favor specific canting angle; (ii) the Dzyaloshinskii-Moriya interaction (DMI) is not allowed by the inversion symmetry of NiI₂ (Note that incommensurate spin patterns are too weak to generate non-negligible DMI); and (iii) interlayer Heisenberg terms are proved to have effects neither on propagation directions nor cantings Régnault et al. (1982). On the other hand, new forms of interactions, i.e., Kitaev interaction Stavropoulos et al. (2019); Amoroso et al. (2020); Riedl et al. (2022) and biquadratic interactions Ni et al. (2021), have recently been proposed to be non-negligible in NiI₂, but their effects and interplays are still not clearly understood. Hence, any highly desired realistic model of NiI₂ has to not only incorporate all these aforementioned important mechanisms, but also reproduce the correct ground state – which is currently lacking.

In this work, we build a first-principle-based spin Hamiltonian for NiI₂, taking advantage of a symmetry-adapted cluster expansion and machine learning methods. The resulting Hamiltonian can well reproduce the observed PS state of NiI₂, with the propagation, period and canting angle comparing well with experiments on bulk systems. By further developing a phase diagram, it is demonstrated that (i) Heisenberg terms actually lead to ${\langle 110\rangle}$ propagation; and (ii) it is the Kitaev interaction that not only results in the actual ${\langle 1\bar{1}0\rangle}$ propagation, but also dominantly determines the canting of the rotation plane. The roles of biquadratic interaction and interlayer couplings are also carefully examined. Monte Carlo (MC) simulations further predict diverse spin textures and topological defects.

Our newly developed symmetry-adapted cluster expansion method, as implemented in the PASP software, is applied to build the spin Hamiltonian of NiI₂ Lou et al. (2021); Xu et al. (2022). Such method roots in cluster expansion that goes over all combinations of spin components of $S_{\alpha}(\alpha=x,y,z)$. By further applying crystal symmetries to those combinations, only the symmetry-allowed terms, i.e., the invariants, are kept. The coefficients of these invariants can be fitted from total energies obtained from DFT calculations via a machine learning algorithm Li et al. (2020). Such method can thus in principle consider all possible interactions to any body and any order [see Supplemental Materials (SM) for details sm ].

To construct the spin Hamiltonian of NiI₂, we start with distant neighbors going up to fifth nearest neighbors, spin-orbit coupling (SOC) effects, and up to four-body interactions (see SM sm ). Energies of random spin structures are calculated with HSE06 hybrid functional Krukau et al. (2006), but also with PBE+U for comparison Perdew et al. (1996). After repeated fitting and refining, the model finally reads

with $n=1,2,3$ and where $\langle i,j\rangle_{n}$ denotes pairs of $n$th nearest neighbors (NN) within each layer, while the $\perp$ symbol refers to interlayer couplings; $\gamma$ chooses its value from $X,Y$ and $Z$ from the Kitaev basis (see Fig. 1d and SM sm ), which shows the bond-dependent feature. Note that the SOC effects are reflected by the Kitaev term and SIA. For the sum running over $\langle i,j\rangle_{1}$, $J$ quantifies the isotropic exchange coupling, $K$ the Kitaev interaction, and $B$ a biquadratic term. Note that one can also define $J_{1}=\frac{1}{3}(3J+K)$, which can be thought of as the real isotropic exchange. $A_{zz}$ denotes the SIA. As shown in Table I, the 1NN isotropic exchange favors FM since $J=-4.976$ meV, which is the largest coefficient in magnitude. $J_{2}$ also favors FM because of its negative sign, but is relatively very small. On the other hand, $J_{3}=2.250$ meV favors AFM and thus competes with the 1NN $J$. Regarding the interlayer couplings, $J_{1}^{\perp}$ is FM in nature but very small in magnitude. In contrast, $J_{2}^{\perp}=0.685$ meV favors AFM and is the strongest interlayer coupling. Moreover, sizable AFM Kitaev $K=0.858$ meV and $B=-0.719$ meV biquadratic interactions are predicted, which are in line with previous studies Stavropoulos et al. (2019); Amoroso et al. (2020); Ni et al. (2021); Riedl et al. (2022); Xu et al. (2018, 2020a). Such spin Hamiltonian of Eq. (1) yields a very small mean averaged error (MAE) of 0.063 meV/Ni, as indicated in the SM sm .

The ground state of NiI₂ is determined employing the Hamiltonian of Eq. (1) within MC and conjugate gradient (CG) methods. The predicted ground state indeed yields a canted PS state with an in-plane $\langle 1\bar{1}0\rangle$ propagation and antiparallel interlayer alignments, which agree well with measurements. The period is determined to be $\lambda=7.3{\bm{a}}$ if neglecting interlayer couplings, which compares well with the experimental value of $\lambda=7.23{\bm{a}}$ (where ${\bm{a}}$ denotes the in-plane lattice constant) Kuindersma et al. (1981); Kurumaji et al. (2013). Strikingly the canting angle of the rotation plane is numerically found to be 46^∘ for bulk, which is consistent with the corresponding measured value of 55^∘$\pm$10^∘ Kuindersma et al. (1981). Our model therefore reproduces well the correct PS state for bulk, where the spin texture in a single layer will be referred to as PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ state. Note that the parameters from PBE result in the $\langle 110\rangle$ propagation, as a result of rather strong $J_{3}/J$. It is also important to know that isotropic Heisenberg terms, by themselves, do not support in-plane $\langle 1\bar{1}0\rangle$ propagation, as $J_{2}$ and $J$ both favor FM while $J_{3}$ and $J$ compete against each other (since $J_{3}>0$ and thus favor AFM while $J_{3}/J=-0.45$). Such isotropic Heisenberg terms lead to an incommensurate state along $\langle 110\rangle$ (IC^⟨110⟩), which is consistent with both analytical results Okubo et al. (2012) and previous models from DFT Amoroso et al. (2020); Riedl et al. (2022); Ni et al. (2021, 2022). It therefore indicates that the $\langle 1\bar{1}0\rangle$ propagation is stabilized by mechanisms other than the isotropic Heisenberg terms.

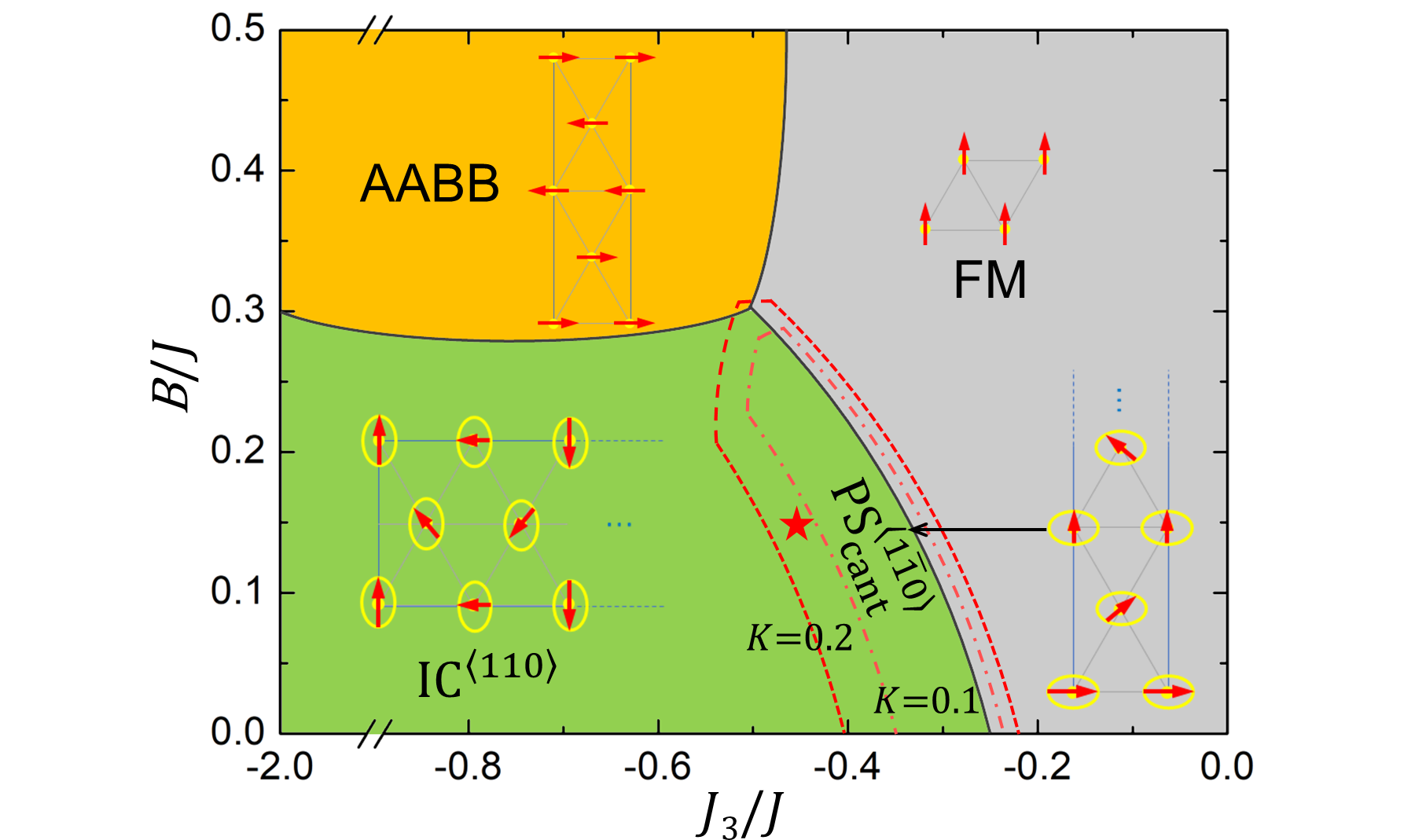
To unravel the puzzling mechanisms that stabilize such $\langle 1\bar{1}0\rangle$ propagation, we built a phase diagram. More precisely, we chose $J=-1$ meV and sweep over $J_{3}$ $\geq$ 0 and $B$ $\leq$ 0 (in this phase diagram, “only” $J$, $J_{3}$ and $B$ are thus included for now). As shown in Fig. 2, for $B/J=0$, the chosen negative $J$ stabilizes the FM state when $J_{3}$ is weak; while the system adopts IC^⟨110⟩ states when $J_{3}/J<-0.25$, which is consistent with the analytical results of Ref.Okubo et al. (2012). For $B/J>0$, the negative biquadratic term shifts the IC^⟨110⟩-FM boundary toward larger magnitude of $J_{3}/J$, which can be understood by the fact that $B<0$ favors collinear arrangements and thus helps stabilize the FM state. When $B/J\gtrsim 0.3$ and $J_{3}/J\lesssim-0.5$, a so-called AABB AFM state becomes the ground state Wu et al. (2022). Moreover, calculations varying the interlayer Heisenberg terms ($J_{n}^{\perp}$, $n=1,2,3$) were also performed, but their results are not shown in the phase diagram. It is found that $J_{n}^{\perp}$ can only modify the period of IC states or induce collinear states, but not alter the propagation direction, which is in line with a previous work too Régnault et al. (1982). The phase diagram discussed so far thus indicates that $J$, $J_{3}$, $B$ and $J_{n}^{\perp}$, by themselves, can not lead to the $\langle 1\bar{1}0\rangle$ propagation in the investigated parameter space.

The Kitaev interaction is therefore now further incorporated into the computations and resulting phase diagram (consequently, $J$, $J_{3}$, $B$ and $K$ are now included in this new phase diagram). Surprisingly, with $K=0.1$ meV (resulting thus in $K/J=-0.1$), an incommensurate state propagating along $\langle 1\bar{1}0\rangle$ (IC${}^{\langle 1\bar{1}0\rangle}$) emerges at the border of the previous IC^⟨110⟩-FM transition, as additionally shown in Fig. 2. Such IC${}^{\langle 1\bar{1}0\rangle}$ state takes a slim area of the previous FM zone and a relatively large area of the previous IC^⟨110⟩ state. When increasing the Kitaev interaction even more to $K=0.2$ meV, the area of IC${}^{\langle 1\bar{1}0\rangle}$ state further expands. As a result, the phase points defined by, e.g., $J_{3}/J=-0.4$ and $B/J=0$, as well as $J_{3}/J=-0.5$ and $B/J=0.2$, transform from the IC^⟨110⟩ to IC${}^{\langle 1\bar{1}0\rangle}$ state. It is thus clear that, for NiI₂, the ratios $J_{3}/J=-0.45$ and $B/J=0.14$ favor the IC^⟨110⟩ state, but $K/J=-0.17$ renders the ground state to become the IC${}^{\langle 1\bar{1}0\rangle}$ state. Such results therefore demonstrate that the Kitaev interaction (with $K>0$), along with the frustration between $J$ and $J_{3}$, tends to stabilize the ${\langle 1\bar{1}0\rangle}$ propagation.

Moreover, it is found that the aforementioned IC${}^{\langle 1\bar{1}0\rangle}$ state resulted from the $J$-$K$-$J_{3}$(-$B$) model (i.e. a model with only such terms) also exhibits canted rotation plane. This canting angle between the $Y$ axis and out-of-plane direction yields 54.7^∘, implying that the canting plane locates exactly in the $XZ$ plane (see Fig. 1d for the Kitaev basis). If we focus on a single layer, such canted IC${}^{\langle 1\bar{1}0\rangle}$ state is actually the PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ state of NiI₂. Such fact strongly suggests that the canting of the PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ state for NiI₂ is strongly related to the Kitaev interaction. To verify such point, we turned on only the intralayer terms of Eq. (1) and compare the energies of three phases: (i) PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ state with a period of $\lambda=7.25{\bm{a}}$; (ii) artificially made PS${}^{\langle 1\bar{1}0\rangle}$ state (that has no canting) with $\lambda=7.25{\bm{a}}$; and (iii) artificially made PS^⟨110⟩ state (that has also no canting) with $\lambda=6.25{\bm{a}}$. Note that the chosen periods lead to the lowest energy of the corresponding propagation. The total and decomposed energies of such three phases are listed in Table II. It is found that, (a) PS${}^{\langle 1\bar{1}0\rangle}$ is 0.03 meV/Ni higher in energy than PS^⟨110⟩ and the Kitaev term contributes the same energy to both states, indicating that the Kitaev interaction favor PS${}^{\langle 1\bar{1}0\rangle}$ and PS^⟨110⟩ equally; while (b) PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ is 0.08 meV/Ni lower in energy than PS${}^{\langle 1\bar{1}0\rangle}$, and the Kitaev interaction, as well as the SIA, contributes dominantly to this energy gain. Such comparisons thus demonstrate that the Kitaev interaction favors canting altogether with the ${\langle 1\bar{1}0\rangle}$ propagation. Moreover, it indicates that Kitaev interaction favors spins rotating in $ZX$, $XY$ or $YZ$ planes with a canting angle of 54.7^∘, while the in-plane SIA further pushes the rotation plane toward the basal plane with a canting angle of 46^∘.

We then develop a model to better understand why Kitaev interaction favors ${\langle 1\bar{1}0\rangle}$ propagation, as well as, a canting in rotation plane (see details in SM sm ). Here, we construct PS${}^{\langle 1\bar{1}0\rangle}$ and PS^⟨110⟩ states and adopt only the Kitaev interaction. The resulted energies are expressed as $E^{1\bar{1}0}/K=c_{1}({\rm cos}2\theta_{1}-2\sqrt{2}{\rm sin}2\theta_{1})+c_{2}$ and $E^{110}/K=c_{3}{\rm cos}2\theta_{1}+c_{4}$, where $E^{1\bar{1}0}$ and $E^{110}$ are the total energies of the corresponding PS states, $\theta_{1}$ is the angle from the [001] direction to the normal of the rotation plane, and $c_{n}(n=1-4)$ are positive constants. It is found that (i) $E^{1\bar{1}0}$ has its minimum at $\theta_{1}=54.7^{\circ}$, which is the angle between the [001] direction and the $Y$ ($Z$ or $X$, respectively) axis, demonstrating that the Kitaev interaction prefers the rotation plane of the PS${}^{\langle 1\bar{1}0\rangle}$ pattern within the $XZ$ ($XY$ or $YZ$, respectively) plane; (ii) $E^{110}$ has its minimum at $\theta_{1}=\pm 90^{\circ}$, indicating an exact PS state with rotation plane being perpendicular to the propagation direction; and (iii) $E^{1\bar{1}0}_{min}<E^{110}_{min}$, confirming that ${\langle 1\bar{1}0\rangle}$ propagation, together with a canting, is energetically more favorable (see Fig. S3 of SM sm ).

The critical role of Kitaev interaction in reproducing the canting in spin rotation plane demonstrates the significance of SOC effects on the spin model of NiI₂. Moreover, our DFT results (see Fig. S7 of SM) show that the strength of electric polarization depends largely on the orientation of the spin rotation plane. It thus indicates that the Kitaev interaction is closely related to the ferroelectricity. Such findings are thus in line with previous work, which demonstrates that the ferroelectric order is controlled by the SOC of iodine Fumega and Lado (2022).

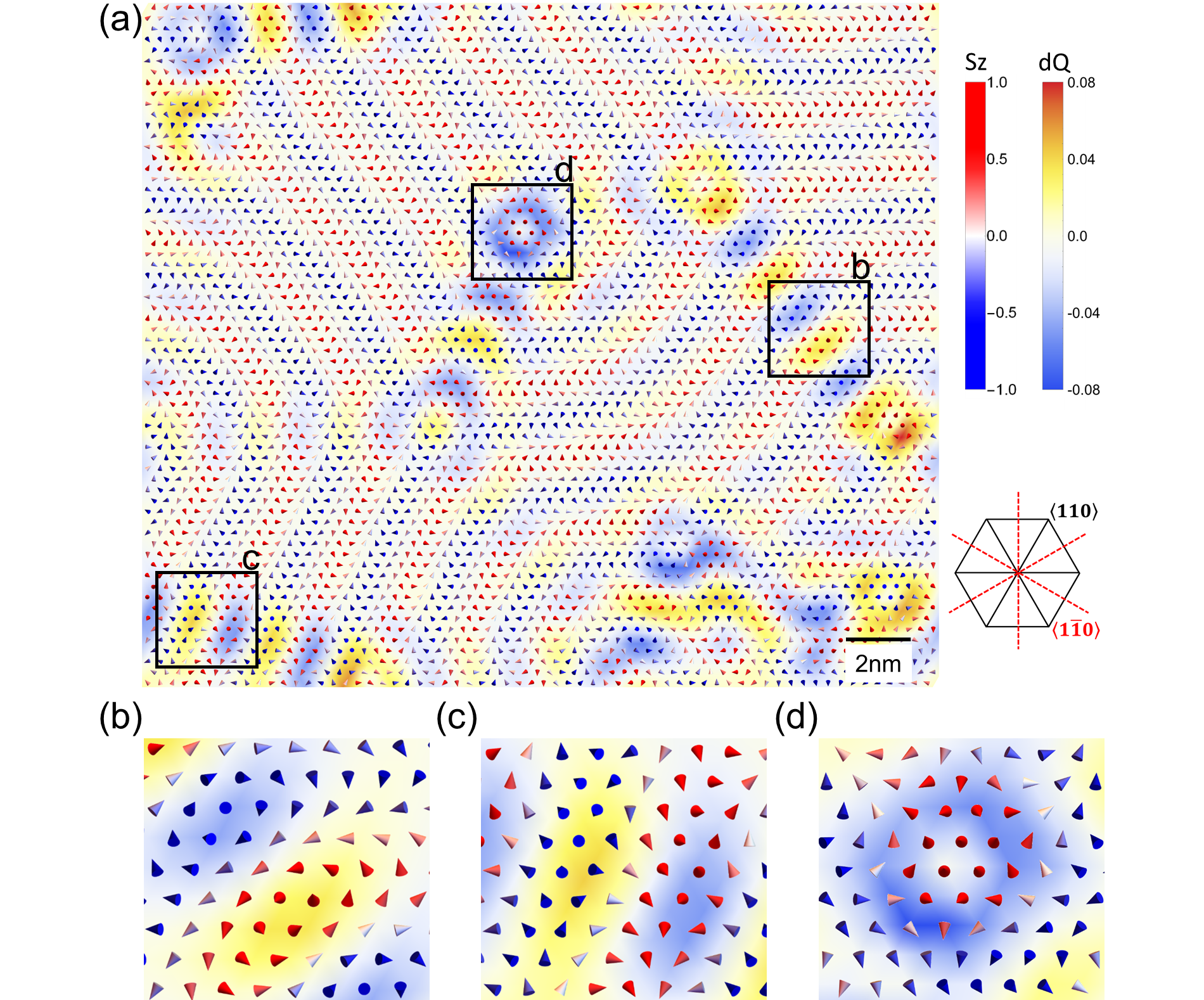
Furthermore, Monte-Carlo simulations, as well as a conjugate gradient (CG) algorithm, are performed on large supercells using the Hamiltonian of Eq. (1). Since bulk only differs from the monolayer only by a longer period of propagation and interlayer AFM alignments, we focus on the monolayer hereafter for simplicity. As shown in Fig. 3(a), these simulations found that canted PS states form stripy domains and cover most of the area at low temperatures, which is consistent with the fact that the PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ states are the ground states of NiI₂ bulk. There are three domains that propagate along $\langle 1\bar{1}0\rangle$ or the equivalent $\langle 120\rangle$ and $\langle\bar{2}\bar{1}0\rangle$ directions, which is also in line with the observed three domains of NiI₂ monolayer Song et al. (2022). Note that the spin pattern shown in Fig. 3a is only 0.038 meV/Ni higher in energy than the ground state of PS${}^{\langle 1\bar{1}0\rangle}_{cant}$ monodomain. Interestingly, topological defects are predicted to occur at phase boundaries (see Fig. 3), which is in line with the prediction of skyrmion lattice in monolayer NiI₂ Amoroso et al. (2020).

To conclude, we adopted the symmetry-adapted cluster expansion method and built a realistic spin model for multiferroic NiI₂. Such model can reproduce well the experimental $\langle 1\bar{1}0\rangle$ propagating proper screw state, as well as the canting in its spin rotation plane. The Kitaev interaction is found to play a key role in NiI₂, and is proved to impose anisotropy on coplanar spin texture. Our work thus leads to a better understanding on the magnetism of NiI₂, as well as its type-II multiferroicity.