Real-Time Motion Planning of a Hydraulic Excavator
using Trajectory Optimization and Model Predictive Control

We classify studies on excavator trajectory planning into three classes: 1) trajectory-optimization-based approach, 2) receding horizon optimization-based approach, and 3) non-optimization-based approach.

Given a specified cost function, constraints, and system dynamics, trajectory optimization generates an optimized trajectory in the defined state and input space which satisfies a set of constraints and system dynamics. Thanks to this property of explicit satisfaction of constraints, [6, 7, 9] successfully reflect the system dynamics with force/torque input, operational constraints, and physical constraints while minimizing overall effort or operation time. However, considering that optimization over the entire trajectory entails burdensome computation in general, the trajectories are usually parameterized using relatively simple kernel functions [7, 8]. Additionally, although soil model is employed to consider soil-bucket interaction forces [7, 9], the actual soil-bucket interaction may not be suitably addressed. There also exist studies regarding trajectory optimization of a new platform, e.g. a walking excavator [10, 11]. Nevertheless, unlike other studies for conventional hydraulic excavator, they focus on planning and control of locomotion using newly added degrees of freedom (DoF) which is out of our scope.

As a variation of trajectory optimization, receding horizon trajectory optimization or model predictive control (MPC), which optimizes trajectory in a receding horizon manner, is introduced [12, 13]. [12] applies offset-free MPC to track the reference trajectory even in the presence of soil interaction disturbance while satisfying input box constraints. However, only decoupled dynamics, each with single input and no state constraints, are considered in MPC. In [13], MPC is implemented for trajectory planning of an excavator, but system dynamics is modeled only with a double integrator, and the computation time seems to be insufficient for real-time application ($\approx$ 3.3 Hz).

Different from trajectory optimization, [14] computes a kinematically feasible reachability map of the bucket pose and linear movements offline. In [1], the authors apply dynamic motion primitives (DMP) to plan a trajectory which emulates experts’ operation while being robust to various soil conditions. However, since these approaches cannot explicitly consider constraints, violation of constraints, especially physical constraints, can occur. To handle such physical constraints, studies with a walking excavator [15, 16] present a hierarchical optimization-based controller. Nevertheless, feasibility cannot be always guaranteed due to the imposed hierarchy among constraints, and nonlinear constraints such as power constraint may not be directly considered in the optimization. In [15], additional force controller tracking a force reference instead of a position reference is implemented in simulation to adjust to unknown soil conditions.

To address both operational constraints and physical constraints in the presence of external disturbance during excavation, we present an integrated planner consisting of an online global planner and a real-time local planner as in Fig. 2. Considering that the global planning does not require any measurement feedback, the integrated planner can be executed in real-time if the global planner is computed within the trajectory run time.

In the global planning phase, a small-sized nonlinear optimization problem with a reduced number of constraints is solved. The obtained global trajectory is tracked by the model-predictive-control-based local planner, which plans high-fidelity local trajectories. The local planner runs alongside with a disturbance estimator, and takes the estimation results into consideration. To the best of our knowledge, this work is the first real-time trajectory planning framework for autonomous excavation with guarantee of dynamic feasibility, physical constraint satisfaction, and disturbance-awareness. We summarize our main contributions as follows:

• •

  Integration of global planner and local planner for considering both operational and physical constraints.

• •

  Formulation of the global trajectory optimization problem of the reduced dimension, which permits computation time shorter than a few seconds.

• •

  Real-time constrained trajectory generation considering external disturbance.

Let $\mathscr{F}_{B}$ and $\mathscr{F}_{C}$ be the base frame and cabin frame where the base frame’s relative orientation is defined by the ground slope, and the orientation of $\mathscr{F}_{C}$ differs from that of $\mathscr{F}_{B}$ by the amount of swing rotation. The origin and $x,z$-axis of $\mathscr{F}_{C}$ are illustrated in Fig. 3. The configuration of the mechanical system of a hydraulic excavator can be either defined with $\mathbf{q}_{\theta}=[\psi_{U}\ \theta_{B}\ \theta_{A}\ \theta_{K}]^{\top}\in\mathbb{R}^{4}$ or $\mathbf{q}_{L}=[\psi_{U}\ L_{B}\ L_{A}\ L_{K}]^{\top}\in\mathbb{R}^{4}$ where $\psi_{U},\theta_{B},\theta_{A},\theta_{K}$ are swing angle, rotation angles of boom, arm, and bucket, and $L_{B},L_{A},L_{K}$ are cylinder displacements of boom, arm, and bucket as shown in Fig. 1. The nonlinear, bijective¹¹1This is true within a physically feasible region, and the region is considered in the local planning as a cylinder displacement constraint. mapping between $\mathbf{q}_{\theta}$ and $\mathbf{q}_{L}$ can be derived by solving closed-chain kinematics, denoted by

	$\displaystyle\mathbf{q}_{\theta}$	$\displaystyle=g_{L}(\mathbf{q}_{L}),$	$\displaystyle\ \mathbf{q}_{L}$	$\displaystyle=g_{\theta}(\mathbf{q}_{\theta}),$		(1)
	$\displaystyle\dot{\mathbf{q}}_{\theta}$	$\displaystyle=J_{L}(\mathbf{q}_{L})\dot{\mathbf{q}}_{L},$	$\displaystyle\ \dot{\mathbf{q}}_{L}$	$\displaystyle=J_{\theta}(\mathbf{q}_{\theta})\dot{\mathbf{q}}_{\theta},$

where $J_{L},J_{\theta}$ are corresponding Jacobian matrices.

In some parts of this paper, the $\mathbf{q}_{L}$-configuration with fixed $\psi_{U}$ is used. For the sake of notational simplicity, we denote this subconfiguration by $\mathbf{L}=[L_{B}\ L_{A}\ L_{K}]^{\top}\in\mathbb{R}^{3}$. We also denote the pose of the bucket tip with respect to the $\mathscr{F}_{C}$ frame by $\mathbf{E}=[E_{x}\ E_{z}\ \theta]^{\top}\in\mathbb{R}^{3}$ where $E_{x},E_{z}$ are the bucket tip’s $x$, $z$-directional positions, and $\theta$ is its orientation, i.e., $\theta=\theta_{B}+\theta_{A}+\theta_{K}$. The components of $\mathbf{E}$ can be computed from $\mathbf{L}$ using the forward kinematics. We write them as $\mathbf{E}=[E_{x}(\mathbf{L})\ E_{z}(\mathbf{L})\ \theta(\mathbf{L})]^{\top}$.

By defining the system state $\mathbf{x}_{\theta}=[\mathbf{q}_{\theta}^{\top}\ \dot{\mathbf{q}}_{\theta}^{\top}]^{\top}\in\mathbb{R}^{8}$ and control input $\mathbf{u}=[T_{U}\ F_{B}\ F_{A}\ F_{K}]^{\top}\in\mathbb{R}^{4}$ where $T_{U},\ F_{B},\ F_{A},\ F_{K}$ are swing torque, hydraulic forces of boom, arm, and bucket cylinder, the system dynamics can be derived with the Euler-Lagrange equation:

$$\dot{\mathbf{x}}_{\theta}=\left[\begin{matrix}\dot{\mathbf{q}}_{\theta}\\ \ddot{\mathbf{q}}_{\theta}\end{matrix}\right]=\left[\begin{matrix}\dot{\mathbf{q}}_{\theta}\\ M_{\theta}^{-1}(-h_{\theta}+J_{\theta}^{\top}\mathbf{u}+\Delta)\end{matrix}\right]\eqqcolon f_{\theta}(\mathbf{x}_{\theta},\mathbf{u},\Delta)$$

(2)

where $M_{\theta}(\mathbf{q}_{\theta})\in\mathbb{R}^{4\times 4}$, $h_{\theta}(\mathbf{q}_{\theta},\dot{\mathbf{q}}_{\theta})\in\mathbb{R}^{4}$ are the mass matrix and combined term for the Coriolis-centrifugal and gravitational effects. $\Delta\in\mathbb{R}^{4}$ is a lumped disturbance describing unmodeled dynamics, e.g. friction in hydraulic cylinders, soil-bucket interaction, and model uncertainties.

As explained in section III and IV, since several state constraints considered in global and local planning can be expressed as linear constraints with respect to the hydraulic cylinder’s motion, we further modify the system dynamics (2) with the newly defined system state $\mathbf{x}_{L}=[\mathbf{q}_{L}^{\top}\ \dot{\mathbf{q}}_{L}^{\top}]^{\top}$. The equations of motion (2) can be rewritten with respect to $\mathbf{x}_{L}$ and $\mathbf{u}$ as follows:

$$\dot{\mathbf{x}}_{L}=\left[\begin{matrix}\dot{\mathbf{q}}_{L}\\ \ddot{\mathbf{q}}_{L}\end{matrix}\right]=\left[\begin{matrix}\dot{\mathbf{q}}_{L}\\ M_{L}^{-1}(-h_{L}+\mathbf{u}+\Delta_{L})\end{matrix}\right]\eqqcolon f_{L}(\mathbf{x}_{L},\mathbf{u},\Delta_{L})$$

(3)

where $h_{L}(\mathbf{q}_{L},\dot{\mathbf{q}}_{L})=J_{L}^{\top}(\tilde{M}_{L}\dot{J}_{L}\dot{\mathbf{q}}_{L}+\tilde{h}_{L})$, $\Delta_{L}=J_{L}^{\top}\Delta$, and $M_{L}(\mathbf{q}_{L})=J_{L}^{\top}\tilde{M}_{L}J_{L}$. Here, by inserting the results of kinematics (1) into the $M_{\theta}(\mathbf{q}_{\theta})$ and $h_{\theta}(\mathbf{q}_{\theta},\dot{\mathbf{q}}_{\theta})$, $\tilde{M}_{L}$ and $\tilde{h}_{L}$ are defined as $\tilde{M}_{L}(\mathbf{q}_{L})\coloneqq M_{\theta}(g_{L}(\mathbf{q}_{L}))$ and $\tilde{h}_{L}(\mathbf{q}_{L},\dot{\mathbf{q}}_{L})\coloneqq h_{\theta}(g_{L}(\mathbf{q}_{L}),J_{L}(\mathbf{q}_{L})\dot{\mathbf{q}}_{L})$.

In this subsection, we set up the trajectory optimization problem for phase 2. For phase 2, we constrain the cabin part of the excavator from moving, in order to prevent the side plates of the bucket from pushing against the soil. The goal of phase 2 global planning is to minimize the length travelled by the hydraulic cylinders during the excavation task. Unlike phases 1 and 3, the excavator faces large and unpredictable external disturbance which originates from the direct contact between the earth and the bucket. Traditional torque- or force-minimizing strategies are therefore not suitable, since their optimality would be degraded due to external forces. The travelled distance of the hydraulic cylinders should preferably serve as a cost measure, as the earth shall always resist the bucket’s motion while in phase 2. At the same time, we should prefer large excavation volume, because digging more volume will naturally reduce the number of repetitive excavation tasks needed to complete a mission. To take the aforementioned considerations into account, we first discretize the phase 2 trajectory using $n_{2}+1$ waypoints, $\mathbf{L}_{0}$, $\mathbf{L}_{1}$, $\cdots$, $\mathbf{L}_{n_{2}}$ and propose the following cost function:

$$J_{\mathrm{Phase2}}=w_{{d}}\sum_{k=1}^{n_{2}}\mathinner{\!\left\lVert\mathbf{L}_{k}-\mathbf{L}_{k-1}\right\rVert}_{W}^{2}-w_{{v}}V,$$

(4)

where $V$ is the volume of the removed soil, $w_{{d}}>0$ and $w_{{v}}>0$ are weights associated with the distance travelled by the cylinder and $V$, respectively. $W$ is a positive-definite weight matrix, where $\lVert x\rVert_{Y}$ ($Y>0$) denotes a weighted 2-norm of a vector $x$ with a matrix $Y$.

In phase 2, earth surface $z_{\mathrm{surf}}$ and target shape $z_{\mathrm{target}}$ are described using polynomials over $x$, where $x$ and $z$ are given with respect to the frame $\mathscr{F}_{C}$ (Fig. 3):

	$\displaystyle z_{\mathrm{surf}}$	$\displaystyle=a_{0}^{\mathrm{surf}}+a_{1}^{\mathrm{surf}}x+\cdots+a_{n_{\mathrm{surf}}}^{\mathrm{surf}}x^{n_{\mathrm{surf}}}$		(5)
	$\displaystyle z_{\mathrm{target}}$	$\displaystyle=a_{0}^{\mathrm{target}}+a_{1}^{\mathrm{target}}x+\cdots+a_{n_{\mathrm{target}}}^{\mathrm{target}}x^{n_{\mathrm{target}}}.$

Within the region of interest $x\in[x_{\mathrm{min}},x_{\mathrm{max}}]$, the earth surface should be above the target, i.e., $z_{\mathrm{target}}(x)\leq z_{\mathrm{surf}}(x)$. Now, we consider the following constraints for the bucket tip.

1. 1.

   The bucket tip should always be located within the region of interest, above the target surface and below the earth. At initial and final conditions, it must be located on the earth surface.

2. 2.

   The rotation angle $\theta$ of the bucket tip must be monotonically increasing; otherwise, the bucket plate pushes the dirt out of the bucket, which is energy-inefficient.

3. 3.

   The bucket must maintain positive clearance angle ($\alpha>0$) while digging. This ensures that the bucket parts other than the tip do not push against the ground.

4. 4.

   In the similar sense, the whole bucket body must move above the tip path.

5. 5.

   The bucket rotation $\theta$ must be smaller than $\pi$: otherwise, the excavator will spill the dirt onto its wrist, which will escalate the risk of equipment malfunctioning. (Fig. 4)

The mentioned constraints are explained in Fig. 5.

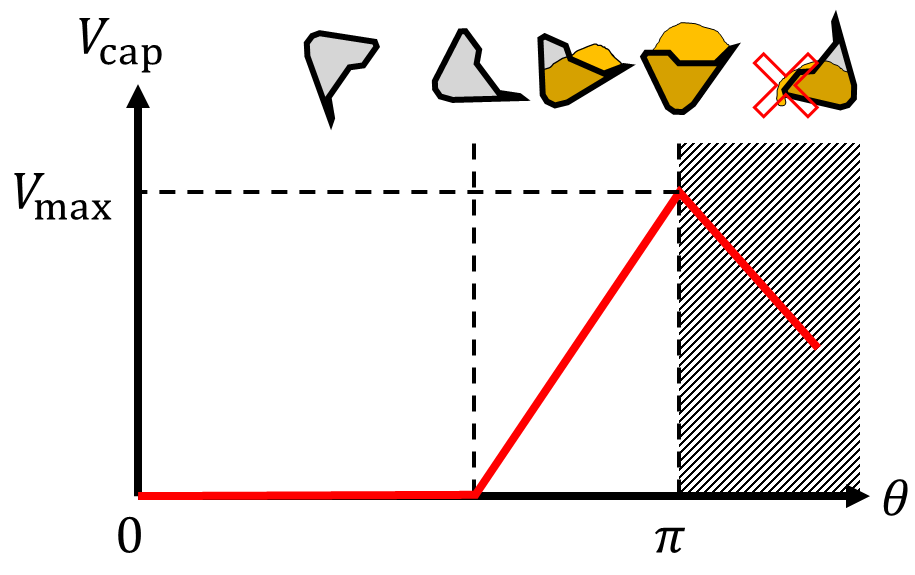
Basically, the volume of the removed dirt is geometrically determined using the swept volume between the earth surface and the bucket tip trajectory. However, if the swept volume is greater than the bucket capacity, the excavator shall spill the excess dirt, thus $V=\min{\left\{V_{\mathrm{swept}},V_{\mathrm{cap}}(\theta(\mathbf{L}_{n_{2}}))\right\}}$, where

	$\displaystyle V_{\mathrm{swept}}=$	$\displaystyle\int_{x_{n_{2}}}^{x_{0}}{z_{\mathrm{surf}}(x)\;dx}$		(6)
	$\displaystyle{}-$	$\displaystyle{}\frac{z_{0}+2z_{1}+\cdots+2z_{n_{2}-1}+z_{n_{2}}}{2n_{2}}\cdot\left(x_{0}-x_{n_{2}}\right)$

is the (approximate) swept volume calculated using the trapezoidal integration rule, $x_{i}=E_{x}(\mathbf{L}_{i})$, $z_{i}=E_{z}(\mathbf{L}_{i})$, and $\theta_{i}=\theta(\mathbf{L}_{i})$. The maximum capacity of the bucket, which is a function of $\theta_{n_{2}}$, is modeled as described in Fig. 4.

Unlike phase 2, in phases 1 and 3, the bucket travels a long distance while influenced by fewer constraints. Therefore, in order to reduce the computation burden, we parameterize the trajectory using a pre-selected set of bases. In this paper, Bernstein polynomials are used to parameterize the $\mathbf{q}_{L}$ trajectory. Bernstein polynomial is written as

$$p(s)=\sum_{k=0}^{n}\beta_{k}\cdot\binom{n}{k}s^{k}(1-s)^{n-k},$$

(7)

where $s\in[0,1]$. Bernstein bases are used because the convex hull property of the bases allows to incorporate the box constraint for $\mathbf{q}_{L}$ and linear inequality constraints for $\dot{\mathbf{q}}_{L}$ easily. Furthermore, their time-derivatives can be easily calculated, so faster computation speed can be achieved. For phases 1 and 3, we minimize the force cost during travel.

	$\displaystyle\underset{\beta_{k},\;T}{\mathrm{min.}}$	$\displaystyle\quad\int_{0}^{T}{\frac{1}{2}\mathbf{u}^{\top}W_{u}\mathbf{u}}\;dt$		(8)
	$\displaystyle\mathrm{s.t.}$	$\displaystyle\quad\mathbf{q}_{L}(t)=\sum_{k=0}^{n}{\beta_{k}\binom{n}{k}\left(\frac{t}{T}\right)^{k}\left(1-\frac{t}{T}\right)^{n-k}}$
		$\displaystyle\quad{\mathbf{q}}_{L}^{l}\leq\beta_{k}\leq{\mathbf{q}}_{L}^{u}\quad\forall 0\leq k\leq n$
		$\displaystyle\quad{\dot{\mathbf{q}}}_{L}^{l}\leq\frac{n\cdot(\beta_{k+1}-\beta_{k})}{T}\leq{\dot{\mathbf{q}}}_{L}^{u}\quad\forall 0\leq k\leq n-1$
		$\displaystyle\quad\mathbf{q}_{L}(0)=\mathbf{q}_{L\cdot 0},\;\dot{\mathbf{q}}_{L}(0)=\dot{\mathbf{q}}_{L\cdot 0}$
		$\displaystyle\quad\mathbf{q}_{L}(T)=\mathbf{q}_{L\cdot T},\;\dot{\mathbf{q}}_{L}(T)=\dot{\mathbf{q}}_{L\cdot T},$

where $\beta_{k}$ is the $k$-th control point for the Bernstein polynomial representation of $\mathbf{q}_{L}$, and $T$ is the time cost for complete traversal. Superscripts $(\cdot)^{l}$ and $(\cdot)^{u}$ denote lower and upper bounds for the state variables, respectively. The boundary values $\mathbf{q}_{L\cdot 0}$, $\mathbf{q}_{L\cdot T}$, $\dot{\mathbf{q}}_{L\cdot 0}$, $\dot{\mathbf{q}}_{L\cdot T}$ are chosen such that the transition between any two consecutive phases is smooth. $W_{u}$ is a positive-definite weighting matrix. The middle term in the third constraint is the control points for $\dot{\mathbf{q}}_{L}$ and was derived from the properties of Bernstein bases. For phase 3, to keep the excavator from spilling the dirt, we introduce one additional constraint:

$$\theta_{0}\leq\theta(\beta_{k})\leq\pi,$$

(9)

where $\theta_{0}$ is the bucket rotation angle at which phase 2 ended.

Similar to other existing researches for trajectory optimization of a hydraulic excavator [6, 7], we consider four types of physical constraints in the local planning: 1) actuation (force/torque) limit, 2) power limit, 3) cylinder displacement limit, and 4) pump flow rate limit. They are modeled as

	$$\displaystyle\begin{split}\mathbf{u}^{l}\leq\mathbf{u}\leq\mathbf{u}^{u}\end{split}$$		(10a)
	$$\displaystyle\begin{split}p=\mathbf{u}^{\top}\dot{\mathbf{q}}_{L}\leq p^{u}\end{split}$$		(10b)
	$$\displaystyle\begin{split}\mathbf{L}^{l}\leq\mathbf{L}\leq\mathbf{L}^{u}\end{split}$$		(10c)
	$$\displaystyle\begin{split}f_{i}=A_{i}(\text{sgn}(\dot{\mathbf{q}}_{L}))^{\top}\dot{\mathbf{q}}_{L}^{\text{abs}}\leq f^{u}_{i},\ i=1,2\end{split}$$		(10d)

where $\mathbf{u}^{l},\mathbf{u}^{u}\in\mathbb{R}^{4}$ in (10a) are the lower and upper bounds of the control input $\mathbf{u}$, and $p^{u}\in\mathbb{R}$ in (10b) is the upper bound of the overall power generated by the hydraulic pump. It is required to impose this overall power limit because of the actuation mechanism of the hydraulic excavator where all four control inputs are powered by the same actuation source. $\mathbf{L}^{l},\mathbf{L}^{u}\in\mathbb{R}^{3}$ in (10c) are the lower and upper bounds of the hydraulic cylinder displacement $\mathbf{L}$. Lastly, $f^{u}_{i}\in\mathbb{R}$ and $A_{i}=[A_{U,i}\ A_{B,i}\ A_{A,i}\ A_{K,i}]^{\top}\in\mathbb{R}^{4}$ in (10d) are the upper bound of the pump flow rate and cross-section areas corresponding to swing motion, boom, arm, and bucket cylinder displacement, respectively. Because the cross-section area differs depending on the motion of a hydraulic cylinder, either contraction or expansion, $A_{i}$ is defined to include such effect and modeled as a function of sign of $\dot{\mathbf{q}}_{L}$ [6]. $(\cdot)^{\text{abs}}$ is used to denote an element-wise absolute-valued vector mapped from a vector $(\cdot)$. To consider the flow rates of two hydraulic pumps, the subscript $i$ is used.

As mentioned in [21, 22], if disturbance is not properly considered in the system dynamics of MPC, constraints, especially state constraints, can be violated even if they were satisfied in the predicted trajectory computed with nominal dynamics. To alleviate such feasibility issue, inspired by successful demonstrations of integration between model predictive control and disturbance estimation in robotics [23, 24], we combined disturbance estimation and model predictive control for disturbance-awareness of the computed local reference trajectory.

We design a real-time disturbance estimation algorithm based on momentum-based disturbance estimation [1, 25]. Considering the system dynamics based on the joint angles of the excavator (2), the momentum-based disturbance estimation algorithm is formulated as follows:

	$\displaystyle\hat{\Delta}$	$\displaystyle=K_{E}\left(p-p(0)-\int_{0}^{t}\left(J_{\theta}^{\top}\mathbf{u}+C_{\theta}^{\top}\dot{\mathbf{q}}_{\theta}-G_{\theta}+\hat{\Delta}\right)\,d\tau\right)$		(11)
	$\displaystyle p$	$\displaystyle=M_{\theta}\dot{\mathbf{q}}_{\theta}$

where $C_{\theta}\in\mathbb{R}^{4\times 4},G_{\theta}\in\mathbb{R}^{4}$ are Coriolis matrix and gravity vector computed from the Euler-Lagrange equation. Utilizing the fact that $\dot{M}_{\theta}=C_{\theta}+C_{\theta}^{\top}$, the estimation algorithm can be analyzed to operate as a low pass filter of the actual disturbance $\Delta$ as $\dot{\hat{\Delta}}=K_{E}(\Delta-\hat{\Delta}).$ The disturbance estimate of the cylinder displacement-based dynamics (3) then can be computed as $\hat{\Delta}_{L}=J_{L}^{\top}\hat{\Delta}\eqqcolon[\hat{\Delta}_{U}\ \hat{\Delta}_{B}\ \hat{\Delta}_{A}\ \hat{\Delta}_{K}]^{\top}.$

Based on the system dynamics (3) and constraints (10), the MPC problem is formulated as follows:

	$\displaystyle\underset{\mathbf{u}_{k}}{\textrm{min.}}$	$\displaystyle\ \lVert\mathbf{x}_{N}-\mathbf{x}_{r,N}\rVert_{P}^{2}+\sum_{k=0}^{N-1}\lVert\mathbf{x}_{k}-\mathbf{x}_{r,k}\rVert_{Q}^{2}+\lVert\mathbf{u}_{k}\rVert_{R}^{2},$		(12)
	s.t.	$\displaystyle\ \mathbf{x}_{k+1}=f_{d}(\mathbf{x}_{k},\mathbf{u}_{k},\hat{\Delta}_{k})$
		$\displaystyle\ c_{k,i}(\mathbf{x}_{k},\mathbf{u}_{k})\geq 0\ \quad\forall 0\leq i\leq m_{k}-1$
		$\displaystyle\ c_{N,i}(\mathbf{x}_{k})\geq 0\ \quad\forall 0\leq i\leq m_{N}-1$

where $N$ is the number of the prediction horizon, $f_{d}$ is the discretized dynamics of (3), $c_{k,i},c_{N,i}$ are the inequality constraints (10), and $m_{k},m_{N}$ are the number of inequality constraints. $P$, $Q$, $R$ are positive-definite weighting matrices. Here, the subscript $L$ is omitted in the state $\mathbf{x}$, dynamics $f_{d}$, and disturbance estimate $\hat{\Delta}$ for brevity. A quadratic objective function is designed to allow the excavator to track the global reference trajectory $\mathbf{x}_{r}$ while minimizing the overall effort $\sum\lVert\mathbf{u}\rVert_{R}$. Lastly, similar to the widely adopted assumptions in papers on disturbance-aware model predictive control [22, 24, 23], we assume that the disturbance does not vary significantly over a short time horizon, i.e. $\hat{\Delta}_{k+1}=\hat{\Delta}_{k}$.

To solve the formulated MPC problem (12), most optimal control solvers require partial derivatives, either numerical or analytic, of the dynamics (3) and constraints (10) with respect to the state $\mathbf{x}$ and the input $\mathbf{u}$. However, due to the high nonlinearity of the system dynamics (3), especially the matrix inverse of the mass matrix $M_{L}$ which inheres in the closed-chain kinematics, it is difficult to obtain an optimized solution in real-time. Therefore, we simplify the MPC problem by introducing a virtual input $\mathbf{v}\in\mathbb{R}^{4}$ and a feedback-linearization-based control law $\mathbf{u}=\text{FL}(\mathbf{x},\mathbf{v})\coloneqq h_{L}+M_{L}\mathbf{v}-\hat{\Delta}_{L}$ through which the original nonlinear dynamics (3) is transformed into a linear dynamics as

$$\begin{gathered}\dot{\mathbf{x}}=A_{c}\mathbf{x}+B_{c}\mathbf{v}\\ A_{c}=\left[\begin{matrix}0_{4\times 4}&I_{4}\\ 0_{4\times 4}&0_{4\times 4}\end{matrix}\right],B_{c}=\left[\begin{matrix}0_{4\times 4}\\ I_{4}\end{matrix}\right]\end{gathered}$$

(13)

where $0_{4\times 4},I_{4}\in\mathbb{R}^{4\times 4}$ are zero and identity matrices. The feedback-linearization-based MPC problem is then formulated as follows:

	$\displaystyle\underset{\mathbf{v}_{k}}{\textrm{min.}}$	$\displaystyle\ \lVert\mathbf{x}_{N}-\mathbf{x}_{r,N}\rVert_{\tilde{P}}^{2}+\sum_{k=0}^{N-1}\lVert\mathbf{x}_{k}-\mathbf{x}_{r,k}\rVert_{\tilde{Q}}^{2}+\lVert\mathbf{v}_{k}\rVert_{\tilde{R}}^{2},$		(14)
	s.t.	$\displaystyle\ \mathbf{x}_{k+1}=A_{d}\mathbf{x}_{k}+B_{d}\mathbf{v}_{k}$
		$\displaystyle\ c_{k,i}(\mathbf{x}_{k},\text{FL}(\mathbf{x}_{k},\mathbf{v}_{k}))\geq 0\ \quad\forall 0\leq i\leq m_{k}-1$
		$\displaystyle\ c_{N,i}(\mathbf{x}_{k})\geq 0\ \quad\forall 0\leq i\leq m_{N}-1$

where $\tilde{P}$, $\tilde{Q}$, $\tilde{R}$ are positive-definite weight matrices, and $A_{d},B_{d}$ are constant matrices in the discretized dynamics, corresponding to $A_{c}$ and $B_{c}$ in the continuous counterpart (13).

We validate the proposed planning algorithms in simulation. The overall flow chart during simulation is illustrated in Fig. 2. All modules in Fig. 2 are individually implemented in Robot Operating System (ROS) using C++. Excavator dynamics simulator (PLANT in Fig. 2) is based on the derived system dynamics (2) where the external disturbance $\Delta$ is modeled with a steady-state modified LuGre friction model [26] for cylinder friction and modified Fundamental Earth-moving Equation (FEE) [27, 7] for soil-bucket interaction. Note that friction and soil-bucket interaction models are introduced only to construct a realistic simulation environment and are unknown to the planning algorithms. Parameters in the system dynamics and physical constraints are from the Hyundai HX300L model in Fig. 1.

As a motion controller, which computes the control input $\mathbf{u}$ based on the reference trajectory $\mathbf{x}_{d}$ generated from the local planning module, we adopt a feedback linearization-based PID controller: $\mathbf{u}=J_{\theta}^{-\top}(h_{\theta}-\hat{\Delta}+M_{\theta}\mathbf{u}_{\text{PID}})$. Applying the control input $\mathbf{u}$ to the system equation (2), input-output stability of the closed-loop system can be derived [28, Ch. 5] where the input is the estimation error of the external disturbance $\tilde{\Delta}=\Delta-\hat{\Delta}$ multiplied by the inverse of the mass matrix $M_{\theta}$, and the output is the state $\mathbf{x}$.

The global planner is implemented using ALGLIB [29], an open-source nonlinear optimization solver. We use 9 Bernstein control points for phases 1 and 3, respectively, and 20 via points for phase 2. Next, to solve the formulated model predictive control problem (14), we implement differential dynamic programming (DDP) with augmented Lagrangian method [30], which is an algorithm widely exploited in various robotic application for real-time trajectory optimization [19, 17, 18]. It transforms the original constrained MPC problem into an unconstrained problem using the Lagrangian and quadratic penalty function, which is then solved with the conventional DDP algorithm. For MPC implementation, we employ the time horizon of 1000 ms, control discretization and integration rate of 20 ms. Except for the results of cylinder displacements $\mathbf{L}$, which are normalized with constant bias and constant normalization factors, the other results related to physical limits of Hyundai HX300L displayed in Fig. 7 and Fig. 8 are normalized with constant normalization factors, denoted with $\bar{(\cdot)}$. Each element of control inputs and the corresponding channel of disturbance estimates are normalized with the same factor for comparison.

To validate the proposed framework, we conducted two simulation scenarios on a desktop computer equipped with an Intel Core i7-9750 CPU at 2.6 GHz, by varying the target excavation depth: 1) shallow excavation and 2) deep excavation. As depicted in Fig. 2, we assume prior knowledge of the environment, i.e. the ground shape, which can be obtained either from onboard sensors like lidars and cameras, or from external sensors like total station in real experiment.