Reactive Multi-Robot Navigation in Outdoor Environments Through Uncertainty-Aware Active Learning of Human Preference Landscape
Abstract
Compared with single robots, Multi-Robot Systems (MRS) can perform missions more efficiently due to the presence of multiple members with diverse capabilities. However, deploying an MRS in wide real-world environments is still challenging due to uncertain and various obstacles (e.g., building clusters and trees). With a limited understanding of environmental uncertainty on performance, an MRS cannot flexibly adjust its behaviors (e.g., teaming, load sharing, trajectory planning) to ensure both environment adaptation and task accomplishments. In this work, a novel joint preference landscape learning and behavior adjusting framework (PLBA) is designed. PLBA efficiently integrates real-time human guidance to MRS coordination and utilizes Sparse Variational Gaussian Processes with Varying Output Noise to quickly assess human preferences by leveraging spatial correlations between environment characteristics. An optimization-based behavior-adjusting method then safely adapts MRS behaviors to environments. To validate PLBA’s effectiveness in MRS behavior adaption, a flood disaster search and rescue task was designed. 20 human users provided feedback based on human preferences obtained from MRS behaviors related to {”task quality”, ”task progress”, ”robot safety”}. The prediction accuracy and adaptation speed results show the effectiveness of PLBA in preference learning and MRS behavior adaption.
I Introduction
MRS has been widely used in complex real-world applications, such as disaster search-and-rescue [1] and planetary exploration [2]. However, deploying MRS in wide and unstructured environments remains challenging [3]. A significant contributor is the difficulty in smoothly and seamlessly integrating human guidance into the robot’s decision-making. But wide unstructured environments have various physical and logistical constraints [4], such as uncertain surroundings, limited communication, and unexpected obstacles. It’s challenging for humans to gain precise understandings of priority and safety factors in missions and adjust the behavior of the MRS in real-time [5].
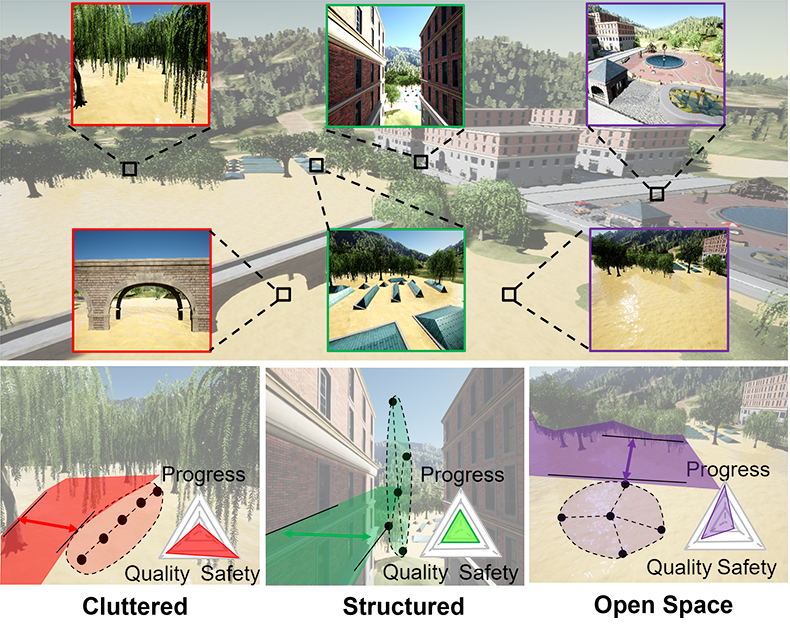
Currently, to enable more seamless integration and further improve robot survivability in real-world environments, many studies leverage machine learning methods to accurately predict human preferences for safe MRS deployments[6]. Although the learned human preference model can provide robots with a fast and comprehensive understanding of human expectations, its learning and deployment still have the following flaws. First, human preference is dynamically associated with robot behaviors, task progress, and environmental conditions. Estimating human preferences by using only pre-defined motions and ignoring the above factors is challenging. For example, as illustrated in Fig. 1, MRS deployed in open spaces flies fast and focuses more on task execution speeds, which is unacceptable for those deployed in a cluttered environment where robot safety is the primary consideration [7]. Second, humans may not always be capable of accurately determining their preferences, which results in uncertainty and noise in their feedback, hampering robots to utilize human preference for planning [8].
To improve the human-robot teaming with seamless human analysis and robot planning integrations, we proposed a novel joint preference landscape learning and MRS behavior-adjusting framework (PLBA), shown in Fig. 2. In PLBA, the Gaussian Process was used to quickly assess human preferences from noisy human feedback by leveraging spatial correlations between environment characteristics, and an optimization-based behavior control method was also used to ensure safe MRS behavior adjustments. As shown in Fig. 1, PLBA helps an MRS adapts to {”cluttered”, ”structured”, ”open space”} environments by balancing the task progress, execution quality, and robot safety. This paper has three major contributions:
-
1.
A novel joint preference landscape learning and MRS behavior-adjusting framework (PLBA) is developed to help robots understand relations between human preference landscape and environment’s characteristics. This framework largely reduces robots’ dependency on humans and improves robots’ autonomy level.
-
2.
An active collaboration-calibration scheme is designed to improve the human-MRS teaming. Instead of waiting for human corrections, PLBA actively requests human guidance based on its learning needs (predicted uncertainty level), which can reduce the negative impact of feedback unreliability.
II Related Work
Robots Adaptation to Unstructured Environments. In [9, 10, 11], a global environment classification model was learned to enable a robot to understand its surroundings and react in real-time. In [9], to develop a model for real-time perception and understanding of various environments, a lightweight neural network architecture was developed for real-time segmentation of navigable spaces. To efficiently learn an environment characterization model, [11] used the Probabilistic Gaussian method with sparse approximation to update parameters quickly. Although a global model can consider various features that may impact robots’ movements, one of the main challenges in deploying global models is that global models are large and require a lot of computational and memory resources. As a result, global models can be slow to generate predictions, limiting their practical applications in real-time scenarios. Instead of learning a global model, [12, 13] developed several approaches to train an accurate local model for robot autonomous navigation. Even with local performance, these models need to be updated and retrained for each new environment. The model does not retrain well in new environments, which may lead to unsafe robot behavior. In environments where the trained model has low accuracy, our PLBA method will seek guidance directly from the human operator, exploit the spatial correlations among similar environments for fast model updates, optimize robot behaviors, and improve planning safety even if the preference predictions are inaccurate.
Human Preference Model for Effective Humans-Robots Collaboration. Recent research was done to learn human preferences to better integrate humans into robot teaming. In [14, 15], active learning, addressing data inefficiencies by choosing the most informative queries, was used for robot learning as much as possible from a few questions. In [16, 17], the volume removal method, which aims to maximize the information gained from each query, was used to evaluate the performance of query methods. However, the above studies represented human preferences via a linear weighted sum of robot behaviors (e.g., moving speed, trajectory smoothness, and distance to obstacles), which can lead to the loss of valuable and informative information due to ignoring the dynamic and nonlinear influence entanglements among these behaviors [18]. Furthermore, human preference is subjective and dynamically related to task progress and environmental conditions, making linear assumptions unsuitable for human preference representation [19]. To solve the above issues, [20, 21, 22] adopted methods based on reinforcement learning and neural networks to model human preferences. Even though neural networks can learn the complex, non-linear relationship between human preferences and robot behaviors, their performance was significantly impacted by the inherent noise present in human feedback [8]. In response to this, our prior work[23] developed the Meta Preference Learning (MPL) method, which uses a meta-learning framework to adapt quickly to user preferences with minimal user input. This approach streamlines the integration of human guidance into MRS behavior adjustment, significantly reducing the cognitive load and frequency of human interventions required. In this work, to deal with varying levels of noise present in human feedback, the Gaussian Processes with Varying Output Noise is used to estimate the noise in the human feedback based on input. Then, the optimization-based MRS behavior adjustment approach can reliably and safely realize the predicted human preferences even with high-level uncertainty.
III Methods
III-A Problem statement
Human preference is parameterized by a set of actions with . Each action represents one factor characterizing the multi-robot flocking process. In this work, multi-output Gaussian Processes (GPs) are used to model the underlying human preference function , which doesn’t have strong assumptions about the form of . Human preference feedbacks in trial are collected into a data set , where denotes the total number of collected human feedbacks, represents noises in human feedback. Defining as the maximum posterior (MAP) estimation of given , we aim at using a Bayesian approach to iteratively update the parameters of to minimize the prediction error ().
III-B Multi-output GPs with varying output noise
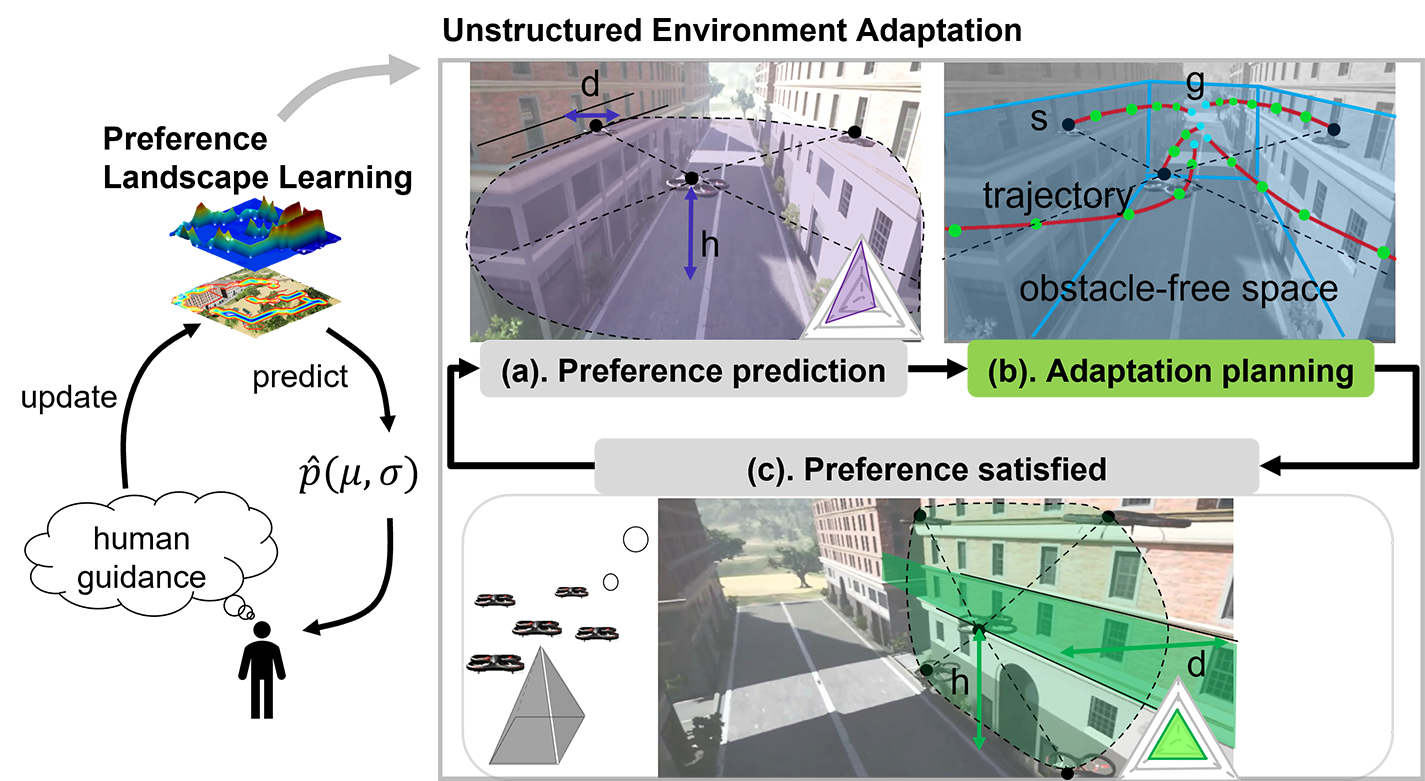
After the problem statement, we are now ready to use multi-output Gaussian Processes [24] to learn human preference function . The output of is denoted as . And the distribution of the stacked outputs () for all inputs is Gaussian distributed, where and the input is -dimension combined features. Like single-output GPs, multi-output GPs are fully specified by their mean and kernel functions. The matrix-valued kernel obeys the same positive definiteness properties where the input space is extended by the index of the output:
| (1) |
Then the distribution of can be denoted as:
| (2) |
| (3) |
Then, a linear transformation of independent functions is used to construct multi-output function :
| (4) |
| (5) |
where is a squared exponential kernel.
Given that the human feedback for each output has a different noise level, a Gaussian process model where different noises are assumed for the data points is used:
| (6) |
| (7) |
In this paper, the covariance of noise () is represented as a diagonal matrix:
| (8) |
where and are hyper-parameters related to human feedback noise. Then the distribution of combined with noise is shown as follows:
| (9) |
where is a diagonal matrix. With -dimension outputs and samples, a covariance matrix with computational complexity is needed for obtaining an accurate multi-output GP. Hence, a posterior approximation method (stochastic variational inference) is used. By introducing a set of inducing variables (), the computational complexity can be reduced to . At last, the Adam optimizer can optimize the noise variance and the variational parameters separately. Capturing the essence of our theoretical groundwork, Procedure 1 streamlines the execution of the PLBA framework (shown in Fig. 2), from mission initiation to MRS safety assurance during ongoing operations. The algorithmic procedure outlined offers a succinct roadmap for dynamic decision-making, integrating path planning and real-time adaptive behavior modeling, which is pivotal for the MRS’s performance in diverse environments. As for the optimization details, please refer to [24, 25].
III-C Preference-based safe MRS behavior adjustment
In this work, we extended the flocking method proposed in [26] by involving obstacle-free largest convex region searching and optimization-based MRS behavior planning for stable and safe robot behaviors. The desired MRS behavior adjusting velocity is calculated by:
| (10) |
where is the index of a drone and denotes the flocking speed. represents MRS team formation maintaining term. is short-range repulsion term and similarly denotes long-range attraction term. keeps a safe distance between robots and obstacles. maintains the robot at a preferred flying height. is velocity alignment term. Then to prevent from largely exceeding the human preferred flying speed, an upper limit is introduced:
| (11) |
Specifically, each type of speed can be parameterized by one or a few human preferences in the set . denotes the minimal distance between robots; denotes the flying height of robot system; represents the flying speed of multi-robot system; represents the minimal distance between robots and obstacles; and denotes coordination pattern. Next, we determine the largest convex region of obstacle-free space using an iterative regional inflation method based on semi-definite programming [27]. Drones are then assigned to the vertices of this convex region to establish the formation. The flocking model helps the drones maintain their relative positions within the formation throughout the operation.
To maintain informative and helpful interactions with humans and learn a more representative preference model via human feedback (developed in Section A), Algorithm 1 was developed to decide the timing and manner of seeking human guidance. In Algorithm 1, an interactive learning framework was designed by utilizing active learning to inquire informative guidance from humans. The mean and covariance of human preference predictions are calculated during the learning process. A high covariance value means that the human preference model does not generalize well to the current environment; thus, more human guidance is needed to refine the preference model. With the guidance of low-variance human preference, which means good preference estimation, MRS can adjust robot behavior safely without aggressive or unexpected adjustments.
IV Evaluation
A multi-robot search and rescue task in a flood disaster site was designed to evaluate PLBA’s effectiveness in supporting unstructured environment adaptation. The following two aspects were mainly validated: (i) the effectiveness of PLBA in fast human preference learning, which is for MRS fast adapt to the unstructured environment; (ii) the effectiveness of environment similarity for fast human preference learning.
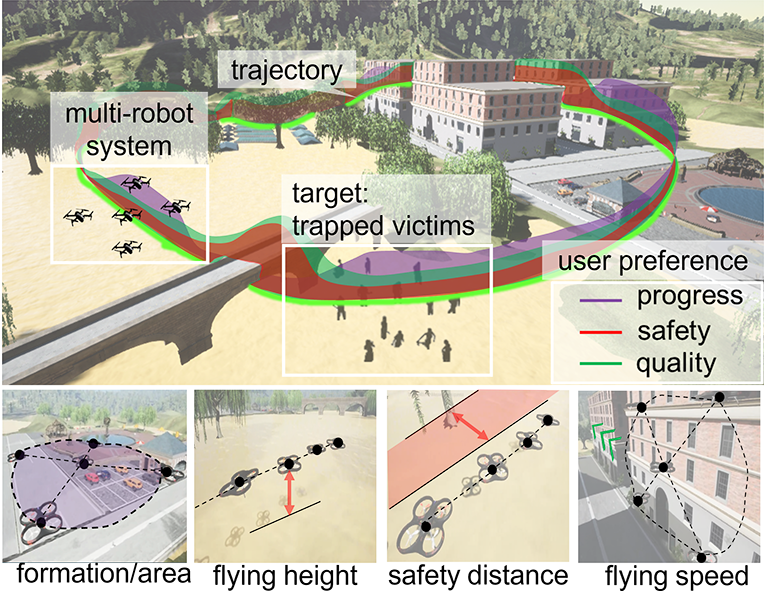
IV-A Experiment setting
In Fig. 3, an ”MRS search and rescue in flood disaster” environment was designed based on the software AirSim [29] and Unreal Engine [30]. The environment (400 400 ) was designed to include various scenes (city, bridge, forest, park, etc.), which is enough to test PLBA’s effectiveness in supporting unstructured environment adaptation. Five kinds of flocking behaviors that can illustrate human preferences were considered: 1). The ”flying height” denotes the average flying altitude of the MRS; 2). ”Coverage area” is represented by the minimum distance between drones; 3). The ”safe distance to the obstacle” is the minimum distance between the drone and obstacles; 4). ”Flying speed” represents the average speed of MRS; 5). ”Team formation” is represented by the assigned Cartesian positions of all robots.
In this work, outdoor environments mainly consist of four typical scenarios – ”City”, ”Park”, ”Forest”, ”County”, and ”River”. According to obstacle density, these scenarios can be roughly classified into three categories ”Cluttered”, ”Structured”, and ”Open Space”. ”Open Space” represents a scenario where there are no or few physical obstacles (e.g., lake and park). In ”Open Space” environments, humans can operate MRS more aggressively to achieve fast mission progress. ”Cluttered” represents areas that are characterized by an excessive accumulation of objects or debris, which can make it challenging to move around or perform activities (e.g., forest). Therefore, humans should operate MRS more reserved to pay more attention to robot safety. ”Structured” refers to spaces that are designed and organized with well-defined boundaries and guidelines, which are helpful to promote safety and consistency outcomes (e.g., city). Fig. 4 shows expected robot behavior corresponding to three specific environment types.
To analyze the effectiveness of PLBA in adaptation to outdoor environments, a test procedure for MRS to continuously adapt to multiple environments was designed; two baseline methods (linear regression and neural network regression) were used as comparison groups. The adaptation speed and prediction errors of human preferences in unfamiliar environments were comparatively analyzed. In addition, the relationship between environmental similarity and human preference prediction error was also analyzed, illustrating that the spatial correlation between environmental features can be used for environmental adaptation.
IV-B Result analysis
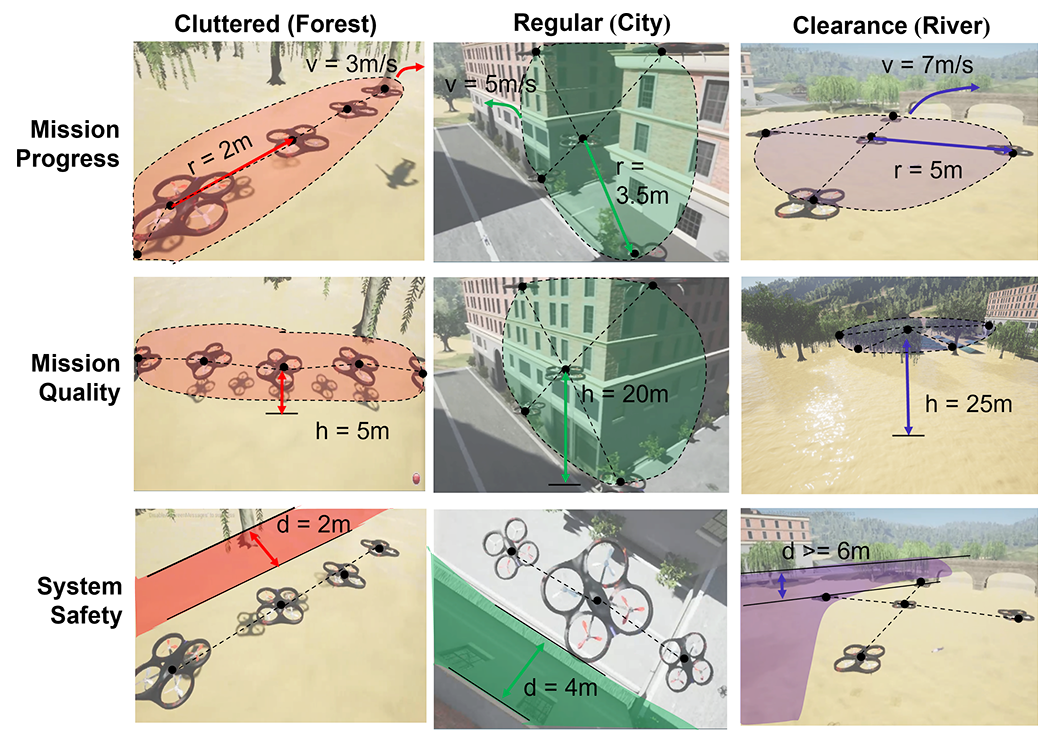
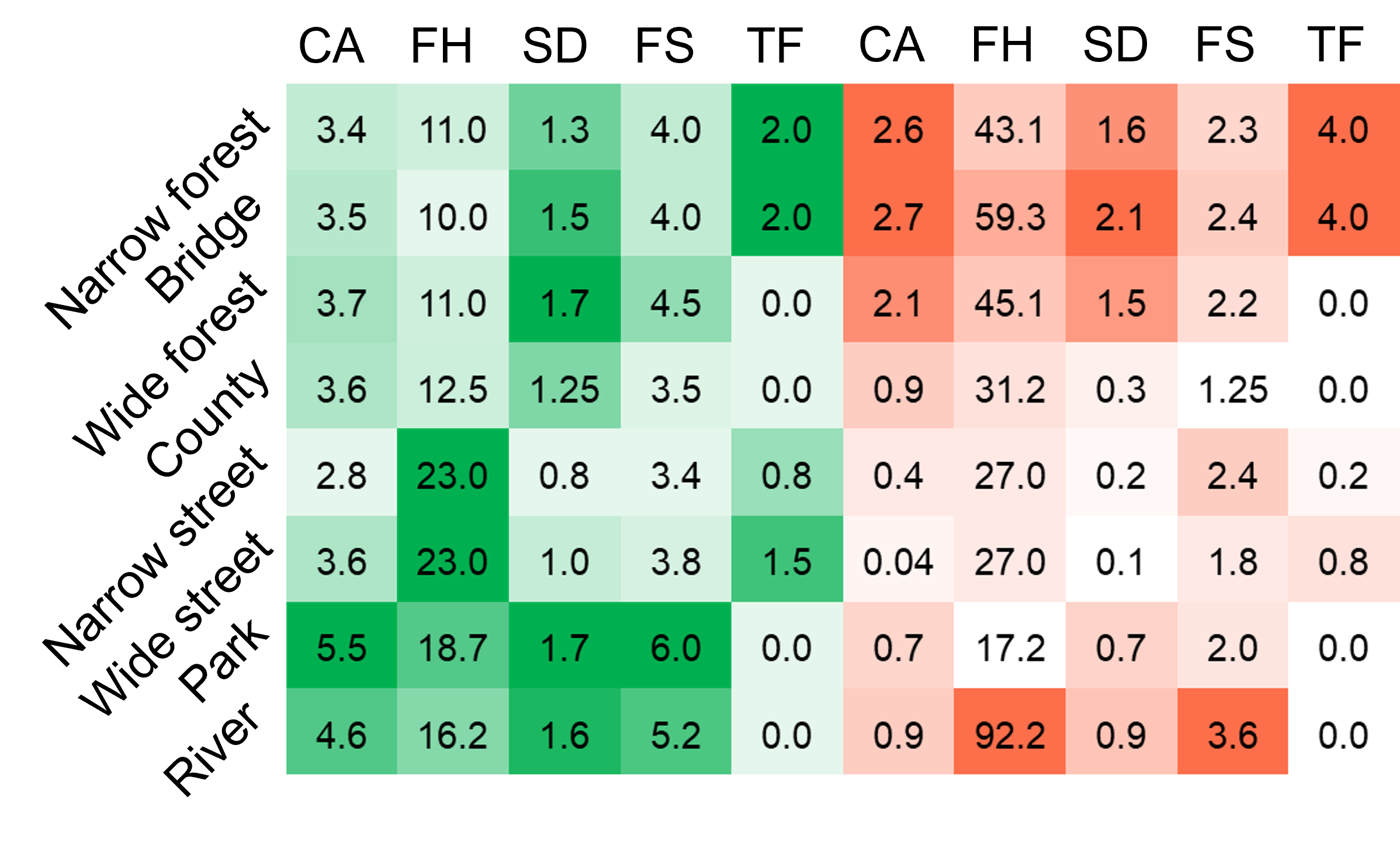
Human User Study. With the pioneer user study involving 20 human volunteers, the mean and variance human preference values in various environments were calculated. Then, two kinds of human preferences – simple human preference only with mean values and complex human preference with mean and variance values were conducted to validate the effectiveness of PLBA in rapid adaptation to unstructured environments. The details of human preferences are listed in Fig. 5. The sample behavior illustrations for human preferences in different environments are shown in Fig. 4.
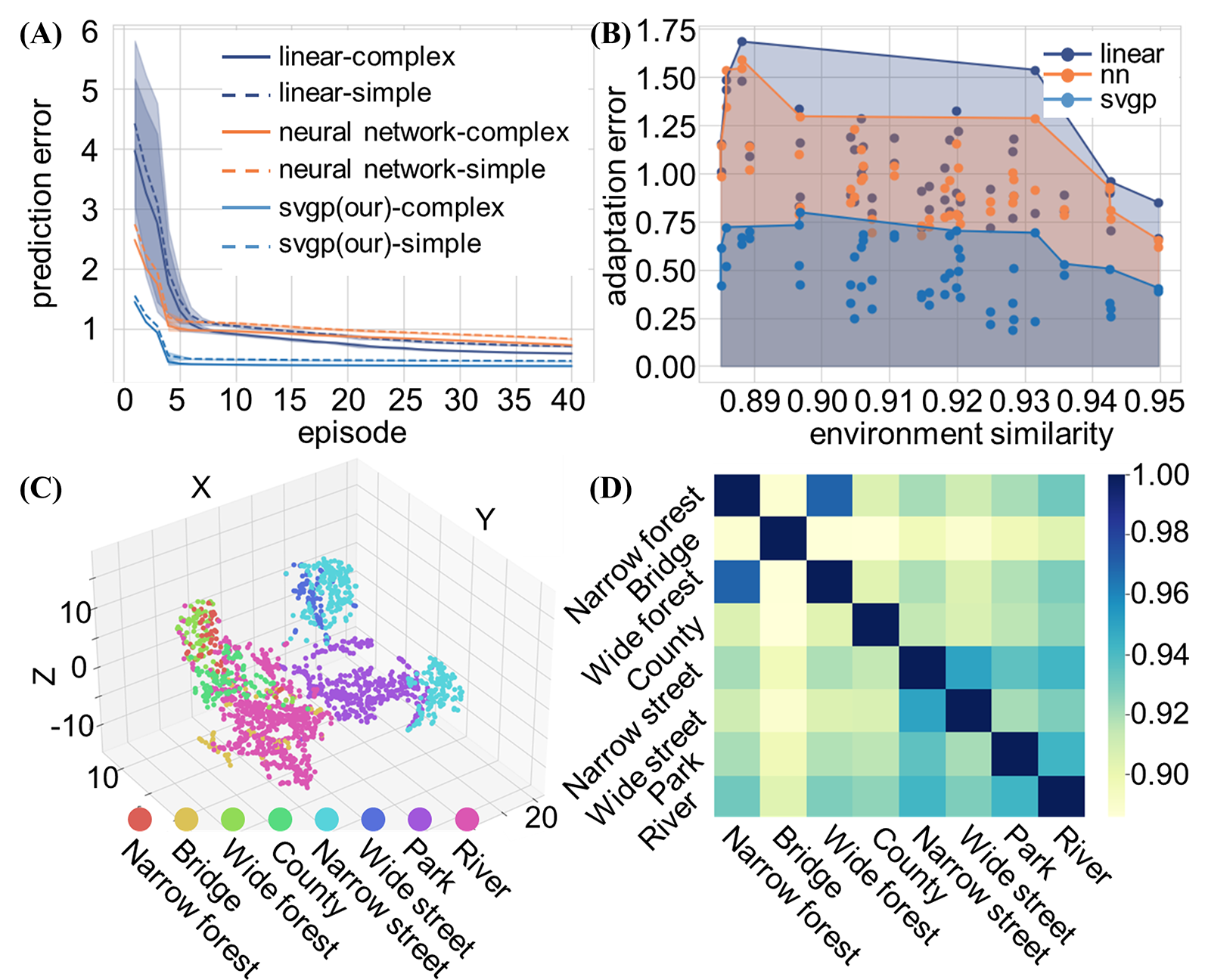
Environment analysis and learning Performance Validation. Under the guidance of volunteers, human preference over motion behaviors such as {”covering area”, ”flying height”, ”distance to an obstacle”, ”flying speed”, and ”team formation” } were collected to generate a data set with samples; the data set is mainly sampled from a flood disaster site which can be mainly categorized into eight typical environments. Each category includes about 12.5% of the total data samples. Each sample consists of environment features and corresponding human preference guidance. The environment features are concatenated by environment visual features, MRS status, and the relationship between MRS and the environment. The distribution and similarity of various environments are illustrated in Fig. 6 (C) and (D). As shown in Fig. 6 (A), after five updates, the losses between predicted human preference and real human preference generated by PLBA is less than 0.05; while the losses obtained from baseline methods are greater than 1.00. THey show the proposed method PLBA has a faster convergence speed to customize MRS motions for unstructured environment adaptation.
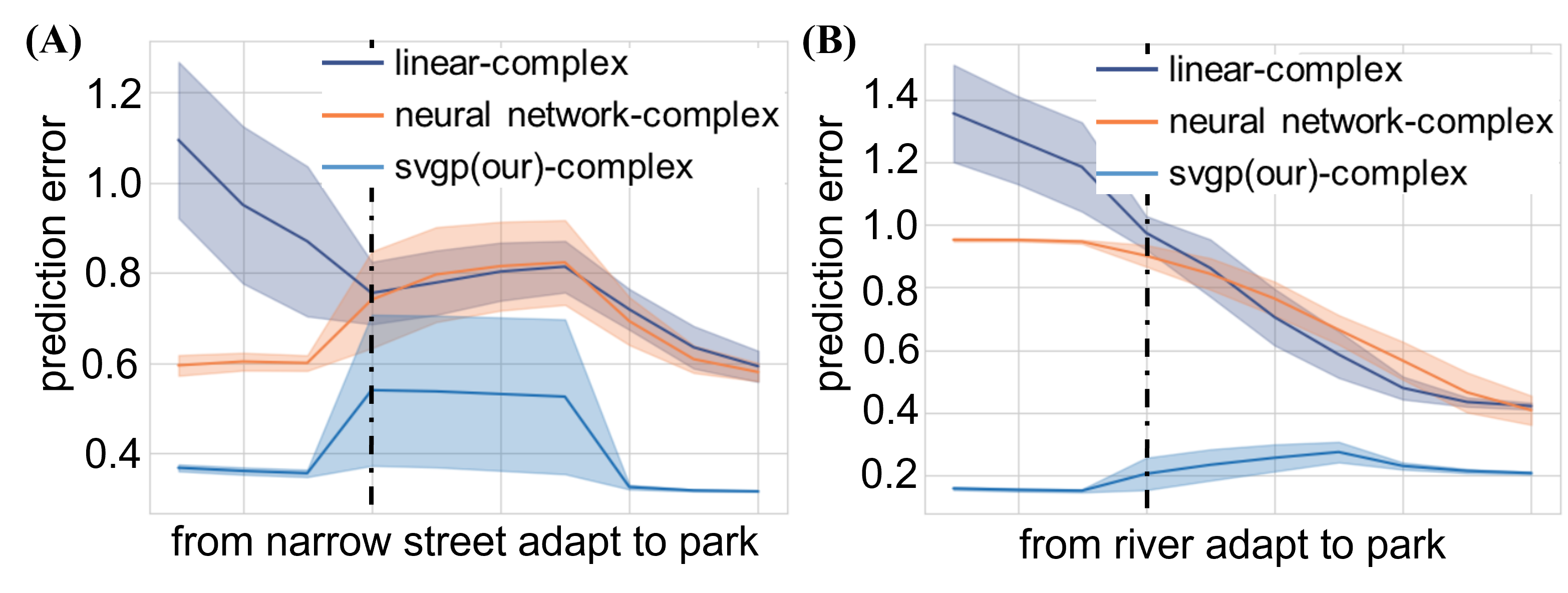
Adaptation Effectiveness Validation. The relationship between the prediction errors and environment similarity was analyzed to validate the method’s effectiveness in facilitating adaptation of unstructured environments. The rationale is that when two environments are similar, the prediction errors of a model trained in an old environment but used in new environments will be minimal. Two examples of changes in human preference prediction errors from one environment to another new environment were illustrated. As shown in Fig. 6 (B), the human preference adaptation error will decrease with the increase of similarity between the previous and new environments for our proposed method and all the baseline methods. That means the spatial correlation between environments can be leveraged for fast unstructured environment adaptation. Besides, the adaptation error of PLBA is 0.5 less than that of baseline methods, which means our proposed method is more suitable for fast and accurate unstructured environment adaptation. Fig. 7 shows two samples of new environment adaptation. (A) The human preference prediction error for MRS to adapt from a narrow street to a park environment is around 0.5; (B) while the human preference prediction error for MRS to adapt from a river to a park environment is around 0.3. That means the model trained in a river environment can quickly adapt to the park environment because the part environment is more similar to the river environment than the narrow street environment, verified in Fig. 6 (D).
V Conclusion and Future Work
This paper developed a novel joint preference landscape learning and MRS behavior-adjusting framework (PLBA) to establish a mapping between human preference landscape and unstructured environment’s characteristics and adjust MRS motions to follow human preferences over mission progress, quality, and system safety. To validate method effectiveness, a five-UAV-based multi-robot team was deployed for victim search in a flood disaster site; with 20 volunteer-based user studies, two types of user preferences were identified as ”simple-preference” – without variances and ”complex-preference” – with variance. Our proposed method’s effectiveness for unstructured environment adaptation was validated by the reduced update number and the adaptation error calculated by models updated only once in a new environment. Given the capability of enabling safe and cognitive teaming, PLBA can be extended to guide the flexible teaming of multiple robots and even the cooperation between vehicles and human units.
In the future, the adaptation method could be enriched by on-board sensing information to improve human-MRS collaboration further.
References
- [1] B. Reily, J. G. Rogers, and C. Reardon, “Balancing mission and comprehensibility in multi-robot systems for disaster response,” in 2021 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), pp. 146–151, 2021.
- [2] M. Kaufmann, T. S. Vaquero, G. J. Correa, K. Otstr, M. F. Ginting, G. Beltrame, and A.-A. Agha-Mohammadi, “Copilot mike: An autonomous assistant for multi-robot operations in cave exploration,” in 2021 IEEE Aerospace Conference (50100), pp. 1–9, 2021.
- [3] A. P. Cohen, S. A. Shaheen, and E. M. Farrar, “Urban air mobility: History, ecosystem, market potential, and challenges,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 9, pp. 6074–6087, 2021.
- [4] Q. Yu, Z. Shen, Y. Pang, and R. Liu, “Proficiency constrained multi-agent reinforcement learning for environment-adaptive multi uav-ugv teaming,” in 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), pp. 2114–2118, 2021.
- [5] S. Bansal, M. Chen, K. Tanabe, and C. J. Tomlin, “Provably safe and scalable multivehicle trajectory planning,” IEEE Transactions on Control Systems Technology, vol. 29, no. 6, pp. 2473–2489, 2021.
- [6] D. Callegaro, S. Baidya, G. S. Ramachandran, B. Krishnamachari, and M. Levorato, “Information autonomy: Self-adaptive information management for edge-assisted autonomous uav systems,” in MILCOM 2019 - 2019 IEEE Military Communications Conference (MILCOM), pp. 40–45, 2019.
- [7] G. Canal, G. Alenyà, and C. Torras, “Adapting robot task planning to user preferences: an assistive shoe dressing example,” Autonomous Robots, vol. 43, no. 6, pp. 1343–1356, 2019.
- [8] N. Imtiaz, J. Middleton, P. Girouard, and E. Murphy-Hill, “Sentiment and politeness analysis tools on developer discussions are unreliable, but so are people,” in Proceedings of the 3rd International Workshop on Emotion Awareness in Software Engineering, pp. 55–61, 2018.
- [9] K. Asadi, P. Chen, K. Han, T. Wu, and E. Lobaton, “Real-time scene segmentation using a light deep neural network architecture for autonomous robot navigation on construction sites,” in ASCE International Conference on Computing in Civil Engineering 2019, pp. 320–327, American Society of Civil Engineers Reston, VA, 2019.
- [10] E. Trautmann and L. Ray, “Mobility characterization for autonomous mobile robots using machine learning,” Autonomous Robots, vol. 30, no. 4, pp. 369–383, 2011.
- [11] C. Plagemann, S. Mischke, S. Prentice, K. Kersting, N. Roy, and W. Burgard, “Learning predictive terrain models for legged robot locomotion,” in 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 3545–3552, 2008.
- [12] S. Levine and P. Abbeel, “Learning neural network policies with guided policy search under unknown dynamics,” Advances in neural information processing systems, vol. 27, 2014.
- [13] A. D. Buchan, D. W. Haldane, and R. S. Fearing, “Automatic identification of dynamic piecewise affine models for a running robot,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 5600–5607, 2013.
- [14] E. Bıyık, M. Palan, N. C. Landolfi, D. P. Losey, and D. Sadigh, “Asking easy questions: A user-friendly approach to active reward learning,” arXiv preprint arXiv:1910.04365, 2019.
- [15] B. Settles, “Active learning literature survey,” 2009.
- [16] E. Biyik and D. Sadigh, “Batch active preference-based learning of reward functions,” in Conference on robot learning, pp. 519–528, PMLR, 2018.
- [17] S. M. Katz, A.-C. Le Bihan, and M. J. Kochenderfer, “Learning an urban air mobility encounter model from expert preferences,” in 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), pp. 1–8, 2019.
- [18] Y. Pang, C. Huang, and R. Liu, “Synthesized trust learning from limited human feedback for human-load-reduced multi-robot deployments,” in 2021 30th IEEE International Conference on Robot & Human Interactive Communication (RO-MAN), pp. 778–783, 2021.
- [19] N. Wilde, D. Kulić, and S. L. Smith, “Active preference learning using maximum regret,” in 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 10952–10959, 2020.
- [20] P. Ménard, O. D. Domingues, A. Jonsson, E. Kaufmann, E. Leurent, and M. Valko, “Fast active learning for pure exploration in reinforcement learning,” in International Conference on Machine Learning, pp. 7599–7608, PMLR, 2021.
- [21] S. Krening and K. M. Feigh, “Interaction algorithm effect on human experience with reinforcement learning,” ACM Transactions on Human-Robot Interaction (THRI), vol. 7, no. 2, pp. 1–22, 2018.
- [22] H. Zhan, F. Tao, and Y. Cao, “Human-guided robot behavior learning: A gan-assisted preference-based reinforcement learning approach,” IEEE Robotics and Automation Letters, vol. 6, no. 2, pp. 3545–3552, 2021.
- [23] C. Huang, W. Luo, and R. Liu, “Meta preference learning for fast user adaptation in human-supervisory multi-robot deployments,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 5851–5856, IEEE, 2021.
- [24] M. Van der Wilk, V. Dutordoir, S. John, A. Artemev, V. Adam, and J. Hensman, “A framework for interdomain and multioutput gaussian processes,” arXiv preprint arXiv:2003.01115, 2020.
- [25] J. Hensman, N. Fusi, and N. D. Lawrence, “Gaussian processes for big data,” arXiv preprint arXiv:1309.6835, 2013.
- [26] G. Vásárhelyi, C. Virágh, G. Somorjai, T. Nepusz, A. E. Eiben, and T. Vicsek, “Optimized flocking of autonomous drones in confined environments,” Science Robotics, vol. 3, no. 20, p. eaat3536, 2018.
- [27] R. Deits and R. Tedrake, Computing Large Convex Regions of Obstacle-Free Space Through Semidefinite Programming, pp. 109–124. Cham: Springer International Publishing, 2015.
- [28] P. E. Hart, N. J. Nilsson, and B. Raphael, “A formal basis for the heuristic determination of minimum cost paths,” IEEE transactions on Systems Science and Cybernetics, vol. 4, no. 2, pp. 100–107, 1968.
- [29] S. Shah, D. Dey, C. Lovett, and A. Kapoor, “Airsim: High-fidelity visual and physical simulation for autonomous vehicles,” in Field and Service Robotics: Results of the 11th International Conference, pp. 621–635, Springer, 2018.
- [30] E. Games, “Unreal engine,@ unrealengine,” 2019.