lemmaathm \aliascntresetthelemmaa \newaliascntpropathma \aliascntresetthepropa
Rationalizing Path-Independent Choice Rules
Abstract.
Path independence is arguably one of the most important choice rule properties in economic theory. We show that a choice rule is path independent if and only if it is rationalizable by a utility function satisfying ordinal concavity, a concept closely related to concavity notions in discrete mathematics. We also provide a rationalization result for choice rules that satisfy path independence and the law of aggregate demand.
An earlier version of this paper was circulated under the title “Representation theorems for path-independent choice rules.” We would like to thank David Ahn, Christopher Chambers, Federico Echenique, SangMok Lee, three anonymous referees, and the editor for their helpful comments and suggestions. Nanami Aoi, Kento Hashimoto, Asuka Hirano, Wataru Ishida, Shinji Koiso, Sota Minowa, Daiji Nagara, Leo Nonaka, Rin Nitta, Ryosuke Sato, Kazuki Sekiya, Haruka Sawazaki, Ryo Shirakawa, Yuji Tamakoshi, and Kenji Utagawa provided excellent research assistance. Koji Yokote is supported by the JSPS KAKENHI Grant-In-Aid 22KJ0717. Fuhito Kojima is supported by the JSPS KAKENHI Grant-In-Aid 21H04979 and JST ERATO Grant Number JPMJER2301, Japan. Yokote is affiliated with the Graduate School of Economics, the University of Tokyo, Tokyo, Japan; Hafalir is with the UTS Business School, University of Technology Sydney, Sydney, Australia; Kojima is with the Department of Economics, the University of Tokyo, Tokyo, Japan; Yenmez is with the Department of Economics, Washington University, St. Louis, MO, USA and Durham University Business School, Durham, United Kingdom. Emails: [email protected], [email protected], [email protected], [email protected].
1. Introduction
Path independence is a fundamental property of combinatorial choice rules. For example, consider a firm that needs to choose a subset from a set of available contracts. We say that the firm’s choice rule is path independent if the chosen set of contracts from any set remains unchanged when the firm divides the set into segments, applies the rule to each segment first, and then applies the rule to the combined set of chosen contracts from all segments. This property is desirable for at least two reasons. First, without path independence, the set of chosen contracts can depend on the order in which contracts are reviewed. Therefore, firms whose choice rules are not path independent may not only regret rejecting offers but also may suffer from the malpractice of favoritism and other manipulations. Second, path independence is intimately related to other well-known properties of interest: A choice rule is path independent if and only if it satisfies the substitutes condition and the irrelevance of rejected contracts (Aizerman and Malishevski, 1981).
Plott (1973) introduces path independence as a property of social choice formalizing an idea in Arrow’s book Social Choice and Individual Values. Although originating in social choice, path independence has found applications in different areas of economic theory, such as market design and decision theory. For example, in two-sided matching markets, when agents have path-independent choice rules, a stable matching exists (Blair, 1988).111The substitutes condition is not sufficient for the existence of a stable matching when choice rules are the primitive of the model rather than utility functions or preferences. See the discussion in Aygün and Sönmez (2013) and Chambers and Yenmez (2017). In decision theory, path independence and its stochastic versions have been studied extensively (Kalai and Megiddo, 1980).222See also Machina and Parks (1981) and a recent treatment by Ahn et al. (2018) Path independence has also been studied in other fields, such as discrete mathematics, law, philosophy, and systems design.333For discrete mathematics see Danilov and Koshevoy (2005) and Gratzer and Wehrung (2016), for law Chapman (1997) and Hammond and Thomas (1989), for philosophy Rott (2001) and Stewart (2022), and for systems design Levin (1998).
Economic agents are usually modeled as utility maximizers: They have a utility function and, given a set of contracts, they choose a subset with the highest utility. An alternative approach is to endow agents with choice rules, for example, when agents do not necessarily have a well-defined utility function or when the utility function is not observable.444For example, choice rules are used to model diversity policies of schools (Hafalir et al., 2013; Ehlers et al., 2014; Echenique and Yenmez, 2015). A fundamental question linking these two approaches is whether a choice rule is rationalizable by a utility function so that the choice from any set of contracts is the subset with the highest utility among all subsets. Results of this nature that connect choice rules with certain properties to utility functions with corresponding properties are called rationalization theorems.555It is, in general, useful to identify rationalization of given choice rules by preference relations or utility functions as an intellectual foundation for almost all economic analysis using preference relations or utility functions. See, for example, Chapter 1 of Mas-Colell et al. (1995). We provide rationalization theorems for path independent choice rules.
First, we show that a choice rule is path independent if and only if it is rationalizable by a utility function satisfying ordinal concavity (Theorem 1). Ordinal concavity is a property introduced in Murota and Shioura (2003) to study discrete optimization problems.666Murota and Shioura (2003) introduce semi-strict quasi M-concavity (SSQM-concavity) as an ordinal implication of M-concavity. M-concavity is a cardinal notion, and it has a weaker variant called M♮-concavity. Analogous to weakening M-concavity to M♮-concavity, SSQM♮-concavity is the natural counterpart of SSQM-concavity (see Murota and Shioura (2024)). Ordinal concavity is equivalent to SSQM♮-concavity. Roughly, it requires that when two sets of contracts are made closer to each other, the value of the utility function either increases on at least one side or remains unchanged on both sides. In this context, getting closer may either mean adding or removing a contract to or from the original set that we start with or the existence of a second contract such that we add one of the contracts and remove the other one.
Hafalir et al. (2022b) show that ordinal concavity is implied by M♮-concavity,777See also Murota and Shioura (2024). which is a standard notion of concavity used in the discrete convex analysis literature. Fujishige and Yang (2003) show that the gross substitutes property of Kelso and Crawford (1982) is equivalent to M♮-concavity.888M♮-concavity is also equivalent to the single-improvement property introduced by Gul and Stacchetti (1999); see Corollary 19 of Murota and Tamura (2003). Therefore, one implication of our result is that the difference between the gross substitutes property and the substitutes condition (or path independence) can be attributed to the difference between M♮-concavity and ordinal concavity.999To be more precise, this statement holds for rationalizable choice functions that satisfy the substitutes condition and for path-independent choice rules. In fact, these two classes of choice rules are the same.
Submodularity is another well-known condition that is often associated with a variety of substitutability notions. Indeed, M♮-concavity, or equivalently the gross substitutes condition, implies submodularity (Murota and Shioura, 2001). Likewise, supermodularity is used to study complementarities in different settings (Topkis, 1998). For instance, Rostek and Yoder (2020) show that supermodularity of a utility function implies that the induced choice rule satisfies a notion of complementarities.101010The setting in Rostek and Yoder (2020) is different from ours in that they allow for externalities in a multi-agent setting. Their Lemma 1 shows that when the utility function is quasisupermodular and satisfies a single-crossing condition, the choice rule has complementarities. Quasisupermodularity is an ordinal implication of supermodularity, and the single-crossing condition is trivially satisfied when there are no externalities as in our setting. Analogously, one could conjecture that submodularity implies the substitutes condition. However, submodularity and ordinal concavity are logically unrelated, and in fact rationalizability by a submodular function does not imply the substitutes condition or path independence.111111See Claims 1 and 2. We also show that M♮-concavity and other related notions fail to give the desired rationalization result (see Section 4). At a high level, one of our contributions is to identify an appropriate condition on utility functions that is tightly connected with path independence and the substitutes condition (Theorem 1).
In the market-design literature, another choice rule property that plays a crucial role is the law of aggregate demand (Hatfield and Milgrom, 2005). The law of aggregate demand states that when a larger set of contracts becomes available, the number of chosen contracts weakly increases. The law of aggregate demand, together with path independence, yields numerous results. It implies, for instance, the rural hospitals theorem in two-sided matching markets, which states that the number of contracts an agent gets is the same across all stable matchings (Fleiner, 2003). In addition, in the doctor-hospital matching problem, a generalization of the doctor-proposing deferred-acceptance mechanism of Gale and Shapley (1962) is strategy-proof for doctors (Hatfield and Milgrom, 2005).
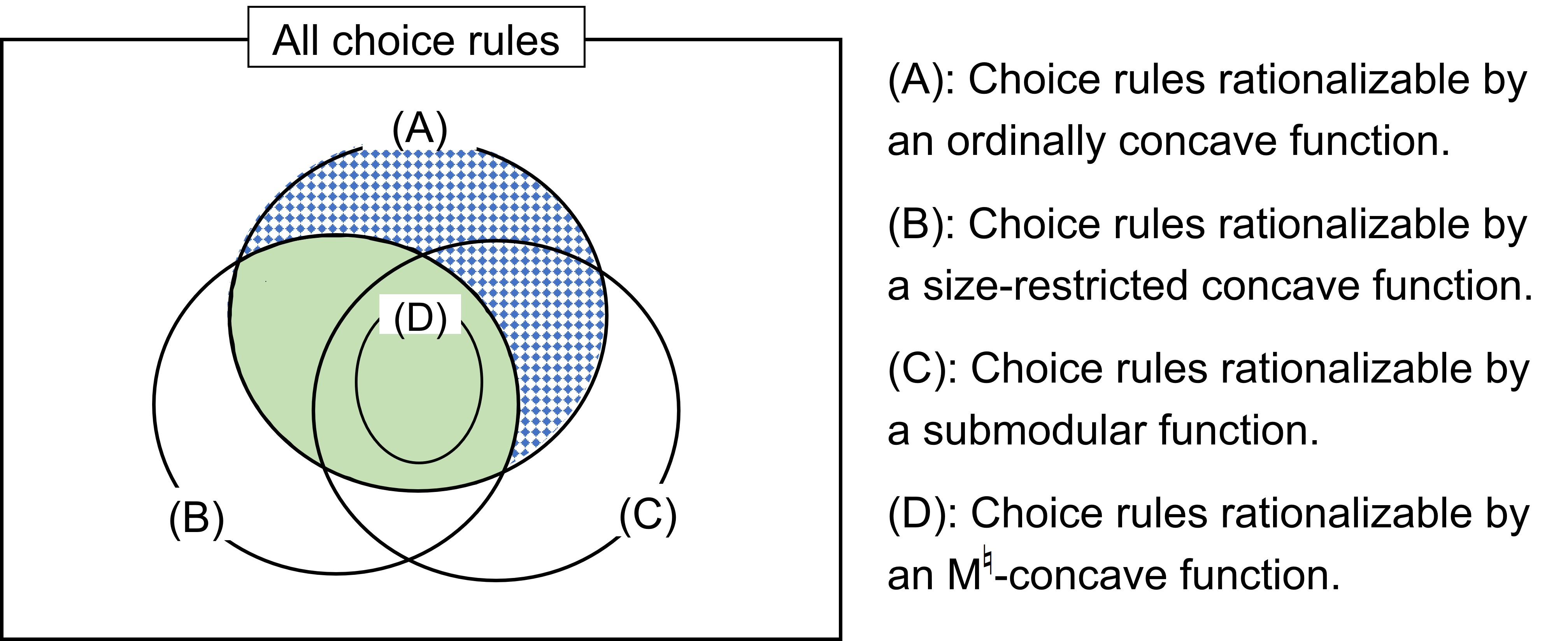
In our second result, we show that a choice rule satisfies path independence and the law of aggregate demand if and only if it is rationalizable by a utility function that satisfies ordinal concavity and size-restricted concavity (Theorem 2). Size-restricted concavity is a concept of discrete concavity with a quantifier such that the implication is required only for sets of contracts with different sizes. Figure 1 illustrates the relationships between choice rules that are rationalizable by utility functions satisfying different notions of concavity.
Path independence and the law of aggregate demand are testable conditions on individual choice. Consider a data set consisting of observed choices of a decision maker, which may or may not include choices from all possible bundles. If there is a violation of path independence in the data, then we can refute the theory that the decision maker has a utility function satisfying ordinal concavity. Likewise, if there is a violation of the law of aggregate demand (even when there is no violation of path independence), then we can refute the theory that the decision maker has a utility function that satisfies ordinal concavity and size-restricted concavity.
The main difference between our work and the classical literature on social choice is that we assume the utility function (or the preference relation) is over sets of contracts, whereas in the classic setting, the utility function (or the preference relation) is over individual contracts (see Moulin (1985) for a summary). Likewise, our choice rule is combinatorial,121212Combinatorial choice is a common characteristic of many allocation problems in the real world. It plays a crucial role in combinatorial auctions (Cramton et al., 2006; De Vries and Vohra, 2003), land allocation (Bleakley and Ferrie, 2014), and allocation of airport landing slots (Schummer and Vohra, 2013), among other cases. See Milgrom (2017) who provides in-depth discussions of practical examples and highlights the importance of the combinatorial nature of many allocation problems. whereas in the classical setting, multiple contracts represent the indecision of the agent, and the agent is eventually assigned only one contract. Therefore, our results are independent of the social choice literature on rationalizability.131313At the same time, we note that the appeal of path independence as a normatively desirable property is not affected by these differences, and hence is as relevant in our combinatorial choice context as in the classical setting. Recall our discussion in the first paragraph of the Introduction for the interpretation of path independence in our context.
Even though path independence has been studied in the context of combinatorial choice (e.g., Echenique (2007) and Alva (2018)), there are only a few papers that study rationalizability of these choice rules. In a recent work, Yang (2020) shows that path-independent choice rules are rationalizable,141414For a detailed discussion of rationalizability of path-independent choice rules, see Section 5 of Yang (2020) as well as Alva (2018). but he does not provide necessary or sufficient conditions for a utility function to ensure that the corresponding choice rule satisfies path independence. Less relatedly, Chambers and Echenique (2018) consider a setting with continuous transfers and characterize combinatorial demand functions that can be rationalized by quasi-linear preferences, through continuity and the law of demand.
One of the major contributions of our paper is to establish a close connection between choice rules in economics and concavity concepts in discrete mathematics. This connection allows us to shed light on economic problems with discrete optimization techniques. For instance, in an abstract setting, Eguchi et al. (2003) show that choice rules that are rationalizable by M♮-concave functions satisfy path independence and Murota and Yokoi (2015) show that they satisfy the law of aggregate demand. On an applied front, Kojima et al. (2018) build upon their results to find M♮-concave functions that rationalize a variety of practically relevant choice rules and establish their desirable properties including computational efficiency. Hafalir et al. (2022b) establish connections between ordinal concavity and choice rules in markets with dual objectives such as college admissions where diversity and meritocracy are typical goals. While advancing this research program further, the present paper is distinctive in that it provides conditions of discrete concavity that are equivalent to rationalizability of desirable choice rules, thus giving a complete answer to a foundational issue in this research agenda.
There is also a significant literature on menu choice (where a menu is a set of items or contracts). In this literature, a decision maker has preferences over menus anticipating consumption of an item from the available menu in the future. In this context, Kreps (1979) provides a model of preferences for flexibility and a representation of such preferences using state-dependent utility functions over individual items.151515Other notable papers include Gul and Pesendorfer (2001) who provide a model of temptation and Dekel et al. (2001) who study an extension of Kreps (1979) that also allows preferences for commitment. Although the decision maker in the menu choice literature ultimately consumes just one item, subsets of items or contracts arise naturally as the objects of interest as the decision maker has preferences and associated choice behavior over them, leading to a combinatorial problem such as ours.
The rest of the paper is organized as follows. We define choice rules and their properties in Section 2, present our rationalization results in Section 3, discuss rationalizability by a utility function satisfying concavity notions other than ordinal concavity in Section 4, and conclude in Section 5. We provide all proofs in the Appendix.
2. Preliminaries
Let denote a finite set of contracts. A choice rule is a function such that, for any , we have .161616In a typical model, is a choice rule of a single agent and is the set of contracts that the agent can sign. We allow the agent to have multiple contracts with the same partner as in Alkan and Gale (2003) and Hatfield and Kominers (2012). Hatfield and Kominers (2012) consider a discrete setting like ours whereas Alkan and Gale (2003) allow fractional allocations. We study two key properties of choice rules.
Definition 1 (Plott (1973)).
A choice rule satisfies path independence if, for any ,
Path independence plays a fundamental role in social choice, market design, and decision theory.171717Path independence is equivalent to the following condition: for any , (Plott, 1973, Theorem 1). It has also been used in different areas such as discrete mathematics, law, philosophy, and systems design.181818See the references in the Introduction.
As explained in the Introduction, path independence has a normative interpretation on its own. Moreover, it is equivalent to two properties that are commonly assumed in market design. A choice rule satisfies the substitutes condition (Roth and Sotomayor, 1990) if, for any ,
A choice rule satisfies irrelevance of rejected contracts (Aygün and Sönmez, 2013) if, for any ,
Proposition 1 (Aizerman and Malishevski (1981)).
A choice rule satisfies path independence if and only if it satisfies irrelevance of rejected contracts and the substitutes condition.
It is well known that a stable matching exists if the choice rule of every agent satisfies the substitutes condition and the irrelevance of rejected contracts.191919Roth and Sotomayor (1990) show this result in a model of matching without contracts (i.e., there exists exactly one contract associated with each pair of a firm and a worker). Hatfield and Milgrom (2005) generalize the result to a setting with contracts. Aygün and Sönmez (2013) point out that the result goes through only under irrelevance of rejected contracts, a condition that the proof of Hatfield and Milgrom (2005) uses without explicitly assuming. Therefore, path independence guarantees the existence of stable matchings in two-sided markets (Blair, 1984).
We next introduce another important property in market design called the law of aggregate demand.202020Alkan (2002) calls it cardinal monotonicity and Alkan and Gale (2003) call it size monotonicity. These papers address matching problems without contracts, while our results hold for general matching problems with contracts.
Definition 2 (Hatfield and Milgrom (2005)).
A choice rule C satisfies the law of aggregate demand if, for any ,
The law of aggregate demand, together with path independence, produces classic results such as the rural hospitals theorem (Fleiner, 2003) and strategy-proofness of a generalization of the doctor-proposing Gale-Shapley deferred-acceptance mechanism for doctors (Hatfield and Milgrom, 2005).
A utility function assigns a value to every set of contracts.212121 represents the set of real numbers. A choice rule is rationalizable by a utility function if, for any ,
In other words, when a choice rule is rationalizable by a utility function, from any set of available contracts, the choice rule selects the unique subset with the highest utility.
3. Results
In this section, we provide two rationalization theorems using utility functions that satisfy notions of discrete concavity. To define these notions, we introduce some notation. For any and , let and . Similarly, for any , let and .
Definition 3.
A utility function satisfies ordinal concavity if, for any and , there exists such that
-
(i)
, or
-
(ii)
, or
-
(iii)
and .
In other words, ordinal concavity requires that when is brought closer to by removing and adding , and is brought closer to by adding and removing , either at least one of the two function values strictly increases or both values remain unchanged.
Our main result is a rationalization theorem for path-independent choice rules.
Theorem 1.
A choice rule is path independent if and only if it is rationalizable by a utility function satisfying ordinal concavity.
Proof.
See Section A.1. ∎
The if direction easily follows from the existing literature, although we provide a self-contained proof.222222See Theorem 2 of Hafalir et al. (2022b). Our main contribution is to show the only-if direction.232323In Section 4, we show that the only-if direction does not hold for other concavity notions used in prior work. We note that this direction is an existence result, and its proof is constructive. In what follows, we give the main idea of our construction.242424The proof presented in the main text is based on a suggestion made by one of the anonymous referees. We gratefully acknowledge their helpful comment. The Online Appendix provides our original proof.
Our utility function construction relies on the decomposition lemma of Aizerman and Malishevski (1981): for any path-independent choice rule, there exists a finite sequence of linear orders over contracts such that the choice from each set is given by the union of the most-preferred contracts according to each linear order (a formal statement of this lemma is given in Appendix A).252525Chambers and Yenmez (2017) use the decomposition lemma to make a connection between the theory of path-independent choice rules and matching theory and utilize this connection to advance both fields. To represent each order numerically, we construct a value function over contracts that assigns a higher value to a more preferred contract according to . We define the utility from a set by the weighted sum of the highest contract values among according to for each . Then, for any , the derived utility function assigns the highest utility to the chosen set among all subsets of , because collects the most-preferred (equivalently, highest-valued) contracts according to each order . Using this observation, we show that the utility function rationalizes (see step 2 in Section A.1.2).262626Precisely speaking, we need to modify the utility function so that the utility from a set is smaller than that from when . See the construction of in equation 4. This formulation is also useful for establishing ordinal concavity because the highest contract value among a set is tractable when we add or remove one contract from the set (see step 3 in Section A.1.2).
Mathematically, the construction is similar to that of Kreps (1979) in the sense that a rationalizing utility function is defined by the weighted sum of the maximum values of multiple functions. We note that there are at least two differences between Kreps’ model and ours. First, Kreps takes a preference over sets of contracts as primitive, while we take a choice rule as primitive. Second, Kreps assumes monotonicity of preferences in the sense that the agent prefers any set to its subsets, which cannot hold for utility functions rationalizing some path-independent choice rules.272727For example, let and, for any with , , and, otherwise when , . It is easy to see that this choice rule is path independent and any utility function that rationalizes it must assign a strictly higher utility to than , violating monotonicity.
Theorem 1 states that, for any path-independent choice rule, there exists some ordinally concave utility function. In general, there could be utility functions that are not ordinally concave while rationalizing a path-independent choice rule. In fact, it is obvious that the values assigned to sets of contracts that are never chosen can be lowered without changing the rationalized choice rule, and such changes in a utility function do not necessarily preserve ordinal concavity. This simple observation suggests that it is likely to be elusive to single out one condition on utility functions for the rationalization result.282828In fact, there is a large degree of freedom in choosing utility functions for rationalizing a given path-independent choice rule. Alkan (2002) shows that the set of all chosen sets by a path-independent choice rule forms a lattice under a natural revealed preference relation. Any utility function that gives higher values to more preferred chosen subsets and gives sufficiently low values to never-chosen subsets rationalizes the choice rule. However, we also show that the rationalization result fails for many other conditions that are seemingly related to substitutability, so our rationalization result offers meaningful restrictions on rationalizing functions; see the discussions in the Introduction and Section 4.
In practice, it is often the case that a choice rule chooses subsets of cardinality of up to some constant , which could be interpreted as a capacity. If we consider such a choice rule in the only-if direction of Theorem 1, we can construct a rationalizing utility function whose effective domain is the subsets that have cardinality of at most .292929We are grateful to an anonymous referee for their suggestion, which led us to consider this case. Specifically, we can construct such that (i) for all with , (ii) rationalizes , and (iii) for any with and and any , the requirement of ordinal concavity is satisfied.303030To construct such a utility function, it suffices to modify the definition of in the proof (see step 1 in Section A.1.2) so that the utility from with is equal to . Even though the stronger version of ordinal concavity that we call ordinal concavity++ is no longer satisfied, the proof of satisfying ordinal concavity still goes through with a minor modification.
Next, we introduce another concavity notion that proves crucial for rationalizable choice rules to satisfy the law of aggregate demand.
Definition 4.
A utility function satisfies size-restricted concavity if, for any with , there exists such that
-
(i)
, or
-
(ii)
, or
-
(iii)
and .
Like ordinal concavity, this condition states that either the function value strictly increases on at least one side or the function values remain unchanged on both sides when two sets move closer to each other. Size-restricted concavity differs from ordinal concavity in that it requires to have a strictly larger cardinality than , and furthermore, only one contract is added or removed when sets are brought closer to each other. It is easy to see that size-restricted concavity is implied by M♮-concavity but is logically independent of ordinal concavity.313131We define M♮-concavity in Section 4. If a utility function satisfies M♮-concavity, then it has the following property: for any with , there exists such that . In fact, M♮-concavity is equivalent to this property in our setting (Murota and Shioura, 2018, Corollary 1.4). It can be easily verified that size-restricted concavity is an ordinal implication of this inequality. Therefore, M♮-concavity implies size-restricted concavity.
Our second rationalization theorem uses size-restricted concavity.
Theorem 2.
A choice rule satisfies path independence and the law of aggregate demand if and only if it is rationalizable by a utility function that satisfies ordinal concavity and size-restricted concavity.
Proof.
See Section A.2. ∎
By Theorem 1, a choice rule that is rationalizable by an ordinally concave utility function satisfies path independence. To complete the if direction, we show that when the utility function also satisfies size-restricted concavity, the induced choice rule satisfies the law of aggregate demand as well. For the only-if direction, we show that the utility function we construct in the proof of Theorem 1 satisfies size-restricted concavity when the choice rule satisfies both path independence and the law of aggregate demand. This completes the proof using Theorem 1, which shows that the utility function satisfies ordinal concavity.
We note that the path independence of the choice rule and the ordinal concavity of the rationalizing utility function are indispensable in Theorem 2. More precisely, without these assumptions, the law of aggregate demand is logically unrelated to rationalizability by a size-restricted concave function.
4. Rationalizability by concavity notions related to ordinal concavity
In this section, we focus on concavity notions other than ordinal concavity that have been used in economic analysis. We show that they do not constitute a necessary and sufficient condition for rationalizing choice rules with path independence and the law of aggregate demand. We then discuss some variants of ordinal concavity and size-restricted concavity.
4.1. Submodularity
A typical assumption on functions with a combinatorial structure is submodularity. It is assumed in various economic models such as combinatorial auctions (Ausubel and Milgrom, 2002) and cost-sharing problems (Moulin and Shenker, 2001).
Definition 5.
A utility function satisfies submodularity if, for any , we have
Take any and distinct . By substituting for and for in the above definition, we obtain
| (1) |
This condition captures nonincreasing marginal utility: the marginal utility of adding to set does not increase when expands to .323232It is well known that submodularity is equivalent to nonincreasing marginal utility; for a formal statement, see, e.g., Proposition 6.1 of Shioura and Tamura (2015). In other words, if is present, then the agent is less willing to accept , so this captures a kind of substitutability between and . Contrary to this intuition, submodular functions do not necessarily induce substitutable or path-independent choice rules.
Claim 1.
There exists a choice rule that is rationalizable by a submodular function but does not satisfy substitutability. In particular, the choice rule does not satisfy path independence.
Proof.
We provide an example in Section B.1. ∎
Therefore, Theorem 1 does not hold if we replace ordinal concavity with submodularity. Indeed, the two notions are logically independent.
Claim 2.
Submodularity and ordinal concavity are logically independent of each other.
Proof.
See Section B.2. ∎
4.2. M♮-concavity
Claim 1 suggests that submodularity is too weak to capture the substitutes condition (and hence path independence). Therefore, we turn our attention to a stronger notion than submodularity, called M♮-concavity. M♮-concavity is a central concavity notion in discrete convex analysis (Murota, 2003). M♮-concavity implies submodularity (Murota and Shioura, 2001), and M♮-concavity guarantees the existence of equilibrium in markets with indivisibilities (Kelso and Crawford, 1982),333333Kelso and Crawford (1982) use a condition called the gross substitutes condition, which is equivalent to M♮-concavity; see Section 4.3 for a detailed discussion. or stable outcomes in matching markets (Kojima et al., 2018).
Definition 6.
A utility function satisfies M♮-concavity if, for any and , there exists such that
M♮-concavity implies ordinal concavity (Hafalir et al., 2022b). Moreover, when a choice rule is rationalizable by an M♮-concave function, the following result holds.
Proposition 2 (Eguchi et al. (2003) and Murota and Yokoi (2015)).
Let be a choice rule that is rationalizable by an M♮-concave utility function. Then satisfies path independence and the law of aggregate demand.
However, M♮-concavity does not cover all choice rules that satisfy path independence and the law of aggregate demand.
Claim 3.
There exists a choice rule that satisfies path independence and the law of aggregate demand but is not rationalizable by any M♮-concave utility function.
Proof.
We provide an example in Section B.3. ∎
4.3. Ordinal content of M♮-concavity
M♮-concavity is a cardinal notion because the definition compares the sum of function values. Meanwhile, rationalization is an ordinal concept because only the ordinal ranking among utility values is taken into account. Therefore, Proposition 2 still holds when is a choice rule that is rationalizable by a monotonic transformation of an M♮-concave utility function.343434A utility function is a monotonic transformation of another utility function if there exists a strictly increasing function such that for all . In other words, if we replace M♮-concavity with “the ordinal content of M♮-concavity” in Proposition 2, the result continues to hold.353535The ordinal content of cardinal notions has drawn some attention in the literature. For example, Chambers and Echenique (2009) study the ordinal content of supermodularity and Chambers and Echenique (2008) consider ordinal notions of submodularity.
One important implication of this discussion is that ordinal concavity is not equivalent to the ordinal content of M♮-concavity. This can be seen by noting that under ordinal concavity, the induced choice rule does not need to satisfy the law of aggregate demand, but under the ordinal content of M♮-concavity the law of aggregate demand holds. For example, consider a path-independent choice rule that does not satisfy the law of aggregate demand and the corresponding utility function that we construct in the proof of Theorem 1.363636For example, let . Define choice rule as follows: if , then , and otherwise. It is easy to check that is path independent but does not satisfy the law of aggregate demand. We know that the utility function satisfies ordinal concavity by Theorem 1. However, since the choice rule does not satisfy the law of aggregate demand, the utility function cannot be a monotonic transformation of an M♮-concave utility function by Proposition 2. In fact, even though both ordinal concavity and size-restricted concavity are implied by M♮-concavity, their conjunction is not equivalent to its ordinal content.373737If the conjunction of ordinal concavity and size-restricted concavity were equivalent to the ordinal content of M♮-concavity, then the choice rule constructed in the proof of Claim 3 would also be rationalizable by an M♮-concave utility function, which contradicts Claim 3.
The preceding discussion elucidates the relationships between different concepts of substitutability. The substitutes condition of Hatfield and Milgrom (2005) is closely related to the gross substitutes property of Kelso and Crawford (1982), which is the standard concept of substitutability in markets with continuous transfers. These two conditions are often regarded as natural counterparts in markets with and without transfers, with the gross substitutes property being stronger than the substitutes condition. Our analysis precisely pins down how much stronger the former is than the latter for rationalizable choice rules. To see this, we note that Fujishige and Yang (2003) show that the gross substitutes property is equivalent to M♮-concavity in the present setting. Since Theorem 1 provides an equivalence result for rationalizable choice rules satisfying the substitutes condition (rationalizability and the substitutes condition are jointly equivalent to path independence, see Proposition 1 and Theorems 4 and 5 in Yang (2020)), one can attribute the difference between the two notions of substitutability to the difference between two kinds of discrete concavity, namely M♮-concavity and ordinal concavity. Similarly, Theorem 2 shows that size-restricted concavity is precisely the additional restriction on utility functions that corresponds to imposing the law of aggregate demand on choice rules in addition to path independence.
4.4. Pseudo M♮-concavity
Hafalir et al. (2022a) introduce a variant of M♮-concavity, called pseudo M♮-concavity.
Definition 7.
A utility function satisfies pseudo M♮-concavity if, for any and , there exists such that
A notable characteristic of pseudo M♮-concavity is that upper contour sets form well-behaved discrete convex sets (see Lemma 1 of Hafalir et al. (2022a)). In view of rationalizing choice rules with path independence and the law of aggregate demand, pseudo M♮-concavity is similar to M♮-concavity: it is a sufficient condition, but not a necessary condition.
Proposition 3.
Let be a choice rule that is rationalizable by a pseudo M♮-concave utility function. Then satisfies path independence and the law of aggregate demand.
Proof.
See Section B.4. ∎
Claim 4.
There exists a choice rule that satisfies path independence and the law of aggregate demand but is not rationalizable by any pseudo M♮-concave utility function.
Proof.
We provide an example in Section B.5. ∎
4.5. Variants of ordinal concavity and size-restricted concavity
The preceding results reveal that Theorem 1 does not hold if we replace ordinal concavity with submodularity, M♮-concavity, or pseudo M♮-concavity. In this section, we introduce new variants of ordinal concavity and strengthen Theorem 1 by using these notions.
Definition 8.
A utility function satisfies ordinal concavity- if, for any and , there exists such that
-
(i)
, or
-
(ii)
.
To see that ordinal concavity implies ordinal concavity-,383838Ordinal concavity- is implied by condition QM in Murota and Shioura (2003). note first that conditions (i) and (ii) of the former are the strict-inequality versions of conditions (i) and (ii) in the latter. Moreover, condition (iii) of ordinal concavity implies that both conditions (i) and (ii) of ordinal concavity- hold with equality.
Definition 9.
A utility function satisfies ordinal concavity+ if, for any and , there exists such that one of the following two conditions holds:
-
(i)
, or
-
(ii)
.
Ordinal concavity+ implies ordinal concavity because conditions (i) and (ii) of the former are identical to conditions (i) and (ii) of the latter. We now provide a generalization of Theorem 1 using these concavity notions.
Theorem 1’ \thelemmaa.
The following hold:
-
(I)
If a choice rule is rationalizable by a utility function satisfying ordinal concavity-, then it satisfies path independence.
-
(II)
If a choice rule is path independent, then it is rationalizable by a utility function satisfying ordinal concavity+.
Proof.
See Section A.1. ∎
Theorem subsection 4.5 implies that Theorem 1 holds for any property of utility functions that implies ordinal concavity- and is implied by ordinal concavity+. In particular, Theorem 1 can be stated using either ordinal concavity+ or ordinal concavity-. However, we regard rationalization by ordinal concavity as our main result for two reasons. First, ordinally concave functions have a computational advantage: there exists an algorithm that finds a maximizer of an ordinally concave function in polynomial time in the number of contracts.393939See Hafalir et al. (2022b) or Murota and Shioura (2024). Therefore, if we can identify a utility function used in practice and verify that the function satisfies ordinal concavity, then we can compute its maximizers very fast. Second, for applications such as school choice, the utility function known to rationalize a given choice rule often satisfies ordinal concavity.404040See, for example, the applications in Kojima et al. (2018). Ordinal concavity strikes a balance between these two properties—note that the first property does not hold if the condition on the utility function is too permissive, while the second property does not hold if the condition is too restrictive.
Furthermore, rationalization by a utility function is useful because numerical evaluations of candidates are commonplace in practice. For example, a school authority often admits students based on test scores. The necessity part of our rationalization theorem indicates that ordinally concave functions are a sufficiently large class of utility functions in the sense that any path-independent choice rule is ordinally concave rationalizable. Therefore, it would potentially be useful to identify computationally tractable numerical evaluations behind path-independent choice rules.
Finally, we introduce variants of size-restricted concavity.
Definition 10.
A utility function satisfies size-restricted concavity- if, for any with , there exists such that
-
(i)
, or
-
(ii)
.
Definition 11.
A utility function satisfies size-restricted concavity+ if, for any with , there exists such that
-
(i)
, or
-
(ii)
.
It is easy to check that size-restricted concavity+ implies size-restricted concavity. Likewise, size-restricted concavity implies size-restricted concavity-. Similar to Theorem subsection 4.5 generalizing Theorem 1, the following result generalizes Theorem 2.
Theorem 2’ \thepropa.
The following hold:
-
(I)
If a choice rule is rationalizable by a utility function satisfying ordinal concavity- and size-restricted concavity-, then it satisfies path independence and the law of aggregate demand.
-
(II)
If a choice rule satisfies path independence and the law of aggregate demand, then it is rationalizable by a utility function satisfying ordinal concavity+ and size-restricted concavity+.
Proof.
See Section A.2. ∎
Therefore, Theorem subsection 4.5 holds for any combination of two notions such that (i) one implies ordinal concavity- and is implied by ordinal concavity+ and (ii) the other implies size-restricted concavity- and is implied by size-restricted concavity+.
5. Concluding remarks
Concavity has been a central assumption in the analysis of economies with divisible goods. Our analysis reveals a sense in which it is essential in economies with indivisible goods as well. In particular, we show that a path-independent choice rule is rationalizable by a utility function that satisfies a particular notion of discrete concavity, namely ordinal concavity. In fact, we show that the relationship between path independence and rationalizability by a utility function with ordinal concavity is tight. In economies with divisible goods, it is often the case that maximization techniques of concave functions help us characterize equilibrium outcomes. Our rationalization theorems may prove useful in the analysis of economies with indivisible goods.
To our knowledge, the present paper is one of the first to provide rationalization theorems for combinatorial choice rules. One possible direction for future research is to provide rationalization results for other choice rules. It is not arduous to provide such results for canonical choice rules such as the responsive ones (Roth, 1985) as well as the -acceptant and substitutable ones (Kojima and Manea, 2010).414141The rationalization results are available from the authors upon request. They are not included in the present paper because the conditions on the utility functions are not naturally interpretable as concavity properties, which are the main focus of the current paper. Meanwhile, rationalization results are still an open problem for most other choice rules, such as those with type-specific quotas (Abdulkadi̇roğlu and Sönmez, 2003) and with reserves (Hafalir et al., 2013). More generally, it would be interesting to establish rationalization theorems for practically relevant choice rules.
References
- (1)
- Abdulkadi̇roğlu and Sönmez (2003) Abdulkadi̇roğlu, Atila and Tayfun Sönmez, “School choice: A mechanism design approach,” American Economic Review, June 2003, 93 (3), 729–747.
- Ahn et al. (2018) Ahn, David S., Federico Echenique, and Kota Saito, “On path independent stochastic choice,” Theoretical Economics, 2018, 13 (1), 61–85.
- Aizerman and Malishevski (1981) Aizerman, Mark A. and Andrew V. Malishevski, “General theory of best variants choice: Some aspects,” IEEE Transactions on Automatic Control, 1981, 26 (5), 1030–1040.
- Alkan (2002) Alkan, Ahmet, “A class of multipartner matching markets with a strong lattice structure,” Economic Theory, 2002, 19, 737–746.
- Alkan and Gale (2003) by same author and David Gale, “Stable schedule matching under revealed preference,” Journal of Economic Theory, 2003, 112 (2), 289 – 306.
- Alva (2018) Alva, Samson, “WARP and combinatorial choice,” Journal of Economic Theory, 2018, 173, 320–333.
- Alva and Dogan (2023) by same author and Battal Dogan, “Choice and market design,” in “Online and matching-based market design” 2023, pp. 238–263.
- Ausubel and Milgrom (2002) Ausubel, Lawrence M and Paul R Milgrom, “Ascending auctions with package bidding,” The BE Journal of Theoretical Economics, 2002, 1 (1), 20011001.
- Aygün and Sönmez (2013) Aygün, Orhan and Tayfun Sönmez, “Matching with Contracts: Comment,” American Economic Review, 2013, 103 (5), 2050–2051.
- Blair (1984) Blair, Charles, “Every Finite Distributive Lattice is a Set of Stable Matchings,” Journal of Combinatorial Theory (A), 1984, 37, 353–356.
- Blair (1988) by same author, “The Lattice Structure of the Set of Stable Matchings with Multiple Partners,” Mathematics of Operations Research, November 1988, 13 (4), 619–628.
- Bleakley and Ferrie (2014) Bleakley, Hoyt and Joseph Ferrie, “Land openings on the Georgia frontier and the coase theorem in the short-and long-run,” 2014. working paper.
- Chambers and Echenique (2008) Chambers, Christopher P. and Federico Echenique, “Ordinal notions of submodularity,” Journal of Mathematical Economics, 2008, 44 (11), 1243–1245.
- Chambers and Echenique (2009) by same author and by same author, “Supermodularity and preferences,” Journal of Economic Theory, 2009, 144 (3), 1004–1014.
- Chambers and Echenique (2018) by same author and by same author, “A characterization of combinatorial demand,” Mathematics of Operations Research, 2018, 43 (1), 222–227.
- Chambers and Yenmez (2017) by same author and M. Bumin Yenmez, “Choice and Matching,” American Economic Journal: Microeconomics, August 2017, 9 (3), 126–47.
- Chapman (1997) Chapman, Bruce, “Law, incommensurability, and conceptually sequenced argument,” University of Pennsylvania Law Review, 1997, 146, 1487.
- Cramton et al. (2006) Cramton, Peter C, Yoav Shoham, Richard Steinberg, and Vernon L Smith, Combinatorial auctions, Vol. 1, MIT press Cambridge, 2006.
- Danilov and Koshevoy (2005) Danilov, Vladimir and Gleb Koshevoy, “Mathematics of Plott choice functions,” Mathematical Social Sciences, 2005, 49 (3), 245–272.
- Dekel et al. (2001) Dekel, Eddie, Barton L. Lipman, and Aldo Rustichini, “Representing Preferences with a Unique Subjective State Space,” Econometrica, 2001, 69 (4), 891–934.
- Echenique (2007) Echenique, Federico, “Counting combinatorial choice rules,” Games and Economic Behavior, 2007, 58 (2), 231 – 245.
- Echenique and Yenmez (2015) by same author and M. Bumin Yenmez, “How to Control Controlled School Choice,” American Economic Review, August 2015, 105 (8), 2679–2694.
- Eguchi et al. (2003) Eguchi, Akinobu, Satoru Fujishige, and Akihisa Tamura, “A generalized Gale-Shapley algorithm for a discrete-concave stable-marriage model,” in “International Symposium on Algorithms and Computation” Springer 2003, pp. 495–504.
- Ehlers et al. (2014) Ehlers, Lars, Isa E. Hafalir, M. Bumin Yenmez, and Muhammed A. Yildirim, “School choice with controlled choice constraints: Hard bounds versus soft bounds,” Journal of Economic Theory, 2014, 153, 648–683.
- Fleiner (2003) Fleiner, Tamás, “A Fixed-Point Approach to Stable Matchings and Some Applications,” Mathematics of Operations Research, February 2003, 28 (1), 103–126.
- Fujishige and Yang (2003) Fujishige, Satoru and Zaifu Yang, “A Note On Kelso And Crawford’s Gross Substitutes Condition,” Mathematics of Operations Research, August 2003, 28 (3), 433–462.
- Gale and Shapley (1962) Gale, David and Lloyd S. Shapley, “College Admissions and the Stability of Marriage,” The American Mathematical Monthly, January 1962, 69 (1), 9–15.
- Gratzer and Wehrung (2016) Gratzer, George A and Friedrich Wehrung, Lattice theory: special topics and applications, Springer, 2016.
- Gul and Stacchetti (1999) Gul, Faruk and Ennio Stacchetti, “Walrasian Equilibrium with Gross Substitutes,” Journal of Economic Theory, July 1999, 87 (1), 95–124.
- Gul and Pesendorfer (2001) by same author and Wolfgang Pesendorfer, “Temptation and self-control,” Econometrica, 2001, 69 (6), 1403–1435.
- Hafalir et al. (2022a) Hafalir, Isa E., Fuhito Kojima, and M. Bumin Yenmez, “Efficient market design with distributional objectives,” 2022. Working paper.
- Hafalir et al. (2022b) by same author, by same author, by same author, and Koji Yokote, “Design on Matroids: Diversity vs. Meritocracy,” 2022. Working paper.
- Hafalir et al. (2013) by same author, M. Bumin Yenmez, and Muhammed A. Yildirim, “Effective affirmative action in school choice,” Theoretical Economics, May 2013, 8 (2), 325–363.
- Hammond and Thomas (1989) Hammond, Thomas H. and Paul A. Thomas, “The impossibility of a neutral hierarchy,” The Journal of Law, Economics, and Organization, 1989, 5, 155.
- Hatfield and Milgrom (2005) Hatfield, John William and Paul R. Milgrom, “Matching with Contracts,” American Economic Review, September 2005, 95 (4), 913–935.
- Hatfield and Kominers (2012) by same author and Scott Duke Kominers, “Matching in Networks with Bilateral Contracts,” American Economic Journal: Microeconomics, 2012, 4 (1), 176–208.
- Kalai and Megiddo (1980) Kalai, Ehud and Nimrod Megiddo, “Path Independent Choices,” Econometrica, 1980, 48 (3), 781—784.
- Kelso and Crawford (1982) Kelso, Alexander S. and Vincent P. Crawford, “Job Matching, Coalition Formation, and Gross Substitutes,” Econometrica, 1982, 50, 1483–1504.
- Kojima et al. (2018) Kojima, Fuhito, Akihisa Tamura, and Makoto Yokoo, “Designing matching mechanisms under constraints: An approach from discrete convex analysis,” Journal of Economic Theory, 2018, 176, 803 – 833.
- Kojima and Manea (2010) by same author and Mihai Manea, “Axioms for Deferred Acceptance,” Econometrica, 2010, 78 (2), 633–653.
- Kreps (1979) Kreps, David M, “A representation theorem for” preference for flexibility”,” Econometrica: Journal of the Econometric Society, 1979, pp. 565–577.
- Levin (1998) Levin, Mark, Combinatorial engineering of decomposable systems, Vol. 2, Springer Science & Business Media, 1998.
- Machina and Parks (1981) Machina, Mark J. and Robert P. Parks, “On Path Independent Randomized Choice,” Econometrica, 1981, 49 (5), 1345–1347.
- Mas-Colell et al. (1995) Mas-Colell, A., M. D. Whinston, and J. R. Green, Microeconomic Theory, Oxford University Press, New York, 1995.
- Milgrom (2017) Milgrom, Paul, Discovering prices: auction design in markets with complex constraints, Columbia University Press, 2017.
- Moulin (1985) Moulin, Hervé, “Choice functions over a finite set: A summary,” Social Choice and Welfare, 1985, 2 (2), 147–160.
- Moulin and Shenker (2001) by same author and Scott Shenker, “Strategyproof sharing of submodular costs: budget balance versus efficiency,” Economic Theory, 2001, 18, 511–533.
- Murota (2003) Murota, Kazuo, Discrete Convex Analysis, Society for Industrial and Applied Mathematics, 2003.
- Murota (2016) by same author, “Discrete Convex Analysis: A Tool for Economics and Game Theory,” Journal of Mechanism and Institution Design, 2016, 1, 151–273.
- Murota and Tamura (2003) by same author and Akihisa Tamura, “New characterizations of M-convex functions and their applications to economic equilibrium models with indivisibilities,” Discrete Applied Mathematics, 2003, 131 (2), 495–512.
- Murota and Shioura (2001) by same author and Akiyoshi Shioura, “Relationship of M-/L-convex functions with discrete convex functions by Miller and Favati-Tardella,” Discrete Applied Mathematics, 2001, 115 (1), 151–176. First Japanese-Hungarian Symposium for Discrete Mathematics and i ts Applications.
- Murota and Shioura (2003) by same author and by same author, “Quasi M-convex and L-convex functions—quasiconvexity in discrete optimization,” Discrete Applied Mathematics, 2003, 131 (2), 467–494.
- Murota and Shioura (2018) by same author and by same author, “Simpler exchange axioms for M-concave functions on generalized polymatroids,” Japan Journal of Industrial and Applied Mathematics, 2018, 35 (1), 235–259.
- Murota and Shioura (2024) by same author and by same author, “Note on minimization of quasi M♮-convex functions,” Japan Journal of Industrial and Applied Mathematics, 2024, 41 (2), 857–880.
- Murota and Yokoi (2015) by same author and Yu Yokoi, “On the Lattice Structure of Stable Allocations in Two-Sided Discrete-Concave Market,” Mathematics of Operations Research, 2015, 40, 460–473.
- Plott (1973) Plott, Charles R., “Path independence, rationality, and social choice,” Econometrica, 1973, 41 (6), 1075–1091.
- Rostek and Yoder (2020) Rostek, Marzena and Nathan Yoder, “Matching With Complementary Contracts,” Econometrica, 2020, 88 (5), 1793–1827.
- Roth (1985) Roth, Alvin E., “The College Admissions Problem is not equivalent to the Marriage Problem,” Journal of Economic Theory, aug 1985, 36 (2), 277–288.
- Roth and Sotomayor (1990) by same author and Marilda Sotomayor, Two-sided Matching: A Study in Game-Theoretic Modelling and Analysis, Vol. 18 of Econometric Society Monographs, Cambridge University Press, Cambridge England, 1990.
- Rott (2001) Rott, Hans, Change, choice and inference: A study of belief revision and nonmonotonic reasoning number 42, Oxford University Press, 2001.
- Schummer and Vohra (2013) Schummer, James and Rakesh V Vohra, “Assignment of arrival slots,” American Economic Journal: Microeconomics, 2013, 5 (2), 164–185.
- Shioura and Tamura (2015) Shioura, Akiyoshi and Akihisa Tamura, “Gross substitutes condition and discrete concavity for multi-unit valuations: a survey,” Journal of the Operations Research Society of Japan, 2015, 58 (1), 61–103.
- Stewart (2022) Stewart, Rush T., “Path Independence and a Persistent Paradox of Population Ethics,” 2022. Forthcoming in Journal of Philosophy.
- Topkis (1998) Topkis, Donald M., Supermodularity and complementarity, Princeton university press, 1998.
- De Vries and Vohra (2003) Vries, Sven De and Rakesh V Vohra, “Combinatorial auctions: A survey,” INFORMS Journal on computing, 2003, 15 (3), 284–309.
- Yang (2020) Yang, Yi-You, “Rationalizable choice functions,” Games and Economic Behavior, 2020, 123, 120–126.
- Yokoi (2019) Yokoi, Yu, “Matroidal choice functions,” SIAM Journal on Discrete Mathematics, 2019, 33 (3), 1712–1724.
Appendix A Proofs of Theorems in Section 3
In the Appendix, we provide the proofs of our results.
A.1. Proof of Theorems 1 and subsection 4.5
In this section we prove Theorem subsection 4.5. As discussed in Section 4.5, the if and only-if directions of Theorem 1 follow from Theorem subsection 4.5 (I) and (II), respectively.
Before starting the proof, we refer to an existing result on path-independent choice rules. For a choice rule , we define
| (2) |
If satisfies the substitutes condition, then if and only if for some . For a linear order over and , we define
Note that is a singleton or the empty set. By using this function, we can represent a path-independent choice rule , as stated below.424242A formal proof of this proposition can be found in Moulin (1985) (Theorem 5) or Alva and Dogan (2023) (Theorem 11.19).
Lemma 1 (Aizerman and Malishevski (1981)).
Let be a choice rule such that . Then, satisfies path independence if and only if there exists a finite sequence of linear orders over , , such that
| (3) |
A.1.1. Proof of Theorem subsection 4.5 (I)
Let be a choice rule and be a utility function that rationalizes and satisfies ordinal concavity-. Our goal is to prove that satisfies path independence. By Proposition 1, it suffices to prove that satisfies the substitutes condition and irrelevance of rejected contracts. One easily verifies that, if a choice rule is rationalized by some utility function, then it satisfies irrelevance of rejected contracts. In the following we prove that satisfies the substitutes condition.
Suppose, for contradiction, that the substitutes condition fails, i.e., there exist and distinct such that and .434343We note that the substitutes condition is equivalent to the following condition: for any and any distinct , if , then . Here, we consider the negation of this condition. Consider two subsets , and . By ordinal concavity-, there exists such that
-
(i)
, or
-
(ii)
.
If , then , which implies
If , then the above set inclusion clearly holds. Therefore, condition (i) contradicts uniquely maximizing among all subsets of . By , we have . Therefore, condition (ii) contradicts uniquely maximizing among all subsets of . ∎
A.1.2. Proof of Theorem subsection 4.5 (II)
Let be a choice rule that satisfies path independence. By Proposition 1, it also satisfies irrelevance of rejected contracts and the substitutes condition. We assume that (recall (2)).444444If , then for all (see the sentence after (2)). For such a choice rule, we can easily construct a utility function that rationalizes and satisfies ordinal concavity; for example, defined by satisfies the desired conditions. Therefore, we consider only choice rules with .
We proceed in three steps. In step 1, we construct a utility function . In step 2, we prove that rationalizes . In step 3, we prove that satisfies ordinal concavity+.
Step 1: Construction of a utility function.
Set . By Lemma 1, there exists a sequence of linear orders over , , such that (3) holds. Let . For each , let denote the rank of in the order .454545For example, if and is given by , then , , and . We define by
Notice that gives a higher value to a contract with a higher priority according to . Therefore, for any , it holds that .464646If , then this equality holds in the sense that both sides coincide with the empty set.
We define by
where the maximum over the emptyset is defined to be . Hence, implies . Note that, for any with , we have . Let and we define by
| (4) |
Note that the second term on the right-hand side is sufficiently small in the sense that
| (5) |
We prove a claim.
Claim 5.
Let . Suppose that there exists such that
| (6) | |||
| (7) |
Then, .
Proof.
By (7) and the fact that takes integer values, we have . This means that and
where the last inequality follows from (5). Therefore, the desired claim follows if (which implies ). In what follows, we assume that .
For each , let be contracts such that
Then,
where
-
•
the first inequality follows from (5) and ,
-
•
the second inequality follows from (6),
-
•
the third inequality follows from (7) and the definition of ,
-
•
the fourth inequality follows from and for all with ,474747We remark that, if , then , so the left-hand side of the fourth inequality is equal to , and hence, the desired inequality follows. and
-
•
the last equality follows from the formula of a finite geometric series (with first term and common ratio ).
The above displayed inequality establishes the desired inequality. ∎
Step 2: Proof of rationalizing .
Let and with . Our goal is to prove that
We consider two cases.
Case 1: Suppose that . By and irrelevance of rejected contracts, we have
By (3), the left-hand side is equal to . Therefore, for any , we have , which together with implies
It follows that . By irrelevance of rejected contracts, we have , which implies . Meanwhile, implies . Therefore, we obtain
as desired.
Case 2: Suppose that , which is equivalent to . By (3), we have . Therefore,
| (8) | there exists such that . |
Take such a with the lowest index, i.e., implies . By and , we have
which implies
Furthermore, by (8) and ,
By Claim 5 applied to and , we obtain the desired inequality.
Step 3: Proof of ordinal concavity+ of .
Instead of directly proving that satisfies ordinal concavity+, we show that it satisfies a stronger notion defined below.
Definition 12.
A utility function satisfies ordinal concavity++ if, for any and , one of the following two conditions holds:
-
(i)
there exists such that , or
-
(ii)
.
Note that ordinal concavity++ implies ordinal concavity+.484848To verify this claim, take any and . If condition (i) of ordinal concavity++ holds for , then condition (i) of ordinal concavity+ holds for the . If condition (ii) of ordinal concavity++ holds, then condition (ii) of ordinal concavity+ holds for . Since conditions (i) and (ii) of ordinal concavity+ are equivalent to the first two conditions of ordinal concavity, the above argument also shows that ordinal concavity++ implies ordinal concavity.
Case 1: Suppose that . By (3), for any , we have . This condition implies
By and irrelevance of rejected contracts, we have , which implies . This inequality together with the above displayed equality implies that . Therefore, condition (i) of ordinal concavity++ holds for .
Case 2: Suppose that , which implies (recall the sentence after (2)). By (3), there exists such that . Take such a with the lowest index, i.e.,
| (9) | implies . |
Subcase 2-1: Suppose that
| (10) | there exists such that . |
Since , we have . We also have
where the former inequality follows from (9) and the latter inequality follows from and (10). Claim 5 applied to and implies that condition (i) of ordinal concavity++ holds.
Subcase 2-2: Suppose that for all .494949This case subsumes . Then,
Since takes only integer values, the above inequality implies that the left-hand side is bigger than the right-hand side by no less than 1. Therefore,
| (11) |
It follows that
where
-
•
the first inequality follows from ,
-
•
the second inequality follows from (11), and
-
•
the last inequality follows from (5).
We conclude that condition (ii) of ordinal concavity++ holds. As ordinal concavity++ implies ordinal concavity+, the desired conclusion follows. ∎
A.2. Proof of Theorems 2 and subsection 4.5
In this section, we prove Theorem subsection 4.5. Note that the if and only-if directions of Theorem 2 follow from Theorem subsection 4.5 (I) and (II), respectively.
A.2.1. Proof of Theorem subsection 4.5 (I)
Let be a choice rule and be a utility function that rationalizes and satisfies ordinal concavity- and size-restricted concavity-. By Theorem subsection 4.5 (I), satisfies path independence. It remains to prove that satisfies the law of aggregate demand. The proof is similar to that of Theorem 3.10 in Murota (2016). Suppose, for contradiction, that the law of aggregate demand is violated, i.e., there exist and such that and . By size-restricted concavity- of , there exists such that
-
(i)
, or
-
(ii)
.
If (i) holds, then we obtain a contradiction to uniquely maximizing among all subsets of . If (ii) holds, then together with , we obtain a contradiction to uniquely maximizing among all subsets of .
A.2.2. Proof of Theorem subsection 4.5 (II)
Let be a choice rule that satisfies path independence and the law of aggregate demand. We define as in (4). As proven in Section A.1.2, rationalizes and satisfies ordinal concavity+. It remains to prove that satisfies size-restricted concavity+. Let with . We consider two cases.
Case 1:505050The proof of this case is similar to that of Subcase 2-2 of step 3 in Section A.1.2. Suppose that there exist and such that
Since takes only integer values, the left-hand side is bigger than the right-hand side by no less than 1. Therefore,
| (12) |
It follows that
where
-
•
the first inequality follows from ,
-
•
the second inequality follows from (12), and
-
•
the last inequality follows from (5).
We conclude that condition (ii) of size-restricted concavity+ holds.
Case 2: Suppose that, for any , we have
This condition implies
which is equivalent to
By (3), we have
| (13) |
Subcase 2-1: Suppose that . Since satisfies path independence, by Proposition 1, satisfies the substitutes condition. Hence, the following set-inclusion holds:515151To see that (14) holds, suppose that there exists with . By and (the latter condition follows from (13)), we have . Together with , it implies . By combining , , and , we obtain a contradiction to the substitutes condition.
| (14) |
Since ,
| (15) |
Then,
where the first inequality follows from (14), the second inequality follows from (15), and the last inequality follows from , where
-
•
the first set-inclusion follows from the assumption of Subcase 2-1, and
-
•
the second set-inclusion follows from (which follows from (13)).
The above displayed inequality implies . We obtain a contradiction to the law of aggregate demand. Hence, Subcase 2-1 is not possible.
Subcase 2-2:525252The proof of this case is similar to that of Case 1 of step 3 in Section A.1.2. Suppose that . Let . By (3), for any , we have . This condition implies
By and irrelevance of rejected contracts, we have , which implies . This inequality together with the above displayed equality implies that . Therefore, condition (i) of size-restricted concavity+ holds. ∎
Appendix B Proof of claims in Section 4
B.1. Proof of Claim 1
Let and consider defined as follows:
One easily verifies that is submodular. However, the choice rule rationalized by this utility function violates the substitutes condition because
B.2. Proof of Claim 2
We first show that submodularity does not imply ordinal concavity. Consider the utility function in Section B.1, which satisfies submodularity. To verify that this function violates ordinal concavity, consider , , and . We have
Therefore, ordinal concavity does not hold.
To see that ordinal concavity does not imply submodularity, let and define by
One can verify that this function satisfies ordinal concavity. However, it violates submodularity because . ∎
B.3. Proof of Claim 3
We consider a choice rule introduced by Yokoi (2019).535353Yokoi (2019) studies a class of choice rules called matroidal choice functions. Yokoi (2019) proves that the choice rule given in this section is a matroidal choice function that is not rationalizable by any monotonic M♮-concave function. We strengthen this claim by showing that there exists no rationalizing M♮-concave function (including non-monotonic ones). Let and we define seven subsets of , denoted through ,545454These seven subsets arise as cycles of an undirected graph; see Figure 6.1 of Yokoi (2019). and for , as follows:
Let be a choice rule given by
This choice rule satisfies path-independence and the law of aggregate demand (see Yokoi (2019)). Our goal is to prove that there exists no M♮-concave utility function that rationalizes . Suppose, for contradiction, that there exists a rationalizing M♮-concave function .
It is known that an M♮-concave function satisfies the following condition:555555See, e.g., Corollary 1.3 of Murota and Shioura (2018).
In the following, we apply the above condition to two subsets with the same size and derive equations that must satisfy. We abbreviate to for notational simplicity.
-
1.
For and and ,
For and and ,
By and ,
Combining the above three displayed conditions leads to .565656We explain why this equation holds. Applying the strict inequalities in the third displayed condition to the first displayed condition, we have . Similarly, applying the strict inequalities to the second displayed condition, we have . Combining these two inequalities establish the desired equation. The other 7 equations below are derived in the same manner.
-
2.
For and and ,
For and and ,
By and ,
We obtain .
-
3.
For and and ,
For and and ,
By and ,
We obtain .
-
4.
For and and ,
For and and ,
By and ,
We obtain .
-
5.
For and and ,
For and and ,
By and ,
We obtain .
-
6.
For and and ,
For and and ,
By and ,
We obtain .
-
7.
For and and ,
For and and ,
By and ,
We obtain .
-
8.
For and and ,
For and and ,
By and ,
We obtain .
Let denote the 14 subsets appearing in the above 8 equations.
We define , where is the matrix that represents the 8 equations. Specifically, is given as follows:
Letting denote the vector such that for all , we must have .575757To see why this claim holds, note that we have thus far shown that any utility function satisfying M♮-concavity and rationalizing must satisfy the 8 equations. Equivalently, . One can verify the following assertion.
Fact 1.
The matrix has full row rank.
Notice that is the null space of the linear function given by the matrix . Applying existing results in linear algebra, we obtain:
Proposition 4 (Known result in linear algebra).
is a linear space and .
We define
Fact 2.
is a linear space and .
Proof.
It is easy to verify that is a linear space. To see that the inclusion relation holds, take . Then, there exists such that for all . Our goal is to show that satisfies the 8 equations; we only deal with the first equation because the other equations can be handled analogously.
as desired. ∎
Our next goal is to prove that . To this end, we introduce two existing results.
Proposition 5 (Known result in linear algebra).
For two linear spaces and , if and , then .
We say that two linear spaces and are isomorphic if there exists a function such that
-
1
is one-to-one.
-
2
is onto.
-
3
is linear (i.e., and ).
Proposition 6 (Known result in linear algebra).
Two linear spaces are isomorphic if and only if they have the same dimension.
Let be a function that maps to given by
To prove that , it suffices to prove that satisfies the three conditions of isomorphism.585858We explain why this claim holds. If satisfies the three conditions of isomorphism, then and are isomorphic, which together with Proposition 6 implies . This equation and Proposition 4 implies . Furthermore, by Fact 2, . Applying Proposition 5, we obtain . It is easy to see that is onto and linear. We prove that is one-to-one. Let and be such that . We show that . By the definition of , the following equation holds:
Note that the 6 subsets appearing on the right-hand side are included in . The same equation holds with replaced with . One can verify that the above matrix has full rank. Therefore, .
It follows that . Since (recall footnote 57), there exists such that
| (16) |
Again, we apply M♮-concavity (in particular, the condition stated after footnote 55) to two subsets with the same size 3. For and and ,
Note that 126 and 136 are not included in , while the other subsets are included in .
- •
- •
Therefore, in either case, we have
| (17) |
B.4. Proof of Proposition 3
Let be a choice rule and be a utility function that rationalizes and satisfies pseudo M♮-concavity. Our goal is to prove that satisfies path independence and the law of aggregate demand.
B.4.1. Proof of satisfying path independence
The proof is similar to that of Theorem subsection 4.5 (I) in Section A.1.1. By Proposition 1, it suffices to prove that satisfies the substitutes condition and irrelevance of rejected contracts. One easily verifies that, if a choice rule is rationalizable by some utility function, then it satisfies irrelevance of rejected contracts. In the following we prove that satisfies the substitutes condition.
Suppose, for contradiction, that the substitutes condition fails, i.e., there exist and distinct such that and .595959We consider the negation of the condition stated in footnote 43. Considet two subsets , and . By pseudo M♮-concavity, there exists such that
We consider two cases.
Case 1: Suppose that the left-hand side is equal to . Then, . We obtain a contradiction to uniquely maximizing among all subsets in .
Case 2: Suppose that the left-hand side is equal to . Then, . By , we obtain a contradiction to uniquely maximizing among all subsets in .
B.4.2. Proof of satisfying the law of aggregate demand
Instead of directly proving that satisfies the law of aggregate demand, we prove that satisfies the following condition: for any and ,
| (18) |
This condition and irrelevance of rejected contracts of (which follows from the fact that is rationalizable by some utility function) imply that satisfies the law of aggregate demand.606060To see that this implication holds, take with . Let . We first show that . If , then by irrelevance of rejected contracts, we have , which establishes the desired inequality. If , then (18) implies that the desired inequality holds. Repeating this procedure, we obtain .
Suppose, for contradiction, that the above condition fails, i.e., there exist and such that
| (19) |
Applying pseudo M♮-concavity to , and , there exists such that
By (which follows from uniquely maximizing among all subsets in ), the left-hand side is equal to . Therefore,
By (19), we have . Since (whenever ), it holds that . This condition and the above displayed inequality yield a contradiction to uniquely maximizing among all subsets in . ∎
B.5. Proof of Claim 4
We revisit the choice rule in Section B.3. Suppose, for contradiction, that there exists a pseudo M♮-concave function that rationalizes . Applying pseudo M♮-concavity to and and , we have
| (20) |
By (which follows from ) and (which follows from ), if the first inequality holds, then the third inequality holds. By (which follows from ) and (which follows from ), if the second inequality holds, then the third inequality holds. Therefore, in any case, the third inequality (20) holds.
Applying pseudo M♮-concavity to and and , we have
| (21) |
By (which follows from ) and (which follows from ), if the first inequality holds, then the third inequality holds. By (which follows from ) and (which follows from ), the second inequality never holds. Therefore, the third inequality (21) holds.
Combining (20) and (21), we have
By (which follows from ), the left-hand side is equal to . If , then we obtain a contradiction to (which follows from ). If , then we obtain a contradiction to (which follows from ). ∎
Online Appendix
Alternative Proof of Theorem 1
B.6. Construction of a utility function
Let . For any , we define for , inductively as follows:
We define for , inductively (from to ) as follows:
We define by
| (22) |
For any and , we define by
where is a sufficiently small number with . We define by
| (23) |
The following inequalities hold:
| (24) |
where the strict inequality follows from .
Claim 6.
Let with . Then,
Proof.
The proof is by mathematical induction. The claim trivially holds for because . Suppose that it holds for . We show the claim for .
By the definition of , our goal is to prove that
| (25) |
Let . By and the induction hypothesis,
| (26) |
By , we have (i) or (ii) . If (i) holds, then by , the induction hypothesis, and the substitutes condition,616161We use the following equivalent condition to the substitutes condition: for any with , it holds that . we have , which implies . Together with (26), it implies that is included in the right-hand side of (25). If (ii) holds, then , which implies , and so . Together with (26), it implies that is included in the right-hand side of (25). ∎
B.7. Proof of rationalizing
Fix an arbitrary with and let . Our goal is to prove that uniquely maximizes among all subsets of . The proof works in a number of steps. At each step , where , we provide two statements labeled as and below.
In step 1, we show that either Claim or Claim holds. The proof is completed if holds. If holds, then we go to step 2. In step 2, we show that either Claim or Claim holds. Again, if holds then the proof is completed, and otherwise we go to step 3. We continue this process until Claim holds for some .
We define for inductively as follows:
Note that .
Step ().
Suppose that one of the following two conditions holds:
-
•
, or
-
•
and holds in every step .
Then, one of the following two claims holds:
- :
-
uniquely maximizes among all elements in ; or
- :
-
for every , and satisfies the following four conditions:
-
(i):
,
-
(ii):
for every ,
-
(iii):
for every , and
-
(iv):
for every and .
-
(i):
Moreover, if , then holds.
Proof of the statement for step .
By the definition of , . Together with the substitutes condition, it implies that
| (27) |
The following equality holds:
| (28) |
To see that (28) holds, let with . Then, , which implies . Since for every , we obtain . Conversely, let with . Then,
where the first equality follows from , the strict inequality follows from (27) and , and the last equality follows from . By the above displayed inequality and (which follows from (i)),626262If , then follows from . we get . It follows that (28) holds.
For any and ,636363If , then the summation is defined to be .
where
-
•
the first inequality follows from ,
-
•
the second equality follows from (ii) for every with ,646464If , then the second equality trivially holds.
-
•
the third equality follows from (if ), and and (iii) (if ),
-
•
the second inequality follows from and , and
-
•
the last inequality follows from the definition of .
Hence,
| (30) |
We consider two cases.
Case 1: Suppose . We prove that holds.
By and irrelevance of rejected contracts,
| (31) |
Fix with . The above equality and (28) imply
Together with (31) and , it implies
| (32) |
By (29), , and (iii),656565If , then (33) follows from . we have
| (33) |
Together with (31) and (32), it yields
| (34) |
which implies and . By the definition of ,
Together with (33) and (34), it implies
| (35) |
By (ii) for every with ,666666If , then we do not need (36) in order to establish (37).
| (36) |
| (37) |
By the first claim of for every with , (34), and the definition of ,
| (38) |
We obtain
| (39) | ||||
| (40) |
where the first and last equalities follow from (38), the second equality follows from (34), and the strict inequality follows from (34) and (37).
Furthermore, for any and any ,
| (41) |
where the first inequality follows from (29) and (30) and the other inequalities follow from (iv) for every with .
Hence, for any , we have , where the equality follows from (39), the strict inequality follows from (41),
and the weak inequality follows from the former inequality of (24).
Together with (40) for every with , it yields .
Case 2: Suppose . We prove that holds. For any , by the assumption of Case 2 and (which follows from ), we have (where the equality follows from (iii)),676767If , then the equality follows from . The same comment applies to the equation in the remaining part. which implies . Thus,
the first claim of holds.
By (29), we obtain (i).
For any , by (28), we have . Together with (which follows from ), it yields
| (42) |
Together with (which follows from (iii)), it implies (ii).
For any , we have
where the second equality follows from (which follows from (iii)) and the fourth equality follows from (42). Together with (which follows from the assumption of Case 2), it yields (iii). Finally, (iv) follows from (30). We conclude that holds.
Finally, we prove the claim that holds for . By (iii) for with , we get . Together with and (which follows from the definition of ), we get . Hence, . As proven in Case 1, holds. ∎
By the statement for step (), there exists such that holds. Therefore, we obtain the desired claim. ∎
B.8. Proof of ordinal concavity of
As in the proof of Theorem subsection 4.5 (I) in the main text, we show that satisfies ordinal concavity++ (see step 3 in Section A.1.2). Since ordinal concavity++ is stronger than ordinal concavity (see footnote 48 in the main text), the desired claim follows.
Definition (Same as Definition 9 in the main text).
A utility function satisfies ordinal concavity++ if, for any and , one of the following two conditions holds:
-
(i)
there exists such that , or
-
(ii)
.
Let and . We show that defined by (23) satisfies (i) or (ii) in the above definition.
Let and . By following the same line of the proof in Section B.7, there exists such that
-
•
For every with , Case 2 holds in step and we obtain , and
-
•
Case 1 holds in step and we obtain .
As shown in the proof, there exists a sequence of collections of subsets of , , such that satisfies the conditions in for every with . We define by
Let . By (28) and for every with ,
Together with , it implies
These conditions and (28) imply
| (43) | |||
| (44) |
We consider two cases.
Case 1:
Suppose . By the definition of , we have and . Together with and (28),
it yields
Since , the above conditions have two implications. First, the former set-inclusion and imply
| (45) |
Second, there exists such that
| (46) |
By (43) and ,
| (47) |
We obtain
where
-
•
the first inequality follows from ,
-
•
the second equality follows from (which is implied by (47)), , and (ii) for every with ,
-
•
the third equality follows from (which is implied by (47)), , and (iii),686868If , then the third equality follows from .
- •
-
•
the last inequality follows from the definition of .
It follows that , which together with (24) implies . Hence, condition (i) of ordinal concavity++ holds.
Case 2: Suppose . We consider two subcases.
Subcase 2-1: Suppose that for every .
By (28) and the definition of , we have for every with . Together with the assumption of Subcase 2-1, it yields
This condition and (28) imply
These conditions, together with (43), yield
| (48) |
We consider two further subcases.
Subcase 2-1-1: Suppose .
As we noted in the beginning of Section B.8 (after the definition of ordinal concavity++), Case 1 holds in the proof of step in Section B.7, which
implies (see the first sentence of Case 1 after (30)).
We consider two further subcases.
Subcase 2-1-1-1: Suppose .
By (which follows from (48)), , and (iii),696969If , then (49) follows from .
we have
| (49) |
Together with the assumptions of Subcases 2-1 and 2-1-1-1, these equations imply
| (50) |
If , then by the definition of and (50), we get
which together with (50) imply and . Repeating this procedure,
| (51) | |||
We obtain the following:707070If , then the summation is defined to be .
where
-
•
the second equality follows from (which is implied by (48)), and (ii) for every with , and
-
•
the third equality follows from (51).
Hence,
| (52) |
By , and the first statement of for every with , we have
| (53) |
We obtain
where the two equalities follow from (50), (53), and the definition of , and the strict inequality follows from (49) and (50). This inequality and (52) imply
Hence, condition (i) of ordinal concavity++ holds for .
Subcase 2-1-1-2: Suppose . Since and (which follows from the assumption of Subcase 2-1-1), there exists such that . Then,
where
-
•
the first inequality follows from ,
-
•
the second equality follows from (which is implied by (48)), , and (ii) for every with ,
-
•
the third equality follows from (which is implied by (48)), , and (iii),717171If , then the third equality follows from .
-
•
the fourth equality follows from the assumption of Subcase 2-1 and , and
-
•
the last inequality follows from the definition of .
It follows that , which together with (24) implies . Hence, condition (i) of ordinal concavity++ holds.
Subcase 2-1-2 Suppose , which implies . By (28), we have .
By following the same line of the proof of Subcase 2-1-1-2 (with playing the role of ),
there exists with . Hence, condition (i) of ordinal concavity++ holds.
Subcase 2-2: Suppose that there exists such that . Together with
-
•
for every (which follows from and Claim 6),
-
•
(where the set-inclusion follows from the definition of ) for every , and
-
•
the substitutes condition,
it implies that there exists with . Let denote the minimum index such that .
By (28) and for every with ,
Together with (ii) for every with , it implies
| (54) |
By and (iii) for every with , we have
| (55) |
If , then
where the second equality follows from (which follows from and the minimality of ) and the third equality follows from (55). If , then by the same argument as above, we obtain . Repeating this procedure, we obtain
This condition and (55) imply
| (56) |
Together with the minimality of , it yields
| (57) |
We obtain
where
-
•
the first inequality follows from ,
- •
-
•
the third equality follows from (56) and , and
-
•
the last inequality follows from the definition of .
It follows that , which together with (24) implies . Hence, condition (ii) of ordinal concavity++ holds. ∎