Rationality based Innate-Values-driven
Reinforcement Learning
Abstract
Innate values describe agents’ intrinsic motivations, which reflect their inherent interests and preferences to pursue goals and drive them to develop diverse skills satisfying their various needs. The essence of reinforcement learning (RL) is learning from interaction based on reward-driven behaviors, much like natural agents. It is an excellent model to describe the innate-values-driven (IV) behaviors of AI agents. Especially developing the awareness of the AI agent through balancing internal and external utilities based on its needs in different tasks is a crucial problem for individuals learning to support AI agents integrating human society with safety and harmony in the long term. This paper proposes a hierarchical compound intrinsic value reinforcement learning model – innate-values-driven reinforcement learning termed IVRL to describe the complex behaviors of AI agents’ interaction. We formulated the IVRL model and proposed two IVRL models: DQN and A2C. By comparing them with benchmark algorithms such as DQN, DDQN, A2C, and PPO in the Role-Playing Game (RPG) reinforcement learning test platform VIZDoom, we demonstrated that rationally organizing various individual needs can effectively achieve better performance.
1 Introduction
In natural systems, motivation is concerned explicitly with the activities of creatures that reflect the pursuit of a particular goal and form a meaningful unit of behavior in this function heckhausen2018motivation . Furthermore, intrinsic motivations describe incentives relating to an activity itself, and these incentives residing in pursuing an activity are intrinsic. Intrinsic motivations deriving from an activity may be driven primarily by interest or activity-specific incentives, depending on whether the object of an activity or its performance provides the main incentive schiefele1996motivation . They also fall in the category of cognitive motivation theories, which include theories of the mind that tend to be abstracted from the biological system of the behaving organism merrick2013novelty .
However, when we analyze natural agents, such as humans, they are usually combined motivation entities. They have biological motivations, including physiological, safety, and existence needs; social motivation, such as love and esteem needs; and cognitive motivation, like self-actualization or relatedness and growth needs merrick2009motivated . The combined motivation theories include Maslow’s Hierarchy of Needs maslow1958dynamic and Alderfer’s Existence Relatedness Growth (ERG) theory alderfer1972existence . Fig. 2 and 2 illustrate the general innate values (intrinsic motivations) model and various models with three-level needs of different amounts, respectively.
Many researchers regard motivated behavior as behavior that involves the assessment of the consequences of behavior through learned expectations, which makes motivation theories tend to be intimately linked to theories of learning and decision-making baldassarre2013intrinsically . In particular, intrinsic motivation leads organisms to engage in exploration, play, strategies, and skills driven by expected rewards. The computational theory of reinforcement learning (RL) addresses how predictive values can be learned and used to direct behavior, making RL naturally relevant to studying motivation.
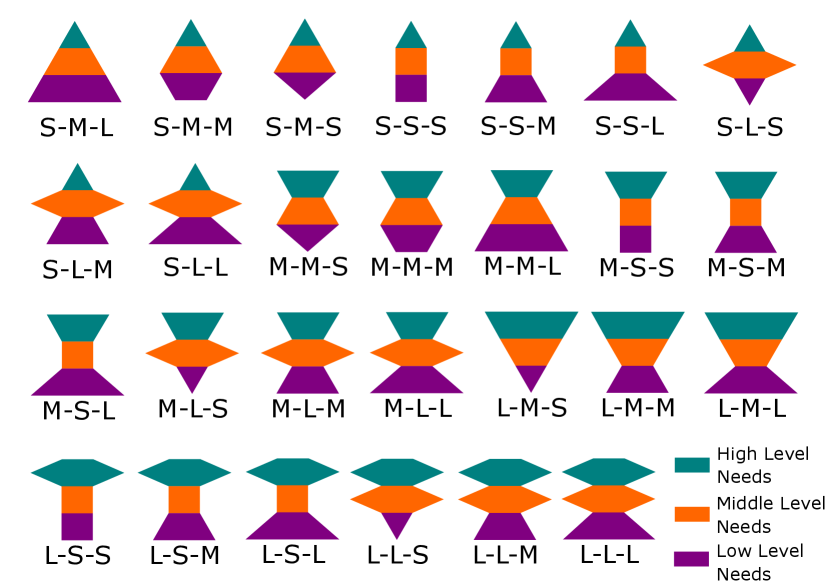
In artificial intelligence, researchers propose various abstract computational structures to form the fundamental units of cognition and motivations, such as states, goals, actions, and strategies. For intrinsic motivation modeling, the approaches can be generally classified into three categories: prediction-based schmidhuber1991curious ; schmidhuber2010formal , novelty-based marsland2000real ; merrick2009motivated , and competence-based barto2004intrinsically ; schembri2007evolution . Furthermore, the concept of intrinsic motivation was introduced in machine learning and robotics to develop artificial systems learning diverse skills autonomously yang2024bayesian . The idea is that intelligent machines and robots could autonomously acquire skills and knowledge under the guidance of intrinsic motivations and later exploit such knowledge and skills to accomplish tasks more efficiently and faster than if they had to acquire them from scratch baldassarre2013intrinsically .
In other words, by investigating intrinsically motivated learning systems, we would clearly improve the utility and autonomy of intelligent artificial systems in dynamic, complex, and dangerous environments yang2022game ; yang2023hierarchical . Specifically, compared with the traditional RL model, intrinsically motivated RL refines it by dividing the environment into an external environment and an internal environment, which clearly generates all reward signals within the organism111Here, the organism represents all the components of the internal environment in the AI agent. baldassarre2013intrinsically . However, although the extrinsic reward signals are triggered by the objects and events of the external environment, and activities of the internal environment cause the intrinsic reward signals, it is hard to determine the complexity and variability of the intrinsic rewards (innate values) generating mechanism.
To address those gaps, we introduce the innate-values-driven reinforcement learning (IVRL) model to describe the complex behaviors in AI agents’ interactions by integrating with combined motivation theories. We formalize the idea and propose two IVRL models based on classic DQN and A2C algorithms. Then, we compare them with benchmark RL algorithms such as DQN mnih2015human , DDQN wang2016dueling , A2C mnih2016asynchronous , and PPO schulman2017proximal in the RPG RL test platform VIZDoom Kempka2016ViZDoom ; Wydmuch2019ViZdoom . The results demonstrate that the IVRL model can achieve convergence and adapt efficiently to complex and challenging tasks.
2 Approach Overview
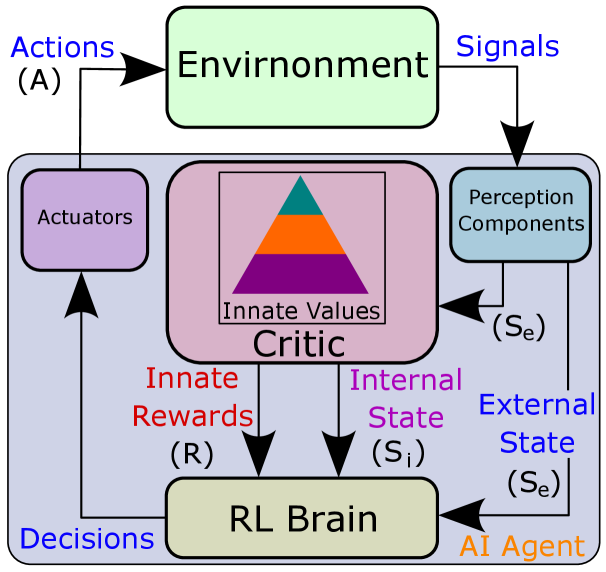
We assume that all the AI agents (like robots) interact in the same working scenario, and their external environment includes all the other group members and mission setting. In contrast, the internal environment consists of individual perception components including various sensors (such as Lidar and camera), the critic module involving intrinsic motivation analysis and innate values generation, the RL brain making the decision based on the feedback of rewards and description of the current state (including internal and external) from the critic module, and actuators relating to all the manipulators and operators executing the RL brain’s decisions as action sequence and strategies. Fig. 4 illustrates the proposed IVRL model.
Compared with the traditional RL model, our model generates the input state and rewards from the critic module instead of directly from the environment. This means that the individual needs to calculate rewards based on the innate value and current utilities and then update its current internal status – the hierarchical needs model. For example, supposing two agents and have different innate value models: Fig. 2 S-M-L and L-M-S. We use health points, energy levels, and task achievement to represent their safety needs (low-level intrinsic motivations), basic needs (middle-level intrinsic motivations), and teaming needs (High-level intrinsic motivations) yang2020hierarchical ; yang2020needs ; yang2021can , respectively. Considering , , and , if and receive the external repairing signal simultaneously, the innate rewards will larger than based on their innate value model (low-level safety needs ). In contrast, if they get the order to collaborate with other agents fulfilling a task (high-level teaming needs ) at the same time, the agent will receive more credits from it (). In other words, due to different innate value models, their intrinsic motivations present significant differences, which will lead to different innate rewards for performing the same task.
Specifically, we formalize the IVRL of an AI agent with an external environment using a Markov decision process (MDP) puterman2014markov . The MDP is defined by the tuple where represents the finite sets of internal state 222The internal state describes an agent’s innate value distribution and presents the dominant intrinsic motivation based on the external state . and external states . represents a finite set of actions. The transition function : [0, 1] determines the probability of a transition from any state to any state given any possible action . Assuming the critic function is , which describes the individual innate value model. The reward function defines the immediate and possibly stochastic innate reward that an agent would receive given that the agent executes action which in state and it is transitioned to state the discount factor that balances the trade-off between innate immediate and future rewards.
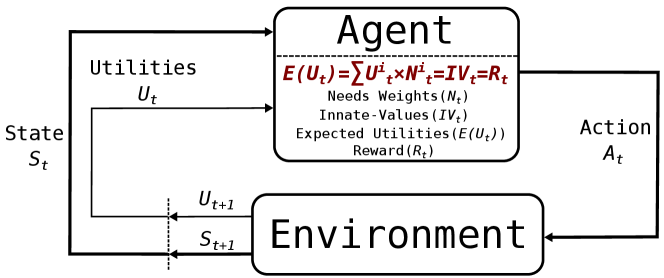
2.1 The Source of Randomness
In our model, the randomness comes from three sources. The randomness in action is from the policy function: ; the needs weight function: makes the randomness of innate values; the state-transition function: causes the randomness in state.
Supposing at current state an agent has a needs weight matrix (Eq. (1)) in a mission, which presents its innate value weights for different levels of needs. Correspondingly, it has a utility matrix (Eq. (1)) for specific needs resulting from action . Then, we can calculate its reward for through Eq. (2) at the state .
| (1) |
| (2) |
In the process, the agent will first generate the needs weight and action based on the current state, then, according to the feedback utilities and the needs weights, calculate the current reward and iterate the process until the end of an episode. Fig. 3 illustrates the trajectory of state , needs weight , action , and reward in the IVRL model.
2.2 Randomness in Discounted Returns
According to the above discussion, we define the discounted return at time as cumulative discounted rewards in the IVRL model (Eq. (3)) and is the discount factor.
| (3) |
At time , the randomness of the return comes from the the rewards . Since the reward depends on the state , action , and needs weight , the return also relies on them. Furthermore, we can describe their randomness as follows:
| (4) | |||
| (5) | |||
| (6) |
2.3 Action-Innate-Value Function
Based on the discounted return Eq. (3) and its random factors – Eq. (4), (5), and (6), we can define the Action-Innate-Value function as the expectation of the discounted return at time (Eq. (7)).
| (7) |
describes the quality of the action taken by the agent in the state , using the needs weight generating from the needs weight function as the innate value judgment to execute the policy .
2.4 State-Innate-Value Function
Furthermore, we can define the State-Innate-Value function as Eq. (8), which calculates the expectation of for action and reflects the situation in the state with the innate value judgment .
| (8) |
2.5 Approximate the Action-Innate-Value Function
The agent’s goal is to interact with the environment by selecting actions to maximize future rewards based on its innate value judgment. We make the standard assumption that a factor of per time-step discounts future rewards and define the future discounted return at time as Eq. (3). Moreover, we can define the optimal action-value function as the maximum expected return achievable by following any strategy after seeing some sequence , making corresponding innate value judgment , and then taking action , where is a needs weight function describing sequences about innate value weights and is a policy mapping sequences to actions.
| (9) |
Since the optimal action-innate-value function obeys the Bellman equation, we can estimate the function by using the Bellman equation as an iterative update. This is based on the following intuition: if the optimal innate-value of sequence at the next time-step was known for all possible actions and needs weights , then the optimal strategy is to select the reasonable action and rational innate value weight , maximising the expected innate value of ,
| (10) |
Furthermore, the same as the DQN mnih2015human , we use a function approximator (Eq. (11)) to estimate the action-innate-value function.
| (11) |
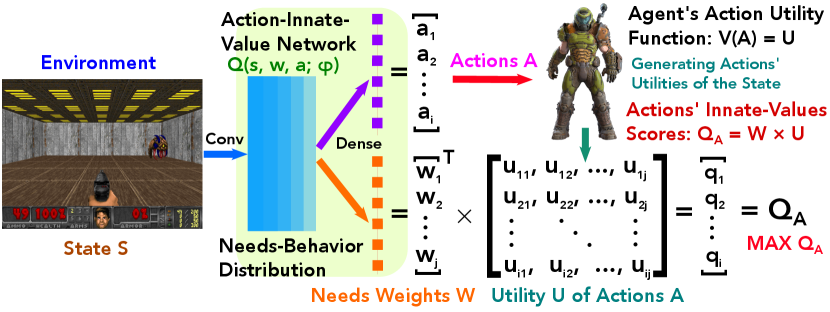
We refer to a neural network function approximator with weights as a Q-network. It can be trained by minimising a sequence of loss function that changes at each iteration ,
| (12) |
| (13) |
Where Eq. 13 is the target for iteration and is a probability distribution over sequences , needs weights , and action that we refer to as the needs-behavior distribution. We can approximate the gradient as follows:
| (14) |
Instead of computing the full expectations in the Eq. (14), stochastic gradient descent is usually computationally expedient to optimize the loss function. Here, the weights are updated after every time step, and single samples from the needs-behavior distribution and the emulator replace the expectations, respectively.
Our approach is a model-free and off-policy algorithm, which learns about the greedy strategy following a needs-behavior distribution to ensure adequate state space exploration. Moreover, the needs-behavior distribution selects action based on an -greedy strategy that follows the greedy strategy with probability and selects a random action with probability . Fig. 5 illustrates the action-innate-value network generating Needs-Behavior distribution.
Moreover, we utilize the experience replay technique lin1992reinforcement , which stores the agent’s experiences at each time-step, in a data-set , pooled over many episodes into a replay memory. During the algorithm’s inner loop, we apply Q-learning updates, or minibatch updates, to samples of experience, , drawn at random from the pool of stored samples. After performing experience replay, the agent selects and executes an action according to an -greedy policy, as we discussed. Since implementing arbitrary length histories as inputs to a neural network is difficult, we use a function to produce our action-innate-value Q-function. Alg. 1 presents the algorithm of the IVRL DQN.
2.6 IVRL Advantage Actor-Critic (A2C) Model
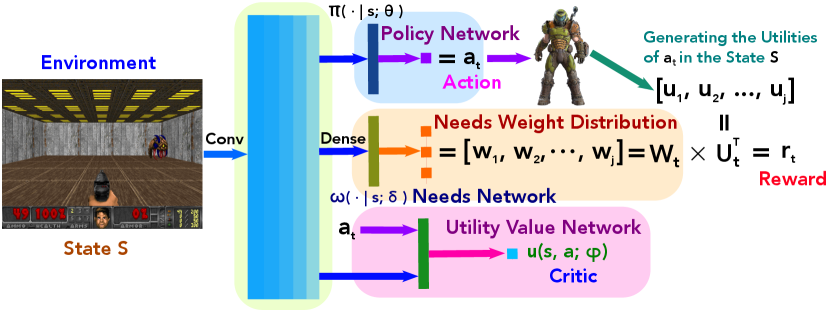
Furthermore, we extend our IVRL method to the Advantage Actor-Critic (A2C) version. Specifically, our IVRL A2C maintains a policy network , a needs network , and a utility value network . Since the reward in each step is equal to the current utilities multiplying the corresponding weight of needs, the state innated-values function can be approximated by presenting it as Eq. (15). Then, we can get the policy gradient Eq. (16) and needs gradient Eq. (17) of the Eq. (15) deriving according to the Multi-variable Chain Rule, respectively. We can update the policy network and needs network by implementing policy gradient and needs gradient, and using the temporal difference (TD) to update the value network .
| (15) |
| (16) |
| (17) |
Using an estimate of the utility function as the baseline function, we subtract the V value term as the advantage value. Intuitively, this means how much better it is to take a specific action and a needs weight compared to the average, general action and the needs weights at the given state Eq. (18). Fig. 6 illustrates the architecture of the IVRL actor-critic version and Alg. 2 presents the algorithm of the IVRL A2C.
| (18) |
3 Experiments




Considering cross-platform support and the ease of creating custom scenarios, we selected the VIZDoom Role-Playing Game (RPG) reinforcement learning test platform Kempka2016ViZDoom ; Wydmuch2019ViZdoom to evaluate the performance of the proposed innate-value-driven reinforcement learning model. We choose four scenarios: Defend the Center, Defend the Line, Deadly Corridor, and Arens (Fig. 7), and compare our models with several benchmark algorithms, such as DQN mnih2015human , DDQN wang2016dueling , A2C mnih2016asynchronous , and PPO schulman2017proximal . These models were trained on an NVIDIA GeForce RTX 3080Ti GPU with 16 GiB of RAM.
3.1 Environment Setting
In our experiments, we define four categories of utilities (health points, amount of ammo, environment rewards, and number of killed enemies), presenting three different levels of needs: low-level safety and basic needs, medium-level recognition needs, and high-level achievement needs. When the agent executes an action, it receives all the corresponding innate utilities, such as health points and ammo costs, and external utilities, such as environment rewards (living time) and the number of killed enemies. At each step, the agent can calculate the rewards for the action by multiplying the current utilities and the needed weight for them. In our experiments, the initial needs weight for each utility category is 0.25, which has been fixed in the benchmark DRL algorithms’ training, such as DQN, DDQN, and PPO. For more details about the experiment code, please check the supplementary materials.
a. Defend the Center – Fig. 7(a): For this scenario, the map is a large circle where the agent is in the middle, and monsters spawn along the wall. The agent’s basic actions are turn-left, turn-right, and attack, and the action space is 8. It needs to survive in the scenario as long as possible.
b. Defend the Line. – Fig. 7(b): The agent is located on a rectangular map, and the monsters are on the opposite side. Similar to the defend the center scenario, the agent needs to survive as long as possible. Its basic actions are move-left, move-right, turn-left, turn-right, and attack, and the action space is 32.
c. Deadly Corridor. – Fig. 7(c): In this scenario, the map is a corridor. The agent is spawned at one end of the corridor, and a green vest is placed at the other end. Three pairs of monsters are placed on both sides of the corridor. The agent needs to pass the corridor and get the vest. Its basic actions are move-left, move-right, move-forward, turn-left, turn-right, and attack, and the action space is 64.
d. Arena. – Fig. 7(d): This scenario is the most challenging map compared with the other three. The agent’s start point is in the middle of the map, and it needs to eliminate various enemies to survive as long as possible. Its basic actions are move-left, move-right, move-forward, move-backward, turn-left, turn-right, and attack, and the action space is 128.
3.2 Evaluation
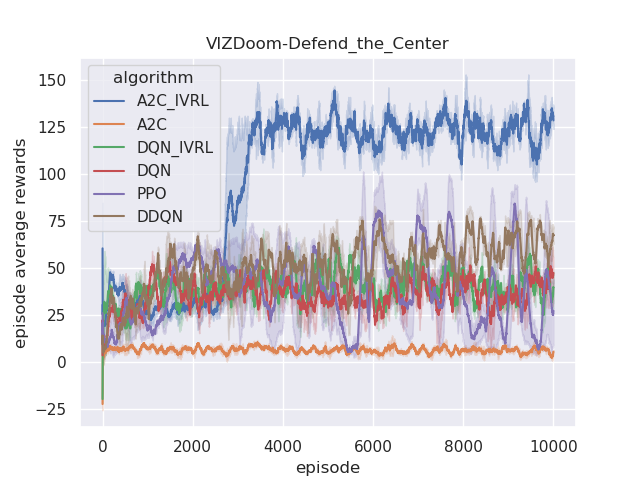
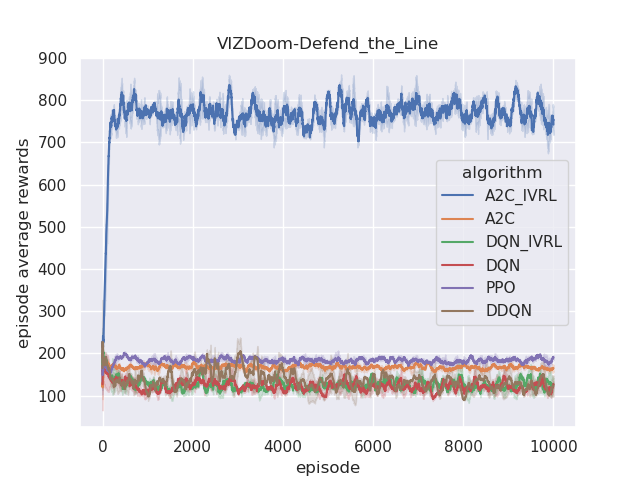
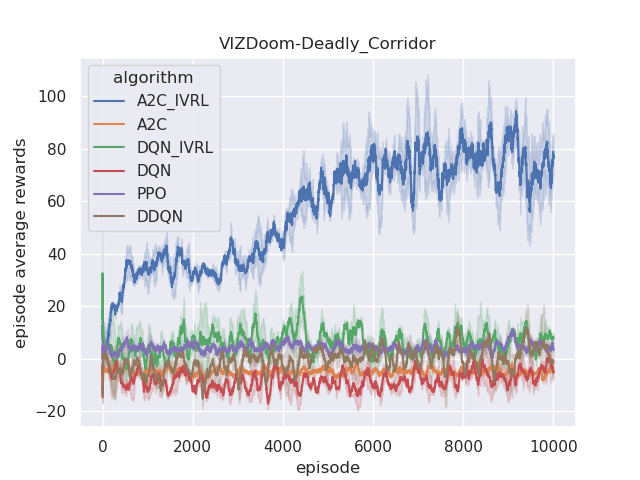
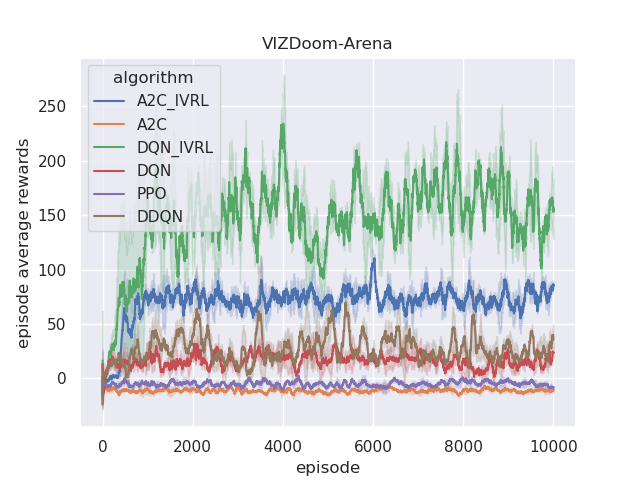
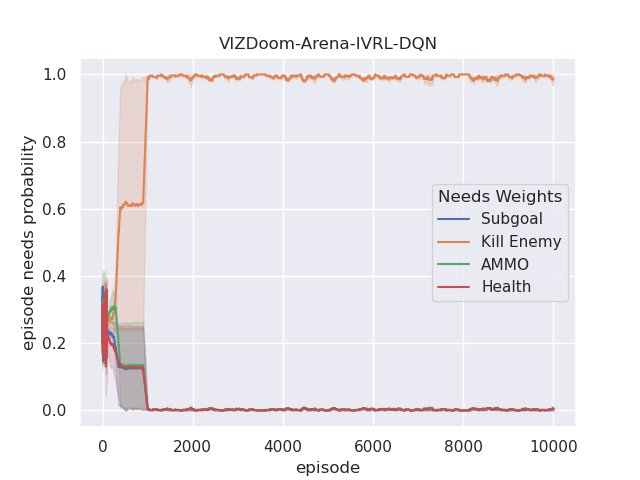
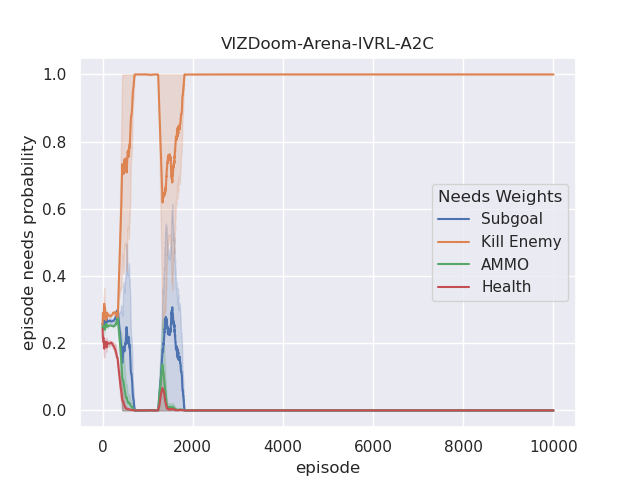
The performance of the proposed IVRL DQN and A2C models is shown in the Fig 8. Fig. 7(a), 7(b), 7(c), and 7(d) demonstrate that IVRL models can achieve higher average scores than traditional RL benchmark methods (Fig. 8, 8, 8, and 8). Especially for the IVRL A2C algorithm, it presents more robust, stable, and efficient properties than the IVRL DQN model. Although the IVRL DQN shows better performance in the Arena scenario (Fig. 8), the small perturbation introduced by the innate-values utilities may have made the network weights in some topology difficult to reach convergence.
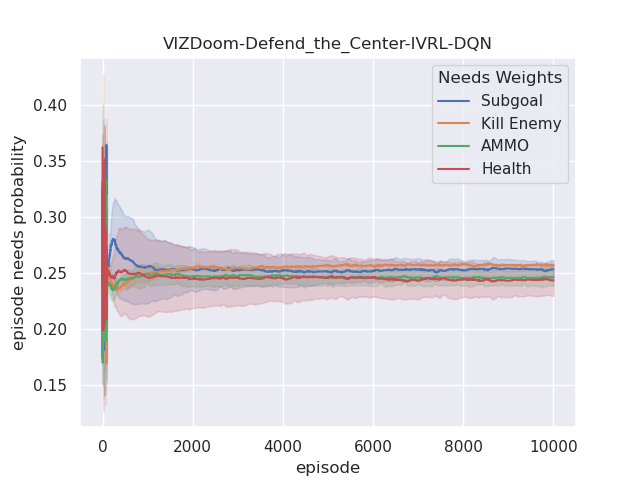
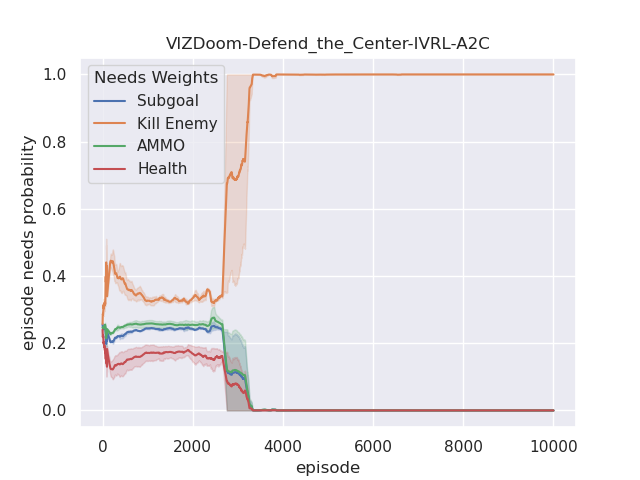
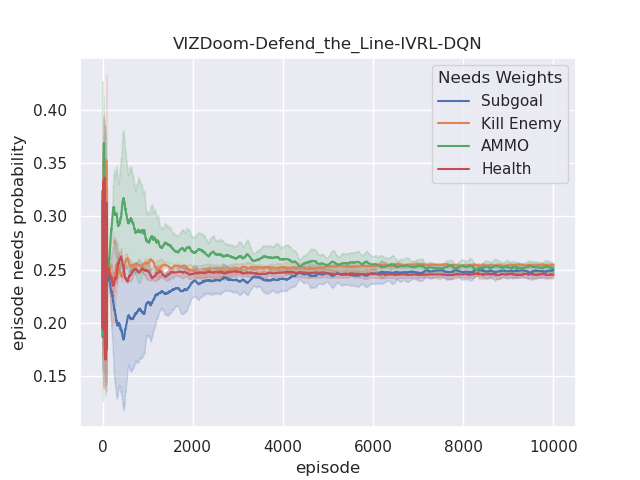
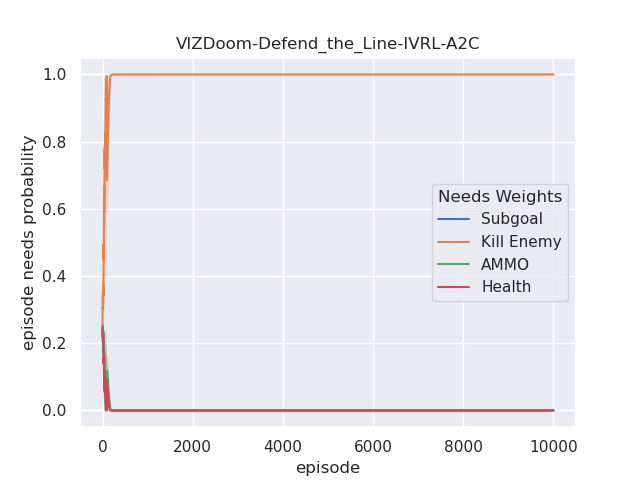
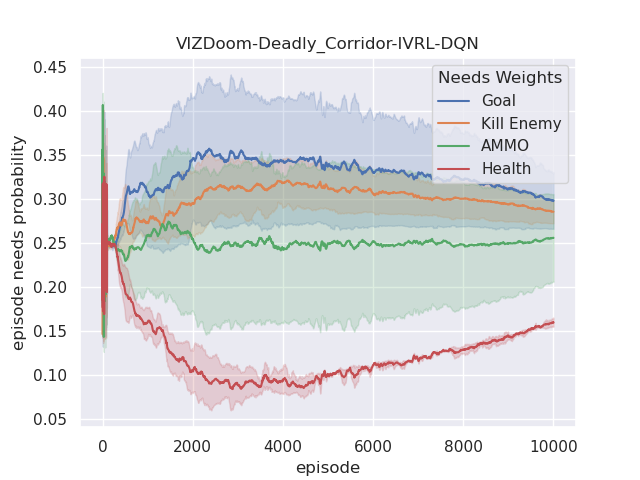
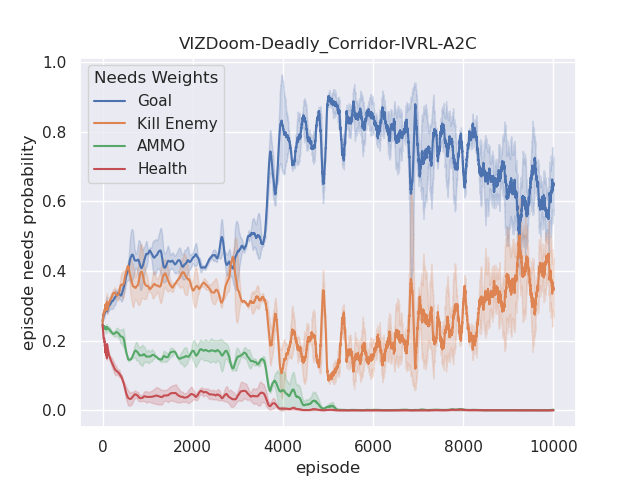
Furthermore, we also analyze their corresponding tendencies in different scenarios to compare the needs weight differences between the IVRL DQN and A2C models. In the defend-the-center and defend-the-line experiments, each category of the need weight in the IVRL DQN model does not split and converges to a specific range compared with its initial setting in our training (Fig. 8 and 8). In contrast, the weights of health depletion, ammo cost, and sub-goal (environment rewards) shrink to approximately zero, and the weight of the number of killed enemies converges to one in the IVRL A2C model. This means that the top priority of the IVRL A2C agent is to eliminate all the threats or adversaries in those scenarios so that it can survive, which is similar to the Arena task. According to the performance in those three scenarios (Fig. 8, 8, and 8), the IVRL A2C agent represents the characteristics of bravery and fearlessness, much like the human hero in a real battle. However, in the deadly corridor mission, the needs weight of the task goal (getting the vest) becomes the main priority, and the killing enemy weight switches to the second for the IVRL A2C agent (Fig. 8). They converge to around 0.6 and 0.4, respectively. In training, by adjusting its different needs weights to maximize rewards, the IVRL A2C agent develops various strategies and skills to kill the encounter adversaries and get the vast efficiently, much like a military spy.
In our experiments, we found that selecting the suitable utilities to consist of the agent innate-values system is critically important for building its reward mechanism, which decides the training speed and sample efficiency. Moreover, the difference in the selected utility might cause some irrelevant experiences to disrupt the learning process, and this perturbation leads to high oscillations of both innate-value rewards and needs weight.
Generally, the innate value system serves as a unique reward mechanism driving agents to develop diverse actions or strategies satisfying their various needs in the systems. It also builds different personalities and characteristics of agents in their interaction. From the environmental perspective, due to the various properties of the tasks, agents need to adjust their innate value system (needs weights) to adapt to different tasks’ requirements. These experiences also shape their intrinsic values in the long term, similar to humans building value systems in their lives. Moreover, organizing agents with similar interests and innate values in the mission can optimize the group utilities and reduce costs effectively, just like “Birds of a feather flock together." in human society.
4 Conclusion
This paper introduces the innate-values-driven reinforcement learning (IVRL) model mimicking the complex behaviors of agent interactions. By adjusting needs weights in its innate-values system, it can adapt to different tasks representing corresponding characteristics to maximize the rewards efficiently. For theoretical derivation, we formulated the IVRL model and proposed two types of IVRL models: DQN and A2C. Furthermore, we compared them with benchmark algorithms such as DQN, DDQN, A2C, and PPO in the RPG reinforcement learning test platform VIZDoom. The results prove that rationally organizing various individual needs can effectively achieve better performance.
For future work, we want to improve the IVRL further and develop a more comprehensive system to personalize individual characteristics to achieve various tasks testing in several standard MAS testbeds, such as StarCraft II, OpenAI Gym, Unity, etc. Especially in multi-object and multi-agent interaction scenarios, building the awareness of AI agents to balance the group utilities and system costs and satisfy group members’ needs in their cooperation is a crucial problem for individuals learning to support their community and integrate human society in the long term. Moreover, integrating efficient deep RL algorithms with the IVRL can help agents evolve diverse skills to adapt to complex environments in MAS cooperation. Furthermore, implementing the IVRL in real-world systems, such as human-robot interaction, multi-robot systems, and self-driving cars, would be challenging and exciting.
References
- [1] Jutta Heckhausen and Heinz Heckhausen. Motivation and action. Springer, 2018.
- [2] Ulrich Schiefele. Motivation und Lernen mit Texten. Hogrefe Göttingen, 1996.
- [3] Kathryn E Merrick. Novelty and beyond: Towards combined motivation models and integrated learning architectures. Intrinsically motivated learning in natural and artificial systems, pages 209–233, 2013.
- [4] Kathryn E Merrick and Mary Lou Maher. Motivated reinforcement learning: curious characters for multiuser games. Springer Science & Business Media, 2009.
- [5] Abraham Harold Maslow. A dynamic theory of human motivation. 1958.
- [6] Clayton P Alderfer. Existence, relatedness, and growth: Human needs in organizational settings. 1972.
- [7] Gianluca Baldassarre and Marco Mirolli. Intrinsically motivated learning systems: an overview. Intrinsically motivated learning in natural and artificial systems, pages 1–14, 2013.
- [8] Jürgen Schmidhuber. Curious model-building control systems. In Proc. international joint conference on neural networks, pages 1458–1463, 1991.
- [9] Jürgen Schmidhuber. Formal theory of creativity, fun, and intrinsic motivation (1990–2010). IEEE transactions on autonomous mental development, 2(3):230–247, 2010.
- [10] Stephen Marsland, Ulrich Nehmzow, and Jonathan Shapiro. A real-time novelty detector for a mobile robot. EUREL European Advanced Robotics Systems Masterclass and Conference, 2000.
- [11] Andrew G Barto, Satinder Singh, Nuttapong Chentanez, et al. Intrinsically motivated learning of hierarchical collections of skills. In Proceedings of the 3rd International Conference on Development and Learning, volume 112, page 19. Citeseer, 2004.
- [12] Massimiliano Schembri, Marco Mirolli, and Gianluca Baldassarre. Evolution and learning in an intrinsically motivated reinforcement learning robot. In Advances in Artificial Life: 9th European Conference, ECAL 2007, Lisbon, Portugal, September 10-14, 2007. Proceedings 9, pages 294–303. Springer, 2007.
- [13] Qin Yang and Ramviyas Parasuraman. Bayesian strategy networks based soft actor-critic learning. ACM Transactions on Intelligent Systems and Technology, 15(3):1–24, 2024.
- [14] Qin Yang and Ramviyas Parasuraman. Game-theoretic utility tree for multi-robot cooperative pursuit strategy. In ISR Europe 2022; 54th International Symposium on Robotics, pages 1–7. VDE, 2022.
- [15] Qin Yang and Ramviyas Parasuraman. A hierarchical game-theoretic decision-making for cooperative multiagent systems under the presence of adversarial agents. In Proceedings of the 38th ACM/SIGAPP Symposium on Applied Computing, pages 773–782, 2023.
- [16] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. Human-level control through deep reinforcement learning. nature, 518(7540):529–533, 2015.
- [17] Ziyu Wang, Tom Schaul, Matteo Hessel, Hado Hasselt, Marc Lanctot, and Nando Freitas. Dueling network architectures for deep reinforcement learning. In International conference on machine learning, pages 1995–2003. PMLR, 2016.
- [18] Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asynchronous methods for deep reinforcement learning. In International conference on machine learning, pages 1928–1937. PMLR, 2016.
- [19] John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
- [20] Michał Kempka, Marek Wydmuch, Grzegorz Runc, Jakub Toczek, and Wojciech Jaśkowski. ViZDoom: A Doom-based AI research platform for visual reinforcement learning. In IEEE Conference on Computational Intelligence and Games, pages 341–348, Santorini, Greece, Sep 2016. IEEE. The Best Paper Award.
- [21] Marek Wydmuch, Michał Kempka, and Wojciech Jaśkowski. ViZDoom Competitions: Playing Doom from Pixels. IEEE Transactions on Games, 11(3):248–259, 2019. The 2022 IEEE Transactions on Games Outstanding Paper Award.
- [22] Qin Yang and Ramviyas Parasuraman. Hierarchical needs based self-adaptive framework for cooperative multi-robot system. In 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), pages 2991–2998. IEEE, 2020.
- [23] Qin Yang and Ramviyas Parasuraman. Needs-driven heterogeneous multi-robot cooperation in rescue missions. In 2020 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), pages 252–259. IEEE, 2020.
- [24] Qin Yang and Ramviyas Parasuraman. How can robots trust each other for better cooperation? a relative needs entropy based robot-robot trust assessment model. In 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), pages 2656–2663. IEEE, 2021.
- [25] Martin L Puterman. Markov decision processes: discrete stochastic dynamic programming. John Wiley & Sons, 2014.
- [26] Long-Ji Lin. Reinforcement learning for robots using neural networks. Carnegie Mellon University, 1992.