Random magnetic anisotropy driven transitions in layered perovskite LaSrCoO4
Abstract
Attempts to unravel the nature of magnetic ordering in LaSrCoO4 (Co3+), a compound intermediate between antiferromagnetic (AFM) La2CoO4 (Co2+) and ferromagnetic (FM) Sr2CoO4 (Co4+), have met with a limited success so far. In this report, the results of a thorough investigation of dc magnetization and ac susceptibility (ACS) in single-phase LaSrCoO4 provide clinching evidence for a thermodynamic paramagnetic (PM) - ferromagnetic (FM) phase transition at Tc = 220.5 K, followed at lower temperature (Tg = 7.7 K) by a transition to the cluster spin glass (CSG) state. Analysis of the low-field Arrott plot isotherms, in the critical region near Tc, in terms of the Aharony-Pytte scaling equation of state clearly establishes that the PM-FM transition is basically driven by random magnetic anisotropy (RMA). For temperatures below 30 K, large enough RMA destroys long-range FM order by breaking up the infinite FM network into FM clusters of finite size and leads to the formation of a CSG state at temperatures T 8 K by promoting freezing of finite FM clusters in random orientations. Increasing strength of the single-ion magnetocrystalline anisotropy (and hence RMA) with decreasing temperature is taken to reflect an increase in the number of low-spin (LS) Co3+ ions at the expense of that of high-spin (HS) Co3+ ions. At intermediate temperatures (30 K 180 K), spin dynamics has contributions from the infinite FM network (fast relaxation governed by a single anisotropy energy barrier) and finite FM clusters (extremely slow stretched exponential relaxation due to hierarchical energy barriers).
I Introduction
Low-dimensional magnetic systems are susceptible to a variety of external perturbations, such as doping, magnetic field, and strain, etc. [1]. Their higher sensitivity to external stimuli compared to the 3D counterparts opens up room for new applications, , control of exchange bias in a single unit cell [2]. Moreover, in low-dimensional systems, control of spin moment can provide tremendous application opportunities for spintronics devices (layered cobaltates are potential candidates). LaCoO3 (Co3+), an often studied 3D compound, exhibits peculiar properties such as a metal-insulator transition, high-spin (HS) state to low-spin (LS) state transitions, magneto-electronic phase separation and ferromagnetic (FM) correlations [3]. A fascinating cobaltate and its 2D analog, La2CoO4 (Co2+) is an antiferromagnetic insulator (AFI) [4], but not explored enough mainly due to its topotactic oxidation [5]. Its counterpart Sr2CoO4 (Co4+) has a similar structure and shows ferromagnetism and half-metallicity [6]. In LaSrCoO4 (an intermediate composition of the above-mentioned end compounds), La/SrCoO3 3D blocks are separated by rock-salt La/SrO layers.
Depending upon how the energy-splitting between the and orbitals, caused by the crystal-field, compares in magnitude with the exchange energy associated with the Hund’s rule coupling, the Co3+ ion can exist in three different spin states [7]: the magnetically-active Co3+ high-spin (HS; , S = 2) state when , intermediate-spin (IS; , S = 1) state when and non-magnetic low-spin (LS; , S = 0) state when . In the LaSrCoO4 (LSCO) compound, the spin-state of Co3+ ions has been a controversial issue. For instance, LSCO is reported [8, 9, 10, 11, 12] to have a mixture of LS and (thermally-activated) HS states of the Co3+ ions. Presence of homogeneous IS state of Co3+ ions has also been claimed [13] and subsequently challenged [14]. In our previous study [7], we probed the spin-states in La2-xSrxCoO4 (0.5 x 1) compounds and found existence of the HS and LS states together at room temperature, discarding the presence of IS state. First-principles calculations [9] support the view that mixed spin-states (HS and LS) of Co3+ ions inhabit the ground state of LaSrCoO4.
Existence of mixed spin-states of the Co3+ ions in LSCO is expected to have an important bearing on the magnetic and transport properties, since the super-exchange interaction between the HS Co3+ ions mediated by the intervening LS Co3+ ion can induce long-range FM order, while the superexchange interaction between the adjacent HS Co3+ neighbors can give rise to antiferromagnetic (AFM) order. The competing FM and AFM exchange interactions, in turn, could result in a spin glass (SG) state. Conflicting reports [15, 16, 17, 18, 19, 20] about the nature of magnetism in LSCO, however, render the existing magnetic data inconclusive, as elucidated below. While a paramagnetic (PM)-SG transition at 20 K [15] ( 8 K [16]) is construed as a transition from the HS to IS state, no PM-SG transition is observed down to 2 K (the temperature up to which an insulating PM state persists [18]) and a broad hump in the thermomagnetic data, observed at 250 K, is attributed to the ferromagnetic (La,Sr)CoO3 impurity [18]. This insulating PM ground state is taken to reflect [18] the IS spin state of Co3+ ions. In sharp contrast, two magnetic transitions, PM-FM transition at Tc 250 K [19, 20] and the SG-like transition at 12 K [19] or at 60 K [20], have been reported. Considering that the spin and valence states of Co are inextricably linked in cobaltates, presence of valence states (Co2+ and/or Co4+) of Co, arising from the varying degree of oxygen off-stoichiometry in the LSCO samples used in such investigations, could be at the root of these apparent discrepancies.
In this work, the intrinsic magnetic behavior near the PM - FM and SG transitions is unraveled by ensuring close to a pure Co3+ state in our LaSrCoO4 sample. DC magnetization and frequency-dependent ac susceptibility (ACS) data, taken on the LaSrCoO4 compound, unambiguously confirm the existence of two magnetic transitions: a thermodynamic (frequency-independent) PM - FM phase transition at Tc = 220.5 K and a frequency-dependent cluster spin glass (SG) transition, approaching the value Tg = 7.7 K in the zero-frequency limit. Both of these transitions are basically driven by random magnetic anisotropy (RMA). Increasing strength of the single-ion magnetocrystalline anisotropy (and hence RMA) with decreasing temperature is shown to be a manifestation of an increase in the number of low-spin (LS) Co3+ ions at the expense of that of high-spin (HS) Co3+ ions.
II Experimental method
The details of sample synthesis are reported elsewhere [7]. Synchrotron X-ray diffraction (XRD) pattern was measured at room temperature using the BL-12 ADXRD beamline of RRCAT, India. To avoid possible fluorescence from Co, an x-ray photon energy of 7690 eV ( = 1.612 Å), which lies below the absorption edge, was used for XRD measurements. X-ray absorption near edge spectra (XANES) were recorded in the fluorescence mode at the same beamline. Energy resolution at the Co K-edge energy was 0.7 eV. ‘Zero-field’ (H = 0) and ‘in-field’ (H = 80 kOe) electrical resistivities as functions of temperature were measured by four-probe method, using the Oxford cryostat. Magnetization measurements were carried out utilizing the 7 Tesla Quantum design MPMS 3 magnetometer. M(H) hysteresis loops at fixed temperatures were recorded following the ‘field-cooled’ (FC) protocol. Magnetization was measured as a function of temperature, M(T), over the temperature range extending from 5 K to 300 K at fixed fields, employing the FC and ‘zero-field-cooled’ (ZFC) protocols. The virgin M(H) curves were recorded after demagnetizing the sample and the superconducting magnet by setting field to zero in the oscillatory mode. For constructing the Arrott plots from the virgin M(H) isotherms, the applied field has been corrected for the demagnetizing field to arrive at the internal effective magnetic field [21] Heff, in accordance with the relation, Heff = Happlied - (4N) M, where N is the demagnetizing factor, which was determined from the low-field portions of the M(H) isotherms taken at T Tc. ZFC relaxation measurement has been performed by cooling the sample down to 150 K in zero field and after waiting for 100 s (tw), a static magnetic field of 50 Oe was applied and the time evolution of magnetization at 150 K was measured upto 8000 s. The real () and imaginary () components of ac magnetic susceptibility were measured in the temperature range of 2 - 300 K, at fixed frequencies (1.1 Hz - 941 Hz) of the ac driving field of rms amplitude, = 3 Oe employing the Quantum Design MPMS 3 system equipped with an ac susceptibility option.
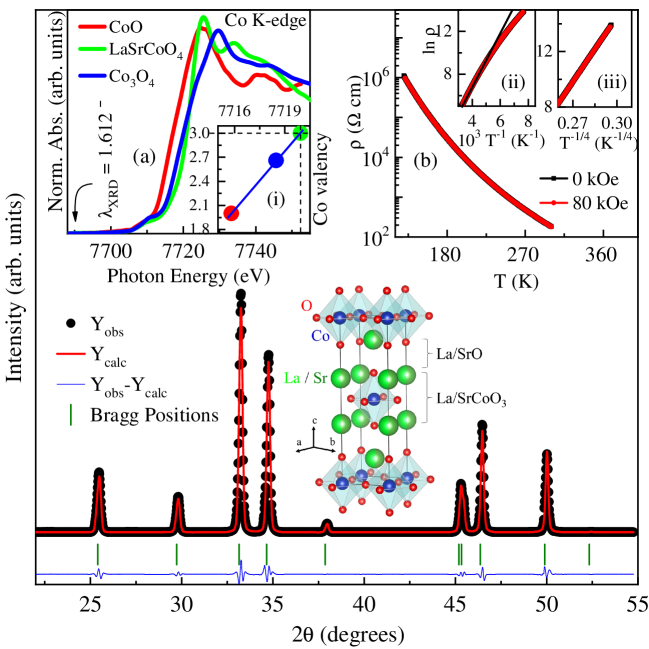
III Results and discussion
Fig. 1 shows room temperature synchrotron XRD pattern of the LaSrCoO4 (LSCO) compound together with the Rietveld fit. Absence of any extra Bragg peaks, attributable to the impurity phases such as La2CoO4 (Co2+) and Sr2CoO4 (Co4+), confirms the single-phase nature of the LaSrCoO4 sample. Rietveld refinement yielded the lattice parameters, corresponding to the tetragonal space group 4/, as = 3.8025(3) Å and = 12.4985(2) Å . Inset (a) compares the Co K-edge XANES data of LaSrCoO4 with those of the reference compounds CoO and Co3O4. Linear Co-valency versus Co K-edge photon energy plot in the inset (i) yields the value +2.98(2) for the Co valence and thereby confirms the Co-valency of +3 in the LSCO sample. Data points, depicted by circles in the linear plot shown in inset (i), correspond to the first derivative of the absorption edge.
Inset (b) of Fig. 1 clearly demonstrates semiconducting-like temperature variation of the ‘zero-field’ ((H = 0)) and ‘in-field’ ((H = 80 kOe)) resistivity in the LSCO sample. If, apart from Co3+ ions, Co2+ and Co4+ ions were also present in the sample, double exchange, involving charge hopping, would have resulted in a metallic state (characterized by low resistivity, typically 10 - 100 , and increasing with temperature) as opposed to the observed semiconducting-like state with very large resistivity decreasing from at 130 K to at 310 K. Consistent with the conclusion drawn from the Co K-edge XANES data, this finding completely rules out the presence of Co2+ and Co4+ ions in our LSCO sample. Furthermore, negligibly small magnetoresistance (MR), [((T,H = 80 kOe) - (T,H = 0)]/(T,H = 0), observed in the present case, sharply contrasts the reasonably large negative MR, expected in double-exchange ferromagnets. The insets (ii) and (iii) of Fig. 1(b) bear out clearly that the processes such as the thermal activation of charge carriers across the band gap (described by expression ) and Mott variable-range polaron hopping (represented by the expression ) [22, 23, 24] operate within the temperature ranges 225 K - 300 K (T Tc) and 130 K - 220 K (T Tc), respectively.
After ensuring that the sample is of very good quality (free from the impurity phases), in the following, we attempt to unravel the intrinsic magnetic behavior of the LaSrCoO4 compound. Fig. 2(a) displays the ‘field-cooled’ (FC) and ‘zero-field-cooled’ (ZFC) thermomagnetic curves, M(T), at fixed magnetic fields in the range 10 Oe - 10 kOe. A clear bifurcation between FC and ZFC M(T) is observed at low fields. Such bifurcations are indicative of either a spin-glass (SG) phase [25] or cluster spin-glass (CG) phase or magnetic anisotropy energy barriers or super-paramagnetism (SPM) [26]. A closer look at the low-temperature ZFC M(T) data shows a clear cusp (inset (b) of Fig. 2) at Tg 8 K. Similar feature was observed previously [17, 19, 16] and denoted as a freezing temperature. An interesting point to note is that on cooling below TIrr (the temperature at which FC and ZFC M(T) bifurcate), MFC increases, which is taken to be a characteristic feature of cluster spin glass behavior in various systems [27]. The increase in MFC with decreasing temperature, even below Tg, points to the presence of a cluster spin glass (CSG) state [28] because MFC normally exhibits a plateau for canonical spin glass [29]. It is noteworthy to mention that, for a typical re-entrant SG systems, the irreversibility occurs far below Tc while for CSG TIrr Tc [30]. In this connection, it is also reported [3] that if the bifurcation temperature TIrr Tg, the compound exhibits cluster spin glass type behavior while, for canonical SG [31], the TIrr coincides with the Tg. Thus, we conclude that the signatures discussed above basically reflect the CSG state in LaSrCoO4 at low temperatures.
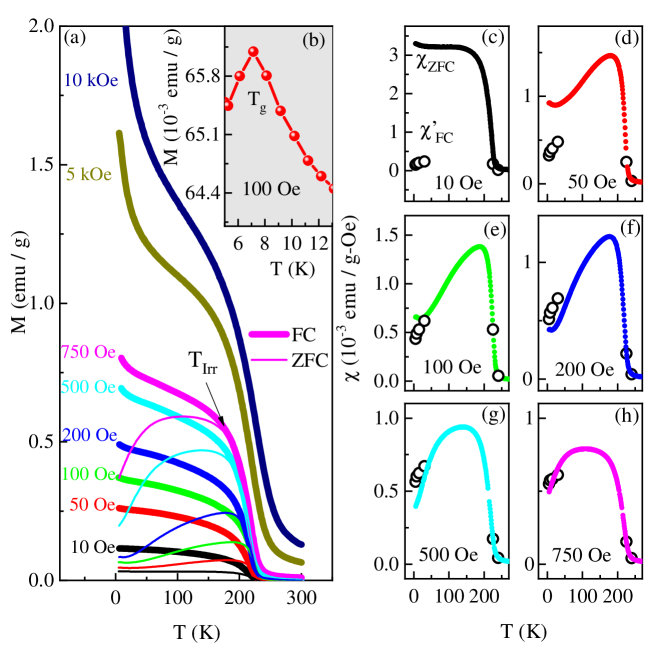
Next, we discuss the role of magnetic anisotropy as a possible source of bifurcation in M(T). Because of the prevalent elongated octahedra in the crystal structures similar to that of LaSrCoO4, the pseudo orbital moment of Co3+ HS, = 1 [32], prefers to lie in-plane and forces the spin moment also to lie within the plane [33] due to the spin-orbit coupling. Neutron diffraction studies on iso-structural compounds LaSrFeO4 [34] and half-doped La1.5Sr0.5CoO4 [35] have clearly borne out that, in these systems, magnetic moments are confined to the plane but can rotate within the plane. This is indicative of an XY-type anisotropy and hence -axis may not be the easy axis of magnetization. To ascertain whether or not magnetic anisotropy plays a role, we adopted the approach, proposed by Joy [26], according to which, if the decrease in MZFC at low temperatures is due to magnetocrystalline anisotropy, MZFC should follow the relation, . That this is indeed the case for the fields 100 Oe, is evident from Fig. 2(e - h). However, at 50 Oe, () strongly deviates from () (see Fig. 2(c, d)) in the low temperature region. The demagnetization-limited behavior of at for 10 Oe, suggests that the shape anisotropy also becomes important at low fields 50 Oe. Note that, in the calculation of , we have used the coercive field, Hc(T), data shown in the inset of Fig. 3.
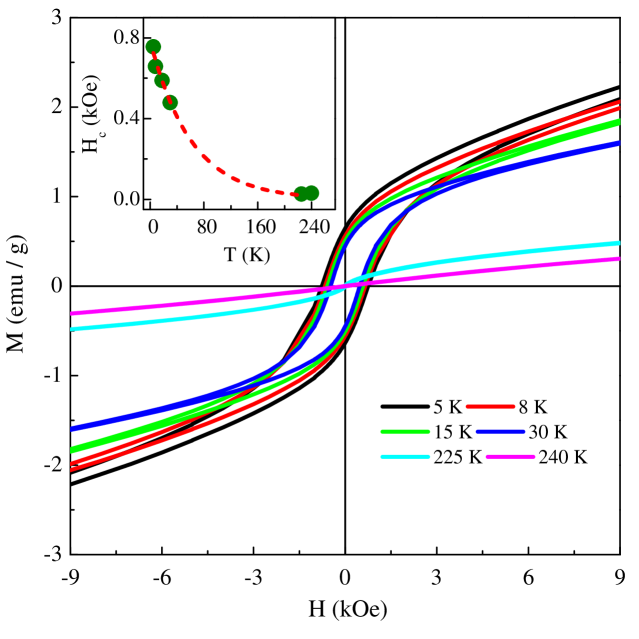
Fig. 3 presents the M(H) hysteresis loops at fixed temperatures, taken in the ‘field-cooled’ (H = 70 kOe) mode at temperatures below and above the PM-FM transition temperature, Tc = 220.5 K, (corresponding to the dip in dMZFC(T)/dT at low fields H = 10 - 100 Oe, not shown here). With temperature decreasing from T Tc, where the sample is in the PM state and as such the M(H) isotherms are linear, the coercive field, Hc, increases from zero at T = Tc = 220.5 K to about 800 Oe at 5 K; the rate of increase in Hc picks up for temperatures below 30 K, as is evident from the inset of Fig. 3. A steep increase in Hc as the temperature falls below 30 K is indicative of an increase in the random magnetic anisotropy (RMA). The observation that magnetization does not saturate even in fields as high as 70 kOe at low temperatures (Fig.5(a)) and the presence of RMA (as inferred from the critical-point analysis in the following section) support the existence of a CSG state at low temperatures.
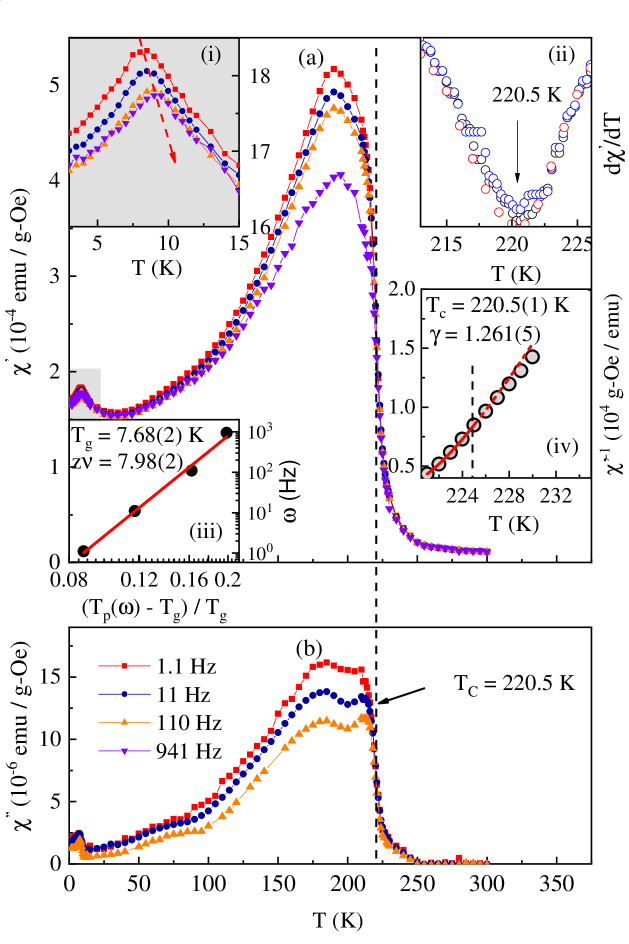
The panels (a) and (b) of Fig. 4 display the temperature variations of the real () and imaginary () parts of ac magnetic susceptibility, respectively. While the inset (i) of panel (a) highlights the frequency-induced shift in the peak in (T) at T = 8 K, the inset (ii) clearly brings out the frequency-independence of the dip in the d/dT T plots at = 220.5 K, which corresponds to the inflection point in (T). The frequency-independent value of = 220.5 K confirms the true thermodynamic nature of the FM - PM phase transition at .
The shift in per decade of frequency ( = 3.2 10-2) is an order of magnitude greater than that ( 10-3)) observed [31] in canonical spin glasses but is typical of the cluster spin glasses [31, 36]. The frequency dependence of the peak temperature, , is analyzed in terms of the following expression given by the ‘critical slowing down’ model [31, 36]
| (1) |
where is the relaxation time due to the correlated spin dynamics, is the spin-glass transition temperature in the zero-frequency limit, is the spin-spin correlation length critical exponent and is the dynamical critical exponent. The linear fit through the versus data (solid circles) in the inset (iii) of Fig. 4, based on the Eq. (1) with the parameter values = 2.49(1) 10-8 s, = 7.68(2) K and the product = 7.98(2), testifies to the validity of the critical slowing down model. Note that, in the canonical spin glasses, relaxation time, , is typically of the order of 10-12 s [31, 36]. Several orders of magnitude larger (i.e., much slower spin dynamics), in the present case, further confirms the existence of a cluster spin glass ground state.
Next, we focus our attention on the FM - PM transition at = 220.5 K. In the critical region above , the inverse of measured ac susceptibility, (T) (T), is related to the inverse intrinsic susceptibility, (T) as (T) = 4 N + (T), where N is the demagnetizing factor. As the temperature approaches from above, diverges (or equivalently, goes to zero) at in accordance with the relation
| (2) |
where and are the critical amplitude and critical exponent, respectively. Inset (iv) of Fig. 4 depicts the best theoretical fit (continuous curve) to the data, based on the Eq. (2), yields = 220.5 K, = 5.9(1) 105 and = 1.261(5). This value of will be put into a proper context later in the text.
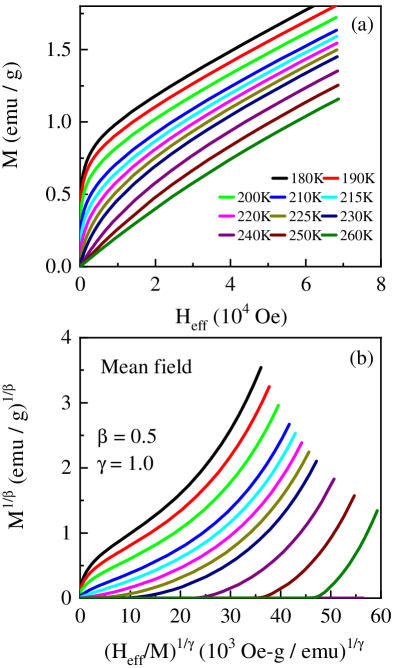
It is well-known that the critical-point (CP) analysis of magnetization, M(T,H), data taken in the critical region near Tc provides a powerful means to unravel the true nature of magnetic ordering prevalent in a spin system. As elucidated below, the CP analysis makes use of the critical exponents , and for the spontaneous magnetization (order parameter), ‘zero-field’ susceptibility and the critical M(H) isotherm, (characterizing a continuous FM-PM phase transition at Tc), that are defined as [37]
| (3) |
| (4) |
| (5) |
where , A, B and M0 are the critical amplitudes [37, 38]. Diverse systems having exactly the same values for the critical exponents , and , fall into a single universality class. Universality class, in turn, is governed by the order parameter (spin) dimensionality () and spatial dimensionality () [37, 39] as long as the interaction coupling the spins is of short range. The presence of different valence and spin states in the present system is expected to have a profound effect on the critical behavior. This expectation called for a detailed study of the critical behavior of LaSrCoO4 at temperatures in the vicinity of the FM-PM phase transition. To this end, we have analyzed the virgin M(H) isotherms in the critical region (shown in Fig. 5(a)) using the scaling equation of state (SES) method, detailed in the reference [37]. Instead of following the customary practice of using, at first, the Arrott [40] SES, we use the generalized form of the Arrott SES, given by Arrott and Noakes [41] (AN), i.e.,
| (6) |
to arrive at the correct choice of the critical exponents that makes the AN, versus , plots a set of parallel straight lines in the critical region near Tc. The temperature at which the linear AN plot isotherm passes through the origin marks the Tc. To begin with, we ascertain if the values of critical exponents and , theoretically predicted for any universality class, make the AN plot isotherms at temperatures close to Tc linear. For example, in Fig. 5 (b) it is evident that the mean-field (MF) critical exponent values = 0.5 and = 1 do not yield linear AN isotherm in the critical region. The data presented in Fig. S1 of the supplementary material demonstrate that, like the MF critical exponent values, none of the universality class critical exponent choices: = 0.365, = 1.386 for three-dimensional (3D) Heisenberg; = 0.345, = 1.316 for 3D-XY; = 0.325, = 1.241 for 3D Ising and = 0.25, = 1.0 for mean-field tricritical, results in the linear AN plot isotherms.
Furthermore, regardless of the choice of the critical exponents and , extrapolation of the high-field portions of the AN isotherms to does not give any intercept on the axis. No intercept on the ordinate axis implies no spontaneous magnetization and hence absence of long-range FM order. This result prompted us to look for even the non-universal exponent values that could lead to the desired linear AN plot isotherms.
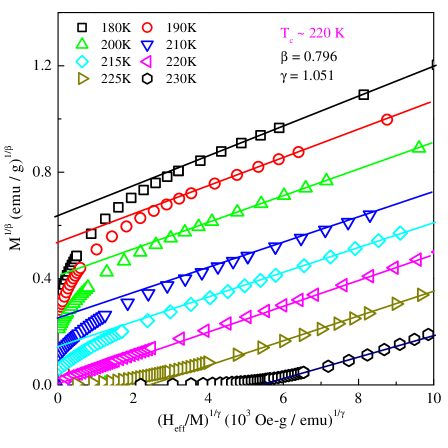
By varying the values of and in Eq. (6), we succeeded in making the AN plot isotherms nearly straight over the field range 1.5 kOe 10 kOe with the critical exponent values, = 0.796, = 1.051. Note that the field range for the linear AN isotherms is much wider in the immediate vicinity of Tc. From the modified Arrott plot (Fig. 6), it is evident that the extrapolation of the linear portions of the AN isotherms to H = 0 yields finite spontaneous magnetization, , (inverse susceptibility, ) below (above) Tc and both and are zero at the transition temperature Tc 220 K. This value of Tc is very close to that deduced from the ac susceptibility data. Using the critical exponent values, = 0.796 and = 1.051, in the Widom scaling relation [42] , we obtained the critical isotherm critical exponent as 2.32. To crosscheck this value, the relation (Eq. (5)) is used to fit the virgin M(H) isotherm at Tc 220 K. Fig. 7(c) shows the critical M(H) isotherm plotted as the ln M versus ln Heff plot. As expected from Eq. (5), this log-log plot is linear with inverse slope = 2.35(5). This value of is in excellent agreement with that obtained using the Widom scaling relation.
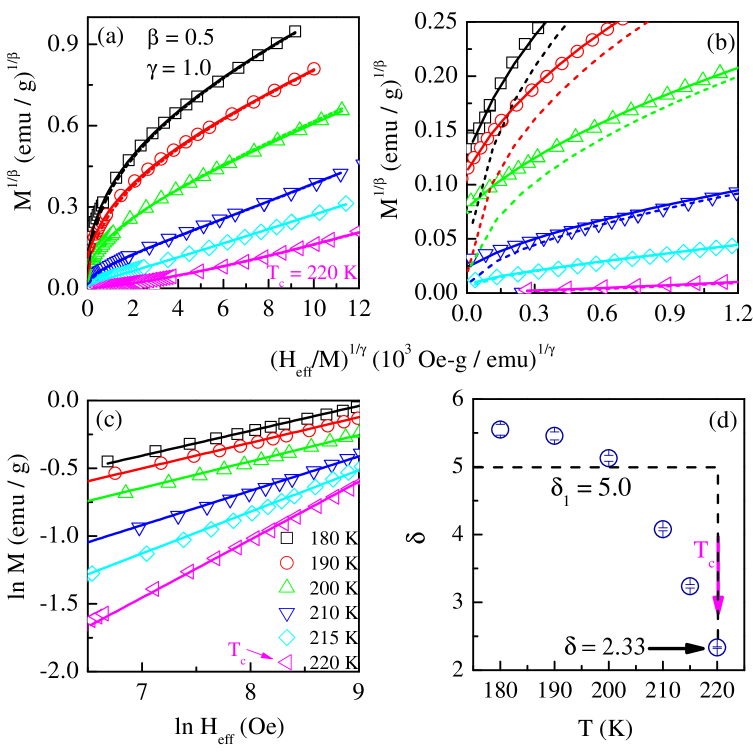
Despite a close agreement between the value of directly determined from the critical isotherm and that from the exponent values = 0.796 and = 1.051 via the Widom scaling relation, two basic questions arise: (i) how does one reconcile with the non-universal critical exponent values, and (ii) what causes the deviations from the linear AN isotherms at sufficiently low fields. Considering that the random magnetic anisotropy (RMA) model [43] yields nonlinear mean-field AN isotherms at low fields, it is worth investigating if the SES form given by Aharony and Pytte [43] helps resolve the above issues. Note that nonlinear mean-field isotherms have been observed in the past in a number of amorphous rare earth - transition metal systems and explained [44] in terms of the Aharony and Pytte model.
Neglecting the critical fluctuations, Aharony and Pytte (AP) make the following predictions for a (, ) spin system with RMA. (I) The M(H) isotherms follow the relation at and at all temperatures below , with the exponents and given by
| (7) |
For a three-dimensional ( = 3) system, Eq. (7) gives = 7/3 = 2.33 and = 5.0. While the theoretical estimate = 2.33 is in perfect agreement with the presently determined value = 2.35(5), the observed values do not reproduce the theoretically-predicted abrupt jump in at T to the value = 5.0, which remains constant for T (as evidenced in Fig. 7(d)). This discrepancy between theory and experiment can be traced back to a total neglect of critical fluctuations of the order parameter, leading to Eq. (7). (II) According to the AP model, the scaling equation of state has the following form [43] for a = 3, = 3 system with random uniaxial and cubic anisotropies
| (8) |
where = 0.5, = 1.0, , and are a measure of random uniaxial and cubic anisotropies, respectively, and signifies the exchange interaction. Eq. (8) permits a clear distinction between the cases: (i) = 0 when only the random uniaxial anisotropy exists, and (ii) 0 when, in addition to the random uniaxial anisotropy, cubic anisotropy is present. The low-field data, plotted in the form of the Arrott plot (i.e., plot with mean-field exponents and ) isotherms, and the theoretical fits based on the AP SES, Eq. (8), for the cases = 0 (dashed curves) and 0 (continuous curves), are displayed in Fig. 7 (a). Fig. 7 (b) provides an enlarged view of the data and fits at fields not very far from zero. Evidently, the AP SES correctly reproduces the observed change in the curvature of the Arrott plot isotherms from concave-downward to concave-upward at Tc. Furthermore, superiority of the 0 fits over those corresponding to = 0, particularly at fields close to zero, asserts that the inclusion of cubic anisotropy is necessary. Consequently, in conformity with the observed behavior, an extrapolation to = 0 gives finite intercepts on the ordinate (finite Ms) for T Tc and on the abscissa (finite ) for T Tc; both Ms and go to zero at T = Tc. However, due to sizable gradients of the AP isotherms at very low fields ( 0) for temperatures on either side of Tc, the intercepts on the ordinate and abscissa depend on the range of chosen for extrapolation. Thus, the Ms(T) and (T), so obtained, are not accurate enough for the determination of critical exponents and . In sharp contrast, the ‘zero-field’ ac susceptibility (ACS) does not suffer from such extrapolation errors. The value = 1.261(5) of the susceptibility critical exponent, determined from the ACS data, is thus reliable. The deviation of this value of from the mean-field value, = 1.0, underscores the importance of critical fluctuations (neglected in the AP RMA model). Thus, the RMA model, due to Aharony and Pytte [43], captures the main physical essence in that the curvature in the mean-field Arrott isotherms at low fields has its origin in the random uniaxial and cubic anisotropies, but fails to yield correct values for the critical exponents and .
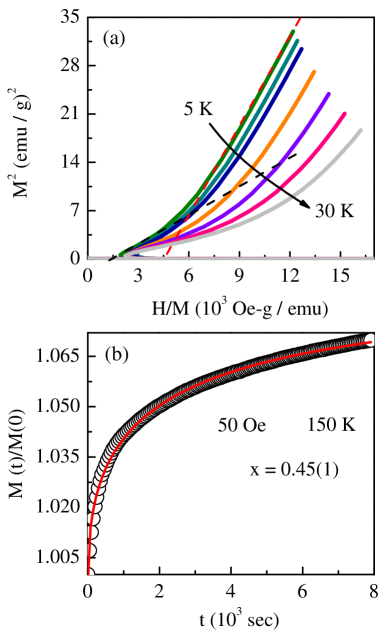
The evidence presented so far asserts that (i) at temperatures in range 180 K T Tc = 220.5 K, RMA is too weak to destroy long-range FM order, and (ii) the transition to a cluster spin glass (CSG) state occurs at Tg = 7.7 K. It remains to be verified if, in the intermediate temperature range, a mixed state is formed in which long-range FM order coexists with the CSG order. In this connection, Fig. 8(a) makes it obvious that, in the low temperature region (T 30 K), the Arrott (M2 versus H/M) plots, when extrapolated to H = 0, do not yield any intercept on the ordinate axis regardless of the field-range chosen for extrapolation. It immediately follows that no spontaneous magnetization, and hence no long-range FM order, exists at these temperatures. Concurrently, in the same temperature range T 30 K, a steep rise in RMA (reflected in a sharp increase in the coercive field, as noticed in the inset of Fig. 3) occurs. Within the framework of the RMA models [43, 45], sizable magnitude of RMA at T 30 K can account for both the breakdown of long-range FM order [43] and the freezing of spin clusters in random orientations at T = Tg, leading to the formation of cluster (correlated) spin glass state (with a finite FM correlation length [45]) at temperatures below Tg.
With a view to gain more insight into the nature of magnetism at temperatures intermediate between the spin glass transition temperature Tg 8 K and Tc 220.5 K, the time (t) evolution of the ZFC magnetization, (t), at 150 K was measured in a static magnetic field of 50 Oe switched on after a fixed waiting time, , ranging between and s. The (t) data, so obtained, were fitted to the stretched exponential function given by expression
| (9) |
where represents the FM component while and are the spin-glass magnetization component and the characteristic SG relaxation time, respectively [46]. The value of exponent reflects the type of energy barriers present. For instance, = 1 describes the relaxation behavior of a FM system with a single anisotropy energy barrier separating the ZFC and FC states [47]. 0.5, on the other hand, is associated with the stretched exponential relaxation, caused by hierarchical energy barriers in spin glasses [31]. From the fit (solid red curve through the data points), based on the above expression (Eq. (9)), to the data (Fig. 8(b)), we obtain , = 1.083(1), = 0.086(1) and = 2252 sec, where M(0) = 1.0348 is magnetization value, recorded at the time when the field was applied. The determined value of is in good agreement with those generally reported for spin glass systems [31]. This result provides an evidence for the coexistence of a glassy (a cluster spin glass-like) phase with ferromagnetic order at intermediate temperatures. Note that, within the uncertainty limits, the above-mentioned parameter values seem to be insensitive to the choice of presumably because constitutes a tiny fraction of the total magnetization at the measurement temperature of 150 K, which lies well above Tg 8 K.
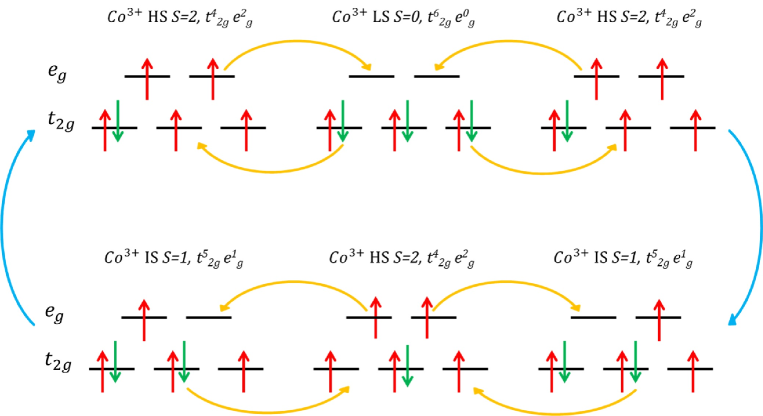
Finally, an attempt is made to ascertain how the present results can be understood in terms of the HS/IS/LS spin states of Co3+ ions in the LaSrCoO4 compound. At first, we recall that the single-ion magneto-crystalline anisotropy (MCA) has its origin in the combined action of the crystal-field interaction (CFI) and spin-orbit coupling (SOC). Since the LS state is associated with S = 0, the LS Co3+ ions, neither in isolation nor as neighbors, contribute to spin magnetic moment and MCA (due to the lack of SOC). However, in the case of LS Co3+ ions with HS neighbors, the spin-state configurations, fluctuating [12, 11] between the Co3+ HS - O2- - Co3+ LS - O2- - Co3+ HS and Co3+ IS - O2- - Co3+ HS - O2- - Co3+ IS configurations (refer to the schematic diagram shown in Fig. 9), can lead to FM superexchange interaction between the spins of Co3+ HS ions. This process involves correlated hopping [12, 11] of and electrons between Co3+ LS and its Co3+ HS neighbors without any charge transfer as shown in Fig. 9 and results in a finite effective S at the LS Co3+ ion site. Finite S, in turn, enables SOC and ensures a significant contribution to spin magnetic moment. In conformity with the observed steep rise in MCA as the temperature drops below 80 K, MCA increases with decreasing temperature because LS Co3+ ions with SOC and much stronger CFI (and hence MCA) increase [11, 12, 48] in number at the expense of HS Co3+ ions. In sharp contrast, arguments based on the mixed HS-IS or IS ground state (similar to those presented above), at best, lead to a much slower increase in MCA with lowering temperature because of their low CFI relative to LS. A competition between the above-mentioned FM interaction and the AFM interaction between the spins of neighboring Co3+ HS ions, caused by the Co3+ HS - O2- - Co3+ HS superexchange, give rise to a spin glass (SG) ground state.
IV Summary and Conclusion
In the LaSrCoO4 compound, as functions of temperature, ‘zero-field-cooled’ (ZFC) dc susceptibility, , at low fields (H 100 Oe), and ac susceptibility, , (ACS), at different frequencies of the driving ac field of rms amplitude = 3 Oe, exhibit peaks at around 200 K and 8 K. While the low-temperature peak in (T) shifts to higher temperatures with increasing frequency, the inflection-point in (T) (or equivalently, a dip in ) at 220.5 K is frequency-independent. Note that the dip in also occurs at exactly the same temperature. This observation provides strong experimental evidence for the existence of a thermodynamic PM - FM phase transition at Tc = 220.5 K. The frequency-induced shift in the low-temperature peak is described well by the critical slowing down model for a cluster spin glass (CSG). According to this model, the transition to the CSG state takes place at Tg = 7.7 K in the zero-frequency limit. The Aharony-Pytte (AP) model for a (d = 3, n = 3) Heisenberg spin system with random magnetic anisotropy (RMA) yields the value ( = 7/3) of the critical exponent for the critical isotherm at Tc = 220.5 K, which agrees closely with the observed value of = 2.35(5). Moreover, the AP scaling equation of state correctly describes the observed crossover from the concave-downward to concave-upwards curvature in the low-field Arrott plot isotherms, as the temperature is increased through Tc. These findings clearly establish that the PM-FM transition is basically driven by RMA.
For temperatures below 30 K, large enough RMA destroys long-range FM order by breaking up the infinite FM network into FM clusters of finite size and leads to the formation of a CSG state at temperatures T 8 K by promoting freezing of finite FM clusters in random orientations. Increasing strength of the single-ion magnetocrystalline anisotropy (and hence RMA) with decreasing temperature reflects an increase in the number of low-spin (LS) Co3+ ions at the expense of that of high-spin (HS) Co3+ ions. At intermediate temperatures (30 K 180 K), spin dynamics has contributions from the infinite FM network (fast relaxation governed by a single anisotropy energy barrier) and finite FM clusters (extremely slow stretched exponential relaxation due to hierarchical energy barriers).
Acknowledgements
The authors acknowledge Kranti Sharma for AC susceptibility measurements. S.S.M. acknowledges the financial support from SERB, India, in the form of the national post doctoral fellowship (NPDF) award (PDF/2021/002137). R.S. acknowledge the financial support provided by the Ministry of Science and Technology in Taiwan under project numbers MOST-111-2124-M-001-009 & MOST-110-2112-M-001-065-MY3 & AS- iMATE-111-12.
References
- Gong and Zhang [2019] C. Gong and X. Zhang, Two-dimensional magnetic crystals and emergent heterostructure devices, Science 363 (2019).
- Ahad et al. [2020] A. Ahad, K. Gautam, K. Dey, S. Majid, F. Rahman, S. Sharma, J. Coaquira, I. da Silva, E. Welter, and D. Shukla, Magnetic correlations in subsystems of the misfit [Ca2CoO3]0.62 [CoO2] cobaltate, Phys. Rev. B 102, 094428 (2020).
- Wu and Leighton [2003] J. Wu and C. Leighton, Glassy ferromagnetism and magnetic phase separation in La1-xSrxCoO3, Phys. Rev. B 67, 174408 (2003).
- Ram et al. [1988] R. A. M. Ram, P. Ganguly, and C. N. R. Rao, Preparation and characterization of La2CoO4, Mat. Res. Bull. 23, 501 (1988).
- Nemudry et al. [1998] A. Nemudry, P. Rudolf, and R. Schollhorn, Room temperature topotactic oxidation of lanthanum cobalt oxide La2CoO4, Solid State Ionics 109, 213 (1998).
- Pandey et al. [2013] P. K. Pandey, R. J. Choudhary, and D. M. Phase, Magnetic behavior of layered perovskite Sr2CoO4 thin film, Appl. Phys. Lett. 103, 132413 (2013).
- Ahad et al. [2017] A. Ahad, D. Shukla, F. Rahman, S. Majid, G. Okram, A. Sinha, and D. Phase, Colossal thermopower, spin states and delocalization effects in single layered La2-xSrxCoO4, Acta Mater. 135, 233 (2017).
- Wang et al. [2000] J. Wang, W. Zhang, and D. Y. Xing, Magnetic structure of the layered perovskite LaSrCoO4, Phys. Rev. B 62, 14140 (2000).
- Wu [2010] H. Wu, High-spin and low-spin mixed state in LaSrCoO4: An ab initio study, Phys. Rev. B 81, 115127 (2010).
- Hollmann et al. [2008] N. Hollmann, M. W. Haverkort, M. Cwik, M. Benomar, M. Reuther, A. Tanaka, and T. Lorenz, Anisotropic susceptibility of La2-xSrxCoO4 related to the spin states of cobalt, N. J. Phys. 10, 023018 (2008).
- Merz et al. [2010] M. Merz, P. Nagel, C. Pinta, A. Samartsev, H. v. Löhneysen, M. Wissinger, S. Uebe, A. Assmann, D. Fuchs, and S. Schuppler, X-ray absorption and magnetic circular dichroism of LaCoO3, La0.7Ce0.3CoO3, and La0.7Sr0.3CoO3 films: Evidence for cobalt-valence-dependent magnetism, Phys. Rev. B 82, 174416 (2010).
- Merz et al. [2011] M. Merz, D. Fuchs, A. Assmann, S. Uebe, H. V. Lohneysen, P. Nagel, and S. Schuppler, Spin and orbital states in single-layered La2-xSrxCoO4 studied by doping- and temperature-dependent near-edge x-ray absorption fine structure, Phys. Rev. B 84, 014436 (2011).
- Ang et al. [2008] R. Ang, Y. P. Sun, X. Luo, C. Y. Hao, and W. H. Song, Studies of structural, magnetic, electrical and thermal properties in layered perovskite cobaltite SrLnCoO4 (ln= la, ce, pr, nd, eu, gd and tb), J. Phys. D: Appl. Phys. 41, 045404 (2008).
- Subías et al. [2020] G. Subías, J. Blasco, S. Lafuerza, V. Cuartero, M. C. Sánchez, R. Boada, S. Díaz-Moreno, F. Fauth, and J. García, Relation among oxygen stoichiometry, structure, and Co valence and spin state in single-layer La2-xAxCoO4±δ (A= Ca, Sr) perovskites, Inorg. Chem. 59, 15757 (2020).
- Moritomo et al. [1997] Y. Moritomo, K. Higashi, K. Matsuda, and A. Nakamura, Spin-state transition in layered perovskite cobalt oxides: La2-xSrxCoO4 (0.4 x 1.0), Phys. Rev. B 55, R14725 (1997).
- Shimada et al. [2006] Y. Shimada, S. Miyasaka, R. Kumai, and Y. Tokura, Semiconducsemi ferromagnetic states in La1-xSr1+xCoO4, Phys. Rev. B 73, 134424 (2006).
- Guo et al. [2016] H. Guo, Z. Hu, T.-W. Pi, L. H. Tjeng, and A. C. Komarek, Single crystal growth of pure Co3+ oxidation state material LaSrCoO4, Crystals 6, 98 (2016).
- Chichev et al. [2006] A. V. Chichev, M. Dlouha, S. Vratislav, K. Knizek, J. Hejtmanek, M. Marysko, M. Veverka, Z. Jirak, N. O. Golosova, D. P. Kozlenko, and B. N. Savenko, Structural, magnetic, and transport properties of the single-layered perovskites La2-xSrxCoO4 (x=1.0-1.4), Phys. Rev. B, 74, 134414 (2006).
- Liu et al. [2005] Y. Y. Liu, X. M. Chen, and X. Q. Liu, Magnetic properties and magnetoresistance of polycrystalline SrLaCoO4, Solid State Commun. 136, 576 (2005).
- Andujar et al. [2006] M. S. Andujar, D. Rinaldi, R. Caciuffo, J. Mira, J. Rivas, and M. A. S. Rodriguez, Magnetotransport properties of spin-glass-like layered compounds La1-xSr1+xCoO4 (0 < x < 0.40), Solid State Sciences 8, 901 (2006).
- Srinath and Kaul [1999] S. Srinath and S. N. Kaul, Static universality class for gadolinium, Phys. Rev. B 60, 12166 (1999).
- Mott [1968] N. Mott, Conduction in glasses containing transition metal ions, J. Non-Cryst. Solids 1, 1 (1968).
- Mott [1993] N. Mott, Conduction in non-crystalline materials (1993).
- Bitla et al. [2020] Y. Bitla, P. Babu, and S. N. Kaul, Magnetotransport in under and optimally hole-doped bulk nanocrystalline La1-xCaxMnO3 manganites, J. Magn. Magn. Mater. 501, 166291 (2020).
- Kriener et al. [2004] M. Kriener, C. Zobel, A. Reichl, J. Baier, M. Cwik, K. Berggold, H. Kierspel, O. Zabara, A. Freimuth, and T. Lorenz, Structure, magnetization, and resistivity of La1-xMxCoO3 (M= Ca, Sr, and Ba), Phys. Rev. B 69, 094417 (2004).
- Joy et al. [1998] P. A. Joy, P. S. A. Kumar, and S. K. Date, The relationship between field-cooled and zero-field-cooled susceptibilities of some ordered magnetic systems, J. Phys.: Condens. Matter 10, 11049 (1998).
- Freitas et al. [2001] R. S. Freitas, L. Ghivelder, F. Damay, F. Dias, and L. F. Cohen, Magnetic relaxation phenomena and cluster glass properties of La0.7-xYxCa0.3MnO3 manganites, Phys. Rev. B 64, 144404 (2001).
- Kaul and Srinath [1998] S. N. Kaul and S. Srinath, Irreversibility lines in the H-T phase diagram of re-entrant amorphous ferromagnets, J. Phys.: Condens. Matter 10, 11067 (1998).
- Pejaković et al. [2000] D. A. Pejaković, J. L. Manson, J. S. Miller, and A. J. Epstein, Photoinduced magnetism, dynamics, and cluster glass behavior of a molecule-based magnet, Phys. Rev. Lett. 85, 1994 (2000).
- Mukherjee et al. [1996] S. Mukherjee, R. Ranganathan, P. S. Anilkumar, and P. A. Joy, Static and dynamic response of cluster glass in La0.5Sr0.5CoO3, Phys. Rev. B 54, 9267 (1996).
- Mydosh [2015] J. Mydosh, Spin glasses: redux: an updated experimental/materials survey, Rep. Prog. Phys. 78, 052501 (2015).
- Haverkort et al. [2006] M. W. Haverkort, Z. Hu, J. C. Cezar, T. Burnus, H. Hartmann, M. Reuther, C. Zobel, T. Lorenz, A. Tanaka, N. B. Brookes, et al., Spin state transition in LaCoO3 studied using soft X-ray absorption spectroscopy and magnetic circular dichroism, Phys. Rev. Lett. 97, 176405 (2006).
- Csiszar et al. [2005] S. Csiszar, M. Haverkort, Z. Hu, A. Tanaka, H. Hsieh, H.-J. Lin, C. Chen, T. Hibma, and L. Tjeng, Controlling orbital moment and spin orientation in CoO layers by strain, Phys. Rev. Lett. 95, 187205 (2005).
- Qureshi et al. [2013] N. Qureshi, H. Ulbrich, Y. Sidis, A. Cousson, and M. Braden, Magnetic structure and magnon dispersion in LaSrFeO4, Phys. Rev. B 87, 054433 (2013).
- Helme et al. [2009] L. M. Helme, A. T. Boothroyd, R. Coldea, D. Prabhakaran, C. D. Frost, D. A. Keen, L. P. Regnault, P. G. Freeman, M. Enderle, and J. Kulda, Magnetic order and dynamics of the charge-ordered antiferromagnet La1.5Sr0.5CoO4, Phys. Rev. B 80, 134414 (2009).
- Bitla et al. [2012] Y. Bitla, S. N. Kaul, and L. F. Barquín, Nonlinear susceptibilities as a probe to unambiguously distinguish between canonical and cluster spin glasses, Phys. Rev. B 86, 094405 (2012).
- Kaul [1985] S. N. Kaul, Static critical phenomena in ferromagnets with quenched disorder, J. Magn. Magn. Mater. 53, 5 (1985).
- Khan et al. [2010] N. Khan, A. Midya, K. Mydeen, P. Mandal, A. Loidl, and D. Prabhakaran, Critical behavior in single-crystalline La0.67Sr0.33CoO3, Phys. Rev. B 82, 064422 (2010).
- Reisser et al. [1995] R. Reisser, R. Kremer, and A. Simon, 3d-XY critical behavior of the layered metal-rich halides Gd2IFe2, Gd2ICo2 and Gd2BrFe2, Physica B 204, 265 (1995).
- Arrott [1957] A. Arrott, Criterion for ferromagnetism from observations of magnetic isotherms, Phys. Rev. 108, 1394 (1957).
- Arrott and Noakes [1967] A. Arrott and J. E. Noakes, Approximate equation of state for nickel near its critical temperature, Phys. Rev. Lett. 19, 786 (1967).
- Lago et al. [2012] J. Lago, S. J. Blundell, A. Eguia, M. Jansen, and T. Rojo, Three-dimensional heisenberg spin-glass behavior in SrFe0.90Co0.10O3.0, Phys. Rev. B 86, 064412 (2012).
- Aharony and Pytte [1980] A. Aharony and E. Pytte, Infinite susceptibility phase in random uniaxial anisotropy magnets, Phys. Rev. Lett. 45, 1583 (1980).
- Dieny and Barbara [1985] B. Dieny and B. Barbara, Random anisotropy effects on the phase transition of amorphous DyxGd1-xNi, J. Phys. 46, 293 (1985).
- Chudnovsky et al. [1986] E. M. Chudnovsky, W. M. Saslow, and R. A. Serota, Ordering in ferromagnets with random anisotropy, Phys. Rev. B 33, 251 (1986).
- Ahad et al. [2019] A. Ahad, K. Gautam, S. Majid, K. Dey, F. Rahman, R. Choudhary, and D. Shukla, Magnetic correlations in mixed valent layered La1.2Sr0.8CoO4, Physica B 570, 308 (2019).
- Mathew and Kaul [2012] S. P. Mathew and S. N. Kaul, Magnetization processes in nanocrystalline gadolinium, J. Phys.: Condens. Matter 24, 256008 (2012).
- Sehlin et al. [1995] S. R. Sehlin, H. U. Anderson, and D. M. Sparlin, Semiempirical model for the electrical properties of La1-xCaxCoO3, Phys. Rev. B 40, 11681 (1995).