Radiative decays of the spin- partner of
Abstract
It has been generally expected that the has a spin-2 partner, , with quantum numbers . In the hadronic molecular model, its mass was predicted to be below the threshold, and the new structure reported in the invariant mass distribution by the Belle Collaboration with mass MeV and decay width MeV, with a global significance of 2.8 , is a nice candidate for it. We consider the radiative decay widths for the with treating the as a shallow bound state, and estimate the events of in two-photon collisions that can be collected in the () final states at Belle. Based on the upper limit for the ratio of decay widths of and measured by BESIII, we predict the similar ratio to be smaller than . We suggest searching for the signal in the invariant mass distribution via two-photon fusions. The results will lead to insights into both the and the new structure observed by Belle.
I Introduction
The hadron spectroscopy of mesons and baryons with heavy quarks (charm and bottom) has been an important laboratory in the quest for understanding quantum chromodynamics (QCD) at the confinement scale due to the large bulk of experimental information accumulated over the last two decades. Many new hadronic states observed in the heavy sector seem to not fit into the predictions from the potential quark models such as the well-known Godfrey-Isgur quark model [1]. This fact has triggered a debate about the nature of those hadrons, and assumptions of different multiquark configurations beyond the conventional quark-antiquark/three quarks were put forward in order to explain their properties, such as mass, decay width, and the quantum numbers, i.e., the total angular momentum , parity , and charge conjugation (see the reviews [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]).
Among these models, the molecular picture seems to be a natural one since the majority of the new hadrons are near some hadron-hadron threshold. In the charm sector, for instance, the state is just at the threshold, and its properties are suitably described considering the as a molecular state (for a review focusing on the hadonic molecular model of the , see Ref. [14]). In fact, the was the first among those new hadrons observed experimentally by the Belle Collaboration in 2003 [15], with quantum numbers determined by the LHCb Collaboration a decade later [16]. It is, to date, the most well-studied state, and it is not a surprise that its experimental and theoretical information is used as inputs for predictions of new hadronic states in the heavy quark sector. In Ref. [17], the authors assumed the as a molecule and concluded that a state should exist as a consequence of the heavy-quark spin symmetry for the system under consideration. Specifically, using a contact-range (pionless) effective field theory, they claimed that the new state, from now on called , is the spin- partner of the , with a similar value for the binding energy and mass of about MeV. Such a state was first predicted in Ref. [18] long ago with a mass MeV and later in Refs. [19, 17, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34] using various phenomenological models.
Recently, the Belle collaboration reported a hint of an isoscalar structure with mass MeV and width MeV, seen in the invariant mass distribution via a two-photon process [35]. The global significance is . This new structure is located near the threshold which leads us to conclude that it is a promising candidate for the shallow bound state.111In Refs. [36, 37], this structure was assumed to be a molecule with . In addition, the mass value predicted in Refs. [17, 23] is in good agreement with the experimental one reported by Belle [35], and the measured width well matches the predicted one, of the order of a few MeV, in Ref. [27] despite that there is a sizeable uncertainty in the theoretical predictions [27, 28]. Thus, this narrow structure could be a hint for the state, supporting the theoretical predictions in Refs. [17, 18, 23].
Alternatively, by looking at the spectra of tetraquarks, there also exists spin partners of states that reproduce the quantum numbers of as well as its mass [38, 39, 40, 41]. Although the authors of these works were not particularly aiming at the state, it is still possible to assign the results to such a structure. On the other hand, a tensor state with a similar mass could also be described as a conventional charmonium state [1, 42]; in this case, the [43] would be an exotic meson.
One way to disentangle those different multiquark configurations from the molecular point of view is to check the mass splitting between the and states. In Refs. [17, 23], the corresponding mass splitting is approximately equal to that between the vector and pseudoscalar charmed mesons, that is
| (1) |
with the pseudoscalar (vector) charmed meson mass. On the other hand, within the tetraquark approach, for instance, in Ref. [38] the is about MeV, which is smaller than the difference given in Eq. (1). A similar conclusion is found for the difference between the first radially excited charmonia and by looking at the results for both the Godfrey-Isgur quark model [1] and the one using a screened potential [42], which are about MeV and MeV, respectively.
Even though only the Belle experiment has reported a signal relevant to the spin- partner of the , such a structure can also be searched for in other ongoing and future experiments, e.g., BESIII and its upgrade, LHCb, and PANDA. Belle II also has plans to search for the state soon. In line with the current and upcoming experiments that will provide more information about such a structure, it is crucial to extend the theoretical studies surveying the system. In other words, we should further explore the tensor state to help discriminate the various multiquark models used to describe the structure.
The decays of a tensor structure have been studied in Refs. [44, 45]. In particular, considering that state as the first radial excitation of the -wave () charmonium, the quark model adopted in Ref. [44, 45] provides width estimates for the decay to charmed mesons around tens of MeV. Moreover, the hadronic decays of the -wave hadronic molecule, into and meson pairs were estimated to be of the order of a few MeV in Ref. [27] and can be as large as 50 MeV in Ref. [28].
Furthermore, the decay width was also calculated in Ref. [27] to be of the keV order. In contrast to the hadronic decays that, according to Ref. [27], has a strong dependence on the ultraviolet (UV) form factors and therefore are sensitive to the short-distance details, radiative decays into are more sensitive to the long-distance structure of the resonance. Thus, as argued in Ref. [27], one can extract valuable information about the wave function, as well as about interactions, by surveying such decays. It is not difficult to understand this feature. In the process, the final state receives leading contribution from the one-body transition , which has no direct relation to the two-body interaction accounting for the short-distance part of the state. Therefore, the long-range structure of that determines its coupling to has an essential role in its radiative decay into .
Additional interesting decay modes of the which have not been explored before include the radiative decays into and channels. Such a study may help to discriminate the nature from the meson possibility. As discussed in, e.g., Ref. [46], the radiative decay matrix element is proportional to the overlap between the wave functions corresponding to the initial and final states. Specifically, for transitions between two charmonia, that overlap is influenced by the position of the nodes of the wave function. Hence, the one-node wave function for the state has an overlap with the larger than that for the one, which is nodeless, such that the following ratio
| (2) |
should be much larger than the one if the initial particle is the charmonium. Table 1 shows some results for obtained in different quark models [44, 45]. Therefore, to confront these results, we evaluate the radiative decays into and , assuming that the resonance is a molecular partner of the state, predicted in Refs. [17, 23] according to heavy quark spin symmetry (HQSS).
| [keV] | [keV] | ||
| Ref. [44] | 53 | 207 | 3.9 |
| Ref. [45] | 81 | 304 | 3.8 |
In order to calculate those radiative decay widths, we employ the couplings of the mesons to charmed mesons respecting HQSS and the magnetic and electric couplings of charmed mesons and a photon. The nonrelativistic effective field theory is applied to depict the coupling of the to , which is related to the binding energy of . After calculating the radiative decay widths for with , the upper limit of the ratio is predicted with the use of the experimental result reported by the BESIII collaboration at confidence level [47], and the results for the radiative decays of in the hadronic molecular picture [46]. Taking into account the signal yield of in the invariant mass distribution measured by Belle [35], and the predicted upper bound of , we also estimate the lower limit of the signal yield of in the mode via the two-photon process at Belle, with reconstructed in lepton-antilepton pairs.
The structure of the paper is as follows. In Section II, we discuss the interaction Lagrangians and the main parameters used as well as the relevant Feynman diagrams contributing to the decay process . The radiative decay ratio and the signal yield of in the mode are predicted in Section III. A summary is given in Section IV. Finally, in Appendix A, we provide an update for the results corresponding to the radiative decay widths for discussed in Ref. [46].
II Formalism
II.1 The Lagrangian and vertices
As discussed in Refs. [48, 49, 50] hadron loops play an important role in certain hadron transitions. For pure hadronic molecules, those loops are the leading order contribution to the corresponding transition amplitudes due to the large coupling of the molecule to its constituents. In our case, the radiative decays under consideration proceeds through the loops depicted in Fig. 1.





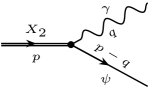
In order to evaluate each diagram displayed in Fig. 1, we need first to define the interaction Lagrangian that describes all the vertices involved in such loops. We start by the interaction vertex that is described by the following Lagrangian
| (3) |
where and are the couplings to the neutral (0) and charged charmed mesons, while the subscript “nr” stands for “nonrelativistic”. As we know, there is a slight difference between the neutral and charged meson masses that leads to an isospin-breaking effect. However, according to Refs. [17, 27], this effect is small so that the couplings and are approximately the same. In addition, the relative size of is much smaller compared to the Bohr radius of a ground-state hadronic atom, made out of the charged and mesons, so that the electromagnetic effects can be ignored in such a scenario. Therefore, we follow Ref. [46] and set . The vertex is then
| (4) |
Next, the interaction vertex between the and charmed and mesons can be extracted from
| (5) |
encoding HQSS [51, 52]. In Eq. (5), is the four-velocity of the charmed meson. By defining the four-momentum as , with a residual momentum of , and recalling that , we can write as
| (6) |
where is the charmed meson mass. Furthermore, we can write the coupling constant in terms of the relativistic couplings , and as given in Refs. [52, 49, 46], that is
| (7) |
where is the mass of the meson. From Eq. (5) we extract the interaction vertices and , which are
| (8) | ||||
| (9) |
Now, we move on to the interaction between the charmed mesons and the photon. In this case, we have two couplings corresponding to the electric and magnetic interactions. The former is obtained by gauging the kinetic term associated with the charged mesons, which is
| (10) |
with standing for the electric charge of the heavy meson, and . The vertex reads
| (11) |
Note that this vertex satisfies the Ward-Takahashi identity, as discussed in Ref. [46]. Besides, after gauging the vertex of Eq. (9), a four-point vertex for , see the diagram in Fig. 1 (e), reads
| (12) |
On the other hand, the magnetic vertices are extracted from the Lagrangian [53]
| (13) |
where is the light quark charge matrix, and corresponds to the charge of the charm quark, while the stands for the electromagnetic field tensor. In addition, is the charm quark mass, and the parameter is discussed in Ref. [54]. From Eq. (13) the vertices , , and are
| (14) | ||||
| (15) | ||||
| (16) | ||||
| (17) |
As in Eq. (11), these vertices also satisfy the appropriate Ward identity.
II.2 The amplitude
Once we have all the vertices in the loop diagrams in Fig. 1, we are able to write the amplitude for the decay. Namely,
| (18) |
with , and the polarization vectors for the state, the photon, and mesons (, and ), respectively. The tensor structure in Eq. (18) encodes the contributions of all the diagrams in Fig. 1, and it is written as
| (19) |
where the superscripts (a)-(e) match the labels of each individual diagram in Fig. 1. Yet, the contributions in Eq. (19) with the labels and corresponds to the magnetic and electric couplings, respectively. Explicitly, each contribution in Eq. (19) reads
| (20) | ||||
| (21) | ||||
| (22) | ||||
| (23) | ||||
| (24) | ||||
| (25) | ||||
| (26) |
with and the propagator for the heavy fields and , respectively, given by
| (27) |
The factor in Eq. (19) accounts for the normalization of the heavy meson fields.222Except for the electric coupling in Eq. (11), we use the nonrelativistic normalization for the heavy mesons (including the charmonium, charmed mesons, and ), which differs from the traditional relativistic normalization by a factor . It is worth noticing that, as a consistency check, the loop amplitude in Eq. (19) is gauge invariant, as we must expect.
The loop amplitude defined in Eq. (19) is a UV divergent integral. In order to have a well-defined amplitude from which we can get consistent results, we add a counterterm amplitude like the case for the [46], depicted in Fig. 1(f), to the one given in Eq. (19). Specifically, it is
| (28) |
which is straightforward to see its manifest gauge invariance. These terms are defined such that (), which is subject to renormalization, absorbs the UV divergence from the loops in Eq. (19), as done in Ref. [46]. On the one hand, the counterterm defined in Ref. [46] has only one parameter ; on the other hand, in our case, Eq. (28) has five terms with each one having its strength . However, for our purposes, we do not consider relations among them.
The two-body decay width is given by the following formula
| (29) |
where stands for the momentum of the final states ( or ) in the center-of-mass frame,
| (30) |
Furthermore, in Eq. (29) is the projection operator corresponding to the summation over the polarizations of , which is given by [55]
| (31) |
where denotes the summation over the polarization vectors
| (32) |
with four-momentum and mass .
In the next subsection, we shall discuss the parameters used in our numerical analysis, which will be presented later in Section III.
II.3 The parameters
In order to numerically calculate the radiative decay widths of , we should fix the values for the parameters used. The values for the meson masses are [43]
where () is the average mass between the neutral and charged () mesons, and the mass is taken from Ref. [35]. The charm quark mass and the parameter related to the magnetic coupling are fixed by the partial electromagnetic widths for and [54],
| (33) |
The coupling constant for to the charged and neutral charmed mesons is extracted from the binding energy of [56, 57],
| (34) |
where and are the binding energy of relative to the threshold and the reduced mass, respectively. is identified with the range of forces, where in the weak binding limit [58]. We assume that the is a pure bound state, , and then we obtain the coupling constant , where the uncertainty is derived from the uncertainties of () and masses. Besides, and denote the and couplings to the charmed mesons, respectively.
We evaluate the loop integrals in Fig. 1 by using the dimensional regularization method. In particular, we adopt the subtraction scheme. As for the strength of the interaction corresponding to the counterterms, denoted by the parameters, following the idea in Ref. [46], we set to zero the contribution of the finite part of the counterterms in Eq. (28) and vary the energy scale in a large range, 1.5–7.0 GeV, in the UV divergent loop integrals. We define the ratios
| (35) |
where () is the coupling constant between () and charmed mesons in Eq. (7). We take and with the latter from the model-dependent estimates discussed in Refs. [52, 49]. The coupling to is denoted as , and its benchmark value is set to [59].
III Numerical results
In Table 2, we show our numerical results for the partial decays with and as given in Eq. (29), along with the corresponding ratio . These observables depend on the products among the quantities defined in Eq. (35). In order to fix those quantities, we have to make assumptions on the coupling constants and since their values are not well established in the literature. Besides, we have also to fix the contribution from the contact terms, that is, to fix the size of ’s in Eq. (28), which is unknown; however, as discussed Ref. [46], we may estimate their size by noticing that any change in must also change the counterterms accordingly so that the overall result does not depend on the renormalization scale . Thus, we set and vary the scale within a large range from GeV up to , with the mass, as mentioned above. In Table 2, we can see such behavior in the partial decays under consideration by noticing their corresponding changes as varies. In other words, such variation in each partial decay width we are concerned with may be considered a measure of the size of ’s.
| (GeV) | 1.5 | 2.0 | 4.0 | 7.0 |
| (keV) | 162 | 176 | 212 | 244 |
| (keV) | 17.5 | 18.4 | 20.8 | 22.7 |
| (keV) | 139 | 161 | 224 | 284 |
| (keV) | 25.0 | 27.1 | 32.7 | 37.6 |
| 0.11 | 0.10 | 0.10 | 0.09 | |
| 0.18 | 0.17 | 0.15 | 0.13 | |
| 1.67 | 1.61 | 1.49 | 1.43 | |
| 35 | 36 | 39 | 41 |
As for the ratio , we set the finite part of the counterterm to zero and will depend only on the ratio at a given scale. In order to fix this latter ratio, we consider some model-dependent estimates. If is assumed to equal to unity, for the case the channel is relatively suppressed [46]. Similarly, in our case, by considering , we find that the channel is also suppressed. In Ref. [63], the ratio was fixed to by modeling the couplings in a vector-meson dominance picture [52]; in this case, the channel is still suppressed relatively to the channel. Alternatively, we can fix by using the upper limit for the ratio corresponding to the and , reported by BESIII in Ref. [47]. The radiative decays are discussed in Ref. [46] (see Appendix A which updates a couple of expressions in Ref. [46]). The results for the state are also shown in Table 2. Note that, in this case, the barely changes as we vary the scale . Thus, we can choose one specific value for , for instance, GeV, and then, by using the BESIII measurement for , we obtain from Table 2
| (36) |


As a matter of checking, in Fig. 2, we show the plots for both ratios and as a function of the scale . As we can see, within the range , those ratios are, to a good approximation, independent of , as we expect.
As discussed above, both ratios and depend on value, whose value is not fixed and model dependent. However, we can determine independently of the couplings and , using the experimental information for , measured by BESIII in Ref. [47], as an input. Specifically, in Fig. 3 we show the double ratio as a function of . Note that this observable only slightly decreases from to as the renormalization scale varies within the large range . This flat variation indicates that we can set any value within that range for , and then use the upper boundary provided by BESIII such that we obtain an upper limit for :
| (37) |

Next, we shall estimate the number of events of that can be collected in the final state of the two-photon process at the Belle experiment. The signal yield of in such a process is given by
| (38) |
where is the two-photon decay width of , is the branching fraction for , is the efficiency, and is the total integrated luminosity of the Belle data sample. In addition, for the reconstructed from as done in Ref. [35] and from the lepton pairs (), one has and . The factor is related to the two-photon luminosity function [64, 35]
| (39) |
with the effective energy of the two-photon collision and the spin for . Since the two-photon decay width , the efficiency , the total integrated luminosity and the factor are the same for and , the signal yield of in the with is given by
| (40) |
The signal yield of is in Ref. [35], and the branching fraction for is [43]. As discussed above, for GeV we have , the yield of is
| (41) |
Therefore, we estimate that the signal yield of observed in the invariant mass distribution is at least about 35 for the two-photon collision at Belle. Besides, the minimal yields of estimated with other energy scales are listed in Table 2. The prediction can be checked with the Belle data.
IV Summary
By assuming the existence of a tensor state , that, according to HQSS, is a spin partner of the state in the hadronic molecular model, as predicted in Refs. [17, 18, 23], we have evaluated its radiative decays into and channels. Although with low statistics, a candidate of such a state was recently observed by the Belle Collaboration in Ref. [35], with mass and width in accordance with the corresponding values predicted in Refs. [17, 18, 23].
In particular, in our case, the decays we are concerned with proceed through hadronic loops with charmed mesons as intermediate particles. These loops are UV divergent, requesting an introduction of additional counterterm amplitude, in which the strength of that contact interaction absorbs the infinities after renormalization. However, with the available theoretical information, it is impossible to determine the contribution from the counterterms precisely. Notwithstanding, we estimated their contributions by varying the renormalization scale, as done in Ref. [46] for the case, such that the changes in the partial decay widths encode the size of the counterterm.
Moreover, we have used effective Lagrangians to describe the couplings to the charmed and mesons, and the couplings of those mesons with the charmonia and . Since these latter set of couplings are not well-determined in literature, we have written the partial decays and in terms of ratios involving those couplings, that allows us to draw conclusions based on the relations among them.
According to our findings, for values of close to one, we always find suppression of the channel against the one. On the other hand, as increases the ratios and increase accordingly. We have fixed the range of to be using input from the BESIII measurement of . Consequently, we found . As a matter of comparison, estimated using the quark model assuming the to be the meson leads to a value about 4, as displayed in Table 1, significantly larger than the one we obtained in the hadronic molecular picture. In principle, future experimental measurements of the observable may shed light on the internal structure of .
Finally, we predict the signal yield of in the spectrum from the two-photon process based on our findings for , and also the yields of in the reaction reported by the Belle Collaboration [35]. As a result, we expect that the yield of in the final states should be at least about , that is larger than the number of events observed by the Belle collaboration in Ref. [35].
Acknowledgements.
We would like to thank Alexey Nefediev for valuable discussions. This work is partly supported by the Chinese Academy of Sciences under Grant No. XDB34030000; by the National Natural Science Foundation of China (NSFC) under Grants No. 12125507, No. 11835015, and No. 12047503; and by the NSFC and the Deutsche Forschungsgemeinschaft (DFG) through the funds provided to the Sino-German Collaborative Research Center “Symmetries and the Emergence of Structure in QCD” (NSFC Grant No. 12070131001, DFG Project-ID 196253076 - TRR110).Appendix A radiative decays into and channels
The radiative decays into the and channels have been evaluated in Ref. [46], adopting a molecular picture as the quark configuration for the state. The findings reported in Ref. [46] are in line with the experimental ratio measured by the BESIII Collaboration [47]. In particular, it is stressed in Ref. [46] that those specific decays take place through hadron loops involving charmed mesons plus short-distance contributions in the form of a counterterm. For pure hadronic molecular states the hadron loops are the leading order contribution and play an important role in such processes. However, the charged conjugated diagrams in the loops are not considered in Ref. [46]; these contributions will lead to a factor of 2 for all the loop contributions but does not affect the ratio which was the main concern in Ref. [46]. In addition, in Eq. (24) and in Eq. (28) in Ref. [46] should be changed to and , respectively, which has also been noticed in Ref. [30]. That is because the four-velocity of heavy mesons with respect to the magnetic vertices in Eqs. (14) and (16) are related to the charmed-meson momentum inside the loop, instead of the four-velocity. The updated expressions of Eqs.(24)-(29) in Ref. [46] for the individual contributions to the process are (we use the same notation as in Ref. [46])
| (42) |
where and are the masses of and mesons, respectively, and the magnetic coupling parameter is the in Eq. (33).
| [keV] | [keV] | |||
| Ref. [46] | 23.5 | 4.9 | 0.21 | |
| Updated | 211 | 20.6 | 0.10 |
The updated numerical results for the partial decay widths of and are shown in Table 3, where we have kept the results from Ref. [46] for a comparison. As can be seen, they are much larger than the ones in Ref. [46]. As for the ratio , the new result is about half of the previous one. Nevertheless, the conclusion in Ref. [46], that is the hadronic molecular picture of the is compatible with the measured ratio , is not altered.
References
- Godfrey and Isgur [1985] S. Godfrey and N. Isgur, Mesons in a Relativized Quark Model with Chromodynamics, Phys. Rev. D 32, 189 (1985).
- Chen et al. [2016] H.-X. Chen, W. Chen, X. Liu, and S.-L. Zhu, The hidden-charm pentaquark and tetraquark states, Phys. Rep. 639, 1 (2016), arXiv:1601.02092 [hep-ph] .
- Hosaka et al. [2016] A. Hosaka, T. Iijima, K. Miyabayashi, Y. Sakai, and S. Yasui, Exotic hadrons with heavy flavors: , and related states, Prog. Theor. Exp. Phys. 2016, 062C01 (2016), arXiv:1603.09229 [hep-ph] .
- Esposito et al. [2017] A. Esposito, A. Pilloni, and A. D. Polosa, Multiquark Resonances, Phys. Rept. 668, 1 (2017), arXiv:1611.07920 [hep-ph] .
- Lebed et al. [2017] R. F. Lebed, R. E. Mitchell, and E. S. Swanson, Heavy-quark QCD exotica, Prog. Part. Nucl. Phys. 93, 143 (2017), arXiv:1610.04528 [hep-ph] .
- Ali et al. [2017] A. Ali, J. S. Lange, and S. Stone, Exotics: Heavy pentaquarks and tetraquarks, Prog. Part. Nucl. Phys. 97, 123 (2017), arXiv:1706.00610 [hep-ph] .
- Olsen et al. [2018] S. L. Olsen, T. Skwarnicki, and D. Zieminska, Nonstandard heavy mesons and baryons: Experimental evidence, Rev. Mod. Phys. 90, 015003 (2018), arXiv:1708.04012 [hep-ph] .
- Guo et al. [2018] F.-K. Guo, C. Hanhart, U.-G. Meißner, Q. Wang, Q. Zhao, and B.-S. Zou, Hadronic molecules, Rev. Mod. Phys. 90, 015004 (2018), [Erratum: Rev.Mod.Phys. 94, 029901 (2022)], arXiv:1705.00141 [hep-ph] .
- Albuquerque et al. [2019] R. M. Albuquerque, J. M. Dias, K. P. Khemchandani, A. Martínez Torres, F. S. Navarra, M. Nielsen, and C. M. Zanetti, QCD sum rules approach to the and states, J. Phys. G 46, 093002 (2019), arXiv:1812.08207 [hep-ph] .
- Liu et al. [2019] Y.-R. Liu, H.-X. Chen, W. Chen, X. Liu, and S.-L. Zhu, Pentaquark and tetraquark states, Prog. Part. Nucl. Phys. 107, 237 (2019), arXiv:1903.11976 [hep-ph] .
- Guo et al. [2020] F.-K. Guo, X.-H. Liu, and S. Sakai, Threshold cusps and triangle singularities in hadronic reactions, Prog. Part. Nucl. Phys. 112, 103757 (2020), arXiv:1912.07030 [hep-ph] .
- Brambilla et al. [2020] N. Brambilla, S. Eidelman, C. Hanhart, A. Nefediev, C.-P. Shen, C. E. Thomas, A. Vairo, and C.-Z. Yuan, The states: Experimental and theoretical status and perspectives, Phys. Rep. 873, 1 (2020), arXiv:1907.07583 [hep-ex] .
- Chen et al. [2023] H.-X. Chen, W. Chen, X. Liu, Y.-R. Liu, and S.-L. Zhu, An updated review of the new hadron states, Rept. Prog. Phys. 86, 026201 (2023), arXiv:2204.02649 [hep-ph] .
- Kalashnikova and Nefediev [2019] Y. S. Kalashnikova and A. V. Nefediev, in the molecular model, Phys. Usp. 62, 568 (2019), arXiv:1811.01324 [hep-ph] .
- Choi et al. [2003] S. K. Choi et al. (Belle), Observation of a narrow charmonium-like state in exclusive decays, Phys. Rev. Lett. 91, 262001 (2003), arXiv:hep-ex/0309032 .
- Aaij et al. [2013] R. Aaij et al. (LHCb), Determination of the Meson Quantum Numbers, Phys. Rev. Lett. 110, 222001 (2013), arXiv:1302.6269 [hep-ex] .
- Nieves and Valderrama [2012] J. Nieves and M. P. Valderrama, The Heavy Quark Spin Symmetry Partners of the , Phys. Rev. D 86, 056004 (2012), arXiv:1204.2790 [hep-ph] .
- Törnqvist [1994] N. A. Törnqvist, From the deuteron to deusons, an analysis of deuteron-like meson meson bound states, Z. Phys. C 61, 525 (1994), arXiv:hep-ph/9310247 .
- Molina and Oset [2009] R. Molina and E. Oset, The , and the as dynamically generated resonances from the vector-vector interaction, Phys. Rev. D 80, 114013 (2009), arXiv:0907.3043 [hep-ph] .
- Hidalgo-Duque et al. [2013a] C. Hidalgo-Duque, J. Nieves, and M. P. Valderrama, Light flavor and heavy quark spin symmetry in heavy meson molecules, Phys. Rev. D 87, 076006 (2013a), arXiv:1210.5431 [hep-ph] .
- Sun et al. [2012] Z.-F. Sun, Z.-G. Luo, J. He, X. Liu, and S.-L. Zhu, A note on the , , , molecular states, Chin. Phys. C 36, 194 (2012).
- Hidalgo-Duque et al. [2013b] C. Hidalgo-Duque, J. Nieves, A. Ozpineci, and V. Zamiralov, and its Partners in the Heavy Quark Limit of QCD, Phys. Lett. B 727, 432 (2013b), arXiv:1305.4487 [hep-ph] .
- Guo et al. [2013a] F.-K. Guo, C. Hidalgo-Duque, J. Nieves, and M. P. Valderrama, Consequences of Heavy Quark Symmetries for Hadronic Molecules, Phys. Rev. D 88, 054007 (2013a), arXiv:1303.6608 [hep-ph] .
- Albaladejo et al. [2013] M. Albaladejo, C. Hidalgo-Duque, J. Nieves, and E. Oset, Hidden charm molecules in finite volume, Phys. Rev. D 88, 014510 (2013), arXiv:1304.1439 [hep-lat] .
- Liang et al. [2010] W. H. Liang, R. Molina, and E. Oset, Radiative open charm decay of the , , resonances, Eur. Phys. J. A 44, 479 (2010), arXiv:0912.4359 [hep-ph] .
- Swanson [2005] E. S. Swanson, and molecules, J. Phys. Conf. Ser. 9, 79 (2005).
- Albaladejo et al. [2015] M. Albaladejo, F. K. Guo, C. Hidalgo-Duque, J. Nieves, and M. P. Valderrama, Decay widths of the spin-2 partners of the , Eur. Phys. J. C 75, 547 (2015), arXiv:1504.00861 [hep-ph] .
- Baru et al. [2016] V. Baru, E. Epelbaum, A. A. Filin, C. Hanhart, U.-G. Meißner, and A. V. Nefediev, Heavy-quark spin symmetry partners of the revisited, Phys. Lett. B 763, 20 (2016), arXiv:1605.09649 [hep-ph] .
- Cincioglu et al. [2016] E. Cincioglu, J. Nieves, A. Ozpineci, and A. U. Yilmazer, Quarkonium Contribution to Meson Molecules, Eur. Phys. J. C 76, 576 (2016), arXiv:1606.03239 [hep-ph] .
- Baru et al. [2017] V. Baru, C. Hanhart, and A. V. Nefediev, Can be the tensor partner of the ?, JHEP 06, 010, arXiv:1703.01230 [hep-ph] .
- Ortega et al. [2018] P. G. Ortega, J. Segovia, D. R. Entem, and F. Fernández, Charmonium resonances in the 3.9 GeV/ energy region and the puzzle, Phys. Lett. B 778, 1 (2018), arXiv:1706.02639 [hep-ph] .
- Wang [2021] Z.-G. Wang, Analysis of the Hidden-charm Tetraquark molecule mass spectrum with the QCD sum rules, Int. J. Mod. Phys. A 36, 2150107 (2021), arXiv:2012.11869 [hep-ph] .
- Dong et al. [2021] X.-K. Dong, F.-K. Guo, and B.-S. Zou, A survey of heavy-antiheavy hadronic molecules, Progr. Phys. 41, 65 (2021), arXiv:2101.01021 [hep-ph] .
- Montaña et al. [2022] G. Montaña, A. Ramos, L. Tolos, and J. M. Torres-Rincon, The , the , and their bottom partners at finite temperature, (2022), arXiv:2211.01896 [hep-ph] .
- Wang et al. [2022] X. L. Wang et al. (Belle), Study of →(2S) at Belle, Phys. Rev. D 105, 112011 (2022), arXiv:2105.06605 [hep-ex] .
- Duan et al. [2022] M.-Y. Duan, D.-Y. Chen, and E. Wang, The possibility of as a molecular state, Eur. Phys. J. C 82, 968 (2022), arXiv:2207.03930 [hep-ph] .
- Yue et al. [2022] Z.-L. Yue, M.-Y. Duan, C.-H. Liu, D.-Y. Chen, and Y.-B. Dong, Hidden charm decays of in a molecule scenario, Phys. Rev. D 106, 054008 (2022), arXiv:2208.12796 [hep-ph] .
- Maiani et al. [2014] L. Maiani, F. Piccinini, A. D. Polosa, and V. Riquer, The and a New Paradigm for Spin Interactions in Tetraquarks, Phys. Rev. D 89, 114010 (2014), arXiv:1405.1551 [hep-ph] .
- Wu et al. [2019] J. Wu, X. Liu, Y.-R. Liu, and S.-L. Zhu, Systematic studies of charmonium-, bottomonium-, and -like tetraquark states, Phys. Rev. D 99, 014037 (2019), arXiv:1810.06886 [hep-ph] .
- Shi et al. [2021] P.-P. Shi, F. Huang, and W.-L. Wang, Hidden charm tetraquark states in a diquark model, Phys. Rev. D 103, 094038 (2021), arXiv:2105.02397 [hep-ph] .
- Giron et al. [2021] J. F. Giron, R. F. Lebed, and S. R. Martinez, Spectrum of hidden-charm, open-strange exotics in the dynamical diquark model, Phys. Rev. D 104, 054001 (2021), arXiv:2106.05883 [hep-ph] .
- Li et al. [2009] B.-Q. Li, C. Meng, and K.-T. Chao, Coupled-Channel and Screening Effects in Charmonium Spectrum, Phys. Rev. D 80, 014012 (2009), arXiv:0904.4068 [hep-ph] .
- Workman et al. [2022] R. L. Workman et al. (Particle Data Group), Review of Particle Physics, PTEP 2022, 083C01 (2022).
- Barnes and Godfrey [2004] T. Barnes and S. Godfrey, Charmonium options for the , Phys. Rev. D 69, 054008 (2004), arXiv:hep-ph/0311162 .
- Barnes et al. [2005] T. Barnes, S. Godfrey, and E. S. Swanson, Higher charmonia, Phys. Rev. D 72, 054026 (2005), arXiv:hep-ph/0505002 .
- Guo et al. [2015] F.-K. Guo, C. Hanhart, Y. S. Kalashnikova, U.-G. Meißner, and A. V. Nefediev, What can radiative decays of the teach us about its nature?, Phys. Lett. B 742, 394 (2015), arXiv:1410.6712 [hep-ph] .
- Ablikim et al. [2020] M. Ablikim et al. (BESIII), Study of Open-Charm Decays and Radiative Transitions of the , Phys. Rev. Lett. 124, 242001 (2020), arXiv:2001.01156 [hep-ex] .
- Guo et al. [2009] F.-K. Guo, C. Hanhart, and U.-G. Meißner, On the extraction of the light quark mass ratio from the decays , Phys. Rev. Lett. 103, 082003 (2009), [Erratum: Phys.Rev.Lett. 104, 109901 (2010)], arXiv:0907.0521 [hep-ph] .
- Guo et al. [2011] F.-K. Guo, C. Hanhart, G. Li, U.-G. Meißner, and Q. Zhao, Effect of charmed meson loops on charmonium transitions, Phys. Rev. D 83, 034013 (2011), arXiv:1008.3632 [hep-ph] .
- Guo et al. [2010] F.-K. Guo, C. Hanhart, and U.-G. Meißner, Extracting the light quark mass ratio from bottomonia transitions, Phys. Rev. Lett. 105, 162001 (2010), arXiv:1007.4682 [hep-ph] .
- Jenkins et al. [1993] E. E. Jenkins, M. E. Luke, A. V. Manohar, and M. J. Savage, Semileptonic decay and heavy quark spin symmetry, Nucl. Phys. B 390, 463 (1993), arXiv:hep-ph/9204238 .
- Colangelo et al. [2004] P. Colangelo, F. De Fazio, and T. N. Pham, Nonfactorizable contributions in decays to charmonium: The Case of , Phys. Rev. D 69, 054023 (2004), arXiv:hep-ph/0310084 .
- Amundson et al. [1992] J. F. Amundson, C. G. Boyd, E. E. Jenkins, M. E. Luke, A. V. Manohar, J. L. Rosner, M. J. Savage, and M. B. Wise, Radiative decay using heavy quark and chiral symmetry, Phys. Lett. B 296, 415 (1992), arXiv:hep-ph/9209241 .
- Hu and Mehen [2006] J. Hu and T. Mehen, Chiral Lagrangian with heavy quark-diquark symmetry, Phys. Rev. D 73, 054003 (2006), arXiv:hep-ph/0511321 .
- Chung [1971] S. U. Chung, Spin formalisms, CERN-71-08 10.5170/CERN-1971-008 (1971).
- Weinberg [1965] S. Weinberg, Evidence That the Deuteron Is Not an Elementary Particle, Phys. Rev. 137, B672 (1965).
- Baru et al. [2004] V. Baru, J. Haidenbauer, C. Hanhart, Y. Kalashnikova, and A. E. Kudryavtsev, Evidence that the and are not elementary particles, Phys. Lett. B 586, 53 (2004), arXiv:hep-ph/0308129 .
- Baru et al. [2022] V. Baru, X.-K. Dong, M.-L. Du, A. Filin, F.-K. Guo, C. Hanhart, A. Nefediev, J. Nieves, and Q. Wang, Effective range expansion for narrow near-threshold resonances, Phys. Lett. B 833, 137290 (2022), arXiv:2110.07484 [hep-ph] .
- Guo et al. [2013b] F.-K. Guo, C. Hanhart, U.-G. Meißner, Q. Wang, and Q. Zhao, Production of the in charmonia radiative decays, Phys. Lett. B 725, 127 (2013b), arXiv:1306.3096 [hep-ph] .
- Shtabovenko et al. [2020] V. Shtabovenko, R. Mertig, and F. Orellana, FeynCalc 9.3: New features and improvements, Comput. Phys. Commun. 256, 107478 (2020), arXiv:2001.04407 [hep-ph] .
- Shtabovenko [2017] V. Shtabovenko, FeynHelpers: Connecting FeynCalc to FIRE and Package-X, Comput. Phys. Commun. 218, 48 (2017), arXiv:1611.06793 [physics.comp-ph] .
- Patel [2017] H. H. Patel, Package-X 2.0: A Mathematica package for the analytic calculation of one-loop integrals, Comput. Phys. Commun. 218, 66 (2017), arXiv:1612.00009 [hep-ph] .
- Dong et al. [2011] Y. Dong, A. Faessler, T. Gutsche, and V. E. Lyubovitskij, and decay modes of the , J. Phys. G 38, 015001 (2011), arXiv:0909.0380 [hep-ph] .
- Uehara [1996] S. Uehara, TREPS: A Monte-Carlo Event Generator for Two-photon Processes at Colliders using an Equivalent Photon Approximation, (1996), arXiv:1310.0157 [hep-ph] .