Quasi-two-body $B_{(s)}\to V\pi\pi$ Decays with Resonance $f_{0}(980)$ in PQCD Approach

In recent years, non-leptonic three-body decays of $B$ mesons have been paid more attention on both experimental and theoretical sides, as these decays can be used to test the standard model (SM), to extract the CKM angles, and to search for the sources of the $CP$ violation. From last century, a large number of three-body $B$ decays have been measured by BaBar Lees:2012kxa , Belle Nakahama:2010nj , CLEO Eckhart:2002qr and LHCb Aaij:2018rol ; Aaij:2016qnm ; Aaij:2019nmr ; Aaij:2017zgz ; Aaij:2019jaq ; Aaij:2020ypa ; Aaij:2020dsq . Meanwhile, on the factorization hypothesis, a few of theoretical methods have been proposed to study these decays, such as approaches based on the symmetry principle He:2014xha , the QCD factorization approachKrankl:2015fha ; Virto:2016fbw ; Cheng:2007si ; Cheng:2016shb ; Li:2014oca , the perturbative QCD approach (PQCD) Wang:2016rlo ; Li:2016tpn ; Zou:2020atb ; Zou:2020fax ; Zou:2021lex ; Zou:2020dpg , and other theoretical methods Wang:2015ula .

Unlike the two-body decays where the kinematics is fixed, three-body decay amplitudes depend on two kinematic variables. For a decay $B(p_{B})\to M_{1}(p_{1})M_{2}(p_{2})M_{3}(p_{3})$, it is general to define the variables as two invariant masses of two pairs of final state particles, for instance, $s_{12}$ and $s_{13}$ with the definition $s_{ij}=2(p_{i}\cdot p_{j})/m_{B}^{2}$. All physical kinematics configurations could define a two-dimensional region in the $s_{12}-s_{13}$ plane, and the density plot of the differential decay rate $d\Gamma/ds_{12}ds_{13}$ in this region is called a Dalitz plot. Specially, when the final states are the light mesons such as the $\pi$ and $K$ mesons, the corresponding configuration reduces to a triangle region. In general, the Dalitz plot has three typical regions according to the characteristic kinematics. The central region so-called “Mercedes Star” configuration corresponds to the case where all the invariant masses are roughly the same and of order of $m_{B}$. In this region all three light mesons have a large energy in the $B$ meson rest frame and fly apart at about $120^{\circ}$ angles. The corners regions correspond to the cases where one final state is soft and the others fly back-to-back with large energy about $m_{B}/2$. At the edges of the Dalitz plot one invariant mass is small and the other two are large, which implies that two particles move collinearly and the third bachelor particle recoils back. The interactions between two collinear mesons leads eventually to the resonances. Compared with two other regions, the physics picture at the edges of the Dalitz plot is very similar to a two-body decay by viewing the two-meson pair as a whole, and we thus call it quasi-two-body decay. In the past twenty years, PQCD approach based on the $k_{T}$ factorization has been used to study the $B$ meson two-body decays successfully, therefore it can be generalized for studying the quasi-two-body decays.

In the past few years, a large number of charmless quasi-two-body $B/B_{s}\to V(f_{0}(980)\to)\pi^{+}\pi^{-}$ decays have been measured in the experiments Zyla:2020zbs , and some branching fractions or upper limits of them are summarized as follows

Except the decay $B_{s}\to\phi f_{0},f_{0}\to\pi^{+}\pi^{-}$, other decays have not been studied theoretically in the literatures. Motivated by this, we shall study above decays in PQCD approach, so as to further check the reliability of PQCD in multi-body decays and present more predictions.For the sake of convenience $f_{0}(980)$ is abbreviated to $f_{0}$ in the following context unless special statement.

In the framework of PQCD, the decay amplitude $\mathcal{A}$ of $B\to V(f_{0}(980)\to)\pi^{+}\pi^{-}$ decay can be decomposed as the convolution

where $x_{i}$ are the momentum fractions of the light quarks, $b_{i}$ are the conjugate variables of the quarks’ transverse momenta $k_{iT}$. $\Phi_{B}$ and $\Phi_{V}$ are the wave functions of the $B$ mesons and vector mesons, while the $\Phi_{\pi\pi}$ is the $S$-wave $\pi\pi$-pair wave function. These wave functions are non-perturbative and universal. The exponential term is the so-called Sudakov form factor caused by the additional scale introduced by the intrinsic transverse momenta $k_{T}$, which suppresses the soft dynamics effectively Li:2001ay ; Lu:2000hj . $\mathcal{H}(x_{i},b_{i},t)$ is the hard kernel, which can be calculated perturbatively. The parameter $t$ is the largest scale in the hard kernel, which ensures the higher order corrections as small as possible.

In PQCD, the most important inputs are the initial and final mesons’ wave functions. For the $B$ meson and the light vector mesons, their wave functions have been studied extensively and the inner parameters have been fixed by the well measured two-body $B$ meson decays Liu:2019ymi ; Li:2004ep , so we will not discuss them in this work. For the $\pi\pi$-pair, its $S$-wave wave function can be written as Diehl:1998dk ; Diehl:2000uv ; Pire:2002ut ; Xing:2019xti ; Wang:2018xux

with $z$ being the momentum fraction of the light quark in the $\pi\pi$-pair. The parameter $\xi$ is the momentum fraction of one $\pi$ meson in the $\pi\pi$-pair. The momentum of the $\pi\pi$-pair $P$ satisfies the condition $P^{2}=\omega^{2}$, $\omega$ being the invariant mass of $\pi\pi$-pair. $n=(1,0,\vec{0})$ and $v=(0,1,\vec{0})$ are the light-like vectors. For the explicit expressions of the light-core distributions $\phi_{S}^{(s,t)}$, we adopt the form Wang:2014ira ; Wang:2015uea

with Gegenbauer moment $a_{s}=0.3\pm 0.2$ Xing:2019xti . $F_{S}(\omega)$ is the time-like form factor. In particular, for a narrow intermediate resonance, the time-like form factor $F_{S}(\omega)$ can be well described by the relative Breit-Wigner lineshape Back:2017zqt . However, due to the remarkable interference between two decays $f_{0}\to\pi\pi$ and $f_{0}\to K\overline{K}$, the relative Breit-Wigner lineshape cannot work well for the time-like form factor of $f_{0}$. In this case, the Flatt$\acute{e}$ lineshape is proposed to describe that of $f_{0}$ Flatte:1976xu ; Back:2017zqt , which is given as

with

The $g_{\pi\pi}$ and $g_{KK}$ are the coupling constants corresponding to $f_{0}\to\pi\pi$ and $f_{0}\to K\overline{K}$ decays, respectively, whose values are taken as $g_{\pi\pi}=(0.165\pm 0.018)~{}\mathrm{GeV}^{2}$ and $g_{KK}/g_{\pi\pi}=4.21\pm 0.33$ Back:2017zqt . In addition, the factor $F_{KK}=e^{-\alpha q^{2}}$ is introduced to suppress the $f_{0}$ width above the $KK$ threshold. The parameter $\alpha$ is taken $2.0\pm 1.0~{}\mathrm{GeV}^{-2}$, which does not affect the predictions remarkably Aaij:2014emv . It is noted that this lineshape has been also adopted extensively in analyzing data in the LHCb experiment Aaij:2014emv .

Although the quark model has achieved great successes, the underlying structures of the scalar mesons are not well established so far. There are many scenarios for the classification of the scalar mesons. One scenario is the naive 2-quark model, and the light scalar mesons below or near 1 GeV are identified as the lowest lying states. Another consistent picture Close:2002zu provided by the data implies that light scalar mesons below or near 1 GeV can be described by the $q^{2}\bar{q}^{2}$, while scalars above 1 GeV will form a conventional $q\bar{q}$ nonet with with some possible glue content Cheng:2005ye ; Jaffe:1976ig ; Alford:2000mm . This picture can be used to interpret the mass degeneracy of $f_{0}$ and $a_{0}(980)$, the reason why the widths of $\kappa(800)$ and $\sigma(600)$ is broader than those of $a_{0}(980)$ and $f_{0}$, and the large couplings of $f_{0}$ and $a_{0}(980)$ to $K\overline{K}$. However, in practice it is hard for us to make quantitative predictions on $B$ decays based on the four-quark picture for light scalar mesons as it involves the unknown form factors and decay constants that are beyond the conventional quark model. Hence, we here only discuss the two-quark scenario for $f_{0}$. Moreover, some experimental evidences indicate the existence of the non-strange and strange quark contents in $f_{0}$, we therefore regard it as a mixture of $s\bar{s}$ and $n\bar{n}=(u\bar{u}+d\bar{d})/\sqrt{2}$

where $\theta$ is the mixing angle. Recent studies Cheng:2002ai ; Anisovich:2002wy ; Gokalp:2004ny show that the mixing angle $\theta$ lies in the ranges of $25^{\circ}<\theta<40^{\circ}$ and $140^{\circ}<\theta<165^{\circ}$, and studies based on the $B$ decays favor the later range.

With the initial and final wave functions, we can calculate the whole amplitude of each decay mode in PQCD approach. In the leading order, the diagrams contributing to the decay $B^{+}\to\rho^{+}\pi^{+}\pi^{-}$ are shown in the Fig.1. The first two diagrams are the emission type diagrams with the first one emitting the $\pi\pi$-pair and the second one with the vector meson emitted. The last two are the annihilation type diagrams. Because the decay amplitudes are very similar to those presented in the ref.Zou:2020dpg , for the sake of simplicity, we shall not present them in this work. The other parameters used in the numerical calculations, such as the mass of the mesons, CKM matrix elements and the life times of $B$ mesons, are taken from the Particle Data Group Zyla:2020zbs .

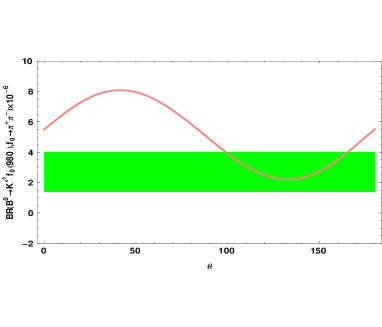
As aforementioned, the mixing angle of $f_{0}$ have not yet been determined. At first, we set $\theta$ as a free parameter and plot the branching fractions of $B_{u,d,s}\to Vf_{0}\to V\pi^{+}\pi^{-}$ decays dependent on it in Fig. 2, where the green bands are the allowed regions in the experiments. Combining the experimental data of $B^{0}\to\rho^{0}(f_{0}\to)\pi^{+}\pi^{-}$ and $B^{0}\to K^{*}(892)^{0}(f_{0}\to)\pi^{+}\pi^{-}$ decays, we get the range of the mixing angle $135^{\circ}\leq\theta\leq 155^{\circ}$, which is consistent with the results obtained from $\phi\to f_{0}\gamma$ and $f_{0}\to\gamma\gamma$. In our previous work Li:2019jlp , the decays $B\to K^{*}_{0,2}(1430)f_{0}/\sigma$ have been investigated, and we obtained $\theta\approx 145^{\circ}$ after comparing with experimental result Lees:2011dq . If the mixing angle $\theta=145^{\circ}$ is adopted, the branching ratios of the $B^{0}\to\rho^{0}(f_{0}\to)\pi^{+}\pi^{-}$ and $B^{0}\to K^{*}(892)^{0}(f_{0}\to)\pi^{+}\pi^{-}$ decays are given as

which well match the experimental measurements:

In view of this, we present all calculated results of the $CP$-averaged branching fractions and the local direct $CP$ asymmetries of the concerned decay modes with $\theta=145^{\circ}$ in Table. 1. For comparison, the available experimental data are also listed. One can find that adopting the appropriate wave functions of initial and final states, our predictions are in good agreement with the current experimental data, although there are only upper limits for the $B^{0}\to\omega(f_{0}\to)\pi^{+}\pi^{-}$ and $B^{+}\to\rho^{+}(f_{0}\to)\pi^{+}\pi^{-}$ decays. Finally, we plot all the branching fractions dependent on the mixing angle $\theta$, which may shed light on the mixing angle by combining the ongoing experimental measurements.

We acknowledge that there are many uncertainties in our calculations. In this work, we mainly evaluate three kinds of errors, namely the parameters in wave functions of the initial and final states, the higher order and power corrections, and the CKM matrix elements, respectively. In fact, the first kind of errors come from the uncertainties of nonperturbative parameters, such as the $B_{(s)}$ meson decay constants $f_{B}/f_{B_{s}}=0.19\pm 0.02/0.23\pm 0.02~{}\mathrm{GeV}$, the sharp parameters $\omega/\omega_{s}=0.4\pm 0.04/0.5\pm 0.05~{}\mathrm{GeV}$ in the distribution amplitudes of $B$ mesons, the Gegenbauer moments in the LCDAs of vector mesons, and the Gagenbauer moment $a_{S}$ in the $S$-wave LCDAs of the $\pi\pi$-pair, et.al. We can find from the table that this kind of uncertainties are dominant. Fortunately, this kind of uncertainties could be reduced with the developments of the experiments or other nonperturbative theoretical approaches in future. The second kind of errors arise from the unknown higher order of $\alpha_{s}$ and higher power corrections, which are reflected by varying the $\Lambda_{QCD}=0.25\pm 0.05~{}\mathrm{GeV}$ and the factorization scale $t$ from $0.8t$ to $1.2t$, respectively. The last ones are caused by the uncertainties of the CKM matrix elements.

If the narrow-width approximation (NWA) holds in these decays, the branching fraction of the quasi-two-body $B$ meson decay can be decomposed as

with $R$ represents a resonance. If two decays have a same resonance, we then define a ratio as

Based on the predictions in Table. 1, the ratio between the $B^{0}\to\rho^{0}f_{0}$ and $B^{0}\to\omega f_{0}$ is given as

which is agreement with the results of QCDF Cheng:2013fba . Within the isospin relation

we obtain the relation

which can be used to predict the branching fractions of the corresponding quasi-two-body $B\to V(f_{0}\to)\pi^{0}\pi^{0}$ decays.

Now we turn to discuss the local direct $CP$ asymmetries of these decays. In the quark level, $B\to K^{*}(f_{0}\to)\pi^{+}\pi^{-}$, $B_{s}\to\rho^{0}/\omega(f_{0}\to)\pi^{+}\pi^{-}$, and $B_{s}\to\phi(f_{0}(980)\to)\pi^{+}\pi^{-}$ are induced by $\bar{b}\to\bar{s}q\bar{q}$ transition, while $B\to(\rho,\omega)(f_{0}\to)\pi^{+}\pi^{-}$ and $B_{s}\to K^{*}(f_{0}(980)\to)\pi^{+}\pi^{-}$ are controlled by $\bar{b}\to\bar{d}q\bar{q}$ transition. From Table. 1, it is found that the local $CP$ asymmetries of decays $B^{0}\to K^{*0}(f_{0}\to)\pi^{+}\pi^{-}$ and $B_{s}\to\rho^{0}/\omega(f_{0}\to)\pi^{+}\pi^{-}$ are very small, and the reason is that the tree diagrams contributions are both color and CKM elements suppressed. However, for the decay $B^{+}\to K^{*+}(f_{0}\to)\pi^{+}\pi^{-}$, because the spectator $u$ quark enters into not only $K^{*+}$ meson but also $\pi\pi$-pair, the contributions from tree and penguin operators are comparable, leading to a large $CP$ asymmetry. For the decays $B^{0}\to\rho^{0}/\omega(f_{0}\to)\pi^{+}\pi^{-}$, although the contributions from tree operators are color suppressed, the destructive interference between the diagrams with vector meson emitted and ones with $\pi\pi$-pair emitted decreases the effects of penguin operators remarkably, therefore the $CP$ asymmetries are as small as about $10\%$. For $B^{+}\to\rho^{+}(f_{0}\to)\pi^{+}\pi^{-}$ decay, its amplitude is more complicated. In eq. (7), if the mixing angle $\theta$ of $f_{0}(980)$ is an obtuse angle, the sign of $n\bar{n}$ is negative. The spectator $u$-quark of $B^{+}\to\rho^{+}(f_{0}\to)\pi^{+}\pi^{-}$ can enter into both $f_{0}$ and $\pi\pi$-pair, so the negative sign leads to the cancellation between two tree operators contributions. With the sizable contributions of penguin operators, the $CP$ asymmetry of this decay is as large as $-55\%$. The decay of $B_{s}\to\bar{K}^{*0}(f_{0}\to)\pi^{+}\pi^{-}$ is very similar to $B^{+}\to\rho^{+}(f_{0}\to)\pi^{+}\pi^{-}$, but the spectator is a strange quark. When the spectator enters into the kaon, both the tree and penguin operators contribute, and the tree operators are color suppressed. However, when it enters into the $\pi\pi$-pair, only penguin operators play roles. Due to large interference between two kinds of above contributions, the large $CP$ asymmetry in $B_{s}\to\bar{K}^{*0}(f_{0}\to)\pi^{+}\pi^{-}$ is reasonable. On the experimental side, these $CP$ asymmetries have not been measured, and we hope these predictions can be tested in future.

In this work, we investigated the quasi-two-body $B/B_{s}\to V(f_{0}(980)\to)\pi^{+}\pi^{-}$ decays in PQCD approach, assuming that $f_{0}(980)$ is a mixture of $n\bar{n}=(u\bar{u}+d\bar{d})/{\sqrt{2}}$ and $s\bar{s}$ with the mixing angle $\theta$. Within the $S$-wave two-pion wave function, both the branching fractions and the located $CP$ asymmetries have been calculated. When the mixing angle $\theta$ is around $145^{\circ}$, the obtained branching fractions of the $B^{0}\to\rho^{0}(f_{0}(980)\to)\pi^{+}\pi^{-}$ and $B^{0}\to K^{*0}(f_{0}(980)\to)\pi^{+}\pi^{-}$ are in good agreement with the experimental data, and other results could be tested in the future experiments. In addition, the branching fractions of $B/B_{s}\to V(f_{0}\to)\pi^{0}\pi^{0}$ could be predicted based on the isospin symmetry, which can be measured in the LHCb and Belle II experiments. We note that the calculated $CP$ asymmetries of the $B^{+}\to\rho^{+}(f_{0}\to)\pi^{+}\pi^{-}$ and $B_{s}\to\bar{K}^{*0}(f_{0}\to)\pi^{+}\pi^{-}$ decays are very large, which can be tested in the ongoing experiments. We acknowledge that there are many uncertainties in the calculation, and the dominant one is the two-meson wave function. Therefore, more precise multi-meson wave functions from non-perturbative approach are needed.

This work is supported in part by the National Science Foundation of China under the Grant Nos. 11705159, 11975195, 11875033, and 11765012, and the Natural Science Foundation of Shandong province under the Grant No.ZR2019JQ04. This work is also supported by the Project of Shandong Province Higher Educational Science and Technology Program under Grants No. 2019KJJ007.