Quasi-Monte Carlo Quasi-Newton for variational Bayes
Abstract
Many machine learning problems optimize an objective that must be measured with noise. The primary method is a first order stochastic gradient descent using one or more Monte Carlo (MC) samples at each step. There are settings where ill-conditioning makes second order methods such as L-BFGS more effective. We study the use of randomized quasi-Monte Carlo (RQMC) sampling for such problems. When MC sampling has a root mean squared error (RMSE) of then RQMC has an RMSE of that can be close to in favorable settings. We prove that improved sampling accuracy translates directly to improved optimization. In our empirical investigations for variational Bayes, using RQMC with stochastic L-BFGS greatly speeds up the optimization, and sometimes finds a better parameter value than MC does.
1 Introduction
Many practical problems take the form
| (1) |
and is random vector with a known distribution . Classic problems of simulation-optimization (Andradóttir,, 1998) take this form and recently it has become very important in machine learning with variational Bayes (VB) (Blei et al.,, 2017) and Bayesian optimization (Frazier,, 2018) being prominent examples.
First order optimizers (Beck,, 2017) use a sequence of steps for step sizes and an operator that we always take to be the gradient with respect to . Very commonly, neither nor its gradient is available at reasonable computational cost and a Monte Carlo (MC) approximation is used instead. The update
| (2) |
for is a simple form of stochastic gradient descent (SGD) (Duchi,, 2018). There are many versions of SGD, notably AdaGrad (Duchi et al.,, 2011) and Adam (Kingma and Ba,, 2014) which are prominent in optimization of neural networks among other learning algorithms. Very often SGD involves sampling a mini-batch of observations. In this paper we consider SGD that samples instead some random quantities from a continuous distribution.
While a simple SGD is often very useful, there are settings where it can be improved. SGD is known to have slow convergence when the Hessian of is ill-conditioned (Bottou et al.,, 2018). When is not very high dimensional, the second order methods such as Newton iteration using exact or approximate Hessians can perform better. Quasi-Newton methods such as BFGS and L-BFGS (Nocedal and Wright,, 2006) that we describe in more details below can handle much higher dimensional parameters than Newton methods can while still improving upon first order methods. We note that quasi second-order methods cannot be proved to have better convergence rate than SGD. See Agarwal et al., (2012). They can however have a better implied constant.
A second difficulty with SGD is that MC sampling to estimate the gradient can be error prone or inefficient. For a survey of MC methods to estimate a gradient see Mohamed et al., (2020). Improvements based on variance reduction methods have been adopted to improve SGD. For instance Paisley et al., (2012) and Miller et al., (2017) both employ control variates in VB. Recently, randomized quasi-Monte Carlo (RQMC) methods, that we describe below, have been used in place of MC to improve upon SGD. Notable examples are Balandat et al., (2020) for Bayesian optimization and Buchholz et al., (2018) for VB. RQMC can greatly improve the accuracy with which integrals are estimated. The theory in Buchholz et al., (2018) shows how the improved integration accuracy from RQMC translates into faster optimization for SGD. The primary benefit is that RQMC can use a much smaller value of . This is also seen empirically in Balandat et al., (2020) for Bayesian optimization.
Our contribution is to combine RQMC with a second order limited memory method known as L-BFGS. We show theoretically that improved integration leads to improved optimization. We show empirically for some VB examples that the optimization is improved. We find that RQMC regularly allows one to use fewer samples per iteration and in a crossed random effects example it found a better solution than we got with MC.
At step of our stochastic optimization we will use some number of sample values, . It is notationally convenient to group these all together into . We also write
| (3) |
for gradient estimation at step .
The closest works to ours are Balandat et al., (2020) and Buchholz et al., (2018). Like Balandat et al., (2020) we incorporate RQMC into L-BFGS. Our algorithm differs in that we take fresh RQMC samples at each iteration where they had a fixed sample of size that they used in a ‘common random numbers’ approach. They prove consistency as for both MC and RQMC sampling. Their proof for RQMC required the recent strong law of large numbers for RQMC from Owen and Rudolf, (2021). Our analysis incorporates the geometric decay of estimation error as the number of iterations increases, similar to that used by Buchholz et al., (2018) for SGD. Our error bounds include sampling variances through which RQMC brings an advantage.
An outline of this paper is as follows. Section 2 reviews the optimization methods we need. Section 3 gives basic properties of scrambled net sampling, a form of RQMC. Section 4 presents our main theoretical findings. The optimality gap after steps of stochastic quasi-Newton is where is the optimal value. Theorem 4.1 bounds the expected optimality gap by a term that decays exponentially in plus a second term that is linear in a measure of sampling variance. RQMC greatly reduces that second non-exponentially decaying term which will often dominate. A similar bound holds for tail probabilities of the optimality gap. Theorem 4.2 obtains a comparable bound for . Section 5 gives numerical examples on some VB problems. In a linear regression problem where the optimal parameters are known, we verify that RQMC converges to them at an improved rate in . In logistic regression, crossed random effects and variational autoencoder examples we see the second order methods greatly outperform SGD in terms of wall clock time to improve . Since the true parameters are unknown we cannot compare accuracy of MC and RQMC sampling algorithms for those examples. In some examples RQMC finds a better ELBO than MC does when both use SGD, but the BFGS algorithms find yet better ELBOs. Section 6 gives some conclusions. The proofs of our main results are in an appendix.
2 Quasi-Newton optimization
We write for the Hessian matrix of . The classic Newton update is
| (4) |
Under ideal circumstances it converges quadratically to the optimal parameter value . That is . Newton’s method is unsuitable for the problems we consider here because forming may take too much space and solving the equation in (4) can cost which is prohibitively expensive. The quasi-Newton methods we consider do not form explicit Hessians. We also need to consider stochastic versions of them.
2.1 BFGS and L-BFGS
The BFGS method is named after four independent discoverers: Broyden, Fletcher, Goldfarb and Shanno. See Nocedal and Wright, (2006, Chapter 6). BFGS avoids explicitly computing and inverting the Hessian of . Instead it maintains at step an approximation to the inverse of . After an initialization such as setting to the identity matrix, the algorithm updates and via
respectively, where
The stepsize is found by a line search.
2.2 Stochastic quasi-Newton
Ordinarily in quasi-Newton algorithms the objective function remains constant through all the iterations. In stochastic quasi-Newton algorithms the sample points change at each iteration which is like having the objective function change in a random way at iteration . Despite this Bottou et al., (2018) find that quasi-Newton can work well in simulation-optimization with these random changes.
We will need to use sample methods to evaluate gradients. Given the sample gradient is as given at (3). Stochastic quasi-Newton algorithms like the one we study also require randomized Hessian information.
Byrd et al., (2016) develop a stochastic L-BFGS algorithm in the mini-batch setting. Instead of adding every correction pair to the buffer after each iteration, their algorithm updates the buffer every steps using the averaged correction pairs. Specifically, after every iterations, for , it computes the average parameter value over the most recent steps. It then computes the correction pairs by and
and adds the pair to the buffer. Here is a random sample of size Hessian update samples. The samples for are completely different from and independent of for used to update gradient estimates at step . This method is called SQN (stochastic quasi-Newton). As suggested by the authors, is often taken to be 10 or 20. So one can afford to use relatively large because the amortized average number of gradient evaluations per iteration is .
The objective function from Byrd et al., (2016) has the form , and is a fixed training set. At each iteration, their random sample is a subset of points in the dataset, not a sample generated from some continuous distribution. However, it is straightforward to adapt their algorithm to our setting. The details are in Algorithm 1 in Section 3.
2.3 Literature review
Many authors have studied how to use L-BFGS in stochastic settings. Bollapragada et al., (2018) proposes several techniques for stochastic L-BFGS, including increasing the sample size with iterations (progressive batching), choosing the initial step length for backtracking line search so that the expected value of the objective function decreases, and computing the correction pairs using overlapping samples in consecutive steps (Berahas et al.,, 2016).
Another way to prevent noisy updates is by a lengthening strategy from Xie et al., (2020) and Shi et al., (2020). Classical BFGS would use the correction pair , where is the update direction, and encodes the randomness in estimating the gradients. Because the correction pairs may be dominated by noise, Xie et al., (2020) suggested the lengthening correction pairs
Shi et al., (2020) propose to choose by the Armijo-Wolfe condition, while choosing large enough so that is sufficiently large.
Gower et al., (2016) utilizes sketching strategies to update the inverse Hessian approximations by compressed Hessians. Moritz et al., (2016) combines the stochastic quasi-Newton algorithm in Byrd et al., (2016) and stochastic variance reduced gradients (SVRG) (Johnson and Zhang,, 2013) by occasionally computing the gradient using a full batch.
Balandat et al., (2020) also applied RQMC with L-BFGS in Bayesian optimization. At each step of Bayesian optimization, one needs to maximize the acquisition function of the form , where is a Gaussian process and is a loss function. They use the sample average approximation , where . They prove that the maximizer of converges to that of when for both MC and RQMC sampling under certain conditions. The RQMC result relies on the recent discovery of the strong law of large numbers for RQMC (Owen and Rudolf,, 2021).
3 Scrambled net sampling
Scrambled nets are a form of RQMC sampling. We begin by briefly describing plain quasi-Monte Carlo (QMC) sampling. QMC is most easily described for computing expectations of for . In our present context will be a component of and not the same as the in equation (1). In practice we must ordinarily transform the random variables to some other distribution such as a Gaussian via . We suppose that for some transformation . The text by Devroye, (1986) has many examples of such transformations. Here we subsume any such transformation into the definition of .
In QMC sampling, we estimate by , just like in MC sampling except that distinct points are chosen so that the discrete uniform distribution is made very close to the continuous distribution. The difference between these two distributions can be quantified in many ways, called discrepancies (Chen et al.,, 2014). For a comprehensive treatment of QMC see Dick and Pillichshammer, (2010) or Niederreiter, (1992) or Dick et al., (2013).
When is of bounded variation in the sense of Hardy and Krause (BVHK) (see Owen, (2005)) then QMC attains the asymptotic error rate for any . QMC is deterministic and to get practical error estimates RQMC methods were introduced. In RQMC, each individual while collectively still retain the low discrepancy property. Uniformity of makes RQMC unbiased: . Then if we get an RMSE of . The whole RQMC process can then be replicated independently to quantify uncertainty. See Cranley and Patterson, (1976) and Owen, (1995) for methods and a survey in L’Ecuyer and Lemieux, (2002).
Scrambled net sampling (Owen,, 1995) is a form of RQMC that operates by randomly permuting the bits (more generally digits) of QMC methods called digital nets. The best known are those of Sobol’, (1969) and Faure, (1982). In addition to error estimation, scrambled nets give the user some control over the powers of in the QMC rate and also extend the domain of QMC from Riemann integrable functions of which BVHK is a subset to much more general functions including some with integrable singularities. For any integrand , MC has RMSE while scrambled nets have RMSE without requiring or even that is Riemann integrable (Owen, 1997a, ). For fixed , each construction of scrambled nets has a ‘gain constant’ so that the RMSE is below for any . This effectively counters the powers of . For smooth enough , an error cancellation phenomenon for scrambled nets yields an RMSE of (Owen, 1997b, ; Yue and Mao,, 1999; Owen,, 2008). The logarithmic powers here cannot ‘set in’ until they are small enough to obey the upper bound. Some forms of scrambled net sampling satisfy a central limit theorem (Loh,, 2003; Basu and Mukherjee,, 2017).
Very recently, a strong law of large numbers
has been proved for scrambled net sampling assuming only that for some (Owen and Rudolf,, 2021). The motivation for this result was that Balandat et al., (2020) needed a strong law of large numbers to prove consistency for their use for scrambled nets in Bayesian optimization.
Figure 1 graphically compares MC, QMC and RQMC points for . The underlying QMC method is a Sobol’ sequence using ‘direction numbers’ from Joe and Kuo, (2008). We can see that MC points leave voids and create clumps. The QMC points are spread out more equally and show a strong diagonal structure. The RQMC points satisfy the same discrepancy bounds as the QMC points do but have broken up some of the structure.
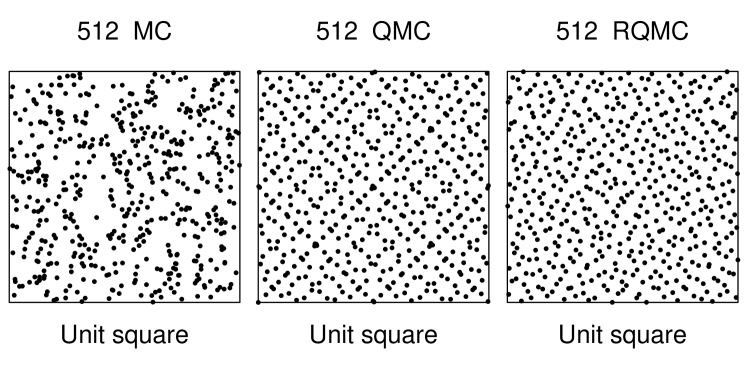
In favorable settings the empirical behaviour of QMC and RQMC for realistic can be as good as their asymptotic rates. In less favorable settings RQMC can be like MC with some reduced variance. The favorable integrands are those where is nearly additive or at least dominated by sums of only a few of their inputs at a time. See Caflisch et al., (1997) for a definition of functions of ‘low effective dimension’ and Dick et al., (2013) for a survey of work on reproducing kernel Hilbert spaces of favorable integrands.
We propose to combine the stochastic quasi-Newton method with RQMC samples to create a randomized quasi-stochastic quasi-Newton (RQSQN) algorithm. At the ’th iteration, we draw an independently scrambled refreshing sample of size via RQMC to compute the gradient estimator . Then we find the descent direction using an L-BFGS two-loop recursion. Then we update the solution by
Here may be found by line search with the Wolfe condition when using L-BFGS. See Chapter 3.1 in Nocedal and Wright, (2006).
Algorithm 1 shows pseudo-code for an RQMC version of SQN based on L-BFGS. It resembles the SQN algorithm in Byrd et al., (2016), except that the random samples are drawn by using RQMC instead of being sampled without replacement from a finite data set. Note that we don’t compute the Hessian directly. We either compute the Hessian-vector product or use gradient differences .
4 Theoretical guarantees
In this section, we study the convergence rate of a general quasi-Newton iteration based on sample points at stage . The algorithm iterates as follows
| (5) | ||||
Here is an approximate inverse Hessian. We let . We assume that the gradient estimator is unbiased conditionally on , i.e., . The are random because they depend on for .
The Hessian estimates for are also random because they depend directly on some additional inputs for those Hessian update epochs which occur prior to step . They also depend on for because those random variables affect . In our algorithms is independent of . For RQMC this involves fresh rerandomizations of the underlying QMC points at step . The alternative of ‘going deeper’ into a given RQMC sequence using points through would not satisfy independence. While it might possibly perform better it is harder to analyze and we saw little difference empirically in doing that. Our theory requires regularity of the problem as follows.
Assumption 1
We impose these three conditions:
-
(a)
Strong convexity. For some ,
-
(b)
Lipschitz continuous objective gradients. For some ,
-
(c)
Bounded variance of the gradient estimator. For some ,
These are standard assumptions in the study of SGD. For example, see Assumptions 4.1 and 4.5 of Bottou et al., (2018). Strong convexity implies that there exists a unique minimizer to estimate. We write , for the best possible value of . We must have some smoothness and Lipshitz continuity is a mild assumption. The quantity will prove to be important below. We can get a better from RQMC than from MC. The other way to reduce is to increase . When RQMC has an advantage it is because it gets a smaller for the same , or to put it another way, it can get comparable with smaller .
For two symmetric matrices and , means that is positive semi-definite. We denote the spectral norm of by .
Theorem 4.1 (Convergence of optimality gap)
Suppose that our simulation-optimization problem satisfies the regularity conditions in Assumption 1. Assume that we run updates as in equation (5) where the approximate inverse Hessian matrices satisfy for some and all . Next, assume constant step sizes with . Then for every
| (6) |
Furthermore, if for some constant for all and , then for any
| (7) |
holds with probability at least .
Proof
See Section A.1 in the Appendix.
Remark 4.1
As the expected optimality gap is no larger than . The variance bound (for points ) depends on the sampling method we choose. From the results in Section 3, scrambled nets can reduce from for MC to attaining or even in favorable cases. When for MC then for scrambled net RQMC, which limits the harm if any that could come from RQMC.
Remark 4.2
The following theorem states the convergence rate of .
Theorem 4.2 (Convergence of variables)
Proof
See Section A.2 in the Appendix.
Remark 4.3
When , the limiting expected squared error is bounded by . Once again the potential gain from RQMC is in reducing compared to MC or getting a good with smaller .
5 Variational Bayes
In this section we investigate quasi-Newton quasi-Monte Carlo optimization for some VB problems. Variational Bayes begins with a posterior distribution that is too inconvenient to work with. This usually means that we cannot readily sample . We turn instead to a distribution for from which we can easily sample . We now want to make a good choice of and in VB the optimal value is taken to be the minimizer of the KL divergence between distributions:
In this section we are using the symbol as a generic probability distribution. It is the distribution of whatever random variable’s symbol is inside the parentheses and not necessarily the same from the introduction. We use to denote expectation with respect to .
We suppose that has a prior distribution . Then Bayes rule gives
The last term does not depend on and so we may minimize by maximizing
This is known as the evidence lower bound (ELBO). The first term expresses a preference for having a large value of the likelihood of the observed data given the latent data . The second term can be regarded as a regularization, penalizing parameter values for which is too far from the prior distribution .
To optimize we need . It is usual to choose a family for which and its gradient are analytically tractable. We still need to estimate the gradient of the first term, i.e.,
One method is to use the score function and Fisher’s identity
with . Unfortunately an MC strategy based on this approach can suffer from large variance.
The most commonly used method is to write the parameter as a function of some underlying common random variables. This is known as the reparameterization trick (Kingma and Welling,, 2014). Suppose that there is a base distribution and a transformation , such that if , then . Then
It is often easy to sample from the base distribution , and thus to approximate the expectation by MC or RQMC samples. This is the method we use in our examples.
5.1 Bayesian linear regression
We start with a toy example where we can find analytically. This will let us study empirically. We consider the hierarchical linear model
where is a given matrix of full rank and is a known error variance. Here is the number of data points in our simulation and not the number of MC or RQMC gradient evaluations. The entries in are IID random variables and we used .
Translating this problem into the VB setup, we make our latent variable the unknown parameter vector , and we choose a very convenient variational distribution with for . Now , and plays the role of the observations . We also write and for the parts of .
The ELBO has the expression
where . In this example, the ELBO has a closed form and the optimal variational parameters are given by
where is the ’th column of .
In this setting the Hessian is simply and so stochastic quasi-Newton gradient estimates are not needed. We can however compare the effectiveness of MC and RQMC in SGD. We estimate the gradient by MC or RQMC samples and use SGD via AdaGrad (Duchi et al.,, 2011) to maximize the ELBO.
Our computations used one example data set with data points, variables and iterations. At each iteration, we draw a new sample of sample size of the -dimensional Gaussian used to sample . The sample size is fixed in each run, but we vary it between over the range through powers of in order to explore how quickly MC and RQMC converge.
For RQMC, we use the scrambled Sobol’ points implemented in PyTorch (Balandat et al.,, 2020) using the inverse Gaussian CDF to translate uniform random variables into standard Gaussians that are then multiplied by and shifted by to get the random that we need. We compute the log errors and and average these over the last 50 iterations. The learning rate in AdaGrad was taken to be .
The results are shown in Figure 2. We see there that RQMC achieves a higher accuracy than plain MC. This happens because RQMC estimates the gradient with lower variance. In this simple setting the rate of convergence is improved. Balandat et al., (2020) report similar rate improvements in Bayesian optimization.



5.2 Bayesian logistic regression
Next we consider another simple example, though it is one with no closed form expression for . We use it to compare first and second order methods. The Bayesian logistic regression model is defined by
As before, is the unknown , and has , for . The ELBO has the form
where denotes the sigmoid function .
In our experiments, we take and . With it is very likely that the data can be perfectly linearly separated and then a Bayesian approach provides a form of regularization. The integral to be computed is in dimensions, and the parameter to be optimized is in dimensions. We generate the data from , then and finally with probability are sampled independently for .
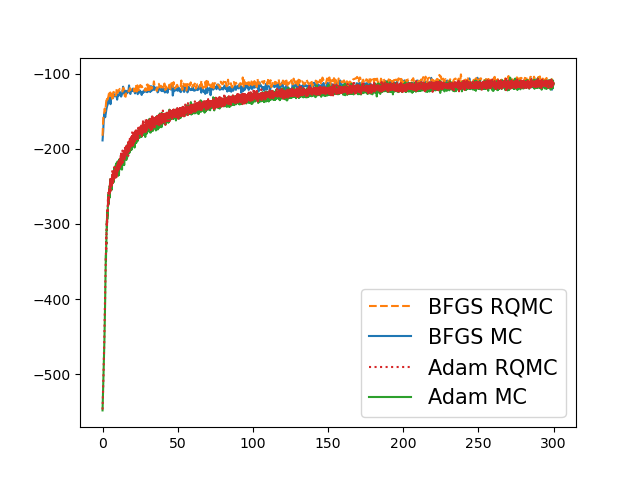
In Figure 3, we show the convergence of ELBO versus wall clock times for different combinations of sampling methods (MC, RQMC) and optimization methods (AdaGrad, L-BFGS). The left panel draws samples in each optimization iterations, while the right panel takes . The initial learning rate for AdaGrad is 0.01. The L-BFGS is described in Algorithm 1, with Hessian evaluations every steps with memory size and . Because L-BFGS uses some additional gradient function evaluations to update the Hessian information at every ’th iteration that the first order methods do not use, we compare wall clock times. The maximum iteration count in the line search was 20. We used the Wolfe condition (Condition 3.6 in Nocedal and Wright, (2006)) with and .
For this problem, L-BFGS always converges faster than AdaGrad. We can also see that plain MC is noisier than RQMC. The ELBOs for AdaGrad still seem to be increasing slowly even at the end of the time interval shown. For AdaGrad, RQMC consistently has a slightly higher ELBO than MC does.


5.3 Crossed random effects
In this section, we consider a crossed random effects model. Both Bayesian and frequentist approaches to crossed random effects can be a challenge with costs scaling like or worse. See Papaspiliopoulos et al., (2020) and Ghosh et al., (2020) for Bayesian and frequentist approaches and also the dissertation of Gao, (2017).
An intercept only version of this model has
given , , and where and are both . All of , , and the log standard deviations are independent.
We use VB to approximate the posterior distribution of the dimensional parameter . In our example, we take and . As before is chosen to be Gaussian with independent coordinates and has their means and standard deviations. In Figure 4, we plot the convergence of ELBO for different combinations of sampling methods and optimization methods. The BFGS method takes , , . We used a learning rate of in AdaGrad. We observe that when the sample size is 8 (left), plain Monte Carlo has large fluctuations even when converged, especially for BFGS. When the sample size is 128 (right), the fluctuations disappear. But RQMC still achieves a higher ELBO than plain Monte Carlo for BFGS. In both cases, BFGS finds the optimum faster than AdaGrad.


5.4 Variational autoencoder
A variational autoencoder (VAE, Kingma and Welling, (2014)) learns a generative model for a dataset. A VAE has a probabilistic encoder and a probabilistic decoder. The encoder first produces a distribution over the latent variable given a data point , then the decoder reconstructs a distribution over the corresponding from the latent variable . The goal is to maximize the marginal probability . Observe that the ELBO provides a lower bound of :
where denotes expection for random given with parameter . In this section is the latent variable, and not a part of the that we use in our MC or RQMC algorithms. We do not refer to those variables in our VAE description below.
The usual objective is to maximize the ELBO for a sample of IID and now we have to optimize over as well as . The first term in the ELBO is the reconstruction error, while the second term penalizes parameters that give a posterior too different from the prior . Most commonly, , and , so that the KL-divergence term has a closed form. The decoding term is usually chosen to be a Gaussian or Bernoulli distribution, depending on the data type of . The expectation is ordinarily estimated by MC. We implement both plain MC and RQMC in our experiments. To maximize the ELBO, the easiest way is to use SGD or its variants. We also compare SGD with L-BFGS in the experiments.
The experiment uses the MNIST dataset in PyTorch. It has 60,000 gray scale images, and so the dimension is 784. All experiments were conducted on a cluster node with 2 CPUs and 4GB memory. The training was conducted in a mini-batch manner with batch size 128. The encoder has a hidden layer with 800 nodes, and an output layer with 40 nodes, 20 for and 20 for . Our takes the form . The decoder has one hidden layer with 400 nodes.
In Figure 5(a), we plot the ELBO versus wall clock time for different combinations of sampling methods (MC, RQMC) and optimization methods (Adam, BFGS). The learning rate for Adam is 0.0001. For BFGS, the memory size is . The other tuning parameters are set to the defaults from PyTorch. We observe that BFGS converged faster than Adam. For BFGS, we can also see that RQMC achieves a slightly higher ELBO than MC. Figure 5(b) through 5(e) shows some reconstructed images using the four algorithms.




6 Discussion
RQMC methods are finding uses in simulation optimization problems in machine learning, especially in first order SGD algorithms. We have looked at their use in a second order, L-BFGS algorithm. RQMC is known theoretically and empirically to improve the accuracy in integration problems compared to both MC and QMC. We have shown that improved estimation of expected gradients translates directly into improved optimization for quasi-Newton methods. There is a small burden in reprogramming algorithms to use RQMC instead of MC, but that is greatly mitigated by the appearance of RQMC algorithms in tools such as BoTorch (Balandat et al.,, 2020) and the forthcoming scipy 1.7 (scipy.stats.qmc.Sobol) and QMCPy at https://pypi.org/project/qmcpy/.
Our empirical examples have used VB. The approach has potential value in Bayesian optimization (Frazier,, 2018) and optimal transport (El Moselhy and Marzouk,, 2012; Bigoni et al.,, 2016) as well.
The examples we chose were of modest scale where both first and second order methods could be used. In these settings, we saw that second order methods improve upon first order ones. For the autoencoder problem the second order methods converged faster than the first order ones did. This also happenend for the crossed random effects problem where the second order methods found better ELBOs than the first order ones did and RQMC-based quasi-Newton algorithm found a better ELBO than the MC-based quasi-Newton did without increasing the wall clock time.
It is possible that RQMC will bring an advantage to conjugate gradient approaches as they have some similarities to L-BFGS. We have not investigated them.
Acknowledgments
This work was supported by the National Science Foundation under grant IIS-1837931.
References
- Agarwal et al., (2012) Agarwal, A., Bartlett, P. L., Ravikumar, P., and Wainwright, M. J. (2012). Information-theoretic lower bounds on the oracle complexity of stochastic convex optimization. IEEE Transactions on Information Theory, 58(5):3235–3249.
- Andradóttir, (1998) Andradóttir, S. (1998). A review of simulation optimization techniques. In 1998 winter simulation conference, volume 1, pages 151–158. IEEE.
- Azuma, (1967) Azuma, K. (1967). Weighted sums of certain dependent random variables. Tohoku Mathematical Journal, Second Series, 19(3):357–367.
- Balandat et al., (2020) Balandat, M., Karrer, B., Jiang, D. R., Daulton, S., Letham, B., Wilson, A. G., and Bakshy, E. (2020). BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization. In Advances in Neural Information Processing Systems 33.
- Basu and Mukherjee, (2017) Basu, K. and Mukherjee, R. (2017). Asymptotic normality of scrambled geometric net quadrature. Annals of Statistics, 45(4):1759–1788.
- Beck, (2017) Beck, A. (2017). First-order methods in optimization. SIAM, Philadelphia.
- Berahas et al., (2016) Berahas, A. S., Nocedal, J., and Takáč, M. (2016). A multi-batch L-BFGS method for machine learning. Advances in Neural Information Processing Systems, pages 1063–1071.
- Bigoni et al., (2016) Bigoni, D., Spantini, A., and Marzouk, Y. (2016). Adaptive construction of measure transports for Bayesian inference. In NIPS workshop on Approximate Inference.
- Blei et al., (2017) Blei, D. M., Kucukelbir, A., and McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518):859–877.
- Bollapragada et al., (2018) Bollapragada, R., Nocedal, J., Mudigere, D., Shi, H. J., and Tang, P. T. P. (2018). A progressive batching L-BFGS method for machine learning. In International Conference on Machine Learning, pages 620–629. PMLR.
- Bottou et al., (2018) Bottou, L., Curtis, F. E., and Nocedal, J. (2018). Optimization methods for large-scale machine learning. Siam Review, 60(2):223–311.
- Buchholz et al., (2018) Buchholz, A., Wenzel, F., and Mandt, S. (2018). Quasi-Monte Carlo variational inference. In International Conference on Machine Learning, pages 668–677. PMLR.
- Byrd et al., (2016) Byrd, R. H., Hansen, S. L., Nocedal, J., and Singer, Y. (2016). A stochastic quasi-Newton method for large-scale optimization. SIAM Journal on Optimization, 26(2):1008–1031.
- Caflisch et al., (1997) Caflisch, R. E., Morokoff, W., and Owen, A. B. (1997). Valuation of mortgage backed securities using Brownian bridges to reduce effective dimension. Journal of Computational Finance, 1(1):27–46.
- Chen et al., (2014) Chen, W., Srivastav, A., and Travaglini, G., editors (2014). A panorama of discrepancy theory. Springer, Cham, Switzerland.
- Cranley and Patterson, (1976) Cranley, R. and Patterson, T. N. L. (1976). Randomization of number theoretic methods for multiple integration. SIAM Journal of Numerical Analysis, 13(6):904–914.
- Devroye, (1986) Devroye, L. (1986). Non-uniform Random Variate Generation. Springer, New York.
- Dick et al., (2013) Dick, J., Kuo, F. Y., and Sloan, I. H. (2013). High-dimensional integration: the quasi-Monte Carlo way. Acta Numerica, 22:133–288.
- Dick and Pillichshammer, (2010) Dick, J. and Pillichshammer, F. (2010). Digital sequences, discrepancy and quasi-Monte Carlo integration. Cambridge University Press, Cambridge.
- Duchi et al., (2011) Duchi, J., Hazan, E., and Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(7).
- Duchi, (2018) Duchi, J. C. (2018). Introductory lectures on stochastic optimization. In Mahoney, M. W., Duchi, J. C., and Gilbert, A. C., editors, The mathematics of data, volume 25, pages 99–186. American Mathematical Society, Providence, RI.
- El Moselhy and Marzouk, (2012) El Moselhy, T. A. and Marzouk, Y. M. (2012). Bayesian inference with optimal maps. Journal of Computational Physics, 231(23):7815–7850.
- Faure, (1982) Faure, H. (1982). Discrépance de suites associées à un système de numération (en dimension ). Acta Arithmetica, 41:337–351.
- Frazier, (2018) Frazier, P. I. (2018). A tutorial on Bayesian optimization. Technical report, arXiv:1807.02811.
- Gao, (2017) Gao, K. (2017). Scalable Estimation and Inference for Massive Linear Mixed Models with Crossed Random Effects. PhD thesis, Stanford University.
- Ghosh et al., (2020) Ghosh, S., Hastie, T., and Owen, A. B. (2020). Backfitting for large scale crossed random effects regressions. Technical report, arXiv:2007.10612.
- Gower et al., (2016) Gower, R., Goldfarb, D., and Richtárik, P. (2016). Stochastic block BFGS: Squeezing more curvature out of data. In International Conference on Machine Learning, pages 1869–1878.
- Joe and Kuo, (2008) Joe, S. and Kuo, F. Y. (2008). Constructing Sobol’ sequences with better two-dimensional projections. SIAM Journal on Scientific Computing, 30(5):2635–2654.
- Johnson and Zhang, (2013) Johnson, R. and Zhang, T. (2013). Accelerating stochastic gradient descent using predictive variance reduction. In Advances in Neural Information Processing Systems, volume 26, pages 315–323.
- Kingma and Ba, (2014) Kingma, D. P. and Ba, J. (2014). Adam: A method for stochastic optimization. Technical report, arXiv:1412.6980.
- Kingma and Welling, (2014) Kingma, D. P. and Welling, M. (2014). Auto-encoding variational Bayes. stat, 1050:1.
- L’Ecuyer and Lemieux, (2002) L’Ecuyer, P. and Lemieux, C. (2002). A survey of randomized quasi-Monte Carlo methods. In Dror, M., L’Ecuyer, P., and Szidarovszki, F., editors, Modeling Uncertainty: An Examination of Stochastic Theory, Methods, and Applications, pages 419–474. Kluwer Academic Publishers.
- Loh, (2003) Loh, W.-L. (2003). On the asymptotic distribution of scrambled net quadrature. Annals of Statistics, 31(4):1282–1324.
- Miller et al., (2017) Miller, A. C., Foti, N. J., D Amour, A., and Adams, R. P. (2017). Reducing reparameterization gradient variance. In Advances in Neural Information Processing Systems.
- Mohamed et al., (2020) Mohamed, S., Rosca, M., Figurnov, M., and Mnih, A. (2020). Monte Carlo gradient estimation in machine learning. Journal of Machine Learning Research, 21(132):1–62.
- Moritz et al., (2016) Moritz, P., Nishihara, R., and Jordan, M. (2016). A linearly-convergent stochastic L-BFGS algorithm. In Artificial Intelligence and Statistics, pages 249–258.
- Niederreiter, (1992) Niederreiter, H. (1992). Random Number Generation and Quasi-Monte Carlo Methods. SIAM, Philadelphia, PA.
- Nocedal, (1980) Nocedal, J. (1980). Updating quasi-Newton matrices with limited storage. Mathematics of computation, 35(151):773–782.
- Nocedal and Wright, (2006) Nocedal, J. and Wright, S. (2006). Numerical Optimization. Springer Science & Business Media, New York, second edition.
- Owen, (1995) Owen, A. B. (1995). Randomly permuted -nets and -sequences. In Niederreiter, H. and Shiue, P. J.-S., editors, Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing, pages 299–317, New York. Springer-Verlag.
- (41) Owen, A. B. (1997a). Monte Carlo variance of scrambled net quadrature. SIAM Journal of Numerical Analysis, 34(5):1884–1910.
- (42) Owen, A. B. (1997b). Scrambled net variance for integrals of smooth functions. Annals of Statistics, 25(4):1541–1562.
- Owen, (2005) Owen, A. B. (2005). Multidimensional variation for quasi-Monte Carlo. In Fan, J. and Li, G., editors, International Conference on Statistics in honour of Professor Kai-Tai Fang’s 65th birthday.
- Owen, (2008) Owen, A. B. (2008). Local antithetic sampling with scrambled nets. Annals of Statistics, 36(5):2319–2343.
- Owen and Rudolf, (2021) Owen, A. B. and Rudolf, D. (2021). A strong law of large numbers for scrambled net integration. SIAM Review, 63(2):360–372.
- Paisley et al., (2012) Paisley, J., Blei, D. M., and Jordan, M. I. (2012). Variational Bayesian inference with stochastic search. In Proceedings of the 29th International Coference on International Conference on Machine Learning, pages 1363–1370.
- Papaspiliopoulos et al., (2020) Papaspiliopoulos, O., Roberts, G. O., and Zanella, G. (2020). Scalable inference for crossed random effects models. Biometrika, 107(1):25–40.
- Shi et al., (2020) Shi, H. J., Xie, Y., Byrd, R., and Nocedal, J. (2020). A noise-tolerant quasi-Newton algorithm for unconstrained optimization. Technical report, arXiv:2010.04352.
- Sobol’, (1969) Sobol’, I. M. (1969). Multidimensional Quadrature Formulas and Haar Functions. Nauka, Moscow. (In Russian).
- Xie et al., (2020) Xie, Y., Byrd, R. H., and Nocedal, J. (2020). Analysis of the BFGS method with errors. SIAM Journal on Optimization, 30(1):182–209.
- Yue and Mao, (1999) Yue, R.-X. and Mao, S.-S. (1999). On the variance of quadrature over scrambled nets and sequences. Statistics & probability letters, 44(3):267–280.
Appendix A Proof of main theorems
Our approach is similar to that used by Buchholz et al., (2018). They studied RQMC with SGD whereas we consider L-BFGS, a second order method.
A.1 Proof of Theorem 4.1
Proof Let be the error in estimating the gradient at step . By the unbiasedness assumption, . Starting from the Lipschitz condition, we have
Because , we have . Because strong convexity implies
we have
Adding to both sides gives
| (8) |
where
Let be the filtration generated by the random inputs to our sampling process. Because are mutually independent and is independent of , we have and . Then
Therefore, is a martingale difference sequence w.r.t. . Let
Then is also a martingale difference sequence w.r.t. . So we can write
where
is a martingale difference sequence, and is a deterministic sequence. Recursively applying equation (8) gives
By the bounded variance assumption, for all . Hence,
Taking expectations on both sides proves (6).
To prove the finite sample guarantee (7), it remains to bound the martingale with high probability. We assumed a bound on which implies one for as well for any fixed . When the norms of the gradient and gradient estimator are bounded by such a constant for all and , then , and we have the bound
where the second inequality uses that the largest eigenvalue of is upper bounded by . By the Azuma-Hoeffding inequality (Azuma,, 1967), for all ,
Setting gives
So we have proved that with probability at least ,
A.2 Proof of Theorem 4.2
Our proof uses the following lemma.
Lemma 1
Let satisfy and let be symmetric with where . Then
Proof Without loss of generality, we can assume that is a diagonal matrix. Otherwise, let be the eigen-decomposition of . Then , , , and , and we can replace by .
Let be the diagonal entries of . Then . Let and . Note that , . Then for any ,
Now we are ready to prove Theorem 4.2.
Proof We start by decomposing
Note that only and depend on . Taking expectation w.r.t. on both sides gives
| (9) |
By strong convexity of ,