Quarkonium in a bulk viscous QGP medium
Abstract
The non-equilibrium properties of quark-gluon plasma (QGP) have been a topic of intensive research. In this contribution, we explore the nature of heavy quarkonia immersed in a QGP with bulk viscosity. We incorporate the bulk viscous effect through the deformation of the distribution functions of thermal quarks and gluons, with which the color dielectric permittivity can be computed. We use the color dielectric permittivity to compute the heavy quark potential inside a bulk viscous plasma and solve the Schrödinger equation using the potential to obtain the physical properties such as binding energies and decay widths. We discuss the effect of the bulk viscous correction on the quarkonium properties and the melting temperatures.
pacs:
14.40.Pq, 12.38.Mh, 21.65.Qr, 25.75.-q, 11.25.Tq, 47.17.+eday month yearday month year \keysQuark-gluon plasma, heavy quarkonia, bulk viscosity
1 Introduction
Heavy quarkonia have been one of the key probes of quark-gluon plasma (QGP) created in heavy-ion collisions. The suppression of quarkonium states was predicted to indicate the formation of QGP [1]. This suppression occurs because of the Debye screening, which is reflected in the deformation of the real part of a heavy quark potential [1], and the in-medium transitions, which are encoded in the imaginary part of the potential [2, 3].
In this contribution, we examine the effect of non-equilibrium bulk viscosity on the properties of heavy quarkonia [4]. Recent works show that the bulk viscosity of the QCD medium is enhanced near the critical point [5, 6, 7, 8, 9, 10], which may give rise to observable effects in the beam energy scan program [11]. The purpose of this study is to test how sensitive heavy quarkonia are to the bulk viscous nature of a QGP fluid. If they indeed are sensitive, there is a possibility to use heavy quarkonia as a probe of the changes of the bulk viscosity of a QGP.
The outline of the computational procedure is as follows. To encode the bulk viscous effect, we first deform the thermal distribution of quarks and gluons, and compute the color dielectric permittivity of the medium using the Hard Thermal Loop (HTL) approximation at one loop [12, 4]. Using the modified dielectric permittivity, we compute the heavy quark potential of a bulk viscous medium. We solve the Schrödinger equation using the real part of the obtained heavy quark potential and compute the physical properties of heavy quarkonium states such as binding energies and decay widths.
2 Color dielectric permittivity of a bulk viscous medium
Here, we outline the computation of the dielectric permittivity of a bulk viscous medium.
We incorporate the non-equilibrium bulk viscous effect by modifying the distribution functions of thermal quarks and gluons,
| (1) |
where is the equilibrium distribution and is the bulk viscous correction, which we parametrize in the following way [12],
| (2) |
where indicates the Bose (Fermi) distribution. The parameters and control the strength of the bulk viscous correction.
Using the deformed distribution function (2), the retarded self-energy in the presence of bulk correction becomes
| (3) |
where is the four momenta, , and is the equilibrium Debye mass. The correction from the bulk viscosity is written as
| (4) |
where and are dimensionless quantities [12]. The symmetric self-energy can also be computed in a similar manner, and again the effect of the bulk viscous correction enters through the modification of the Debye mass, . Using the self energies, one can compute the retarded, advanced and symmetric propagators. Based on these quantities, the dielectric permittivity is expressed using the modified Debye masses as
| (5) |
3 In-medium heavy quark potential
The color dielectric permittivity (5) encodes the bulk viscous effect of the medium. In the spirit of the linear-response theory[13, 14], we compute the in-medium heavy quark potential by modifying (the Fourier transform of) the Cornell potential with the color dielectric permittivity. The real part of the modified potential reads
| (6) |
and the imaginary part is
| (7) |
where , is the Fourier transform of the Cornell potential, and with . We take the string tension to be , and to be the one-loop coupling constant [4].


In Fig. 1, we plot the real and imaginary parts of the modified potential. Different lines correspond to different values of the parameter . The real part of the potential becomes flattened for a larger value of because of a stronger screening effect (larger Debye mass). The influence of the bulk viscosity on the imaginary part is more nontrivial. Its magnitude, , shows an enhancement in the small region and a suppression in the large region in the presence of .
4 Heavy quarkonia in a bulk viscous medium
Let us now study the properties of heavy quarkonia in a bulk viscous medium. Using the modified potential (6), we solve the Schrödinger equation for the radial wave function,
| (8) |
where is the reduced mass of the quarkonium system. We take for and for . Equation (8) is solved numerically to obtain the wave functions and eigenvalues. The binding energy, , and the decay width, , are given by
| (9) | ||||
| (10) |
In Fig. 2, we plot the binding energies (left) and decay widths (right) for charmonium (top) and bottomonium (bottom) states. The solid and dashed lines correspond to cases with and without bulk viscous corrections, respectively. We observe that the binding energy is a decreasing function of the bulk viscous correction, which is because of a stronger screening effect. The decay width shows an enhancement as a function of .



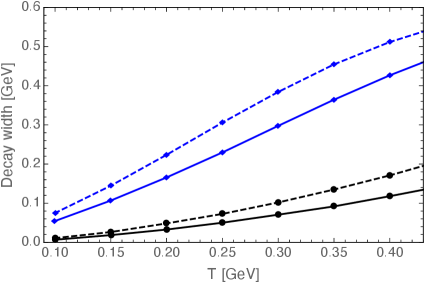

In Fig. 3, we plot the binding energies (black line) and decay widths (blue line) of states for different values of at . The melting temperatures of quarkonium states are estimated based on a standard criterion that the binding energy intersects with the decay width at the melting temperature, . In Table 1, we compare the melting temperatures computed in the current computation for with the results from Ref. [15], which are based on the extraction of the potential from lattice QCD data. The current model reproduces the former results, at least qualitatively. To make an estimate of a systematic dependence, we varied the value of parameter in the one-loop coupling. The upper and lower number in the table correspond to and , respectively.
Now, let us see the influence of the bulk viscosity on the melting temperatures. Fig. 4 shows the melting temperatures of the , and states as a function of . We observe that the melting temperatures of the quarkonium states decrease slightly as a function of . If there is a sudden enhancement in the bulk viscous effect at a certain collision energy, the behaviour of observables related to heavy quarkonia might show anomalous behaviour. It would be interesting to look at those observables and their collision energy dependence on the beam energy scan program, since the bulk viscous effect is expected to become larger near the critical point.


| [GeV] | Ref. [15] | |
|---|---|---|
5 Conclusion
In this contribution, we have discussed the effects of bulk viscous corrections on the properties of quarkonium states. We computed the color dielectric permittivity of a bulk viscous QGP and computed a modified heavy quark potential. We have discussed how the bulk viscous correction deforms the real and imaginary parts of the potential. Using the modified potential, we solved the Schrödinger equation to obtain the wave functions, binding energies and decay widths of the quarkonium states. We found that the binding energy decreases and decay width increases as a function of for a fixed temperature. We also found that the melting temperatures of the quarkonium states are reduced for . We expect that the bulk viscous effect is enhanced near the critical point and it would be interesting to look at how the physical observables such as behaves as a function of collision energy.
6 Acknowledgement
L. T. would like to thank the organizers of the HADRON 2021 Conference for the opportunity to give this parallel talk. L. T. and Y. H. are supported by National Research Foundation (NRF) funded by the Ministry of Science of Korea with Grant No. 2021R1F1A1061387(LT) and 2020R1F1A1076267(YH). N. H. is supported by Department of Atomic Energy (DAE), India via National Institute of Science Education and Research.
References
- . T. Matsui and H. Satz, “ Suppression by Quark-Gluon Plasma Formation,” Phys. Lett. B178 (1986) 416–422.
- . M. Laine, O. Philipsen, P. Romatschke, and M. Tassler, “Real-time static potential in hot QCD,” JHEP 03 (2007) 054, arXiv:hep-ph/0611300 [hep-ph].
- . N. Brambilla, J. Ghiglieri, A. Vairo, and P. Petreczky, “Static quark-antiquark pairs at finite temperature,” Phys. Rev. D 78 (2008) 014017, arXiv:0804.0993 [hep-ph].
- . L. Thakur, N. Haque, and Y. Hirono, “Heavy quarkonia in a bulk viscous medium,” JHEP 06 (2020) 071, arXiv:2004.03426 [hep-ph].
- . D. Kharzeev and K. Tuchin, “Bulk viscosity of QCD matter near the critical temperature,” JHEP 09 (2008) 093, arXiv:0705.4280 [hep-ph].
- . F. Karsch, D. Kharzeev, and K. Tuchin, “Universal properties of bulk viscosity near the QCD phase transition,” Phys. Lett. B663 (2008) 217–221, arXiv:0711.0914 [hep-ph].
- . G. D. Moore and O. Saremi, “Bulk viscosity and spectral functions in QCD,” JHEP 09 (2008) 015, arXiv:0805.4201 [hep-ph].
- . J. Noronha-Hostler, J. Noronha, and C. Greiner, “Transport Coefficients of Hadronic Matter near T(c),” Phys. Rev. Lett. 103 (2009) 172302, arXiv:0811.1571 [nucl-th].
- . S. Ryu, J. F. Paquet, C. Shen, G. S. Denicol, B. Schenke, S. Jeon, and C. Gale, “Importance of the Bulk Viscosity of QCD in Ultrarelativistic Heavy-Ion Collisions,” Phys. Rev. Lett. 115 no. 13, (2015) 132301, arXiv:1502.01675 [nucl-th].
- . A. Monnai, S. Mukherjee, and Y. Yin, “Phenomenological Consequences of Enhanced Bulk Viscosity Near the QCD Critical Point,” Phys. Rev. C 95 no. 3, (2017) 034902, arXiv:1606.00771 [nucl-th].
- . A. Bzdak, S. Esumi, V. Koch, J. Liao, M. Stephanov, and N. Xu, “Mapping the Phases of Quantum Chromodynamics with Beam Energy Scan,” Phys. Rept. 853 (2020) 1–87, arXiv:1906.00936 [nucl-th].
- . Q. Du, A. Dumitru, Y. Guo, and M. Strickland, “Bulk viscous corrections to screening and damping in QCD at high temperatures,” JHEP 01 (2017) 123, arXiv:1611.08379 [hep-ph].
- . L. Thakur, U. Kakade, and B. K. Patra, “Dissociation of Quarkonium in a Complex Potential,” Phys. Rev. D89 no. 9, (2014) 094020, arXiv:1401.0172 [hep-ph].
- . L. Thakur, N. Haque, and H. Mishra, “Heavy quarkonium moving in hot and dense deconfined nuclear matter,” Phys. Rev. D95 no. 3, (2017) 036014, arXiv:1611.04568 [hep-ph].
- . D. Lafferty and A. Rothkopf, “Improved Gauss law model and in-medium heavy quarkonium at finite density and velocity,” Phys. Rev. D 101 no. 5, (2020) 056010, arXiv:1906.00035 [hep-ph].